Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning models for predicting configuration of modified knuckle epitope peptides of BMP-2 protein using mesoscale simulation data†
Ricky Anshuman
Dash
and
Esmaiel
Jabbari
 *
*
Biomimetic Materials and Tissue Engineering Laboratory, Chemical Engineering Department, University of South Carolina, 301 Main Street, Columbia, SC, USA 29208. E-mail: jabbari@cec.sc.edu
First published on 31st March 2025
Abstract
The high doses of bone morphogenetic proteins (BMPs) cause undesired side effects in skeletal tissue regeneration. An alternative approach is to use the bioactive knuckle epitope domain of BMP-2 (BMP2-KEP) with an open-arm structure as part of the protein for engineering skeletal tissues. However, the osteogenic activity of this peptide, in the free state, is orders of magnitude lower than the native protein which is attributed to the closed-arm structure of the free peptide. The objective of this work was to develop a quantitative structure activity relationship (QSAR) using different machine learning (ML) models to correlate the different 20-mer sequences of the modified BMP2-KEP to their configurational properties. As the existing structure–property data for osteogenic peptides are insufficient for training ML models, the SIMFIM mesoscale simulation model was used to obtain structural properties, such as radius of gyration (Rg) and end-to-end distance (EtE), of the modified BMP2-KEP sequences to create a database. For ML modeling, the residues in the 20-mer sequences, as the input features of the database, were represented by different amino acid descriptor (AAD) scales. The performances of all the models were compared using the R2 performance metric. Permutation importance and SHAP interaction analysis were done to determine which residue positions and properties had highest contribution to the structural properties of the sequences. These studies led to developing trained and tested QSARs for predicting the structural properties of any modified BMP2-KEP sequence for the purpose of discovering novel 20-mer sequences with open-arm structures.
Introduction
Resorbable materials loaded with bone morphogenetic proteins (BMPs) are used clinically as a regenerative alternative to autologous bone transplantation for treating skeletal defects to restore continuity.1,2 The BMP induces migration of progenitor cells from the surrounding tissue to the injury site followed by their differentiation to pre-osteoblasts and bone morphogenesis. The resorption of the graft concurrent with osteogenesis provides volume for the apposition of new bone. However, the short half-life of the recombinant human bone morphogenetic protein-2 (rhBMP-2, see Fig. 1(A)) necessitates administering 3–4 orders of magnitude higher doses (1 mg mL−1) than the endogenous amount (0.2 μg mL−1) for bone formation and healing.3 The high doses combined with BMPs’ role in the development of a wide range of tissues from embryonic to adulthood cause undesired side effects such as bone overgrowth, immune response, tumorigenesis, and neurological complications.4,5 Consequently, the FDA has issued warning to physicians against off-label use of rhBMP-2 in clinical procedures which has limited the widespread use of BMPs in orthopaedics.6It is reported that the amino acid residues 73–92 of the knuckle epitope of rhBMP-2 homodimer (see Fig. 1(A)), hereafter abbreviated by BMP2-KEP, is the ligand that interacts with BMP receptors on the surface of human mesenchymal stem cells (hMSCs) to induce their migration and osteogenic differentiation to osteoblasts to form mineralized bone tissue.7 An alternative to BMPs to mitigate its undesired side effects in bone regeneration is the use of short bioactive peptides corresponding to the active domains of rhBMP-2, like the BMP2-KEP peptide.8–19 However, we and others have shown that the osteogenic activity of these morphogenetic peptides in the free state (not as part of the protein) is orders of magnitude lower than the identical peptide as part of the parent protein.20,21 Hence, none of the peptides corresponding to the active domains of rhBMP-2 protein or other soluble proteins in the bone matrix have reached clinical trial.22
The native BMP2-KEP ligand with 20 amino acids (AAs) has an open-arm, extended, configuration as part of the protein with radius of gyration (Rg) and end-to-end distance (EtE) of 15.95 Å and 46.85 Å, respectively, based on a single nuclear magnetic resonance (NMR) spectrum of the protein in the protein databank (PDB), as shown in Fig. 1(B),23 whereas the free BMP2-KEP sequence has a closed-arm, partially collapsed, configuration with 〈Rg〉 and 〈EtE〉 of 9.47 Å and 21.18 Å as determined from our mesoscale simulations (Fig. 1(C)).24 The amount of free BMP2-KEP required to stimulate osteogenic differentiation of hMSCs to the same level as that of rhBMP-2 was 3000-fold higher, as we previously reported.20,21 The free, partially collapsed BMP2-KEP sequence has a much wider distribution (many orders of magnitude) of entropically-favourable configurational states as compared to the native, extended BMP2-KEP ligand with a relatively narrow distribution of entropically-less favourable states. Consequently, it is much less probable for the free BMP2-KEP to possess the desired configuration for interaction with BMP receptors on the surface of hMSCs as compared to the native BMP2-KEP ligand as part of rhBMP-2 protein. We hypothesize that the many folds lower osteogenic activity of the free peptide as compared to the native BMP2-KEP is related to differences in their configuration and the likelihood of the sequence to acquire the desired extended configuration for interaction with BMP receptors on the surface of hMSCs. Therefore, there is a need to design novel peptide sequences that mimic the configuration of BMP2-KEP sequence in its native state as part of rhBMP-2 protein and test the effect of peptide configuration on osteogenic activity.
For the 20-mer BMP2-KEP sequence, vast number of sequences would have to be tested to identify those with morphogenetic activity. A novel approach is to utilize the existing bioactivity data to train machine learning (ML) models and then use the best trained model to find novel peptide sequences mimicking the native configuration of the BMP2-KEP peptide. The best trained ML model is known as quantitative structure–activity relationship (QSAR).25 Machine learning algorithms in combination with protein/peptide databanks have been used in clustering, classification, and prediction of biological activities of different peptides. Currently, there are public databases on, among others, antimicrobial, anticancer, anti-inflammatory, and anti-hypertension properties of peptides.26 Andreu et al. used antimicrobial properties of peptides from publicly accessible databases to train and test an artificial neural network model and used it to predict antimicrobial properties of unknown peptides.27 Kumar et al. built a support vector regression (SVR) ML model, trained and tested with publicly available data, to predict the inhibitory activity of short antihypertensive peptides.28 The input features used in the model were amino acid composition and chemical descriptors such as hydrophobicity, charge, and molecular weight of the amino acids. Du et al. built two models, namely random forest and partial least squares regression, to predict antioxidant activity of peptides.29 The input features used in the model were divided physicochemical property scores (DPPS), and structural, quantum, and topological descriptors. Rong et al. developed a convolutional neural network model using online repositories of molecular graphs data of peptides to predict angiotensin I-converting enzyme (ACE) inhibitory activity of peptides.30 Karasev et al. used a publicly available database to train and build a predictive ML model for haemolytic activity properties of peptides.31 Each peptide in the model was represented by 440 input features which were based on physicochemical properties of the amino acids in the sequence. Li et al. used an online repository with data on peptide activity as a function of amino acid composition to train and build an ML model for prediction of inhibitory activity of anti-coronavirus peptides.32 These previous ML models for predicting bioactivity of unknown peptides were built using publicly available databanks. However, due to the large number of input amino acid descriptors (AADs) to quantitatively describe different peptide sequences, the existing structure–property and bioactivity data for osteogenic peptides in public databases and online repositories are insufficient for training ML models.8–19 Furthermore, experimental studies to relate structural properties at the molecular scale to biological activity are limited by the number of peptides that can be investigated in practical times.26 Hence, there is a need to generate big data on structure–property and osteogenic activity of thousands of peptides for training ML models.
One approach to create a database for structure–property of randomly generated 20-mer peptide sequences is mesoscale dissipative particle dynamics (DPD) simulation.33 As peptides exhibit diverse molecular fragments or beads with different modes of energetic interaction including non-polar, polar, neutral, hydrophobic, hydrophilic, amphipathic, charged, hydrophobic-charged, and hydrophilic-charged interactions, robust models are required to account for these energetic interactions. In this respect, we recently developed and tested a uniquely parameterized mesoscale model named Structure Independent Molecular Fragment Interfuse Model, abbreviated as SIMFIM, to simulate by DPD the structural properties of a large number of sequences in a practical time scale.24 This model is remarkably suited for simulation of structural properties of peptides because non-bonded pairwise bead interactions are determined using the energy of mixing to account for subtle differences in the structure of fragments. Electrostatic interactions are incorporated in this model using a normal distribution of charges around the centre of the beads.
We previously showed that the SIMFIM predicted radius of gyration values of peptides with known structures were close to the values determined from the actual structures with low deviation between the predicted and actual values.24
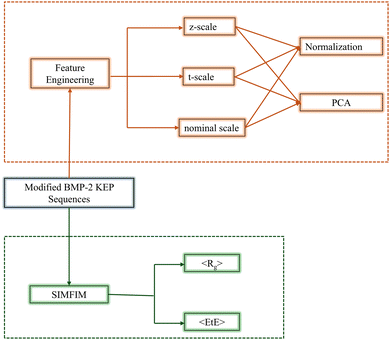
The objective of this work was to build a structure-configuration database of osteogenic peptides by DPD simulation using the SIMFIM model of pairwise secondary interactions between the beads to train ML models to predict configurational descriptors of modified BMP2-KEP sequences. The input of the database was amino acid descriptors (AADs) of the peptide sequences and the output was the configuration descriptors which were the average radius of gyration (〈Rg〉) and average end-to-end distance (〈EtE〉) as a measure of size and openness of the sequences, respectively. The 20-mer free BMP2-KEP was the lead peptide, and the new sequences were generated by modifying the lead peptide using the following approach: (a) modifying residues in the sheet forming domains with uncharged amino acid (AA) residues, (b) modifying residues in the random coil domain with uncharged AA residues, and (c) modifying the residues in the sheet and coil domains with charged residues. The ML models used to relate the output descriptors to the input included regularized linear regression models such as ridge (RR), lasso (LR), and elastic net (ER); non-linear regression models like support vector regression (SVR), Kernel ridge (KRR), and random forest (RFR); and the neural network (NN) model. The database was used to train each ML model and fine-tune its hyperparameters. The importance of features in the ML models that achieved high R2 scores were analysed using the Permutation Importance approach. The combined effect of pairs of these important features was analysed by SHAP interaction analysis. The best performing ML models were used as QSARs to predict new sequences with the desired configuration descriptors by minimum modification of the lead BMP2-KEP peptide.
Methods
Study design
The lead peptide was the knuckle epitope sequence KIPKASSVPTELSAISTLYL (BMP2-KEP) of rhBMP-2 protein. Based on the reported structure of rhBMP-2 in the protein databank (NMR spectra for PDB ID:3BMP), this sequence has an open-arm configuration as a part of the protein (Fig. 1(B)). The residues SSVPT (residues 78–82) and ISTLYL (residues 87–92) form β-sheets as part of the protein (Fig. 1(A) and 2) whereas the remaining residues KIPKA (residues 73–77) and ELSA (residues 83–86) form random coils (Fig. 1(A) and 2). The following approaches were used to replace the residues in the lead peptide with AAs containing hydrophobic, hydrophilic, positively and negatively charged side chains and amino acids with high propensity for β-sheet formation. In the first approach, three randomly picked residues in the β-sheet forming domains (residues 78, 80, and 90 in translucent red boxes in the dotted arrow domains of Fig. 2) were replaced with six randomly selected AAs having hydrophobic, hydrophilic, and high propensity for β-sheet forming side chains (2 of each AA type). The selected AAs were hydrophobic proline and phenylalanine, hydrophilic serine and threonine, and β-sheet forming valine and tyrosine. In the second approach, three randomly picked residues in the coil forming domains (residues 75, 83, and 84 in translucent teal boxes in the dotted line domains of Fig. 2) were replaced with randomly selected AAs as described in the first approach (2 of each AA type). The randomly selected AAs in the second approach were hydrophobic leucine and phenylalanine, hydrophilic asparagine and threonine, and β-sheet forming valine and isoleucine. In the third approach, four randomly picked residues from the remaining residues (not picked in the first and second approaches; residues 81, 86, 91, and 92) were replaced with two positively charged and two negatively charged AAs. The selected AAs in the third approach were positively charged arginine and histidine and negatively charged aspartic acid and glutamic acid. The three approaches to replace the BMP2-KEP residues generated ∼700 sequences for mesoscale simulation and ML modelling. The sequences are shown in Table S1 of the ESI† file.Mesoscale simulation
The configuration descriptors of the modified BMP2-KEP sequences, that is 〈Rg〉 and 〈EtE〉, were determined by mesoscale simulation using our SIMFIM model, as described previously.24 Briefly, molecular fragments corresponding to groups of atoms in different AAs as well as the solvent (water) were coarse grained into beads. Next, the beads were used to construct the mesomolecule model of the peptide sequence. Then, the constructed peptide mesomolecule was randomly placed in a box of size 200 Å × 200 Å × 200 Å with periodic boundary conditions. A box of this size was chosen to avoid the finite size effect, which arises when the number of beads in the simulation box is insufficient to provide a statistically consistent depiction of the conditions of the actual physical system.24,34 The concentrations were adjusted so that there was only one peptide mesomolecule present in the simulation box and the rest of the volume was filled with water beads. The peptide was placed in the box with a random initial configuration and counter ions were placed in the vicinity of the charged beads to maintain electrical neutrality of the system. The charges on the charged amino acid beads were represented by a normal distribution around the beads.35 The geometry of the peptide mesomolecule was optimized by the Geometry Optimization task in the Mesocite module of the Materials Studio software (BIOVIA, Dassault Systèmes, Materials Studio, 24.1.0.0321190, San Diego, CA, USA; Dassault Systèmes, 2024). Following geometry optimization, the system was subjected to Dissipative Particle Dynamics (DPD) simulation using the DPD task in the Mesocite module of the Materials Studio software. The simulations were performed in NVT ensemble with the temperature of the system set at 298 K.36 The SIMFIM model for pairwise secondary interactions between the beads, the bonded interactions such as bond stretching, bond angles, and dihedral angles, and the forcefield governing the motion of the mesomolecule during geometry optimization and DPD simulation were described by us previously.24 A 3-1 mapping was used for the beads, that is, each bead was mapped into three water molecules. The system was simulated for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ps which was sufficiently long for the system to equilibrate. Other input parameters needed for the DPD runs can be found in our previous work.24 After equilibration, data was collected at ∼2000 time points. The coordinates of the backbone beads of the peptide mesomolecule at each time point were obtained using a Perl script.37 These coordinates were then used to determine the radius of gyration (Rg) and end-to-end distance (EtE) at each time point using the following equations:
000 ps which was sufficiently long for the system to equilibrate. Other input parameters needed for the DPD runs can be found in our previous work.24 After equilibration, data was collected at ∼2000 time points. The coordinates of the backbone beads of the peptide mesomolecule at each time point were obtained using a Perl script.37 These coordinates were then used to determine the radius of gyration (Rg) and end-to-end distance (EtE) at each time point using the following equations: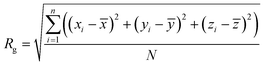 | (1) |
 | (2) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , ȳ and
, ȳ and ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) were the coordinates of the centre of mass of the backbone beads; xN, yN, and zN were the coordinates of the Nth backbone bead of the simulated peptide and N was the total number of AA residues in the peptide sequence (N = 20). These calculations were done using in-house codes in MATLAB. The 〈Rg〉 and 〈EtE〉 are the average values of Rg and EtE over all collected time points, respectively. The simulations in Materials studio were performed in an in-house CPU system.
were the coordinates of the centre of mass of the backbone beads; xN, yN, and zN were the coordinates of the Nth backbone bead of the simulated peptide and N was the total number of AA residues in the peptide sequence (N = 20). These calculations were done using in-house codes in MATLAB. The 〈Rg〉 and 〈EtE〉 are the average values of Rg and EtE over all collected time points, respectively. The simulations in Materials studio were performed in an in-house CPU system.
Feature engineering of amino acid descriptors
The input to the database used by the algorithm for machine learning were the modified BMP2-KEP amino acid sequences and the output were the configuration descriptors of the sequences predicted by the described mesoscale simulation. Each modified BMP2-KEP consisted of a sequence of AAs uniquely defined by their chemical properties. The Chemical properties of AAs were defined by various scales or amino acid descriptors (AADs). In machine learning, these AADs are referred to as the features of the ML model and the performance of an ML model is improved by engineering these features with respect to output predictions, that is, the configuration descriptors.38,39In this work, three different AAD scales, namely nominal scale, z-scale, and t-scale, were used to numerically define the AAs.40,41 In the nominal scale, all AAs were represented equally by randomly assigning integers 1 through 20 to the twenty natural amino acids. This scale does not assign any property to the AAs to serve as a reference scale for evaluating the other scales that assign specific properties to the AAs. The amino acids were categorized in the nominal scale without any inherent order or ranking. In the z-scale, each AA is defined by a unique set of three numbers z1, z2, and z3. The z1, z2, and z3 represent hydrophilicity, molecular size, and electronic nature of the AA, respectively. In the z-scale, each BMP2-KEP sequence was defined by a unique set of 20 × 3 = 60 descriptors.40 In the t-scale, each AA is defined by a unique set of five descriptors. The five descriptors are derived by performing principal component analysis (PCA) on 67 different types of structural and topological parameters of AAs followed by reducing the dimensionality to five with <9% loss of information after dimensionality reduction.41 As the five descriptors of each AA result from PCA and dimensionality reduction, the descriptors for each AA in t-scale are not directly related to specific properties of AAs. In the t-scale, each BMP2-KEP sequence was defined by a unique set of 20 × 5 = 100 descriptors.41
Normalization and dimensional reduction
The AADs in general are not normalized with respect to different descriptors. Normalization of the input data results not only in scale uniformity across all structural features, but it also eliminates domination of one or more features over the others which improves interpretability of the ML models. The scale for any feature in the database was normalized by the following equation:42 | (3) |
ML models
Using feature engineering and SIMFIM, we developed a database for the modified BMP2-KEP sequences with the engineered features of amino acids of the sequences as the input and 〈Rg〉 and 〈EtE〉 values simulated by SIMFIM as the output (Fig. 3). The sequences were converted into numbers using the different AADs as described in the feature engineering section. Different ML algorithms were imported from the Scikit-learn library in Python.44 The entire database was split into training and testing datasets in 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ratio. The training dataset was used to train different ML models which included basic linear regression (BL), ridge regression (RR), lasso regression (LR), rlastic net (EN), support vector regression (SVR), Kernel ridge regression (KRR), random forest (RF) and neural network (NN).45–51 The training dataset was used to fine-tune the hyperparameters of different models using ‘GridSearchCV’ in the Scikit library, which is a search technique for determination of the best combination of hyperparameters for a given model.52 Table S2 of the ESI† file shows the range of values of hyperparameters that were used in the grid search for all the models. In EN model, a large search range was used for the hyperparameters alpha and l1_ratio to avoid overfitting by covering both low and high regularization and to balance the penalty terms L1 and L2.53 For RF model, the range of hyperparameter values for min_samples_leaf, and max_depth were adjusted to avoid overfitting the data.54 For NN model, the size of hidden layers was chosen in such a way to accommodate different features irrespective of the type of scale or dimensionality of the features.55 After defining the hyperparameter search grid, the number of cross-validation folds was set to 5 as defined previously to divide the training dataset into 5 subsets.56,57 This implies that the model was trained with four randomly selected subsets and validated with the one remaining subset. This step was repeated for all possible splits of the training subsets to train and validate the model multiple times. After cross-validation, the R2 correlation coefficient (discussed later), as an average performance metric, was calculated for each hyperparameter combination. The hyperparameter combination with the best average performance metric was chosen to train the ML models on the entire training dataset. The trained ML models were then used to predict the output 〈Rg〉 and 〈EtE〉 of the sequences in the testing dataset.
20 ratio. The training dataset was used to train different ML models which included basic linear regression (BL), ridge regression (RR), lasso regression (LR), rlastic net (EN), support vector regression (SVR), Kernel ridge regression (KRR), random forest (RF) and neural network (NN).45–51 The training dataset was used to fine-tune the hyperparameters of different models using ‘GridSearchCV’ in the Scikit library, which is a search technique for determination of the best combination of hyperparameters for a given model.52 Table S2 of the ESI† file shows the range of values of hyperparameters that were used in the grid search for all the models. In EN model, a large search range was used for the hyperparameters alpha and l1_ratio to avoid overfitting by covering both low and high regularization and to balance the penalty terms L1 and L2.53 For RF model, the range of hyperparameter values for min_samples_leaf, and max_depth were adjusted to avoid overfitting the data.54 For NN model, the size of hidden layers was chosen in such a way to accommodate different features irrespective of the type of scale or dimensionality of the features.55 After defining the hyperparameter search grid, the number of cross-validation folds was set to 5 as defined previously to divide the training dataset into 5 subsets.56,57 This implies that the model was trained with four randomly selected subsets and validated with the one remaining subset. This step was repeated for all possible splits of the training subsets to train and validate the model multiple times. After cross-validation, the R2 correlation coefficient (discussed later), as an average performance metric, was calculated for each hyperparameter combination. The hyperparameter combination with the best average performance metric was chosen to train the ML models on the entire training dataset. The trained ML models were then used to predict the output 〈Rg〉 and 〈EtE〉 of the sequences in the testing dataset.
Model performance evaluation
The performance of the trained models was evaluated by calculating the coefficient of determination of fitting (R2 score) which reflects the goodness of the fit of predicted versus observed by simulation of the values of the target output in the dataset. R2 score was calculated using the following equation:58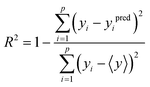 | (4) |
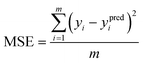 | (5) |
 | (6) |
 | (7) |
 | (8) |
Feature analysis
Permutation Importance was done to assess the impact of different residue properties and their positions in the sequence on predicted 〈Rg〉 and 〈EtE〉 of the BMP2-KEP peptides using different ML models.62 Briefly, the baseline performance score was defined as the R2 of the ML model with highest R2 score and low MSE value trained on the input feature matrix X and the target output matrix Y. This baseline performance score was designated by Rbase2. Next, the values of Xj in the jth column of the feature matrix, corresponding to the jth input feature of all datapoints, were randomly shuffled to break the correlation between Xj and the target matrix Y. The model performance score after shuffling was recalculated. This random shuffling of the values in the jth column of X was repeated fifty times to account for variability in the models’ predictions due to randomness in the permutations, and the recalculated performance scores were designated by Rkj2 for the kth random shuffling of Xj values. The index of permutation importance, Ikj, for the kth shuffling of the values of Xj was defined as follows:63| Ikj = Rbase2 − Rkj2 | (9) |
Effect of important features
The effect of important features on the predicted outputs was studied by determining basic Shapley values and SHAP (SHapley Additive exPlanations) interaction values using Permutation Importance values.64,65 The Shapley value of feature ‘i’, which was found to be important by Permutation Importance, was defined as the average of the marginal contributions of feature ‘i’ over all possible subsets of the features and is given by the following equation:64,65 | (10) |
 | (11) |
QSAR prediction
The important features of the best performing model predicting 〈Rg〉 or 〈EtE〉 were determined from permutation importance. The SHAP interaction analysis determined which pairs of these features, when combined, significantly affected the model's outputs. Next, the lead peptide was modified by replacing residues in these pairs of locations to generate a new set of modified BMP2-KEP sequences. Then, the QSARs (best performing models predicting 〈Rg〉 and 〈EtE〉) were used to predict the configurational descriptors of these new set of sequences to determine which sequences had the highest 〈Rg〉 and 〈EtE〉 following minimum modification to the lead peptide.Statistical analysis
R 2 scores of different ML models were analysed before and after normalization or dimensionality reduction using paired t-test where the null hypothesis was there is no significant difference between R2 scores of the models before and after dimensionality reduction or normalization. To analyse the effect of different scales on R2 scores of different ML models, one way ANOVA analysis was performed on R2 scores followed by a Tukey post hoc test to further investigate the differences between different AAD scales on R2 scores of different ML models.68Results and discussion
Effect of sequence modification
Three approaches, as described in the study design subsection of the methods, were used to replace the residues in the lead BMP2-KEP sequence with AAs of different properties to generate ∼700 sequences for mesoscale simulation and ML modelling. After designing the sequences, the configuration descriptors of the modified peptides, namely Rg and EtE, were determined at different simulation timepoints using the SIMFIM model and averaged over all time points. The violin-like plots in Fig. 4 show the effect of different approaches used to modify the BMP2-KEP sequence on distribution of the values of 〈Rg〉 and 〈EtE〉 of the modified peptides. The dashed magenta lines in the plots are the 〈Rg〉 and 〈EtE〉 values of the free BMP2-KEP sequence. The sequences modified using the first approach had a median 〈Rg〉 and 〈EtE〉 values of 9.37 Å and 21.35 Å, respectively, which did not differ significantly from those of the free BMP2-KEP sequence. This implied that modifying the residues in the β-sheet forming regions alone did not significantly affect the openness of the configuration of the BMP2-KEP sequence. The sequences modified using the second approach had a median 〈Rg〉 and 〈EtE〉 values of 10.74 Å and 26.42 Å, respectively, which differed significantly from those of the free BMP2-KEP sequence. This implied that modifying the residues in the coil forming regions significantly opened the configuration of the BMP2-KEP sequence. The sequences modified using the third approach had a median 〈Rg〉 and 〈EtE〉 values of 7.89 Å and 14.42 Å, respectively, which were significantly less than those of the free BMP-2 KEP sequence. This implied that the addition of positive or negative charged groups led to the collapse of the configuration of the BMP2-KEP sequence. Some sequences modified using the third approach with multiple histidine residues had higher 〈Rg〉 and 〈EtE〉 values (outliers) which was attributed to the bulky nature and repulsion between the positively charged histidine side groups.Effect of number of datapoints
The performances of all the ML models with different number of datapoints for testing and training were analysed using the R2 score performance metric. The ML models were trained and tested with 80% and 20% of the database, respectively, and the z-scale was used as the descriptor for the AAs in the sequences. The R2 scores of models built with 50, 100, and 200 datapoints were relatively low implying that the dataset size was insufficient to find any correlation between the input features and the target outputs. The R2 scores improved significantly after the number of datapoints was increased from 200 to 600 in increments of 100. Furthermore, R2 scores of the models did not improve significantly when the number of datapoints increased from 600 to 700 implying that the models had reached their learning limits. Fig. S1 and S2 in the ESI† file show the effect of number of datapoints on R2 scores of the ML models in predicting 〈Rg〉 and 〈EtE〉 of the modified BMP2-KEP sequences. Fig. S3 in the ESI† file shows the learning curves for the best two RF models where the MSE is plotted against size of the dataset used to train the models. According to the learning curves, the MSE values stabilized and plateaued with increasing dataset size indicating saturation of learning curves. Furthermore, the minimal gap between the MSE values of the training and testing datasets implied the absence of data overfitting.69Effect of scale for describing AAs
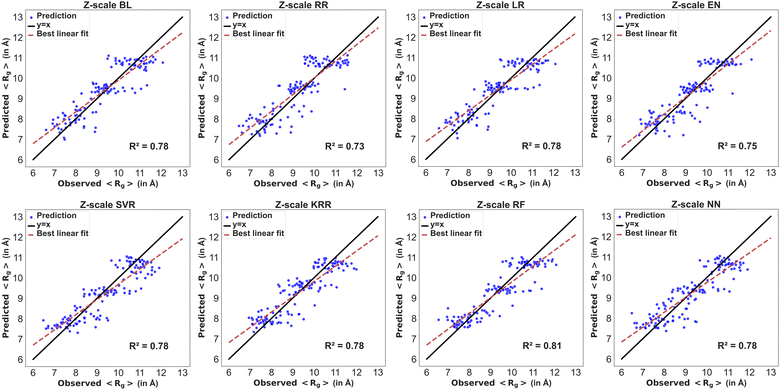
The residues in the modified BMP2-KEP sequences were described using z-scale, t-scale or nominal scale. Fig. 5 and 6 show the parity plots of the observed versus predicted values of 〈Rg〉 and 〈EtE〉 by different models for the testing dataset using z-scale to describe the residues. The observed and predicted values were fitted to the equation for a linear line and compared with the reference line y = x for a perfect model. The best performing model for predicting 〈Rg〉 with z-scale was RF with an R2 score of 0.81, followed by NN, KRR, SVR, BL, and LR models with R2 scores of 0.78, and EN and RR models with R2 scores of 0.75 and 0.73, respectively. The SVR model showed bias toward lower 〈Rg〉 values, that is, the model predicted higher 〈Rg〉 for sequences that had lower 〈Rg〉 values. The MBEs for SVR model in the lower, intermediate, and higher ranges of the observed 〈Rg〉 were 0.25 Å, −0.15 Å, and −0.46 Å, respectively, whereas the MBEs for the best performing RF model were 0.22 Å, −0.05 Å, and −0.33 Å. The best performing models for predicting 〈EtE〉 with z-scale were RF and NN with R2 scores of 0.8, followed by SVR, BL, and KRR models with R2 scores of 0.78, and RR and EN models with R2 scores of 0.71 and 0.72, respectively. The SVR model with an R2 score of 0.78 underestimated 〈EtE〉 of some sequences and overestimated 〈EtE〉 of some others. The MBEs for SVR model in the lower, intermediate, and higher ranges of observed 〈EtE〉 were 1.67 Å, −0.50 Å, and −1.83 Å, respectively, whereas the MBEs for the best performing RF model in the same ranges were 0.99 Å, −0.01 Å, and −1.23 Å.Fig. 7 and 8 show the parity plots of the observed versus predicted values of 〈Rg〉 and 〈EtE〉 by different models for the testing dataset using t-scale to describe the residues. The best performing models for predicting 〈Rg〉 with t-scale were RF and NN with R2 scores of 0.81 and 0.80, respectively, whereas KRR and RR models were the lowest performing models with R2 scores of 0.75 and 0.74. The SVR model underestimated higher observed 〈Rg〉 values of the modified sequences. The MBEs for SVR model in the lower, intermediate, and higher ranges of observed 〈Rg〉 were 0.23 Å, −0.14 Å, and −0.44 Å, respectively, whereas the MBEs for the best performing RF model in the same ranges were 0.19 Å, −0.06 Å, and −0.34 Å. The best performing model for predicting 〈EtE〉 with t-scale was RF with an R2 score of 0.8 followed by SVR, NN, and LR with R2 scores of 0.79, 0.78 and 0.78 respectively. RR and KRR had the poorest performance among all the models with R2 scores of 0.72 each. The SVR model overestimated 〈EtE〉 of sequences with lower observed 〈EtE〉 and underestimated 〈EtE〉 of sequences with higher observed 〈EtE〉. The MBEs for the SVR model in the lower, intermediate, and higher ranges of observed 〈EtE〉 were 1.59 Å, −0.48 Å, and −1.75 Å, respectively, whereas MBEs for the best performing RF model in the same ranges were 0.92 Å, −0.05 Å, and −1.04 Å.
Fig. S4 and S5 in the ESI† file show the parity plots of 〈Rg〉 and 〈EtE〉 by different models for testing the dataset using the nominal scale. Unlike the ML models based on z-scale and t-scale as AADs, there was a relatively poorer correlation between the predicted and observed values of 〈Rg〉 and 〈EtE〉 when the nominal scale was used in different models. The best performing model for 〈Rg〉 was RF with an R2 score of 0.73 whereas BL, RR, LR, EN models performed poorly each with an R2 score of 0.66.
Based on one-way ANOVA analysis of R2 scores, the AA descriptor scale significantly affected predictions of 〈Rg〉 [F(22, p < 0.05) = 32.92] and 〈EtE〉 [F(22, p<0.05) = 20.5] by different models. Tukey's post hoc test for multiple comparisons (see Tables S4 and S5 in the ESI† file) showed that there was a statistically significant difference in R2 scores of the models between z-scale or t-scale as AADs and the nominal scale. There was no significant difference in R2 scores between z-scale and t-scale for prediction of 〈Rg〉 and 〈EtE〉 by different models. These results show that the material properties of AAs as well as their location in the sequence contribute to the configuration of the peptides. In other words, the location of AAs in the sequence is insufficient for predicting the structural properties of the modified BMP2-KEP sequences.
Dimensionality reduction
The graphs in Fig. S6 in the ESI† file show the parity plots of the best performing RF model (Fig. 6(A) and (B)) and comparison of the performances of all the models (Fig. 6(C) and (D)) for predicting 〈Rg〉 and 〈EtE〉 of the peptides using z-scale before and after PCA of AADs from 60 to 30. Paired t-test analysis showed no statistically significant difference in R2 scores of the models using z-scale for predicting 〈Rg〉 [t(7) = −0.19, p = 0.85] and 〈EtE〉 [t(7) = 0, p = 1] before and after PCA. The graphs in Fig. S7 in the ESI† file show the parity plots of the best performing RF model (Fig. 7(A) and (B)) and comparison of the performances of all the models (Fig. 7(C) and (D)) for predicting 〈Rg〉 and 〈EtE〉 of the peptides using t-scale before and after PCA of AADs from 100 to 50. Paired t-test analysis showed no statistically significant difference in R2 scores of the models using t-scale for predicting 〈Rg〉 [t(7) = 0.35, p = 1] and 〈EtE〉 [t(7) = 0.121, p = 0.90] before and after dimensionality reduction. The graphs in Fig. S8 in the ESI† file show the parity plots of the best performing RF model (Fig. 8(A) and (B)) and comparison of the performances of all the models (Fig. 8(C) and (D)) for predicting 〈Rg〉 and 〈EtE〉 of the peptides using nominal scale before and after PCA of AADs from 20 to 10. Paired t-test analysis showed no statistically significant difference in R2 scores of the models using nominal scale for predicting 〈Rg〉 [t(7) = −0.60, p = 0.56] and 〈EtE〉 [t(7) = 0.60, p = 0.56] before and after dimensionality reduction. These results imply that the learning curves for different models had reached saturation with 700 datapoint from different BMP2-KEP sequences such that dimensionality reduction did not affect R2 scores. The models captured most of the underlying patterns in the dataset with 600 datapoints.Normalization of features
The graphs in Fig. S9 in the ESI† file show the parity plots of the best performing RF model (Fig. 9(A) and (B)) and comparison of the performances of all the models (Fig. 9(C) and (D)) for predicting 〈Rg〉 and 〈EtE〉 of the peptides using z-scale before and after normalization. Paired t-test analysis showed no statistically significant difference in R2 scores of the models using z-scale for predicting 〈Rg〉 [t(7) = 0, p = 1] and 〈EtE〉 [t(7) = 0.97, p = 0.38] before and after normalization. The graphs in Fig. S10 in the ESI† file show the parity plots of the best performing RF model (Fig. 10(A) and (B)) and comparison of the performances of all the models (Fig. 10(C) and (D)) for predicting 〈Rg〉 and 〈EtE〉 of the peptides using t-scale before and after normalization. Paired t-test analysis showed no statistically significant difference in R2 scores of the models using t-scale for predicting 〈Rg〉 [t(7) = −1.52, p = 0.17] and 〈EtE〉 [t(7) = −2.04, p = 0.07] before and after normalization. The graphs in Fig. S11 in the ESI† file show the parity plots of the best performing RF model (Fig. 11(A) and (B)) and comparison of the performances of all the models (Fig. 11(C) and (D)) for predicting 〈Rg〉 and 〈EtE〉 of the peptides using nominal scale before and after normalization. Paired t-test analysis showed no statistically significant difference in R2 scores of the models using nominal scale for predicting 〈Rg〉 [t(7) = 1, p = 0.35] and 〈EtE〉 [t(7) = 0.55, p = 0.59] before and after normalization. Therefore, normalization did not significantly affect R2 scores of the models for the three AAD scales used in this work.Feature importance
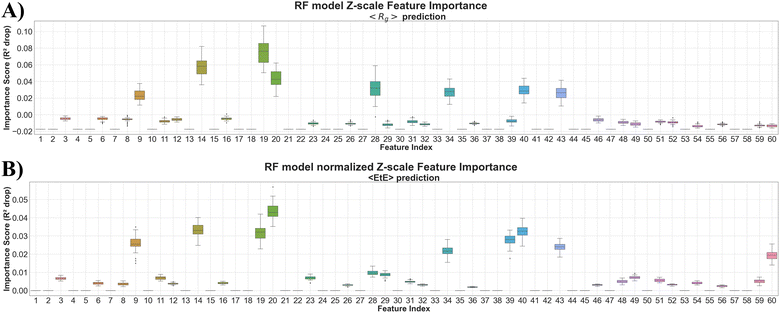
The best performing model for predicting 〈Rg〉 was RF. Table S6 in the ESI† file shows the MSE, PCC, and MAE values of the RF model for predicting 〈Rg〉 using testing dataset with z-scale and t-scale before and after dimensionality reduction or normalization. The MSE and MAE of the RF model with z-scale were lower than those with t-scale regardless of reduction or normalization. The RF model with z-scale without reduction and without normalization had the least MSE and MAE values and highest PCC value. Fig. 9(A) shows the distribution of drops for R2 scores of the RF model for predicting 〈Rg〉 from the baseline R2 score (0.81) with z-scale without dimensionality reduction and without normalization (MSE = 0.601 from Table S6 the ESI† file). The drop in R2 scores was calculated by randomly permuting each input feature column 50 times to break the model's correlation between the feature inputs and the target outputs. The 9th (electronic nature), 14th (size), 19th (hydrophilicity), 20th (size), 28th (hydrophilicity), 34th (hydrophilicity), 40th (hydrophilicity), and 43rd (hydrophilicity) features showed high median drops of R2 scores and these features corresponded to the 3rd, 5th, 7th, 10th, 12th, 14th, and 15th residue positions in the BMP2-KEP sequence.Table S7 in the ESI† file shows the MSE, PCC, and MAE values of the best performing models for predicting 〈EtE〉 which were RF using z-scale, t-scale, and normalized z-scale. As the RF model with normalized z-scale had the least MSE and MAE values as well as highest PCC value, this model was used for feature analysis. Fig. 9(B) shows the distribution of drops for R2 scores of the RF model for predicting 〈EtE〉 from the baseline R2 score (0.80) with normalized z-scale (MSE = 2.71 from Table S7 the ESI† file) by random permutation of each input feature 50 times. The 9th (electronic nature), 14th (size), 19th (hydrophilicity), 20th (size), 34th (hydrophilicity), 39th (electronic nature), 40th (hydrophilicity), and 43rd (hydrophilicity), and 60th (electronic nature) features showed high median drops of R2 scores and these features corresponded to 3rd, 5th, 7th, 12th, 13th, 14th, 15th, and 20th residue positions in the BMP2-KEP sequence. The residue locations with high importance in the QSARs for predicting 〈Rg〉 and 〈EtE〉 were 3rd (electronic nature), 5th (size), 7th (hydrophilicity and size), 10th (hydrophilicity), 12th (hydrophilicity), 13th (electronic nature), 14th (hydrophilicity), 15th (hydrophilicity) and 20th (electronic nature).
SHAP interaction analysis
From permutation analysis, 10 features were determined to be important in the QSARs for predicting the configurational descriptors. Shapley values for these features were calculated for all datapoints and the SHAP interaction values of all possible pairs of these important features were also determined. Fig. 10(A)–(D) show the scatter plots of the SHAP interaction values of pairs of important QSARs features for predicting 〈Rg〉. The scatter plots show those pairs of features having a maximum SHAP interaction value greater than 1 as the other pairs showed relatively weaker interaction values. A cluster of high SHAP interaction values (yellow points) was observed at high Shapley values of the 7th residue's size and 12th residue's hydrophilicity (Fig. 10(A)). There were very few purple points indicating very few cases where the interactions of these two features did not significantly affect the model's predictions (Fig. 10(A)). The highest SHAP interaction values were observed at ∼−0.1 Shapley value of 7th residue's size and ∼0.1 of 13th residue's electronic nature (Fig. 10(B)). A small cluster of moderate SHAP interaction values was observed at high values of 7th residue's size (Fig. 10(B)). Very few purple points were observed for these residues indicating that the combination of these two features had a dominant contribution to the model's output (Fig. 10(B)). In the interaction between 12th residue's hydrophilicity and 13th residue's electronic nature, highest SHAP interaction values were observed at ∼0.1 Shapley value of both features (Fig. 10(C)). Several low SHAP interaction values (purple points) were observed at negative Shapley values of 12th residue's hydrophilicity (Fig. 10(C)). A cluster of moderate to high SHAP interaction values was observed at high Shapley values of both 12th residue's hydrophilicity and 14th residue's hydrophilicity (Fig. 10(D)). Several purple points were observed at negative Shapley values of both features indicating their combined weak effects contributed to these datapoints (Fig. 10(D)).Fig. 11(A)–(E) show the scatter plots of SHAP interaction values of the pairs of important QSARs features for predicting 〈EtE〉. The plots show those pairs of features having a maximum SHAP interaction value greater than 1.5 as the other pairs showed relatively weaker interaction values. The highest SHAP interaction value was observed at ∼−0.2 Shapley value of 3rd residue's electronic nature and ∼0 of 13th residue's electronic nature (Fig. 11(A)). A cluster of moderate SHAP interaction values was observed at high Shapley values of 3rd residue's electronic nature (Fig. 11(A)). The highest SHAP interaction value was observed at ∼−0.2 Shapley value of 5th residue's size and ∼0.2 of 13th residue's electronic nature (Fig. 11(B)). A cluster of moderate SHAP interaction values was observed at high Shapley values of 5th residue's size (Fig. 11(B)). In the interaction between 12th residue's hydrophilicity and 13th residue's electronic nature, the highest SHAP interaction value was observed at ∼0 Shapley value of the former and ∼0.2 of the latter (Fig. 11(C)). Purple points indicating low SHAP interaction values were scattered at ∼−0.8 to ∼−0.6 Shapley values of 12th residue's hydrophilicity (Fig. 11(C)). A vertical cluster of moderate SHAP interaction values was observed at ∼0.1 Shapley value of 13th residue's electronic nature (Fig. 11(D)). A horizontal cluster of low SHAP interaction values was observed at ∼−0.2 Shapley value of 15th residue's hydrophilicity and negative values of 13th residue's electronic nature indicating that neither the 15th residue's electronic nature alone nor the combined effect of the two features affected the model's output at these datapoints (Fig. 11(D)). The highest SHAP interaction value was observed at ∼0.2 Shapley value of 13th electronic nature and ∼−0.2 of 15th residue's hydrophilicity (Fig. 11(D)). Several clusters with different SHAP interaction values were observed for 13th residue's electronic nature and 20th residue's electronic nature (Fig. 11(E)). At negative Shapley values of both features, a small cluster of low SHAP interaction values was observed (Fig. 11(E)). The highest SHAP interaction value was observed at ∼0.2 Shapley value of 13th residue's electronic nature and ∼−0.2 of 20th residue's electronic nature (Fig. 11(E)).
From SHAP interaction analysis, the following pairs of features were identified to have a significant combined effect on the model's outputs: (a) 3rd residue's electronic nature and 13th residue's electronic nature, (b) 5th residue's size and 13th residue's electronic nature, (c) 7th residue's size and 12th residue's hydrophilicity, (d) 7th residue's size and 13th residue's electronic nature, (e) 12th residue's hydrophilicity and 13th residue's electronic nature, (f) 12th residue's hydrophilicity and 14th residue's hydrophilicity, (g) 13th residue's electronic nature and 15th residue's hydrophilicity, and (h) 13th residue's electronic nature and 20th residue's electronic nature.
QSAR predictions
From permutation importance and SHAP interaction analysis, the residues of the following location pairs in the free BMP2-KEP sequence were replaced with the pairs of residue locations with other natural AAs: (a) 3rd and 13th, (b) 5th and 13th, (c) 7th and 12th, (d) 7th and 12th, (e) 12th and 13th, (f) 12th and 14th, (g) 13th and 15th, and (h) 13th and 20th. It is important to note that only two positions in the free BMP2-KEP sequence were replaced at a time which generated ∼3000 new modified BMP2-KEP sequences. After removing duplicate sequences, the 〈Rg〉 and 〈EtE〉 of these new set of modified BMP2-KEP sequences were predicted by the QSARs. The sequence with largest predicted 〈Rg〉 and 〈EtE〉 by the QSARs was KIKKASSVPTELWAISTLYL which was obtained by replacing the 3rd and 13th residues of the free BMP2-KEP sequence. The predicted 〈Rg〉 was 11.11 Å and 〈EtE〉 was 26.23 Å. This QSAR-predicted peptide was simulated by SIMFIM and its 〈Rg〉 and 〈EtE〉 were 11.4 Å and 26.72 Å, respectively. This slight underestimation by the QSARs was expected as observed by MBE values calculated from QSARs at higher ranges of configurational descriptors. The free BMP2-KEP peptide was compared to the QSAR-predicted peptide and the peptide from database (KIIKASSVPTNLSAISTLYL) with highest 〈Rg〉 and 〈EtE〉 values. Fig. 12 shows the probability distribution of the simulated Rg and EtE of these three peptides. There is quantifiable probability for the QSAR peptide and peptide from the database to exist in states with configurational descriptors close to that of the native BMP2-KEP sequence as part of rhBMP-2 protein whereas there is almost zero probability for the free BMP2-KEP to exist in those states as seen in Fig. 12. Fig. 13 shows snapshots of the backbone of several peptides from the database from simulation as well as few peptides predicted by the QSARs to be relatively more open. The snapshots of the sequences from the database in the Figure show a wide range of configurational descriptor values near their average value. | ||
| Fig. 12 Distribution of simulated Rg (left) and simulated EtE (right) of QSAR predicted peptide, most open peptide in the database, and the free BMP2-KEP sequence. | ||
Conclusion
A list of modified BMP2-KEP sequences were generated using three different strategies. These sequences were subjected to mesoscale simulation using SIMFIM to determine their structural properties like 〈Rg〉 and 〈EtE〉. Next, the residues in the generated sequences were quantified using different AADs like z-scale, t-scale or nominal scale. Then, a database was constructed using the AADs and their SIMFIM simulated configuration descriptors. The database was split into training and testing datasets. The training dataset was used to fine tune the hyperparameters of several models following cross validation and then used to train the models. The trained models were then used to predict the target outputs (〈Rg〉 or 〈EtE〉) and compare with the simulated outputs. The R2 scores improved significantly as the number of datapoints was increased from 50 to 700 and the ML models reached their learning limit at 600 datapoints. The performance of the ML models, as measured by R2 scores, improved significantly by using z-scale or t-scale as AADs as compared to the nominal scale. This led to the conclusion that structural properties of the sequences were dependent on both location within the sequence and physiochemical properties of the amino acid residues. Dimensionality reduction and normalization of the features did not significantly affect the performance of the models. The best performing models in predicting 〈Rg〉 and 〈EtE〉 were random forest with z-scale and random forest with normalized z-scale, respectively, with R2 scores of 0.81 and 0.8, which was close to the R2 score of 0.89 representing the natural variation in configuration of the peptides. Permutation importance was utilized to determine residue locations and properties that had the most impact on structural properties of different sequences. Using SHAP interaction analysis, we found 8 pairs of these important features which in combination had a significant effect on the QSAR's output. We then generated another set of modified BMP2-KEP sequences by replacing pairs of residue locations as determined by permutation importance and SHAP interaction analysis. The QSAR predicted peptide with highest 〈Rg〉 and 〈EtE〉 values of 11.4 Å and 26.72 Å (actual values verified by SIMFIM), respectively, was compared with those of the peptide from the database having the highest values of 12.19 Å and 33.4 Å, and the free BMP2-KEP sequence with values of 9.47 Å and 21.18 Å. Compared to the free BMP2-KEP the other two sequences were relatively more open but not as fully open as the native BMP-KEP as part of the protein with 〈Rg〉 and 〈EtE〉 values of 15.95 Å and 46.85 Å. The other two sequences were observed to have higher probability to exist in the native open-arm configuration of BMP2-KEP sequence than the free BMP2-KEP as evidenced from their probability distribution. In this work, we were able to combine the techniques of mesoscale simulation and machine learning to generate 20-mer sequences by just replacing 2 residues in the free BMP2-KEP sequence to achieve relatively open structures. The mesoscale dissipative particle dynamics (DPD) model SIMFIM was used to build the database, which samples peptide configurations across all local energy minima in the configurational landscape. Unlike methods that focus on identifying a single global minimum, SIMFIM explores the full range of accessible states. Since the secondary structures of these peptides are unknown, the model's forcefield does not enforce dihedral constraints on the peptide backbones, allowing for unbiased exploration of the entire configurational space. This approach contrasts with the traditional brute-force molecular dynamics (MD) methods—such as annealing, replica exchange MD (REMD), or extended production runs—which primarily aim to overcome energy barriers to sample thermodynamically stable global energy minima states.70 The QSARs models trained on this database incorporate configurational descriptors derived from sampling all equilibrated states of the peptides. By capturing the full diversity of configurations, including those in local minima, the QSARs successfully predicted output descriptors for the modified BMP2-KEP sequences, revealing greater structural openness compared to the free BMP2-KEP sequence. The future work will investigate computationally the energetic interactions and binding of the QSARs-predicted open-arm BMP2-KEP sequences with BMP receptors on the surface of hMSCs. This will involve using techniques such as molecular mechanics simulation to dynamically assess binding, which enables the selection of a few sequences for experimental validation of osteogenic activity using cell culture.Author contributions
Conceptualization: R. A. D. and E. J.; data curation: R. A. D.; formal analysis: R. A. D. and E. J.; investigation: R. A. D. and E. J.; methodology: R. A. D. and E. J.; project administration; E. J.; Resources: E. J.; supervision: E. J.; validation: R. A. D.; visualization: R. A. D.; writing (original draft) – R. A. D.; writing (review and editing) – R. A. D. and E. J.Data availability
The list of sequences simulated for the database can be found in the ESI† file. Details of the mesoscale simulation conditions are provided in this manuscript and further details on the forcefield can be found in our previous publication. The file containing the raw trajectories for the simulated peptides are too large to be shared in a public repository. The Perl scripts which run in the Materials Studio software to perform geometry optimization and dissipative particle dynamics tasks are provided as supplementary codes 1 and 2 in the ESI† file. However, the analysis of the simulation data to obtain structural properties of the sequences and their probabilities are discussed in this manuscript. The libraries imported in python to build machine learning models are provided in this manuscript. The ranges of hyperparameters in different models that were used in grid search are also provided in the ESI.†Conflicts of interest
There are no conflicts to declare. This work is protected by an institutional IP disclosure.Acknowledgements
R. A. D. was supported by a teaching assistantship from the Chemical Engineering Department and the license for Materials Studio software was supported by the department. The authors thank Mr. Mubarak Bello in the Department of Chemical Engineering (U. South Carolina) for consultation with parity plots, Mr. Zhymir Thompson and Dr. Austin Downey in the department of Mechanical Engineering (U. South Carolina) for consultation regarding normalization of features.Notes and references
- Medtronic ST. Indications, safety, and warnings - infuse bone graft: Spine and trauma 2024 [updated January 2024; cited 2024 June]. Available from: https://www.medtronic.com/us-en/healthcare-professionals/products/spinal-orthopaedic/bone-grafting/infuse-bone-graft/indications-safety-warnings.html.
- Medtronic OMD. Infuse Bone Graft: Bone Grafting (Oral Maxillofacial and Dental) 2024 updated January 2019. Available from: https://www.medtronic.com/us-en/healthcare-professionals/products/oral-maxillofacial-dental/bone-grafting/infuse-bone-graft.html#:~:text=RECOMBINANT%20HUMAN%20BONE%20MORPHOGENETIC%20PROTEIN,and%20localized%20alveolar%20ridge%20augmentation.
- E. J. Lytle, D. Slavnic, D. Tong, M. Bahoura, L. Govila and R. Gonda, et al., Minimally Effective Dose of Bone Morphogenetic Protein in Minimally Invasive Lumbar Interbody Fusions, Spine, 2019, 44(14), 989–995 CrossRef PubMed.
- A. W. James, G. LaChaud, J. Shen, G. Asatrian, V. Nguyen and X. L. Zhang, et al., A Review of the Clinical Side Effects of Bone Morphogenetic Protein-2, Tissue Eng., Part B, 2016, 22(4), 284–297 CAS.
- D. S. Weinberg, J. H. Eoh, W. J. Manz, O. P. Fakunle, A. M. Dawes and E. T. Park, et al., Off-label usage of RhBMP-2 in posterior cervical fusion is not associated with early increased complication rate and has similar clinical outcomes, Spine J., 2022, 22(7), 1079–1088 Search PubMed.
- E. P. Ramly, A. R. Alfonso, R. S. Kantar, M. M. Wang, J. R. D. Siso and A. Ibrahim, et al., Safety and Efficacy of Recombinant Human Bone Morphogenetic Protein-2 (rhBMP-2) in Craniofacial Surgery, Plast. Reconstr. Surg. Glob. Open., 2019, 7(8), e2347 Search PubMed.
- G. Z. Zhao, L. Q. Zhang, L. F. Che, H. Z. Li, Y. Liu and J. Fang, Revisiting bone morphogenetic protein-2 knuckle epitope and redesigning the epitope-derived peptides, J. Pept. Sci., 2021, 27(6), e3309 CrossRef CAS PubMed.
- M. Halder, A. Singh, D. Negi and Y. Singh, Investigating the Role of Amino Acids in Short Peptides for Hydroxyapatite Binding and Osteogenic Differentiation of Mesenchymal Stem Cells to Aid Bone Regeneration, Biomacromolecules, 2024, 25(4), 2286–2301 CAS.
- S. J. Li, S. X. Zhang, S. Dong, M. E. Zhao, W. Zhang and C. Zhang, et al., Stiffness and BMP-2 Mimetic Peptide Jointly Regulate the Osteogenic Differentiation of Rat Bone Marrow Stromal Cells in a Gelatin Cryogel, Biomacromolecules, 2024, 25(2), 890–902 CAS.
- Y. M. Song, H. J. Li, Z. X. Wang, J. M. Shi, J. Li and L. Wang, et al., Define of Optimal Addition Period of Osteogenic Peptide to Accelerate the Osteogenic Differentiation of Human Pluripotent Stem Cells, Tissue Eng. Regener. Med., 2024, 21(2), 291–308 CAS.
- J. K. Seon, S. S. Kuppa, J. Y. Kang, J. S. Lee, S. A. Park and T. R. Yoon, et al., Peptide derived from stromal cell-derived factor 1δ enhances the in vitro expression of osteogenic proteins via bone marrow stromal cell differentiation and promotes bone formation in in vivo models, Biomater. Sci., 2023, 11(19), 6587–6599 CAS.
- A. Ginjaume, J. Hoyland and A. Saiani, BMP2-Incorporated Peptide-Based Bioinks For Promoting Osteogenic Differentiation, Tissue Eng., Part A, 2023, 29 Search PubMed.
- J. R. Camassari, I. T. C. de Sousa, K. Cogo-Müller and R. M. Puppin-Rontani, The Self-assembling peptide P-4 influences viability and osteogenic differentiation of stem cells of the apical papilla (SCAP)*, J. Dent., 2023, 134, 104551 CAS.
- Z. B. Y. Çevik, O. Karaman and N. Topaloglu, Synergistic effects of integrin binding peptide (RGD) and photobiomodulation therapies on bone-like microtissues to enhance osteogenic differentiation, Biomater. Adv., 2023, 149, 213392 Search PubMed.
- H. Yue, Z. B. Leng, Y. Y. Bo, Y. Y. Tian, Z. Y. Yan and C. H. Xue, et al., Novel Peptides from Sea Cucumber Intestinal Enzyme Hydrolysates Promote Osteogenic Differentiation of Bone Mesenchymal Stem Cells via Phosphorylation of PPARγ at Serine 112, Mol. Nutr. Food Res., 2023, 67(9), 13212–13222 CrossRef PubMed.
- J. W. Hwang and Y. H. Han, Novel bone Morphogenetic Protein (BMP)-2/4 Consensus Peptide (BCP) for the Osteogenic Differentiation of C2C12 Cells, Curr. Protein Pept. Sci., 2023, 24(7), 610–619 CrossRef CAS PubMed.
- Y. P. Zuo, Q. C. Xiong, Q. W. Li, B. Zhao, F. Xue and L. X. Shen, et al., Osteogenic growth peptide (OGP)-loaded amphiphilic peptide (NapFFY) supramolecular hydrogel promotes osteogenesis and bone tissue reconstruction, Int. J. Biol. Macromol., 2022, 195, 558–564 CrossRef CAS PubMed.
- J. S. Lee, M. E. Kim, J. K. Seon, J. Y. Kang, T. R. Yoon and Y. D. Park, et al., Bone-forming peptide-3 induces osteogenic differentiation of bone marrow stromal cells via regulation of the ERK1/2 and Smad1/5/8 pathways, Stem Cell Res., 2018, 26, 28–35 CAS.
- R. Z. Li, C. Zhou, J. Chen, H. T. Luo, R. Y. Li and D. Y. Chen, et al., Synergistic osteogenic and angiogenic effects of KP and QK peptides incorporated with an injectable and self-healing hydrogel for efficient bone regeneration, Bioact Mater., 2022, 18, 267–283 CAS.
- Z. Tong, J. X. Guo, R. C. Glen, N. W. Morrell and W. Li, A Bone Morphogenetic Protein (BMP)-derived Peptide Based on the Type I Receptor-binding Site Modifies Cell-type Dependent BMP Signalling, Sci. Rep., 2019, 9, 13446 CrossRef PubMed.
- S. Moeinzadeh, D. Barati, S. K. Sarvestani, T. Karimi and E. Jabbari, Experimental and Computational Investigation of the Effect of Hydrophobicity on Aggregation and Osteoinductive Potential of BMP-2-Derived Peptide in a Hydrogel Matrix, Tissue Eng., Part A, 2015, 21(1–2), 134–146 CrossRef CAS PubMed.
- I. Pountos, M. Panteli, A. Lampropoulos, E. Jones, G. M. Calori and P. V. Giannoudis, The role of peptides in bone healing and regeneration: a systematic review, BMC Med., 2016, 14 Search PubMed.
- C. Scheufler, W. Sebald and M. Huelsmeyer, 3BMP: Human Bone Morphogenetic Protein-2 (BMP-2) 2000 updated March 12, 2000. Available from: https://www.rcsb.org/structure/3BMP.
- R. A. Dash and E. Jabbari, A Structure Independent Molecular Fragment Interfuse Model for Mesoscale Dissipative Particle Dynamics Simulation of Peptides, ACS Omega, 2024, 9(16), 18001–18022 CrossRef CAS PubMed.
- P. Zhou, Q. Liu, T. Wu, Q. Q. Miao, S. Y. Shang and H. Y. Wang, et al., Systematic Comparison and Comprehensive Evaluation of 80 Amino Acid Descriptors in Peptide QSAR Modeling, J. Chem. Inf. Model., 2021, 61(4), 1718–1731 CrossRef CAS PubMed.
- S. Basith, B. Manavalan, T. H. Shin and G. Lee, Machine intelligence in peptide therapeutics: A next-generation tool for rapid disease screening, Med. Res. Rev., 2020, 40(4), 1276–1314 CAS.
- D. Andreu and M. Torrent, Prediction of Bioactive Peptides Using Artificial Neural Networks, in Artificial Neural Networks, ed. H. Cartwright, Springer, New York, 2015, vol. 1260, pp. 101–118 Search PubMed.
- R. Kumar, K. Chaudhary, J. Singh Chauhan, G. Nagpal, R. Kumar and M. Sharma, et al., An in silico platform for predicting, screening and designing of antihypertensive peptides, Sci. Rep., 2015, 5(1), 12512 Search PubMed.
- A. Du, W. Jia and R. Zhang, Machine learning methods for unveiling the potential of antioxidant short peptides in goat milk-derived proteins during in vitro gastrointestinal digestion, J. Dairy Sci., 2024, 107(11), 8837–8851 CAS.
- Y. Rong, B. Feng, X. Cai, H. Song, L. Wang and Y. Wang, et al., Predicting variable-length ACE inhibitory peptides based on graph convolutional network, Int. J. Biol. Macromol., 2024, 282, 137060 CAS.
- D. A. Karasev, G. S. Malakhov and B. N. Sobolev, Quantitative prediction of hemolytic activity of peptides, Comput. Toxicol., 2024, 32, 100335 CAS.
- M. Li, Y. Wu, B. Li, C. Lu, G. Jian and X. Shang, et al., ACVPICPred: Inhibitory activity prediction of anti-coronavirus peptides based on artificial neural network, Comput. Struct. Biotechnol. J., 2024, 23, 3625–3633 CAS.
- P. M. Pieczywek, W. Plazinski and A. Zdunek, Dissipative particle dynamics model of homogalacturonan based on molecular dynamics simulations, Sci. Rep., 2020, 10(1), 14691 CAS.
- F. Cheng, X. Guan, H. Cao, T. Su, J. Cao and Y. Chen, et al., Characteristic of core materials in polymeric micelles effect on their micellar properties studied by experimental and dpd simulation methods, Int. J. Pharm., 2015, 492(1–2), 152–160 CAS.
- P. B. Warren, Screening properties of four mesoscale smoothed charge models, with application to dissipative particle dynamics, J. Chem. Phys., 2014, 084904 Search PubMed.
- K. P. Santo and A. V. Neimark, Dissipative particle dynamics simulations in colloid and Interface science: a review, Adv. Colloid Interface Sci., 2021, 298, 102545 CAS.
- J. Andress, Introduction to Perl, Coding for Penetration Testers, 2017, pp. 81–110 Search PubMed.
- M. Bazeley, The Feature Engineering Guide 2023 Available from: https://www.featureform.com/post/feature-engineering-guide.
- A. M. F. Mumuni, Automated data processing and feature engineering for deep learning and big data applications: A survey, J. Inf. Intell., 2024, 113–135 Search PubMed.
- S. Hellberg, M. Sjoestroem, B. Skagerberg and S. Wold, Peptide quantitative structure–activity relationships, a multivariate approach, J. Med. Chem., 1987, 30(7), 1126–1135 CAS.
- F. Tian, P. Zhou and Z. Li, T-scale as a novel vector of topological descriptors for amino acids and its application in QSARs of peptides, J. Mol. Struct., 2007, 830(1–3), 106–115 CAS.
- Y.-S. Kim, Investigating the Impact of Data Normalization Methods on Predicting Electricity Consumption in a Building Using different Artificial Neural Network Models, Sustain. Cities Soc., 2024, 105570 Search PubMed.
- A. Géron, Hands-on Machine Learning with Scikit-Learn and TensorFlow, 2017, p. 551 Search PubMed.
- J. Santos-Pereira, L. Gruenwald and J. Bernardino, Top data mining tools for the healthcare industry, J. King Saud Univ. – Comput. Inf. Sci., 2022, 34(8), 4968–4982 Search PubMed.
- Y.-A. Wang, Q. Huang, Z. Yao and Y. Zhang, On a class of linear regression methods, J. Complex., 2024, 82, 101826 Search PubMed.
- M. V. Lakshmi and J. R. Winkler, Numerical properties of solutions of LASSO regression, Appl. Numer. Math., 2024, 297–309 Search PubMed.
- A. Guedon, C. Thepenier, E. Shotar, J. Gabrieli, B. Mathon and K. Premat, et al., Predictive score for complete occlusion of intracranial aneurysms treated by flow-diverter stents using machine learning, J. Neurointerv. Surg., 2021, 13(4), 341–346 CrossRef PubMed.
- A. Mohammadian, Z. Mortezaei and Y. NejatyJahromy, Fast rank-based normalization of miRNA qPCR arrays using support vector regression, Inform. Med. Unlocked, 2023, 39, 101265 CrossRef.
- S. Xiao, M. Shen and L. Yu, Energy Saving Analysis of refrigeration room Group Control Based on Kernel Ridge Regression Algorithm, Int. J. Refrig., 2023, 153, 345–355 CrossRef.
- L. Blanchet, R. Vitale, R. van Vorstenbosch, G. Stavropoulos, J. Pender and D. Jonkers, et al., Constructing bi-plots for random forest: Tutorial, Anal. Chim. Acta, 2020, 1131, 146–155 CrossRef CAS PubMed.
- A. Shah, M. Shah, A. Pandya, R. Sushra, R. Sushra and M. Mehta, et al., A comprehensive study on skin cancer detection using artificial neural network (ANN) and convolutional neural network (CNN), Clin. eHealth, 2023, 6, 76–84 CrossRef.
- T. Puślecki, Hyperparameters Optimization Using GridSearchCV Method for TinyML Models, in International Conference on Computer Recognition Systems, ed. K. Walkowiak, Springer, Cham, 2023 Search PubMed.
- P. E. Dewitt and T. D. Bennett, ensr: R Package for Simultaneous Selection of Elastic Net Tuning Parameters. arXiv: Computation, 2019.
- L. Amusa, D. North and T. Zewotir, Optimal hyperparameter tuning of random forests for estimating causal treatment effects, Songklanakarin J. Sci. Technol., 2021, 43, 1004–1009 Search PubMed.
- M. A. K. Raiaan, S. Sakib, N. M. Fahad, A. A. Mamun, M. A. Rahman and S. Shatabda, et al., A systematic review of hyperparameter optimization techniques in Convolutional Neural Networks, Decis. Anal. J., 2024, 11, 100470 CrossRef.
- Automatic Termination for Hyperparameter Optimization, ed. A. Makarova, H. Shen, V. Perrone, A. Klein, J. B. Faddoul and A. Krause, et al., AutoML, 2021 Search PubMed.
- J. Kaliappan, A. R. Bagepalli, S. Almal, R. Mishra, Y.-C. Hu and K. Srinivasan, Impact of Cross-Validation on Machine Learning Models for Early Detection of Intrauterine Fetal Demise, Diagnostics, 2023, 13(10), 1692 CrossRef PubMed.
- Y. He and X. He, Molecular design and genetic optimization of antimicrobial peptides containing unnatural amino acids against antibiotic-resistant bacterial infections: Molecular Design and Genetic Optimization, Biopolymers, 2016, 106(5), 746–756 CrossRef CAS PubMed.
- S. Chatterjee, P. W. Khan and Y.-C. Byun, Recent advances and applications of machine learning in the variable renewable energy sector, Energy Rep., 2024, 12, 5044–5065 CrossRef.
- F. S. L. G. Duarte, R. A. Rios, E. R. Hruschka and R. F. de Mello, Decomposing time series into deterministic and stochastic influences: A survey, Digit. Signal Process, 2019, 95, 102582 CrossRef.
- A. Botchkarev, A New Typology Design of Performance Metrics to Measure Errors in Machine Learning Regression Algorithms, Interdiscip. J. Inf. Knowl. Manag., 2019, 14, 045–076 Search PubMed.
- D. Thakur and S. Biswas, Permutation importance based modified guided regularized random forest in human activity recognition with smartphone, Eng. Appl. Artif. Intell., 2024, 129, 107681 CrossRef.
- Developers S-l. Permutation Importance—Scikit-learn 1.5 documentation 2024 Available from: https://scikit-learn.org/1.5/modules/permutation_importance.html.
- S. M. Lundberg, G. G. Erion and S.-I. Lee Consistent Individualized Feature Attribution for Tree Ensembles. arXiv, 2018.
- S. M. Lundberg and S.-I. Lee A unified approach to interpreting model predictions. Proceedings of the 31st International Conference on Neural Information Processing Systems; Long Beach, California, USA: Curran Associates Inc., 2017, pp. 4768–4777.
- A. Cremades, S. Hoyas and R. Vinuesa, Additive-feature-attribution methods: A review on explainable artificial intelligence for fluid dynamics and heat transfer, Int. J. Heat Fluid Flow, 2025, 112, 109662 CrossRef.
- R. Jia, D. Dao, B. Wang, F. A. Hubis, N. Hynes and N. M. Gürel, et al., Towards Efficient Data Valuation Based on the Shapley Value, in Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, ed. C. Kamalika and S. Masashi, Proceedings of Machine Learning Research: PMLR, 2019. pp. 1167–1176 Search PubMed.
- K. Cabello-Solorzano, I. Araujo, M. Peña Cubillos, L. Correia and A. J. Tallón-Ballesteros, The Impact of Data Normalization on the Accuracy of Machine Learning Algorithms: A Comparative Analysis, 2023, pp. 344–353 Search PubMed.
- Brownlee j. 2019. Available from: https://machinelearningmastery.com/learning-curves-for-diagnosing-machine-learning-model-performance/.
- R. C. Bernardi, M. C. R. Melo and K. Schulten, Enhanced sampling techniques in molecular dynamics simulations of biological systems, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850(5), 872–877 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00407a |
| This journal is © the Owner Societies 2025 |