 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Proton affinities of aldehyde molecules determined from the forward and backward gas-phase proton transfer reactions in a selected ion flow-drift tube†
Maroua
Omezzine Gnioua
 ab,
Anatolii
Spesyvyi
ab,
Anatolii
Spesyvyi
 a and
Patrik
Španěl
a and
Patrik
Španěl
 *a
*a
aJ Heyrovský Institute of Physical Chemistry of the CAS, v. v. i., Dolejškova 2155/3, 182 23 Prague 8, Czechia. E-mail: patrik.spanel@jh-inst.cas.cz
bFaculty of Mathematics and Physics, Charles University, V Holešovičkách 2/747, Prague 8, Czechia
First published on 28th February 2025
Abstract
Proton affinity (PA) and gas-phase basicity (GB) are important thermodynamic properties that provide insights into ion–molecule interactions. Aldehydes play a significant role in biology, the environment, and industry, but their PAs remain unknown for those with more than 5 C atoms. This study aims to experimentally determine PAs and GBs of hexanal, heptanal, and octanal using pentanal as a reference. A selected ion flow drift tube (SIFDT) was used to study proton transfer reactions among all possible combinations of protonated and neutral molecules from this set. Rate coefficients (k), equilibrium constants (K), and effective temperatures (Teff) were used to calculate Gibbs free energy changes (ΔG) and enthalpy changes (ΔH). PAs and GBs were then determined relative to the known values of pentanal. Experimental PAs were found to increase with aldehyde chain length: pentanal 796.6 kJ mol−1 < hexanal 809.6 kJ mol−1 < heptanal 813.4 kJ mol−1 < octanal 824.0 kJ mol−1. Theoretical enthalpies and entropies were obtained via density functional theory (DFT) B3LYP/6-311++G(d,p) with D4 dispersion correction for both open and bent protonated structures, allowing comparison with experimental data. The theoretical calculations for open structures underestimate the observed PAs, while the bent structures align more closely with experimental trends, indicating that larger protonated aldehydes may have bent and cyclic shapes. These findings contribute to bridging the gaps in knowledge about protonated aldehydes, providing a better understanding of their ion chemistry.
1. Introduction
Proton affinity (PA) and gas-phase basicity (GB) are key thermodynamic properties that indicate a molecule's ability to accept a proton in the gas phase.1,2 These properties are important for understanding chemical ionisation in mass spectrometry, catalysis, and molecular interactions.PA measures the enthalpy change when a molecule accepts a proton in a notional reaction:
| A + H+ → AH+ | (1) |
| GB = −ΔG | (2) |
Over the decades, significant efforts have been devoted to measuring and estimating PA for various compounds, resulting in extensive data collection.3 These data are currently summarised in the NIST WebBook, which critically evaluates both experimental and theoretical data.2
Experimental determination of PA typically relies on mass spectrometry techniques. While relative PA values are measured with reasonable accuracy, obtaining absolute values remains challenging.3 One of the experimental methods4 involves the calculation of GB from measured equilibrium constants (K) for reversible proton transfer reactions. In the present study, this was done by using a selected-ion flow drift tube (SIFDT).5 Complementary to experimental approaches, ab initio quantum chemistry calculations employing density functional theory (DFT) have been used to predict enthalpy (ΔH) and entropy (ΔS) changes associated with PA values. A comprehensive overview of PA from a theoretical perspective is given by Maksić et al.1 The use of the B3LYP functional and standard Pople basis sets, such as 6-311++G(d,p) or 6-31G*, is currently considered good practice for performing PA calculations.6,7
Until now, the proton affinities of saturated aldehydes have only been studied for compounds with up to five carbon atoms. Given that the analyses of trace amounts of their vapours using SIFT-MS8 and PTR-MS9,10 are important in biological, medical, and food applications, it is crucial to understand the trends in their proton affinity (PA) and gas phase basicity (GB) values. Additionally, gaining insights into the structure of their protonated molecules is important, as our previous mobility studies suggested that larger protonated aldehyde molecules may have cyclic structures.11 Pentanal can serve as a reference compound because its proton affinity (796.6 kJ mol−1) and gas phase basicity (764.8 kJ mol−1) were well established based on ammonia (NH3) by Taff et al. in an unpublished study reported in ref. 12 and by Wolf et al.,13 and by Aue et al. referenced against dimethyl ether.14 The agreement between these results is within 0.1 kJ mol−1, which indicates pentanal's suitability as a benchmark compound. The objective of the present study was to experimentally determine the gas-phase basicity (GB) and proton affinity (PA) of hexanal, heptanal, and octanal, using pentanal as a reference. We conducted 12 separate SIFDT investigations into the kinetics of proton transfer reactions among all possible combinations of proton donors and proton acceptors involving these four compounds. DFT calculations were used to explain the experimental trends observed in GB and PA by changes in the structures of the aldehyde molecules on protonation.
2. Methods
2.1 Selected ion flow drift tube instrument
This study used a selected ion flow drift tube (SIFDT) instrument designed and developed in our laboratory,15–17 which is described in detail in recent publications.11,18 Only a brief description is provided here to highlight a specific modification made for this study involving the addition of a new port to introduce neutral molecules into the drift tube reactor, facilitating the study of ion–molecule reactions.19The scheme of the present configuration is shown in Fig. 1. H3O+ ions were produced in a hollow cathode (HC) discharge through water vapour and transferred via a source drift tube (SDT) filled with helium carrier gas (He) into the octopole (OP) ion guide. To convert H3O+ ions to protonated aldehydes for some experiments, a mixture of aldehyde vapour and clean air from a zero-air generator contained in a Nalophan bag was introduced into the ion source via a needle valve and a stainless-steel capillary VOC vapour port (labelled M0 in Fig. 1). In the OP, the H3O+ ions may then undergo proton transfer reactions with the aldehyde molecules forming M0H+ ions. The reagent ions (either H3O+ or M0H+) are selected in the quadrupole mass filter (QMF) by their mass-to-charge ratio (m/z). The selected ions are then injected through the Venturi inlet (VI) with a helium stream into a Venturi drift tube (VDT) maintained at an electric field strength of E = 5 V cm−1. Within the VDT, the ion energy is reduced through multiple collisions with He atoms, and ions are thermalised to a Maxwell–Boltzman distribution of kinetic and internal energies at an effective temperature close to 300 to 400 K. The ions are then carried downstream by the He flow to the drift tube reactor (DTR) at a pressure of 2 mbar.
 | ||
| Fig. 1 Schematic representation of the current SIFDT arrangement with designated main operational parts and the vacuum system. Adapted from ref. 11 (available under the CC BY 4.0 open-access license). | ||
A separate port (labelled M1) introduced neutral aldehyde molecules (again as a mixture of vapour in clean air in a Nalophan bag) into the DTR at varying flow rates controlled by a flow controller (Alicat 5 sccm). The ion residence time is determined by Hadamard modulation as detailed in previous publications.20–22 The helium flow in the DTR is counter to that in the VDT, with both flows evacuated between the drift tubes via a valve-regulated booster port of an Edwards nEXT300 turbomolecular pump (Fig. 1). This counterflow setup ensures a homogeneous gas composition within the DTR, unaffected by the gas from the VDT.
The applied voltage across the DTR (U) is monitored and adjusted to achieve a constant reduced field strength (E/N) 30 Td for the present experiments. After the ion–molecule reactions occur in the DTR, the resulting product and remaining reagent ions are sampled through a sampling nose cone (NC) and introduced to a downstream quadrupole mass spectrometer (QMS), where they are analysed based on m/z and detected by an electron multiplier.
The reagents were purchased from Sigma-Aldrich: pentanal (valeraldehyde) 97%, hexanal 98%, heptanal 95% and octanal 99%.
2.2 Determination of rate coefficients and branching ratios
In the present study, reaction kinetics were determined for six combinations of M0H+ and M1 always complemented by a reference experiment on the reaction kinetics of H3O+ and M1. The H3O+ reactions proceed as follows:| H3O+ + M1 → M1H+ + H2O | (3a) |
| →(M1–OH)+ + 2H2O | (3b) |
The total rate coefficients for these exothermic proton transfer reactions are assumed to be collisional23 and thus their rate coefficients were calculated according to ref. 24 for pentanal, hexanal, heptanal, and octanal as 3.39 × 10−9 cm3 s−1, 3.37 × 10−9 cm3 s−1, 3.47 × 10−9 cm3 s−1, and 3.38 × 10−9 cm3 s−1, respectively. The decay rate of H3O+ with a variable flow of the M1 mixture serves as a reference to determine the rate coefficient for the M0H+ reaction, as will be discussed later.
To determine the product ion branching ratios, the first aldehyde (M0) was introduced into the ion source, where it reacted with H3O+ ions to produce M0H+. The second aldehyde (M1) was introduced in the DTR at several flow rates, and the resulting mass spectra were obtained using QMS. These mass spectra allow the identification of product ions of the reaction.
| M0H+ + M1 → M0H+M1 | (4a) |
| →M1H+ + M0 | (4b) |
| →(M1–OH)+ + M0 + H2O | (4c) |
To determine the reaction rate coefficients, the decays of the H3O+ and M0H+ were monitored as a function of the flow rate of M1. These follow the relationships:
 | (5a) |
 | (5b) |
The concentration of the neutral molecules M1 in the DTR is directly proportional to its flow rate ΦM1 as:
 | (6) |
| [M1] = CΦM1 | (7) |
 | (8) |
 | (9a) |
 | (9b) |
 | (10) |
2.3 Determination of equilibrium constants and Gibbs free energy changes
For each pair of aldehydes, the forward (kf) and backward rate coefficients (kb) were determined as the partial proton transfer reaction channel (4b) rate coefficients: | (11) |
 | (12) |
The internal energy of the neutral molecules M1 and M0 corresponds to the carrier gas temperature. However, the ions M0H+ and M1H+ entering the reaction have elevated translational and internal energies due to the drift field. To account for this when interpreting the equilibrium constant, we have to consider the effective temperature of the reaction complex {M0H+M1}* that influences the rate coefficients, especially for the endothermic direction of the proton transfer. The effective temperature of ions results from a balance between the kinetic energy gained from the electric field and the energy lost during collisions. This temperature corresponds to the effective thermal energy of the ions, which is influenced by their interactions with helium atoms.
The average kinetic energy of the drifting ions MH+ is given by the Wannier formula:25
 | (13) |
The mean relative kinetic energy of the collisions between ions and He gas atoms in the centre-of-mass frame can then be calculated as follows:
 | (14) |
Similarly, the mean relative collision energy between ions and neutral reactant molecules in the centre-of-mass frame is determined as follows:
 | (15) |
The effective temperature of the reagent ions M0H+ drifting through He before they react was then determined according to Viehland's classical kinetic theory of drift tube experiments involving molecular ion–neutral systems26 as follows:
 | (16) |
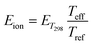 | (17) |
The total energy of the reaction system, involving the drifting ion impacting the neutral molecule M0H+ M1, is calculated by summing as follows:
| Etotal = Eion + Eneutral + Er | (18) |
The effective temperature of the reaction system was determined as follows:
 | (19) |
This calculation was performed for each flow rate using the measured vd values, and the average value was then used as Teff to calculate ΔG from the experimental K using the following equation:
ΔG = −kBTeff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K) ln(K) | (20) |
2.4 Thermodynamic cycles for relative gas-phase basicity
As mentioned in the introduction, the GB of pentanal is a reliable reference for determining the GB of other aldehydes included in this study, using a thermodynamic cycle approach.27,28 The experiments yielded twelve values for ΔG for different proton transfer reactions between each pair of aldehydes. These values denoted as Δ1 = ΔGPen-Hex, Δ2 = ΔGHex-Pen, Δ3 = ΔGPen-Hep, Δ4 = ΔGHep-Pen, Δ5 = ΔGPen-Oct, Δ6 = ΔGOct-Pen, Δ7 = ΔGHex-Hep, Δ8 = ΔGHep-Hex, Δ9 = ΔGHex-Oct, Δ10 = ΔGOct-Hex, Δ11 = ΔGHep-Oct, and Δ12 = ΔGOct-Hep.These experimentally determined values are not independent, as they reflect differences in gas phase basicity between the aldehydes. The relationship between these aldehydes and their Gibbs free energy differences is visually represented in the diagram in Fig. 2. This figure illustrates the thermodynamic cycle framework, where each arrow corresponds to a measured ΔG and provides a way to interpret the relative differences in GB from the interconnectivity of the aldehyde pairs.
 | ||
| Fig. 2 The thermodynamic cycle represents the relationship between experimental ΔG values for proton transfer reactions between aldehyde pairs and the optimised ladder of the gas phase basicity GB. | ||
We obtained optimised relative Gibbs free energy differences for the aldehyde pairs by combining the multiple experimental values into evaluated gas-phase basicity values. These differences are denoted as ΔGHex-Pen, ΔGHep-Hex and ΔGOct-Hep and can be calculated from an overdetermined set of linear equations using the Moore–Penrose pseudo-inverse method. This method minimises the sum of squared residuals between the experimental and calculated ΔG values, ensuring the best-fit solution. Thus, the relationship between the measured and unknown ΔG values was expressed as a system of linear equations in matrix form, represented as
| A·x = b | (21) |
The right side is the vector of the experimental ΔG values b = [Δ1, Δ2, Δ3, Δ4, Δ5, Δ6, Δ7, Δ8, Δ9, Δ10, Δ11, Δ12]T. For the present study, the matrices are thus:
| x = A+·b | (22) |
2.5 Determination of proton affinities
After optimising the ΔG values using the Moore–Penrose pseudoinverse method and aligning them to a common baseline with pentanal chosen as the reference point, the GBs of each aldehyde were derived by adding the experimental ΔG values to the known GB of pentanal.To obtain the experimental proton affinities (PA) of aldehydes, thermodynamic relationships involving Gibbs free energy (ΔG) and enthalpy changes (ΔH) were utilised.
The ΔH for each proton transfer reaction was derived using Teff and the entropy changes ΔSp(M):
| ΔH = ΔG + TeffΔSp(M) | (23) |
| ΔSp(M) = S(MH+) − S(M) | (24) |
2.6 Computational methods and thermodynamic calculations
The molecular geometries of the neutral aldehyde molecules and protonated MH+ ions for all four aldehydes were initially drawn using AVOGADRO software.29 Geometry optimisations were subsequently obtained using ORCA 5.0.1 software.30 The calculations employed the density functional theory (DFT) method with the well-established functional B3LYP and the sufficiently extensive basis set 6-311++G(d,p) incorporating the D4 dispersion correction.31 The choice of the basis set and functional was based on good agreement with the known value of PA for pentanal and on the current established practice.32 Optimisations were achieved for all feasible structures of the neutral molecules and protonated ions that are obtained by placing the H+ proton near the oxygen site of the aldehydes. It is worth noting that the protonated aldehyde molecules may exhibit both open and bent structures. Therefore, both configurations were considered, and the lowest energy structure was chosen. The enthalpy (H), entropy (S) and Gibbs free energy (G) values were calculated for each optimised structure, which was subsequently used to determine ΔH, ΔS and ΔG. Thermal corrections from the ORCA output files at a standard temperature of 298.15 K were scaled to match the experimental temperature Teff, ensuring accurate thermodynamic values reflective of the experimental conditions. The calculated lowest energy ion geometries, charge distributions and thermodynamic data are available in ORCA output files in the data repository.3. Results and discussion
3.1 SIFDT experimental results
The rate coefficients for the reactions (4) and the branching ratios of their channels obtained using the SIFDT are given in Table 1. Note that most experimentally obtained total rate coefficients are near the collisional limits, kc, calculated from the reduced masses, polarisabilities and dipole moments according to Su.24 The relatively slowest reaction is between protonated hexanal and pentanal at 1/3 of collisional, and the reactions with neutral octanal proceed fast, apparently above the collisional limit. This can be explained by large geometrical cross-sections of ions and neutral molecules for which point approximation implied by Su does not apply, and all-atom trajectory simulations would have to be used.33 In all reactions, association (4a) is the dominant channel (67% to 99%), whilst the proton transfer channel is only minor (1% to 8%) and the H2O loss channel ranges from 0 to 33%. These kinetics data were used to calculate the equilibrium rate constants (12) from which the thermochemical properties were determined.| Reaction | M1 (RMM per Da) | |||
|---|---|---|---|---|
| M0H+ (RMM per Da) | Pentanal (86)ab C5H10O | Hexanal (101)ab C6H12O | Heptanal (115)ab C7H14O | Octanal (128)ab C8H16O |
| a For each reaction, the experimental k is given followed by the calculated collisional k24 in the units of 10−9 cm3 s−1. b The product ions are given symbolically, followed by their branching ratios, followed by the branching ratio in parentheses. | ||||
| Pentanal (87) C5H10OH+ | 1.3 [2.1] | 2.1 [2.2] | 3.3 [2.0] | |
| M0H+M1 95% M1H+ 4% | M0H+M1 95% M1H+ 4% | M0H+M1 89% M1H+ 4% | ||
| (M1–OH)+ 1% | (M1–OH)+ 1% | (M1–OH)+ 1% | ||
| Hexanal (101) C6H12OH+ | 0.7 [2.1] | 1.8 [2.0] | 2.7 [2.0] | |
| M0H+M1 99% | M0H+M1 97% M1H+ 3% | M0H+M1 94% M1H+ 5% | ||
| M1H+ 1% | (M1–OH)+ 1% | |||
| Heptanal (115) C7H14OH+ | 0.9 [2.0] | 1.6 [2.0] | 2.1 [1.9] | |
| M0H+M1 98% | M0H+M1 98% M1H+ 2% | M0H+M1 92% M1H+ 8% | ||
| M1H+ 1% | ||||
| (M1–OH)+ 1% | ||||
| Octanal (129) C8H16OH+ | 1.2 [2.0] | 1.6 [1.9] | 1.8 [1.9] | |
| M0H+M1 67% | M0H+M1 92% M1H+ 2% | M0H+M1 98% M1H+ 2% | ||
| M1H+ 1% | (M1–OH)+ 6% | |||
| (M1–OH)+ 33% | ||||
Table 2 gives the experimental results derived from the reaction kinetics data for each reaction pair between two different aldehydes, including the effective temperatures (Teff) of the reaction systems, equilibrium constants (K), Gibbs free energy changes (ΔG) calculated using eqn (20) and enthalpy changes (ΔH) calculated using eqn (23).
| Compound | T eff (K) | K | ΔG (kJ mol−1) | ΔH (kJ mol−1) | |
|---|---|---|---|---|---|
| M0H+ | M1 | ||||
| Protonated pentanal | Hexanal | 383 | 7.2 | −6.3 | −12.99 |
| Protonated hexanal | Pentanal | 380 | 0.1 | 6.3 | 12.87 |
| Protonated pentanal | Heptanal | 363 | 9.5 | −6.8 | −11.06 |
| Protonated heptanal | Pentanal | 370 | 0.1 | 6.9 | 11.28 |
| Protonated pentanal | Octanal | 381 | 28.0 | −10.6 | −21.31 |
| Protonated octanal | Pentanal | 352 | 0.04 | 9.8 | 19.60 |
| Protonated hexanal | Heptanal | 375 | 1.7 | −1.7 | −3.84 |
| Protonated heptanal | Hexanal | 364 | 0.6 | 1.7 | −0.42 |
| Protonated hexanal | Octanal | 376 | 4.2 | −4.5 | −8.46 |
| Protonated octanal | Hexanal | 356 | 0.2 | 4.2 | 8.01 |
| Protonated heptanal | Octanal | 370 | 4.4 | −4.6 | −10.62 |
| Protonated octanal | Heptanal | 365 | 0.2 | 4.5 | 10.47 |
The effective temperatures (Teff) of the reactions, as calculated from eqn (19), range from 352 K to 383 K. Higher Teff values were observed for reactions involving lighter reagents, while lower values correspond to heavier protonated aldehydes.
The equilibrium constants (K) and the Gibbs free energy changes (ΔG) for the proton transfer reactions exhibit a wide range of values, reflecting the varying tendencies of protonated aldehydes (M0H+) to transfer a proton to neutral aldehydes (M1). A more negative ΔG corresponds to a higher gas-phase basicity. For instance, the reactions involving protonated pentanal demonstrate thermodynamically favourable proton transfer to hexanal (K = 7.2, ΔG = −6.3 kJ mol−1), heptanal (K = 9.5, ΔG = −6.8 kJ mol−1), and octanal (K = 28.0, ΔG = −10.6 kJ mol−1), indicating that gas-phase basicities relative to pentanal increase with the number of the carbon atoms in the protonated molecules (see Table 3). In contrast, when protonated hexanal or heptanal reacts with pentanal, the reactions are endergonic and have positive ΔG values. The experimental results show that octanal exhibits the highest gas-phase basicity in this study; for example, reactions of protonated octanal with hexanal (K = 0.2, ΔG = 4.2 kJ mol−1) and heptanal (K = 0.2, ΔG = 4.5 kJ mol−1) are also endergonic. These ΔG values were combined using the Moore–Penrose pseudoinverse method (eqn (22)) to calculate relative gas-phase basicities, with pentanal serving as the reference. The results are given in Table 3. Note that the GB and PA values follow a clear trend: pentanal < hexanal < heptanal < octanal.
| Compound (RMM) | Experimental gas phase basicities GBexpa (kJ mol−1) | Experimental proton affinity PAa (kJ mol−1) | Theoretical gas phase basicities GBtheob (kJ mol−1) | Theoretical proton affinity PAb (kJ mol−1) |
|---|---|---|---|---|
| a Experimental values determined using the SIFDT technique, with pentanal as the reference compound accounting for the effective Teff. b Theoretical values are calculated for the lowest energy (bent) structures using B3LYP 6-311++G(d,p) D4 DFT. c Taken from the NIST2 as a reference for this study. | ||||
| Pentanal (86) | 764.8c | 796.6c | 759.6 | 791.1 |
| Hexanal (100) | 770.7 | 809.6 | 760.0 | 796.6 |
| Heptanal (114) | 777.5 | 813.4 | 766.4 | 801.4 |
| Octanal (128) | 788.1 | 824.0 | 769.3 | 809.1 |
3.2 Comparison between the experimental results and the initial DFT calculations: open protonated structures
The initial theoretical results were obtained from DFT calculations at T = 298 K using the open chain structures of protonated molecules corresponding to optimised geometries starting from adding a proton to the oxygen of the neutral molecule (see Fig. 4). From the calculated Gibbs free energies, the following ΔG values were obtained for the six reaction pairs: protonated pentanal to hexanal −1.2 kJ mol−1, protonated pentanal to heptanal −1.9 kJ mol−1, protonated pentanal to octanal −2.3 kJ mol−1, protonated hexanal to heptanal −0.7 kJ mol−1, protonated hexanal to octanal −1.1 kJ mol−1 and protonated heptanal to octanal −0.4 kJ mol−1. These theoretical ΔG values are consistently smaller than the experimental results across all aldehyde pairs. This is because these initial DFT calculations assumed idealised open geometries that may not fully consider the dynamic molecular interactions that can change the structure of the protonated molecules formed in reactions (4b). Alternative geometries, such as cyclic (bent) structures, could be more stable and have lower total energy. Thus, we attempted to calculate several different structures, starting from cyclic configurations of the ions as a potential resolution to the differences observed between theoretical and experimental results; these are also shown in Fig. 4.3.3 DFT calculations of the bent structures of protonated aldehydes
The results from the DFT calculations for the lowest energy structures of protonated aldehydes are presented in Table 3, alongside the experimentally obtained gas-phase basicities (GB) and proton affinities (PA). The geometries illustrated in Fig. 4 are given in the repository in the form of ORCA output files. Notably, for protonated pentanal, the lowest energy structure retains an open configuration, similar to the neutral molecule. However, for hexanal and heptanal, the lowest energy protonated structure adopts a bent or a U-shaped geometry, and for octanal, the protonated structure approaches a near-closed cyclic configuration (see Fig. 4).The enthalpies and entropies obtained by DFT for the lowest energy structures of the protonated aldehydes again confirm the rising trend of the gas phase basicity with the number of carbon atoms. For instance, the bent structure of protonated octanal exhibits the highest theoretical GB (769.3 kJ mol−1) and PA (809.1 kJ mol−1).
The theoretical GB and PA values for pentanal are slightly lower than the reference values,12 and the calculated GB of 759.6 kJ mol−1 is 5.2 kJ mol−1 lower than the literature value of 764.8 kJ mol−1. Whilst this is not strictly within the so-called chemical accuracy of ±4 kJ mol−1 (±1 kcal mol−1), it is in an acceptable agreement for the B3LYP 6-311++G(d,p) DFT method.
The ladder diagram shown in Fig. 3 compares the experimental and theoretical proton affinities (PA) for pentanal, hexanal, heptanal, and octanal. The experimental data, shown as steps in blue, demonstrate a consistent trend of increasing PA with the number of carbon atoms in the aldehyde chain: pentanal < hexanal < heptanal < octanal. There is only one theoretical value for protonated pentanal, as the DFT optimisation for both bent and open initial geometries yields identical open structures corresponding to the PA of 791.1 kJ mol−1. This reflects the stability of the open geometry for this smaller aldehyde.
 | ||
| Fig. 3 Proton affinities of the four aldehydes obtained by SIFDT experiments (blue), DFT calculations for the open structures of the protonated molecules (orange) and for the bent structures (green). | ||
 | ||
| Fig. 4 Bent and open aldehyde structures with the corresponding enthalpy values (in Hartree) for each structure and the enthalpy difference between open and bent structures (in kJ mol−1). | ||
For hexanal, the experimental PA = 809.6 kJ mol−1 is greater than the theoretical value of 796.6 kJ mol−1 by another 13 kJ mol−1. The value for the open structure would be even lower at 7963 kJ mol−1. The experimental PA for heptanal (813.4 kJ mol−1) is again greater than the theoretical value for the lower energy bent structure (801.4 kJ mol−1), which is notably higher than that for the open structure (792.6 kJ mol−1). Octanal exhibits the highest experimental PA (824.0 kJ mol−1) in this study, consistent with the highest theoretical PA (809.1 kJ mol−1) for the bent ion. Again, the open structure (corresponding to the PA of only 793.3 kJ mol−1) has significantly higher energy. The near-cyclic geometry of protonated octanal, as predicted in the bent theoretical model, likely provides additional stabilisation through intramolecular interactions, explaining its higher PA. While the ladder diagram in Fig. 3 shows the PA values, the corresponding gas-phase basicity (GB) values are summarised in Table 3. Together, these results demonstrate the increasing stability of protonated aldehydes with longer carbon chains and indicate that the protonated aldehydes have bent geometries.
Overall, the experimental values show a clear trend of increasing GB and PA with the size of the aldehyde molecule; the values of octanal GB and PA are more than 21 kJ mol−1 and 27.4 kJ mol−1 greater than those of pentanal. The theoretical model that considers protons attached to linear chain molecules predicts that the GB should increase by no more than 2.5 kJ mol−1 and the PA by no more than 2.2 kJ mol−1. However, considering the bending or cyclisation of larger protonated aldehydes somewhat improves the predictions, suggesting an increase of GB by 9.7 kJ mol−1 and PA by 18 kJ mol−1. Therefore, in proton transfer reactions, it is possible that even more energetically favourable structures are formed, which we did not identify through DFT optimisations, potentially involving bond rearrangements. Note that these results support the speculation arising from ion mobility measurements11 that protonated heptanal and octanal adopt a cyclic geometry.
4. Conclusion
The primary results of this study are original experimental data on the gas-phase basicities (GB) and proton affinities (PA) of hexanal, heptanal, and octanal using selected ion flow drift tube (SIFDT) studies of proton transfer between different pairs of aldehydes. The elevated temperatures of reactions caused by suprathermal ion–neutral interaction energies in the drift tube facilitate the low proton-transfer channel (less than 8% for all aldehyde pairs), which is otherwise not accessible at room temperatures in the SIFT. These results revealed a clear trend in gas-phase basicity and proton affinity, increasing with molecular size in the order of pentanal < hexanal < heptanal < octanal. Octanal thus has a PA more than 27 kJ mol−1 greater than pentanal. This is a surprisingly large difference, considering their great chemical similarity.The initial theoretical results obtained by DFT for open-chain protonated structures predicted very little change in PA (only 2 kJ mol−1) in this series of aldehydes and did not explain the experimentally observed trend of increasing PA with the number of C atoms. To explain such a trend, U-shaped or cyclic configurations of protonated aldehyde molecules needed to be included in the DFT calculations. Bent and cyclic configurations were found to have lower energies than the open chain structures and resulted in an increase of the PA of octanal by 16 kJ mol−1, in better qualitative agreement with the experiment. Presumably, the remaining discrepancy indicates that more rearrangement takes place upon the protonation of larger aldehydes. To fully investigate this, we suggest further work using conformational searches34 or molecular dynamics to explore the details of the proton transfer reaction.
Data availability
The data supporting this study are openly available in the National Data Repository at https://doi.org/10.48700/datst.grwf8-3c725.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the Praemium Academiae funding by the Czech Academy of Sciences project no. AP2102.References
- Z. B. Maksic, B. Kovacevic and R. Vianello, Advances in Determining the Absolute Proton Affinities of Neutral Organic Molecules in the Gas Phase and Their Interpretation: A Theoretical Account, Chem. Rev., 2012, 112, 5240–5270, DOI:10.1021/cr100458v.
- E. P. Hunter and S. G. Lias, Proton Affinity Evaluation, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD 20899, 2013 Search PubMed.
- S. Kolboe, Proton Affinity Calculations with High Level Methods, J. Chem. Theory Comput., 2014, 10, 3123–3128, DOI:10.1021/ct500315c.
- J. E. Szulejko and T. B. Mcmahon, Progress toward an Absolute Gas-Phase Proton Affinity Scale, J. Am. Chem. Soc., 1993, 115, 7839–7848, DOI:10.1021/ja00070a033.
- M. Tichý, N. D. Twiddy, D. P. Wareing, N. G. Adams and D. Smith, Sifdt Studies of the Reactions of N4+ Ions with H2, D2, and Ar, Int. J. Mass Spectrom. Ion Processes, 1987, 81, 235–246, DOI:10.1016/0168-1176(87)80016-2.
- J. K.-C. Lau, V. Romanov, S. Lukow, A. C. Hopkinson and U. H. Verkerk, Collision-induced dissociation of protonated fentanyl: A DFT study, Comput. Theor. Chem., 2021, 1196, 113117, DOI:10.1016/j.comptc.2020.113117.
- E. H. Denis, J. L. Bade, R. S. Renslow, K. A. Morrison, M. K. Nims, N. Govind and R. G. Ewing, Proton Affinity Values of Fentanyl and Fentanyl Analogues Pertinent to Ambient Ionization and Detection, J. Am. Soc. Mass Spectrom., 2022, 33, 482–490, DOI:10.1021/jasms.1c00320.
- B. M. Ross, S. Puukila, I. Malik, S. Babay, M. Lecours, A. Agostino, T. Wondimu and N. Khaper, The Use of SIFT-MS to Investigate Headspace Aldehydes as Markers of Lipid Peroxidation, Curr. Anal. Chem., 2013, 9, 600–613, DOI:10.2174/15734110113099990025.
- T. Majchrzak, M. Marc and A. Wasik, Understanding the early-stage release of volatile organic compounds from rapeseed oil during deep-frying of tubers by targeted and omics-inspired approaches using PTR-MS and gas chromatography, Food Res. Int., 2022, 160, 8, DOI:10.1016/j.foodres.2022.111716.
- J. Beauchamp, E. Zardin, P. Silcock and P. J. Bremer, Monitoring photooxidation-induced dynamic changes in the volatile composition of extended shelf life bovine milk by PTR-MS, J. Mass Spectrom., 2014, 49, 952–958, DOI:10.1002/jms.3430.
- M. Omezzine Gnioua, P. Španěl and A. Spesyvyi, Gas-phase ion mobility of protonated aldehydes in helium measured using a selected ion flow-drift tube, Rapid Commun. Mass Spectrom., 2024, 38, e9767, DOI:10.1002/rcm.9767.
- E. P. L. Hunter and S. G. Lias, Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update, J. Phys. Chem. Ref. Data, 1998, 27, 413–656, DOI:10.1063/1.556018.
- J. F. Wolf, R. H. Staley, I. Koppel, M. Taagepera, J. McIver, J. L. Beauchamp and R. W. Taft, Gas phase basicities and relative proton affinities of compounds between water and ammonia from pulsed ion cyclotron resonance thermal equilibria measurements, J. Am. Chem. Soc., 1977, 99, 5417–5429, DOI:10.1021/ja00458a032.
- D. H. Aue and M. T. Bowers, in Gas Phase Ion Chemistry, ed. M. T. Bowers, Academic Press, 1979, pp. 1–51 DOI:10.1016/B978-0-12-120802-8.50007-2.
- P. Španěl, A. Spesyvyi and D. Smith, Electrostatic Switching and Selection of H3O+, NO+, and O2− (+center dot) Reagent Ions for Selected Ion Flow-Drift Tube Mass Spectrometric Analyses of Air and Breath, Anal. Chem., 2019, 91, 5380–5388, DOI:10.1021/acs.analchem.9b00530.
- A. Spesyvyi, D. Smith and P. Španěl, Ion chemistry at elevated ion-molecule interaction energies in a selected ion flow-drift tube: reactions of H3O+, NO+ and O2+ with saturated aliphatic ketones, Phys. Chem. Chem. Phys., 2017, 19, 31714–31723, 10.1039/c7cp05795d.
- A. Spesyvyi, K. Sovova and P. Španěl, In-tube collision-induced dissociation for selected ion flow-drift tube mass spectrometry, SIFDT-MS: a case study of NO+ reactions with isomeric monoterpenes, Rapid Commun. Mass Spectrom., 2016, 30, 2009–2016, DOI:10.1002/rcm.7679.
- P. Španěl, K. Dryahina, M. Omezzine Gnioua and D. Smith, Different reactivities of H3O+(H2O)n with unsaturated and saturated aldehydes: ligand-switching reactions govern the quantitative analytical sensitivity of SESI-MS, Rapid Commun. Mass Spectrom., 2023, 37, e9496, DOI:10.1002/rcm.9496.
- A. Spesyvyi, K. Sovová, D. Smith and P. Španěl, Increase of the Charge Transfer Rate Coefficients for NO+ and O2+˙ Reactions with Isoprene Molecules at Elevated Interaction Energies, J. Phys. Chem. A, 2018, 122, 9733–9737, DOI:10.1021/acs.jpca.8b08580.
- A. Spesyvyi, M. Lacko, K. Dryahina, D. Smith and P. Španěl, Ligand Switching Ion Chemistry: An SIFDT Case Study of the Primary and Secondary Reactions of Protonated Acetic Acid Hydrates with Acetone, J. Am. Soc. Mass Spectrom., 2021, 32, 2251–2260, DOI:10.1021/jasms.1c00174.
- A. Spesyvyi and P. Španěl, Determination of residence times of ions in a resistive glass selected ion flow-drift tube using the Hadamard transformation, Rapid Commun. Mass Spectrom., 2015, 29, 1563–1570, DOI:10.1002/rcm.7254.
- A. Spesyvyi, D. Smith and P. Španěl, Selected Ion Flow-Drift Tube Mass Spectrometry: Quantification of Volatile Compounds in Air and Breath, Anal. Chem., 2015, 87, 12151–12160, DOI:10.1021/acs.analchem.5b02994.
- D. K. Bohme, G. I. Mackay and H. I. Schiff, Determination of proton affinities from the kinetics of proton transfer reactions. VII. The proton affinities of O2, H2, Kr, O, N2, Xe, CO2, CH4, N2O, and CO, J. Chem. Phys., 1980, 73, 4976–4986, DOI:10.1063/1.439975.
- T. Su, Parametrization of Kinetic-Energy Dependences of Ion Polar Molecule Collision Rate Constants by Trajectory Calculations, J. Chem. Phys., 1994, 100, 4703, DOI:10.1063/1.466255.
- J. Sanderson, H. Tanuma, N. Kobayashi and Y. Kaneko, Ion mobility measurements for O+ and N+ in helium gas at 4.35 K, J. Chem. Phys., 1995, 103, 7098–7103, DOI:10.1063/1.470338.
- L. A. Viehland, Classical Kinetic-Theory of Drift Tube Experiments Involving Molecular Ion Neutral Systems, Chem. Phys., 1986, 101, 1–16, DOI:10.1016/0301-0104(86)87018-5.
- R. S. Mason, in Thermochemistry and Its Applications to Chemical and Biochemical Systems: The Thermochemistry of Molecules, Ionic Species and Free Radicals in Relation to the Understanding of Chemical and Biochemical Systems, ed. M. A. V. Ribeiro da Silva, Springer Netherlands, Dordrecht, 1984, pp. 627–651 DOI:10.1007/978-94-009-6312-2_31.
- G. Bouchoux, Gas-phase basicities of polyfunctional molecules. part 1: theory and methods, Mass Spectrom. Rev., 2007, 26, 775–835, DOI:10.1002/mas.20151.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 17, DOI:10.1186/1758-2946-4-17.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, DOI:10.1002/wcms.1327.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 034112, DOI:10.1063/1.4993215.
- M. Gray, P. E. Bowling and J. M. Herbert, Comment on “Benchmarking Basis Sets for Density Functional Theory Thermochemistry Calculations: Why Unpolarized Basis Sets and the Polarized 6-311G Family Should Be Avoided”, J. Phys. Chem. A, 2024, 128, 7739–7745, DOI:10.1021/acs.jpca.4c00283.
- I. Neefjes, R. Halonen, H. Vehkamäki and B. Reischl, Modeling approaches for atmospheric ion–dipole collisions: all-atom trajectory simulations and central field methods, Atmos. Chem. Phys., 2022, 22, 11155–11172, DOI:10.5194/acp-22-11155-2022.
- C. C. Lam and J. M. Goodman, CONFPASS: Fast DFT Re-Optimizations of Structures from Conformation Searches, J. Chem. Inf. Model., 2023, 63, 4364–4375, DOI:10.1021/acs.jcim.3c00649.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00328h |
| This journal is © the Owner Societies 2025 |

