Oscillatory motion of a self-propelled object determined by the mass transport path

Abstract

Oscillatory self-propulsion can be achieved under nonequilibrium conditions. In the case of a camphor boat, the periods of oscillatory motion were determined by the lateral (two-dimensional) transport length of camphor molecules at the solid plastic/water interface. However, the control of self-propulsion by different mass transport paths has not yet been explored. We observed new fluidic behaviors in the oscillatory motion of self-propelled objects. The period of oscillatory motion was determined by the mass transport path of the energy source molecules depending on the room temperature, T_r, and the temperature gradient, ΔT (= T_b − T_r, where T_b denotes the temperature at the bottom of the water chamber). We found that the oscillation period was determined by three types of mass transport paths for camphor molecules: lateral, downward, and complex. This study suggests that the three-dimensional transport path of energy source molecules can control the periods of oscillatory motion.

---

Introduction

Spontaneous oscillatory phenomena are generated under non-equilibrium conditions corresponding to the difference in the chemical potential around examined systems.^1–3 Self-propulsion is the ability of an object to move with a driving force produced by itself, and it is essential for living organisms to move spontaneously in response to environments. Inanimate systems that mimic the self-propulsion of biological systems have been widely studied for potential applications in cargo transport^4–11 and environmental remediation.^12,13 Self-propulsion with periodic changes in the speed of motion, that is, oscillatory motion, is observed in several types of inanimate systems, for example, a gel or a droplet synchronized with oscillating chemical reactions, such as the Belousov–Zhabotinsky (BZ) reaction and the Briggs–Rauscher (BR) reaction,^14–19 a solid in couple with a chemical reaction or interaction at an air/aqueous interface,^20–22 and a camphor boat depending on the diffusion length of camphor molecules on water.^23–27 The periods of oscillatory motion for the BZ and BR systems, chemical reaction-coupled solid system, and camphor system were determined by the oscillating chemical reactions,^14–19 threshold value of the reactant concentration,^20–22 and concentration of the driving force molecule around the self-propelled objects,^23–27 respectively.

When a smaller camphor disk adhered to the basement and the center of a larger plastic disk floated on water as a self-propelled object named “self-propelled camphor object (SPC),” oscillatory motion between rest and motion was observed periodically.^23–28 We previously reported that the period of oscillatory motion changes depending on the radius of the plastic disk, temperature, and viscosity of the water phase.^25,28 In these studies, the periods of oscillatory motion were determined by the lateral (or two-dimensional) mass transport length of camphor molecules at the solid plastic/water interface.^25,28 However, the control of self-propulsion by different mass transport paths, that is, the three-dimensional transport path, has not been explored.

In this study, we propose a simple self-propelled system using an SPC that is sensitive to the temperature conditions of not only the solid/water interface but also the water phase. Mass transport of camphor molecules in water was indirectly visualized using 7-hydroxycoumarin (7-HC) solid microparticles as a fluorescent indicator mixed in a solid camphor disk under UV light irradiation. We found three types of mass transport of camphor molecules; (1) lateral transport originated from the diffusion and the Marangoni flow by the difference in surface tension under a constant room temperature (T_r), (2) downward transport originated from the diffusion and the flow induced by the difference between densities of pure water and camphor solution under a constant T_r, and (3) complex transport originated from the diffusion and the thermal convection under the difference in the temperature, ΔT (= T_b − T_r, where T_b denotes the temperature at the bottom of the water chamber). The resting SPC accelerated when the camphor molecules reached the water surface from the water phase. In particular, we confirmed that the period of oscillatory motion is almost equal to the resting time. For types (1) and (2) under constant T_r, the period of oscillatory motion was determined by the ratio of types (1) and (2) depending on T_r. In type (3), for ΔT > 0, the oscillation period shortened with an increase in ΔT. We discuss the period of oscillatory motion in relation to the visualization of camphor molecules as a function of T_r and ΔT. These results suggest that the period of the oscillatory motion can be controlled not only by the two-dimensional mass transport of the energy source molecule around the solid/liquid interface but also the three-dimensional mass transport in the water phase, which was induced by ΔT.

Materials and methods

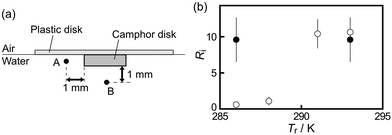
(+)-Camphor was purchased from FUJIFILM, Inc. (Kyoto, Japan). The 7-HC was purchased from Tokyo Chemical Industry Co., Ltd (Tokyo, Japan). A solid disk (thickness: 1 mm, diameter: 3 mm, mass: 5 mg) comprising 99 wt% camphor and 1 wt% 7-HC was manufactured based on a previous study.²⁷ Here, 7-HC was mixed with camphor to indirectly visualize camphor distribution in the water phase. Fig. 1a shows the SPC comprising a solid camphor disk and a polyester plastic disk (diameter: 10 mm, thickness: 0.1 mm). We confirmed that the period of the oscillatory motion of the SPC composed of 99 wt% camphor and 1 wt% 7-HC (111.1 ± 24.3 s) was similar to that of the SPC composed of 100 wt% camphor without 7-HC (81.2 ± 10.2 s) at T_r = 293 K. Water was purified by filtering through active carbon, ion-exchange resin, a water distillation apparatus (RFD24ONC, ADVANTEC Co. Ltd, Tokyo, Japan), and Millipore Milli-Q filtering system (Merck Direct-Q 3UV, Germany; resistance: 18 MΩ cm). Purified water (V = 12 mL) was poured into a cylindrical glass cell (inner diameter: 55 mm, height: 42 mm) to form the water phase (water depth: 5 mm; Fig. 1b).

Fig. 1 Schematic illustration of experiments. (a) SPC. (b)(i) Experimental setup for experiment I which was performed in the fridge to keep the constant value of each T_r. (ii) Experimental setup for experiment II which was performed in the cold room (the room temperature, T_r = 280 K) at ΔT > 0, where ΔT = T_b − T_r. T_b represents the temperature of the basement of the water chamber. The glass cell was placed on the electronic thermostat, and the SPC was floated on water in experiment II. The depth of the water phase was 5 mm in experiments I and II.

The behaviors of the SPC under the absence and presence of temperature gradient in the water phase were monitored in experiments I and II, respectively. In experiment I, self-propulsion of the SPC and the camphor distribution at a constant temperature, T_r, were monitored from the top and side simultaneously. The SPC floated on water in the glass cell was examined in a fridge (Mitsubishi Electric Engineering Co., Ltd, SLC-25A, Tokyo, Japan, temperature range: 276–330 ± 1 K) to keep a constant value of T_r, as shown in Fig. 1b(i). To indirectly visualize the diffusion of camphor, UV light (wavelength: 365 nm, AS ONE Corporation, Handy UV Lamp UV-16, Tokyo, Japan) was irradiated, and the emitted light from 7-HC was monitored. In experiment II, the visualization of the camphor distribution and monitoring of the SPC were performed under the existence of a temperature gradient in the water phase, ΔT. Here, the glass cell was placed on the electronic thermostat (Matsuo Electronic Co. Ltd, METIII, Tokyo, Japan, the size of Peltier element: 50 mm × 50 mm) to control T_b, as shown in Fig. 1b(ii). Experiment II was performed in the cold room (T_r = 280 ± 1 K).

The motion of the SPC was monitored from the top and side views using digital video cameras (HDR-CX680, SONY, Tokyo, Japan; HC-W590MS-T, Panasonic, Tokyo, Japan; minimum time resolution, 1/30 s), and the images were analyzed using an image processing system (ImageJ, National Institute of Health, Bethesda, MD, USA). At least four examinations were performed under each experimental condition, and the SPC was replaced for each examination to confirm the reproducibility of the results.

Results

First, we observed oscillatory motion of the SPC as a function of T_r or ΔT. Fig. 2a and b show the time variation of the speed for the SPC in experiments I and II, respectively. At ΔT = 0 K, the period of the oscillatory motion decreased with increasing T_r (Fig. 2a). On the other hand, the periods of oscillatory motion at ΔT ≠ 0 and individually examined T_r in experiment II (Fig. 2b) were shorter than those at ΔT = 0 K in experiment I. In particular, the period of oscillatory motion at T_r = 286 K and ΔT = 6 K (Fig. 2b(i)) was four times shorter than that at T_r = 286 K and ΔT = 0 K (Fig. 2a(ii)). In contrast, the period of oscillatory motion at T_r = 293 K and ΔT = 0 K (Fig. 2a(iii)) was similar to that at ΔT = 13 K (Fig. 2b(ii)).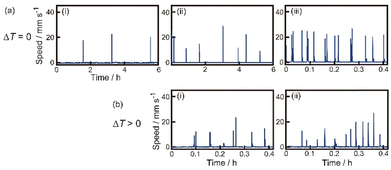

Fig. 2 Oscillatory motion of the SPC. (a) Time-variation on the speed of the SPC at T_r = (i) 280, (ii) 286, and (iii) 293 K in experiment I. The data obtained in (i), (ii), and (iii) are from the Movies S1, S2, and S3 in ESI,† respectively. (b) Time-variation on the speed of the SPC at T_b = (i) 286 K (ΔT = 6 K) and (ii) 293 K (ΔT = 13 K), respectively, in experiment II. Experiment II was performed in the cold room (T_r = 280 K). The data in (i) and (ii) were obtained from the Movies S4 and S5 in ESI,† respectively.

Fig. 3a shows the period of oscillatory motion depending on T_r at ΔT = 0 K in experiment I. With an increase in T_r, the period of the oscillatory motion decreased in the range of 280–290 K; however, the period of oscillatory motion slightly decreased above 290 K. Fig. 3b shows the period of the oscillatory motion depending on ΔT at T_r = 280 K in experiment II. With an increase in ΔT, the period of oscillatory motion decreased in the range of 280–285 K; however, the period of oscillatory motion slightly decreased above 285 K. The period of oscillatory motion in experiment II was shorter than that in experiment I in the range of 283–288 K.

Fig. 3 Oscillatory motion depending on the temperature. (a) Period of oscillatory motion depending on T_r in experiment I. (b) Period of oscillatory motion depending on T_b (or ΔT) in experiment II. Error bars represent the standard deviation obtained from the four examinations.

Next, the UV light was irradiated to the water phase to indirectly visualize the distribution of the camphor molecules dissolved from the camphor disk. Fig. 4 shows the time variation of the snapshots of the water phase during the resting state under different conditions of T_r and ΔT. At T_r = 280 and 286 K in experiment I, downward mass transport of camphor molecules from the disk to the base of the water chamber, in addition to lateral mass transport, was observed (Fig. 4a(i) and a(ii)). The amount of camphor that accumulated around the chamber base at T_r = 280 K (Fig. 4a(i)) was larger than that at T_r = 286 K (Fig. 4a(ii)). The downward mass transport was observed rather than the lateral transport at T_r ≤ 288 K. In contrast, lateral transport around the bottom of the plastic disk was mainly observed at T_r = 293 K in experiment I (Fig. 4a(iii)). When camphor molecules spilled from the edge of the plastic disk to the water surface, the resting object was accelerated.

Fig. 4 Visualization of mass transport of camphor molecules around the SPC (side view). (a) Time-variation of snapshots at T_r = (i) 280, (ii) 286, and (iii) 293 K in experiment I. The corresponding snapshots in (i), (ii), and (iii) were obtained from the Movies S6, S7, and S8 (ESI†), respectively. (b) Time-variation of snapshots at ΔT = (i) 6 and (ii) 13 K in experiment II. The corresponding snapshots in (i) and (ii) were obtained from the Movies S9 and S10 (ESI†), respectively. The experimental conditions for (a) and (b) were the same as those for (a) and (b) in Fig. 1, respectively. The values beside the snapshots denote the elapsed time after the object was floated on the water surface (t = 0). A 1 wt% 7-hydroxycoumarin was mixed with camphor to visualize the distribution of camphor dissolved from the camphor disk under UV light irradiation.

Fig. 4b shows the camphor distribution in the water phase at T_r = 280 K in experiment II. At ΔT = 6 K and 13 K, the downward transport of camphor molecules was mainly observed, and the direction of transport then changed upward. The resting object accelerates when the upward transport approaches the water surface.

Fig. 5 shows aqueous 7 mM camphor solution densities and those for water at different temperatures. At temperatures lower than 290 K, the density of the camphor solution tended to be higher than that of water. At temperatures higher than 290 K, the density of the camphor solution was similar to that of water.

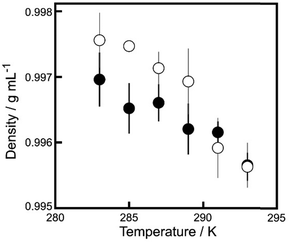Fig. 5 Density of 7 mM camphor aqueous solution (empty circles) and water (filled circles) at different temperatures. Error bars represent the standard deviation obtained from the four examinations.

We measured the light intensity at points A and B to evaluate the degree of the lateral and downward transport as a function of T_r. The light intensity at points A and B was measured just before the SPC accelerated from the resting state. Points A and B were 1 mm off from the edge of the camphor disk, as shown in Fig. 6a. Fig. 6b shows the light intensity ratio at point A (I_A) to that at point B (I_B), R_i (= I_A/I_B), as a function of T_r. R_i increased with an increase in T_r. The downward mass transport was clearly observed rather than the lateral transport in pure water at T_r ≤ 288 K. Here, we also investigated the light intensity in an aqueous NaCl solution to elucidate the effect of the density of the water phase on the nature of mass transport. When SPC was floated on 1.0 M aqueous NaCl solution, the lateral mass transport was mainly observed at T_r = 286 K and ΔT = 0 K (see filled circles in Fig. 6b). In this case, the period of the oscillatory motion of the SPC was 0.072 ± 0.017 h. This value was apparently lower than that on pure water (see Fig. 3a).

Fig. 6 Evaluation of the degree of the lateral and downward transport. (a) Definition of the points A and B for light intensity analysis. (b) The ratio of the light intensity at point A to that at point B, R_i (= light intensity at point A/light intensity at point B), as a function of T_r. Empty and filled circles were obtained from the experiments using pure water and 1.0 M aqueous NaCl solution as the water phase, respectively. Error bars denote the standard deviations obtained from the three examinations.

Discussion

Based on the experimental results and related studies,^25,28 we discuss the effects of room temperature (T_r) and temperature difference (ΔT) on the period of oscillatory motion for a SPC floating on water. In addition, we discuss the relationship between the mass transport path of the camphor molecules and the period of oscillatory motion as illustrated in Fig. 7.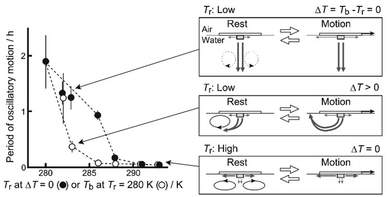

Fig. 7 Schematic illustration of three types of the mass transport of camphor molecules depending on T_r and ΔT.

First of all, three main mass-transport paths must be considered to understand the motion of the SPC (Fig. 4 and 7). First, the lateral mass transport of the camphor molecules originates from diffusion and the Marangoni flow, which is driven by the difference in surface tension due to the camphor concentration gradient around the SPC. Second, downward mass transport is generated by camphor diffusion and camphor sedimentation, originating from the density difference between the camphor aqueous solution and water. Third, convection is generated under a temperature gradient (ΔT > 0), contributing to the upward transport of camphor and helping the molecules reach the air/liquid interface faster. We note that this convection appears to be caused by the density instability driven by the vertical thermal gradient.

The period of the oscillatory motion at T_r ≥ 291 K and ΔT = 0 K was significantly shorter than that at T_r ≤ 288 K and ΔT = 0 K (refer to Fig. 3a). In previous studies, the period of oscillatory motion changed depending on the radius of the plastic disk and water temperature.^23,25,27,28 The diffusion rate of camphor molecules in water depends on the temperature, and the period of oscillatory motion is determined by the time (t_s) required to reach the threshold value of camphor molecules at the edge of the plastic disk to accelerate from the resting state.²⁵ Therefore, t_s at higher temperatures were shorter than those at lower temperatures. In addition, the density difference between the saturated camphor solution and water decreased with increasing temperature (Fig. 5). Fig. 5 and 6b suggest that the degree of the downward transport of camphor molecules generated by sedimentation at lower temperatures was greater than that at higher temperatures. Therefore, the ratio of the lateral transport of camphor molecules to the downward transport decreased with a decrease in T_r at ΔT = 0 (refer to Fig. 5). Consequently, the period of the oscillatory motion under ΔT = 0 at T_r ≤ 288 K is significantly longer than that at T_r ≥ 291 K. This is because it takes a long time to reach the threshold value to obtain the acceleration owing to downward diffusion. Consequently, oscillatory motion with an extended period (∼1.8 h) was observed at T_r = 280 K and ΔT = 0 K.

Next, we discuss the mass transport paths of the camphor molecules at ΔT > 0. The convective flow around the SPC at T_r = 280 K and 0 < ΔT ≤ 13 K is generated by the Marangoni flow due to the existence of ΔT.²⁹ The period of oscillatory motion depending on T_b at T_r = 280 K is shorter than that depending on T_r at ΔT = 0 in the range of 282–288 K (refer to Fig. 7). This result suggests that the time for camphor molecules to reach the water surface owing to convective flow is shorter than that required to reach the edge of the plastic plate owing to lateral transport. Large values of ΔT may induce shorter periods of oscillatory motion owing to rapid convective flow. However, the period of oscillatory motion at T_b ≥ 291 K and ΔT ≥ 11 K was similar to that at T_r ≥ 291 K and ΔT = 0 K (refer to Fig. 7). This is because the downward flow was weakened by the low-density difference (Fig. 5), and the period of the oscillatory motion was determined by lateral transport at temperatures higher than 291 K. Fig. 6 suggests that behaviors of the SPC and mass transport of camphor molecules were strongly affected by the density difference between the water phase and dissolved camphor solution.

Conclusions

In this study, we demonstrate the oscillatory motion of a self-propelled object comprising a camphor disk and a plastic disk floating on water. Three types of mass transport paths as functions of T_r and ΔT were visualized by mixing 7-HC with camphor under UV light irradiation. When ΔT = 0, the lateral and downward transport paths around the object determine the short and long periods of oscillatory motion at higher and lower temperatures, respectively. When ΔT > 0, convective flow enhanced the camphor mass transport. Consequently, the period of oscillatory motion under ΔT > 0 was shorter than that under ΔT = 0 in the range of 282–288 K. This study suggests that the features of self-propelled motion can be controlled by the three-dimensional transport paths of the energy source molecules; that is, we can design novel types of self-propelled systems that are sensitive to the environment of not only the self-propelled object, such as the size and shape of the object, but also the bulk phase, such as the shape and volume of the chamber.

Author contributions

Conceptualization: SN; data curation: MK, NK; formal analysis: MK, NK; investigation: MK, NK; methodology: MM, SN; supervision: SN; validation: MM, NJS, IL, SN; writing – original draft: MK, SN; writing – review and editing: MM, NJS, IL, SN.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Mr Yujin Kubodera for his technical assistant. This study was supported by JSPS KAKENHI No. JP20H02712, JP21H00996, and 24K22324, the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (No. 20221004), and The Iketani Science and Technology Foundation 0351181A to S. N. The JSPS-Hungary Bilateral Joint Research Project (JPJSBP120213801) to N. J. S.

References

1. R. J. Field and M. Burger, Oscillations and Traveling Waves in Chemical Systems, Wiley, New York, USA, 1985.
2. I. R. Epstein and K. Showalter, Nonlinear Chemical Dynamics:  Oscillations, Patterns, and Chaos, J. Phys. Chem., 1996, 100, 13132–13147.
3. I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos, Oxford University Press, Inc., Oxford, UK, 1998.
4. H. Jin, A. Marmur, O. Ikkala and R. H. A. Ras, Vapour-driven Marangoni propulsion: continuous, prolonged and tunable motion, Chem. Sci., 2012, 3, 2526–2529.
5. J. R. Baylis, J. H. Yeon, M. H. Thomson, A. Kazerooni, X. Wang, A. E. St John, E. B. Lim, D. Chien, A. Lee, J. Q. Zhang, J. M. Piret, L. S. Machan, T. F. Burke, N. J. White and C. J. Kastrup, Self-propelled particles that transport cargo through flowing blood and halt hemorrhage, Sci. Adv., 2015, 1, e1500379.
6. M. Paven, H. Mayama, T. Sekido, H.-J. Butt, Y. Nakamura and S. Fujii, Light-driven delivery and release of materials using liquid marbles, Adv. Funct. Mater., 2016, 26, 3199–3206.
7. Y. Yang and M. A. Bevan, Cargo capture and transport by colloidal swarms, Sci. Adv., 2020, 6, eaay7679.
8. C. Wang, B. E. Fernandez de Avila, R. Mundaca-Uribe, M. A. Lopez-Ramirez, D. E. Ramirez-Herrera, S. Shukla, N. F. Steinmetz and J. Wang, Active delivery of VLPs promotes anti-tumor activity in a mouse ovarian tumor model, Small, 2020, 16, e1907150.
9. X. Arqué, T. Patiño and S. Sánchez, Enzyme-powered micro- and nano-motors: key parameters for an application-oriented design, Chem. Sci., 2022, 13, 9128–9146.
10. C. P. Thome, W. S. Hoertdoerfer, J. R. Bendorf, J. G. Lee and C. W. I. Shields, Electrokinetic active particles for motion-based biomolecule detection, Nano Lett., 2023, 23, 2379–2387.
11. A. Shi, H. Wu and D. K. Schwartz, Nanomotor-enhanced transport of passive Brownian particles in porous media, Sci. Adv., 2023, 9, eadj2208.
12. L. Soler, V. Magdanz, V. M. Fomin, S. Sanchez and O. G. Schmidt, Self-propelled micromotors for cleaning polluted water, ACS Nano, 2013, 7, 9611–9620.
13. W. Li, C. Wu, Z. Xiong, C. Liang, Z. Li, B. Liu, Q. Cao, J. Wang, J. Tang and D. Li, Self-driven magnetorobots for recyclable and scalable micro/nanoplastic removal from nonmarine waters, Sci. Adv., 2022, 8, eade1731.
14. S. Nakata, M. Yoshii, S. Suzuki and R. Yoshida, Periodic reciprocating motion of a polymer gel on an aqueous phase synchronized with the Belousov–Zhabotinsky reaction, Langmuir, 2014, 30, 517–521.
15. H. Kitahata, R. Aihara, N. Magome and K. Yoshikawa, Convective and periodic motion driven by a chemical wave, J. Chem. Phys., 2002, 116, 5666–5672.
16. S. Thutupalli, R. Seemann and S. Herminghaus, Swarming behavior of simple model squirmers, New J. Phys., 2011, 13, 073021.
17. N. Yoshinaga, K. H. Nagai, Y. Sumino and H. Kitahata, Drift instability in the motion of a fluid droplet with a chemically reactive surface driven, Phys. Rev. E, 2012, 86, 016108.
18. N. J. Suematsu, Y. Mori, T. Amemiya and S. Nakata, Oscillation of speed of a self-propelled Belousov−Zhabotinsky droplet, J. Phys. Chem. Lett., 2016, 7, 3424–3428.
19. M. Kuze, Y. Kubodera, H. Hashishita, M. Matsuo, H. Nishimori and S. Nakata, Self-propulsion mode switching of a Briggs–Rauscher droplet, ChemSystemsChem, 2022, e202200030.
20. P. Kumar, Q. Wang, D. Horváth, A. Tóth and O. Steinbock, Collective motion of self-propelled chemical garden tubes, Soft Matter, 2022, 18, 4389–4395.
21. T. Fujino, M. Matsuo, V. Pimienta and S. Nakata, Oscillatory motion of an organic droplet reflecting a reaction scheme, J. Phys. Chem. Lett., 2023, 14, 9279–9284.
22. R. Fujita, M. Matsuo and S. Nakata, Self-propelled object that generates a boundary with amphiphiles at an air/aqueous interface, J. Colloid Interface Sci., 2024, 663, 329–335.
23. N. J. Suematsu, Y. Ikura, M. Nagayama, H. Kitahata, N. Kawagishi, M. Murakami and S. Nakata, Mode-switching of the self-motion of a camphor boat depending on the diffusion distance of camphor molecules, J. Phys. Chem. C, 2010, 114, 9876–9882.
24. S. Nakata, M. Yoshii, Y. Matsuda and N. J. Suematsu, Characteristic oscillatory motion of a camphor boat sensitive to physicochemical environment., Chaos, 2015, 25, 064610.
25. R. Tenno, Y. Gunjima, M. Yoshii, H. Kitahata, J. Gorecki, N. J. Suematsu and S. Nakata, Period of oscillatory motion of a camphor boat determined by the dissolution and diffusion of camphor molecules., J. Phys. Chem. B, 2018, 122, 2610–2615.
26. R. J. G. Löffler, T. Roliński, H. Kitahata, Y. Koyano and J. Górecki, New types of complex motion of a simple camphor boat, Phys. Chem. Chem. Phys., 2023, 25, 7794–7804.
27. R. Fujita, N. Takayama, M. Matsuo, M. Iima and S. Nakata, Height-dependent oscillatory motion of a plastic cup with a camphor disk floated on water, Phys. Chem. Chem. Phys., 2023, 25, 14546–14551.
28. S. Nakata and S. Hiromatsu, Intermittent motion of a camphor float, Colloids Surf., A, 2003, 224, 157–163.
29. M. Lappa, Thermal Convection: Patterns, Evolution and Stability, John Wiley & Sons, Ltd., Chichester, England, 2009.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04832f

---