Estimating protein binding upon treatment with radionuclide ions

Abstract

Several types of radioactive isotopes are used for cancer treatment. While most are embedded in chelating agents, ²²³Ra is given as RaCl₂ salt and ⁹⁰Y in microspherical particles. If ionic radionuclides are free, they have the potential to bind to proteins instead of their endogenous ions, interfere with their activity and be transported by them. In this study, a computational approach was used to estimate the binding affinities of Y³⁺, Ra²⁺ and Pb²⁺ (²⁰⁷Pb is the decay product of ²²³Ra) to proteins, instead of their native cofactors Ca²⁺ and Mn²⁺. Y³⁺ was found to bind strongly to proteins with the ability to replace Ca²⁺ and to some degree also Mn²⁺. Ra²⁺ does not bind to the studied proteins but Pb²⁺ can replace Ca²⁺ in Ca²⁺ binding proteins. A recently identified coordination compound was found to be highly selective for ²²³Ra.

---

1 Introduction

Radionuclides have been used in cancer therapy since the beginning of the 20th century. Initially, radium salts were used for skin cancers.¹ Thereafter, instruments were developed to deliver the radiation directly to the tumour,² whereby the use of solid salts had a benefit over radiation therapy. The common isotope of radium, ²²⁶Ra, however, has a long half-life of 1599 years and is not considered safe for therapy. Nevertheless, radioactive salts have emerged as potential therapies and in 1951 the use of ¹³¹I was approved by the U.S. Food and Drug Administration (FDA) for thyroid cancer.³ With a half-life of 8 days and decay through β- and γ- rays to stable and inert ¹³¹Xe, ¹³¹I has been shown to be a safe and effective therapy. Meanwhile, treatment with radium isotopes, was reintroduced and has been used since 2013 for castration-resistant prostate cancer with symptomatic bone metastases. To this end, the less stable isotope ²²³Ra is given as RaCl₂ salt. ²²³Ra has a half-life of 11.43 days and decays by α- and β-radiation to form stable ²⁰⁷Pb. It is believed that the radioactive ions adsorb preferentially to the bones. Early clinical studies have shown improved overall survival⁴ (albeit by a median of 3 months), and a good safety profile in a three years follow-up study.⁵ On the other hand, a recent study⁶ reported haematological toxicities in ∼15% of the patients and second primary malignancies in ∼1%.

Delivery of radionuclides to the tumour can be made directly when the radionuclide is given as salt (as is the case for ¹³¹I), through chelating agents that strongly bind a radioactive ion (these can be further attached to peptides or antibodies for specific delivery), or through the use of microspheres. The latter method has so far been used exclusively with the ⁹⁰Y isotope. This therapy, known as radioembolisation, is used for liver tumours. The radioactive microspheres are injected directly into blood vessels that supply blood to the tumour and get stuck in tiny blood vessels in the tumour. ⁹⁰Y decays to stable ⁹⁰Zr through release of β radiation. The isotope has a half-life of 2.67 days. There are two different ways to deliver ⁹⁰Y to the tumour, namely glass spheres which encapsulate the radionuclides and resin spheres where ⁹⁰Y is bound to the surface. These treatments are effective and relatively safe. However, a systemic review showed gastrointestinal, hepatic and respiratory toxicities with both types of microspheres.⁷ It is likely that the decay product is released from the microsphere with the impact from the radiation. In addition, the release of energy can lead to unbinding of ⁹⁰Y³⁺ ions from microspheres in the immediate vicinity of the β emitter.

Multivalent metal ions such as Mg²⁺, Ca²⁺, Zn²⁺, Mn²⁺ and others are important cofactors of proteins and maintain proper protein structure and function. The binding of xenobiotic ions instead of endogenous ones can lead to toxicities, by modifying the protein's structure, hindering catalysis, or reducing the affinity to substrates. Treatment with radionuclides that are multivalent metal ions could lead to the radionuclide binding to proteins, thereby being transported and also affecting protein activity. With respect to the latter risk, not only the metal ions themselves but also their decay products should be considered. ²²³Ra poses a particular risk since it is given as soluble salt, whereas ⁹⁰Y could mediate such risks if unbound from the microspheres. In the case of ²²³Ra, especially with repeated therapy, even the decay product ²⁰⁷Pb might cause a risk. ⁹⁰Y however decays to ⁹⁰Zr. The latter form stable Zr⁴⁺ ions that are strongly hydrated and carry low if any health risk.

Little is known about the biological activity of Ra²⁺ and Y³⁺ and whether these ions can bind to proteins. The scarcity and radioactivity of radium, and the difficulty to separate Y³⁺ from other rare-earth metals make it difficult to experimentally study their effects in biology in general and binding to proteins in particular. Here, a computational approach is used to estimate the risks with binding of the radioactive ions to proteins in the body. Since Ra²⁺ binds to bone instead of Ca²⁺, and as lanthanides were shown to bind strongly to Ca²⁺ binding proteins,⁸ the bindings to such proteins were studied first. To this end, calmodulin (CaM) was used as a prototype of Ca²⁺ binding proteins, as it exhibits the common EF-hand domain that binds Ca²⁺ in many proteins. EF domains are remarkably similar between different proteins and the binding to the EF domain in calmodulin can thus inform on the interference of ions with most Ca²⁺-binding proteins in the human body. Protein kinase A (PKA) is also considered, as it exhibits a different Ca²⁺ binding site and can accommodate larger ions as well. Finally, Mn²⁺ can form coordination complexes with varied (often high) coordination numbers where it binds to hard ligands and hence DNA polymerase ι that preferentially uses Mn²⁺ as a cofactor was also considered in this study. The binding of Ra²⁺'s decay product Pb²⁺ to those proteins was examined as well. For the Ca²⁺ binding proteins, the affinity to Sr²⁺ was considered a reference for the calculations, since it is known that Sr²⁺ is chemically similar to Ca²⁺ and might replace it.

2 Theory and methods

2.1 Theory

2.1.1 Binding energy differences upon ion exchange. When referring to the difference between the affinity of protein for an ion M^M+ with respect to a natural ionic cofactor, L^L+ (e.g. Ra²⁺ and Ca²⁺, respectively), the property of interest is ΔΔG^bind and it is given by:

ΔΔG^bind = Δ_fG°(prot·M) − Δ_fG°(prot·L) − [G°(M) − G°(L)] (1)

where Δ_fG°(prot·□) is the standard free energy of formation for the complex in the protein environment and G°(□) is the standard free energy of an ion in solution; M and L are the two ions M^M+ and L^L+ and the empty box □ symbolises any of the ions.

In reality, it is not possible to consider the full environment (protein, other cofactors, substrate(s), water, additional ions, etc.) for the complex. In calculations of ion binding affinities it is therefore assumed that the coordinating groups have the most significant influence on the interaction energy and selectivity for ions.^8–10 Thus, eqn (1) is approximated as:

Here, Δ_fG°(prot·□) was replaced by Δ_fG(bs·□) where bs stands for ‘binding site’, surrounded by implicit solvent (here, using the SMD model¹¹). Gibbs energies of the ions in solvent were replaced by their values in the same solvent model, G(□)_SMD. The approximate nature of the implicit solvent model necessitates careful calibration of the radii of ions to reproduce the correct hydration energy,¹² while the ionic radius has a limited effect in the complex because the ion is totally surrounded by larger moieties. Since the ionic radii are hard-coded in some quantum chemistry software packages, instead of modifying the radius it is possible to correct for the difference between the real value of the hydration energy (estimated from experiments) and the value calculated with the implicit solvent model which is referred to here as ΔG^corr_hyd(□). Explicitly, the values were calculated as:

ΔG^corr_hyd = ΔG^exp_hyd − ΔG^SMD_hyd (3)

ΔG^exp_hyd is the experimental value for the hydration energy of an ion and ΔG^SMD_hyd is the calculated value.

To mimic the environment inside a protein metal binding site, which is partially exposed to the solvent and includes many polar residues, ethanol (ε = 24.5) was used as the solvent of the complex.

The free energies of formation of the binding site here include the internal (Gibbs) energy calculated with a quantum mechanical (QM) method of choice (here, density functional theory, DFT) in implicit solvent. Although a single point energy calculation without considering thermochemical corrections is formally the Gibbs energy in solvent, corrections for the enthalpy in finite temperature (here, 300 K), vibrational, rotational and translational entropies of the complex are included in the values for Δ_fG(bs·□).

2.1.2 Energy decomposition analysis for protein–ion binding. EDA deals with decomposition of the interaction energies into various contributions that can be used in an explanatory fashion. In the PCMEDA¹³ approach used here, the energy is decomposed as follows:

ΔG^total = ΔG^ele + ΔG^ex + ΔG^rep + ΔG^pol + ΔG^corr + ΔG^disp + ΔG^desolv (4)

The interaction energy ΔG^total is the energy of the complex in solution minus the energy of the components in solution. Here, it refers to the energy of the protein–ion complex subtracted by the energies of the ion and the protein (in practice, representing the protein by the ion binding site under the assumption that the most significant contributions are captured, vide supra). ΔG^ele, ΔG^ex, ΔG^rep, ΔG^pol, ΔG^corr, ΔG^disp and ΔG^desolv are the electrostatics, exchange, repulsion, polarisation, quantum-mechanical correlation, dispersion and desolvation contributions. Understanding the relative share of each contribution can be used to explain what stabilises the complex or shed light on differences between complexes (e.g. when different ions bind to the same protein). The exchange and repulsion terms are often merged together into ΔG^exrep. When using DFT to calculate the energies, ΔG^disp is an empirical correction for the inability of DFT to correctly model the attractive dispersion. For binding of monoatomic ions, this value is much smaller than other attractive contributions. ΔG^desolv is calculated by the use of an implicit solvent model (as above, eqn (3)), except that ΔG^SMD_hyd was replaced by the corresponding value in ethanol since here the values are calculated for each ion separately as ΔG not ΔΔG upon replacing one ion (Ca²⁺) by another. It is necessary to correct this term for the difference between the experimental hydration energy of an ion and the value calculated by the implicit solvent model; differences can amount to tens or even hundreds of kcal mol⁻¹.

It is important to note that thermochemistry (corrections for the enthalpy and entropy of the solutes in finite temperature) is not included in the EDA. In addition, calculating the EDA necessitates the use of the same geometry for the complex and its components, i.e. the protein binding site is assumed to be pre-formed. This is however not important when comparing between multiple ions binding to the same protein, since the free protein (or binding site) always has the same structure.

2.2 Computational methods

2.2.1 Models. Unless otherwise stated, amino acid residues where modelled by their functional groups: acetate for Asp and Glu, acetamide for Asn, and ethylamine for Lys. Backbone carbonyls were modelled as H₂C=O. All optimisations were carried out in implicit solvent model (SMD¹¹), with ethanol (ε = 24.5) as a solvent to model the protein environment.
2.2.1.1 Calmodulin. The PDB structure 1CLL¹⁴ was used to build the model. Binding site 1 was modelled with the side chains of residues Asp²⁰, Asp²², Asp²⁴ and Glu³¹, the backbone carbonyl of Thr²⁶, and one water molecule (36 atoms). Binding site 2 was modelled with the side chains of residues Asp⁵⁶, Asp⁵⁸, Asn⁶⁰ and Glu⁶⁷, the backbone carbonyl of Thr⁶², and one water molecule (38 atoms).
2.2.1.2 Protein kinase A. The structure of PKA with two Ba²⁺ ions (PDB code 4IAZ¹⁵) was used as a starting structure for optimisations. Preliminary calculations showed that starting the optimisations with a structure where PKA binds to Sr²⁺ did not modify the results. The two cations in the binding site were modelled with the backbone of Asn¹⁷¹ (modelled as acetamide), the side chain of Asp¹⁸⁴, ADP modelled as diphosphoricacid, monomethylester with −3 charge, the side chain of pSer⁶²¹ modelled as methylphosphate with −3 charge and six water molecules. Residue Lys⁷² and four additional water molecules were included for solvation of the negative charges. There were 81 atoms in the structure.
2.2.1.3 DNA polymerase ι. The non-truncated structure of DNA polymerase ι (residues 1–455) with a short DNA sequence, a DNA template and two Mn²⁺ with PDB code 5KT7¹⁶ was used. The side chains of residues Asp³⁴, Asp¹²⁶ and Glu¹²⁷, the backbone carbonyl of Leu³⁵ (all residues in the PDB structure numbering), a dCTP analogue truncated at the phosphates with a methyl, and a hydroxyl oxygen from the DNA primer were included, for a total of 50 atoms.

2.2.2 Geometry optimisation. Calculations were performed with ORCA.^17–20 Atoms with atomic numbers up to 25 (Mn) were modelled with Dunning's cc-pVDZ basis set,^21–24 augmented²⁵ for O atoms. The cc-pVDZ-pp basis set with effective core potentials (ECP)^26–30 was used for the heavier atoms. M06 was used as the DFT functional³¹ with dispersion correction (DFT-D3³²). The same general-purpose meta hybrid functional has been used by us before to study protein–metal systems^8,33 and was hence selected for this study. Of note, in a study of ²²³Ra complexation, the choice of a DFT functional led to only few percent difference in energies, and the calculated geometries were almost identical,³⁴ suggesting that the choice of functional is not critical. All calculations used dense grid (DEFGRID3 in ORCA). Optimisation runs were carried out until the calculated frequencies did not include any imaginary terms to ensure that the structures were at minimum. No scaling of the frequencies was performed.

2.2.3 Binding energy differences. Binding energy differences for the complexes with the ions were calculated using eqn (2). The software, functional and basis sets were the same as above (Section 2.2.2). The experimental values for the hydration energies of the ions, which were used to calculate ΔG^corr_hyd (eqn (3)) were taken from the work by Marcus.³⁵ ΔG^exp_hyd Ra²⁺ in ref. 35 was estimated to be the same as the value for Ba²⁺. However, it is not likely that these two ions will have the same values while in general the hydration energies of alkaline earth metal ions decline with the atomic number. Differences in the hydration energies between Ra²⁺ and Ba²⁺ were estimated as 8.3,³⁶ 9.3,³⁷ 10³⁸ and 12.0³⁴ kcal mol⁻¹. Here, a choice was made to adopt the difference as calculated by Persson et al.,³⁷ who suggested that the hydration energy is a function of the ion to water oxygen distances, since this approach was found to be accurate with other ion seria (lanthanides and actinides¹²). The difference between the hydration energies was used rather than the absolute value from ref. 37 since an estimation of the hydration energies depends on the hydration energy of a proton used as a reference, and different authors (i.e. Persson et al. and Marcus) used difference values. It is noted that this has no bearing on values of ΔΔG^bind which are the subject of interest here as long as the choice for the reference hydration energies is consistent. For clarity, the reference hydration energy values as used in eqn (3) are given in Table 1.

Table 1 Reference hydration energy values as used in this study, see the text for details and references. These values are standard hydration free energies with respect to the ion in the liquid state; to convert to the gaseous 1 ATM standard state 2.1 kcal mol⁻¹ should be added, making each value slightly less negative. All values are in kcal mol⁻¹

Ion	ΔG^exphyd
Ca^2+	−363.5
Mn^2+	−437.4
Sr^2+	−329.8
Y^3+	−824.6
Ba^2+	−298.8
Pb^2+	−340.6
Ra^2+	−289.5

---

Galland and co-workers³⁴ pointed out the importance of spin orbit coupling (SOC) for calculations of binding energies of chelators to Ra²⁺. Indeed, preliminary calculations with a recently described radium binding complex³⁹ have shown that the binding energy of Ra²⁺ to this complex was lowered (i.e. became more favourable) by −10.9 kcal mol⁻¹ when SOC was considered. For the same complex with Pb²⁺, the second heaviest ion studied here, SOC was negligible (−0.2 kcal mol⁻¹). Thus, SOC was included when calculating differences in the binding of Ra²⁺ to other ions in all complexes. A SOC correction, ΔE^SOC was added to Δ_fG(bs·M) in eqn (2) when M was Ra²⁺. This correction was calculated as:

ΔE^SOC = [E(bs·M)^SODFT − E(M)^SODFT] − [E(bs·M)^DFT − E(M)^DFT] (5)

To this end, the energies of the complexes, E(bs·M), and the ion E(M) were calculated with NWCHEM^40,41 twice, once using DFT without SOC and once using spin–orbit DFT (SODFT). The same basis set and DFT functional were used as for the calculation of geometries and binding energies.

2.2.4 Energy decomposition analysis. EDA was performed with XEDA,⁴² using the M06 functional and DFT-D3 as above. The cc-pVDZ-pp basis set is not implemented in XEDA and a correlation consistent, triple-ζ basis set, MCP-TZP^29,43–46 with ECP was used for the EDA calculations. SOC was calculated as above and added a posteriori to the total energy.

3 Results

Given that Ra²⁺ binds to hydroxyapatite in bones and that lanthanides, which are similar to Y³⁺ in many aspects, can bind to Ca²⁺-binding proteins,⁸ the potential bindings of Ra²⁺, its decay product Pb²⁺, and Y³⁺ were estimated for calmodulin (CaM), a prototype calcium-binding protein with the typical calcium binding sites. Thereafter, the binding of the ions was studied to protein kinase A (PKA), an enzyme that has two metal-ion binding sites in its catalytic pocket where the metals are coordinated to amino acids, water and a phosphate. PKA is known to be able to bind Mg²⁺, Ca²⁺, Sr²⁺ and Ba²⁺, while maintaining activity.¹⁵ Finally, the ability of Ra²⁺ and Y³⁺ to bind to an Mn-dependent enzyme, DNA polymerase ι, was also examined.

3.1 Calmodulin

CaM binds Ca²⁺ in four binding sites, each comprising of an EF-hand which is a typical Ca²⁺-binding motif in proteins (Fig. 1). The sites are overall similar, with seven oxygen ligands, but differ in the number of carboxylate oxygens that coordinate to the metal ion: five in sites 1 and 4, four in sites 2 and 3. The different coordinations can lead to different binding energies and preferences for coordination of ions besides Ca²⁺. For this reason, sites 1 (prototype of a binding site with five coordinating carboxylate atoms) and 2 (prototype of a binding site with four coordinating carboxylate atoms) were studied here.

Fig. 1 The structure of calmodulin (PDB code: 1CLL). The location of the four Ca²⁺ ions is indicated as green spheres.

The Gibbs energy differences with respect to Ca²⁺, for binding of the ions to the two binding sites of CaM, are shown in Table 2. Sr²⁺, an alkali earth metal and an analogue of Ca²⁺ is known to be able to bind CaM when present in high enough concentrations⁴⁷ and was included in this study as a control. Indeed, the calculations show that binding of the Sr²⁺ ions to calmodulin is disfavoured by 2.4 to 2.9 kcal mol⁻¹ in comparison to Ca²⁺, suggesting that the concentration of Sr²⁺ should be about 100 times larger than that of Ca²⁺ in order to bind the protein. In contrast, both Pb²⁺ and Y³⁺ strongly interact with CaM, with the first preferring site 2 and the second site 1. Finally, with an energy difference of over 6 kcal mol⁻¹ disfavouring its binding, it cannot be expected that Ra²⁺ will replace Ca²⁺ in CaM or other EF-hand proteins.

Table 2 Gibbs energies for binding of ions to CaM binding sites 1 and 2 instead of Ca²⁺

Ion	ΔΔG^bind	ΔΔG^bind
	Site 1	Site 2
Sr^2+	2.4	2.9
Pb^2+	−6.7	−9.9
Y^3+	−28.5	−20.6
Ra^2+	6.0	9.6

---

To better understand the reasons for the preferred binding of Y³⁺ and Pb²⁺ to CaM, and the inability of Ra²⁺ to replace Ca²⁺, the interactions of the ions with the binding site were subject to energy decomposition analysis (EDA) calculations using the PCM-EDA approach.¹³ The EDA results (Table 3) reveal that pure electrostatic interactions are weaker for Pb²⁺ when compared with Ca²⁺, but polarisation for Pb²⁺ is stronger and there is a lower cost of desolvation for the binding of this ion. Y³⁺ binds better due to increased electrostatics and polarisation and in spite of the higher cost of desolvating the ion. Sr²⁺ behaves as Ca²⁺ in general. Finally, Ra²⁺ behaves like a hard ion, with a less pronounced contribution from polarisation relative to electrostatics and otherwise weaker interactions than all other ions (except for dispersion and correlation that do not constitute important contributions to ion binding). Of note, the total interaction energies as calculated by EDA are different than those used to obtain the values presented in Table 2. This is due to the fact that the binding energies calculated in EDA do not include rotational and vibrational entropy, and corrections to the enthalpy. Basis set differences account for a smaller share of the difference.

Table 3 Energy decomposition analysis of the ions binding to CaM. The values are interaction energies in solvent (ΔG^int, in kcal mol⁻¹) and correspond to the binding of an ion to a pre-formed binding site. The differences between the ions do not correspond to Table 2, because of the use of different basis sets and since corrections for the vibrational enthalpy and entropy are not included in the EDA calculations. The interaction energies from XEDA were adjusted taking into account the spin–orbit coupling in the Ra-complexes. The desolvation energies were corrected to account for the difference between the calculated ion solvation values in ethanol and the experimental values in solvent

	Ca	Sr	Pb	Y	Ra
Site 1
ΔG^ele	−929.8	−893.7	−774.5	−1412.3	−825.1
ΔG^exrep	89.7	90.6	102.4	177.0	72.8
ΔG^pol	−120.5	−101.8	−233.3	−340	−77.9
ΔG^corr	−0.5	−6.8	−28.3	−24.4	−12.9
ΔG^disp	−3.5	−4.2	−5.8	−3.6	−5.5
ΔG^desolv	736.2	690.8	683.4	1229.0	679.2
ΔE^soc					−6.4
ΔG^total	−228.4	−225.2	−256.1	−374.3	−175.8
Site 2
ΔG^ele	−786.2	−754.9	−686.1	−1175.5	−705.4
ΔG^exrep	91.1	91.2	99.0	176.6	67.1
ΔG^pol	−123.2	−104.2	−205.5	−352.8	−68.5
ΔG^corr	0.8	−4.9	−31.6	−23	−9.6
ΔG^disp	−3.5	−4.2	−5.3	−3.8	−5.5
ΔG^desolv	609.4	563.3	577.0	1014.3	570.5
ΔE^soc					−5.8
ΔG^total	−211.5	−213.7	−252.6	−364.2	−157.2

---

3.2 Protein kinase A

PKA was crystallised with Mg²⁺, Ca²⁺, Sr²⁺ and Ba²⁺. The structures and metal binding sites are overall highly similar, with small differences due to the different size of the ions (Fig. 2). The coordinating moieties for the two ions included the amide oxygen of Asn¹⁷¹, one carboxylate oxygen of Asp¹⁸⁴, phosphate groups from ADP, the substrate phosphate oxygens, and six water oxygens. The binding energies for the ions, relative to Ca²⁺ are shown in Table 4 (values are for a pair of ions in each case). The results reveal that Sr²⁺ binds somewhat worse than Ca²⁺, with Ba²⁺ binding even less, Pb²⁺ binds better and will likely impair the protein, and Y³⁺ even better than Pb²⁺. Surprisingly, Ra²⁺ binds only slightly weaker than Ca²⁺ and better than Sr²⁺ and Ba²⁺. This is due to SOC effects, that amount to −17.5 kcal mol⁻¹. However, the high physiological concentration of Ca²⁺, about 1 mM in the blood, makes it unlikely that ²²³Ra will bind PKA in appreciable amounts.

Fig. 2 The crystal structures of PKA with (A) Mg²⁺, (B) Ca²⁺, (C) Sr²⁺ and (D) Ba²⁺ (PDB codes: 4IAF, 4IAI, 4IAL and 4IAZ, respectively). The locations of the ions are indicated as green spheres.

Table 4 Gibbs energies for binding of ions to PKA instead of Ca²⁺

Ion	ΔΔG^bind
Sr^2+	3.4
Ba^2+	10.8
Pb^2+	−7.3
Y^3+	−43.0
Ra^2+	1.1

---

As it is clear from the experiment that PKA can bind Ba²⁺, the values in Table 4 indicate that it can bind all ions. Thus, it is interesting to examine the structures of the optimised complexes. Overall, the ion binding sites are quite similar (Fig. 3). There are some differences when compared to the X-ray structures, that are due to the optimisation. It is likely that in solution the binding site of the ions can adopt multiple conformations that cannot all be adequately sampled here, as also shown in the two structures of the same protein with Sr²⁺. In the optimised complexes, the ion–ligand distances increase within the alkali earth series, as expected (Table 5). The coordination number (CN) is smaller for Ca²⁺ in comparison with the larger alkali-earth ions. Interestingly, while Sr²⁺ and Ba²⁺ bind to the second site in PKA with a higher CN, Ra²⁺ on the contrary binds to the first site with higher CN; this reveals some differences in the binding. Pb²⁺ binds with higher CN to the first site, in similarity with Ra²⁺. Y³⁺ binds to PKA as Ca²⁺ but with smaller ion–ligand distances.

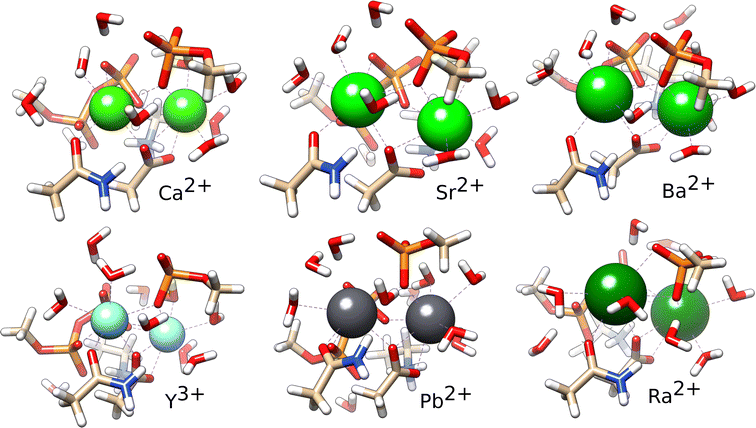Fig. 3 Optimised complexes of the ion binding site of PKA with Ca²⁺, Sr²⁺, Ba²⁺, Y³⁺, Pb²⁺ and Ra²⁺.

Table 5 Coordination numbers (CN) and average ion–ligand distances (d, in Å) for ions in the PKA binding site

Ion	Site	Optimised		X-ray
		CN	d	CN	d
a There are two structures with Sr^2+, 4IAK (left) and 4IAY (right).
Ca^2+	1	8	2.46	8	2.44
	2	8	2.48	7	2.40
Sr^2+ ^a	1	8	2.60	9/8	2.60/2.66
	2	9	2.67	7/6	2.54/2.61
Ba^2+	1	8	2.79	8	2.75
	2	9	2.84	6	2.67
Pb^2+	1	8	2.70
	2	7	2.67
Y^3+	1	8	2.38
	2	8	2.40
Ra^2+	1	9	2.94
	2	8	2.89

---

3.3 DNA polymerase ι

DNA polymerase ι achieves high activity with Mn²⁺ as cofactor. The structure of the protein reveals that it binds two Mn²⁺ ions through one backbone oxygen, five carboxylate oxygens, three phosphate groups, and one oxygen from the primer that is added to the substrate, yielding a 5 + 6 coordinated binding site (Fig. 4). The results of the calculation of the binding energies show that the protein binds somewhat better to Y³⁺ than Mn²⁺ and much less to Pb²⁺ and Ra²⁺. In practice it cannot be expected that the protein will bind Ra²⁺ at all (Table 6).

Fig. 4 The ion binding site of DNA polymerase ι. Mn²⁺ ions are shown as violet spheres.

Table 6 Gibbs energies for binding of ions to DNA polymerase ι instead of Mn²⁺

Ion	ΔΔG^bind
Pb^2+	17.6
Y^3+	−16.0
Ra^2+	53.0

---

4 Discussion

4.1 Radium does not significantly replace other ions in proteins

The results show that Ra²⁺ binds to proteins less than Ca²⁺ and Mn²⁺. It was further shown to be a hard ion, displaying low polarisability while at the same time its electrostatic interactions are weaker than those of Ca²⁺. Interestingly, analysing binding to water as a ligand, Matsuda and Mori have shown a similar trend with contributions from electrostatics and polarisation steadily declining along the alkaline-earth series.⁴⁸ Toxicities of ²²³Ra therapy can thus be attributed to direct effects of its decay outside of the tumour tissue. It is not likely that it is transported by proteins or affects protein activity.

4.2 Pb²⁺ binds to proteins instead of Ca²⁺

Unlike ²²³Ra, its decay product ²⁰⁷Pb can bind to proteins as a doubly charged ion and shows affinity to typical (CaM) Ca²⁺-bind proteins and to PKA that is higher than the affinities of these proteins to Ca²⁺. Its binding energy was estimated to be up to ∼10 kcal mol⁻¹ more favourable than that of Ca²⁺. Pb²⁺ is a soft ion, and contribution from polarisation has been high (almost twice that of Ca²⁺) even with hard ligands such as oxygen. On the other hand, Pb²⁺ is also adsorbed to the bone tissue and its release is slow. It remains to be seen if repeated exposure to ²²³Ra treatment poses a risk of Pb²⁺ poisoning. However, this study points out that accidental overdose of ²²³Ra Cl₂ can mitigate not only too much radiation (acute toxicity) but also lead exposure (chronic toxicity).

4.3 Yttrium binds strongly to proteins

Despite its strong hydration Y³⁺ has shown significant binding to proteins, with the ability to replace Ca²⁺ and potentially also Mn²⁺. The short lifetime of ⁹⁰Y is beneficial in this respect, since it is mostly trapped in the liver. Toxicities associated with ⁹⁰Y therapy were indicated to be somewhat higher with resin compared to glass microspheres,⁶ which might have to do with the binding of the ions at the surface of such spheres from which they can presumably more easily escape and thereafter bind to proteins. Considering the accuracy of the calculations, it should be noted that Y³⁺ is the only ion that differs in charge from the others. Estimations of the hydration free energies in this work were taken from the seminal work of Marcus.³⁵ Such estimations depend on the value that is used for calculating the hydration energy of a proton (ΔG_hyd(H⁺) = −252.4 kcal mol⁻¹). As Marcus noted, other estimations were more negative (by up to 11.2 kcal mol⁻¹). Comparing between ions, the choice of this value will only affect ΔΔG^bind values for Y³⁺, reducing its Gibbs hydration energy by the same amount. Had the lowest estimation of ΔG_hyd(H⁺) been used, the results with respect to binding of Y³⁺ would have been shifted up. Qualitatively, this would have meant that Y³⁺ could still have replaced Ca²⁺ and Mn²⁺ in proteins.

4.4 Targeted delivery of radium

While ²²³Ra is used for bone metastases it is difficult to see how it can be used to target other organs than the bone. For targeted delivery, there is a need to design chelators that will bind to ²²³Ra. It has been difficult to develop coordination complexes with high affinity to ²²³Ra that must not be replaced by physiological ions such as Ca²⁺. The radioactivity and scarcity of Ra on the one hand, and its lower ability to bind many ligands on the other have hindered the development of Ra-chelators, with the first crystallographic structure of a radium complex described only recently.³⁹ The neutral crown ether cage that binds the ion in such host–guest complexes (Fig. 5) was shown to be able to bind ²²³Ra and Ba²⁺ with preferences that depend on the co-anions.³⁹ For such complexes that are injected or ingested in the body, it is important to verify if other ions might displace ²²³Ra. Examination of the affinities of the ions Ba²⁺, Pb²⁺, Y³⁺ and Ca²⁺ to this crown ether complex leads to the conclusion that this particular host–guest complex binds Ra²⁺ better than those other ions (Table 7). Nevertheless, it is important to analyse the risks to release of decay products in the body. The high energy release with the first alpha-particle upon decay from ²²³Ra to ²¹⁹Rn will likely break down the coordination compound and release gaseous, radioactive ²¹⁹Rn with a half-life of ∼4 s. The radon atom will diffuse in the nearby tissue before decaying further. Thus, the risks associated with radon diffusion also need to be taken into account when considering targeted delivery of radium.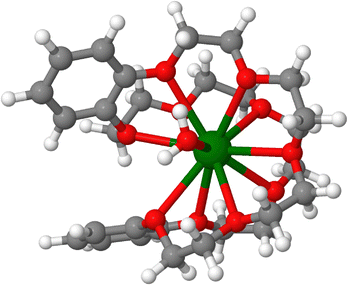

Fig. 5 A crown ether complex bound to Ra²⁺. Optimised structure, with the coordinates from ref. 39.

Table 7 Gibbs energies for binding of ions to the crown ether complex shown in Fig. 5 in comparison with Ra²⁺. The calculations were carried out by use of a similar approach as for the protein complexes (transfer from solution to the complex). No counter ions were included, assuming that such anions will dissolve in the body

Ion	ΔΔG^bind
Ca^2+	18.5
Pb^2+	7.6
Ba^2+	6.9
Y^3+	28.1

---

Data availability

All calculations were performed with open source or academic licence software as described in the main text. Optimised structures of metal complexes are available at https://dx.doi.org/10.6084/m9.figshare.27613200.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computations (except EDA) were enabled by resources provided by LUNARC, The Centre for Scientific and Technical Computing at Lund University, and the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement no. 2022-06725. EDA calculations were run on the Xiamen Atomistic Computing Suite (XACS).

Notes and references

1. J. H. Sequeira, BMJ, 1915, 1, 365–366.
2. A. Dronsfield and P. Ellis, Educ. Chem., 2011, 48, 56.
3. P. Borges de Souza and C. J. McCabe, Endocr.-Relat. Cancer, 2021, 28, T121–T124.
4. C. Parker, S. Nilsson, D. Heinrich, S. Helle, J. OSullivan, S. FossÅ, A. Chodacki, P. Wiechno, J. Logue, M. Seke, A. Widmark, D. Johannessen, P. Hoskin, D. Bottomley, N. James, A. Solberg, I. Syndikus, J. Kliment, S. Wedel, S. Boehmer, M. DallOglio, L. Franzén, R. Coleman, N. Vogelzang, C. OBryan-Tear, K. Staudacher, J. Garcia-Vargas, M. Shan, Ø. Bruland and O. Sartor, N. Engl. J. Med., 2013, 369, 213–223.
5. C. C. Parker, R. E. Coleman, O. Sartor, N. J. Vogelzang, D. Bottomley, D. Heinrich, S. I. Helle, J. M. OSullivan, S. D. FossÅ, A. Chodacki, P. Wiechno, J. Logue, M. Seke, A. Widmark, D. C. Johannessen, P. Hoskin, N. D. James, A. Solberg, I. Syndikus, J. Kliment, S. Wedel, S. Boehmer, M. DallOglio, L. Franzén, Ø. S. Bruland, O. Petrenciuc, K. Staudacher, R. Li and S. Nilsson, Eur. Urol., 2018, 73, 427–435.
6. C. S. Higano, D. J. George, N. D. Shore, O. Sartor, K. Miller, P. S. Conti, C. N. Sternberg, F. Saad, J. P. Sade, J. Bellmunt, M. R. Smith, K. Chandrawansa, P. Sandström, F. Verholen and B. Tombal, eClinicalMedicine, 2023, 60, 101993.
7. J. R. Kallini, A. Gabr, K. Thorlund, C. Balijepalli, D. Ayres, S. Kanters, S. Ebrahim, E. Mills, R. J. Lewandowski and R. Salem, Cardiovasc. Intervent. Rad., 2017, 40, 1033–1043.
8. R. Friedman, J. Phys. Chem. B, 2021, 125, 2251–2257.
9. R. Friedman, Dalton Trans., 2014, 43, 2878–2887.
10. L. Moretto, M. Ušaj, O. Matusovsky, D. E. Rassier, R. Friedman and A. Månsson, Nat. Commun., 2022, 13, 4575.
11. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
12. R. Friedman, ChemPhysChem, 2022, 24, e202200516.
13. P. Su, H. Liu and W. Wu, J. Chem. Phys., 2012, 137, 034111.
14. R. Chattopadhyaya, W. E. Meador, A. R. Means and F. A. Quiocho, J. Mol. Biol., 1992, 228, 1177–1192.
15. O. Gerlits, M. J. Waltman, S. Taylor, P. Langan and A. Kovalevsky, Biochemistry, 2013, 52, 3721–3727.
16. J.-Y. Choi, A. Patra, M. Yeom, Y.-S. Lee, Q. Zhang, M. Egli and F. P. Guengerich, J. Biol. Chem., 2016, 291, 21063–21073.
17. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2e, 73–78.
18. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
19. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
20. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e70019.
21. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
22. J. Koput and K. A. Peterson, J. Phys. Chem. A, 2002, 106, 9595–9599.
23. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
24. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2006, 125, 074110.
25. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
26. B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569.
27. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112.
28. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
29. Y. Osanai, E. Soejima, T. Noro, H. Mori, M. S. Mon, M. Klobukowski and E. Miyoshi, Chem. Phys. Lett., 2008, 463, 230–234.
30. J. G. Hill and K. A. Peterson, J. Chem. Phys., 2017, 147, 244106.
31. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. E. Ahlstrand, D. Spångberg, K. Hermansson and R. Friedman, Int. J. Quantum Chem., 2013, 113, 2554–2562.
34. H. Mohaman, S. Happel, G. Montavon and N. Galland, New J. Chem., 2023, 47, 12914–12925.
35. Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999.
36. R. M. Noyes, J. Am. Chem. Soc., 1962, 84, 513–522.
37. I. Persson, M. Sandström and H. Yokoyama, Z. Naturforsch., A: Phys. Sci., 1995, 50, 21–37.
38. R. R. Pappalardo, D. Z. Caralampio, J. M. Martínez and E. Sánchez Marcos, Inorg. Chem., 2021, 60, 13578–13587.
39. F. D. White, N. A. Thiele, M. E. Simms and S. K. Cary, Nat. Chem., 2023, 16, 168–172.
40. M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. V. Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
41. E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102.
42. Z. Tang, Y. Song, S. Zhang, W. Wang, Y. Xu, D. Wu, W. Wu and P. Su, J. Comput. Chem., 2021, 42, 2341–2351.
43. Y. Sakai, E. Miyoshi, M. Klobukowski and S. Huzinaga, J. Comput. Chem., 1987, 8, 226–255.
44. Y. Sakai, E. Miyoshi, M. Klobukowski and S. Huzinaga, J. Comput. Chem., 1987, 8, 256–264.
45. Y. Sakai, E. Miyoshi, M. Klobukowski and S. Huzinaga, J. Chem. Phys., 1997, 106, 8084–8092.
46. H. Anjima, S. Tsukamoto, H. Mori, M. Mine, M. Klobukowski and E. Miyoshi, J. Comput. Chem., 2007, 28, 2424–2430.
47. P. Kursula, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 70, 24–30.
48. A. Matsuda and H. Mori, J. Comput. Chem., Jpn., 2014, 13, 105–113.

---