Non-adiabatic photodissociation dynamics of vinyl iodide from nσ* and nπ* transitions

Abstract

The photodissociation dynamics of vinyl iodide upon photoexcitation at 199.2 and 200 nm are investigated in a joint theoretical and experimental study. The gas-phase absorption spectrum measured by Fourier transform spectroscopy along with the use of synchrotron radiation is reported and a reassignment of the excited electronic states responsible for the absorption at the energy range of interest is proposed. Femtosecond time-resolved velocity map imaging in conjunction with resonance enhanced multiphoton ionization detection of the I(²P_3/2) and I*(²P_1/2) photofragments have been carried out. The experimental results are discussed in view of high-level ab initio calculations including potential energy curves and semiclassical dynamics. Three conical intersections (CIs) governing the dynamics are identified in a search for stationary points using spin–orbit gradients. Based on these results, a complete picture of the photodissociation dynamics of vinyl iodide is obtained. Photoexcitation at 200 nm, associated with a n_I(⊥)σ* transition, leads to a fast dissociation occurring in a repulsive potential energy surface, which is mediated by a CI with a low-lying excited electronic state. This mechanism resembles the typical dissociation of alkyl iodides in the first absorption A-band. In contrast, one-photon excitation at 199.2 nm into a well-defined vibronic structure of the absorption spectrum is assigned to a n_I(‖)π* transition. The subsequent dissociation dynamics from that state features an ultrafast electronic predissociation with sub-200 femtosecond reaction time. State-switching at a first CI with a low-lying electronic state governing the mechanism involves states of completely different character, occurring in less than 20 fs. This remarkably fast process takes place through an initial stretch of the C=C bond, followed by a C–I elongation with subsequent vibrational activity in the C=C stretch mode.

---

1 Introduction

Some of the most fundamental processes in nature, such as vision or photosynthesis, are induced by absorption of light. The evolution of the wave packet created in an excited electronic state by photon absorption can lead to a variety of outcomes from fragmentation to isomerization or internal relaxation back to the ground state. Chemical dynamics are typically described within the Born–Oppenheimer approximation, i.e. assuming a complete separation of the nuclear and electronic degrees of freedom. The photoinduced dynamics, and the eventual outcome, are however often governed by crossings between electronic states where strong couplings between electronic and nuclear motions arise and allow the wave packet to switch from one surface to another. Such dynamics and the associated timescales are dependent on the structure of the molecule. The presence of electrons in π orbitals, e.g. double bonds or aromatic compounds, strongly modifies the electronic excited states and hence the photodynamics taking place. Ultrafast internal conversion between ππ* and nπ* electronic states has been largely reported as a first step following photoabsorption in organic chromophores and nucleobases. For instance, this internal conversion was reported to occur in 60 fs following photoexcitation of thymine.¹ A similar timescale was obtained for this mechanism in 2-nitronaphthalene.² In contrast, the decay through a crossing between ππ* and nσ* is often associated with longer timescales since such coupling requires a double excitation. For instance, fragmentation through such crossing is characterized by a 600 fs lifetime in iodobenzene^3,4 and a 900 fs in iodonaphthalene.^5,6 In the present work, we report an ultrafast predissociation in vinyl iodide taking place through a coupling between n_‖π* and n_⊥π* thus requiring a modification of both the excited electron and the hole, leading however to dissociation in ∼160 fs.

Vinyl iodide, CH₂=CHI, constitutes the simplest alkyl iodide including in the molecular structure a C=C double bond. Alkyl iodides can be considered as prototypes for molecular photodynamics involving a non-negligible spin–orbit coupling. The absorption spectra of these molecules is in general characterized by a first structureless continuum band in the UV, named A-band, while a second absorption band, the B-band, lying around 200 nm, is characterized by the presence of a main sharp peak. The A-band is assigned to a σ* ← np_(I) transition, where several completely repulsive optically-active excited states lead to a fast dissociation. A conical intersection (CI) controls the quantum yield between the two open channels producing iodine atoms in their ground and excited spin–orbit states, I(²P_3/2) and I(²P_1/2), respectively – henceforth I and I*. In contrast, the second absorption band is attributed to a transition into the 6s Rydberg state from the np_(I) orbital. This Rydberg state presents a pronounced well and typical electronic predissociation taking place in the picosecond scale leads predominately to dissociation into I* in correlation with the co-fragment in its ground electronic state. The presence of a C=C double bond in vinyl iodide, and hence of π and π* valence orbitals, is expected to strongly modify the photodissociation dynamics following excitation at around 200 nm.

The photochemistry of ethylene, CH₂=CH₂, specifically in the VUV region, has attracted considerable interest as a model for ab initio calculations of several-atom systems and for its dissociation mechanisms.^7–18 Two main dissociation channels, associated with either H-atom elimination or H₂ formation, have been investigated. Halogen-atom substitution in ethylene has also shown to considerably modify the electronic structure and subsequent photodissociation dynamics. Halogen-substituted ethylenes, CH₂=CHX (X = F, Cl, Br or I), can undergo photodissociation pathways via simple C–H and C–X bond cleavage, molecular eliminations (HX, H₂), and three-body dissociation. The molecular dissociation/atomic dissociation ratio, in terms of HX/X, varies depending on the halogen atom.¹⁹ For CH₂=CHF, molecular dissociation is the unique pathway, whereas for CH₂=CHI, atomic photodissociation is the major route.^20,21 In the case of CH₂=CHBr and CH₂=CHCl, both channels are produced.

The electronic structure and thus the absorption spectrum of halogen-subtituted ethylenes is considerably dependent on the halogen atom. Based on electron energy loss spectroscopy and photoelectron spectroscopy,²² the valence molecular orbitals were shown to be reversed for vinyl iodide. In contrast to the π_CC character of the HOMO orbital for others vinyl halides, in CH₂=CHI it is assigned to the np_(I) lone-pair orbital. Two effects may be responsible for this. First, the presence of a lone pair orbital from the halogen atom along with the π_CC orbital results in a resonance interaction leading to the destabilization of the π_CC bonding orbital. Second, an electrostatic inductive effect, due to the dipole moment of the C–X bond stabilizes the π_CC orbital. While the magnitude of the second is expected to be similar for all the former leads to a considerable stabilization of the π_CC orbital and a destabilization of the np_(I) orbital in vinyl iodide.

Four bands up to 200 nm (∼6 eV) are observed in the reported gas-phase absorption spectrum^22,23 of vinyl iodide, centered around 4.9, 5.7, 6.06 and 6.23 eV and assigned to transitions σ* ← n_I(⊥), , σ* ← n_I(‖) and to a transition into the 6s Rydberg state, respectively.

The photodissociation dynamics have been scarcely investigated.^19–21,24 Cao et al.²⁴ investigated the photodissociation following excitation in the first absorption band, at 248 nm, using photofragment translational spectroscopy. The results, showing dissociation into two channels, i.e., CH₂=CH˙ + I* and CH₂=CH˙ + I, are consistent with a fast dissociation mechanism in a repulsive potential energy surface, similar to the photodissociation of other alkyl iodides in the A-band. More recently, Zou et al.¹⁹ reported a detailed and comprehensive study using three different techniques: time-resolved Fourier transform emission spectroscopy, multiple-pass laser absorption spectroscopy and ion velocity map imaging. Quantum yields were determined at different excitation wavelengths along with average translational energies and anisotropy parameters. The experimental results were complemented by calculations of ground-state potential energy surfaces and the discussion focused on understanding the halogen atom dependence of photodissociation mechanisms in vinyl halides.

In the present work, we employ femtosecond ion velocity map imaging in combination with resonance enhanced multiphoton ionization (REMPI) for the detection of I and I* photofragments in order to investigate the photodissociation dynamics upon excitation at two close wavelengths, i.e. 199.2 and 200 nm. The experimental results including translational energy distributions and angular distributions at asymptotic time delays as well as the iodine transients, and hence the reaction times determined for the C–I bond cleavage, are complemented by high-level ab initio and semiclassical dynamics calculations. In addition, the gas-phase high-resolution absorption spectrum of vinyl iodide measured using Fourier transform spectroscopy (FTS) is reported. A reassignment of the first bands is proposed based on the experimental and theoretical results presented.

2 Methodology

2.1 Experimental methodology

2.1.1 VUV Fourier transform spectrometer. The Fourier transform spectrometer (FTS),²⁵ one of the permanent end-stations of the VUV beamline DESIRS^26,27 of the synchrotron SOLEIL facility, was employed to measure the high-resolution UV-VUV absorption spectrum of gas-phase vinyl iodide. The detailed description of the beamline and the VUV FTS instrument can be found in ref. 27 and 28 and only a brief description is given here. A large spectral window from 4 to 30 eV can be covered with a minimum linewidth of 0.08 cm⁻¹ and a spectral resolution of ΔE/E = 7%. A two-step procedure is followed. A first absorption measurement covering the full VUV spectral range is completed using a windowless cell. A reservoir filled with the liquid sample is connected to the main sample environmental/vacuum chamber. After a series of freeze pump–thaw purification steps of the sample, the sample in the gas phase controlled using a needle valve is allowed to flow through a 10 cm cylindrical windowless cell with two rectangular tubes at both ends. The synchrotron beam is going through the cell and is ultimately recorded using the FTS instrument. In order to calibrate the column density, another measurement at a moderate spectral resolution is performed inside a 9 cm long MgF₂ windowed cell. This time, only a few spectral windows are recorded, providing absolute absorption cross sections. The windowless spectrum is scaled upon these reference points as described in ref. 27. As the VUV FTS is extremely sensitive to external perturbations, a statistical study gave an estimated uncertainty for the absolute cross section of ±10%. Concerning the energy scale, no further calibration is required for this experiment since the accuracy is intrinsically referred to the indexation of a He–Ne stabilized laser, leading already to a relative error in the range of 10⁻⁶. The spectral resolution was set to 4.3 cm⁻¹, which is more than enough to properly resolve the absorption spectrum of vinyl iodide.

2.1.2 Femtosecond velocity map imaging setup. The femtosecond laser system consists of a chirped pulse amplified Ti:sapphire laser, delivering 3.2 mJ pulses of 50 fs duration at 1 kHz repetition rate, and with a central wavelength set at 800 nm. About 1 mJ of the total was used to pump a two-stage femtosecond automated optical parametric amplifier of white light continuum (TOPAS Prime Spectra Physics). The output signal beam was two-step frequency quadrupled in a second stage by means of two β-barium borate (BBO) crystals yielding tunable pulses centered at 304.5–306 nm with energies typically around 7–9 μJ and with a full width at half maximum (FWHM) bandwidth of ≈1.5 nm. With these pulses, the iodine fragment atoms arising from the photodissociation of vinyl iodide were probed by two different (2 + 1) REMPI schemes: the I(²P_3/2) fragments through the 6p ⁴P_1/2, 6p ⁴D_7/2 and 6p ⁴D_1/2 states, and the I*(²P_1/2) fragments through the corresponding 6p ⁴D_1/2 and 6p ⁴P_3/2 states.²⁹ Given the bandwidth of the probe laser (FWHM = 1.5 nm) by appropriately selecting the wavelength of the probe laser, it was possible to detect the two spin–orbit states of the iodine atoms: both I(²P_3/2) and I*(²P_1/2) fragments simultaneously at 304.5 nm, or exclusively the excited spin–orbit I*(²P_1/2) fragment at 306 nm.

Another ∼1 mJ of the main 800 nm beam was frequency quadrupled in a home-made setup consisting of a tripling unit followed by a sum-frequency mixing unit between the third harmonic and the fundamental.³⁰ Radiation around 200 nm was produced for one-photon excitation of vinyl iodide with a FWHM bandwidth of ≈0.3 nm, and typical pulse energies of ∼1 μJ with some tunability around this value by fine adjustments of the quadrupling crystal. The spectrum of the 199–200 nm pulses is recorded using a spectrometer (Spectral Products SM440), which allows us to determine the exact pump wavelength and an approximate full-width-at-half-maximum (FWHM) of around 0.3 nm, ensuring a complete separation of the region pumped by each selected wavelength. The polarization of both the pump and probe lasers was set horizontal by means of half-wave plates and the propagation conditions were controlled through adjustable telescopes. They were propagated co-linearly and focused with a 25 cm focal length lens into a vacuum chamber where they interacted with a pulsed molecular beam. The pump–probe delay was controlled by a motorized delay stage placed at the probe laser arm that allows time steps as low as 1 fs. The instrument's temporal response time, considered as the temporal cross correlation of the pump and probe pulses, was measured through multiphoton ionization (MPI) of Xe, obtaining typical values of 160 fs.

The molecular beam was generated by a supersonic expansion of vinyl iodide (Fluorochem Limited, 85%) seeded in helium gas at a backing pressure of 1 bar, through a 0.5 mm diameter nozzle and a 1 kHz homemade cantilever piezoelectric pulsed valve. A 1 mm diameter skimmer separates the expansion and ionization chambers, where the molecular beam interacts with the laser pulses. The ionized iodine fragments are extracted by a set of electrostatic lenses working in velocity mapping configuration with repeller voltages of 5200 V and optimum conditions found for V_extractor/V_repeller = 0.76 through a field-free time-of-flight (TOF) region (50 cm), until they reach a Chevron configuration dual microchannel plate (MCP), with gated front MCP to achieve mass selection, and coupled to a phosphor screen (P47). The images are recorded with a Peltier-cooled 12 bit charge-coupled device camera (LaVision Imager QE) and later Abel inverted using the polar basis set expansion (pBasex) method.³¹ A Levenberg–Marquardt^32,33 squared residuals minimization algorithm was used for fitting the data. The pixel to energy calibration was done using the known kinetic energy release (KER) of the CH₃ (ν = 0) + I*(²P_1/2) and CH₃ (ν₁ = 1) + I*(²P_1/2) channels from 201.19 nm photodissociation of CH₃I.³⁴

2.2 Theoretical methods

To characterize the electronic structure of vinyl iodide, several electronic states were calculated using multireference methods based on state-average CASSCF wave functions. Relativistic effects were taken into account by using a second-order Douglas–Kroll Hamiltonian^35,36 formalism in combination with an ANO-RCC^37,38 basis set contracted to a double zeta polarized (ANO-RCC-VDZP). The two-electron integrals were evaluated using the density fitting approximation where the selected auxiliary basis set was constructed using the uncontracted ANO-RCC basis. The active space used in the CASSCF calculations is composed of eight electrons in seven orbitals. Specifically, the set of orbitals considered in this study contains two lone pairs in the iodine atom, n_I(‖) and n_I(⊥), the bonding and antibonding, σ_(C–I) and π_(C–C), as well as the Rydberg s orbital. Two sets of orbitals were obtained using the state-average technique, the first one considering nineteen singlets and the second one averaging over eighteen triplets. The energy was corrected by perturbation theory in its extended multistate CASPT2 (XMS-CASPT2) formalism³⁹ with an imaginary shift of 0.3 a.u. These calculations were performed using the brilliantly advanced general electronic-structure library (BAGEL) code,⁴⁰ including analytical gradients^41–43 when required. Spin–orbit coupling was taken into account using the atomic mean-field integral (AMFI) approximation,⁴⁴ resulting in a total of 73 electronic states. This calculation was performed extracting the CASSCF wave function (CI vector and orbitals) from the BAGEL code and importing it to the OpenMolcas code,⁴⁵ where the spin–orbit coupling was evaluated using a perturbation modified CASSCF approximation. The calculated states were selected to describe the seven first spin–orbit dissociation levels: I + C₂H₃, I* + C₂H₃, I + C₂H₃* (valence), I* + C₂H₃*, I + C₂H₃* (Rydberg), and I* + C₂H₃* (Rydberg), together with the ion-pair I⁻ + C₂H₃⁺. To estimate the reliability of the method all curves were compared with the equivalent ones calculated only with OpenMolcas.⁴⁵ Potential energy curves were calculated by varying the C–I distance between 2 and 7.

In addition, stationary points were optimized following the procedure of ref. 46 in order to consider the spin–orbit numerical gradients. A new calculator was created in a modified version of the atomic simulation environment⁴⁷ with the FIRE optimizer.⁴⁸ The spin–orbit gradient was estimated by averaging the gradient of the different spin-free states, similar to the SHARC method,⁴⁹ in a recent implementation.⁵⁰ The variation of the spin–orbit operator with the nuclei coordinates and the non-adiabatic elements were neglected for the gradient calculation. In the case of degeneration points, an effective gradient was obtained by constraining the energy difference between the spin–orbit states. This was done by optimizing at the same time the square of the energy difference between the two electronic states and the lowest electronic state (projecting out the previous contribution).

Finally, in order to estimate the most probable path of the dissociation process, the dynamics of the equilibrium geometry were simulated starting from two different excited electronic states. This was carried out using the surface hopping including arbitrary couplings (SHARC) method,⁵¹ where the Hamiltonian and the spin-free gradients were described using the previous electronic structure protocol.

3 Results

3.1 Experimental results

3.1.1 Absorption spectrum and spectroscopic analysis. The absolute high-resolution VUV absorption spectrum of vinyl iodide measured in the photon energy range of 5.0–10.0 eV using the FTS set-up at the DESIRS beamline (Synchrotron SOLEIL), is shown in Fig. 1(a), while an expanded view of the 5.9–6.8 eV energy range is depicted in Fig. 1(b). The present experimental conditions permit a spectral resolution of 4.3 cm⁻¹, higher than those of previous works by Boschi and Salahub,²³ as well as, by Sze et al.²²

Fig. 1 (a) Gas-phase high-resolution VUV absorption spectrum of vinyl iodide in the 5–10 eV photon energy range. (b) Expanded view of the 5.9–6.8 eV photon energy range. Blue and orange combs indicate the assignments proposed (see the text for more details). Purple and cyan vertical bars show the two excitation energies chosen here for the pump–probe experiments, 199.2 and 200 nm, respectively.

The normal mode description has been assigned according to the information in the vibrational spectrum of Torkington and Thompson⁵² and involves mainly the C=C stretching (ν₄) and C–I stretching (ν₅) modes, with energies in the electronic ground state of 0.198 eV (1593 cm⁻¹) and 0.066 eV (535 cm⁻¹), respectively.

An expanded view of the spectrum in the photon energy region of interest, i.e. 5.9–6.8 eV, is depicted in Fig. 1(b), while the electronic bands and assignments are summarized in Table 1. Sections of other spectral regions as well as the corresponding assignments are included in the ESI.†

Table 1 Experimental vertical excitation energies (VEE) of vinyl iodide (in eV) compared to previous data in the literature from Boschi and Salahub,²³ and Sze et al.²² The last decimal of the energy is given in parenthesis for the less resolved features. The cross-section (in Mb) is indicated along with the assignments proposed in the present work

VEE/eV	Cross-section/Mb	Assignment	VEE/eV^23	VEE/eV^22
5.58(5)	12.3		5.579	5.700
6.03(8)	9.9		6.050	6.060
6.230	30.4			6.232
6.291	50.7		∼6.296	6.279
6.361	27.5			6.342

---

The first absorption band (named A-band) between ∼4.2 and ∼5.2 eV, which is not observed in Fig. 1, is assigned to a transition from the 5p lone orbital of iodine to the C–I orbital, , in agreement with previous works.^22,23

A broad structureless continuum is observed in Fig. 1 starting around 5.4 eV and presenting several maxima. In agreement with previous works, two absorption bands are identified with its origin 0⁰₀ at 5.58(5) eV and 6.03(8) eV. The weak progression of broad features observed in between is attributed to the C=C ν₄ stretching mode. The small peak above 6.03 eV is, in addition, assigned to the C–I ν₅ stretching mode. A detailed vibrational assignment of this region is included in the ESI.† These two electronic bands, located at 5.58(5) eV and 6.03(8) eV, were assigned by Sze et al.²² to the transitions and , respectively. Notice that the parallel (‖) and perpendicular (⊥) subscripts refer to the orientation of the lone pair orbital with respect to the π cloud.

A fourth band presenting well-defined vibronic structure is observed at higher energies with its origin 0⁰₀ at 6.166 eV and a maximum at 6.291 eV. The vibrational activity is assigned to the C=C ν₄ stretching mode, coupled with the C–I ν₅ stretching mode. The vibrational assignments, indicated in Fig. 1(b) are summarized in Table 2. This band was assigned to a 6s ← n_I Rydberg transition,²² similarly to the B-band lying at ∼200 nm in saturated alkyl iodides. However, a close inspection of this feature and its role within the associated band, resembles a more valence-like character rather than Rydberg.

Table 2 Proposed vibrational assignments in the 6.0–6.8 eV absorption region for vinyl iodide compared with the previous work of Boschi and Salahub.²³ Shoulder structure (s), weak feature (w), and broad structure (b) are indicated when necessary (the last decimal of the energy value is given in parenthesis for these less-resolved features). Notice that in ref. 23, authors assign the excitation of three vibrational modes: C=C stretching to ν₁, C–I stretching to ν₂, and C–C–I bending to ν₃. ΔE refers to the one-quanta vibrational energy

Photon energy/eV	Assign.	ΔE(ν4)/eV	ΔE(ν5)/eV	Photon energy^23/eV	Assign.^23
6.166	0^00 (?)	—	—	6.221	0^00
6.230	50^1	—	0.064	6.281	20^1
6.291	40^1/50^2	0.125	0.061	6.338	20^2
6.361	50^1 + 40^1	—	—	—	—
6.41(2)(s)	40^2	0.121	—	—	—
6.468	40^2/50^2	—	0.056	—	—
6.538	40^3	0.126	—	—	—
6.67(5)(w,b)	40^4	0.137	—	—	—

---

Based on the present experimental and theoretical results, a different assignment is proposed here for the second, third and fourth bands, located at 5.58(5), 6.03(8) eV and 6.166 eV, respectively. The second and third bands are attributed to and transitions, respectively. This last state is populated upon excitation at 200 nm (see purple bar in Fig. 1(b)). The fourth band is assigned to a transition, excited in the present experiments at 199.2 nm (see cyan bar in Fig. 1(b)). The ab initio calculations including the vertical energies for the excited electronic states, along with the transition dipole moments as well as the difference in electronic density of each state with respect to the ground state, support this new assignment. In contrast to other alkyl iodides, for vinyl iodide the A-band appears really extended in energy and the 6s Rydberg state is located at a significantly higher energy around 7 eV. In addition, the experimental results reflect a fast sub-200 fs dissociation following excitation at 199.2 nm which, taking into account previous studies of the alkyl iodides dissociation in the B-band, seems extremely fast for a predissociation from the 6s Rydberg state. The arguments supporting the new assignment proposed here will be discussed in more detail in the next sections.

3.1.2 Time-resolved velocity map imaging. Fig. 2 shows the Abel-inverted iodine images from the photodissociation of vinyl iodide at 200 nm (a and b) and at 199.2 nm (c and d), using the (2 + 1) REMPI schemes at 304.5 nm and 306 nm for the detection of I + I*, and exclusively I*, respectively, for an asymptotic pump–probe time delay of 10 ps. The corresponding center-of-mass iodine-atom translational energy distributions (TEDs) obtained from angular integration of the images are depicted in Fig. 3.

Fig. 2 Abel-inverted images of the iodine atoms from the photodissociation of vinyl iodide upon excitation at 200 nm (a) and (b) and at 199.2 nm (c) and (d), detected by (2 + 1) REMPI at 304.5 nm (I + I*) (a) and (c), and at 306 nm (I*) (b) and (d), for a time delay between the pump and the probe pulses of 10 ps (asymptotic conditions). The linear polarization of both lasers is set along the vertical axis of the images. The central part of the image has been hidden as it includes all the residuals from the inversion using pBasex.

Fig. 3 Center-of-mass (CM) iodine atom translational energy distributions obtained by angular integration of the corresponding Abel-inverted images measured upon excitation of vinyl iodide at 200 nm (a) and (b), and at 199.2 nm (c) and (d), for either the exclusive detection of I*(²P_1/2) by (2 + 1) REMPI at 306 nm (b) and (d), or joint detection of I(²P_3/2) and I*(²P_1/2) at 304.5 nm (a) and (c). Experimental values are represented by open black circles. The overall result of the fitting is depicted as a blue solid line while the three or four contributions, i.e. the Boltzmann-type and the Gaussian functions, are represented by blue dashed lines. Vertical red bars represent the maximum kinetic energy for the I*(²P_1/2) (lower energy) and I(²P_3/2) (higher energy) dissociation channels. The y-axis corresponds to the normalized intensity, in arbitrary units.

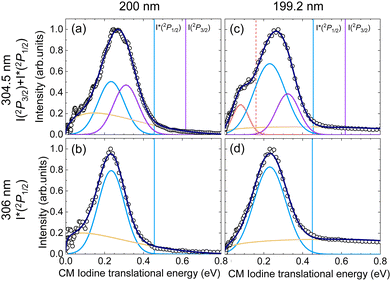
The four ion images shown in Fig. 2 present a well-defined main ring leading to a main structure in the associated TEDs (Fig. 3), despite the fact that two contributions are expected for the detection at 304.5 nm associated with the formation of iodine in the two spin–orbit states. A closer inspection of the images and the TEDS show that the rings and associated peaks are indeed broader at 304.5 nm.

In Fig. 3, the vertical bars indicate the available iodine-atom translational energy, E^I_av, for each dissociation channel, C₂H₃ + I(²P_3/2) and C₂H₃ + I*(²P_1/2), obtained from:

where m_C2H3 and m_C2H3I are the masses of the co-fragment C₂H₃ and of the parent molecule C₂H₃I, respectively, hν is the excitation photon energy, D₀ is the dissociation energy of the C–I bond, 2.684 eV,²⁴E_SO is the spin–orbit splitting of the I(²P) atoms (0.943 eV for I* (ref. 53)), and E^molec_i is the internal energy of the parent molecule, which is considered negligible. The ring and peak observed in Fig. 2(b), (d) and 3(b), (d), respectively, are therefore assigned to the dissociation into C₂H₃ + I*(²P_1/2), while two overlapping contributions lie behind the structure in Fig. 2(a), (c) and 3(a), (c), associated with the dissociation into vinyl radical in its ground state in correlation with I(²P_3/2) and I*(²P_1/2). An inner ring is clearly observed in Fig. 2(c), not appearing in the other images, leading to a shoulder at low translational energies in the corresponding TED in Fig. 3(c). This contribution has been assigned to dissociation into C₂H₃* + I(²P_3/2), where C₂H₃* corresponds to electronically excited vinyl radical. Based on the present results, dissociation into this channel seems to occur exclusively after excitation at 199.2 nm, and specifically yielding I(²P_3/2).

The TEDs obtained in Fig. 3 have been fitted to a number of Gaussian functions to take into account the contribution of each channel, as well as to a Boltzmann-type background broad contribution of the Muckerman form,⁵⁴

I(E_T) = AEⁱ_T(1 − E_T)^j (2)

where E_T is the translational energy and A, i and j are fitting parameters that do not contain physical meaning. This background contribution is observed in all the TEDs depicted in Fig. 3. A typical Boltzmann contribution peaking at low energies is observed at 200 nm (see Fig. 3(a) and (b)), and attributed to a multiphoton ionization process. Similarly, a contribution showing a plateau at higher energies is observed at 199.2 nm (see Fig. 3(c) and (d)) and attributed to some kind of background from the residual gas. Notice that the position of the single Gaussian function employed in Fig. 3(b) and (d) to account for the formation of C₂H₃ + I* is used as a fixed parameter in the fitting when using two or three Gaussian functions in Fig. 3(a) or (c), respectively.

By employing this fitting procedure, a deconvolution of the contribution of the two channels can be achieved in order to extract valuable information, such as the quantum yield for production of I*, defined as . is deduced from the areas of the three Gaussian functions corresponding to the dissociation into C₂H₃ + I, C₂H₃ + I* and C₂H₃* + I, obtained from the fit of the TEDs (see Fig. 3). In order to account for the different REMPI line strengths for I and I* detection, the reported quantum yield for CH₃I at 268 nm⁵³ was used for calibration. The obtained 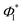values are shown in Table 3 and lie at ∼0.6 at 200 nm, and ∼0.7 at 199.2 nm. The given branching ratios must be considered as approximate considering the deconvolution carried out. Based on the results obtained from different measurements, an error bar of ±0.1 is estimated. Thus, the channel C₂H₃ + I* appears to be slightly more favorable at the two excitation wavelengths. The quantum yield for the production of C₂H₃*, 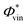, defined as = [C₂H₃*]/([C₂H₃*] + [C₂H₃]), is similarly determined based on the areas of the three Gaussian functions in Fig. 3(c), taking also into account the different REMPI line strength for the detection of I and I*. A of 0.1 is obtained for photoexcitation at 199.2 nm.

Table 3 Iodine and vinyl quantum yield, and , respectively, the fraction of the available energy released into internal energy of the co-fragment (f_int), the anisotropy parameter, β₂ (± 0.05), and the photodissociation reaction time τ_exp, obtained for the two excitation wavelengths (λ_exc = 200 and 199.2 nm). The values are given for either each separated channel (C₂H₃ + I, C₂H₃ + I*, C₂H₃* + I) or for both C₂H₃ + I and C₂H₃ + I* (labeled as I + I*). The indicated values are the average of several experiments

λ exc (nm)			Channel	f int	β 2	τ exp/fs
200	0.6		I + I*		0.83	98 ± 7
			C2H3 + I	0.50
			C2H3 + I*	0.48	0.73	117 ± 14
199.2	0.7	0.1	I + I*		0.03	152 ± 11
			C2H3 + I	0.48
			C2H3 + I*	0.49	−0.14	168 ± 6
			C2H3* + I	0.50	−0.64

---

As shown in Fig. 3, a significant shift between the maximum available iodine-fragment translational energy (E^I_av) and the corresponding measured maximum translational energy, i.e. the maximum of the corresponding Gaussian function, is observed in all cases, reflecting a significant amount of internal (ro-vibrational) energy of the molecular co-fragment. Besides, the broadness of the rings in the images (see Fig. 2) reflects a broad distribution of excited ro-vibrational states of the C₂H₃ co-fragments produced in the dissociation. The most probable fraction of the total available energy released into internal energy of the co-fragment, f_int, is defined as:

where E^max_T denotes the total translational energy at the maximum intensity of the associated Gaussian function. The f_int values, summarized in Table 3, are similar for three channels and at both excitation wavelengths, showing that about half of the available energy is partitioned into translational energy of the fragments, while the other half is partitioned into internal modes. The soft radical impulsive model proposed by Wilson and co-workers⁵⁵ can be easily used to estimate f_int values. Although this model often overestimates the energy partitioning into internal modes, a value of f_int ∼ 0.51 is obtained for the C–I bond cleavage from the photodissociation of vinyl iodide, in good agreement with the experimental values.

The iodine images depicted in Fig. 2 show a different anisotropy depending on the excitation wavelength and iodine fragment detected. While the emission appears preferentially along the linear polarization axis (parallel) at 200 nm, an almost isotropic ring appears at 199.2 nm for I + I* detection, and a perpendicular one for I* detection. The corresponding angular distributions obtained by radial integration of the inverted images are depicted in Fig. 4. We note that the angular distribution cannot be obtained for the I and I* channels separately at 304.5 nm since the two contributions overlap (see Fig. 3). The anisotropy parameters are obtained by fitting the angular distributions to the following equation:

where θ represents the angle between the photolysis laser linear polarization and the fragment recoil velocity, P_2k(cos θ) is the 2kth order Legendre polynomial, and β_2k are the anisotropy parameters, which reflect the photodissociation dynamics and photofragment polarization. For a one-photon dissociation process and a (2 + 1) REMPI detection scheme through a single intermediate J-level, n is constrained by the maximum allowed integers of 2 + 1 or J + 1, whichever is smallest.⁵⁶ While for I* fragment, J is equal to 1/2 and therefore only β₂ is necessary to characterize the angular distribution, for I in its spin–orbit ground state, J is equal to 3/2 and therefore β₂ and β₄ can be necessary. The result of the fitting is highlighted in Fig. 4, while the anisotropy parameters, β₂, are summarized in Table 3. An error bar of ±0.05 is estimated for these values based on the standard deviation of the results obtained from different measurements. The non-negligible values of β₄ obtained for I + I* detection at both excitation wavelengths reflect some photofragment angular momentum alignment of the iodine in its spin–orbit ground state. Further analysis of these effects would require to measure images with different light polarization for the pump and probe pulses and is considered beyond the scope of the present study.

Fig. 4 Angular distributions (black dots) obtained by radial integration of the iodine inverted images from Fig. 2 from excitation of vinyl iodide at 200 nm and 199.2 nm, and detection of I + I* (a) and (c) and only I* (c) and (d) along with the result of the fit to eqn (4) (blue and cyan lines, respectively). The β_2k parameters resulting from the fit are: β₂ = 0.83 and β₄ = −0.26 (a); β₂ = 0.73 (b); β₂ = 0.03 and β₄ = −0.20 (c) and β₂ = −0.14 (d). In (c), grey dots and red line represent the experimental data and the fit with β₂ = −0.64 and β₄ = −0.26, respectively, for the shoulder observed in Fig. 3 associated with the formation of vinyl in its first excited state along with I. The obtained anisotropy parameters β₂ are included in Table 3.

The β₂ anisotropy parameters measured at 200 nm reflect a rather parallel transition although the reported values are considerably lower than the limiting value of 2 for a purely parallel transition. At 199.2 nm, the values reflect a perpendicular transition for I* and an isotropic distribution for I + I*. The excitation of electronic states of different symmetry is responsible for the reported angular distributions in terms of parallel and perpendicular transitions, in agreement with the assignments of the absorption spectrum (see Fig. 1). The angular distribution obtained for the shoulder at lower energies observed in Fig. 3(c) is indeed characterized by a pretty negative value of β₂.

The I* and I + I* images have been recorded as a function of the pump–probe time delay at the two excitation energies using the two (2 + 1) REMPI schemes. A fitting procedure using a Boltzmann-type function and a Gaussian function is employed to extract the transients for either I* or I + I* from the time-dependent TEDs. Notice that for the experiments at 304.5 nm, the contributions of I and I* could not be properly separated using two Gaussian functions due to the considerable overlap of the two channels in the TEDs. Similarly, the reaction time for the C₂H₃* + I channel could not be extracted due to its relatively low intensity and its partial overlap with the two main channels. The resulting transients for I* and I + I*, depicted in Fig. 5, have been fitted to a Boltzmann sigmoidal function S given by:

where A₁ and A₂ are the initial and final intensity values of the function, which is characterized by a center temporal position t₀, i.e., the time delay for which the intensity has reached half its asymptotic value, defined as the reaction time with respect to time zero, and a rise time constant t_c, which describes the steepness of the rise.

Fig. 5 Iodine transients measured (black dots) upon excitation of vinyl iodide at 200 and 199.2 nm for I*(²P_1/2) (b) and (d) and I*(²P_1/2) + I(²P_3/2) (a) and (c) detection, fitted using a Boltzmann sigmoidal function (cyan and blue solid line, respectively). The reaction (clocking) times are referred to the time zero (grey vertical line) found in situ by measuring the multiphoton ionization signal from the center of the images. The reaction time is defined as the time between time zero and the time corresponding to the middle of the rise of the sigmoidal function (shown as grey dashed line). The reaction times obtained as a mean value of several measurements along with the standard deviations are shown in Table 3.

The reaction C–I bond cleavage times, τ_exp, are obtained as a mean value of the t₀ values with respect to time zero obtained for several measurements, along with the standard deviation. Time zero is defined as the maximum of a Gaussian function employed to fit the multiphoton ionization signal evolution which appears in the center of the images. The results are included in Table 3. τ_exp values in the ∼100–200 fs range, reflect in all cases pretty fast dissociation dynamics. At 199.2 nm, the values for both I* and I + I* are larger, reflecting somehow longer reaction dynamics compared to the dissociation at 200 nm. Similarly to previously reported reaction times in the A-band photodissociation of alkyl iodides,⁵⁷ the reaction times for I + I* are slightly shorter, reflecting faster dynamics for iodine formation in its ground spin–orbit state, which seems reasonable considering the larger available energy for dissociation for production of I in comparison with I*.

3.2 Theoretical results

The computed electronic states of vinyl iodide resulting from the ab initio calculations are listed in Table 4 in terms of the vertical excitation energy at the Franck–Condon geometry up to 6.4 eV, as well as the oscillator strength and the singlet or triplet character of the states. The symmetry of each state cannot be determined since the calculations were carried out without symmetry and the spin–orbit coupling mixes different symmetries. As observed in Table 4, two electronic states present high oscillator strength at around 200 nm: states 12 and 13 with values of 0.71 × 10⁻² a.u. and 15.77 × 10⁻² a.u., respectively.

Table 4 Ab initio vertical excitation energies (VEE) of the computed electronic states in the Franck–Condon region for vinyl iodide up to 6.40 eV. The total oscillator strength for each state as well as its singlet or triplet character are also indicated

State number	VEE/eV	Oscillator strength (10^2 a.u.)	State character
1	0.00	0.00	Singlet
2	4.23	0.00	Triplet
3	4.24	0.00	Triplet
4	4.24	0.00	Triplet
5	4.42	0.00	Triplet
6	4.42	0.00	Triplet
7	4.49	0.04	Triplet
8	4.67	0.17	Singlet–triplet
9	4.99	0.00	Triplet
10	5.06	0.05	Triplet
11	5.12	0.20	Singlet–triplet
12	5.45	0.71	Singlet
13	6.10	15.77	Singlet
14	6.38	0.00	Singlet
15	6.38	0.00	Triplet
16	6.40	0.01	Triplet

---

The difference in electronic density between each electronic state and the ground state has been computed and is depicted in Fig. 6. The first three states (numbered 2 to 4), which are dark states, are associated with a ππ* excitation. States 5 to 12 present a n_Iσ* excitation, associated with the A-band of alkyl iodides. Electronic states 13 to 16 correspond to an excitation from the n_I lone pair to the π*. The 6s Rydberg state – state 27 – is considerably higher in energy lying around 7 eV. In agreement with the reported absorption spectrum and the corresponding assignments (see above) as well as the present ab initio calculations, one-photon absorption at 200 nm is attributed to an excitation into state 12, while one-photon excitation at 199.2 nm can lead to the population of both state 12 and 13.

Fig. 6 Electronic density difference between the different excited electronic and the ground electronic states. Red color indicates negative values while blue color shows positive values.

Fig. 7 depicts the adiabatic potential energy curves computed at the XMS-CASPT2 level for vinyl iodide as a function of the C–I internuclear distance (up to energies of 7 eV) highlighting (in yellow) the regions of the potential energy curves with the highest probability of absorption considering the oscillator strength values. In the Franck–Condon region, at the equilibrium geometry, the brightest states are states 12 and 13 with corresponding oscillator strength values of 7.1 × 10⁻³ a.u. and 1.6 × 10⁻¹ a.u. with vertical excitation energies of 5.45 and 6.10 eV, respectively, as reported in Table 4.

Fig. 7 Computed XMS-CASPT2 potential energy curves for vinyl iodide as a function of the C–I distance. The vertical color map indicates the values of the oscillator strength: dark blue indicates the lowest absorption probability while yellow represents the highest absorption probability. The grey box illustrate the Franck–Condon region around the equilibrium geometry indicated by a grey dashed line.

The dissociation energies were obtained by relaxing the last geometry of the potential energy curves in the different electronic states. The obtained values are summarized in Table 5 and compared with experimental values obtained from thermochemical data.⁵⁸ As observed in Fig. 7, two dissociation limits are available below 200 and 199.2 nm. The first dissociation limit, which corresponds to C₂H₃ (X̃) in correlation with I(²P_3/2), appears at 2.7 eV, whereas the second dissociation limit, associated with C₂H₃ (X̃) in correlation with I*(²P_1/2), appears at 3.58 eV, thus 0.88 eV above the first dissociation limit, which is about the spin–orbit coupling energy of I(²P_J). The dissociation limits calculated here are in good agreement with the experimental values. At higher energies, two additional dissociation limits correspond to the formation of the vinyl radical in its first excited electronic state correlated with iodine in either its spin–orbit ground or excited states. We notice that from an energetic point of view the former can be produced from excitation at 199.2 nm and can lead to iodine atoms in the spin–orbit ground state with low translational energy. Using eqn (1), a value of E^I_av ∼ 0.16 eV is obtained in good agreement with the position of the shoulder observed in Fig. 3(c).

Table 5 Dissociation energies (D₀), in eV, obtained from the present XMS-CASPT2(8,6) calculations compared to experimental values from ref. 24

Channel	D 0 (theo.)	D 0 (exp.)
C2H3 (X̃^2A′) + I(^2P3/2)	2.70	2.684
C2H3 (X̃^2A′) + I*(^2P1/2)	3.58	3.627
C2H3 (Ã^2A′′) + I(^2P3/2)	5.30	—
C2H3 (Ã^2A′′) + I*(^2P1/2)	6.16	—

---

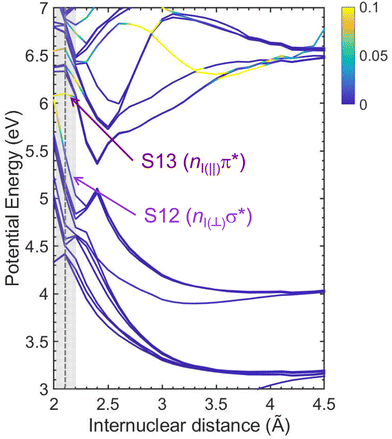
A search for stationary points was carried out following the procedure described in ref. 46 and in Section 2.2. The main results are depicted in Fig. 8, including the geometry and potential energy of each relevant stationary point. The arrows depicted in the chemical structures show the vectors corresponding to the non-adiabatic couplings between the involved electronic states, henceforth referred to as non-adiabatic vectors. The dissociation limits, calculated separately, are included in the figure as a reference. Three relevant conical intersections are found. Following excitation into state 12 (S12), a conical intersection is found between S12 and state 11 (S11). As observed in Fig. 8, this CI appears to be easily reached by elongating the C–I bond. The non-adiabatic vector reflects a subsequent deplanarization and a pyramidalization of the C₂H₃ moiety. A similar nuclear motion was reported at the CI characterizing the dissociation from the ππ* state in ethylene.⁵⁹ Two conical intersections are found following excitation into state 13 (S13). The first CI between S13 and S12 is found at a slightly lower energy and it is associated with a C=C stretch, as reflected by the non-adiabatic vector. A second CI, between S12 and S11 can then be reached and is associated with a strong H–C=C–H torsion, as observed in Fig. 8. A similar pyramidalization of the C₂H₃ moiety is expected in this case.

Fig. 8 Potential energy of relevant stationary points of vinyl iodide found in the dynamics following photoexcitation in the Franck–Condon (FC) region into either state 12 (S12) or state 13 (S13) starting at the equilibrium geometry in the ground state. Dissociation in S12 is mediated through a conical intersection labeled CI_12/11 while two conical intersections labeled CI_13/12 and CI_13,12/11 may be consecutively populated following excitation into S13. The dissociation limits (DLs) computed here are also included in the figure. The geometries associated with the stationary points are plotted in the top and the C–I and C=C distances are indicated. Arrows indicate the non-adiabatic vector characterizing each conical intersection.

On-the-fly adiabatic full-dimension classical trajectory calculations including surface hopping have been run at the ab initio XMS-CASPT2 level. The complete movies can be found in the ESI.†Fig. 9 represents the corresponding geometric evolution along three main degrees of freedom, i.e. the internuclear distance C–I (left panel, solid line), the internuclear distance C=C (left panel, double line) and the dihedral angle H–C=C–H (right panel) for trajectories starting from state 12 (labeled DD) and 13 (labeled CI). Following excitation into state 12 (nσ*), the dynamics is governed by a pretty fast elongation of the C–I bond, characteristic of a ballistic trajectory on a repulsive potential energy surface, leading to a prompt C–I bond dissociation. This motion is accompanied by delayed variation of the C=C distance and a smooth variation of the dihedral angle H–C=C–H. Clear oscillations are observed in the C=C distance, reflecting the formation of the vinyl radical vibrationally excited in the C=C stretching mode. The slight modification of the dihedral angle observed around 30 fs reflects the dynamics at the CI; it allows molecular symmetry to be broken and therefore to transfer population into state 11. In contrast, following excitation into state 13 (nπ*), an elongation of the C=C bond is initially observed along with a simultaneous slightly reduction of the C–I bond, taking place in the first 15 fs. This nuclear motion allows for the transfer from state 13 into state 12 at the CI_13/12 in a sub-20 fs timescale. At later times, an elongation of the C–I bond is observed while the modification of the dihedral angle, breaking the planar symmetry, allows the subsequent switching from state 12 into state 11 through the second conical intersection. This dynamics leads to a continuous elongation and consequent cleavage of the C–I bond and a vibrational excitation of the C=C bond while a strong variation of the dihedral angle is observed reflecting a significant H–C=C–H torsion.

Fig. 9 Average evolution of the C–I internuclear distance, the C=C internuclear distance and the dihedral angle H–C=C–H for the damped dynamics starting from state 12 (DD) and 13 (CI).

4 Discussion

The experimental results from femtosecond velocity map imaging, consisting on the time-resolved I* and I + I* images presented in Section III, can be rationalized with the support of the presented ab initio calculations. Two different excitation energies, i.e. 200 nm and 199.2 nm, were selected. Based on the present experimental and theoretical results, a reassignment of the excited electronic states populated at these two wavelengths is proposed. The excitation at 200 nm into an unstructured broad continuum is attributed to a n_Iσ* excitation, leading to the population of state 12 from the calculations. In contrast, excitation in resonance with the well-defined structure peaking at 199.2 nm observed in the absorption spectrum (Fig. 1) is assigned to the excitation from a n_I lone pair (5p) to the π* and thus the population of state 13. Notice that as observed in Fig. 1(b), the well-defined peak at 199.2 nm lies above a non-negligible continuum. Excitation at 199.2 nm will therefore inevitably lead to some population of state 12 (n_Iσ* excitation). The femtosecond velocity map imaging results reflect then some overlap of the dynamics upon excitation into this last state and from the n_Iπ* (state 13) transition.

Previously reported absorption spectra by Boschi et al.²³ and Sze et al.²² showed similar structures in the energy region of interest while a different assignment was proposed. In particular, the structure at 199.2 nm was attributed to a Rydberg transition, similarly to saturated alkyl iodides, from the 5p iodine orbital into the 6s while the n_Iπ* excitation was reported at lower energies. The new assignment proposed here is based on several aspects. First, it is supported by the high-level ab initio calculations including the vertical energies and the difference in electronic density for each excited electronic state in comparison with the ground state. Second, the width characterizing the structure at 199.2 nm is considerably larger than the well-defined peaks associated with the 6s Rydberg state characterizing the B-band in alkyl iodides lying at around 200 nm. In addition, the photodissociation dynamics following excitation into this Rydberg state has been shown to occur in the picosecond time scale through an electronic predissociation, in the 750–1500 fs range, for all saturated alkyl iodides. The results presented here show in contrast a fast dissociation characterized by reaction times of 168 fs and 152 fs, for I* and I + I*, respectively. The completely different temporal scale supports a different dynamics for vinyl iodide in comparison with saturated analogues. The reported angular distributions for I* and I + I* further supports the assignment proposed here. The pretty positive values of the anisotropy parameters obtained at 200 nm are consistent with the values reported at longer wavelengths¹⁹ as well as with the general parallel character of the n_Iσ* transitions in alkyl iodides. The values are considerably lower than the limiting value of 2 for a transition completely parallel to the C–I distance. While this is often due to some nuclear motion, in particular rotation, occurring before dissociation – leading thus to a failure of the recoil approximation – the ∼100 fs reaction times along with the dynamics observed in the calculations, allows us to discard this. The most probable reason is a transition dipole moment, for the population of state 12, not perfectly aligned with the C–I bond but located at the certain angle. Current ab initio calculations do not reproduce correctly the transition dipole moments for n_Iσ* transitions in alkyl iodides and this hypothesis cannot be confirmed. The values obtained for I* and I + I*, −0.25 and 0.017 reflect two different contributions: a minor positive one from state 12 and a major negative one from state 13. The computed transition dipole moment for the n_Iπ* is located at the C=C–I plane, but pretty perpendicular to the C–I bond. A substantially negative, although not close to the limiting −1 value, would be expected for the transition into state 13.

The experimental results presented here for the formation of I* and I reflect a fast dissociation following excitation at 200 nm and 199.2 nm. The reported f_int values around 0.5 are in good agreement with the soft radical pure impulsive model,⁶⁰ supporting a fast dissociation on a strongly repulsive potential energy surface, where the molecule can be considered quasi-diatomic. In the soft radical limit, the carbon C_α is considered weakly bound to the CH₂ moiety and the two atoms will recoil sharply inducing vibrational and rotational excitation of the molecular fragment. This model is often considered too simplified and the photodissociation dynamics of alkyl iodides was concluded to be semi-rigid. They are indeed somehow better represented by the rigid radical pure impulsive model, in which the molecular moiety acts as a rigid body and can therefore acquire rotational excitation only. Although these are simplified models to understand the measured translational energy distributions, it is particularly interesting the fact that in the presence of a double bond the energy partitioning is so well represented by the soft radical model.

The reaction times reported at 200 nm, 117 and 98 fs, for I* and I + I*, respectively, are consistent with a prompt and direct dissociation associated with a n_Iσ* excitation as in the A-band photodissociation of alkyl iodides. A first conical intersection between state 12, initially populated, and the low-lying state 11, is found to initiate the dissociation dynamics characterized by a direct elongation of the C–I distance leading to prompt dissociation. Subsequent switching between electronic states associated with the n_Iσ* excitation were observed in the dynamics carried out. As discussed in Section 3.2, electronic states associated with a n_Iσ* excitation covers a large energy range in vinyl iodide. State 12 is the higher lying state associated to this transition. Several curve crossings are indeed expected before reaching the dissociation limit, including a last one analogous to the ³Q₀/¹Q₁ (in C_3v symmetry) conical intersection in saturated alkyl iodides. The Φ* value around 0.6 likely reflects the dynamics at this last crossing. The reported value for Φ* is similar to the values of 0.53¹⁹ and 0.57²⁴ reported following excitation at 248 nm, while a lower Φ* (0.27) was found at 266 nm.¹⁹Φ* values in the 0.63–0.76 range obtained for ethyl iodide following excitation in the 245–277 nm range would seem to indicate that the presence of π and π* orbitals is associated to an increased production of iodine in its ground spin–orbit state. A more detailed investigation of the effect of the excitation energy in the I*/I branching ratio will be necessary to get a deeper insight of the effect of a double bond in the dynamics following a n_Iσ* excitation.

The reported reactions times at 199.2 nm are about 50 fs longer compared to the excitation at 200 nm, i.e. 168 and 152 fs, for I* and I + I*, respectively. The well-defined vibronic structure observed in Fig. 1 would seem to indicate a bound potential energy surface associated with the n_Iπ* excitation. The potential energy curves depicted in Fig. 7 show accordingly a slightly bound state. The fast photodissociation dynamics must therefore proceed through non-adiabatic coupling with a repulsive potential energy curve. A first conical intersection was indeed found between state 13 and state 12, corresponding to a state switching from n_I(‖)π* to a n_I(⊥)σ*. Based on the dynamical calculations, this coupling occurs in less than ∼20 fs, which is extremely fast taking into account the fact that both the hole and the excited electron need to change during the switching. Examples of dynamics at CIs involving such double excitation are in general associated with a near picosecond timescale.² The initial dynamics are governed by a C=C bond which does not occur in the case of excitation to state 12, while the C–I bond remains unchanged. Once the state-switching into state 12 is completed, a second conical intersection with state 11 leads to fast dissociation in a repulsive state and a pretty fast C–I bond extension takes place. In contrast to the dissociation in state 12, a remarkable H–C=C–H torsion also occurs then. This particularly fast dynamics seems to be promoted by the presence of an iodine atom with a strong spin–orbit coupling. Sze et al.²² reported a considerable stabilization of the π orbital accompanied by a substantial destabilization of the np halogen lone-pair orbitals for vinyl iodide compared to other vinyl halides. This clearly leads to a different electronic structure and subsequent dynamics. The sub-20 fs state-switching from a n_I(‖)π* (state 13) into a n_I(⊥)σ* character (state 12) reminds the ultrafast charge transfer from a π* to σ* orbital taking place upon dissociative electron attachment, as reported by Kossoski et al.⁶¹ in this particular molecule. This last phenomenon is however a single excitation problem, while here the crossing requires a double excitation, as both the hole and the associated electron need to be modified for the transfer of population to occur.

A third minor dissociation channel was observed in the image and the corresponding TED for excitation at 199.2 nm as a shoulder at lower translational energies. Based on energy considerations, this channel was assigned to the formation of the vinyl radical in an excited state along with iodine in its ground spin–orbit state (C₂H₃* + I(²P_3/2)). In some of the dynamics performed, the wave packet created stays in the n_Iπ* excited electronic state (state 13) – no switching into lower electronic excited states. A slow dissociation in this electronic state is expected although no time-resolved information could be extracted from the present results. Further experiments at shorter wavelengths could be interesting in order to investigate the direct dissociation in this excited state.

5 Conclusions

This work presents a joint theoretical and experimental investigation of the photodissociation dynamics of vinyl iodide upon photoexcitation at 200 and 199.2 nm. Femtosecond velocity map imaging in combination with resonance enhanced multiphoton ionization detection of either I*(²P_1/2), or both I(²P_3/2) and I*(²P_1/2), is employed. Iodine-fragment translational energy distributions and angular distributions are obtained as well as the corresponding transients, and from them the C–I bond cleavage reaction times. The results are complemented by the gas phase absorption spectrum recorded using Fourier transform spectroscopy along with synchrotron radiations, as well as high-level ab initio calculations, including potential energy curves, and semiclassical dynamics. A search of stationary points taking into account the spin–orbit coupling was also carried out and three conical intersections (CIs) governing the dynamics are identified.

Based on the results presented, a reassignment of the excited electronic states responsible of the absorption in the energy range of interest is proposed. One-photon absorption at 200 nm into an unstructured continuum is assigned to a n_I(⊥)σ* transition, similarly to the A-band of alkyl iodides. In contrast, photoexcitation at 199.2 nm into a well-structured vibronic band is attributed to a n_I(‖)π* transition. The photoinduced dynamics from both electronic excited states are discussed. At 200 nm, a fast dissociation in a repulsive surface is observed, mediated through a first CI with a low-lying excited electronic state. This mechanism leads to a C–I bond cleavage characterized by a reaction time around 100 fs. It resembles the typical dissociation of alkyl iodides in the A-band, which in general lies at longer excitation wavelengths. Dissociation following 199.2 nm is characterized by sub-200 fs reaction times, governed by the presence of two conical intersections. State-switching at a first conical intersection with a low-lying electronic state driving the dynamics involves a change in both the excited electron and the left hole, occurring in less than 20 fs. This remarkably fast process for a double excitation takes place through an initial stretch of the C=C bond, followed by a C–I elongation with subsequent vibrational activity in the C=C stretch mode.

Author contributions

Conceptualization: S. M. P., L. B.; funding acquisition: L. B., S. M. P.; methodology: M. L. M.-S., A. Z., J. G.-V., P. L.-V., N. O., L. B., S. M. P.; data curation: M. L. M.-S., A. Z., J. G.-V., P. L.-V., N. O., S. M. P., investigation: M. L. M.-S., A. Z., J. G.-V., S. M. P., L. B.; software: M. L. M.-S., A. Z., J. G.-V.; formal analysis: M. L. M.-S., J. G.-V.; writing – original draft preparation: M. L. M.-S., P. L.-V., J. G.-V., S. M. P.; writing – review and editing: J. G.-V., S. M. P., L. B.

Data availability

The data supporting this article have been included as part of the ESI.† Data are available upon request from the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been carried out within the Unidad Asociada Química Física Molecular between the Departamento de Química Física of the Universidad Complutense de Madrid and CSIC. The financial support from the Spanish Ministry of Science and Innovation under Grants No. PID2021-122549NB-C21 and PID2021-122839NB-I00 is gratefully acknowledged. This work was supported in part by the Madrid Government (Comunidad de Madrid, Spain) under the Multi-annual Agreement with Universidad Complutense de Madrid in the line Research Incentive for Young PhDs, in the context of the V PRICIT (Regional Program of Research and Technological Innovation) (Grant No. PR27/21-010). P. L.-V. acknowledges Fundación Carolina for a mobility grant at Complutense University of Madrid under the Programa de Movilidad de Profesores e Investigadores Portugueses (Fundación Endesa). Part of the experiments presented here was performed at the DESIRS beamline at synchrotron SOLEIL under Proposal No. 20170473. We acknowledge SOLEIL for the smooth provision of the synchrotron radiation facility. We are grateful for the facilities provided by the Center for Ultrafast Lasers of Universidad Complutense de Madrid.

Notes and references

1. T. Wolf, R. H. Myhre, J. Cryan, S. Coriani, R. Squibb, A. Battistoni, N. Berrah, C. Bostedt, P. Bucksbaum and G. Coslovich, et al. , Nat. Commun., 2017, 8, 29.
2. J. P. Zobel, J. J. Nogueira and L. González, Chem. – Eur. J., 2018, 24, 5379–5387.
3. P. Cheng, D. Zhong and A. H. Zewail, Chem. Phys. Lett., 1995, 237, 399–405.
4. D. Zhong and A. H. Zewail, J. Phys. Chem. A, 1998, 102, 4031–4058.
5. M. Dzvonik, S.-C. Yang and R. Bersohn, J. Chem. Phys., 1974, 61, 4408–4421.
6. R. Montero, A. P. Conde, A. Longarte, F. Castaño, M. E. Corrales, R. de Nalda and L. Bañares, Phys. Chem. Chem. Phys., 2010, 12, 7988–7993.
7. A. B. Callear and R. J. Cvetanović, J. Chem. Phys., 1956, 24, 873–878.
8. P. Ausloos and R. Gorden Jr., J. Chem. Phys., 1962, 36, 5–9.
9. H. Okabe and J. R. McNesby, J. Chem. Phys., 1962, 36, 601–604.
10. R. Back and D. Griffiths, J. Chem. Phys., 1967, 46, 4839–4843.
11. H. Hara and I. Tanaka, Bull. Chem. Soc. Jpn., 1973, 46, 3012–3015.
12. H. Hiroshi and T. Ikuzo, Bull. Chem. Soc. Jpn., 1974, 47, 1543–1544.
13. A. H. Laufer, J. Photochem., 1984, 27, 267–271.
14. A. Fahr and A. H. Laufer, J. Photochem., 1986, 34, 261–266.
15. G. J. Collin, in Photochemistry of Simple Olefins: Chemistry of Electronic Excited States or Hot Ground State?, ed. D. H. Volman, G. S. Hammond and K. Gollnick, John Wiley and Sons, 1988, pp. 135–176.
16. S. Satyapal, G. W. Johnston, R. Bersohn and I. Oref, J. Chem. Phys., 1990, 93, 6398–6402.
17. B. Balko, J. Zhang and Y. T. Lee, J. Chem. Phys., 1992, 97, 935–942.
18. A. Stolow, B. A. Balko, E. F. Cromwell, J. Zhang and Y. T. Lee, J. Photochem. Photobiol., A, 1992, 62, 285–300.
19. P. Zou, K. E. Strecker, J. Ramirez-Serrano, L. E. Jusinski, C. A. Taatjes and D. L. Osborn, Phys. Chem. Chem. Phys., 2008, 10, 713–728.
20. S. Yamashita, S. Noguchi and T. Hayakawa, Bull. Chem. Soc. Jpn., 1972, 45, 659–664.
21. S. Yamashita, Chem. Lett., 1975, 967–970.
22. K. Sze, C. Brion, A. Katrib and B. El-Issa, Chem. Phys., 1989, 137, 369–390.
23. R. Boschi and D. Salahub, Mol. Phys., 1972, 24, 735–752.
24. J. Cao, J. Zhang, X. Zhong, Y. Huang, W. Fang, X. Wu and Q. Zhu, Chem. Phys., 1989, 138, 377–382.
25. N. de Oliveira, M. Roudjane, D. Joyeux, D. Phalippou, J.-C. Rodier and L. Nahon, Nat. Photonics, 2011, 5, 149–153.
26. L. Nahon, N. de Oliveira, G. Garcia, J. Gil, D. Joyeux, B. Lagarde and F. Polack, J. Phys.:Conf. Ser., 2013, 425, 122004.
27. N. de Oliveira, D. Joyeux, M. Roudjane, J.-F. Gil, B. Pilette, L. Archer, K. Ito and L. Nahon, J. Synchrotron Radiat., 2016, 23, 887–900.
28. N. de Oliveira, D. Joyeux, D. Phalippou, J.-C. Rodier, F. Polack, M. Vervloet and L. Nahon, Rev. Sci. Instrum., 2009, 80, 043101.
29. A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1998, 109, 4758.
30. P. C. Wright, Generation, characterization and application of the 3rd and 4th harmonics of a Ti:sapphire femtosecond laser, PhD thesis, University of Ottawa, Ottawa, Canada, 2012.
31. G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996.
32. K. Levenberg, Q. Appl. Math., 1944, 2, 164–168.
33. D. W. Marquardt, J. Soc. Ind. Appl. Math., 1963, 11, 431–441.
34. G. Gitzinger, M. E. Corrales, V. Loriot, G. A. Amaral, R. D. Nalda and L. Bañares, J. Chem. Phys., 2010, 132, 234313.
35. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 2037–2047.
36. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956.
37. P. O. Widmark, P. A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306.
38. B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858.
39. T. Shiozaki, W. Gyorffy, P. Celani and H. J. Werner, J. Chem. Phys., 2011, 135, 081106.
40. T. Shiozaki, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2018, 8, e1331.
41. B. Vlaisavljevich and T. Shiozaki, J. Chem. Theory Comput., 2016, 12, 3781–3787.
42. J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 3676–3683.
43. J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 2561–2570.
44. B. Schimmelpfennig, Stockholm University, 1996.
45. I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovacevic, E. Kallman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sorensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesolowski, P. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.
46. J. González-Vázquez, G. A. García, D. V. Chicharro, L. Bañares and S. M. Poullain, Chem. Sci., 2024, 15, 3202.
47. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
48. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201.
49. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
50. J. González-Vázquez, Sharcdyn, Zenodo, 2022.
51. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
52. P. Torkington and H. W. Thompson, J. Chem. Soc., 1944, 303–305.
53. A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1998, 109, 4758.
54. J. Muckerman, J. Phys. Chem., 1989, 93, 179–184.
55. S. J. Riley and K. R. Wilson, Faraday Discuss. Chem. Soc., 1972, 53, 132–146.
56. R. N. Dixon, J. Chem. Phys., 2005, 122, 194302.
57. M. E. Corrales, V. Loriot, G. Balerdi, J. González-Vázquez, R. de Nalda, L. Bañares and A. H. Zewail, Phys. Chem. Chem. Phys., 2014, 16, 8812–8818.
58. B. Ruscic and D. Bross, Active Thermochemical Tables (ATcT) Thermochemical Values ver. 1.130, https://atct.anl.gov/.
59. M. Barbatti, M. Ruckenbauer and H. Lischka, J. Chem. Phys., 2005, 122, 174307.
60. P. T. Reilly, Y. Xie and R. J. Gordon, Chem. Phys. Lett., 1991, 178, 511–516.
61. F. Kossoski and M. Barbatti, Chem. Sci., 2020, 11, 9827–9835.

---

Footnotes

† Electronic supplementary information (ESI) available: Assignments of gas phase high resolution absorption spectrum. Movies of trajectories started from states 12 and 13. See DOI: https://doi.org/10.1039/d5cp00236b

‡ Present address: Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, D-69117 Heidelberg, Germany.

---