DOI:
10.1039/D5CP00178A
(Communication)
Phys. Chem. Chem. Phys., 2025,
27, 6832-6835
Magnetically induced current density from numerical curls of nucleus independent chemical shifts
Received
14th January 2025
, Accepted 28th February 2025
First published on 1st March 2025
Abstract
Instead of computing magnetically induced current densities (MICD) via the wave function and their quantum mechanical definition, one can also use the differential form of the Ampère–Maxwell law to obtain them from curls via spatial derivatives of the induced magnetic field. In magnetic molecular response calculations, the latter can be done by taking the numerical derivative of the so-called “nucleus-independent chemical shifts” (NICS), which are implemented in many standard quantum chemical programs. The resulting numerical MICD data is in contrast to any other first-principles based numerically obtained MICDs computed via the wave function route, virtually divergence-free.
At the conclusion of the fourth and final paper in Schrödinger's seminal series “Quantisierung als Eigenwertproblem”,1 he introduced a vector quantity that is bilinear in the wave function and its complex conjugate similarly to the density function. He interpreted this quantity as the current density (Stromdichte) associated with the probability density (Gewichtsfunktion) in configuration space. Schrödinger further concluded that this current density vanishes for nondegenerate energy eigenstates, leading to his strikingly simple explanation of the radiationlessness of atomic ground states.
The current density (CD), denoted by J, has been of central importance to quantum theory from its earliest days to the present. For the one-particle case, it is defined as
where
ψ is the quantum mechanical wave function describing the state of the particle, and
π is the canonical momentum operator (which itself corresponds to the conjugate of a spatial degree of freedom of the Lagrangian). Today, the CD plays a critical role in theoretical chemistry, as it encodes the complete information on the molecular magnetic response.
2–4 All physical magnetic properties, such as magnetic susceptibilities and shielding constants, can be derived directly from the CD.
In quantum chemistry, the computation of J has traditionally relied on Schrödinger's original defining equation, using the wave function as the starting point within a first-principles framework based purely on quantum mechanics.† Virtually all quantum chemical codes and programs to date (except GIMIC7 which is based on the Biot–Savart equation) employ this approach.3 We propose an alternative strategy inspired by Hirschfelder's notion that his so-called “subobservables”8 can be treated analogously to classical quantities.2 This perspective, in conjunction with the electrodynamic field equations, provides a fresh framework for deriving J, potentially opening up new computational and conceptual pathways.
Electrons in a molecule respond to an external magnetic field Bext by inducing a secondary magnetic field Bind such that in every point in space r, a total magnetic field Btot = Bext + Bind results. These fields are related via the so-called “nuclear magnetic shielding tensor” σ(r), describing the magnetic response of the molecule,
| | | Btot(r) = (1 − σ(r))·Bext(r) | (2) |
| |  | (3) |
The nuclear magnetic shielding tensor can be directly related to the “nucleus-independent chemical shift” tensor or NICS9,10via:
| |  | (4) |
where the first index refers to the response of the molecule in direction
α when the magnetic field points in the
β direction (the second index). In tensor notation, this equals to
where
α and
β (and below also
γ and
δ) denote the tensor component indices for
x,
y,
z. As already has been outlined in ref.
11 the rank-2 current density susceptibility tensor
![[scr J, script letter J]](https://www.rsc.org/images/entities/char_e529.gif) αβ
αβ (CDT) can be expressed
via the magnetostatic Ampère–Maxwell law (in its differential form) and the NICS tensor (see
eqn (4)) as
| | μ0![[scr J, script letter J]](https://www.rsc.org/images/entities/char_e529.gif) αβ(r) = εαγδ∇γNICSδβ(r) αβ(r) = εαγδ∇γNICSδβ(r) | (6) |
where
ε refers to the Levi-Cita tensor,
μ0 is the vacuum susceptibility and summation over repeated Greek indices is implied. This expression is equivalent to
eqn (6) from ref.
11 except that we have replaced
σ by –NICS (
eqn (5)) according to its definition.
9 The computation of the NICS tensor and closely related derived quantities is implemented in many common quantum chemical codes, including the efficient mpshift
12 module of Turbomole.
13–15 It is independent of a prior determination of the current density (susceptibility).
Eqn (6) thus offers a new route for the computation of current densities. Analytical positional derivatives of NICS are not implemented in any quantum chemical codes to the best of our knowledge. However, we found that numerical derivation is a feasible alternative to obtain MICDs. One can formalize a numerical approximation d∇γ to the differentiation operator ∇γ by defining an operator for the finite difference quotient between a forward difference of a vector field component vα(r) at position r and a finite numerical increment d > 0
| |  | (7) |
with
eγ being the unit vector along the
γ component. Note that this operator depends explicitly on the increment size
d and that (under suitable conditions on the operand) lim
d→0d∇
γ = ∇
γ holds. Thus, the main result of this work can be expressed as
| |  | (8) |
where
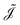
is a numerical approximation to the CDT. For the limit case of
d approximating 0,
eqn (6) is exactly recovered from
eqn (8).
An intriguing property of the current density fields  derived from the contraction of the approximate CDT with the external magnetic field,
derived from the contraction of the approximate CDT with the external magnetic field,
| |  | (9) |
or
| |  | (10) |
lies in its ability to maintain the analytical and defining property of
J—namely that it is divergence-free
for any stationary eigenstate of the system, provided that the numerical representation of the NICS field is sufficiently smooth. This behaviour contrasts with other numerical approximations

to
J obtained from standard quantum chemical software,
3 which are essentially based on expression
eqn (1). Substantial deviations from zero-divergence arise in calculations based on incomplete basis sets and for example perturbative expansions (
vide infra). This is particularly noteworthy because non-zero divergences can pose significant challenges for topological analyses, highlighting the importance of careful numerical treatment. This situation is opposed to by quantum mechanical systems which can be solved analytically or purely theoretical considerations which are independent of numerical data.
At this point, it becomes apparent that ![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) is not equal to the CD obtained from numerical approximations
is not equal to the CD obtained from numerical approximations 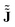 of the magnetically perturbed wave function and the original definition (eqn (1)) by Schrödinger. Monaco, Summa, Zanasi and RB have elaborated on this subject in ref. 11. In short, unlike
of the magnetically perturbed wave function and the original definition (eqn (1)) by Schrödinger. Monaco, Summa, Zanasi and RB have elaborated on this subject in ref. 11. In short, unlike ![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) , approximations of type
, approximations of type  contain a spurious contamination which can be described as the gradient of the Poisson potential of the spurious non-zero divergence,
contain a spurious contamination which can be described as the gradient of the Poisson potential of the spurious non-zero divergence,
| |  | (12) |
Subtraction of the term then yields
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif)
,
11| |  | (13) |
where now ∇·
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif)
= 0. A handful of exemplary calculations of
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif)
are reported and discussed in detail in ref.
11, so we will show only one example calculation on the benzene molecule performed using Turbomole 7.8
13–15 for the magnetic response and NICS calculations as follows.
The calculations were performed at the DFT level with the BP8616,17 functional and the def2-TZVP basis set. The ‘numerical curl’ of the nucleus-independent chemical shieldings was computed on a grid in the molecular plane according to eqn (8) and generated using a Python script.‡ A plot of the obtained ![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) vectors is shown in Fig. 1, along with a plot (Fig. 2) of
vectors is shown in Fig. 1, along with a plot (Fig. 2) of  obtained with GIMIC,7,18 which we denote as JGIMIC in the following. The differences of the currents from the two methods (
obtained with GIMIC,7,18 which we denote as JGIMIC in the following. The differences of the currents from the two methods (![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) –JGIMIC are shown in Fig. 3), and the divergence of the current density obtained from GIMIC at the same level of theory (∇·J) is shown in Fig. 4.
–JGIMIC are shown in Fig. 3), and the divergence of the current density obtained from GIMIC at the same level of theory (∇·J) is shown in Fig. 4.
 |
| | Fig. 1
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) computed viaeqn (8) in the molecular plane of a benzene molecule on a square grid in steps of 0.6 bohr. computed viaeqn (8) in the molecular plane of a benzene molecule on a square grid in steps of 0.6 bohr. | |
 |
| | Fig. 2
J
GIMIC computed with GIMIC in the molecular plane of a benzene molecule on a square grid in steps of 0.6 bohr. | |
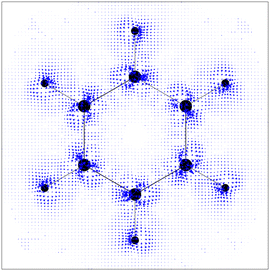 |
| | Fig. 3
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) –JGIMIC in the molecular plane of a benzene molecule on a square grid in steps of 0.3 bohr and scaled by a factor of 10 w.r.t Fig. 1 and 2. –JGIMIC in the molecular plane of a benzene molecule on a square grid in steps of 0.3 bohr and scaled by a factor of 10 w.r.t Fig. 1 and 2. | |
 |
| | Fig. 4 Divergence of JGIMIC (∇·JGIMIC) in the molecular plane of a benzene molecule on a square grid in steps of 0.05 bohr. | |
Prima vista the differences between ![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) (Fig. 1) and JGIMIC (Fig. 2) seem only minor; however, upon subtraction (and upscaling), the differences become more apparent (Fig. 3). As expected, larger deviations appear close to the nuclei. The reason for that is the strong correlation of the differences (explicitly given by eqn (12) and (13)) with the divergence of JGIMIC. These divergences (i.e., breaking of charge conservation) accumulate close to the nuclei where basis set incompleteness is more pronounced,7 which is confirmed by the distribution of ∇·JGIMIC shown in Fig. 4.
(Fig. 1) and JGIMIC (Fig. 2) seem only minor; however, upon subtraction (and upscaling), the differences become more apparent (Fig. 3). As expected, larger deviations appear close to the nuclei. The reason for that is the strong correlation of the differences (explicitly given by eqn (12) and (13)) with the divergence of JGIMIC. These divergences (i.e., breaking of charge conservation) accumulate close to the nuclei where basis set incompleteness is more pronounced,7 which is confirmed by the distribution of ∇·JGIMIC shown in Fig. 4.
In summary, we have devised a new scheme to obtain numerical approximations to the quantum mechanical current density that, unlike previously described methods, does not directly arise from the (perturbed) wave functions but rather from the chemical shift tensor and its spatial derivatives. This approximate CD is virtually divergence-free and can be very simply implemented in any program that can compute chemical shieldings, even interfacing output-data processing scripts. Ongoing work by our groups and collaborators is developing a numerically both efficient and reliable implementation of the scheme proposed here. One key subject thereof will be the choice of the step size of d for the numerical differentiation. We are also currently investigating an approach to decompose J into components for simplified analyses based on the proposed method.
Author contributions
RB conceived the idea, all other contributions are equally shared among the authors.
Data availability
Data for this article, including a “README” file describing the files and their contents, are available on Zenodo at https://zenodo.org/records/14902059.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
RB gratefully acknowledges many insightful discussions with Prof. Dr G. Monaco and Prof. Dr R. Zanasi from the University of Salerno.
References
- E. Schrödinger, Ann. Phys., 1926, 386, 109–139 CrossRef.
- P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Comput. Mol. Biosci., 2016, 6, 639–678 CrossRef CAS.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378 CAS.
- M. Jirásek, H. L. Anderson and M. D. Peeks, Acc. Chem. Res., 2021, 54, 3241–3251 CrossRef PubMed.
- E. Paenurk and R. Gershoni-Poranne, Phys. Chem. Chem. Phys., 2022, 24, 8631–8644 CAS.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 Search PubMed.
- J. O. Hirschfelder, J. Chem. Phys., 1978, 68, 5151–5162 CAS.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CAS.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CAS.
- G. Monaco, F. F. Summa, R. Zanasi and R. J. F. Berger, J. Chem. Phys., 2024, 161, 194105 CAS.
- M. Kollwitz and J. Gauss, Chem. Phys. Lett., 1996, 260, 639–646 CAS.
- TURBOMOLE V7.8 2023, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys, 2020, 152, 184107 CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, WIREs Comput. Mol. Sci., 2013, 4, 91–100 CrossRef.
- J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500 RSC.
Footnotes |
| † In contrast, there also exist semi-empirical approaches that rely on parameterization or fitting procedures of simplified models.5,6 |
| ‡ The scripts and the data are available at https://zenodo.org/records/14902059. |
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Maria
Dimitrova
*a and
Maria
Dimitrova
 *b
*b


![[scr J, script letter J]](https://www.rsc.org/images/entities/char_e529.gif) αβ (CDT) can be expressed via the magnetostatic Ampère–Maxwell law (in its differential form) and the NICS tensor (see eqn (4)) as
αβ (CDT) can be expressed via the magnetostatic Ampère–Maxwell law (in its differential form) and the NICS tensor (see eqn (4)) as![[scr J, script letter J]](https://www.rsc.org/images/entities/char_e529.gif) αβ(r) = εαγδ∇γNICSδβ(r)
αβ(r) = εαγδ∇γNICSδβ(r)

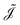 is a numerical approximation to the CDT. For the limit case of d approximating 0, eqn (6) is exactly recovered from eqn (8).
is a numerical approximation to the CDT. For the limit case of d approximating 0, eqn (6) is exactly recovered from eqn (8).
 derived from the contraction of the approximate CDT with the external magnetic field,
derived from the contraction of the approximate CDT with the external magnetic field,

 to J obtained from standard quantum chemical software,3 which are essentially based on expression eqn (1). Substantial deviations from zero-divergence arise in calculations based on incomplete basis sets and for example perturbative expansions (vide infra). This is particularly noteworthy because non-zero divergences can pose significant challenges for topological analyses, highlighting the importance of careful numerical treatment. This situation is opposed to by quantum mechanical systems which can be solved analytically or purely theoretical considerations which are independent of numerical data.
to J obtained from standard quantum chemical software,3 which are essentially based on expression eqn (1). Substantial deviations from zero-divergence arise in calculations based on incomplete basis sets and for example perturbative expansions (vide infra). This is particularly noteworthy because non-zero divergences can pose significant challenges for topological analyses, highlighting the importance of careful numerical treatment. This situation is opposed to by quantum mechanical systems which can be solved analytically or purely theoretical considerations which are independent of numerical data.
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) is not equal to the CD obtained from numerical approximations
is not equal to the CD obtained from numerical approximations 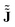 of the magnetically perturbed wave function and the original definition (eqn (1)) by Schrödinger. Monaco, Summa, Zanasi and RB have elaborated on this subject in ref. 11. In short, unlike
of the magnetically perturbed wave function and the original definition (eqn (1)) by Schrödinger. Monaco, Summa, Zanasi and RB have elaborated on this subject in ref. 11. In short, unlike ![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) , approximations of type
, approximations of type  contain a spurious contamination which can be described as the gradient of the Poisson potential of the spurious non-zero divergence,
contain a spurious contamination which can be described as the gradient of the Poisson potential of the spurious non-zero divergence,
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) ,11
,11
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) = 0. A handful of exemplary calculations of
= 0. A handful of exemplary calculations of ![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) are reported and discussed in detail in ref. 11, so we will show only one example calculation on the benzene molecule performed using Turbomole 7.813–15 for the magnetic response and NICS calculations as follows.
are reported and discussed in detail in ref. 11, so we will show only one example calculation on the benzene molecule performed using Turbomole 7.813–15 for the magnetic response and NICS calculations as follows.
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) vectors is shown in Fig. 1, along with a plot (Fig. 2) of
vectors is shown in Fig. 1, along with a plot (Fig. 2) of  obtained with GIMIC,7,18 which we denote as JGIMIC in the following. The differences of the currents from the two methods (
obtained with GIMIC,7,18 which we denote as JGIMIC in the following. The differences of the currents from the two methods (![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) –JGIMIC are shown in Fig. 3), and the divergence of the current density obtained from GIMIC at the same level of theory (∇·J) is shown in Fig. 4.
–JGIMIC are shown in Fig. 3), and the divergence of the current density obtained from GIMIC at the same level of theory (∇·J) is shown in Fig. 4.
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) computed viaeqn (8) in the molecular plane of a benzene molecule on a square grid in steps of 0.6 bohr.
computed viaeqn (8) in the molecular plane of a benzene molecule on a square grid in steps of 0.6 bohr.

![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) –JGIMIC in the molecular plane of a benzene molecule on a square grid in steps of 0.3 bohr and scaled by a factor of 10 w.r.t Fig. 1 and 2.
–JGIMIC in the molecular plane of a benzene molecule on a square grid in steps of 0.3 bohr and scaled by a factor of 10 w.r.t Fig. 1 and 2.
![[J with combining tilde]](https://www.rsc.org/images/entities/b_char_004a_0303.gif) (Fig. 1) and JGIMIC (Fig. 2) seem only minor; however, upon subtraction (and upscaling), the differences become more apparent (Fig. 3). As expected, larger deviations appear close to the nuclei. The reason for that is the strong correlation of the differences (explicitly given by eqn (12) and (13)) with the divergence of JGIMIC. These divergences (i.e., breaking of charge conservation) accumulate close to the nuclei where basis set incompleteness is more pronounced,7 which is confirmed by the distribution of ∇·JGIMIC shown in Fig. 4.
(Fig. 1) and JGIMIC (Fig. 2) seem only minor; however, upon subtraction (and upscaling), the differences become more apparent (Fig. 3). As expected, larger deviations appear close to the nuclei. The reason for that is the strong correlation of the differences (explicitly given by eqn (12) and (13)) with the divergence of JGIMIC. These divergences (i.e., breaking of charge conservation) accumulate close to the nuclei where basis set incompleteness is more pronounced,7 which is confirmed by the distribution of ∇·JGIMIC shown in Fig. 4.