Open Access Article
Open Access ArticleAccounting for the vibrational contribution to the configurational entropy in disordered solids with machine learned forcefields: a case study of garnet electrolyte Li7La3Zr2O12†
Jack
Yang
 *,
Ziqi
Yin
and
Sean
Li
*,
Ziqi
Yin
and
Sean
Li

Materials and Manufacturing Futures Institute, School of Material Science and Engineering, University of New South Wales, Sydney, New South Wales 2052, Australia. E-mail: jianliang.yang1@unsw.edu.au
First published on 2nd April 2025
Abstract
Accounting for lattice vibrations to accurately determine the phase stabilities of site-disordered solids is a long-standing challenge in computational material designs, due to the high computational cost associated with sampling the vast configurational space to obtain the converged thermodynamic quantities. One example is the garnet electrolyte Li7La3Zr2O12, the high-temperature and high-ion-mobility cubic phase of which is disordered in its Li+ site occupations, such that both the vibrational and configurational entropic contributions to its phase stability cannot be ignored. Understanding the subtle interplay between vibrational and configurational entropies in this material will therefore play a critical role in the rational manipulation of dopants and defects to stabilise cubic Li7La3Zr2O12 at room temperature for practical applications. Here, by developing machine learned forcefields based on an equivariant message-passing neural network SO3KRATES, we follow a strict statistical thermodynamic protocol to quantify the phase stability of cubic Li7La3Zr2O12 through structural optimisations, as well as molecular dynamics simulations at 300 and 1500 K, for a total of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 configurations of cubic Li7La3Zr2O12. Although this only covers a tiny fraction of the configurational space (∼7 × 1034 configurations in total), we are able to deterministically show that the vibrational contributions to the total configurational free energy at 1500 K are significant (on the order of 1 eV per atom) in correctly ordering the stability of the cubic Li7La3Zr2O12 over its tetragonal counterpart, thanks to the high data efficiency, accuracy, stability and good transferability of the transformer-based equivariant network architecture behind SO3KRATES. Therefore, our work opens up new avenues to accelerate the accurate computational designs of disordered solids, such as solid electrolytes, for technologically important applications.
120 configurations of cubic Li7La3Zr2O12. Although this only covers a tiny fraction of the configurational space (∼7 × 1034 configurations in total), we are able to deterministically show that the vibrational contributions to the total configurational free energy at 1500 K are significant (on the order of 1 eV per atom) in correctly ordering the stability of the cubic Li7La3Zr2O12 over its tetragonal counterpart, thanks to the high data efficiency, accuracy, stability and good transferability of the transformer-based equivariant network architecture behind SO3KRATES. Therefore, our work opens up new avenues to accelerate the accurate computational designs of disordered solids, such as solid electrolytes, for technologically important applications.
1 Introduction
Computational modelling is an essential component in driving modern scientific discoveries and innovations across multiple fields of physics, chemistry, biology and materials science. These models provide us with the critical insights into the atomistic, and often electronic, origins behind the exotic properties of materials, such as thermal,1,2 optical,3,4 catalytic5 properties and many others. Regardless of which model is employed, fore-mostly, it determines the potential energy of a material system as a function of the atomic positions E(R) with a given composition, a key quantity useful for determining a material's thermodynamic stability, thus providing an answer to the important question of whether the material can exist in the first place. The capability of these energy models, particularly density functional theory (DFT), to reach sub-kcal mol−1 (in chemistry) or meV per atom (in physics and materials science) accuracies compared to experimental thermochemical data as demonstrated by many carefully curated benchmarks6–10 has brought confidence in applying these models as the predictive tools to guide experimental material discoveries. A notable example is the application of organic11,12 and inorganic13,14 crystal structure predictions, which sample the potential energy surface (PES) for structures corresponding to the global energy minimum, and/or a set of low energy local minima, with demonstrated success in materials discoveries such as highly porous organic solids for gas adsorptions,15 complex layered inorganic solids,16 and new ternary inorganic nitrides.17Despite these successes, structure predictions remain one of the Holy Grails in computational chemistry and materials science. This is simply because the size of the search space grows combinatorially large as the degrees-of-freedoms increase, making it impossible to conduct an exhaustive search over the PES, risking important structures being missed18 and/or difficulty in converging thermodynamic properties through ensemble averaging.19 This challenge is often compounded by the necessity to include the (vibrational) free energy contributions for accurate modelling of materials' thermodynamic stability at finite temperatures.7,20–22
Garnet Li7La3Zr2O12 (LLZO) is an interesting example, and is the focus of this work, for demonstrating the challenges behind sampling the PES using computational approaches for comprehensively understanding the phase behaviours of disordered solids at the atomistic level [Fig. 1]. LLZO is a promising solid electrolyte for all solid-state lithium ion batteries because of its high Li+ ion conductivity23 with negligible electronic transports,24 wide electrochemical windows,25 and chemical stability.26 It possesses two different phases [Fig. 1(a)]. The room-temperature tetragonal phase (t-LLZO) with fully ordered Li-sublattice, leading to a low ion conductivity of ∼1 S cm−1 K−1 (ref. 27) in which ion migrations can only be promoted through phonon vibrations.28 Above ∼900 K,29,30 LLZO transforms into its cubic phase (c-LLZO) with a disordered Li-sublattice, in which the presence of Li vacancies significantly enhances the ion conductivity by four orders-of-magnitudes.27 The cubic phase with Li-site disorder is the one that will be investigated in this work. Moving forward [Fig. 1(b)], the thermodynamic stability of c-LLZO can be further affected by the contents of Li+ (and oxygen stoichiometries associated with maintaining charge balance).31,32
 | ||
| Fig. 1 Hierarchical sampling challenge in computational thermodynamics for disordered solids. Using garnet LLZO as an example: (a) the material possesses two (cubic and tetragonal) phases,29,30 and in each phase (b) there is a variation in the chemical compositions of lithium. At any one composition, the Li+ ions can arrange themselves in a different combination of lattice sites, leading to a range of different atomic configurations of LLZO, each with its own enthalpy that is represented by the dots on the energy landscape. The line joining the lowest energy points across all the compositions represents the stability convex hull. More specifically, (c) different configurations of c-LLZO at a given Li content can be categorised based on the relative ratios of 24d to 96h site occupancies in the lattice. For a given ratio of Li site occupancies, (d) the PES of LLZO can be represented as multiple energy wells (grey curves), one for each configuration σ(i). Typically, most of the current research focuses on computing the 0 K enthalpies, which correspond to the transformed PES33 that is determined by the energies of the local minima H(i) as represented by the solid horizontal lines. More accurate computation of materials' stability at finite temperature should also include (e) the vibrational contribution by replacing H(i) with its corresponding temperature-dependent Helmholtz free-energy F(i)vib(T). | ||
Simply focusing on c-LLZO with full Li-stoichiometry, the disorder in the material originates from the total number (120) of lattice sites that can be occupied by the Li+ ions being much larger than the maximum number (56) of Li+ ions per unit cell of LLZO, resulting in an extremely large number34 (∼7 × 1034) of possible ways to arrange Li+ in the unit cell (commonly referred to as configurations). This means that configurational entropy could play a significant role in stabilising c-LLZO at high temperatures, and from a pure statistical thermodynamic perspective, the enthalpies for all these configurations need to be computed to obtain the converged configurational entropy35 for c-LLZO with full Li-stoichiometry, which is computationally infeasible anyway. Crystallographically, different configurations of c-LLZO can be grouped based on the occupancy ratios of two types of Li-sites, namely the 24d and 96h‡ [Fig. 1(c)] (also see Fig. S1 in the ESI†). Importantly, Holland et al.34 established a methodology to generate symmetrically unique configurations of c-LLZO with any site occupancy ratio, particularly in the range with optimum Li–Li distances to promote fast ion conduction. This not only provides the computational community with an exhaustive list of initial atomistic structures of c-LLZO, but also significantly reduces the configurational space, making it more attemptable to compute the thermodynamic stability of LLZO with the explicit inclusion of configurational entropy.
This is the first motivation behind the current work, whereby we examine the temperature-dependent thermodynamic stabilities for a subset of c-LLZO configurations with the 24d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96h site occupancy ratios of 12
96h site occupancy ratios of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 and 11
44 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45, containing 4162 and 65
45, containing 4162 and 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 symmetry unique structures,34 respectively. As in the standard structure prediction workflow, each configuration is first structurally optimised to its corresponding local energy minimum, which essentially provides us with the information of transformed PES at 0 K [Fig. 1(d)]. However, the thermodynamic quantity that truly dictates the stability of each configuration at finite temperature is its Helmholtz free energy,7,20 which takes into account the contribution from lattice vibrations towards structural stability [Fig. 1(e)]. This can be computed with either a finite-displacement phonon36 or molecular dynamics (MD) approach, but the high computational costs associated with these approaches, particularly when combined with a DFT energy model, prohibit these calculations from being individually performed for every configuration. Alternatively, the Helmholtz free energy of a representative configuration (typically the lowest energy one)21 may be used as a constant correction factor across the entire ensemble. The latter assumes Helmholtz free energies vary insignificantly amongst the configurations,20 which may or may not hold.
958 symmetry unique structures,34 respectively. As in the standard structure prediction workflow, each configuration is first structurally optimised to its corresponding local energy minimum, which essentially provides us with the information of transformed PES at 0 K [Fig. 1(d)]. However, the thermodynamic quantity that truly dictates the stability of each configuration at finite temperature is its Helmholtz free energy,7,20 which takes into account the contribution from lattice vibrations towards structural stability [Fig. 1(e)]. This can be computed with either a finite-displacement phonon36 or molecular dynamics (MD) approach, but the high computational costs associated with these approaches, particularly when combined with a DFT energy model, prohibit these calculations from being individually performed for every configuration. Alternatively, the Helmholtz free energy of a representative configuration (typically the lowest energy one)21 may be used as a constant correction factor across the entire ensemble. The latter assumes Helmholtz free energies vary insignificantly amongst the configurations,20 which may or may not hold.
The promising applications of LLZO as a solid electrolyte have already sparked significant interest in applying classical forcefields for conducting molecular dynamics investigations to understand its phase transition and Li-ion diffusion behaviours in pristine and aliovalent-doped LLZO, which have led to some important insights into the subtle interplays between its structural complexity and ion conductivities.37–47 One of the key findings amongst these studies is the importance of increasing configurational entropy as reflected by Li redistributions in the LLZO lattice upon phase transition from the tetragonal to cubic phase.41,42 Although both Ga and Al doping can stabilise LLZO in its high-conductive cubic phase, the Ga-substituted LLZO yields higher conductivity (10−3 S cm−1) compared to the Al-substituted one (10−4 S cm−1),48 which may be attributed to the less repulsive nature of the Al3+ dopant that immobilises the nearby Li-vacancy and blocking the Li-diffusion pathway, as revealed from the forcefield simulation.39,40 Technically, most of these classical forcefields are based on a Buckingham potential and point charge model. While this type of forcefield is fast to evaluate, Chen et al.42 pointed out the difficulty in pinpointing the exact Ta concentration and transition temperature to stabilise the cubic LLZO with Ta doping, due to the inherent limitation of the Buckingham potential. In this regard, Dai et al.44 compared the performances of different forcefields for simulating fast ion conductors, and it is unsurprising to see the polarisable forcefield with an induced dipole model that captures the chemical-environment-dependent polarisation effects performs the best, but the development of an accurate polarisable forcefield is generally more challenging to non-specialists. Moreover, classical forcefields are typically fitted to the vicinity of local minimum, while this is beneficial for modelling the phononic properties, a good description of the long-ranged topological features of the PES is required for studying Li ion diffusions. Lastly, the pair potential also imposed limited flexibility to capture the important many-body atom–atom interactions in a complex system.46
During the past decade, we have seen rapid progress in the development of machine learned forcefields (MLFFs)49–64 with the emergence of the foundational model,65 which offers accuracies in par with modern DFT but few orders of magnitude increase in the computational speed while overcoming the aforementioned limitations in classical forcefields, thus allowing us to bridge the gaps in length and time scales, as well as the compositional complexities in atomistic modelling. A few recent studies applied MLFF to further investigate the phase and ion diffusion behaviours in LLZO,24,66–68 but critical quantitative insights into the role of configurational entropy in determining the thermodynamic properties of LLZO are still lacking. This makes it timely for us to harness the advantages of MLFF to tackle the sampling challenges and determine the temperature-dependent stabilities of LLZO, with the vibrational contributions to the configurational entropy accounted for explicitly, by following the exact statistical mechanics protocol.20 This is the second motivation for the present study. More specifically, we will be using the SO3KRATES62 model to train our material-specific MLFF. It represents one particular implementation of the geometric graph neural networks69 that use the message-passing scheme59,70 to learn the information about connectivities in chemical structures. The architecture is made aware of the rotationally equivariant features by incorporating geometric priors based on the SO(3) rotational group -(special orthogonal group in three dimensions),51,58,71,72 to improve the data efficiency, generalisability and stability in model training and atomistic simulations.73,74 Furthermore, the network is combined with the self-attention mechanism75 to bypass the need for full SO(3) tensor convolution in information exchange to increase the computational speed.
2 Theory
2.1 Thermodynamics of disordered solids
In this section, we briefly outline the fundamental thermodynamics of disordered solids. We begin with a set of structural models for the material of interest, each with symmetrically unique atomic arrangements. This set of structures are most commonly referred to as the configurations which will be collectively denoted as σ = {σ(1), σ(2),…, σ(n)}. As the standard practice in (nearly all) atomistic modelling, we relax each configuration to its local energy minimum, giving us its corresponding enthalpy H(i) at 0 K [Fig. 1(d)]. If we stop here, then the system is said to be stabilised by configurational entropy at T when the temperature-dependent configurational free-energy| Gconf(T) = H − TSconf | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zconf. Here kB is the Boltzmann constant, and the configurational partition function
Zconf. Here kB is the Boltzmann constant, and the configurational partition function | (2) |
 | (3) |
To further account for the vibrational contribution to the thermodynamic stability of each configuration under finite temperature [Fig. 1(e)],20H(i) in eqn (1) needs to be replaced by the corresponding vibrational (Helmholtz) free-energy F(i)vib(T) = H(i)T − TS(i)vib, in which H(i)T includes the internal energies at 0 K and those associated with thermal motion.76 Here, we take H(i)T = 〈U(i)(t)〉MD, which is the time-averaging of the internal energy over an MD trajectory. With this, the configurational partition function becomes
 | (4) |
| Gconf+vib(T) = Fvib(T) − TSconf+vib, | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zconf+vib. Physically, eqn (4) is equivalent of re-normalising the 0 K PES to its corresponding Helmholtz free-energy surface at a finite temperature.
Zconf+vib. Physically, eqn (4) is equivalent of re-normalising the 0 K PES to its corresponding Helmholtz free-energy surface at a finite temperature.
Practically, there exist a multitude of approaches to compute Fvib.76 The most common approach36 is to first perform a frozen phonon calculation to determine the spectrum of phonon eigenfrequencies {ω(i)λ} (where λ = (q,n) with q being the wavevector and n the band index), by diagonalising the Hessian matrix for the i-th configuration. Within the harmonic approximation, the vibrational free energy (ignoring H(i)T) takes the following discrete sum:
 | (6) |
Alternatively, one could take the integral form of the above expression and compute the vibrational free energy from the corresponding phonon density-of-states (PDOS) g(i)(ω) as76–78
 | (7) |
 | (8) |
There exist some notable disadvantages of computing Fvibvia VACF from MD simulations, which include: (a) MD should be performed at different temperatures T to extract the corresponding g(ω,T), if one is interested in the temperature-dependent Helmholtz free energies Fvib(T), for example, to determine the phase-transition temperature. (b) Large supercells, typically with ∼103 atoms or more, need to be used and perform MD runs in sufficiently long times in principle, to obtain fully converged PDOS.76 Both (a) and (b) translate to extremely high computational costs that are only achievable with forcefields, such as the MLFF adopted in this work. Finally, (c) the usage of eqn (7), which was established based on the harmonic approximation may not hold for strongly anharmonic systems. Nevertheless, it offers the advantage of accounting for the variations in PDOS that originate from the multiphonon interactions. Practically, running MD simulations with MLFF takes the advantage from the MD engines in the API (application programming interfaces) of many latest MLFF packages for atomistic simulations, that is either individually implemented or using other well-established APIs such as the atomic simulation environment (ASE),79 as running long-time MD simulations is one of the key driving forces behind these MLFFs.
2.2 The SO3KRATES architecture
A neural network learns the contributions from individual atoms (Ei) towards the total energy of a structure with N atoms (as ) by exchanging the chemical and structural information amongst the constituent atoms through multiple interconnected hidden layers. Different neural networks vary in terms of how such information is exchanged while preserving the important symmetries in the chemical system. More specifically, this information exchange in SO3KRATES (see Fig. S2 ESI† for a detailed illustration) is achieved through T layers of Euclidean transformer blocks, which implements both the message-passing69,70 and self-attention75 mechanisms to iteratively update the per-atom feature as
) by exchanging the chemical and structural information amongst the constituent atoms through multiple interconnected hidden layers. Different neural networks vary in terms of how such information is exchanged while preserving the important symmetries in the chemical system. More specifically, this information exchange in SO3KRATES (see Fig. S2 ESI† for a detailed illustration) is achieved through T layers of Euclidean transformer blocks, which implements both the message-passing69,70 and self-attention75 mechanisms to iteratively update the per-atom feature as | (9) |
 neighbours of i that is identified by a pre-defined cut-off radius rcut. Before the first iteration, the feature vector is initialised purely with the chemical information (in this case, the atomic number zi) of each atom through an embedding function as f(0)i = femb(zi) that maps zi into a F-dimensional vector in the feature space, i.e.
neighbours of i that is identified by a pre-defined cut-off radius rcut. Before the first iteration, the feature vector is initialised purely with the chemical information (in this case, the atomic number zi) of each atom through an embedding function as f(0)i = femb(zi) that maps zi into a F-dimensional vector in the feature space, i.e. . As such, f encodes the invariant information of the system.
. As such, f encodes the invariant information of the system.
In addition, it is crucial for the SO3KRATES network to learn the geometric information of the chemical structure, that also contributes towards Ei and transforms equivariantly with respect to 3D rotations and translations. Here, the spherical harmonic coordinates (SPHC), the basis for the SO(3) rotational group, is used as an inductive basis to preserve the equivariance throughout the network. This is implemented, firstly by embedding the Cartesian vector rij = ri − rj for  into its corresponding Euclidean variable (EV) as a multipolar expansion
into its corresponding Euclidean variable (EV) as a multipolar expansion  with
with
 | (10) |
In the above equation, 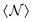 is the average number of atomic neighbours over the whole training data. ϕcut(||rij||) is a cosine cutoff function (eqn (17) in Frank et al.74).
is the average number of atomic neighbours over the whole training data. ϕcut(||rij||) is a cosine cutoff function (eqn (17) in Frank et al.74). ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij = rij/||rij|| is the unit vector, and Yml denotes the spherical harmonic function of degree
ij = rij/||rij|| is the unit vector, and Yml denotes the spherical harmonic function of degree  with m ∈ [−l, −l + 1,…, l − 1, l]. Within each Euclidean transformer block, this SPHC is also updated per-degree-wise, similar to the feature vector as:
with m ∈ [−l, −l + 1,…, l − 1, l]. Within each Euclidean transformer block, this SPHC is also updated per-degree-wise, similar to the feature vector as:
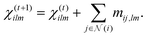 | (11) |
The messages [eqn (9) and (11)] are constructed using the multihead self-attention approach75 (with the number of heads h being a network hyperparameter), to avoid the necessity of performing full SO(3) convolutions repetitively for L times along the feature vector dimension to exchange the invariant and equivariant information,71 bringing down the computational costs from  to
to  . More specifically, we write
. More specifically, we write
| mij = ϕcut(||rij||)αijfj, | (12) |
mij,lm = ϕcut(||rij||)αlijYlm(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij), ij), | (13) |
| αij = kiT(wij⊙qj), | (14) |
 . The weight matrix w is also learnable as the sum of the outcomes from two MLPs as
. The weight matrix w is also learnable as the sum of the outcomes from two MLPs as | (15) |
in which  contracts each degree in cij to the zeroth degree (eqn (14) in Frank et al.74). This completes the Euclidean attention block in the Euclidean transformer. The outputs from the attention block (fattni and χattni) are subsequently passed into the interaction block, which provides the network with additional degree-of-freedoms to exchange the invariant and equivariant information. The outcomes are the refinement dfi and dχi, which are to be combined with the initial inputs to generate the final outputs for a given Euclidean transformer block:
contracts each degree in cij to the zeroth degree (eqn (14) in Frank et al.74). This completes the Euclidean attention block in the Euclidean transformer. The outputs from the attention block (fattni and χattni) are subsequently passed into the interaction block, which provides the network with additional degree-of-freedoms to exchange the invariant and equivariant information. The outcomes are the refinement dfi and dχi, which are to be combined with the initial inputs to generate the final outputs for a given Euclidean transformer block:
| f(t+1)i = f(t)i + dfi, |
| χ(t+1)i = χ(t)i + dχi. |
Finally, autodifferentiation is employed to calculate the atomic forces to ensure energy conservation.56
3 Results
3.1 Accuracy of the model for structural optimisation
Using the equivariant features as an inductive basis in the neural network has demonstrated its advantages in achieving outstanding model performance and data efficiency.62,71 When training the SO3KRATES model on the structural optimisation trajectories using the 12_44_opt set (see Section 5.2 for details), it is found from the learning curves (Fig. S3, ESI†) that using as little as 2000 data points (corresponding to just 2% of the database) is sufficient for the model to reach the meV-level of accuracy in predicting the energies and forces. Beyond that, the model performances only improve slightly with further increase in the size of the training set, and in the subsequent discussions, the model that is applied for structural optimisations is trained with 4000 data points. The accuracy of this particular MLFF is further demonstrated in Fig. 2 which shows both the energies and atomic forces predicted by the MLFF correlate very well with those calculated from DFT, reaching an error level of 7.48 meV and 4.87 meV per (Å atom) in MAE (mean-absolute-error) with 9.62 meV and 6.72 meV per (Å atom) in RMSE (root-mean-squared-error) for energy and force predictions, respectively.To gain some insights into how the performance of the MLFF is affected by the model flexibility, we trained extra versions of MLFFs by changing the dimensionality of the EV χi through varying the degrees of spherical harmonics l. The resulting model performances, which are compared in Table 1, show that compared to the atomic forces, the accuracy in predicting energy is more sensitive to the degrees of multipolar expansions used for constructing the EVs. This can be due to the fact that the models are trained using a loss function that is strongly biased towards accurate force predictions. The largest improvement in the model accuracy can be seen when the dipole moment (l = 1) is incorporated in additional to the monopole moment (l = 0), signifying the importance of learning the orientational information in the chemical environments. Nevertheless, the relative contributions from higher order multipoles reduce as they are progressively introduced into the model. Interestingly, EVs that are expanded to the hexadecapoles while ignoring the monopole contribution shows the best accuracy in energy prediction, with only a small deterioration in forces (compared to the case where the monopole is included). We speculate that this may be because the structural framework of LLZO is made of multiple LiO4, LiO6, LaO6 and ZrO6 polyhedra, which involve many chemical bondings that are strongly directional. In this case, including the monopole term, which is isotropic in nature, is not beneficial to capture the directional bonding characteristics, causing the model to become overfit resulting in worse performance. As such, this choice of l is used throughout the rest of this study.
3.2 Accuracy of the model for molecular dynamics simulations
Unfortunately, the MLFF trained on the structural optimisation trajectories is not sufficiently extrapolative to produce stable MD runs,73 because the latter can sample a much wider configurational space with broader distributions in energies and atomic forces that are far beyond the training data covered in the optimisation trajectories. Hence a separate MLFF is trained on a single AIMD (ab initio molecular dynamics) trajectory which heats up a c-LLZO structure from 10 to 2100 K.63 The lattice constants of c-LLZO were kept fixed during the simulation as the examination of phase transition behaviours in LLZO is not the main goal of the current study.24 Similar to the training of MLFF for structural optimisations discussed in Section 3.1, the top row of Fig. 3 again shows the model is capable of reaching an meV-level of accuracy with a small number of 1000 training data.Apart from the model being accurate, the transferability of the MLFF is also critical, if we would like to use this particular MLFF to determine the vibrational contributions to the configurational entropies from all other configurations in the set. For this, at the bottom row of Fig. 3, we show that the model is capable of reproducing the DFT energies and forces from the 300 K AIMD trajectories of another 50 configurations that are randomly selected from the 12_44_opt set. Note that the prediction errors for this set are seemingly lower than those computed on the AIMD trajectory for model training, because the latter covers much wider ranges in energies and forces. In addition to the equivariant architecture of the SO3KRATES network, the excellent transferability of the trained MLFF could also be attributed to the fact that, despite the configurational space for c-LLZO being very large, the short-ranged chemical environments,51 which are expected to play a dominant contribution to the cohesive energy of a crystal, are much less diverse across configurations.
We also tested the stabilities and performances of using the as-trained MLFF in molecular dynamics simulations across the temperature range (300–1500 K) that we are interested in. Because the key quantity that is needed for computing Fvib is the PDOS [eqn (7)], in Fig. 4, we compare the temperature-dependent PDOS for one configuration of c-LLZO that is computed from AIMD and MLFF-MD via the VACF, respectively. From Fig. 4, it can be seen that the overall shapes of the PDOS from AIMD are well reproduced by the MLFF-MD, particularly the highest PDOS peak that is centred at ∼40 meV. In the phonon energy range of 50–70 meV, MLFF tends to give slightly lower (higher) PDOS values at the lower (higher) temperatures, compared to the ones computed from AIMD. Recent investigation in Li3YCl680 shows the appearance of low-frequency boson-like peaks81 in its PDOS as a signature of strong vibrational anharmonicity and coupled vibration between Li and the rest of the crystal framework plays a key role towards the emergence of the superionic state in this material. However, we did observe similar behaviour from the PDOS of LLZO. Finally, no significant shift in the PDOS peak(s) is observed in both PDOS spectra across the temperature range investigated, suggesting that thermally induced phonon renormalisation in c-LLZO is not expected to be significant. Nevertheless, more investigations of the phononic properties of c-LLZO are subject to future studies.82,83 In Table 2, we further compare the key vibrational thermodynamic quantities that are extracted from AIMD and MLFF-MD simulations. Statistically, compared with DFT over the entire temperature range investigated, the ML potential is found to be slightly more attractive by 121.5 meV per atom (as measured by the time-averaged internal energy 〈U(t)〉t), which may be attributed to the higher PDOS at the higher energy range produced from MLFF-MD as shown in Fig. 4. At the same time, the vibrational entropy Svib computed from MLFF-MD is slightly larger by 18.6 meV per (atom K) compared to the DFT value. It is also shown in Table 2 that, at around 1500 K where c-LLZO is the more stable phase, the vibrational contribution (TSvib) to the free energy, albeit smaller, is on the same order of magnitude as the internal energy 〈U(t)〉t, signifying the importance of accounting for the vibrational contribution in the accurate determination of the material stability.
| Temp. [K] | 〈U(t)〉DFTt [eV per atom] | 〈U(t)〉MLFFt [eV per atom] | S DFTvib [meV per (atom K)] | S MLFFvib [meV per (atom K)] | TS DFTvib [meV per atom] | TS MLFFvib [meV per atom] |
|---|---|---|---|---|---|---|
| 300 | −7.802 | −7.820 | 0.912 | 0.928 | 273.65 | 278.46 |
| 500 | −7.748 | −7.808 | 0.905 | 0.935 | 452.58 | 476.61 |
| 700 | −7.709 | −7.795 | 0.893 | 0.934 | 625.45 | 653.90 |
| 900 | −7.672 | −7.782 | 0.896 | 0.918 | 806.52 | 852.91 |
| 1000 | −7.656 | −7.776 | 0.902 | 0.912 | 902.36 | 911.69 |
| 1100 | −7.636 | −7.769 | 0.887 | 0.910 | 975.64 | 1001.3 |
| 1200 | −7.625 | −7.763 | 0.901 | 0.904 | 1081.6 | 1084.9 |
| 1300 | −7.594 | −7.756 | 0.884 | 0.902 | 1149.1 | 1173.1 |
| 1400 | −7.567 | −7.750 | 0.886 | 0.897 | 1240.3 | 1256.1 |
| 1500 | −7.538 | −7.743 | 0.876 | 0.888 | 1312.4 | 1331.3 |
With the demonstrated accuracy of the trained MLFF, we are able to further examine the effect of supercell size on the PDOS. In Fig. S4 of the ESI,† we show that the changes in the computed PDOS using the supercell with up to 3840 atoms are again minimal, particularly with no sign of soft phonon modes emerging from the PDOS simulated with a larger supercell, thus suggesting that using a single unit cell of c-LLZO is sufficient to converge the PDOS calculations via VACF.
Although this is not the primary focus of the current study, in Section S2 of the ESI† we also compared the Li ion diffusivity and the corresponding activation energies that are further compared to those values extracted from previous experimental and theoretical results, which also showed good agreement between our MLFF-MD results and previously published data.
Finally, we highlight the computational efficiency delivered by MLFF. With AIMD, simulating a 4-ps-long trajectory using a single unit cell of c-LLZO on 56 CPUs over two Broadwell nodes takes ∼34 hours walltime. In contrast, using MLFF executed on a single V100 GPU, we are able to sample a 10-ps-long trajectory in ∼7 minutes, making the comprehensive thermodynamic sampling of disorder solids, such as LLZO, within the reachable computational capabilities.
3.3 Convergence of configurational free energy without the vibrational contribution
Before the trained MLFF can be applied to compute the configurational free energy of c-LLZO, its capability to reproduce the DFT local minima [cf.Fig. 1(d)] from structural optimisations needs to be further verified. Since our primary interest is the configurational free energy, instead of comparing the structural similarities between the DFT- and MLFF-optimised crystal structures of every c-LLZO configuration, we focus on the differences in energies of the local minima that are sampled by these two different energy models. More specifically, we compare the similarity in the distributions of the energies p(H), as the partition function [eqn (2)] can be re-written in the following integral form for a continuous energy spectrum:and the result is shown in Fig. 5. Here, all the starting structures from the 12_44_opt have been re-optimised with MLFF to generate a new set of local minima on the MLFF-PES.
 | ||
| Fig. 5 Performance of MLFF for structure optimisations. (Solid lines) Distributions of energies p(E) for all the local minima on the PES for the 12_44_opt set. These distributions are shown as the Gaussian Kernel Density Estimates (KDEs) of the underlying data, and KDE is used to present other similar data throughout the rest of this paper. (Dashed lines) Evolutions of the configurational entropic contribution to the free energy (−TSconf) at 300 K as more configurations are included (in the order of increasing energy) in the summation [cf.eqn (2)]. | ||
It can be seen from Fig. 5 that, firstly, the overall shapes of pMLFF(H) and pDFT(H) match well with each other, which again demonstrates the trained MLFF for structural optimisation is very accurate. Because structural optimisation essentially traces the shape of the PES near every local minimum, it means this topological feature has been well reproduced by the MLFF, even though it is trained with only 4% of the available data. Secondly, the energies of the local minima tend to be slightly underestimated by MLFF. This could be due to a different structural optimiser and looser convergence criteria that were used in the structural optimisation with MLFF. Nevertheless, as shown by the dashed lines in Fig. 5, the configurational entropies computed from DFT and MLFF converge to the same value as soon as the highest peak in p(E) is passed, and Table 3 further shows that all thermodynamic quantities computed from MLFF are essentially identical to those from DFT.
| Temp. [K] | 〈H〉T [eV per atom] | S conf [meV per (atom K)] | −TSconf [eV per atom] | G conf [eV per atom] | |
|---|---|---|---|---|---|
| 300 | DFT | −7.839 | 0.7112 | −0.2134 | −8.052 |
| MLFF | −7.839 | 0.7118 | −0.2135 | −8.053 | |
| 1500 | DFT | −7.839 | 0.7167 | −1.075 | −8.914 |
| MLFF | −7.839 | 0.7168 | −1.075 | −8.914 |
For comparison, we trained a separate MLFF for t-LLZO and computed its vibrational free energies (see Table S3 of the ESI,† and because this structure is not disordered, no configurational contribution needs to be included). It can be seen from Table 3 that, at 1500 K, although disorder has contributed an additional 1 eV per atom to the stability of c-LLZO leading to a configurational free energy of −8.914 eV per atom, it is still larger than the vibrational free energy of −9.147 eV per atom for t-LLZO.
3.4 Vibrational contribution to the configurational entropy
Now, we are in the position to examine how thermal vibrations renormalise the PES into the corresponding temperature-dependent free energy surfaces, and subsequently affect the configurational contribution to the thermodynamic stability of site-disordered c-LLZO. We begin with a brief look on how PDOS varies across the configurational space, and in Fig. 6 we have plotted the temperature-dependent configurational-averaged PDOS84 for the 12_44_opt set, which are computed aswith the corresponding standard deviation
in which
 with
with ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) (i)(T) = exp(−〈U(i)(t)〉t/kBT). It can be seen from Fig. 6 that, at a given temperature, the variation in the PDOS as measured by σ[g(ω)] is substantial and does not change significantly across the entire phonon energy range, meaning the vibrational behaviour of the LLZO crystal lattice is very sensitive to how the Li ions are arranged in the crystal. This supports the necessity to compute the vibrational free energy per configuration individually as opposed to approximating it with the value of a single configuration for very accurate results. Nevertheless, σ[g(ω)] are larger at 300 K compared to those at 1500 K, possibly because the latter is the temperature at which LLZO is stable at the cubic phase. Fig. 6 also clearly indicates the increase of PDOS in the energy range above 50 meV from 300 to 1500 K, reflecting the excitation of high energy phonons at the elevated temperatures.
(i)(T) = exp(−〈U(i)(t)〉t/kBT). It can be seen from Fig. 6 that, at a given temperature, the variation in the PDOS as measured by σ[g(ω)] is substantial and does not change significantly across the entire phonon energy range, meaning the vibrational behaviour of the LLZO crystal lattice is very sensitive to how the Li ions are arranged in the crystal. This supports the necessity to compute the vibrational free energy per configuration individually as opposed to approximating it with the value of a single configuration for very accurate results. Nevertheless, σ[g(ω)] are larger at 300 K compared to those at 1500 K, possibly because the latter is the temperature at which LLZO is stable at the cubic phase. Fig. 6 also clearly indicates the increase of PDOS in the energy range above 50 meV from 300 to 1500 K, reflecting the excitation of high energy phonons at the elevated temperatures.
With these, Fig. 7 further demonstrates the distributions of vibrational free energies computed for all configurations in the 12_44_opt set. Compared with the distributions of 0 K-enthalpies Fig. 5, it shows that as the temperature increases, the (free) energy distributions gradually widened and shifted to lower energy ranges, indicating the structure is progressively stabilised by lattice vibrations. The changes in the shapes of the (free) energy distributions further show that the vibrational entropic contribution to the free energy is not a simple constant correction factor across the configurational space. By integrating the free energy distributions, the configurational entropy and free energy that include the vibrational contribution at 300 and 1500 K can be obtained and are listed in Table 4. Using the free energies (Gconf+vib) determined in this way, the cubic phase of LLZO is now correctly predicted to be more stable than the tetragonal one by 973 meV at 1500 K (as opposed to being 233 meV less stable with Gconf only), confirming the importance of lattice vibrations in stabilising the cubic phase at high temperature. In contrary, at 300 K, the cubic phase is also predicted to be more stable than the tetragonal phase by 106 meV based on Gconf+vib, and the later was predicted to be more stable by 147 meV if the vibrational contributions were omitted for c-LLZO. This could be indicating that the lattice vibrations and configurational disorders are strongly competing in determining the phase stability at 300 K, which is worth further investigating in the future.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44. The expectation value of the configurational averaged free energy at a given temperature, 〈Fvib〉T, is calculated using eqn(3) by replacing the enthalpy H(i) with the vibrational free energy F(i)vib [eqn(7)] for each configuration, such as, Gconf+vib = 〈Fvib〉T − TSconf+vib
44. The expectation value of the configurational averaged free energy at a given temperature, 〈Fvib〉T, is calculated using eqn(3) by replacing the enthalpy H(i) with the vibrational free energy F(i)vib [eqn(7)] for each configuration, such as, Gconf+vib = 〈Fvib〉T − TSconf+vib
| Temp. [K] | 〈Fvib〉T [eV per atom] | S conf+vib [meV per (atom K)] | −TSconf+vib [eV per atom] | G conf+vib [eV per atom] |
|---|---|---|---|---|
| 300 | −8.107 | 0.6578 | −0.1973 | −8.305 |
| 1500 | −9.093 | 0.6863 | −1.029 | −10.12 |
3.5 Model transferability to c-LLZO with a different Li site occupancy
Having demonstrated the robustness of the MLFFs that are trained on the structural optimisation and AIMD trajectories for c-LLZO structures with an Li site occupancy of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44, in this section, we shall apply these MLFFs to explore the PES of a larger set of c-LLZO with the Li site occupancy of 11
44, in this section, we shall apply these MLFFs to explore the PES of a larger set of c-LLZO with the Li site occupancy of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 that contains a total of 65
45 that contains a total of 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 unique configurations.34 Similar to Fig. 5, in Fig. 8(a), we first compare the distribution of the local minimum energies p(E) that are obtained through structural optimisation using MLFF, using a subset of c-LLZO containing 19
958 unique configurations.34 Similar to Fig. 5, in Fig. 8(a), we first compare the distribution of the local minimum energies p(E) that are obtained through structural optimisation using MLFF, using a subset of c-LLZO containing 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 configurations, for which the corresponding DFT results are available. Once again, we observe good agreement between pMLFF(E) and pDFT(E), whereby the key features of the peak and shoulders in pDFT(E) are well reproduced in pMLFF(E). This suggests that the as-trained MLFF can be well transferred to model c-LLZO of a different Li site occupancy, and again demonstrates the dominant contributions to the cohesive energies of the crystal is the short-range chemical environment rather than the overall site-occupancy in the unit cell.
333 configurations, for which the corresponding DFT results are available. Once again, we observe good agreement between pMLFF(E) and pDFT(E), whereby the key features of the peak and shoulders in pDFT(E) are well reproduced in pMLFF(E). This suggests that the as-trained MLFF can be well transferred to model c-LLZO of a different Li site occupancy, and again demonstrates the dominant contributions to the cohesive energies of the crystal is the short-range chemical environment rather than the overall site-occupancy in the unit cell.
The most significant advantage offered by MLFF is its speed that enables us to perform the structural optimisation, together with MD samplings at 300 and 1500 K for the entire set of 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 c-LLZO configurations in ∼344 days on a single V100 GPU. This is much less than the ∼810 days that it cost us just to perform structural optimisations on 19
958 c-LLZO configurations in ∼344 days on a single V100 GPU. This is much less than the ∼810 days that it cost us just to perform structural optimisations on 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 configurations (29% of the dataset) using periodic DFT. The results are presented in Fig. 8(b–d) and Table 5.
333 configurations (29% of the dataset) using periodic DFT. The results are presented in Fig. 8(b–d) and Table 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45
45
| Without vibrational contribution | ||||
|---|---|---|---|---|
| Temp. [K] | 〈H〉T [eV per atom] | S conf [meV per (atom K)] | −TSconf [eV per atom] | G conf [eV per atom] |
| 300 | −7.839 | 0.9494 | −0.2848 | −8.123 |
| 1500 | −7.839 | 0.9549 | −1.432 | −9.270 |
| With vibrational contribution | ||||
|---|---|---|---|---|
| Temp. [K] | 〈Fvib〉T [eV per atom] | S conf+vib [meV per (atom K)] | −TSconf+vib [eV per atom] | G conf+vib [eV per atom] |
| 300 | −8.106 | 0.8792 | −0.2638 | −8.369 |
| 1500 | −9.092 | 0.9195 | −1.379 | −10.47 |
The p(H) curves in Fig. 8(b) show that the full set [as given by pMLFF(H)] contains more lower energy configurations than the DFT set [as given by pDFT(H)]. Based on these two distributions, at 300 K, the computed configurational entropic contributions to the free energy −TSconfig is −0.2528 eV per atom from the DFT set, which is 11.2% lower than the converged value of −0.2848 eV per atom from MLFF sampling [also see Table 5]. This level of error is qualitatively consistent when ∼20k of MLFF-optimised local minimum energies are used to determine −TSconfig [see Fig. S8, ESI†]. This underestimation in the configurational entropy can be primarily due to incomplete sampling, and this can be tested by using the KDE (Kernel Density Estimate) density of pDFT (H) to sample a full set of 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 958 enthalpy values and compute the corresponding configurational entropy at 300 K, which gives an estimated −TSconfig of −0.2843 eV per atom or 0.176% relative error. Note that the size of the DFT-optimised set (19
958 enthalpy values and compute the corresponding configurational entropy at 300 K, which gives an estimated −TSconfig of −0.2843 eV per atom or 0.176% relative error. Note that the size of the DFT-optimised set (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333) was not chosen based on any statistical insight but merely an arbitrary point at which we thought there would be sufficient data for benchmarking purposes and decided to stop carrying on with more DFT calculations. In the above analysis, as shown by the density estimations, the DFT set is definitely oversampled, consuming more computing time than it is necessarily needed. A promising future direction is to explore generative models to enhance the sampling efficiency for disordered solids,85–87 but it is beyond the scope of the present work.
333) was not chosen based on any statistical insight but merely an arbitrary point at which we thought there would be sufficient data for benchmarking purposes and decided to stop carrying on with more DFT calculations. In the above analysis, as shown by the density estimations, the DFT set is definitely oversampled, consuming more computing time than it is necessarily needed. A promising future direction is to explore generative models to enhance the sampling efficiency for disordered solids,85–87 but it is beyond the scope of the present work.
Moving on to the vibrational free energy landscapes at finite temperatures, Fig. 8(c and d) show again that the distributions of Fvib widen and shift toward the lower energy range as the temperature is increased from 300 to 1500 K, which is consistent with the observations from Fig. 7. On the other hand, although the number of configurations in this set of c-LLZO is an order of magnitude more than the other set with an Li site occupancy of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44, the converged Gconf+vib values for this set of c-LLZO are only 64 and 350 meV lower than those for the 12
44, the converged Gconf+vib values for this set of c-LLZO are only 64 and 350 meV lower than those for the 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 set at 300 and 1500 K, respectively (see Table 5 and Table 4). This is because the distributions of Fvib [Fig. 8(c and d)] are much wider than the thermal energy kBT at the respective temperatures, such that many high-energy metastable configurations contributed insignificantly towards the partition function.
44 set at 300 and 1500 K, respectively (see Table 5 and Table 4). This is because the distributions of Fvib [Fig. 8(c and d)] are much wider than the thermal energy kBT at the respective temperatures, such that many high-energy metastable configurations contributed insignificantly towards the partition function.
A natural extension from here on will be to apply the as-trained MLFFs to compute the configurational entropies for c-LLZO with other Li site occupancies [Fig. 1(c)], from which the total configurational entropy across the global PES may be obtained from the superposition of energy basins.88–91 However, this is merely an exercise of exhausting computational powers, and more informative sampling strategies should be explored to achieve this goal efficiently to advance the field of computational thermodynamics of disordered solids.
4. Conclusions and future outlooks
In this work, for the first time, we are able to follow the exact statistic thermodynamic protocol, to computationally determine the combined contributions from vibrational and configurational entropies towards the phase stabilities of cubic garnet electrolyte LLZO with two specific Li site occupancies. This is enabled by using the equivariant neural network SO3KRATES that is built upon the transformer architecture, delivering high data efficiency, regression accuracy, enhanced stability in MD simulations, as well as good model transferability. Our results show uniquely, that the configurational free energies determined from the 0 K-enthalpies, which correspond to the energies of the local minima on the PES, are insufficient to correctly order the cubic LLZO over its tetragonal counterpart as the stable phase at 1500 K. This can be remedied instead, by computing the configurational free energies from the Helmholtz free energies, to account for the effect of lattice vibrations in renormalising the 0 K PES to the corresponding finite-temperature free energy surface. Most importantly, our results clearly demonstrate significant variations in the PDOSs, which translate to a non-uniform shift from H to Fvib, across different configurations, rendering the necessity to compute Fvib individually for every LLZO configuration. This task is certainly only feasible by using a fast and stable forcefield, like the one being developed in this work.More specifically, we have chosen to compute the Helmholtz free energies by convoluting the PDOS from MLFF-MD simulations. While this offers the advantage to account for the anharmonicity in lattice vibrations, we cannot fully rule out the possibility of Li ions diffusing into other neighbouring sites due to their highly mobile nature. This means that Fvib calculated in this way may have additionally included contributions from neighbouring local minima that may belong to other Li site occupancies, especially at high temperatures. This could be checked, in the future, by recalculating Fvib based on quasiharmonic approximations from frozen-phonon calculations. Another avenue worth exploring is to train the MLFFs to directly predict Fvib using the data generated in this work, which can immediately offer an order of magnitude speed up in the sampling efficiency.
Despite our explicit account for the vibrational contributions to the phase stabilities of c-LLZO at finite temperatures, we have only considered LLZO with perfect stoichiometry and the effects such as dopants together with Li and O non-stoichiometries in lowering the stable temperature of c-LLZO have been neglected.31,32,92,93 These factors not only diversify the chemical space94 but also increase the number of configurations factorially, making the brute-force approach adopted in this work no longer feasible even with an efficient MLFF. The use of foundational models65 trained across the chemical space of possible dopants in LLZO, that is further combined with generative models,85–87 may offer the much needed solutions in the near future.
Finally, we would like to reiterate a key difference between the traditional atom–atom forcefield95 and MLFF. In the language of artificial intelligence, the former can be considered as ‘rule-based’ models, where there is a clear physical motivation behind the design of each functional employed in the forcefield for computing the strengths of atom–atom interactions, such as the two-body bond stretching and dispersion interactions. In contrast, MLFF developed based on neural network architecture is largely relying on information exchange to surrogate a high-dimensional function, or an ansatz, that best describes the behaviours of the training data. In this regard, the development and adaptation of explainable artificial intelligence in computational chemistry and materials science will be an important avenue to explore for advancing our understanding of the structure–property relationships for functional materials at the atomistic level.96
5 Methodologies
5.1 Ab initio calculations
All DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP)97 with the standard projector augmented wave (PAW) method98 and the PBE -(Perdew–Burke–Ernzerhof)99 exchange–correlation functional. We employed the GW-version of the pseudopotential for each element at an energy cut-off of 500 eV. Geometry optimisations were performed only to relax the atomic positions while keeping the lattice constants unchanged, such that the latter are consistent across all training/validation data. The optimisations were terminated when the energy difference between two successive steps is below 10−4 eV. All calculations were performed without spin polarisation and only a single Γ-centered K-point was adopted in order to speed up the computation of a large set of structures. The K-point setting was chosen by considering that the LLZO structures are of a large unit cell with lattice constants a ∼12–14 Å.To generate the data for training the MLFF for MD simulations, one structure of cubic LLZO with an Li-site occupancy of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 was first randomly selected. Then, an AIMD simulation was carried out from 10 to 2610 K at 1 fs per step for 5.2 ps using the velocity-scaling algorithm to generate a total of 5200 frames for model training and validations. A single unit cell of LLZO is used for AIMD and its lattice constants were kept fixed during the simulation. To achieve a stable MD run using MLFF at a target temperature Tc, it is critical that the MLFF model can learn the topology of the PES over an extensive energy range, such that the model ‘knows’ how to restore to a stable structure if some overly distorted structures are generated during the MD run. This can be achieved by including structures that have been sampled over a wide temperature range in AIMD to generate the data to train the MLFF for MD simulations.73 For benchmarking the phonon DOS using VACF, AIMD simulations were performed under the NVE ensemble using the velocity Verlet algorithm at the target temperatures at 1 fs per step for 4 ps. To further test the model transferability for running MD simulations on other structures in the 1244 opt set (see Section 5.2 for details), 50 structures were randomly selected and AIMD simulations were performed under the NVT ensemble at 320 K for 4 ps at 1 fs per step, using an Anderson thermostat with a collision probability of 0.5. Note that the AIMD trajectories generated under this ensemble are not suitable for computing the phonon DOS, because the atomic forces are ‘contaminated’ by the coupling to the heat bath. As such, they will only be used for comparing the accuracies of energies and atomic forces predicted by the MLFF model.
44 was first randomly selected. Then, an AIMD simulation was carried out from 10 to 2610 K at 1 fs per step for 5.2 ps using the velocity-scaling algorithm to generate a total of 5200 frames for model training and validations. A single unit cell of LLZO is used for AIMD and its lattice constants were kept fixed during the simulation. To achieve a stable MD run using MLFF at a target temperature Tc, it is critical that the MLFF model can learn the topology of the PES over an extensive energy range, such that the model ‘knows’ how to restore to a stable structure if some overly distorted structures are generated during the MD run. This can be achieved by including structures that have been sampled over a wide temperature range in AIMD to generate the data to train the MLFF for MD simulations.73 For benchmarking the phonon DOS using VACF, AIMD simulations were performed under the NVE ensemble using the velocity Verlet algorithm at the target temperatures at 1 fs per step for 4 ps. To further test the model transferability for running MD simulations on other structures in the 1244 opt set (see Section 5.2 for details), 50 structures were randomly selected and AIMD simulations were performed under the NVT ensemble at 320 K for 4 ps at 1 fs per step, using an Anderson thermostat with a collision probability of 0.5. Note that the AIMD trajectories generated under this ensemble are not suitable for computing the phonon DOS, because the atomic forces are ‘contaminated’ by the coupling to the heat bath. As such, they will only be used for comparing the accuracies of energies and atomic forces predicted by the MLFF model.
5.2 Training of the SO3KRATES networks
The SO3KRATES models are trained with the following settings. The dimension of the feature vector F is 132, and h = 4 heads are used in the message-passing updates. The cut-off distance rcut = 5 Å is chosen for identifying neighbouring atoms. l = {1,2,3} is selected for constructing the EVs.For the task of structural optimisations, the SO3KRATES model is trained with T = 2 layers. The 12_44_opt set is used for model training and validation. Briefly, all cubic LLZO structures with a 24d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 96h site occupancy ratio of 12
96h site occupancy ratio of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 are retrieved from the dataset published by Holland et al.34 Then the atomic positions in each structure are randomly disturbed using a method implemented in the pymatgen Python API,100 before it is optimised to its nearby local minimum using DFT. The random distributions help to generate a more diversified set of atomic environments for fitting a robust MLFF model. In total, the 12_44_opt contains 95
44 are retrieved from the dataset published by Holland et al.34 Then the atomic positions in each structure are randomly disturbed using a method implemented in the pymatgen Python API,100 before it is optimised to its nearby local minimum using DFT. The random distributions help to generate a more diversified set of atomic environments for fitting a robust MLFF model. In total, the 12_44_opt contains 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 data points, and 1000 are selected for model validation. Model training is terminated after 500 epochs.
271 data points, and 1000 are selected for model validation. Model training is terminated after 500 epochs.
For the task of molecular dynamics simulations, the SO3KRATES model is trained with T = 3 layers, with 1000 data points used for training and 1200 for validation. Model training is terminated after 1000 epochs.
All data points for training and validation were randomly selected from the full (structural optimisation or AIMD trajectories) set without applying any filtering procedure. We note that more informed and robust strategies to select training data exist, for example, in our previous work,101 structural descriptor and kernel-based ML combined with furthest-point sampling was applied to select a set of structurally most distinctive molecular crystals to enhance the model accuracy while reducing the amount of the training data used. However, using this approach would require the hyperparameters for the kernel to be separately optimised to achieve the best expressivity. Computationally, large amounts of disc storage and memories are also necessary to store the pre-computed structural descriptors and/or kernels, which can be particularly significant for LLZO with more than 100 atoms in the unit cell. This means separate and devoted efforts are required to implement this workflow. As such, we did not implement the furthest-point sampling strategy to optimise the training and validation sets in this work, but it is worth exploring in the future.
All models are trained by minimising the following loss function that combines the energy and atomic forces:
 | (16) |
5.3 Structural optimisations and MD simulations with MLFF
Structural optimisations are performed using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm103 to optimise the atomic positions, and are terminated when the maximum atomic force is smaller than 0.08 eV Å−1. MD simulations at the target temperature are carried out under the NVE ensemble for 6 ps at 1fs/step using the velocity Verlet algorithm.Data availability
The raw data for this work can be freely accessed from https://dataverse.harvard.edu/dataverse/unsw_sse_database. Python scripts used for data generations and analysis in this work can be found at https://github.com/yangjackie/futuremat_public.Conflicts of interest
There are no conflicts to declare.Acknowledgements
All authors would like to acknowledge the financial support from the Australian Research Council under the projects DP220103229, as well as the UNSW Materials and Manufacturing Futures Institute. Computations in this work are conducted on the Gadi supercomputer at NCI Australia that is supported by the UNSW Merit Allocation Scheme and the National Computational Merit Allocation Scheme (NCMAS) under the project dy3, as well as the local katana cluster supported by the Research Technology Service, UNSW.References
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals, Nature, 2014, 508, 373 CrossRef CAS PubMed
.
- T. Zhu and E. Ertekin, Mixed phononic and non-phononic transport in hybrid lead halide perovskites: glass-crystal duality, dynamical disorder, and anharmonicity, Energy Environ. Sci., 2019, 12, 216 RSC
.
- M. M. Ugeda, A. J. Bradley, S.-F. Shi, F. H. Da Jornada, Y. Zhang, D. Y. Qiu, W. Ruan, S.-K. Mo, Z. Hussain, Z.-X. Shen, F. Wang, S. G. Louie and M. F. Crommie, Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor, Nat. Mater., 2014, 13, 1091 CrossRef CAS PubMed
.
- X. Jiang, Q. Zheng, Z. Lan, W. A. Saidi, X. Ren and J. Zhao, Real-time GW-BSE investigations on spin-valley exciton dynamics in monolayer transition metal dichalcogenide, Sci. Adv., 2021, 7, eabf3759 CrossRef PubMed
.
- P. You, D. Chen, X. Liu, C. Zhang, A. Selloni and S. Meng, Correlated electron-nuclear dynamics of photoinduced water dissociation on rutile TiO2, Nat. Mater., 2024, 23, 1100 CrossRef CAS PubMed
.
- A. Otero-De-La-Roza and E. R. Johnson, A benchmark for non-covalent interactions in solids, J. Chem. Phys., 2012, 137, 054103 CrossRef CAS PubMed
.
- J. Nyman, O. S. Pundyke and G. M. Day, Accurate force fields and methods for modelling organic molecular crystals at finite temperatures, Phys. Chem. Chem. Phys., 2016, 18, 15828 RSC
.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC
.
- S. A. Tawfik, T. Gould, C. Stampfl and M. J. Ford, Evaluation of van der Waals density functionals for layered materials, Phys. Rev. Mater., 2018, 2, 034005 CrossRef CAS
.
- Y. Zhang, D. A. Kitchaev, J. Yang, T. Chen, S. T. Dacek, R. A. Sarmiento-Pérez, M. A. Marques, H. Peng, G. Ceder, J. P. Perdew and J. Sun, Efficient first-principles prediction of solid stability: Towards chemical accuracy, npj Comput. Mater., 2018, 4, 9 CrossRef
.
- S. L. Price, Predicting crystal structures of organic compounds, Chem. Soc. Rev., 2014, 43, 2098 RSC
.
- D. H. Bowskill, I. J. Sugden, S. Konstantinopoulos, C. S. Adjiman and C. C. Pantelides, Crystal structure prediction methods for organic molecules: State of the art, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 593 CrossRef CAS PubMed
.
- A. R. Oganov, A. O. Lyakhov and M. Valle, How Evolutionary Crystal Structure Prediction Work, and Why, Acc. Chem. Res., 2011, 44, 227 CrossRef CAS PubMed
.
- L. Wei, N. Fu, E. M. Siriwardane, W. Yang, S. S. Omee, R. Dong, R. Xin and J. Hu, TCSP: a template-based crystal structure prediction algorithm for materials discovery, Inorg. Chem., 2022, 61, 8431 CrossRef CAS PubMed
.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. Cooper and G. M. Day, Functional materials discovery using energy-structure-function maps, Nature, 2017, 543, 657 CrossRef CAS PubMed
.
- C. Collins, M. Dyer, M. Pitcher, G. Whitehead, M. Zanella, P. Mandal, J. Claridge, G. Darling and M. Rosseinsky, Accelerated discovery of two crystal structure types in a complex inorganic phase field, Nature, 2017, 546, 280 CrossRef CAS PubMed
.
- W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, A map of the inorganic ternary metal nitrides, Nat. Mater., 2019, 18, 732 CrossRef CAS PubMed
.
- L. M. Hunnisett,
et al., The seventh blind test of crystal structure prediction: structure generation methods, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2024, 80, 517 CrossRef CAS PubMed
.
- X. Liu, J. Zhang and Z. Pei, Machine learning for high-entropy alloys: Progress, challenges and opportunities, Prog. Mater. Sci., 2023, 131, 101018 CrossRef
.
- A. van de Walle and G. Ceder, The effect of lattice vibrations on substitutional alloy thermodynamics, Rev. Mod. Phys., 2002, 74, 11 CrossRef CAS
.
- J. Yang, Mapping temperature-dependent energy-structure-property relationships for solid solutions of inorganic halide perovskites, J. Mater. Chem. C, 2020, 8, 16815 RSC
.
- F. Pan, J. Zhai, J. Chen, L. Yang, H. Dong, F. Yuan, Z. Jiang, W. Ren, Z.-G. Ye, G.-X. Zhang and J. Li, Mixed-Halide Perovskite Alloys CsPb(I1−xBrx)3 and CsPb(Br1−xClx)3: New Insight of Configurational Entropy Effect from First-Principles and Phase Diagrams, Chem. Mater., 2024, 36, 3957 CrossRef CAS
.
- S. Xia, X. Wu, Z. Zhang, Y. Cui and W. Liu, Practical challenges and future perspectives of all-solid-state lithium-metal batteries, Chem, 2019, 5, 753 CAS
.
- Q. Liu, Z. Geng, C. Han, Y. Fu, S. Li, Y. B. He, F. Kang and B. Li, Challenges and perspectives of garnet solid electrolytes for all solid-state lithium batteries, J. Power Sources, 2018, 389, 120 CrossRef CAS
.
- C. Wang, K. Fu, S. P. Kammampata, D. W. McOwen, A. J. Samson, L. Zhang, G. T. Hitz, A. M. Nolan, E. D. Wachsman, Y. Mo, V. Thangadurai and L. Hu, Garnet-type solid-state electrolytes: materials, interfaces, and batteries, Chem. Rev., 2020, 120, 4257 CrossRef CAS PubMed
.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Electrochemical stability of Li10GeP2S12 and Li7La3Zr2O12 solid electrolytes, Adv. Energy Mater., 2016, 6, 1501590 CrossRef
.
- Y. Wang and W. Lai, Phase transition in lithium garnet oxide ionic conductors Li7La3Zr2O12: The role of Ta substitution and H2O/CO2 exposure, J. Power Sources, 2015, 275, 612 CrossRef CAS
.
- S. Muy, R. Schlem, Y. Shao-Horn and W. G. Zeier, Phonon-ion interactions: designing ion mobility based on lattice dynamics, Adv. Energy Mater., 2021, 11, 2002787 CrossRef CAS
.
- Y. Chen, E. Rangasamy, C. R. dela Cruz, C. Liang and K. An, A study of suppressed formation of low-conductivity phases in doped Li7La3Zr2O12 garnets by in situ neutron diffraction, J. Mater. Chem. A, 2015, 3, 22868 RSC
.
- Z. Yan and Y. Zhu, Impact of Lithium Nonstoichiometry on Ionic Diffusion in Tetragonal Garnet-Type Li7La3Zr2O12, Chem. Mater., 2024, 36, 11551 CrossRef CAS
.
- M. Kubicek, A. Wachter-Welzl, D. Rettenwander, R. Wagner, S. Berendts, R. Uecker, G. Amthauer, H. Hutter and J. Fleig, Oxygen vacancies in fast lithium-ion conducting garnets, Chem. Mater., 2017, 29, 7189 CrossRef CAS
.
- A. Paolella, W. Zhu, G. Bertoni, S. Savoie, Z. Feng, H. Demers, V. Gariepy, G. Girard, E. Rivard, N. Delaporte, A. Guerfi, H. Lorrmann, C. George and K. Zaghib, Discovering the influence of lithium loss on garnet Li7La3Zr2O12 electrolyte phase stability, ACS Appl. Energy Mater., 2020, 3, 3415 CrossRef CAS
.
- D. J. Wales and J. P. Doye, Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms, J. Phys. Chem. A, 1997, 101, 5111 CrossRef CAS
.
- J. Holland, T. Demeyere, A. Bhandari, F. Hanke, V. Milman and C.-K. Skylaris, A Workflow for Identifying Viable Crystal Structures with Partially Occupied Sites Applied to the Solid Electrolyte Cubic Li7La3Zr2O12, J. Phys. Chem. Lett., 2023, 14, 10257 CrossRef CAS PubMed
.
- E. P. George, D. Raabe and R. O. Ritchie, High-entropy alloys, Nat. Rev. Mater., 2019, 4, 515 CrossRef CAS
.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1 CrossRef CAS
.
- S. Adams and R. P. Rao, Ion transport and phase transition in Li7−xLa3 (Zr2−xMx)O12 (M = Ta5+, Nb5+, x = 0,0.25), J. Mater. Chem., 2012, 22, 1426 RSC
.
- Y. Wang, A. Huq and W. Lai, Insight into lithium distribution in lithium-stuffed garnet oxides through neutron diffraction and atomistic simulation: Li7−xLa3Zr2−xTaxO12 (x = 0–2) series, Solid State Ionics, 2014, 255, 39 CrossRef CAS
.
- R. Jalem, M. Rushton, W. Manalastas Jr, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Effects of gallium doping in garnet-type Li7La3Zr2O12 solid electrolytes, Chem. Mater., 2015, 27, 2821 CrossRef CAS
.
- F. A. Garcia Daza, M. R. Bonilla, A. Llordés, J. Carrasco and E. Akhmatskaya, Atomistic insight into ion transport and conductivity in Ga/Al-substituted Li7La3Zr2O12 solid electrolytes, ACS Appl. Mater. Interfaces, 2018, 11, 753 CrossRef PubMed
.
- M. Klenk and W. Lai, Local structure and dynamics of lithium garnet ionic conductors: tetragonal and cubic Li7La3Zr2O7, Phys. Chem. Chem. Phys., 2015, 17, 8758 RSC
.
- F. Chen, J. Li, Z. Huang, Y. Yang, Q. Shen and L. Zhang, Origin of the phase transition in lithium garnets, J. Phys. Chem. C, 2018, 122, 1963 CrossRef CAS
.
- M. J. Klenk and W. Lai, Finite-size effects on the molecular dynamics simulation of fast-ion conductors: A case study of lithium garnet oxide Li7La3Zr2O12, Solid State Ionics, 2016, 289, 143 CrossRef CAS
.
- J. Dai, Q. Chen, T. Glossmann and W. Lai, Comparison of interatomic potential models on the molecular dynamics simulation of fast-ion conductors: a case study of a Li garnet oxide Li7La3Zr2O12, Comput. Mater. Sci., 2019, 162, 333 CrossRef CAS
.
- M. R. Bonilla, F. A. G. Daza, J. Carrasco and E. Akhmatskaya, Exploring Li-ion conductivity in cubic, tetragonal and mixed-phase Al-substituted Li7La3Zr2O12 using atomistic simulations and effective medium theory, Acta Mater., 2019, 175, 426 CrossRef CAS
.
- Z. Zhu and Y. Zhu, Developing Classical Interatomic Potentials for Solid Electrolytes, Acc. Mater. Res., 2022, 3, 1101 CrossRef CAS
.
- H. Shiiba, M. Koyama, N. Zettsu and K. Teshima, Li-Ion Conduction Characteristics at Grain Boundaries in Garnet Li7−xLa3Zr2−xNbxO12 (0 ≤ x ≤ 2), Chem. Mater., 2024, 36, 6370 CrossRef CAS
.
- D. Rettenwander, G. Redhammer, F. Preishuber-Pflügl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. M. Doeff, M. Wilkening, J. Fleig and G. Amthauer, Structural and electrochemical consequences of Al and Ga cosubstitution in Li7La3Zr2O12 solid electrolytes, Chem. Mater., 2016, 28, 2384 CrossRef CAS PubMed
.
- J. Behler, Four generations of high-dimensional neural network potentials, Chem. Rev., 2021, 121, 10037 CrossRef CAS PubMed
.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed
.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef
.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian process regression for materials and molecules, Chem. Rev., 2021, 121, 10073 CrossRef CAS PubMed
.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Fast and accurate modeling of molecular atomization energies with machine learning, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed
.
- Z. Li, J. R. Kermode and A. De Vita, Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces, Phys. Rev. Lett., 2015, 114, 096405 CrossRef PubMed
.
- R. Jinnouchi, F. Karsai and G. Kresse, On-the-fly machine learning force field generation: Application to melting points, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS
.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed
.
- J. S. Smith, O. Isayev and A. E. Roitberg, ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost, Chem. Sci., 2017, 8, 3192 RSC
.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Towards exact molecular dynamics simulations with machine-learned force fields, Nat. Commun., 2018, 9, 3887 CrossRef PubMed
.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, Schnet-a deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed
.
- O. T. Unke and M. Meuwly, PhysNet: A neural network for predicting energies, forces, dipole moments, and partial charges, J. Chem. Theory Comput., 2019, 15, 3678 CrossRef CAS PubMed
.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, MACE: Higher order equivariant message passing neural networks for fast and accurate force fields, Advances in Neural Information Processing Systems, 2022, 35, 11423.
- T. Frank, O. Unke and K.-R. Müller, So3krates: Equivariant attention for interactions on arbitrary length-scales in molecular systems, Advances in Neural Information Processing Systems, 2022, 35, 29400.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning local equivariant representations for large-scale atomistic dynamics, Nat. Commun., 2023, 14, 579 CrossRef CAS PubMed
.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5, 1031 CrossRef
.
- I. Batatia, et al., A foundation model for atomistic materials chemistry, arXiv, 2023, preprint, arXiv:2401.00096 Search PubMed.
- A. C. Grieder, K. Kim, L. F. Wan, J. Chapman, B. C. Wood and N. Adelstein, Effects of Nonequilibrium Atomic Structure on Ionic Diffusivity in LLZO: A Classical and Machine Learning Molecular Dynamics Study, J. Phys. Chem. C, 2024, 128, 8560 CrossRef CAS
.
- K. Kim, A. Dive, A. Grieder, N. Adelstein, S. Kang, L. F. Wan and B. C. Wood, Flexible machine-learning interatomic potential for simulating structural disordering behavior of Li7La3Zr2O12 solid electrolytes, J. Chem. Phys., 2022, 156, 221101 CrossRef CAS PubMed
.
- M. Ataya, E. McCalla and R. Z. Khaliullin, Machine Learning for High-Throughput Configuration Sampling of Li-La-Ti-O Disordered Solid-State Electrolyte, J. Phys. Chem. C, 2024, 128, 14149 CrossRef CAS
.
- A. Duval, S. V. Mathis, C. K. Joshi, V. Schmidt, S. Miret, F. D. Malliaros, T. Cohen, P. Lio, Y. Bengio and M. Bronstein, A Hitchhiker's Guide to Geometric GNNs for 3D Atomic Systems, arXiv, 2023, preprint, arXiv:2312.07511 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International Conference in Machine Learning, 2017, 1263.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed
.
- J. Wang, Y. Wang, H. Zhang, Z. Yang, Z. Liang, J. Shi, H.-T. Wang, D. Xing and J. Sun, E(n)-Equivariant cartesian tensor message passing interatomic potential, Nat. Commun., 2024, 15, 7607 CrossRef CAS PubMed
.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. Jaakkola, Forces are not enough: Benchmark and critical evaluation for machine learning force fields with molecular simulations, arXiv, 2022, preprint, arXiv:2210.07237 Search PubMed.
- J. T. Frank, O. T. Unke, K.-R. Müller and S. Chmiela, A Euclidean transformer for fast and stable machine learned force fields, Nat. Commun., 2024, 15, 6539 CrossRef CAS PubMed
.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, Attention Is All You Need, arXiv, 2023, preprint, arXiv:1706.03762 Search PubMed.
- P. Korotaev, M. Belov and A. Yanilkin, Reproducibility of vibrational free energy by different methods, Comput. Mater. Sci., 2018, 150, 47 CrossRef CAS
.
- D.-B. Zhang, T. Sun and R. M. Wentzcovitch, Phonon quasiparticles and anharmonic free energy in complex systems, Phys. Rev. Lett., 2014, 112, 058501 CrossRef PubMed
.
- V. S. Kandagal, M. D. Bharadwaj and U. V. Waghmare, Theoretical prediction of a highly conducting solid electrolyte for sodium batteries: Na10GeP2S12, J. Mater. Chem. A, 2015, 3, 12992 RSC
.
- A. H. Larsen,
et al., The atomic simulation environment a Python library for working with atoms, J. Phys.:Condens. Matter, 2017, 29, 273002 CrossRef PubMed
.
- B. Ahammed and E. Ertekin, Configurational Disorder, Strong Anharmonicity, and Coupled Host Dynamics Lead to Superionic Transport in Li3YCl6 (LYC), Adv. Mater., 2024, 36, 2310537 CrossRef CAS PubMed
.
- M. Baggioli and A. Zaccone, Universal origin of boson peak vibrational anomalies in ordered crystals and in amorphous materials, Phys. Rev. Lett., 2019, 122, 145501 CrossRef CAS PubMed
.
- F. Knoop, T. A. Purcell, M. Scheffler and C. Carbogno, Anharmonicity measure for materials, Phys. Rev. Mater., 2020, 4, 083809 CrossRef CAS
.
- J. Yang, J. Fan and S. Li, Mapping the Room-Temperature Dynamic Stabilities of Inorganic Halide Double Perovskites, Chem. Mater., 2022, 34, 9072 CrossRef CAS
.
- T. D. Humphries, J. Yang, R. A. Mole, M. Paskevicius, J. E. Bird, M. R. Rowles, M. S. Tortoza, M. V. Sofianos, D. Yu and C. E. Buckley, Fluorine substitution in magnesium hydride as a tool for thermodynamic control, J. Phys. Chem. C, 2020, 124, 9109 CrossRef CAS
.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning, Science, 2019, 365, eaaw1147 CrossRef PubMed
.
- S. Mehdi, Z. Smith, L. Herron, Z. Zou and P. Tiwary, Enhanced sampling with machine learning, Ann. Rev. Phys. Chem., 2024, 75, 347 CrossRef CAS PubMed
.
- L. Midgley, V. Stimper, J. Antorán, E. Mathieu, B. Schölkopf and J. M. Hernández-Lobato, SE (3) equivariant augmented coupling flows, Advances in Neural Information Processing Systems, 2024, 36, 79200 Search PubMed.
- F. H. Stillinger and T. A. Weber, Packing structures and transitions in liquids and solids, Science, 1984, 225, 983 CrossRef CAS PubMed
.
- D. J. Wales, Coexistence in small inert gas clusters, Mol. Phys., 1993, 78, 151–171 CrossRef CAS
.
- B. Strodel and D. J. Wales, Free energy surfaces from an extended harmonic superposition approach and kinetics for alanine dipeptide, Chem. Phys. Lett., 2008, 466, 105 CrossRef CAS
.
- V. A. Sharapov, D. Meluzzi and V. A. Mandelshtam, Low-temperature structural transitions: Circumventing the broken-ergodicity problem, Phys. Rev. Lett., 2007, 98, 105701 CrossRef PubMed
.
- Y. Zhu, J. Zhang, W. Li, Y. Zeng, W. Wang, Z. Yin, B. Hao, Q. Meng, Y. Xue, J. Yang and S. Li, Enhanced Li+ conductivity of Li7La3Zr2O12 by increasing lattice entropy and atomic redistribution via Spark Plasma Sintering, J. Alloys Compd., 2023, 967, 171666 CrossRef CAS
.
- Y. Zhu, J. Zhang, W. Li, Y. Xue, J. Yang and S. Li, Realization of superior ionic conductivity by manipulating the atomic rearrangement in Al-doped Li7La3Zr2O12, Ceram. Int., 2023, 49, 10462 CrossRef CAS
.
- E. Anderson, E. Zolfaghar, A. Jonderian, R. Z. Khaliullin and E. McCalla, Comprehensive Dopant Screening in Li7La3Zr2O12 Garnet Solid Electrolyte, Adv. Energy Mater., 2024, 14, 2304025 CrossRef CAS
.
- J. A. Harrison, J. D. Schall, S. Maskey, P. T. Mikulski, M. T. Knippenberg and B. H. Morrow, Review of force fields and intermolecular potentials used in atomistic computational materials research, Appl. Phys. Rev., 2018, 5, 031104 Search PubMed
.
- D. Minh, H. X. Wang, Y. F. Li and T. N. Nguyen, Explainable artificial intelligence: a comprehensive review, Artif. Intell. Rev., 2022, 55, 1 CrossRef
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source
Python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314 CrossRef CAS
.
- F. Musil, S. De, J. Yang, J. E. Campbell, G. M. Day and M. Ceriotti, Machine learning for the structure-energy-property landscapes of molecular crystals, Chem. Sci., 2018, 9, 1289–1300 RSC
.
- D. P. Kingma, Adam: A method for stochastic optimization, arXiv, 2014, preprint, arXiv:1412.6980 Search PubMed.
- D. C. Liu and J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Prog., 1989, 45, 503 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00138b |
‡ By convention, the letters represent the Wyckoff positions, and the numbers signify the total number of equivalent Wyckoff positions, in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group for c-LLZO. d space group for c-LLZO. |
| § In the numerical implementation of eqn (2), H(i) is measured with respect to the energy zero point, which, in this case, is set at min{H(i)}, namely, the global energy minimum for the set of LLZO under consideration. The same principle also applies to eqn (4). |
| This journal is © the Owner Societies 2025 |