Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular dynamics studies of oxide ion transport in Sr-doped LaFeO3: role of cationic environments and cooperativity†
Sanjib
Ray
 and
P. Padma
Kumar
and
P. Padma
Kumar

Department of Physics, Indian Institute of Technology Guwahati, Guwahati, Assam 781039, India. E-mail: padmakumarp@iitg.ac.in
First published on 10th March 2025
Abstract
Classical molecular dynamics simulation is employed to study La1−xSrxFeO3−x/2 at 1200 K over a range of dopant concentrations, x = 0.1 to 0.6. Sr ions tend to improve the energetics of the oxide ion sites, resulting in a higher fraction of vacancies in the vicinity of La. The oxide ion migration in the system involves predominantly intra-octahedral hops along the edges of the FeO6 octahedra. This ion migration is controlled by a triangular bottleneck of cations, formed by two La/Sr ions and one Fe ion, appearing midway between two neighboring oxide ion sites. It is noted that these bottlenecks pose higher barriers as more Sr ions are introduced. This increase in the microscopic energy barriers for oxide ion migration in the system corroborates the observed slowdown of ion transport with dopant concentration. The study also elucidates a dynamic correlation between the mobile species and the cationic framework, wherein as an oxide ion approaches the bottleneck, the cations move apart, increasing the cross-sectional area of the bottleneck.
1 Introduction
One of the key challenges to our society in this century is to reduce our dependency on fossil fuels. Carbon-neutral power generation can be achieved by resorting to energy sources like nuclear, solar, wind, and hydroelectric generators. However, when it comes to portable ‘green’ energy devices, we are limited to the choice of batteries and fuel cells. Fuel cells are primary energy devices, as opposed to batteries, that convert chemical energy in the fuel to electricity. Solid oxide fuel cells (SOFCs) are particularly attractive among their peers, owing to their scalability, longer life, high fuel efficiency, low emission, and fuel flexibility (permitting hydrogen as well as hydrocarbons).1–10The main components of a SOFC are the cathode, anode, and electrolyte. An ideal electrolyte must be a good ionic conductor but highly resistive to electronic conduction, whereas electrodes, i.e. cathode and anode, can be electronic as well as mixed ionic electronic conductors (MIECs). One of the shortcomings of pure electronic conducting cathode materials is that the oxygen reduction reaction is limited only to the triple phase boundary (TPB), the region where the cathode, electrolyte, and air meet, which reduces the efficiency of the fuel cell. MIEC cathodes have the advantage that the oxygen reduction reaction is not limited to TPB but over the entire surface of the cathode exposed to fuel.11–15 Typically, SOFCs suffer from their requirement of a high operating temperature, in the range of 1100–1300 K, which causes material degradation and shortening of their lifespan.14,16–18 Thus, in recent years, more attention has been paid to lowering the operating temperature of SOFCs to the intermediate regime (900–1100 K). One of the key challenges in lowering the operating temperature is the reduced electrocatalytic rate at the cathode.12,13,15–17,19,20 However, this deficiency can be better managed if the ionic conductivity of the cathode can be improved (that is, by overcoming the limitations due to TPB by MIEC). This strategy offers cost reduction and efficiency of SOFCs, which improves their market competitiveness essential for scaling up commercialization.
Over the past two decades, ABO3 based perovskites, where large cations (such as La, Pr, Sm, Nd, Gd, etc.) occupy the A sites and transition metals (such as Mn, Fe, Co, etc.) occupy the B sites, have been extensively studied for their potential applications in SOFCs as electrolytes and cathode materials.8,13,21–31 In general, ion transport in solids occurs primarily through vacancy migration and interstitial mechanisms.32 Oxide ion transport in perovskite materials occurs through the vacancy migration mechanism, where an oxide ion hops to one of its adjacent vacant sites, leaving the original site available for other ions to occupy. These vacancies are typically generated by aliovalent doping of the parent material.8,33 Lanthanum ferrites (LaFeO3), when doped with Sr, generate the necessary oxide ion vacancies for ion migration, while promoting favorable p-type electrical conductivity.34,35 Reportedly, Sr-doping also improves the chemical stability of these ferrites;36 however, their oxide ion (O2−) conductivity is rather low for SOFC applications at intermediate temperatures.
Computational studies in the past have offered valuable insights into ion conduction mechanisms in superionic solids.37–46 In one of the earliest computational studies on lanthanum ferrites, Jones and Islam47 examined the ion migration channels, the nature of bottlenecks for ion migration, and the effect of dopants on the microscopic barriers, using empirical-potential based calculations for the orthorhombic phase of LaFeO3, with the lattice treated static. Since then many density functional theory (DFT) based studies have investigated the role of the Sr dopant in oxygen vacancy formation and migration energy in LaFeO3 giving useful insights.48–51 Very recently, the influence of grain boundaries on oxide ion diffusion was examined using a molecular dynamics study of orthorhombic and cubic phases of polycrystalline Sr substituted LaFeO3 by Bonkowski et al.52
 | ||
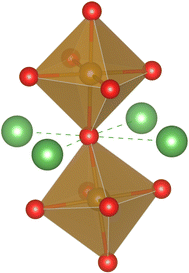
Fig. 1 The rhombohedral structure (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) of LaFeO3 showing corner shared FeO6 octahedra. The red balls represent oxygen, with Fe occupying the center of the octahedra. c) of LaFeO3 showing corner shared FeO6 octahedra. The red balls represent oxygen, with Fe occupying the center of the octahedra. | ||
Over the typical operating temperatures (∼1200 K) these solids generally stabilize in the rhombohedral phase for a wide range of Sr concentrations (x = 0.1 to 0.6).53 However, there are very few theoretical studies that examined the rhombohedral phases. Furthermore, most of the theoretical works available in the literature focus on the energetics of vacancy creation and migration, and hardly any dynamical properties were reported. In fact, except for the study of Bonkowski et al.,52 computational studies have been performed within a frozen cationic sub-lattice approximation. However, at the typical operating temperature of a fuel cell, the dynamics of the framework cations can significantly impact the oxide ion diffusion. In a recent review on the appropriateness of different computational techniques in the study of material properties, Schwarz et al. emphasized the need to invoke a dynamical approach as opposed to static calculations.54
Thus, the present study explores the rhombohedral phase (Fig. 1) of La1−xSrxFeO3−x/2 for Sr concentrations over x = 0.1 to 0.6 employing classical molecular dynamics simulations at 1200 K. The choice of this rather high-temperature simulation is to enhance the ion dynamics for better statistics. The focus of the article is on the microscopic structural and dynamical properties for a better understanding of the mechanism governing the oxide ion transport in these systems and the various factors that influence it.
2 Computational details
Classical molecular dynamics (MD) simulations of La1−xSrxFeO3−x/2 are carried out in an isothermal–isobaric (NPT) ensemble at 1200 K for various Sr dopant concentrations (x = 0.1–0.6). Interactions between the ions are modeled using short-range Buckingham potential coupled with long-range Coulombic interactions, | (1) |
| Pairs | A ij (eV) | ρ ij (Å) | C ij (eV Å6) |
|---|---|---|---|
| La3+⋯O2− | 1545.21 | 0.3590 | 0 |
| Sr2+⋯O2− | 1400.00 | 0.3500 | 0 |
| Fe3+⋯O2− | 1156.36 | 0.3299 | 0 |
| O 2−⋯O2− | 22764.30 | 0.1490 | 43 |
NPT-MD simulations are carried out for 20 ns, after dedicating an initial 4 ns for equilibration. A time step of 2 fs is used for integration, and trajectories are stored at intervals of 1 ps. The simulation cell consists of 5 × 5 × 2 rhombohedral unit cells, each containing six formula units of La1−xSrxFeO3−x/2, such that the undoped system has 1500 number of atoms (300-La, 300-Fe, 900-O). The number of oxide ions in the simulation cell varies from 885 to 810, with the corresponding oxygen vacancies varying from 15 to 90, respectively for x = 0.1 and 0.6. The NPT-MD simulations were started from the experimental structure,55 having unit-cell parameters, a = b = 5.51107 Å and c = 13.41578 Å. Periodic boundary conditions and Ewald summation techniques are employed to mimic the bulk system. The Sr doping is performed at the La sites, picked randomly, and charge neutrality is maintained by removing one oxide ion for every two Sr inserted. Simulations are carried out using the LAMMPS package56 and the trajectories are analyzed using in-house software.
3 Results and discussion
3.1 Structure
In order to establish the reliability of the potential parameters, the structural properties of the system are investigated. The typical time evolution of the lattice parameters of the rhombohedral unit cell of La1−xSrxFeO3−x/2 during the NPT-MD simulations at 1200 K is presented in Fig. S1 in the ESI,† for select compositions. As shown in Fig. 2, the average lattice parameters of the systems increase marginally with Sr doping, and the values are within 3% of the experimental values. | ||
| Fig. 2 The average lattice parameters of a rhombohedral cell of La1−xSrxFeO3−x/2, where x = 0.1 to 0.6, from NPT-MD simulations at 1200 K. | ||
The spatial distributions of the atoms in the system are examined using the radial distribution function (RDF), calculated as
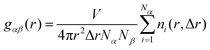 | (2) |
Fig. 3 shows RDFs between La–O, Sr–O, Fe–O, and O–O pairs for different compositions x = 0.1 to 0.6 at 1200 K. The vertical bars correspond to RDFs calculated from the experimentally reported structure for the undoped system.55 As seen the dynamic RDFs of different pairs are in good agreement with their experimental ones, confirming the structural integrity of the simulated system. The broadening in the dynamic RDFs is because of the thermal vibrations of atoms about their mean positions and the successive peaks in the RDFs represent the consecutive position of neighboring atoms of that particular species with respect to the reference atom. It is observed that the Sr–O distance is slightly higher than the La–O distance across the composition, which is attributed to the larger ionic radius of Sr2+ and its relatively weaker Coulombic attraction with O2−.
3.2 Ion transport
As noted earlier, the substitution of Sr2+ at the La3+ sites results in the creation of oxygen vacancies in the matrix, which are quintessential for oxide ion transport in these systems. It shall be noted that the interstitial sites are not energetically favorable for the oxide ions due to their bonding characteristic with the cationic framework.57 Induced by the vacancies, the thermally activated oxide ions hop off from one lattice site to another vacant site, leaving behind a vacancy that is now accessible to other oxygens in the neighborhood. As this process continues, the vacancies essentially migrate in the system in a complementary fashion, though the nature of the dynamics of the ion and its residual vacancies could be different.33,58–60 We shall, however, note that while the vacancies are essential for oxide ion transport, other factors, such as the nature of the dopant ion (Sr), also start controlling the overall transport, as detailed later in the article.The gross transport properties of the system, such as the self-diffusivity and ionic conductivity, can be obtained by calculating the mean squared displacement (MSD) of atoms with time, given by
MSD(t) = 〈|![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (t + τ) − (t + τ) − ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (τ)|2〉 (τ)|2〉 | (3) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (t) is the position vector of the particle at time t and the angular bracket indicates averaging over all the ions and for numerous time origins τ. Shown in Fig. 4 are the MSDs of oxide ions in La1−xSrxFeO3−x/2, for different compositions x = 0.1 to 0.6 at 1200 K. It is observed that MSDs of oxide ions decrease with increasing Sr concentration. The MSDs of the cations in the system (as demonstrated in Fig. S2 in the ESI†) remain flat for all compositions, indicating that their dynamics are limited to vibrations about the mean position, providing further evidence of the structural stability of the simulated system.
(t) is the position vector of the particle at time t and the angular bracket indicates averaging over all the ions and for numerous time origins τ. Shown in Fig. 4 are the MSDs of oxide ions in La1−xSrxFeO3−x/2, for different compositions x = 0.1 to 0.6 at 1200 K. It is observed that MSDs of oxide ions decrease with increasing Sr concentration. The MSDs of the cations in the system (as demonstrated in Fig. S2 in the ESI†) remain flat for all compositions, indicating that their dynamics are limited to vibrations about the mean position, providing further evidence of the structural stability of the simulated system.
 | ||
| Fig. 4 Mean squared displacement of oxide ions in La1−xSrxFeO3−x/2, where x = 0.1 to 0.6, from NPT-MD simulations at 1200 K. | ||
The self-diffusion coefficient of oxide ions is estimated by fitting to the Einstein relation,
 | (4) |
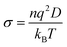 | (5) |
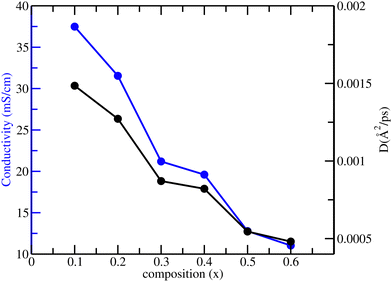 | ||
| Fig. 5 The self-diffusivity of oxide ions (black) and the corresponding conductivity (blue) for La1−xSrxFeO3−x/2, where x = 0.1 to 0.6 from NPT-MD simulations at 1200 K. | ||
As seen in Fig. 5, the calculated self-diffusivity and oxide ion conductivity decrease monotonically with increasing Sr concentration. This behavior can be understood in terms of the changes in the energetics of the local oxide ion environment with increasing Sr concentration, discussed in the later sections. It shall be noted that the oxide ion conductivities in earlier experimental reports are quite scattered, differing from one another by orders of magnitude, thus making it difficult for any direct comparison.61–67 In fact, an earlier experimental study by Patrakeev et al. observed an increase in ionic conductivity with Sr doping, producing a maximum around x = 0.5 and dropping afterward, which is in contrast to the present observations.34
3.3 Microscopic insights
In LaFeO3, oxygen occupies the corners of the FeO6 octahedra and each oxygen is shared by two such octahedra. Thus the structure can be imagined as a network of such octahedra linked through oxide ions. Oxygens are also four coordinated with the La sites that are partially replaced by Sr, as shown in Fig. 6. Thus, based on the number of La and Sr neighbors, five distinct oxygen environments are possible in the matrix. We choose to label these oxygen environments as Sm, where m = 0, 1, 2, 3, and 4, depending on the number of Sr present locally around an oxygen site. For example, S0 represents an oxygen environment where all the four neighbors of the oxygen are La, and S2 represents an environment that has two Sr and two La neighbors. | (6) |
The unanticipated dip in energy profiles, which emerges variably around 0.6–0.9 Å depending on the composition, observed in a recent DFT study as well,49 is attributed to the local distortions of the oxygen sub-lattice, wherein oxygens temporarily relocate closer to the saddle point at instances when the adjacent oxygen site is vacant. A vacancy at the neighboring site results in a temporal imbalance of forces on an oxide ion due to the repulsion from the oxide ions in the other direction. However, a further shift is controlled due to the repulsion of bottleneck cations (detailed in the next sub-section); thus, an intermediate minimum is established. This mechanism is established by examining the potential energy profiles under two possible scenarios (presented in Fig. S3 in the ESI†): (a) when the neighboring oxygen site is occupied – the minimum at the intermediate distance vanishes; (b) but when the neighboring site is vacant – the intermediate minimum is prominently seen.
The sluggish oxide ion mobility in Sr rich environments can be demonstrated from the timescales of oxygen hop from the five different oxygen environments (S0 to S4). For this, we exploit the self-part of the van-Hove correlation function Gs(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , t), given by
, t), given by
 | (7) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) i(t) is the position vector of the ith particle at time t, N is the number of oxide ions, and δ is the Dirac delta function. Gs(
i(t) is the position vector of the ith particle at time t, N is the number of oxide ions, and δ is the Dirac delta function. Gs(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , t) thus describes the probability density that an ion initially (at t = 0) at its original site is found at a distance r (that is, in a spherical shell of volume 4πr2dr around the original site) after time t. Fig. 13 shows the corresponding probability, 4πr2Gs(
, t) thus describes the probability density that an ion initially (at t = 0) at its original site is found at a distance r (that is, in a spherical shell of volume 4πr2dr around the original site) after time t. Fig. 13 shows the corresponding probability, 4πr2Gs(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , t), that an ion is found in a shell of radius r and thickness unity, after an elapsed time t, in the five different environments for two different time intervals. As a note in passing, in a recent study, we have utilized this function to estimate the residence time of oxygens in yttria doped ceria (YxCe1−xO2−δ).71
, t), that an ion is found in a shell of radius r and thickness unity, after an elapsed time t, in the five different environments for two different time intervals. As a note in passing, in a recent study, we have utilized this function to estimate the residence time of oxygens in yttria doped ceria (YxCe1−xO2−δ).71
Fig. 13 suggests that at short time intervals of 10 ps, only the first peak is prominent for all five oxygen environments, while for a larger time interval of 1 ns, the oxide ions start jumping off from their original site to the nearest sites (at a distance of ∼2.7–3.0 Å) leading to the development of second peaks (at the expense of the first). It can be seen that during the 1 ns, a significant fraction of the oxide ions jump off from the S0 environments (having no Sr in the neighborhood), as evident from the height of the second peak. However, as the number of Sr in the environment increases, this fraction decreases systematically, demonstrating that ion hops are becoming sluggish progressively.
4 Conclusions
A comprehensive investigation of various microscopic aspects related to oxide ion mobility in Sr doped LaFeO3 (La1−xSrxFeO3−x/2, x = 0 to x = 0.6) is carried out employing molecular dynamics simulations at 1200 K. The structural features of the rhombohedral phase examined in the present simulation are in agreement with experimental observations across the composition range. The present simulation predicts that the oxide ion conductivity of the La1−xSrxFeO3−x/2 system drops with Sr concentration. However, the available experimental results on the ionic conductivities of these solids from different groups are rather scattered, both quantitatively as well as qualitatively, making it hard to make comparisons.It is noted that the oxide ion diffusion in the system is through intra-octahedral hops, as opposed to inter-octahedral, along the edges of the FeO6 octahedra. The microscopic energy barrier for the oxide ion diffusion along this pathway increases steadily with Sr doping corroborating the nature of the ionic conductivity observed. Further insights on the mechanism of ion transport are derived through analysis of the local oxygen environments and the bottlenecks along the migration channels. The individual energy of oxide ions decreases in the Sr-rich environments favoring higher occupancies of such sites, resulting in oxygen vacancies populating the La-rich environments. Thus, as a result of the random doping of Sr at the La sites, the oxygen vacancies remain positionally disordered in the La1−xSrxFeO3−x/2 matrix.
Interestingly, we observe a cooperative mechanism wherein the triangular bottleneck formed by the cations opens up as the oxygen approaches it for an impending jump. The three kinds of bottlenecks, due to the different La/Sr combinations forming the corners of the triangle, are analyzed individually for their dimensions and energetic barriers. While the dimensions of the triangular bottlenecks are insensitive to the cations (La/Sr) forming its corners, the bottlenecks start posing substantially higher energy barriers as La is replaced by Sr. The larger ionic radius of Sr, as compared to La, results in narrowing of the effective window size, causing higher barriers for oxide ion migration. The resulting slowdown of ion hops in Sr-rich environments is explicitly demonstrated using time correlation functions. Thus doping results in the localization of oxide ions due to the increase in the fraction of Sr-rich environments in the matrix, which accounts for relatively higher oxygen occupancies and poses higher migration barriers. This explains the slower oxide ion transport in La1−xSrxFeO3−x/2 systems with Sr concentration.
The study highlights that an increase in the effective bottleneck radius, which involves an intricate interplay between the lattice parameters and dopant size, could enhance the oxide ion transport. Thus, smaller dopants at A and B sites that do not cause significant contraction of the lattice need to be explored. Alternatively, the oxide ion transport could possibly be enhanced if the fraction of Sr-rich environments can be controlled through tailored synthesis strategies producing uniform distribution of dopants (Sr) in the matrix. The need for further experimental studies is also evident from the scatter of the conductivity data in the literature.
Author contributions
Not applicable.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
No conflict of interest or competing interests to declare.Acknowledgements
We thank the Centre for Development of Advanced Computing (CDAC), Pune, and Param Kamrupa, IIT Guwahati, managed by the National Super Computing Mission (NSM), India, for the generous allowance of CPU hours. The use of the LAMMPS56 package for MD simulations and VMD72 and VESTA73 software for visualization is acknowledged.References
- A. B. Stambouli and E. Traversa, Renewable Sustainable Energy Rev., 2002, 6, 433–455 CrossRef CAS.
- N. Q. Minh, J. Am. Ceram. Soc., 1993, 76, 563–588 CrossRef CAS.
- S. C. Singhal, Solid State Ionics, 2000, 135, 305–313 CrossRef CAS.
- R. M. Ormerod, Chem. Soc. Rev., 2003, 32, 17–28 RSC.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS.
- P. Singh and N. Q. Minh, Int. J. Appl. Ceram. Technol., 2004, 1, 5–15 CAS.
- D. J. Brett, A. Atkinson, N. P. Brandon and S. J. Skinner, Chem. Soc. Rev., 2008, 37, 1568–1578 RSC.
- L. Malavasi, C. A. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387 RSC.
- S. M. Haile, Acta Mater., 2003, 51, 5981–6000 CrossRef CAS.
- T. Elmer, M. Worall, S. Wu and S. B. Riffat, Renewable Sustainable Energy Rev., 2015, 42, 913–931 CrossRef.
- J. Savioli and G. W. Watson, Curr. Opin. Electrochem., 2020, 21, 14–21 CrossRef CAS.
- S. B. Adler, Chem. Rev., 2004, 104, 4791–4844 CrossRef CAS PubMed.
- C. Sun, R. Hui and J. Roller, J. Solid State Electrochem., 2010, 14, 1125–1144 CrossRef CAS.
- A. B. Muñoz-Garca, M. Pavone, A. M. Ritzmann and E. A. Carter, Phys. Chem. Chem. Phys., 2013, 15, 6250–6259 RSC.
- D. Ding, M. Liu, Z. Liu, X. Li, K. Blinn, X. Zhu and M. Liu, Adv. Energy Mater., 2013, 3, 1149–1154 CrossRef CAS.
- A. J. Jacobson, Chem. Mater., 2010, 22, 660–674 CrossRef CAS.
- E. D. Wachsman and K. T. Lee, Science, 2011, 334, 935–939 CrossRef CAS PubMed.
- L. Yang, S. Wang, K. Blinn, M. Liu, Z. Liu, Z. Cheng and M. Liu, Science, 2009, 326, 126–129 CrossRef CAS PubMed.
- J. C. Ruiz-Morales, D. Marrero-López, M. Gálvez-Sánchez, J. Canales-Vázquez, C. Savaniu and S. N. Savvin, Energy Environ. Sci., 2010, 3, 1670–1681 RSC.
- Y. Zhu, W. Zhou, R. Ran, Y. Chen, Z. Shao and M. Liu, Nano Lett., 2016, 16, 512–518 CrossRef CAS PubMed.
- T. Ishihara, Perovskite oxide for solid oxide fuel cells, Springer Science & Business Media, 2009 Search PubMed.
- O. Tripathy and P. P. Kumar, J. Mater. Sci., 2017, 52, 6542–6553 CrossRef CAS.
- P. R. Chandran and T. Arjunan, Int. J. ChemTech Res., 2015, 7, 488–497 Search PubMed.
- T.-L. Wen, H. Tu, Z. Xu and O. Yamamoto, Solid State Ionics, 1999, 121, 25–30 CrossRef CAS.
- J. Richter, P. Holtappels, T. Graule, T. Nakamura and L. J. Gauckler, Monatsh. Chem., 2009, 140, 985–999 CrossRef CAS.
- A. Orera and P. Slater, Chem. Mater., 2010, 22, 675–690 CrossRef CAS.
- Y. Sakaki, Y. Takeda, A. Kato, N. Imanishi, O. Yamamoto, M. Hattori and Y. Esaki, Funtai oyobi Funmatsu Yakin, 1999, 46, 293–299 CAS.
- K. Huang, H. Y. Lee and J. B. Goodenough, J. Electrochem. Soc., 1998, 145, 3220 CrossRef CAS.
- H. Kamata, A. Hosaka, J. Mizusaki and H. Tagawa, Solid State Ionics, 1998, 106, 237–245 CrossRef CAS.
- A. Chroneos, B. Yildiz, A. Tarancón, D. Parfitt and J. A. Kilner, Energy Environ. Sci., 2011, 4, 2774–2789 RSC.
- R. De Souza and J. Kilner, Solid State Ionics, 1998, 106, 175–187 CrossRef CAS.
- P. G. Bruce, Solid state electrochemistry, Cambridge University Press, 1997 Search PubMed.
- A. B. Muñoz-Garca, A. M. Ritzmann, M. Pavone, J. A. Keith and E. A. Carter, Acc. Chem. Res., 2014, 47, 3340–3348 CrossRef PubMed.
- M. Patrakeev, J. Bahteeva, E. Mitberg, I. Leonidov, V. Kozhevnikov and K. Poeppelmeier, J. Solid State Chem., 2003, 172, 219–231 CrossRef CAS.
- J. Mizusaki, T. Sasamoto, W. R. Cannon and H. K. Bowen, J. Am. Ceram. Soc., 1983, 66, 247–252 CrossRef CAS.
- T. Kawada and H. Yokokawa, Key Eng. Mater., 1996, 125, 187–248 Search PubMed.
- A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, J. Mater. Chem., 2010, 20, 266–270 RSC.
- E. Robens, R. Rauschen, J. Kaub, J. P. Parras, D. Kemp, C. L. Freeman and R. A. De Souza, J. Mater. Chem. A, 2022, 10, 2388–2397 RSC.
- F.-F. Lu and H.-K. Tian, Phys. Chem. Chem. Phys., 2023, 25, 18973–18982 RSC.
- M. Jaipal and A. Chatterjee, J. Phys. Chem. C, 2017, 121, 14534–14543 CrossRef CAS.
- P. P. Dholabhai, J. B. Adams, P. Crozier and R. Sharma, Phys. Chem. Chem. Phys., 2010, 12, 7904–7910 RSC.
- M. S. Islam, D. J. Driscoll, C. A. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085–5092 CrossRef CAS.
- S. K. Moharana and P. P. Kumar, Solid State Ionics, 2023, 403, 116409 CrossRef CAS.
- S. Madhual, K. Pramanik and P. P. Kumar, Phys. Chem. Chem. Phys., 2022, 24, 18281–18290 CAS.
- P. P. Dholabhai, S. Anwar, J. B. Adams, P. Crozier and R. Sharma, J. Solid State Chem., 2011, 184, 811–817 CrossRef CAS.
- D. A. Andersson, S. I. Simak, N. V. Skorodumova, I. A. Abrikosov and B. Johansson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3518–3521 CAS.
- A. Jones and M. S. Islam, J. Phys. Chem. C, 2008, 112, 4455–4462 CrossRef CAS.
- Y. A. Mastrikov, R. Merkle, E. A. Kotomin, M. M. Kuklja and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 911–918 CAS.
- T. Das, J. D. Nicholas and Y. Qi, Phys. Chem. Chem. Phys., 2020, 22, 9723–9733 RSC.
- A. M. Ritzmann, A. B. Munñoz-Garca, M. Pavone, J. A. Keith and E. A. Carter, Chem. Mater., 2013, 25, 3011–3019 CrossRef CAS.
- Y.-S. Zheng, M. Zhang, Q. Li, Y.-A. Zhu, Z.-J. Sui, D. Chen and X.-G. Zhou, J. Phys. Chem. C, 2018, 123, 275–290 CrossRef.
- A. Bonkowski, J. A. Kilner and R. A. De Souza, RSC Appl. Interfaces, 2024, 1, 699–710 RSC.
- A. Fossdal, M. Menon, I. Wærnhus, K. Wiik, M.-A. Einarsrud and T. Grande, J. Am. Ceram. Soc., 2004, 87, 1952–1958 CrossRef CAS.
- F. Schwarz, S. Barthel and A. Mace, Chem. Mater., 2024, 36, 11359–11376 CrossRef CAS.
- S. Dann, D. Currie, M. Weller, M. Thomas and A. Al-Rawwas, J. Solid State Chem., 1994, 109, 134–144 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- F. H. Taylor, J. Buckeridge and C. R. A. Catlow, Chem. Mater., 2016, 28, 8210–8220 CrossRef CAS.
- P. P. Kumar and S. Yashonath, J. Chem. Sci., 2006, 118, 135–154 CrossRef CAS.
- H. Mehrer, Diffusion in solids: fundamentals, methods, materials, diffusion-controlled processes, Springer Science & Business Media, 2007, vol. 155 Search PubMed.
- C. Kittel and P. McEuen, Introduction to solid state physics, John Wiley & Sons, 2018 Search PubMed.
- H.-D. Wiemhöfer, H.-G. Bremes, U. Nigge and W. Zipprich, Solid State Ionics, 2002, 150, 63–77 CrossRef.
- F. Bidrawn, S. Lee, J. M. Vohs and R. J. Gorte, J. Electrochem. Soc., 2008, 155, B660 CrossRef CAS.
- J. E. ten Elshof, H. J. Bouwmeester and H. Verweij, Solid State Ionics, 1995, 81, 97–109 CrossRef CAS.
- V. Vashook, M. Al Daroukh and H. Ullmann, Ionics, 2001, 7, 59–66 CrossRef CAS.
- T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, J. Solid State Chem., 1988, 73, 179–187 CrossRef CAS.
- M. Søgaard, P. V. Hendriksen and M. Mogensen, J. Solid State Chem., 2007, 180, 1489–1503 CrossRef.
- T. Ishigaki, S. Yamauchi, J. Mizusaki, K. Fueki, H. Naito and T. Adachi, J. Solid State Chem., 1984, 55, 50–53 CrossRef CAS.
- S. Anand, B. Ouyang, T. Chen and G. Ceder, Phys. Rev. Mater., 2023, 7, 095801 CrossRef CAS.
- J. Kilner and R. Brook, Solid State Ionics, 1982, 6, 237–252 CAS.
- K. Pramanik, K. Sau and P. P. Kumar, J. Phys. Chem. C, 2020, 124, 4001–4009 CAS.
- S. Madhual and P. P. Kumar, J. Mater. Sci., 2023, 58, 4499–4512 CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00131e |
| This journal is © the Owner Societies 2025 |