Intramolecular subtleties in indole azo dyes revealed by multidimensional potential energy surfaces

Abstract

Despite their wide use as molecular photoswitches, the mechanistic photophysics of azo dyes are complex and nuanced, and therefore under-explored. To understand the complex electronic interactions that govern the photoisomerization and thermal reversion of two phenyl-azo-indole dyes that differ by R-sterics near the azo bond, potential energy surfaces that combine the dihedral rotation of the azo bond and the aryl inversion on each side of the azo bond were calculated with density functional theory and time-dependent density functional theory. These multidimensional singlet surfaces provide insights into the correlated rotation and inversion pathways allowing for detailed understanding of both photoisomerization, governed by the excited-state surfaces, and thermal reversion, governed by the ground-state surface, mechanisms to be developed. Large plateaus on the S₁ surface arise from strong intramolecular interactions between a phenyl substituent and one of the aryl groups, extending the experimental photoisomerization lifetime of the dye with a phenyl R-group by two times over the unsubstituted dye. While one might expect the sterics of the larger phenyl substituent to lead to a slower thermal reversion rate, this was not the case. The thermally accessible meta-stable rotamers of the cis-isomer leads to more reversion pathways and a longer cis-lifetime for the unsubstituted dye, by a factor of four in the experiment. Careful computational mapping of multidimensional potential energy surfaces allows accurate mechanistic understanding for systems with interdependent degrees of freedom between meta-stable states.

---

Robust molecular photoswitches are important for a range of applications from dye pigments^1–3 to molecular solar fuels.^4–6 Defined by two aryl groups on either side of a N=N, azo dyes represent of set of chromophores that are highly tunable through changing the aromatic rings or the addition of functional groups on either aryl ring.^7–10 The ground state for the majority of azo dyes is the trans-isomer.¹¹ When excited by ultraviolet (UV) or visible light, these dyes photoisomerize from the trans-isomer to the meta-stable cis-isomer.^1,10,12–14

Detailed mechanisms of photoisomerization (trans → cis) and reversion (cis → trans) have now been worked out for a range of model dyes.^15–22 The lowest-energy singlet excited state, S₁, for most azo dyes, is not accessible from the ground state (S₀) because of its symmetrically forbidden n → π* character. Instead, azo dyes are commonly excited to the optically allowed second singlet excited state, S₂. From the excited S₂, dyes first relax to the S₁, before returning to the vibrationally excited (hot) S₀ surface. Thus the interplay of each of these excited-state potential energy surfaces (PESs) and the ground-state PES govern the behavior of the photoisomerization and reversion processes.

Photoisomerization usually occurs through a dihedral rotation around the azo-bond²⁰ because the curvature of the S₁/S₀ conical intersection is negative or energetically downhill from the initial photoexcited state.^7,8,23,24 Reversion from cis back to trans can occur in the dark, thermally, or with lower-energy light. The CNN in-plane inversion reaction mechanism is often the lowest-energy path for thermal reversion on the S₀ surface.^7,8,15–19 Tuning the lifetime of thermal reversion^25,26 through functional group modification has allowed azo dyes to be used as photoswitchable drugs,^27–31 molecular solar fuels,^4–6 or optical devices.³²

Recently multiple (hetero)aryl groups have been incorporated into azo dyes, including pyridines^8,9 and indoles,^12,13,33 including some substituted at the heteroatom position.³⁴ Here a class of phenyl-azo-indole dyes functionalized at the C2 of the indole ring is investigated. The dyes are named according to each of the key moieties: phenyl (P), azo (A), indole (I) where the R-groups are listed next to the connecting aryl group (Fig. 1 and Fig. S1, ESI†). OMe-P indicates a methoxy on the 4-position of the azo phenyl ring and I-Ph indicates a phenyl R-group on the 2-position of the indole, respectively. The IUPAC name of OMe-PAI is 3-((4-methoxyphenyl)diazenyl)-1-methyl-1H-indole and OMe-PAI-Ph is 3-((4-methoxyphenyl)diazenyl)-1-methyl-2-phenyl-1H-indole. Like most azo dyes, these phenyl-azo-indoles (PAIs) have two meta-stable isomers, trans and cis (Fig. 1). Because of the connection position of the azo to the indole, an additional set of rotational isomers is created around the indole dihedral (D₃₄₅₆, Fig. 1). Looking down the N₄−C₅ bond, in the eclipsed-rotamer the N₃ eclipses the C₆ with an ∼D₃₄₅₆ of 0° and the anti-rotamer has a ∼D₃₄₅₆ of 180° (Table 1).

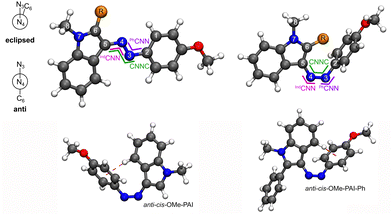Fig. 1 Lowest-energy rotamer structures and angles. Anti-trans-OMe-PAI-R (left) and eclipsed-cis-OMe-PAI-R (right), where trans and cis are defined by the azo dihedral (D₂₃₄₅), eclipsed and anti are defined by the indole dihedral (D₃₄₅₆), and R = H or Ph. The atomic numbers are used to define the geometric coordinates tracked (Table 1) and the azo dihedral (CNNC) and inversion on each side (^IndCNN and ^PhCNN) are marked in green, pink, and purple, respectively. The anti-cis-geometry for each molecule is shown with the (η⁶-phenyl)H interaction highlighted as a dark red dashed line.

Table 1 Geometric parameters of all fully optimized rotamers at CAM-B3LYP/6-311G(d,p)-D3BJ/PCM(MeCN) level of theory. All atomic indices relate to those shown in Fig. 1 and the three azo bond degrees of freedom are highlighted accordingly

		Bond length (Å)				Angle (deg)				Dihedral (deg)
		B 23	B 34	B 45	B 6R	A 123	A 234 (^PhCNN)	A 345 (^IndCNN)	A 456	D 1234	D 2345 (CNNC)	D 3456	D 456R	D R678	D Ph
OMe-PAI	Eclipsed-trans	1.41	1.25	1.39	1.08	125	115	116	130	0	180	0	0	0	—
	Anti-trans	1.41	1.25	1.38	1.08	125	115	116	121	0	180	180	0	0	—
	Eclipsed-cis	1.43	1.25	1.39	1.08	120	120	126	135	90	0	−1	0	0	—
	Anti-cis	1.43	1.25	1.40	1.08	122	123	126	117	51	−9	156	−3	0	—
OMe-PAI-Ph	Eclipsed-trans	1.41	1.25	1.39	1.48	125	115	117	131	0	180	0	0	0	90
	Anti-trans	1.41	1.25	1.38	1.47	125	115	116	121	−1	180	178	−1	−7	141
	Eclipsed-cis	1.43	1.24	1.41	1.47	123	123	124	130	49	7	51	−4	5	34
	Anti-cis	1.42	1.25	1.40	1.47	123	123	125	119	47	10	−149	5	−6	146

---

In this study, an in-depth investigation into the photoisomerization mechanisms of PAIs is conducted by exploring their three lowest-energy singlet potential energy surfaces using density functional theory (DFT) and time-dependent density functional theory (TD-DFT). A combination of potential energy curves (PECs) along the three azo-bond isomerization degrees of freedom, i.e. inversion of each aryl group and the dihedral rotation, along with an expanded potential energy surface between each inversion angle and the dihedral rotation are explored. Together, they provide a clear picture of the complex noncovalent intramolecular interactions of a phenyl R-group on the isomerization mechanism along correlated inversion/rotation coordinates.

The lowest-energy isomer for both PAIs is anti-trans (Table S2, ESI†). Based on Boltzmann weights of the computed energies, at 300 K less than 1% exists as eclipsed-trans-OMe-PAI-Ph and less than 5% exists as eclipsed-trans-OMe-PAI. Thus, most of the photophysics after photoexcitation should originate from the anti-trans-isomer for each dye. The addition of the phenyl R-group has very little effect on the molecular orbitals of the dye (Fig. S13 and S14, ESI†). In fact, the anti-trans of both OMe-PAI and OMe-PAI-Ph have a highest occupied molecular orbital (HOMO) that is a π-orbital across the whole dye, a HOMO−1 that is an indole-π, and a HOMO−2 non-bonding orbital on the azo bond (n). The lowest unoccupied molecular orbital (LUMO) is a π* in both dyes. This leads to similar low energy excited states in both dyes (Tables S10 and S11, ESI†), with S₁ being the symmetry forbidden HOMO−2 → LUMO (n → π*), S₂ is a HOMO → LUMO (π → π*) transition with high oscillator strength, and S₃ is a HOMO−1 → LUMO (indole-π → π*) transition. All three of these excited states populate the same orbital indicating that they should have fast internal conversion between them, as has been seen in other azo dyes.

The indole in the cis-PAIs adopt a variety of orientations in the fully optimized structures (Fig. S11 and S12, ESI†). In many azo dyes, including anthracene aryl groups,⁷ heteroatoms in the aryl rings,⁸ and different functionalization,²³ the cis-isomer has an azo-dihedral angle (CNNC, green in Fig. 1) of about 10° with the two aryl groups attached to the azo bond aligned in a tilted slipped π–π interaction. The unique cis-structures in the PAI dyes arise from a noncovalent interaction between the R-group and the azo-phenyl. For OMe-PAI, where R = H, the anti-cis-isomer adopts a typical cis-geometry with a tilted-slip stack between the indole and azo-phenyl (Fig. S11, ESI†). The eclipsed-cis-OMe-PAI, however, has the H R-group pointed toward the azo-phenyl in an (η⁶-phenyl)H interaction (Fig. 1 and Fig. S11, ESI†). The phenyl R-group prevents an (η⁶-phenyl)R interaction. Instead, in the eclipsed-cis-OMe-PAI-Ph, the phenyl R-group forms a ∼3.48 Å π–π stack with the azo-phenyl (Fig. S12, ESI†). This close interaction between the R-groups and the azo-aryl groups has not been observed in previous studies of meta-substituted azobenzenes.^35,36 In addition, the five-membered ring of the indole allows for greater rotational freedom near the azo bond than other aryl groups. Thus, the lowest-energy anti-cis-OMe-PAI-Ph has an (η⁶-phenyl)H interaction with a hydrogen from the six-membered ring of the indole (Fig. S12, ESI†).

To explore if any of these different cis-geometries are relevant for photoisomerization, potential energy curves (PECs) from the ground state of each dye (anti-trans) were calculated along the three main azo bond degrees of freedom (Fig. 2). Above this ground-state surface (S₀) the first two singlet excited states (S₁ and S₂) were calculated with TD-DFT. The lowest-energy singlet (S₀) surface shows energetic barriers along each degree of freedom: CNNC rotation, and ^IndCNN and ^PhCNN inversion. The barriers between anti-trans and anti-cis for each isomer are slightly less than 2 eV along all reaction coordinates.

Fig. 2 Computed energy curves of the first three singlet states along the three main azo bond degrees of freedom starting from the lowest isomer of each molecule (anti-trans). The S₀ geometry is optimized at each point along the curve with only the angle on the x-axis frozen for OMe-PAI (top) and OMe-PAI-Ph (bottom) along CNNC, ^IndCNN, and ^PhCNN. The discontinuities around CNNC 20° come from a orientation switch of the pheynl ring (Fig. S20, ESI†). The S₁ and S₂ energies are TDDFT energies from these S₀ geometries at CAM-B3LYP/6-311G(d,p)-D3BJ/PCM(MeCN).

The major difference between the PECs is in the curvature of the excited states. The initial photoexcitation of each dye is to the π → π* allowed S₂ (Tables S10 and S11, ESI†). Each S₂ surface has positive curvature in and around the Franck–Condon geometry, i.e. the trans at CNNC ≈ 180° and ^IndCNN = ^PhCNN ≈ 115°. This lack of driving force indicates that the S₂ would quickly relax to the lower energy S₁ without significantly changing geometry.

The S₁ surfaces have the largest variation in shape. Along both inversion coordinates, the S₁ is nearly flat with a slight negative curvature 120° < CNN < 150°. These local S₁ minima are at least 1 eV above the trans-S₀ well, indicating radiative decay of the excited state through these minima, which purely reforms the ground-state trans-isomer. In contrast, along the rotational coordinate (CNNC), the surfaces are similar to many azo dyes, in that the S₁ and S₀ approach each other near the S₀ transition state, indicating a conical intersection. Thus, upon S₁ → S₀ internal conversion some of the molecules go directly back to the trans-ground state and some generate the meta-stable cis-isomer. These PECs suggest that each of the PAIs photoisomerize via an azo-dihedral rotation mechanism.

The different indole R-groups resulted in minimal changes in the two-dimensional PECs so the potential energy surfaces (PESs) between each inversion (^IndCNN and ^PhCNN) and the rotation (CNNC) were calculated (Fig. 3). At first glance, the S₀ and S₂ surfaces appeared similar between the molecules for both the ^IndCNN–CNNC and ^PhCNN–CNNC surfaces for both molecules. The S₀ surfaces show two distinct minima, anti-trans (star) and anti-cis (pentagon), with a high-energy ridge between them. The S₂ surfaces all have prominent global minima at the anti-trans-geometry.

Fig. 3 The first three singlet potential energy surfaces between azo dihedral rotation (CNNC) and inversion on either the indole (^IndCNN, top row) or phenyl (^PhCNN, bottom row) of anti-OMe-PAI (top) and anti-OMe-PAI-Ph (bottom). Each S₀ (left) CAM-B3LYP/6-311G(d,p)-D3BJ/PCM(MeCN) relaxed structure and S₁ (middle) and S₂ (right) point excitation energies are marked with a black dot. The fully optimized trans and cis are marked with a white star and pentagon, respectively. The energies are plotted as a color gradient with smoothed contour lines to help aid the eye. Seams along some surfaces are traced in white to aid in further analysis and the empty points indicate interpolated energies between optimized points on the surface.

The largest differences between surfaces occurs between the OMe-PAI and OMe-PAI-Ph ^IndCNN-CNNC S₀ surfaces; as well as, the ^IndCNN-CNNC and ^PhCNN-CNNC OMe-PAI-Ph S₁ surfaces (highlighted by white seams along the surfaces in Fig. 3). On the ^IndCNN-CNNC surfaces, there is a steeper transition between the high-energy region at larger ^IndCNN angles and at the global minimum on the OMe-PAI-Ph surface compared to OMe-PAI. This sharp decrease in energy can be seen in the closer spacing of the contour lines along the white seams (with black triangles) drawn in Fig. 3. Also, this cliff on the OMe-PAI-Ph ^IndCNN-CNNC surface is not observed on the ^PhCNN-CNNC surface.

Along this seam of the ^IndCNN-CNNC surfaces, the S₀ share a similar shape (Fig. 4) for both OMe-PAI and OMe-PAI-Ph. Looking at the entire surface (Fig. 3) reveals a break in symmetry along the ∼90° dihedral in OMe-PAI-Ph by a subtle shift in the highest crossing point (to the left of the white seam on S₀, Fig. S21, ESI†) along the trans-cis-ridge, while the OMe-PAI surface is symmetric along this line. Both S₂ surfaces are fairly flat along this seam, with the OMe-PAI-Ph being slightly flatter, only decreasing in energy at the last point. On the other hand, the OMe-PAI S₁ energy decreases steadily ∼28 meV deg⁻¹ for CNNC angles between 30–85° and ^IndCNN angles between 135–165°. This indicates clear driving force for trans-OMe-PAI toward the conical intersection through a CNNC dihedral rotation, leading to fast photoisomerization. In contrast, OMe-PAI-Ph S₁ has an energy plateau for ^IndCNN < 145°, which sharply declines where the S₀ begins to rise. Similar plateaus have been observed on other photoexcited surfaces^37,38 for complexes that have extended excited-state lifetimes. Thus, we predict that OMe-PAI-Ph should take longer to photoisomerize than OMe-PAI. Experimentally (methods in Section 1 of the ESI†) the trans → cis isomerization for OMe-PAI-Ph is twice as long as OMe-PAI (Table S1, ESI†), supporting the computational assignment of this mechanism to the rotation pathway, governed by the shape of the S₁ surface.

Fig. 4 First three singlet potential energy curves along the ^IndCNN-CNNC seam (marked in white in Fig. 3) for OMe-PAI and OMe-PAI-Ph. For OMe-PAI-Ph this is the same S₀ seam as the blue in Fig. 5. For OMe-PAI, four indole-side relaxed geometries are extracted from the ^IndCNN-CNNC S₀ surface, and an open circle energy average is added to assist the interpretation. CAM-B3LYP/6-311G(d,p)-D3BJ/PCM(MeCN).

The effect of the unique intramolecular interactions between the azo-phenyl and phenyl R-group are most apparent when comparing the S₀^IndCNN-CNNC and ^PhCNN-CNNC surfaces (Fig. 3, following the white seams). On the ^PhCNN-CNNC surface, along this seam (Fig. 5 red) only small geometric changes around the azo bond are seen, as might be expected from a PEC along a ^PhCNN inversion coordinate (Fig. 2). However, on the ^IndCNN-CNNC surface (Fig. 5 blue) there is a dramatic geometry shift along with a large drop in energy around 155° (between geometry 3 and 4 in Fig. 5). Along both seams, which have nearly identical CNNC angles and respective CNN angles, the first three energies show the same increase followed by a decrease which can be understood in terms of azo bond strain due to the positions of the aryl rings. The ^IndCNN–CNNC surface is 100 meV higher in energy at each of the first three points than the ^PhCNN–CNNC surface, indicating that this effect is caused by strain to the azo backbone caused by maximizing the π–π stacking of the azo-phenyl and the phenyl R-group. Breaking this interaction (between geometry 3 and 4 Fig. 5), leads to a release of this strain, and a sudden drop in energy. This indicates that even though the ground-state surfaces look qualitatively very similar, small changes in noncovalent intramolecular interactions can have a large effect on mixed inversion–rotation energetic barriers and thus dominate the reversion mechanism.

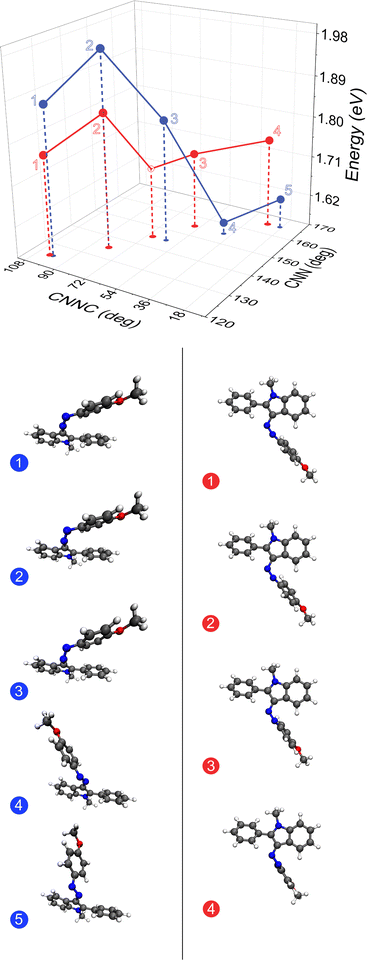Fig. 5 The S₀ seams (marked in white in Fig. 3) of OMe-PAI-Ph along each inversion coordinate, ^IndCNN (blue) and ^PhCNN (red) at CAM-B3LYP/6-311G(d,p)-D3BJ/PCM(MeCN). Five indole-side relaxed geometries are extracted from the ^IndCNN–CNNC S₀ surface, with each displayed with the indole kept as consistent as possible. Four phenol-side relaxed geometries are extracted from the ^PhCNN–CNNC S₀ surface, displayed with the azo-phenyl kept as consistent as possible, with an additional point at CNN = 145° (open circle) added to assist the interpretation. This energy is the average between two neighboring optimized structures with the same CNN angle.

Reversion of most azo dyes from cis to trans occurs thermally on the S₀ surface or through transiently populating the lowest triplet state near the rotational transition state.^39–41 For these dyes, the majority of the low energy transition states are inversion not rotation (Table S9, ESI†) and the lowest energy triplet surfaces only crosses the ground state along the rotation coordinate (Fig. S22, ESI†). Because of this, the rest of the analysis is focused on the singlet manifold. Thus, the exact shape of S₀ and the crossing points between cis and trans can be used to estimate cis-isomer lifetimes.

Although it is clear for OMe-PAI-Ph that the ^IndCNN-CNNC surface has higher barriers (Fig. 3 along the CNNC 90° spine) near the cis- and trans-geometries, the energies across the maximum ridge of the surface vary by 0.3 eV, depending on the extent of ^IndCNN inversion. Comparing the ^IndCNN and ^PhCNN, the maximum and minimum along this ridge (Fig. S21, ESI†) reveals that the minimum energy crossing points for each surface are nearly isoenergetic, with activation energies from the anti-cis-isomer of 1.14 and 1.16 eV, respectively. These results indicate that there is no obvious preferential reaction coordinate for thermal reversion of OMe-PAI-Ph.

The shape of the S₀ surfaces and the lowest transition state energies (Table S9, ESI†) between cis and trans might indicate that the thermal reversion of the two complexes should be fairly similar. Thus, it was surprising to see that the experimental reversion lifetime of OMe-PAI was almost four times longer than that of OMe-PAI-Ph (Table S1, ESI†). That is until one considers that the PECs and PESs focused on the anti-cis to anti-trans barriers but the lowest-energy cis-isomer for both molecules was calculated to be the eclipsed-cis. Optimizing these types of constrained geometries along two structural coordinates (inversion angle and dihedral rotation) has to be done carefully. Finding a set of coordinates between anti-trans and eclipsed-cis would require constraining the indole dihedral angle, likely leading to over-constrained structures and unrealistic or useful surfaces.

To confirm that the difference in the picture of measured and computed reversion arose from considering different parts of the mechanism, two-dimensional nuclear magnetic resonance (NMR) experiments were performed to confirm the structure of the cis-isomer generated upon photoexcitation (ESI,† Section 1). The ¹H–¹H NOESY reveals that OMe-PAI does indeed form the lower energy eclipsed-cis upon exposure to light (Fig. S6–S9, ESI†). While computationally (Tables S2 and S9, ESI†) the eclipsed-cis is the lowest-energy isomer for both dyes, the anti-cis → eclipsed-cis S₁ barrier for OMe-PAI-Ph (Fig. S24, ESI†) is 32.8 meV higher than the barrier in OMe-PAI (Fig. S23, ESI†). This energy barrier seems to be enough to limit the formation of eclipsed-cis for OMe-PAI-Ph during the internal conversion from S₁ back to S₀. The lack of eclipsed-cis-OMe-PAI-Ph is also supported by room temperature NMR (Fig. S10, ESI†) of the photoisomerized OMe-PAI-Ph that shows no evidence of another species beyond the anti-cis-isomer, also observed at low temperature.

In order to rationalize the reversion rates and mechanism for eclispsed-cis-OMe-PAI to anti-trans-OMe-PAI and from anti-cis-OMe-PAI-Ph to anti-trans-OMe-PAI-Ph, fully optimized transition states provide estimates of the thermal activation energies (ESI,† Section 2.5). In OMe-PAI, because the anti-trans → eclipsed-trans and anti-cis → eclipsed-cis barriers are relatively small (Table S9, ESI†), they are in constant equilibrium. After photoisomerization, OMe-PAI equilibrates to a mixture of 79% eclipsed and 21% anti in the cis-isomer leading to the reversion being a combination of the eclipsed-cis → ^IndCNN inversion → eclipsed-trans and anti-cis→ ^IndCNN inversion → anti-trans (Fig. 6 top). In contrast for OMe-PAI-Ph, two low energy transition states between anti-cis and anti-trans were found. Because of their energetics we would predict a anti-cis → rotation mixed ^PhCNN inversion → anti-trans thermal reversion path for OMe-PAI-Ph (Fig. 6 bottom). However, the rotation barrier may be even lower than we estimate here if the CNNC rotation includes population of the triplet surface (Fig. S22, ESI†).³⁹

Fig. 6 Proposed mechanism of photoismoerization and thermal reversion for OMe-PAI and OMe-PAI-Ph. Photoinduced transformations are green and thermal processes are shades of red/orange. The different rotamer singlet surfaces for OMe-PAI are indicated with dotted and dashed lines with the lowest energy isomer shown in orange or red.

Based on these proposed mechanisms (Fig. 6), a weighted rate (Table S9, ESI†) of the lowest-energy paths between cis and trans predicts a longer OMe-PAI reversion rate compared to OMe-PAI-Ph. However, this picture requires experimental support of the isomers formed, as well as extensive mapping of the potential energy surfaces and transition states. These reversion rates indicate once again that the complex interplay of many structural and electronic factors can substantially impact the isomerization kinetics of azo dyes.

In conclusion, extensive exploration of the ground and two lowest-energy singlet excited-state potential energy surfaces for a set of phenyl-azo-indole molecules provides unique insights into their photoisomerization and reversion mechanisms and approximations for cis-isomer lifetimes. Two-dimensional PECs provide an intuitive picture of the various reaction coordinates between the lowest-energy trans- and corresponding cis-isomer. Expanded surfaces between these coordinates explore the subtle interplay between inversion and rotation mechanisms. Here the PESs revealed strong noncovalent intramolecular interactions between the phenyl R-group and the azo-phenyl group along mixed rotation and inversion reaction coordinates. Strong noncovalent intramolecular interactions in OMe-PAI-Ph create large plateaus on the S₁ surface that could increase the excited-state lifetime. For thermal reversion, the S₀ surfaces show that there are a ridge of “transition states” between each cis- and trans-isomer that consists of a mixture of dihedral rotation and inversion coordinates, indicating that PECs along a single coordinate cannot capture thermal reversion well. Instead, the optimized transition states between each pair of isomers reveals that thermal reversion on the S₀ surface is dominated by the number of isomerization paths that are thermally accessible from the formed cis-rotamers. A more unequal distribution of anti- and eclipsed-rotamers in OMe-PAI results in a mixed mechanism of multiple reversion pathways that slows the reversion rate. It is apparant from this work that the complex degrees of freedom in these, and many other azo dyes, requires careful experimental and computational mapping of the meta-stable states and excited-state potential energy surfaces.

Author contributions

AHC computational data collection, curation, and visualization, and co-writing the original draft, review, and editing. ZJK computational data curation, formal analysis, validation, supervision of AHC, and review and editing. CAG experimental data collection, curation, formal analysis, and review and editing. ERY funding acquisition, supervision of CAG, and review and editing. LAF formal analysis, writing of original draft and editing, funding acquisition, project administration, and supervision of AHC and ZJK.

Data availability

All data is available upon request and computed structures are publicly available on GitHub: https://github.com/fredingroup/azodyes/tree/main/indole/.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Research computing resources were provided by Lehigh University partially supported by the NSF CC* Compute program through Grant No. OAC-2019035. This work used Bridges2 at Pittsburgh Supercomputing Center through allocation TG-CHE190011 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296. LAF acknowledges support from a 2024 Sloan Research Fellowship from the Alfred P. Sloan Foundation and LAF and ZJK acknowledge support from the National Science Foundation under Grant No. CHE-2310205. ERY and LAF thank The Pittsburgh Foundation (UN2020-114823) for funding. Acknowledgement is made to the donors of the American Chemical Society Petroleum Research Fund for partial support of this research. This work made use of the Lehigh University (LU) NMR Facility (NSF-MRI-1725883, with support from LU).

References

1. H. M. D. Bandara and S. C. Burdette, Chem. Soc. Rev., 2012, 41, 1809–1825.
2. S. Benkhaya, S. M'rabet and A. El Harfi, Inorg. Chem. Commun., 2020, 115, 107891.
3. R. I. Alsantali, Q. A. Raja, A. Y. Alzahrani, A. Sadiq, N. Naeem, E. U. Mughal, M. M. Al-Rooqi, N. El Guesmi, Z. Moussa and S. A. Ahmed, Dyes Pigm., 2022, 199, 110050.
4. Y. Yang, S. Huang, Y. Ma, J. Yi, Y. Jiang, X. Chang and Q. Li, ACS Appl. Mater. Interfaces, 2022, 14, 35623–35634.
5. B. Zhang, Y. Feng and W. Feng, Azobenzene-Based Solar Thermal Fuels: A Review, Springer Nature, Singapore, 2022, vol. 14, pp. 1–37.
6. D. Kwaria, K. McGehee, S. Liu, Y. Kikkawa, S. Ito and Y. Norikane, ACS Appl. Opt. Mater., 2023, 1, 633–639.
7. R. C. Hamburger, T. Huang, S. M. Martin, C. A. Pointer, L. A. Fredin and E. R. Young, Phys. Chem. Chem. Phys., 2023, 25, 15302–15313.
8. S. M. Martin, Z. J. Knepp, I. A. Thongchai, K. Englehart, K. Sorto, A. Jaffer, L. A. Fredin and E. R. Young, New J. Chem., 2023, 47, 11882–11889.
9. Z. J. Knepp, R. C. Hamburger, I.-A. Thongchai, K. Englehart, K. Sorto, A. Jaffer, E. R. Young and L. A. Fredin, J. Phys. Chem. Lett., 2024, 15, 9593–9600.
10. S. Crespi, N. A. Simeth and B. König, Nat. Rev. Chem., 2019, 3, 133–146.
11. P. Lentes, P. Fruhwirt, H. Freimuth, W. Moormann, F. Kruse, G. Gescheidt and R. Herges, J. Org. Chem., 2021, 86, 4355–4360.
12. S. Crespi, N. A. Simeth, A. Bellisario, M. Fagnoni and B. König, J. Phys. Chem. A, 2019, 123, 1814–1823.
13. N. A. Simeth, S. Crespi, M. Fagnoni and B. König, J. Am. Chem. Soc., 2018, 140, 2940–2946.
14. S. W. Magennis, F. S. Mackay, A. C. Jones, K. M. Tait and P. J. Sadler, Chem. Mater., 2005, 17, 2059–2062.
15. I. K. Lednev, T.-Q. Ye, R. E. Hester and J. N. Moore, J. Phys. Chem., 1996, 100, 13338–13341.
16. I. Lednev, T.-Q. Ye, P. Matousek, M. Towrie, P. Foggi, F. Neuwahl, S. Umapathy, R. Hester and J. Moore, Chem. Phys. Lett., 1998, 290, 68–74.
17. J. Azuma, N. Tamai, A. Shishido and T. Ikeda, Chem. Phys. Lett., 1998, 288, 77–82.
18. C. Slavov, C. Yang, L. Schweighauser, C. Boumrifak, A. Dreuw, H. A. Wegner and J. Wachtveitl, Phys. Chem. Chem. Phys., 2016, 18, 14795–14804.
19. C. J. Otolski, A. M. Raj, V. Ramamurthy and C. G. Elles, Chem. Sci., 2020, 11, 9513–9523.
20. M. Quick, A. L. Dobryakov, M. Gerecke, C. Richter, F. Berndt, I. N. Ioffe, A. A. Granovsky, R. Mahrwald, N. P. Ernsting and S. A. Kovalenko, J. Phys. Chem. B, 2014, 118, 8756–8771.
21. F. Aleotti, L. Soprani, A. Nenov, R. Berardi, A. Arcioni, C. Zannoni and M. Garavelli, J. Chem. Theory Comput., 2019, 15, 6813–6823.
22. Y. Hirose, H. Yui and T. Sawada, J. Phys. Chem. A, 2002, 106, 3067–3071.
23. I.-A. Thongchai, Z. J. Knepp, D. R. Fertal, H. Flynn, E. R. Young and L. A. Fredin, J. Phys. Chem. A, 2024, 128, 785–791.
24. I. Conti, M. Garavelli and G. Orlandi, J. Am. Chem. Soc., 2008, 130, 5216–5230.
25. F. Aleotti, A. Nenov, L. Salvigni, M. Bonfanti, M. M. El-Tahawy, A. Giunchi, M. Gentile, C. Spallacci, A. Ventimiglia, G. Cirillo, L. Montali, S. Scurti, M. Garavelli and I. Conti, J. Phys. Chem. A, 2020, 124, 9513–9523.
26. J. Calbo, C. E. Weston, A. J. P. White, H. S. Rzepa, J. Contreras-García and M. J. Fuchter, J. Am. Chem. Soc., 2017, 139, 1261–1274.
27. W. A. Velema, W. Szymanski and B. L. Feringa, J. Am. Chem. Soc., 2014, 136, 2178–2191.
28. J. Broichhagen, J. A. Frank and D. Trauner, Acc. Chem. Res., 2015, 48, 1947–1960.
29. M. M. Lerch, M. J. Hansen, G. M. van Dam, W. Szymanski and B. L. Feringa, Angew. Chem., Int. Ed., 2016, 55, 10978–10999.
30. K. Hüll, J. Morstein and D. Trauner, Chem. Rev., 2018, 118, 10710–10747.
31. M. J. Fuchter, J. Med. Chem., 2020, 63, 11436–11447.
32. J. Jayabharathi, V. Thanikachalam, K. Brindha Devi and M. Venkatesh Perumal, Spectrochim. Acta, Part A, 2012, 86, 69–75.
33. B. Babür, N. Seferoglu, E. Aktan, T. Hökelek, E. Åžahin and Z. Seferoglu, Dyes Pigm., 2014, 103, 62–70.
34. H. Hu, Y. Liu, J. Li, C. Zhang, C. Gao, C. Sun, Y. Du and B. Hu, Org. Biomol. Chem., 2024, 22, 1225–1233.
35. A. L. Sanna, T. Pachova, A. Catellani, A. Calzolari and G. Sforazzini, Molecules, 2024, 29, 1929.
36. M. B. Pasti-Grigsby, A. Paszczynski, S. Goszczynski, D. L. Crawford and R. L. Crawford, Appl. Environ. Microbiol., 1992, 58, 3605–3613.
37. L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071.
38. L. A. Fredin and P. Persson, J. Phys. Chem. A, 2019, 123, 5293–5299.
39. M. Reimann, E. Teichmann, S. Hecht and M. Kaupp, J. Phys. Chem. Lett., 2022, 13, 10882–10888.
40. N. K. Singer, K. Schlögl, J. P. Zobel, M. D. Mihovilovic and L. González, J. Phys. Chem. Lett., 2023, 14, 8956–8961.
41. A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, J. Am. Chem. Soc., 2004, 126, 3234–3243.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and theoretical methods. Photoisomerization lifetimes and NMR of OMe-PAI and additional DFT/TDDFT data. See DOI: https://doi.org/10.1039/d5cp00110b

---