Guest molecule dynamics and ferroelectric transition in a clathrate compound

Abstract

Low molecular weight glass formers encapsulated within clathrate structures offer a singular testground to study the intricate interplay of confined molecular motion and ferroelectric properties. Using broadband dielectric spectroscopy (BDS), we investigate the dynamic behavior of 1-propyl-1H-imidazole within a supramolecular enclosure formed by duad semicage p-tert-butylcalix[4]arene. Unlike the bulk liquid, where the dielectric spectrum is dominated by the structural relaxation, the clathrates paraelectric phase reveals two distinct molecular relaxation processes. Aided by quantum chemical calculations, the slow process is assigned to head-to-tail reorientations of the guest molecule, while the faster process arises from intramolecular fluctuations of the imidazole ring. These dynamics freeze as the system transitions to the ferroelectric state via a second-order phase change that has been characterized by photopyroelectric calorimetry.

---

Introduction

Clathrate compounds provide a unique opportunity for studying the dynamics of guest molecules in a precisely defined environment formed by the host lattice. If the trapped molecules are polar, broadband dielectric spectroscopy (BDS) becomes a particularly powerful technique to this end because it allows the deconvolution of the distinct dynamic contributions from the host and guest systems within the spectra.¹ This was recognized early on, and the first studies on the dielectric properties of clathrates date back to the middle of the last century.^2–4 In general, the experimental evidence suggests that the individual and collective molecular dynamics in a confined space are determined by the counterbalance between surface- and confinement-effects.^5,6 While the interactions of guest molecules with the host system at the interface between both tend to slow down the dynamics, confinement causes an increase in mobility. The situation is especially interesting in the case of low molecular weight glass formers, for which the topology and dimensionality of the spatial confinement has dramatic consequences. The most prominent feature in the dielectric spectra of glass-forming liquids is the so-called α-relaxation, which reflects the slowing down of the dynamics when approaching the glass transition.^1,7 This structural relaxation is generally associated with the dynamics of cooperatively rearranging regions,⁸ although a consensus regarding the physical interpretation of this process is still lacking, and it is sometimes regarded as the biggest unsolved problem in condensed matter physics.⁹ Interestingly, nanometric spatial confinement can continuously alter this collective bulk behavior to that of single molecules, as in the well-studied example of ethylene glycol confined in various zeolite host systems.⁵

In certain cases, spatial restrictions can give rise to phase transitions and emergent properties, which is a field of increasing interest in its own right. Recently, a paper showcasing the incorporation of 1-propyl-1H-imidazole (hereinafter PIm, see Fig. S1 of the ESI†) into a supramolecular cage formed by duad semicage p-tert-butylcalix[4]arene (BC, see Fig. S1 of the ESI†) was published.¹⁰ The resulting compound (PIm@(BC)₂, see Fig. 1) constitutes the first example of a ferroelectric clathrate featuring a molecule-inclusive supramolecular cage. It is thus an interesting system in which to explore the dynamics of the confined PIm molecule leading to the emergence of spontaneous polar order. Since this kind of systems provides the possibility of switching the polarization of a single trapped molecule,^11–13 they have potential for designing advanced materials to be developed, among other applications, into high-density molecular-scale memory devices at the subnanometric level. In this paper, we present the results of comprehensive BDS experiments on both PIm@(BC)₂ and bulk PIm, alongside quantum chemical calculations to support the interpretation of the dielectric relaxation processes. In addition, we have performed precision calorimetric measurements to clarify the nature of the ferroelectric transition.

Fig. 1 (a) DFT-optimized geometry and dipole moment of the PIm molecule. (b) Crystal structures of the ferroelectric (a) and paraelectric (b) phases of the PIm@(BC)₂ clathrate system determined by single-crystal X-ray diffraction.¹⁰

Experimental section

Materials

PIm@(BC) ₂ single crystals were synthesized as described in ref. 10. These single crystals were then milled with an agate mortar and pestle to a very fine powder. The powder was stored in a desiccator to remove moisture and later compressed with a die into circular plane-parallel pellets (5 mm in diameter) using a hydraulic press at 2 tons of force for 2 minutes at room temperature. PIm (purity > 98%) was purchased from Tokyo Chemical Industry Co., Ltd. It is a clear liquid at room temperature.

Broadband dielectric spectroscopy

Broadband dielectric spectra were recorded in the 10 Hz–1 GHz spectral range. Low-frequency measurements (up to 1 MHz) were performed with an Alpha-A impedance analyzer from Novocontrol Technologies GmbH, while an HP 4191A RF reflectometer was used at higher frequencies (1 MHz–1 GHz). The samples were placed between two circular gold-coated brass electrodes 5 mm in diameter forming a parallel-plate capacitor. The electrode separation was determined by the sample thickness in the case of PIm@(BC)₂ (∼400 μm), while spherical silica spacers 20 μm in diameter were used for PIm. The cell was then placed at the end of a modified HP 16091A coaxial test fixture, using a Quatro Cryostat for temperature control. The complex dielectric permittivity ε*(f) = ε′(f) − iε′′(f) data were fitted to Havriliak–Negami relaxations with a conductivity term: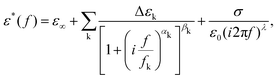where ε_∞ is the high-frequency dielectric permittivity, Δε_k, f_k, α_k and β_k are respectively the dielectric strength, relaxation frequency and broadness exponents of mode k, σ is a measure of the conductivity, and λ is an exponent higher than 0 and lower or equal to 1.

Photopyroelectric calorimetry

Thermal diffusivity measurements of PIm@(BC)₂ were carried out using a high-resolution ac photopyroelectric calorimeter in the back detection configuration. This technique is particularly suited to study phase transitions in detail since a small temperature gradient in the sample gives rise to a high signal-to-noise ratio in the detector. The details of the experimental setup, measurement procedure, and the theory which explains how to obtain thermal parameters from the photopyroelectric signal can be found elsewhere.¹⁴

Quantum chemistry

Density functional theory (DFT) calculations were performed using Gaussian 16.¹⁵ Initial optimization of the molecular geometry was followed by a calculation of vibrational frequencies to confirm that the structure corresponded to an energy minimum. Avogadro software was used for structure visualization.¹⁶

Results and discussion

Firstly, we will focus on PIm in its bulk liquid form. PIm is a small yet highly polar molecule. Its dipole moment calculated at the B3LYP-GD3BJ/aug-cc-pVTZ level of DFT is μ ≈ 4 D (see Fig. 1a). Fig. 2 shows the measured dielectric spectra of PIm (see fit examples and parameters in Fig. S2 and Table S1 of the ESI†). Ignoring conductivity and electrode polarization effects at low frequencies, a single (almost Debye-like) relaxation process is observed in the whole temperature range, which can unambiguously be identified with the α-relaxation. As mentioned in the introduction, this is a universal feature of glass-forming liquids. Following a simplified picture of glassy dynamics, a molecule fluctuates in the cage of its neighbors, and the α-relaxation is associated with reorientations of the molecules forming the cage.¹ As can be seen in Fig. 2, this process slows down dramatically as the temperature is lowered, which precisely reflects its collective nature. Below 193 K, the data became noisy and the α-relaxation could no longer be followed, presumably due to bad contact with the electrodes. It should be mentioned that other imidazole-based liquids were studied in ref. 17.

Fig. 2 Dielectric loss spectra of PIm for various temperatures. Lines are fits to the Havriliak–Negami function.

As mentioned, by trapping the PIm molecule between two BC semicages, a clathrate compound is formed, namely PIm@(BC)₂ (see Fig. 1b). Very remarkably, this clathrate system undergoes a ferroelectric transition at T_C ≈ 189 K, as evidenced by the peak in ε′ shown in Fig. 3. In particular, the suppression of this peak at high frequencies is typical for ferroelectrics of order–disorder type.¹⁸ As evidenced by X-ray diffraction experiments,¹⁰ at this temperature the two BCs within a supramolecular cage undergo relative displacement, resulting in a change in cage symmetry. In particular, the space group changes from P4/nnc in the high-temperature paraelectric phase to P2nn in the low-temperature ferroelectric phase. In Aizu notation, this system belongs to species “4/mmmFmm2”.¹⁹ Since the symmetry elements of the low-temperature phase are contained in those of the high-temperature phase, the ferroelectric transition can, in principle, be second order.²⁰ By fitting the data of Fig. 3 with the Curie–Weiss law at several frequencies (see Fig. S3 of the ESI,† and the corresponding caption) we have obtained C_para/C_ferro ratios in the range 1.9–2.3, which is an indication that the behavior is close to the Landau prediction and a suggestion that the transition is a second-order one.

Fig. 3 Temperature dependence of the real part of the complex dielectric permittivity of PIm@(BC)₂ at selected frequencies. The vertical dashed line corresponds to the ferroelectric phase transition temperature.

In order to obtain additional insights into the ferroelectric transition and elucidate its precise nature, we performed high-precision thermal measurements. Although the differential scanning calorimetry (DSC) curves reported in ref. 10 showed a peak at T_C, thus pointing to a first-order phase transition, it is important to note that pretransitional fluctuations can induce a fictitious enthalpy increase in DSC measurements.²¹ Therefore, ac calorimetry techniques, like photopyroelectric calorimetry, are better suited for this purpose. Through this technique, we obtained the thermal diffusivity K/ρc_p of the sample as a function of temperature, K being the thermal conductivity, ρ the density and c_p the specific heat. The results are shown in Fig. 4. The overall temperature dependence of the observed thermal diffusivity is typical of thermal insulators, in which the thermal transport is dominated by phonons. As the temperature decreases, the phonon mean free path severely increases, thus leading to an increase in diffusivity. The ferroelectric transition appears as a dip at T_C = 188.5 K superimposed on this general behavior. Both the shape of the dip and the fact that we did not observe any hysteresis in our experiments led us to conclude that this is a second-order phase transition. Lastly, it is worth mentioning that the absolute values of the thermal diffusivity are quite low, comparable to those of polymeric materials.²² Nevertheless, this cannot be univocally attributed to the intrinsic material properties but could be the result of the porosity of the prepared polycrystalline hard-pressed sample.

Fig. 4 Temperature dependence of the thermal diffusivity of PIm@(BC)₂.

Coming back to Fig. 3, we notice that, above T_C, a small temperature-evolving bump appears at low frequencies. This corresponds to some kind of dipolar relaxation, to which we now turn our attention. As can be seen in Fig. 5a, a single relaxation process is observed below 1 MHz (see fit examples and parameters in Fig. S4 and Table S2 of the ESI†). This was already observed in ref. 10. At 293 K, it appears almost four decades in frequency below that of bulk PIm. It is reasonable to think that this is partly due to the molecule being trapped inside the supramolecular cage, with which it interacts through C–H⋯π interactions.¹⁰ However, one must remember that this system is a heterogeneous dielectric formed by a matrix (the host lattice) and the guest molecules. In general, the dielectric permittivity is not an additive quantity, so in order to isolate the response of the guest, a quantitative analysis must be performed that accounts for both the dielectric properties of the matrix and the structure of the system.^23–25 The available models for such an analysis are often extremely simplified and of limited applicability, and the conclusions that can be drawn from them are often of limited value, so we will not focus on this issue in the present discussion. Unfortunately, below 209 K, with the relaxation already below 1 kHz, the data became noisy and it could no longer be followed. Remarkably, around this temperature and down to almost T_C, an additional high-frequency relaxation enters the measurement range and it is detected (see Fig. 5b). It appears broader than the low-frequency mode (see fit parameters in Table S2 of the ESI†), and increases in amplitude as the temperature is lowered. Finally, no relaxation is observed in the ferroelectric phase.

Fig. 5 Dielectric loss spectra of PIm@(BC)₂ at (a) low frequencies and (b) high frequencies for various temperatures. Lines are fits to the Havriliak–Negami function.

The interpretation of dielectrically active processes usually requires analyzing the temperature dependence of their absorption frequencies. These are shown in Fig. 6. As inferred from Fig. 2, the α-relaxation in bulk PIm slows down rapidly as the temperature is lowered. This non-Arrhenius behavior is typical of the structural relaxation and is a result of cooperativity.^26,27 The data can be fitted to the Vogel–Fulcher–Tammann equation: f_a = f_∞ exp[−DT₀/(T − T₀)], where f_∞ is a prefactor, T₀ is the Vogel temperature, and D is the so-called strength parameter.¹ The fitting yielded f_∞ = (2.8 ± 0.3) × 10¹¹ Hz, T₀ = 151.8 ± 0.9 K and D = 5.4 ± 0.1. Oftentimes, the condition τ(T_g) = 1/2πf(T_g) ≈ 100 s is used to define the glass-transition temperature T_g. Using the obtained parameters, we arrive at T_g = 177 ± 1 K. It should be mentioned that the slight kink in the experimental data at around 215 K is not an intrinsic feature of this relaxation process, but more likely the result of the deconvolution of the conductivity contribution in the low-frequency measurements. In PIm@(BC)₂, on the other hand, two temperature-activated relaxation processes are observed. Their activation energies E_A can be derived by fitting the data to the Arrhenius equation: f_a = f_∞ exp(−E_A/k_BT), where k_B is the Boltzmann constant. We obtained E_A = 32.7 ± 0.1 kJ mol⁻¹ for the low-frequency mode and E_A = 49 ± 2 kJ mol⁻¹ for the high-frequency one. In ref. 10, the authors assigned the low-frequency process to reorientations of the trapped PIm molecule without involving 180° flips from one semicage to the other one. They drew this conclusion based on the absence of such fluctuation in their molecular dynamics (MD) simulations. In light of the present results, however, we believe this interpretation should be revisited. If the flipping potential energy barrier is high, because of the aforementioned C–H⋯π interactions and limited free volume, for instance, the relaxation rate for such a process will be low and inaccessible to MD simulations. In fact, MD simulations only give access to very fast fluctuations because of their computational cost (simulation time was 2500 ps in ref. 10). Furthermore, it would be reasonable to think that this process drives the ferroelectric transition as the molecules of different cages become correlated, although we could not obtain data close to T_C and possibly observe soft-mode behavior, as in conventional ferroelectrics.²⁸ Of course, this process would then become frozen in the ferroelectric phase. As mentioned in the introduction, ethylene glycol confined in zeolite matrices transitions from collective liquid dynamics to single-molecule behavior as confinement becomes more intense, as originally reported in ref. 29. Out of the three host structures featured in that article, silica sodalite being a clathrasil framework of isolated cages resembles our clatrathe system the most. In that case, BDS measurements in combination with MD simulations showed that the molecular interaction between ethylene glycol guests is impaired. While this phenomenon parallels the low-frequency relaxation mode observed in PIm@(BC)₂, where a perfect Arrhenius behavior is identified, in our case, the interaction cannot be completely impaired, for the ferroelectric transition has to emerge from an increased correlation between PIm molecules of neighboring cages under the constrained spatial conditions. A possibility is that the environment of PIm@(BC)₂ could suppress competing relaxation modes and enhance collective polarization dynamics. This would emphasize the role of structural order and specific molecular interactions in driving the spontaneous polarization.

Fig. 6 Frequencies of maximum absorption of the observed relaxation processes in PIm (circles) and PIm@(BC)₂ (squares). Lines are fits to the Vogel–Fulcher–Tammann equation in the former case and to the Arrhenius equation in the latter case.

The high-frequency mode, on the other hand, must correspond to a more localized molecular fluctuation. A possible interpretation comes from realizing that the PIm molecule has internal rotational freedom of the imidazole ring along the C–N bond. To investigate this in detail, we performed a set of DFT calculations for the isolated molecule in vacuum to obtain the potential energy surface scan for such torsion, as shown in Fig. 7. Very recently, this strategy was followed to interpret the dipolar relaxation observed in a metal–organic framework.³⁰ Due to their computational cost these calculations were performed with a smaller basis set, namely 6-31G(d). The potential energy barrier for these torsional states is small, and we can expect such fluctuations to be active in PIm@(BC)₂ as well. Indeed, these were observed in the MD simulations of the paraelectric phase presented in ref. 10. Moreover, the same MD simulations revealed that these fluctuations were frozen in the ferroelectric phase, as the torsional state of the PIm molecule remained constant. Consequently, at high temperatures in the paraelectric phase, this fluctuation must be active and occur at higher frequencies beyond our measurement capabilities. Close to T_C, however, the energy barrier for this process becomes higher, its relaxation rate decreases and it becomes observable in the dielectric spectrum. Lastly, it becomes frozen in the ferroelectric phase. In addition, although a more involved calculation should consider the C–H⋯π interactions of PIm with the two BCs, the asymmetry in the two maxima of Fig. 7 could explain the broadening of the loss peak in Fig. 5b. It is worth mentioning that, although secondary relaxations involving intramolecular fluctuations were also recently detected in other bulk amorphous imidazole derivatives,³¹ in the present case, the freezing of the high-frequency process is central to the ferroelectric transition and is, thus, of special interest.

Fig. 7 Potential energy surface scan in vacuum for the internal rotation of the imidazole ring of PIm.

As outlined above, PIm@(BC)₂ offers a unique system for the exploration of molecular dynamics under confinement. Future studies that systematically vary the guest molecules and/or clathrate host structures could provide key insights into the mechanisms underlying the dielectric relaxations and phase transitions. Of course, exploring broader classes of systems, such as metal–organic frameworks, hybrid organic–inorganic materials, etc., may also reveal analogous behaviors or novel phenomena.

Conclusions

In this work, we have established a direct comparison between the dynamics of the PIm molecule in its bulk liquid form and in the ferroelectric clathrate system PIm@(BC)₂. While the dielectric spectra in the former case are insensitive to local molecular fluctuations and just reflect the structural relaxation on approaching T_g, two molecular relaxation processes are observed in the paraelectric phase of PIm@(BC)₂. By careful analysis of the dielectric spectra, and aided by quantum chemical calculations, we have provided an interpretation of these processes. The slow process is assigned to head-to-tail reorientations of the PIm molecule, while the fast process is attributed to the intramolecular rotation of the imidazole ring. Both of these processes become frozen in the low-temperature ferroelectric phase. The ferroelectric transition is found to be second order, as revealed by precision calorimetry. In the future, it would be of utmost interest to reproduce the dielectric relaxation processes of PIm@(BC)₂ through MD simulations by calculating the dipolar time-correlation functions. The high-frequency process, in particular, should be easily accessible to MD. A remarkable example in this category of studies is that of the ibuprofen model system. In fact, in a series of articles, the authors were able to reproduce the α-relaxation of this system at high temperatures, as well as the so-called Debye-process, which could be assigned to the rotational dynamics of the O=C–O–H group.^32–34 Alternatively, the investigation of clathrates with varying guest molecules could also aid in the interpretation of the dielectric data.

Data availability

The data that support the findings of this study are available within the article and its ESI.† Additional data will be made available by the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. E. and J. M.-P. acknowledge funding from the Basque Government Project IT1458-22 and from project PID2023-150255NB-I00 from MCIU/AEI/10.13039/5011000-11033/FEDER, UE. A. E. and J. M.-P. also acknowledge the technical and human support provided by IZO-SGI SGIker of UPV/EHU and European funding (ERDF and ESF). A. E. thanks the Department of Education of the Basque Government for a predoctoral fellowship (grant no. PRE_2024_2_0045). Z.-Y. D. and R.-K. H. thank the Natural Science Foundation of China (22465020) and the Natural Science Foundation of Jiangxi Province (20224ACB203002). A. O. acknowledges funding from the Basque Government Project IT1430-22.

References

1. Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003.
2. W. C. Child, Q. Rev., Chem. Soc., 1964, 18, 321.
3. M. Davies and K. Williams, Trans. Faraday Soc., 1968, 64, 529.
4. N. E. Hill, W. E. Vaughan, A. H. Price and M. Davies, Dielectric properties and molecular behaviour, Van Nostrand Reinhold Company, London, 1969.
5. Dynamics in Geometrical Confinement, ed. F. Kremer, Springer International Publishing, Cham, Switzerland, 2014th edn, 2014.
6. Non-equilibrium Phenomena in Confined Soft Matter: Irreversible Adsorption, Physical Aging and Glass Transition at the Nanoscale, ed. S. Napolitano, Springer International Publishing, 2015.
7. K. Ngai, Relaxation and Diffusion in Complex Systems, Springer, New York, 2011.
8. P. Lunkenheimer, U. Schneider, R. Brand and A. Loid, Contemp. Phys., 2000, 41, 15–36.
9. P. W. Anderson, Science, 1995, 267, 1615–1616.
10. L.-Y. Sheng, D.-C. Han, R.-K. Huang, L.-M. Cao, C.-T. He, Z.-Y. Du and T. Nakamura, J. Am. Chem. Soc., 2024, 146, 22893–22898.
11. C. Kato, R. Machida, R. Maruyama, R. Tsunashima, X. Ren, M. Kurmoo, K. Inoue and S. Nishihara, Angew. Chem., 2018, 130, 13617–13620.
12. K. Zhang, C. Wang, M. Zhang, Z. Bai, F.-F. Xie, Y.-Z. Tan, Y. Guo, K.-J. Hu, L. Cao, S. Zhang, X. Tu, D. Pan, L. Kang, J. Chen, P. Wu, X. Wang, J. Wang, J. Liu, Y. Song, G. Wang, F. Song, W. Ji, S.-Y. Xie, S.-F. Shi, M. A. Reed and B. Wang, Nat. Nanotechnol., 2020, 15, 1019–1024.
13. F. Wang, W. Shen, Y. Shui, J. Chen, H. Wang, R. Wang, Y. Qin, X. Wang, J. Wan, M. Zhang, X. Lu, T. Yang and F. Song, Nat. Commun., 2024, 15, 2450.
14. U. Zammit, M. Marinelli, F. Mercuri, S. Paoloni and F. Scudieri, Rev. Sci. Instrum., 2011, 82, 121101.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT.
16. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
17. C. Iacob, J. R. Sangoro, A. Serghei, S. Naumov, Y. Korth, J. Kärger, C. Friedrich and F. Kremer, J. Chem. Phys., 2008, 129, 234511.
18. M. E. Lines and A. M. Glass, Principles and applications of ferroelectrics and related materials, Oxford University Press, London, England, 2001.
19. K. Aizu, J. Phys. Soc. Jpn., 1969, 27, 387–396.
20. L. D. Landau and E. M. Lifshitz, Statistical Physics, Butterworth-Heinemann, Oxford, England, 3rd edn, 1996.
21. J. Thoen, E. Korblova, D. M. Walba, N. A. Clark and C. Glorieux, Liq. Cryst., 2021, 49, 780–789.
22. N. Pech-May, C. Vales-Pinzon, A. Vega-Flick, A. Oleaga, A. Salazar, J. Yanez-Limon and J. Alvarado-Gil, J. Compos. Mater., 2018, 52, 1331–1338.
23. R. Pelster, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 9214–9228.
24. K. Asami, Prog. Polym. Sci., 2002, 27, 1617–1659.
25. R. Richert, Eur. Phys. J.: Spec. Top., 2010, 189, 37–46.
26. The Scaling of Relaxation Processes, ed. F. Kremer and A. Loidl, Springer International Publishing, 2018.
27. M. D. Ediger, C. A. Angell and S. R. Nagel, J. Phys. Chem., 1996, 100, 13200–13212.
28. C. Kittel, Introduction to solid state physics, John Wiley & Sons, Nashville, TN, 8th edn, 2004.
29. A. Huwe, F. Kremer, P. Behrens and W. Schwieger, Phys. Rev. Lett., 1999, 82, 2338–2341.
30. R. Freund, A. Schulz, P. Lunkenheimer, M. Kraft, T. Bergler, H. Oberhofer and D. Volkmer, Adv. Funct. Mater., 2024, 2415376.
31. W. Noor, R. Macovez, P. M. Zamora, J. L. Tamarit and M. Romanini, J. Mol. Liq., 2024, 416, 126518.
32. A. R. Brás, J. P. Noronha, A. M. M. Antunes, M. M. Cardoso, A. Schönhals, F. Affouard, M. Dionísio and N. T. Correia, J. Phys. Chem. B, 2008, 112, 11087–11099.
33. F. Affouard and N. T. Correia, J. Phys. Chem. B, 2010, 114, 11397–11402.
34. M. T. Ottou Abe, M. T. Viciosa, N. T. Correia and F. Affouard, Phys. Chem. Chem. Phys., 2018, 20, 29528–29538.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00100e

---