Dipole orientation of hydrated gas phase proteins

Abstract

In the aerosolization of single proteins from solution, the proteins may be covered by a layer of water. This is relevant to consider in sample delivery for single particle imaging (SPI) with X-ray free-electron lasers. Previous studies suggest that the presence of a 3 Å water layer stabilizes the molecular structure and decreases structural heterogeneity which is important since it facilitates the structure determination in SPI. It has also been shown that SPI would benefit from the possibility of controlling the particle orientation in the interaction region. It has been proposed that such control would be possible by applying a DC electric field that interacts with the intrinsic dipole of the particle. This study investigates how SPI experiments, including dipole orientation, would be affected by the presence of a hydration layer covering the proteins. We investigated this by performing classical MD simulations of a globular protein in gas phase interacting with an external electric field. Two hydration levels were used: a fully desolvated molecule and one with a water layer corresponding to 3 Å covering the proteins surface. Our simulations show that a water layer enables the molecules to orient at lower field amplitudes, and on shorter time scales, as compared to the desolvated case. We also see a marginally larger stability of the molecular structure in the hydrated case at field strengths below 2 V nm⁻¹. The presence of a water layer, in combination with an electric field, also tend to stabilize the dipole axis significantly within the molecular structure.

---

1 Introduction

Proteins play a crucial role in biological processes, with their functions being closely tied to their structures. Traditionally, X-ray crystallography has been the main method for studying protein structures. Crystallography originally precipitated the birth of structure determination, and has been the dominating technique since. However, despite its strengths, including recent developments, it comes with certain limitations.

The crystallization can influence the structures under study, and inescapably purifies a single conformation and oligomeric state from a potentially wide ensemble of structures. Compounding this, the cryogenic temperatures, often used to reduce radiation damage, sequester and shift local dynamics in the structure.

Perhaps most importantly, certain types of proteins (such as membrane proteins) do not readily crystallize, and when they do, the crystallization process can still be arduous. Cryo-electron microscopy (cryo-EM), which has had tremendous impact on structural biology in recent times due to transformative technological developments, alleviates the need for crystals, but requires cryogenic temperatures and is practically limited to sample highly populated low-energy states. As such, both techniques risk obscuring the innate dynamics of protein structures, hiding important clues about their functions and mechanisms.

Over the past decades, there has been an increasing interest in, and rapid development of, techniques for gas phase structural biology. By operating on aerosolised proteins that can be fully devoid of solvent, or carrying a thin layer of water, they offer an avenue that avoids crystallization and cryogenic temperatures.

This approach is an intriguing alternative, as it allows for the study of proteins structures at room temperature and without crystallization, and it opens up for sorting the samples based on mass, charge and folding.¹ It has also been shown that it is to some extent possible to retrieve a protein's structure in solution based on the gas phase structure using classical MD simulations in solution.^2–4

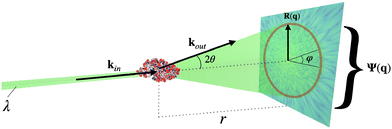
X-ray crystallography exploits the amplification that arises from the crystal lattice to produce measurable diffraction at high resolution, but diffraction from single particles require extremely intense X-ray pulses, such that it leads to extensive ionization causing the particle to explode. Consequently, the probe pulse needs to be in the order of few femtoseconds⁵ to allow the molecular structure to be probed before any defects stemming from radiation damage have time to manifest.^6,7 This outlines the basis for single particle imaging (SPI) of proteins or protein complexes (Fig. 1), which has attained increasing interest in recent years.^8–11 X-ray free electron lasers (XFELs) can produce X-rays with pulse lengths and intensities that meet the prerequisites of SPI, and have been proposed as a potential type of light source for such experiments.¹² SPI could potentially open up the possibility of structure determination of native-like gas phase biomolecules at atomic resolution.¹³

Fig. 1 Upper panel: Standard SPI setup – randomly oriented gas phase proteins are delivered to an X-ray beam and a single-particle diffraction pattern is recorded on a detector. Serial measurements will result in diffraction patterns randomly oriented in reciprocal space. Middle panel: SPI with dipole orientation – with a biased orientation of the gas phase particles (using electric fields) the diffraction images will also have a biased orientation in reciprocal space. Recent studies suggest this can benefit the structure determination. Lower panel: A dipolar single particle is oriented with its dipole [small mu, Greek, vector] along an external electric field E⃑. The deviation angle α is used as a measure of orientation, and is the angle between the protein dipole vector and the electric field. Electric field was implemented in the ẑ-direction in our simulations.

To obtain a 3D image of the molecular structure, multiple diffraction patterns from various directions are needed – such that the diffraction images span the entire reciprocal space volume necessary for structure determination. In standard crystallography, this is solved by simply rotating the sample, exposing it to multiple pulses. This is not possible in SPI, since the target molecule is annihilated by interactions with the XFEL pulse.

Instead, in order to cover enough of reciprocal space, a new particle (ideally identical) must be delivered to the interaction region for each new pulse. A large set of diffraction images is also beneficial due to the low signal-to-noise ratio of SPI measurements.^9,14

The heterogeneity of proteins of the same species poses challenges in this context: serial measurements require large structural homogeneity in the stream of particles delivered to the interaction region.^15,16 A simulation study indicates that structural heterogeneity of the proteins might even be a more severe obstacle towards high resolution SPI using XFEL than radiation damage.¹⁷

Another challenge in SPI imaging of gas phase biomolecules is the unknown orientation of the sample as it is exposed to the X-ray pulse. Unlike conventional crystallography, where the molecular orientation can be manipulated by simply rotating the crystal by macroscopic means, gas phase molecules are free to rotate and will have random orientations in space during imaging. Because of this lack of control of orientation, it is a non-trivial task to relate the 2D diffraction images to each other and assemble them in 3D reciprocal space. This procedure is known as orientation recovery. The iterative expand maximize compress (EMC) algorithm^18,19 can be used to reconstruct the electron density of randomly oriented molecules from a large ensemble of diffraction measurements. However, EMC does not always converge to a meaningful solution, especially when data is scarce or suffers from high noise.

A recent study demonstrated that the performance and utility of EMC can be increased by introducing a bias in the orientation of the molecules during imaging, introducing the so-called enhanced EMC algorithm.²⁰ With additional information about a common orientation direction for the gas phase molecules, the number of patterns required for convergence in the structure reconstruction can be reduced,²⁰ motivating us to pursue means of controlling the orientation of the molecules in the interaction region.

The orientation of single molecules can be influenced by an external electric field in the interaction region.^13,21,22 Alternatively, the orientation can be inferred post-exposure by measuring the direction of the trajectories of the ions ejected by the photo-induced explosion of the protein.^23–26 Electric fields will orient the dipole of the molecules along the field. The field interacts with the dipole of the molecule causing it to exhibit a pendular motion. Due to the non-rigid nature of the molecule, the rotational energy is absorbed by its internal degrees of freedom. This means that at sufficient electric field amplitude, eventually the dipole will orient with the electric field direction. We will refer to this process as dipole orientation. While the method is conceptually promising, there are concerns that the absorption of the rotational energy and the interactions with the electric field may affect the molecular structure. This would lead to increased structural fluctuations within the sample molecules.^21,27

Electrospray ionization (ESI) is commonly used to transfer proteins from solution to gas phase, and increasing evidence show that their structures can survive the non-native conditions.^28–30 Most common applications of ESI uses activation of the injected particles to remove any remaining water and salt, but some water can in principle be left bound to the protein. It turns out that a thin water layer encapsulating the protein slows down the Coulomb explosion of the ionized protein in SPI, reducing the effects of radiation damage in the diffraction images.³¹ In addition, with a minimal water layer the noise associated with structural heterogeneity tends to decrease.^15,16,32

Even a thin layer of water emulates some of the effect of bulk water, allowing single molecules to largely maintain their conformations found in the solution state.¹⁶ It has however also been shown that the addition of a water layer may increase background scattering noise, an effect that increases with layer thickness.³³ Combining SPI with dipole orientation may introduce additional noise due to structural heterogeneity, stemming from vibrations induced by oscillations of the molecular dipole axis around its equilibrium orientation. It is hypothesized that an encapsulating water layer could stabilize the structure by absorbing atomic vibrations and damping the oscillatory motion. The potential stabilizing effect of a water layer on dipole orientation and its implications for SPI have not yet been thoroughly investigated and are the focus of the present study.

Following the method established in earlier studies^{15,16,21,22,27,34} we performed molecular dynamics simulations of gas phase proteins surrounded by a 3 Å layer of water to investigate the effects of water molecules on the protein orientation process, as compared to a completely dehydrated protein. Our analysis focused on the following key aspects:

(i) Stability of the dipole axis. The concept of dipole orientation is based on the assumption that the dipole axis remains fixed relative to the protein molecule, with only small fluctuations. However, this assumption may not hold true due to the non-rigid nature of gas phase molecules. Based on our MD simulations we investigated the dipole axis stability during dipole orientation, and how it is affected by the addition of a 3 Å water layer.

(ii) Dipole orientation. We used the deflection angle α (see Fig. 1) as a measure of how well oriented the molecules were along their dipoles in our simulations. We further examined how rapid the orientation process was, and how this differ for the two hydration conditions.

(iii) Structural stability. We investigated how much the atomic structures of the proteins fluctuate during the dipole orientation process.

(iv) Resolution of diffraction images. We calculated noiseless diffraction images from structures taken from our MD simulations to assess whether the resolution in the diffraction patterns is in agreement with our results in (iii).

2 Method

We performed classical MD simulations of gas phase ubiquitin exposed to a DC electric field using GROMACS 4.6.7.^35,36 A comparison of gas phase protein stability using various force fields revealed minimal influence of the force field on overall stability,³⁴ and consequently, as in our previous studies,^{4,15,16,21,22,27,34,37} the OPLS-AA force field³⁸ was employed in combination with the TIP4P water model.³⁹ To emulate ideal vacuum conditions, no periodic boundary conditions or pressure coupling were applied, and non-bonded interactions were computed without cut-offs. No bond constraints were applied to the protein atoms, while constraints for the water molecules were implemented using the SETTLE algorithm.⁴⁰ The initial structure file of ubiquitin (pdbID:1UBQ)⁴¹ was taken from the RCSB Protein Databank. The crystal structure of ubiquitin has a dipole moment of 244 Debye. In solution the dipole is diminished to 230 Debye, and significantly decreases further when the molecule is transferred to gas phase.

Molecular dynamics simulations of the dipole-field interactions were performed at electric field amplitudes of E ∈ [0, 0.05, 0.10, 0.15, 0.20, 0.4, 0.60, 0.80, 1.00, 1.50, 2.00, 2.50, 3.00] V nm⁻¹ following the protocol described in ref. 42. The electric field was implemented in the ẑ-direction of the simulation box.

As dipole orientation in SPI has not yet been implemented experimentally, we base our choice of range for the electric field strengths on earlier theoretical studies.^21,22

For statistical purposes a total of 10 simulations were performed for each field amplitude. Two simulation sets were carried out: in the first, gas phase ubiquitin was simulated without water (referred to as “0 Å”), and in the second, ubiquitin was covered with water. In the latter case, water molecules were added to generate a 3 Å layer over the protein surface (henceforth referred to as “3 Å”), corresponding to 253 water molecules. After energy minimization, these water molecules redistribute, forming clusters in the hydrophilic regions.²²

For each MD simulation, we performed energy minimization using steepest descent minimization followed by a 10 ps equilibration run with temperature coupling at 300 K with a time step of 0.0005 ps. At this stage, no electric field was applied in the simulations. The Berendsen thermostat was used for the temperature coupling with a coupling time constant of 0.1 ps.⁴³ Following the equilibration run, a 10 ns simulation with external electric field was performed without temperature coupling, mimicking the conditions of a sample being delivered to the interaction region of a SPI experiment. For computational reasons we used a neutral protein in our simulations. In an ESI device the protein will carry a net charge. We assume that our conclusions about the change of dipole magnitude, the heterogeneity of the protein and the direction of the dipole axis will not be significantly affected by our choice of charge state. Simulation input files used are accessible in ref. 44.

We restricted ourselves to standard classical MD, excluding inter-atomic bond breaking and polarization effects resulting from molecule-electric field interactions. These assumptions are justified by previous research, which shows that at our selected field strength magnitudes, the force needed to break covalent bonds is not reached, and the electronic polarization occurs mainly locally, having minimal impact on the total dipole moment of the system.²⁷

We investigated how the dynamics of the protein affect the diffracted signal. Due to the limited access to SPI measurements, we did this by analyzing in silicio data. We calculated instantaneous, noiseless diffraction images using structures with the two hydration levels. Diffraction calculations depend on the X-ray wavelength and intensity, the geometric properties of the detector and the atomic positions x^(a)_j of the sample. Here a denote the atomic species and j ∈ [1,2…N], where is the total number of atoms in the sample. Depending on the atomic species a, different atomic scattering factors f^(λ)_a(θ) are used in calculations – these values are tabulated and depend on the incident X-ray wavelength λ and the scattering angle θ.

The diffraction calculations estimates the wave field Ψ(q) scattered by the sample, where q = k_out − k_in is the scattering vector. The calculations were made as

where r the distance between the sample and detector pixels and r₀ is the Thomson scattering length. This equation holds under the first-order Born approximation and the far field approximation. An illustration of the diffraction setup is shown in Fig. 2.

Fig. 2 Illustration of the diffraction in single particle imaging.

Calculations were performed using Condor, a code introduced by Hantke et al.⁴⁵ as a tool for predicting X-ray far-field scattering amplitudes of isolated particles.

We chose the parameters of the pulse and detector to match what can be expected at an XFEL facility, specifically the coherent X-ray imaging beamline (CXI) at LCLS.⁴⁶ Our virtual detector (side length 200 μm, 1516 × 1516 pixels) was placed orthogonal to the pulse direction, 50 mm from the interaction region. The pulse itself consisted of 10¹² photons using a circular cross section with 100 nm in diameter. Photon energy was fixed at 8 keV, as this is the order of magnitude needed for atomic resolution diffraction imaging.

10 snapshots where taken from each simulation, at even time separations during the last 2 ns of the trajectory. Repeating this for each of the 10 replicas, we obtain n = 100 structures for each of the varied field amplitudes E, each resulting in a calculated diffraction pattern Ψ^(E)(q)_i. From these we constructed an average diffraction image Ψ^(E)₀(q)

We then calculated the Pearson correlation of each diffraction image Ψ^(E)(q)_i with respect to the average Ψ^(E)₀(q) on a ring-by-ring basis, i.e. as a function of q = |q|. The Pearson correlation is implemented as shown in eqn (3) (following the procedure in Östlin et al. (2019).¹⁷)

where the sum indicates a summation over all φ belonging to a circle in the diffraction pattern corresponding to a given value of q (see Fig. 2).

By comparing the average Pearson correlation at increasing q values, we can estimate the resolution possible for structure determination. We used a threshold value for the Pearson correlation at 0.5 as a limit for when structure determination is possible, in accordance with van Ardenne et al.⁴⁷

3 Results

3.1 Stability of dipole axis

We investigated the fluctuations of the dipole direction within individual particles during the process of dipole orientation. For simulations conducted under different field strengths, we calculated the direction of the dipole axis in the molecular body reference frame. This was done by fitting each frame to a common reference structure, and observing the anisotropy of the dipole axis direction. We define the angle ϕ as the deviation of the dipole axis from its mean orientation (Fig. 3). By analyzing the distribution of ϕ, we can assess the stability and consistency of the dipole axis direction within the molecular structure.

Fig. 3 Upper panel: The dipole is not entirely fixed within the molecular structure. For the two hydration levels, the central black line indicate the mean direction of the dipole axis – after fitting to a common reference structure. The red lines are a random selection of the dipole axis at different time steps, to visualize the difference in the dipole axis fluctuations between the two cases. We define the angle ϕ as the deflection angle from the mean dipole direction. In this example the external electric field was 1 V nm⁻¹. Lower panel: Distribution of ϕ, the deflection angle of the molecular total dipole axis with respect to the average. A 3 Å water layer, particularly at larger field strengths, tend to decrease the mean deflection angle, as well as the width of the distribution. This indicate a decreased anisotropy of the dipole axis within the molecule, leading to enhanced dipole orientation.

Fig. 3 shows that the dipole is surprisingly unstable in the absence of a field, with an angular spread that appears to be independent of the presence of a water layer. However, the dipole becomes stabilized by the field both with and without water, but the effect is notably stronger when a water layer is present.

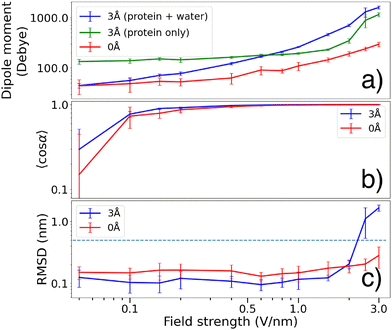
In the presence of an external electric field, polarization effects cause a redistribution of the water molecules, which in turn increases the total dipole of the system (see Fig. 4(b) and 5(a)). The 0 Å dipole magnitude also increases with the electric field, but to a smaller degree. When a protein molecule is transferred to gas phase and is completely dehydrated, conformational changes will occur with respect to its native structure.^2,48,49 Since even a thin water layer on its surface largely emulates the effect of complete hydration, such conformational changes are expected to be less apparent for the 3 Å molecules.¹⁶ We observed that a water layer allows the dipole magnitude of the protein to remain closer to its native state (green curve in Fig. 5(a)) compared to the dehydrated case (red curve in Fig. 5(a)) where the dipole magnitude is diminished due to conformational changes.

Fig. 4 Ubiquitin at the two hydration levels and at different dipole magnitudes. Total dipole moment of the system is displayed by the black vector. (a) Dehydrated protein (0 Å). (b) Examples 3 Å proteins interacting with electric fields. As the water molecules are displaced as a response to the electric field, the total dipole (protein + water) magnitude increases. From left to right: 0 V nm⁻¹, 0.4 V nm⁻¹, 1 V nm⁻¹. Snapshots are taken from the last nanosecond of the simulations.

Fig. 5 (a) Dipole magnitude at increasing electric field strength. For the 3 Å case we display both the total dipole (blue) and the protein dipole (green). The presence of water molecules partly emulates the effect of solvation, which explains why the 3 Å protein dipole is larger than that of the 0 Å protein dipole. Interactions between the field and the molecular structure has polarizing effects, enhancing the dipole at increasing field strength. In the 3 Å case, water molecules are displaced to further increase the total dipole magnitude. (b) Degree of orientation 〈cos α〉 during the last 5 ns for the two hydration levels. The 3 Å molecules tend to reach higher degree of orientation at lower field strengths ccompared to the 0 Å case (c) mean RMSD of the α − C positions of the backbone of the molecular structures. At lower field strengths, a 3 Å water layer reduces the RMSD, indicating larger structural stability compared to the 0 Å case. The dashed line at RMSD = 0.5 nm indicate the threshold for a protein to be considered unfolded.

The observed increase might also come from polarization of the protein itself, and indeed the 0 Å dipole magnitude also increases with the electric field, albeit to a lower degree than with the 3 Å water layer, indicating that the total polarizability depends not only on the water but on the response from the whole system.

3.2 Dipole orientation

The degree of dipole-orientation achieved in the simulations is assessed by the observable 〈cos α〉, α being the angle between the dipole moment vector and the field direction (see Fig. 1). This measure will be close to 1 for a highly oriented molecule. The angle brackets represent a time-average during the last 5 ns of the simulations, along with averaging over the 10 repeated simulations.

Fig. 5(b) shows that for field strengths below 1 V nm⁻¹, the gas phase molecules covered in a 3 Å water layer tend to obtain a slightly higher degree of orientation 〈cos α〉 compared to the dehydrated molecules. At higher field strengths however, both cases seem to reach almost perfect orientation along the electric field (such that 〈cos α〉 ≈ 1).

In Fig. 5(a) we see that the protein dipole of the 3 Å molecules (green curve, calculated without taking water molecules into account) is significantly larger than that of the naked protein. The water layer emulates the effect of solvation, bringing the conformation closer to solution state where the dipole is significantly larger compared to gas phase.¹⁶ At lower fields, the water molecules redistributes such that the total dipole is reduced. This allows for the total dipole to be smaller than that of the protein group. As the electric field strength is increased, polarization effects (as visualized in Fig. 4(b)) forces the waters to be displaced, causing the total dipole to grow larger than the protein dipole.

The time scale required to achieve a high degree of orientation was compared for the two hydration levels. The average time evolution of cos α is shown in Fig. 6 (shown without standard deviations and with a running average for visibility reasons). A few examples of the simulated time-development of cos α without averages are shown in the ESI.†

Fig. 6 Average time evolution of cos θ during the first 1000 ps of simulation. Left figure shows results for 0 Å and right for 3 Å. At sufficient field strength, the 3 Å molecules reach an oriented state faster copared to the 0 Å molecules.

By observing cos θ during the first ns of our simulations, we note that, at intermediate field strengths between 0.2–1 V nm⁻¹, the 3 Å molecules orient faster than the 0 Å molecules. At stronger fields the orientation is reached within 100 ps for both cases, and at lower field strengths, complete orientation is not achieved.

3.3 Structural stability

The root mean square fluctuations (RMSF) of the α-carbons measures how much the molecular structure fluctuates from the initial state during the dipole orientation simulations. In Fig. 7 we present this as distributions fitted to histograms of the RMSF during our simulations.

Fig. 7 Fitted distribution of the α-carbon RMSF of the protein structures for both the 3 Å and 0 Å cases. The presence of a water layer seem to stabilize the protein, causing the RMSF to have a narrower distribution with its peak at lower values as compared to the dehydrated case. This is true for molecules in a electric field below 2 V nm⁻¹. For fields stronger than that, the water layer has the opposite effect, causing large RMSF compared to the 0 Å molecules. Shown here is the 2.5 V nm⁻¹ example, where the 3 Å molecules tend to partially unfold, largly shifting the RMSF distribution outside the shown range.

We see a slight shift in the distribution of RMSF for the two hydration levels, such that the 3 Å case is shifted towards smaller RMSF compared to 0 Å at field strengths below 2 V nm⁻¹. For larger field strengths, the 3 Å molecules display larger structural fluctuations compared to the 0 Å case. This is due to partial unfolding which is also reflected in the RMSD data.

Gas phase molecules in an SPI experiment should ideally remain structurally intact until reaching the interaction region. The time-average change of the α-carbon positions (with respect to the starting structure) were compared using root mean square deviation (RMSD), which indicates if the proteins remain unfolded. RMSD of 0.5 nm is used as threshold for a protein to be considered unfolded.

Fig. 5(c) shows that a 3 Å water layer seems to decrease the RMSD by ∼0.05 nm at field strengths below 2 V nm⁻¹. At stronger field strengths, the water layer causes RMSD to increase above the threshold value of 0.5 nm. Both these observations is in agreement with the RMSF shown in Fig. 7.

3.4 Resolution of diffraction images

A few examples of the calculated diffraction patterns are shown in Fig. 9, and a selection of the Pearson correlations in Fig. 8. Additional calculated resolution limits (for the cases not displayed in Fig. 8) is shown in the ESI.† For a given FRC curve, we can estimate a corresponding resolution limit for structure determination using the same methodology as described in Mandl et al.¹⁵ An example of how the resolution was estimated is also presented in the ESI.† At very high field strengths (above 2 V nm⁻¹), the 3 Å Pearson correlation is diminished in comparison to the 0 Å. At lower field strengths, the 3 Å diffraction images have slightly lower estimated resolution limits. This is indicated by the colored vertical lines in Fig. 8.

Fig. 8 Pearson correlation as a function of q calculated using eqn (3). Results for both hydration levels are shown for some selected values of the electric field strength E. The uncertainties are indicated by the spread of the Pearson correlation after calculations on every pattern in the set. The correlation tend to decrease for larger q – and this effect is enhanced at larger field strengths. The corresponding resolution limit for structure determination are shown for both hydration levels by the vertical lines, and the standard deviation of said resolution limit are indicated by the horizontal lines.

Fig. 9 Calculated mean diffraction patterns of ubiquitin structures taken from the MD trajectory. Each image is the average of 100 patterns. Each structure snapshot was fitted to a reference structure through translation and rotation to ensure them to have same orientation with respect to the incident X-ray pulse. Detector size was 1516 × 1516 pixels and the sample-detector distance was 50 mm. Speckle resolution is similar for both hydration levels, except at large field strengths where speckle contrast decreases. The white circle indicate the diffraction radius at which the Pearson correlation (see eqn (3)) passes the threshold value 0.5 – our threshold for the best possible resolution in structure determination.

4 Discussion and conclusions

The time of flight of gas phase molecules in a typical SPI experiment is several orders of magnitude larger than the time scales possible to examine using MD simulations. Despite this, we are still convinced that our simulations are relevant, since they indicate the timescales of orientation which, for the fields considered, are shorter than our simulations. New implementations of clever techniques such as the FMM (fast multipole method) of calculating electrostatic forces could accelerate simulations of molecular systems in the gas phase.⁵⁰ This would enable studies of considerably larger proteins on experimentally relevant time scales, which would be a natural next step following this investigation.

We do not consider bond-breaking and electric polarization in our simulations as such effect was shown to be negligible for the field strengths used in the simulations. Neglecting ionization is a reasonable assumption as long as the probability of ionization is negligible on the time scales considered, and the electronic polarization has a significantly lower impact of the total dipole compared to the change in dipole induced by the dynamic of the protein.²¹ However, electric polarization could potentially be taken into account using a polarizable force field. Currently, there are no such force fields that have been widely used for simulations in the gas phase.

Another limitation in this study is that our diffraction calculations are instantaneous and does not contain noise due to ionization of the sample caused by an X-ray pulse.¹⁷ Radiation damage caused by ionization would manifest itself slightly different for a sample with or without water. Proteins with water are expected to explode slower,⁵¹ further highlighting the benefits of using a water layer.

The electric fields described in this study are between 0.05 and 3 V nm⁻¹. Experimentally it is complicated to achieve fields at the higher end of this scale, but in the simulations we are able to explore extreme fields, and we consider it relevant to do so. Commercially available miniaturized ultra-FAIMS chips used for ion mobility spectrometry of biomolecules can generate fields reaching 0.075 V nm⁻¹,^52,53 and even stronger fields have been applied to non-protein molecules in the gas phase as well as protein crystals.^54–56

At large field amplitudes, we see apparent changes in the molecular structure due to denaturation. This indicates a limit for field amplitudes suitable for dipole orientation for SPI. Using fields beyond this limit would not be interesting from a structural point of view, but might have applications for studying dynamics and the unfolding pathways of proteins.²⁷

The main objective with this study is to explore if addition of a water layer to proteins that are oriented with an electric field improves the degree of orientation or the structural homogeneity. In a standard sample delivery using ESI, it would not be realistic to expect that the number of water molecules attached to the single particles to be constant in the sample delivery. The thickness of the water layer would therefore be expected to be variable. Previous research indicates that a thicker layer adds noise to the calculated diffraction patterns, having negative effects on orientation recovery.³³ The thickness of the water layer is also likely to have an effect on dipole orientation, influencing the average deviation angle from perfect alignment with the external electric field. As this mean deviation angle is a parameter in the enhanced EMC algorithm, water layer thickness will influence the effectiveness of enhanced EMC.²⁰

This type of inhomogeneity in water layer thickness can potentially be addressed by incorporating mass spectrometry in the sample delivery, whereby particles can be selected for downstream X-ray exposure based on their mass-to-charge ratio, which will differ depending on the number of waters carried by the proteins. A project that experimentally focuses on this aspect is the MS SPIDOC project,⁵⁷ within which ESI and mass spectrometry are combined for controlled particle injection for SPI experiments.^1,13

In the experimental implementation of dipole orientation of gas phase biomolecules, our study could provide some useful information. Our results imply that an electric field of 0.5 V nm⁻¹ is sufficient for achieving a high degree of orientation while not damaging the structure of the single particles. We also show that the existence of water molecules around the delivered single particle is beneficial to the dipole orientation process, both in terms of faster orientation and a more stable molecular structure. A summary of our findings are described more in detail below:

(i) We observed relatively large fluctuations of the dipole axis direction within the molecules. This is highly relevant for developing dipole orientation of single particles, as the orientation occurs along the dipole direction. If the dipole direction is not fixed with respect to the structure, this means additional uncertainty that is not captured by considering orientation of the dipole itself. The addition of a water layer tends to stabilize the total dipole direction with respect to the molecule. This effect becomes more pronounced with increasing field strength, suggesting that a water layer may enhance the dipole orientation by dampening the fluctuations of the dipole. Fluctuations of the dipole axis are caused by vibrations within the molecule. A water layer can absorb such vibrational energy and thus have a dampening factor which fixates the dipole axis within the structure. In addition, the vibrational energy absorbed by water dissipates from the system via evaporation of water molecules, having a cooling effect.^34,58 This likely contributes to the increased stability of the dipole axis that was observed in the 3 Å case.

We also observed that the dipole magnitudes of the 3 Å proteins were consistently larger compared to the 0 Å case. The water layer brings the system closer to solution state, preventing the dipole magnitude to decrease as a response of transferring to gas phase.¹⁶ The water molecules form clusters at hydrophilic regions, causing the total dipole magnitude (blue curve in Fig. 5(a)) to be smaller than that of the protein (green curve in Fig. 5(a)). At larger field strengths the water molecules are however displaced to form clusters that align with the field direction, which is visualized in Fig. 4(b). This removes the stabilizing effects of the water and exposes hydrophobic regions. In addition, the water molecules can facilitate breaking of salt bridges by solvating the charged residues after separation, thereby enabling complete unfolding. This is likely the reason why the 3 Å molecules attain higher RMSDs at large field strengths.

(ii) A 3 Å water layer tends to lead to a higher degree of orientation compared to the waterless proteins. This is most apparent at field strengths below 0.6 V nm⁻¹, and the two cases seem to orient equally well at larger field strengths. We observed a faster orientation time for the 3 Å case at lower field strengths. This, combined with the results in (i), demonstrates the advantage of a water layer for dipole orientation of single particles. Faster orientation means that fewer oscillations occur about the field direction, and since every oscillation may contribute to structural change, a rapid orientation would be beneficial for imaging purposes.

(iii) The RMSD from the initial structure for the 3 Å case is consistently lower than the 0 Å case during our simulations, except at field strengths above 2 V nm⁻¹ where the 3 Å molecules are clearly more affected by the electric field than the 0 Å molecules. In fact, at large field strengths the 3 Å molecules unfold to a higher degree than the 0 Å molecules. Previous studies have suggested ∼0.5 V nm⁻¹ as a suitable field strength for dipole orientation of ubiquitin.²¹ At such field strengths, our results show that a water layer tends to prevent structural changes in the molecule, helping to maintain more native-like structures for delivery to the interaction region. Similar conclusions may be drawn by the analysis of the RMSF distribution, where we saw a clear difference between the two hydration cases. At field strengths <2 V nm⁻¹, water-covered molecules showed smaller C − α fluctuations and a more narrow distribution compared to the naked molecules.

(iv) Simulations of diffraction patterns from the 3 Å and 0 Å molecules show that the structure determination resolution is slightly increased by adding a water layer. This is true at lower field strengths (below 2 V nm⁻¹), whereas the opposite (namely, lower resolution of the 3 Å case in comparison to the 0 Å case) is true at larger field strengths. This should be due to the unfolding discussed in (iii), which reduces the structural heterogeneity. At more modest field strengths, the resolution of the simulated diffraction images are slightly enhanced by a water layer, indicating the benefits of using water-covered sample molecules in SPI.

Author contributions

Conceptualization: CC, EDS; software: HA, ELSJ; formal analysis: HA, ELSJ, GE; resources: CC, EGM; writing – original draft: HA; writing – review & editing: HA, CC, EDS, ELSJ, TM, EGM; visualization: HA; supervision: CC, EDS, EGM.

Data availability

Data for this article, including input files for the simulations are available at GitHub Repository: dipole orientation of hydrated gas phase proteins, https://github.com/agelii92/dipole_orientation_of_hydrated_gas_phase_proteins, (2025-01-03). Additional data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Biophysics network at Uppsala University for insightful discussions. This work was financially supported by the Swedish Research Council via project 2018-00740 and via the Röntgen-Ångström Cluster (2019-03935), as well as by the Center for Interdisciplinary Mathematics (CIM) at Uppsala University. CC acknowledges the Helmholtz Association through the Center for Free-Electron Laser Science at DESY, and SPIDoc's HORIZON-MSCA-2022-DN (GA101120312) for financial support. Computational resources were provided by National Academic Infrastructure for Supercomputing in Sweden (NAISS) via the Tetralith cluster at Linköping University (projects 2024/5-140 and 2024/23-82).

Notes and references

1. A. Kadek, K. Lorenzen and C. Uetrecht, Drug Discovery Today: Technol., 2021, 39, 89–99.
2. T. Meyer, X. de la Cruz and M. Orozco, Structure, 2009, 17, 88–95.
3. M. N. Brodmerkel, E. De Santis, C. Caleman and E. G. Marklund, Protein J., 2023, 42, 205–218.
4. M. N. Brodmerkel, E. De Santis, C. Uetrecht, C. Caleman and E. G. Marklund, Curr. Res. Struct. Biol., 2022, 4, 338–348.
5. R. Neutze, R. Wouts, D. Van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752–757.
6. H. N. Chapman, A. Barty, M. J. Bogan, S. Boutet, M. Frank, S. P. Hau-Riege, S. Marchesini, B. W. Woods, S. Bajt and W. H. Benner, et al., Nat. Phys., 2006, 2, 839–843.
7. H. Chapman, C. Caleman and N. Timneanu, Philos. Trans. R. Soc. London, Ser. B, 2014, 369, 20130313.
8. M. M. Seibert, T. Ekeberg, F. R. N. C. Maia, M. Svenda, J. Andreasson, O. Joensson, D. Odic, B. Iwan, A. Rocker, D. Westphal, M. Hantke, D. P. DePonte, A. Barty, J. Schulz, L. Gumprecht, N. Coppola, A. Aquila, M. Liang, T. A. White, A. Martin, C. Caleman, S. Stern, C. Abergel, V. Seltzer, J.-M. Claverie, C. Bostedt, J. D. Bozek, S. Boutet, A. A. Miahnahri, M. Messerschmidt, J. Krzywinski, G. Williams, K. O. Hodgson, M. J. Bogan, C. Y. Hampton, R. G. Sierra, D. Starodub, I. Andersson, S. Bajt, M. Barthelmess, J. C. H. Spence, P. Fromme, U. Weierstall, R. Kirian, M. Hunter, R. B. Doak, S. Marchesini, S. P. Hau-Riege, M. Frank, R. L. Shoeman, L. Lomb, S. W. Epp, R. Hartmann, D. Rolles, A. Rudenko, C. Schmidt, L. Foucar, N. Kimmel, P. Holl, B. Rudek, B. Erk, A. Hoemke, C. Reich, D. Pietschner, G. Weidenspointner, L. Strueder, G. Hauser, H. Gorke, J. Ullrich, I. Schlichting, S. Herrmann, G. Schaller, F. Schopper, H. Soltau, K.-U. Kuehnel, R. Andritschke, C.-D. Schroeter, F. Krasniqi, M. Bott, S. Schorb, D. Rupp, M. Adolph, T. Gorkhover, H. Hirsemann, G. Potdevin, H. Graafsma, B. Nilsson, H. N. Chapman and J. Hajdu, Nature, 2011, 470, 78–82.
9. T. Ekeberg, D. Assalauova, J. Bielecki, R. Boll, B. J. Daurer, L. A. Eichacker, L. E. Franken, D. E. Galli, L. Gelisio and L. Gumprecht, et al., Light: Sci. Appl., 2024, 13, 15.
10. E. Sobolev, S. Zolotarev, K. Giewekemeyer, J. Bielecki, K. Okamoto, H. K. Reddy, J. Andreasson, K. Ayyer, I. Barak and S. Bari, et al., Commun. Phys., 2020, 3, 97.
11. T. Ekeberg, M. Svenda, C. Abergel, F. R. Maia, V. Seltzer, J.-M. Claverie, M. Hantke, O. Jönsson, C. Nettelblad and G. Van Der Schot, et al., Phys. Rev. Lett., 2015, 114, 098102.
12. J. Hajdu, R. Neutze, R. Wouts, D. van der Spoel and E. Weckert, Nature, 2000, 406, 752–757.
13. T. Kierspel, A. Kadek, P. Barran, B. Bellina, A. Bijedic, M. N. Brodmerkel, J. Commandeur, C. Caleman, T. Damjanović, I. Dawod, E. De Santis, A. Lekkas, K. Lorenzen, L. L. Morillo, T. Mandl, E. G. Marklund, D. Papanastasiou, L. A. I. Ramakers, L. Schweikhard, F. Simke, A. Sinelnikova, A. Smyrnakis, N. Timneanu and C. Uetrecht, Anal. Bioanal. Chem., 2023, 415, 4209–4220.
14. T. V. Yenupuri, S. Rafie-Zinedine, L. Worbs, M. Heymann, J. Schulz, J. Bielecki and F. R. Maia, Sci. Rep., 2024, 14, 4401.
15. T. Mandl, C. Östlin, I. E. Dawod, M. N. Brodmerkel, E. G. Marklund, A. V. Martin, N. Timneanu and C. Caleman, J. Phys. Chem. Lett., 2020, 11, 6077–6083.
16. A. Patriksson, E. Marklund and D. van der Spoel, Biochemistry, 2007, 46, 933–945.
17. C. Östlin, N. Timneanu, C. Caleman and A. V. Martin, Struct. Dyn., 2019, 6, 044103.
18. N.-T. D. Loh and V. Elser, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80, 026705.
19. K. Ayyer, T.-Y. Lan, V. Elser and N. D. Loh, J. Appl. Crystallogr., 2016, 49, 1320–1335.
20. A. Wollter, E. De Santis, T. Ekeberg, E. G. Marklund and C. Caleman, J. Chem. Phys., 2024, 160, 114108.
21. A. Sinelnikova, T. Mandl, H. Agelii, O. Grånäs, E. G. Marklund, C. Caleman and E. De Santis, Biophys. J., 2021, 120, 3709–3717.
22. E. G. Marklund, T. Ekeberg, M. Moog, J. L. P. Benesch and C. Caleman, J. Phys. Chem. Lett., 2017, 8, 4540–4544.
23. C. Östlin, N. Tîmneanu, H. O. Jönsson, T. Ekeberg, A. V. Martin and C. Caleman, Phys. Chem. Chem. Phys., 2018, 20, 12381–12389.
24. E. De Santis, I. Dawod, T. André, S. Cardoch, N. Timneanu and C. Caleman, Europhys. Lett., 2024, 148, 17001.
25. T. André, E. De Santis, N. Timneanu and C. Caleman, arXiv, 2024, preprint, arXiv:2410.15965 DOI:10.48550/arXiv.2410.15965.
26. T. André, I. Dawod, S. Cardoch, E. De Santis, N. Timneanu and C. Caleman, Phys. Rev. Lett., 2025, 134, 128403.
27. A. Sinelnikova, T. Mandl, C. Östlin, O. Grånäs, M. N. Brodmerkel, E. G. Marklund and C. Caleman, Chem. Sci., 2021, 12, 2030–2038.
28. B. T. Ruotolo, K. Giles, I. Campuzano, A. M. Sandercock, R. H. Bateman and C. V. Robinson, Science, 2005, 310, 1658–1661.
29. D. van der Spoel, E. G. Marklund, D. S. D. Larsson and C. Caleman, Macromol. Biosci., 2011, 11, 50–59.
30. T. K. Esser, J. Böhning, A. Önür, D. K. Chinthapalli, L. Eriksson, M. Grabarics, P. Fremdling, A. Konijnenberg, A. Makarov, A. Botman, C. Peter, J. L. P. Benesch, C. V. Robinson, J. Gault, L. Baker, T. A. M. Bharat and S. Rauschenbach, Sci. Adv., 2024, 10, eadl4628.
31. S. P. Hau-Riege, R. A. London and A. Szoke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 051906.
32. F. Wang, E. Weckert, B. Ziaja, D. S. Larsson and D. van der Spoel, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031907.
33. J. E, M. Stransky, Z. Shen, Z. Jurek, C. Fortmann-Grote, R. Bean, R. Santra, B. Ziaja and A. P. Mancuso, Sci. Rep., 2023, 13, 16359.
34. E. G. Marklund, D. S. D. Larsson, D. van der Spoel, A. Patriksson and C. Caleman, Phys. Chem. Chem. Phys., 2009, 11, 8069–8078.
35. H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
36. E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317.
37. M. N. Brodmerkel, L. Thiede, E. De Santis, C. Uetrecht, C. Caleman and E. G. Marklund, Phys. Chem. Chem. Phys., 2024, 26, 13094–13105.
38. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
39. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
40. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
41. S. Vijay-Kumar, C. E. Bugg and W. J. Cook, J. Mol. Biol., 1987, 194, 531–544.
42. C. Caleman and D. van der Spoel, Angew. Chem., Int. Ed., 2008, 47, 1417–1420.
43. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
44. GitHub Repository: dipole orientation of hydrated gas phase proteins, https://github.com/agelii92/dipole_orientation_of_hydrated_gas_phase_proteins, (2025-01-03).
45. M. F. Hantke, T. Ekeberg and F. R. N. C. Maia, J. Appl. Crystallogr., 2016, 49, 1356–1362.
46. M. Liang, G. J. Williams, M. Messerschmidt, M. M. Seibert, P. A. Montanez, M. Hayes, D. Milathianaki, A. Aquila, M. S. Hunter, J. E. Koglin, D. W. Schafer, S. Guillet, A. Busse, R. Bergan, W. Olson, K. Fox, N. Stewart, R. Curtis, A. A. Miahnahri and S. Boutet, J. Synchrotron Radiat., 2015, 22, 514–519.
47. B. von Ardenne, M. Mechelke and H. Grubmüller, Nat. Commun., 2018, 9, 2375–2379.
48. K. Breuker and F. W. McLafferty, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18145–18152.
49. A. D. Rolland and J. S. Prell, TrAC, Trends Anal. Chem., 2019, 116, 282–291.
50. L. J. Persson, C. Sahin, M. Landreh and E. G. Marklund, Anal. Chem., 2024, 96, 15023–15030.
51. S. P. Hau-Riege, R. A. London, H. N. Chapman, A. Szoke and N. Timneanu, Phys. Rev. Lett., 2007, 98, 198302.
52. A. Wilks, M. Hart, A. Koehl, J. Somerville, B. Boyle and D. Ruiz-Alonso, Int. J. Ion Mobility Spectrom., 2012, 15, 199–222.
53. L. J. Brown, D. E. Toutoungi, N. A. Devenport, J. Reynolds, G. Kaur-Atwal, P. Boyle and C. Creaser, Anal. Chem., 2010, 82, 9827–9834.
54. D. A. Horke, Y.-P. Chang, K. Długołecki and J. Küpper, Angew. Chem., Int. Ed., 2014, 53, 11965–11968.
55. S. Y. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828–4878.
56. D. R. Hekstra, K. I. White, M. A. Socolich, R. W. Henning, V. Šrajer and R. Ranganathan, Nature, 2016, 540, 400–405.
57. MS-SPIDOC, https://www.ms-spidoc.eu/.
58. C. Caleman and D. van der Spoel, J. Chem. Phys., 2006, 125, 154508.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00073d

---