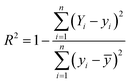Machine learning assisted approximation of descriptors (CO and OH) binding energy on Cu-based bimetallic alloys

Abstract

Data driven machine learning (ML) based methods have the potential to significantly reduce the computational as well as experimental cost for the rapid and high-throughput screening of catalyst materials using binding energy as a descriptor. In this study, a set of eight widely used ML models classified as linear, kernel and tree-based ensemble models were evaluated to predict the binding energy of catalytic descriptors (CO* and OH*) on (111)-terminated Cu₃M alloy surfaces using the readily available metal properties in the periodic table as features. Among all the models tested, the extreme gradient boosting regressor (xGBR) model showed the best performance with the root mean square errors (RMSEs) of 0.091 eV and 0.196 eV for CO and OH binding energy predictions on (111)-terminated A₃B alloy surfaces. Moreover, the xGBR model gave the highest R² scores of 0.970 and 0.890 for CO and OH binding energies. The time taken by the ML predictions for 25 000 fits for each model was varied between 5 and 60 min on a 6 core and 8 GB RAM laptop, which was very negligible as compared to DFT calculations. Our ML model showed remarkable performance for accurately predicting the CO and OH binding energies on a (111)-terminated Cu₃M alloy with a mean absolute error (MAE) of 0.02 to 0.03 eV compared to DFT calculated values. The ML predicted binding energies can be further used with an ab initio microkinetic model (MKM) to efficiently screen A₃B-type bimetallic alloys for the formic acid decomposition reaction.

---

Introduction

Catalyst discovery and optimization play a key role in meeting the ever-growing global demands, developing eco-friendly processes and reducing energy intensity.^1,2 However, the diversity in metal element combinations makes traditional experimental trial-and-error methods difficult for designing new catalyst materials, which provide higher conversions and better selectivity. On the other hand, significant advances in computational power and methods such as density functional theory (DFT) have made computational chemistry a valuable tool for the rational design of catalysts for homogeneous,^3,4 heterogeneous,^5,6 and enzyme catalyses.^7,8 These simulations provide information about catalyst properties and reaction pathways. However, screening of active and selective catalysts from DFT simulations is difficult again, due to the wide choice of catalytic materials and huge computational cost associated with them. Therefore, in order to accelerate the discovery of new catalysts, a tool based on a simple structural or energetic criterion is desirable, which can predict the properties of untested catalysts. To accomplish this, Sabatier principle⁹ based volcano plots¹⁰ are used to predict the catalyst performance using easily accessible descriptor variables.¹¹ For the high-throughput screening of prospective catalysts, these volcano plots use linear scaling relationships to relate the kinetic or thermodynamic performance of the catalyst with the quantitative value of the descriptor.^12,13 For example, Jalid et al. used carbon and oxygen binding energies as descriptors for the volcano plots to screen bimetallic catalysts (Co₃Ni, Ni₃Fe and Co₃Fe) with maximum turnover (10⁻³ s⁻¹) for C–O bond scission of ethanol to produce ethane.¹⁴ Similarly, Chen et al. used volcano plots to design a transition metal doped Ni₃S₂ catalyst for the water splitting reaction.¹⁵ However, the values of descriptors were determined through slow DFT simulations.

An increase in the speed of determining the descriptor variable would definitely accelerate the discovery of catalysts. In this regard, quantum ML models provide instantaneous access to the descriptor.^16,17 Based on the physical and chemical characteristics of materials, ML models have been used for the screening of large material databases to find materials that may perform well.¹⁸ Gradient Boosting Regression (GBR)¹⁹ was used for the prediction of CO binding energy on Pt nanostructures.²⁰ Liu et al. used ML models for the prediction of the binding energies of C and O atoms on bimetallic surfaces and used these binding energies for the steam methane reforming reaction.²¹ Saxena et al. also used an ML based approach for predicting C and O adsorption energies on Cu-based bimetallic surfaces and used these predictions in an MKM for the ethanol decomposition reaction.²² Wang et al. used a similar approach to screen sulphur resistant catalysts for the steam methane reforming reaction by using an ensemble model to predict the binding energies of C, H, S and O on bimetallic surfaces and combined these predictions with the MKM model.²³

Formic acid has been suggested as a suitable material for H₂ storage.^24,25 On transition metal catalysts, formic acid decomposes either via dehydrogenation to form H₂ and CO₂ or dehydrates to produce CO and H₂O.^26–28 But, CO production via the latter pathway deactivates the catalyst surface. In order to develop formic acid as a H₂ storage material, efficient catalysts that can easily decompose formic acid to H₂ and CO₂ are needed. Towards this, pure Cu has been observed to selectively catalyse the dehydrogenation reaction,²⁹ but with reduced rates.³⁰ On the other hand, Cu-based bimetallic catalysts such as Cu₃Pt have shown good activity towards formic acid dissociation into H₂ and also inhibit CO poisoning.^31–33 Furthermore, binding energies of all the reaction species formed during formic acid decomposition can be scaled with CO and OH adsorption energies as they are already involved in the reaction mechanism, and their adsorption energies are known to correlate well with carbon and oxygen adsorption energies respectively.^34,35 Therefore, in this study we have used ML with simple and easily accessible features to train prediction models that can accurately predict the binding energy of descriptors (CO and OH) on (111)-terminated Cu₃M (where M is a guest metal) alloy surfaces. CO and OH binding energies are also the key descriptors for other reactions as well, such as CO₂ reduction reactions,^36,37 reverse water gas shift reactions,^38,39 methanol electro-oxidation,^40,41etc. Furthermore, intermediate CO binding energy on Cu based catalysts makes them selective for the above reactions.^42,43 The ML predicted CO and OH binding energies in this study can be used with an ab initio microkinetic model (MKM) to calculate the catalytic rates for all the above reactions over bimetallic alloys.³² Li et al. have also used an ML based approach to predict OH and CO binding energies on (111)-terminated metal surfaces.⁴⁴ However, the features used in the ML models as input were derived from DFT local density of state calculations, structural optimization and modelling iterations, which increase the time and limit the transferability of the method.²¹ On the other hand, utilizing easily accessible metal properties as features can effectively address the aforementioned issues. Therefore, it is essential to identify the intrinsic properties of catalysts, i.e., features that not only are closely related to the adsorption properties but also have physical meanings.⁴⁵ The features should encapsulate the geometric and electronic properties of the local environment of surface-active sites while also capturing key characteristics of adsorbates. Additionally, they should be readily accessible from databases to enhance the efficiency of machine learning frameworks. Basic elemental properties, such as the atomic number, atomic radius, period number, group number, electronegativity, etc., which can be easily obtained from periodic tables and databases, have been widely used in ML for predicting alloy performance.^46–52 In this study different ML algorithms were evaluated to predict the binding energy of catalytic descriptors (CO* and OH*) on (111)-terminated Cu₃M alloy surfaces using the readily available metal properties in the periodic table as features and to put forward the advantage of extreme gradient boosting regressor (xGBR) over other ML models. As compared to DFT calculations, the computational time required for the ML model prediction was negligible.

Methodology

Different ML models such as Linear Regression (LR), k-Nearest Neighbours Regression (KNN), Support Vector Regression (SVR) and Kernel Ridge Regression (KRR) were used for the predictions. Ensemble-based models such as Random Forest Regression (RFR), Extra Trees Regression (ETR), GBR and xGBR were also included. All these models were trained and tested on a dataset comprised of CO and OH binding energies over (111)-terminated A₃B type bimetallic alloys where ‘A’ is the main metal and ‘B’ is the guest metal. The CO and OH binding energy data on the selected (111)-terminated A₃B alloy surfaces were obtained from a previous DFT study conducted by Zheng et al.⁴⁴ A model representation of the (111)-terminated A₃B alloy surface is shown in Fig. 1. The bimetallic alloy with A₃B (L12 type structure) composition has an FCC crystal structure, with 75 : 25 composition of A and B metals, respectively.^53–55 In this study, only alloys with a formation energy below 0.2 eV per unit cell were deemed potentially stable and were considered.^56,57 Furthermore, surface metal's individual physical properties such as period, group, atomic number, atomic radius, atomic mass, boiling point, melting point, electronegativity, heat of fusion, ionization energy, density, surface energy etc. play an important role in the adsorbate/metal interactions. These elemental properties can be easily obtained from the periodic table and other databases.^58,59 The surface energy dataset was obtained from Tran et al.⁶⁰ The above-mentioned features were used to uniquely represent each bimetallic alloy and have been shown to produce sufficiently accurate results.^48,61 A total of 18 distinct features for the main metal and 18 for the guest metal in the alloy were used and are shown in Table S1 (ESI†).

Fig. 1 A (111)-terminated A₃B bimetallic surface for the ML model development, where A and B represent the metal elements across the periodic table.

The implementation of ML algorithms was carried out by utilizing the popular open-source library, Scikit-Learn.⁶² All the features were used in building the above-mentioned ML models. To assess the predictive efficacy of the ML algorithms, the dataset was initially bifurcated into two subsets: training data and testing data. Various pairs of training and testing data were tested for each model with different separated ratios to gain ideal regression models. The accuracy of the models was evaluated based on the root mean-squared error (RMSE) and coefficient of determination (R²), which are defined as follows:

where Y_i indicates the DFT computed binding energy value, y_i indicates the value predicted by the ML models, n indicates the sample size of the data and ȳ indicates the mean of actual values.

The accuracy of the models is also affected by the values of the hyperparameters. Therefore, for each model, a diverse set of hyperparameters as listed in Table 1, column (i) and (iii) for CO and OH binding energies, respectively, were tested and optimized via randomized search cross validation (RCV)⁶³ in Scikit-Learn. K-Fold cross-validation (k = 10) with 50 iterations was used and repeated 50 times corresponding to 25 000 fits for different splitting ratios of training and testing data. Each split had a unique set of best hyperparameters for the corresponding RMSE, and even the lowest RMSEs across splits corresponded to different hyperparameter combinations. This suggests that while some parameters consistently impacted performance, their optimal values were sensitive to data partitioning. This variability highlights the importance of rigorous tuning and multiple resampling strategies to ensure model robustness and generalizability and avoided data biasing and overfitting. The tuning of each hyperparameter was carefully balanced to avoid over- and under-parametrized models, aiming at models with optimal predictive capabilities. The hyperparameter tuning process was guided by an iterative and adaptive approach. Initially, for each model, the most influential hyperparameters that played a crucial role in controlling underfitting, overfitting, and optimizing the bias-variance trade-off were identified. These parameters were selected based on prior research and their effectiveness in similar machine learning models.^22,48,51,64 Each model was initialized with commonly used parameter ranges. After analysing the RMSE values from the initial tuning phase, the hyperparameter ranges were redefined, tailoring them to each model based on the previously observed best RMSE. This process was repeated multiple times across all chosen hyperparameters until the best possible RMSE values were achieved or no further improvement in RMSE and R² scores was observed. This iterative tuning process, combined with RCV, allowed us to efficiently explore the hyperparameter space while adapting the search to each model's performance characteristics. Furthermore, Sobol Sequence⁶⁵ helped in achieving a more systematic and even distribution of initial points in the hyperparameter space. This aided the searching algorithm to explore promising areas more efficiently, making the tuning process more effective and time saving. The most effective ML model for predicting CO and OH binding energies on (111)-terminated A₃B bimetallic alloys was identified by evaluating the RMSE and R² scores obtained at the optimal hyperparameter settings for each model. The Seaborn library⁶⁶ was used for the construction of the correlation matrix. Moreover, Principal Component Analysis (PCA) was used to extract the essential patterns or information from the original features and to check the effect of dimensionality reduction on the ML model's performance.⁶⁷

Table 1 The range of hyperparameters tested and tuned using RCV for predicting CO and OH binding energies for all ML models (hyperparameters not mentioned were kept at their default values as per scikit-learn/Keras documentation)

S. no.	Model	Tested hyperparameters for CO binding energy	Tuned hyperparameters of the best estimator using RCV for CO	Tested hyperparameters for OH binding energy	Tuned hyperparameters of the best estimator using RCV for OH
		(i)	(ii)	(iii)	(iv)
1	LR	No parameters	No parameters	No parameters	No parameters
2	KNN	Algorithm = [‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’]	Algorithm = [brute]	Algorithm = [‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’]	Algorithm = [ball_tree]
		Leaf_size = np.arange (5, 50, 5)	Leaf_size = [10]	Leaf_size = np.arange (5, 50, 5)	Leaf_size = [45]
		n – neighbors = np.arange (1, 20, 1)	n – neighbors = [4]	n – neighbors = np.arange (1, 20, 1)	n – neighbors = [6]
		P = [1, 2]	P = [1]	P = [1, 2]	P = [1]
		Weights = [‘uniform’, ‘distance’]	Weights = [‘distance’]	Weights = [‘uniform’, ‘distance’]	Weights = [‘distance’]
3	SVR	C = np.arange (500, 1500, 10)	C = [890]	C = np.arange (500, 1500, 10)	C = [500]
		Kernel = [‘rbf’]	Kernel = [‘rbf’]	Kernel = [‘rbf’]	Kernel = [‘rbf’]
		Degree = [2, 3, 4]	Degree = [4]	Degree = [2, 3, 4]	Degree = [4]
		Gamma = [‘scale’]	Gamma = [‘scale’]	Gamma = [‘scale’]	Gamma = [‘scale’]
4	KRR	(Alpha) = uniform (0.01, 100)	(Alpha) = 7.6	(Alpha) = uniform (0.01, 100)	(Alpha) = 79.71
		(Degree) = [2, 3, 4]	(Degree) = 5	(Degree) = [2, 3, 4]	(Degree) = 4
		(‘kernel’) = [‘linear’, ‘rbf’, ‘poly’, ‘sigmoid’]		(‘kernel’) = [‘linear’, ‘rbf’, ‘poly’, ‘sigmoid’]
5	RFR	Max_depth = np.arange (3, 15, 1)	Max_depth = [14]	Max_depth = np.arange (3, 15, 1)	Max_depth = [8]
		n_estimators = np.arange (100, 800, 50)	n_estimators = [400]	n_estimators = np.arange (100, 800, 50)	n_estimators = [200]
6	ETR	Max_depth = np.arange (10, 20, 1)	Max_depth = [10]	Max_depth = np.arange (3, 20, 1)	Max_depth = [4]
		N_estimators = np.arange (100, 400, 10)	N_estimators = [120]	N_estimators = np.arange (100, 800, 10)	N_estimators = [170]
		Random_state = [42]	Random_state = [42]	Random_state = [42]	Random_state = [42]
7	GBR	Alpha = uniform (0.05, 1.0)	Alpha = [0.2268]	Alpha = uniform (0.05, 1)	Alpha = [0.1720]
		Learning_rate = np.arange (0.01, 0.1, 0.01)	Learning_rate = [0.069]	Learning_rate = np.arange (0.1, 0.5, 0.01)	Learning_rate = [0.1599]
		n_estimators = np.arange (100, 500, 25)	n_estimators = [250] random_state = [20]	n_estimators = np.arange (100, 800, 25)	n_estimators = [125]
		Max_depth = np.arange (5, 15, 1)		Random_state = [20]	Random_state = [20]
				Max_depth = np.arange (3, 15, 1)
8	xGBR	Max_depth = np.arange (3, 15, 1)-----	Max_depth = [11]	Max_depth = np.arange (3, 15, 1)	Max_depth = [11]
		Learning_rate = np.arange (0.01, 0.1, 0.01)	Learning_rate = [0.02]	Learning_rate = np.arange (0.01, 0.5, 0.01)	Learning_rate = [0.09]
		N_estimators = np.arange (200, 1000, 25)	N_estimators = [625]	N_estimators = np.arange (400, 1000, 25)	N_estimators = [725]
		Min_child_weight = np.arange (3, 15, 1)	Min_child_weight = [3]	Min_child_weight = np.arange (5, 15, 1)	Min_child_weight = [13]
		Subsample = np.arange (0.7, 1, 0.01)

---

Results and discussion

The ML models were built over a dataset comprised of 156 CO and 69 OH binding energy values on (111)-terminated A₃B type bimetallic alloys. These values for binding energies for CO and OH were taken from a previous study conducted by Zheng et al. and are shown in a matrix form in Fig. 2(a) and (b) respectively.⁴⁴ The dataset did not contain the binding energy datapoints on Cu₃M alloys. However, the CO and OH binding energies were predicted through ML on Cu₃M bimetallic alloys. Predicting the binding energy on bimetallic alloys is a sophisticated non-linear problem, as these alloys tend to diverge from the linear scaling relationship that typically governs the binding energy of related species. This complexity arises due to the unique interactions and anisotropies at the interfaces of the different metals in the alloy.^22,68–70 Therefore, ML models can be used for predicting the binding energy on these alloys due to their ability to learn non-linear interactions.

Fig. 2 The dataset used for ML models for (a) CO and (b) OH binding energies on (111)-terminated A₃B bimetallic surfaces. Highlighted cells indicate the “A” and “B” metals forming the bimetallic alloys, while the cell colours represent the corresponding binding energies of CO/OH, with “A” and “B” representing elements of the periodic table.

For selecting a ML model, features play an important role.^71,72 It is important to choose readily accessible but characteristic values as features that link to the target values i.e. binding energy. Regarding the choice of features for the bimetallics used in our work, we chose 36 physical properties such as the melting point, boiling point, surface energy, electronegativity, group, atomic number, etc. as mentioned in Table S1 (ESI†), 18 for the main metal (A) and 18 for the guest metal (B). These values are easily available from the periodic table and standard reference sources.^58,59 Readily available physical characteristics of metals as features have been used previously as well for the prediction of binding energies of CH₄ related species on Cu-based alloys using tree-based ensemble algorithms.⁴⁸ Similarly, in another study conducted by Saxena et al., physico-chemical properties easily available in the periodic table were used as features in the ML model to predict the binding energy of oxygen and carbon for the screening of bimetallic and single atom alloys using the GBR model.²²

Performance of different ML models

To predict CO and OH binding energies on (111)-terminated Cu₃M bimetallic alloys, a set of eight widely used ML models classified as linear, kernel and tree ensemble models were evaluated, which include LR, KNN, SVR, KRR, RFR, ETR, GBR and xGBR. The optimum hyperparameters for these models for CO and OH binding energies are given in Table 1, column (ii) and (iv) respectively, which were determined using a randomized search approach technique with 10-fold cross-validation for each algorithm. The average training and testing errors for each model using the optimized hyperparameter values along with the minimum and maximum errors observed over 25 000 trials are given in Table 2. During each of these 25 000 trials, the data were randomly split into train and test data. The process of splitting data into training and test sets in various ratios is fundamental in machine learning.^73,74 Different ratios allow us to assess how well a model generalizes to new data, strike a balance between bias and variance, and understand overfitting or underfitting. This practice aids in tuning and optimizing models, especially when dealing with limited data.^75,76 The model was constructed using the training data and the training error was calculated on the same data. Conversely, the testing error was calculated using the testing data. An examination of train and test errors (RMSE) facilitated the comparison and selection of models based on their predictive accuracy. All models consistently demonstrated optimal performance at a test/train ratio of 30/70. Moreover, the R² scores are also given in Table 2 for all the ML models.

Table 2 Train and test errors along with the R² score for predicting CO and OH binding energies on (111)-terminated A₃B bimetallic alloys

S. no.	Model	For CO binding energy (eV)			For OH binding energy (eV)
		Train error mean (min, max)	Test error mean (min, max)	R ^2 score	Train error mean (min, max)	Test error mean (min, max)	R ^2 score
		(i)	(ii)	(iii)	(iv)	(v)	(vi)
1	LR	0.149 (0.149, 0.149)	0.139 (0.139, 0.139)	0.902	0.076 (0.076, 0.076)	0.557 (0.557, 0.557)	0.860
2	KNN	0.025 (0.00, 0.180)	0.232 (0.215, 0.307)	0.781	0.00 (0.00, 0.00)	0.476 (0.451, 0.558)	0.421
3	SVR	0.106 (0.106, 0.106)	0.123 (0.122, 0.124)	0.902	0.128 (0.117, 0.133)	0.309 (0.303, 0.313)	0.841
4	KRR	0.152 (0.150, 0.154)	0.146 (0.142, 0.150)	0.933	0.129 (0.091, 0.130)	0.313 (0.310, 0.395)	0.659
5	RFR	0.058 (0.049, 0.079)	0.089 (0.086, 0.095)	0.964	0.093 (0.086, 0.105)	0.305 (0.282, 0.319)	0.809
6	ETR	0.030 (0.004, 0.038)	0.091 (0.087, 0.093)	0.965	0.069 (0.009, 0.120)	0.235 (0.232, 0.249)	0.836
7	GBR	0.005 (0.00, 0.046)	0.099 (0.095, 0.110)	0.956	0.00 (0.00, 0.002)	0.304 (0.276, 0.353)	0.872
8	xGBR	0.004 (0.001, 0.014)	0.091 (0.086, 0.097)	0.970	0.010 (0.001, 0.028)	0.196 (0.180, 0.216)	0.890

---

LR is a basic statistical technique that models the association between a dependent variable and one or more independent variables by reducing the sum of squared residuals.⁷⁷ Its straightforward nature and ease of interpretation make it a popular choice across diverse scientific fields.⁷⁸ Using the LR model, test RMSE values of 0.139 eV and 0.557 eV were obtained for predicting CO and OH binding energies on (111)-terminated A₃B type bimetallic alloys as shown in Table 2, entries 1(ii) and (v). The value for RMSE for the LR model is lower in the case of CO binding energies than KNN (0.232 eV) and KRR (0.146 eV) models, Table 2, entries 2(ii) and 4(ii) respectively. However, the RMSE values are relatively high in the case of OH binding (0.557 eV, Table 2, entry 1(v)), compared to the counterparts, which can be attributed to the inherent limitations of linear regression. LR excels in capturing linear relationships between features and the target variable.^79,80 However, the prediction of binding energy entails complex nonlinear associations between the features and the response variable. This complexity contributes to the observed variations in the RMSE values.

KNN is a non-parametric distance-based model, which looks at the properties of its nearest neighbours in the training set to predict a target value.^81,82 It is particularly useful for capturing complex, nonlinear relationships in data without requiring prior assumptions about the underlying distribution, though its performance can be sensitive to the choice of distance metric and the number of neighbours.⁸³ Also, for high-dimensional data, calculating the distance between the target and nearest neighbour data points becomes computationally challenging and makes KNN inefficient. In this work also, KNN yielded high RMSEs for predicting CO (0.232 eV) and OH (0.476 eV) binding energies compared to other models as shown in Table 2, entries 2(ii) and (v).

In contrast, kernel-based methods such as the SVR model use a subset of the training data called support vectors for making prediction.^84,85 It maps input features into a high-dimensional space and finds an optimal hyperplane that minimizes prediction errors within a defined margin.⁸⁶ Due to its ability to handle high-dimensional data and nonlinear relationships using kernel functions, SVR is widely applied in scientific and engineering problems.⁸⁷ It shows reduced sensitivity to input dimensionality and often achieves lower generalization error.⁸⁸ SVR in our case outperformed linear models with the test RMSEs of 0.123 and 0.309 eV for predicting CO and OH binding energies as shown in Table 2, entries 3(ii) and (v) respectively. However, compared to tree-based models it still falls short.

On the other hand, by using a different loss function compared to SVR, KRR which is another kernel-based method is known to provide closed-form estimates.^89,90 KRR is a nonlinear regression method that combines ridge regression with kernel functions, enabling it to model complex relationships by mapping data into higher-dimensional spaces.^91,92 By incorporating an [small script l]²-norm regularization term, KRR helps prevent overfitting while maintaining flexibility in capturing intricate patterns, making it particularly effective for small to medium-sized datasets.^93–95 However, for CO binding energy, KRR showed indications of overfitting, with a higher training error (RMSE: 0.152 eV) than the testing error (RMSE: 0.146 eV) as shown in Table 2, entries 4(i) and (ii). Despite KRR's capability to handle nonlinear relationships, its performance in predicting OH binding energy (RMSE: train/test = 0.129 eV/0.313 eV (Table 2, entries 4(iv) and (v)) was less than optimal when compared to other models.

However, tree-based ensemble methods such as RFR, ETR, GBR and xGBR were found to outperform their counterparts, such as the linear model (LR), KNN, and kernel models (SVR and KRR). This was due to their robustness to noise, ability to fit non-linear relationships, scalability in high-dimensional spaces, interpretability through feature importance insights and ease of parameter tuning.^96–98 RFR is a powerful ensemble machine learning technique that builds multiple decision trees, each trained on random data subsets and features, to improve predictive performance and reduce overfitting through bagging and feature randomness.^99,100 By averaging tree predictions, it effectively captures complex, nonlinear relationships. It handles both numerical and categorical data and provides a feature importance mechanism.¹⁰¹ However, it can be computationally expensive and may struggle with high-dimensional, sparse data such as text.¹⁰²

ETR is an ensemble learning method used for regression tasks that builds multiple decision trees, like RFR, but with additional randomness to enhance robustness and reduce overfitting. Instead of selecting the best split at each node, it randomly selects a split for each feature, injecting randomness both at the sample and feature levels. This allows it to capture complex, nonlinear relationships efficiently. While it offers faster training than RFR due to the randomness in splitting, it may lead to slight performance trade-offs.¹⁰³ It is effective with numerical and categorical data, handles missing data, and provides feature importance estimates but may underperform on high-dimensional sparse data, such as text.¹⁰⁴

GBR is a powerful ensemble learning method used for both regression and classification tasks. It sequentially adds weak learners, typically decision trees, to correct the errors of the previous ones, with each new model focusing on the residuals of the previous predictions. The key idea behind GBR is that combining multiple weak learners creates a strong predictive model, leveraging the principle of boosting.¹⁰⁵ The algorithm minimizes the loss function by approximating the gradient of the residuals with respect to the model parameters, effectively improving prediction accuracy. While GBR is highly effective at capturing complex, nonlinear relationships and can handle both categorical and numerical data, it can be prone to overfitting, especially with noisy data, and requires careful hyperparameter tuning, such as the number of estimators, tree depth, and learning rate.¹⁰⁶

On the other hand, xGBR is an efficient and scalable version of GBR that builds an ensemble of decision trees, with each tree correcting the errors of the previous ones. It improves traditional gradient boosting by adding regularization (L1 and L2) to reduce overfitting, as well as incorporating parallelization, handling missing values, and optimizing split finding for faster computation.^106,107

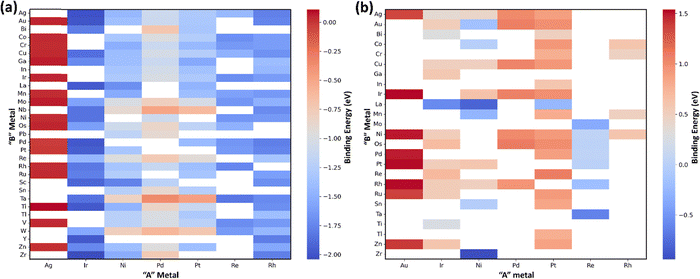
The above models produce more accurate and robust prediction by combining the predictions of weak learners such as decision trees to construct a strong estimator. Each model differs in the way of construction of the decision tree to build an ensemble. Remarkably, low RMSE values were obtained for all four models out of which RFR exhibited the least value of RMSE (0.089 eV) for predicting CO binding energy as shown in Table 2, entry 5(ii), suggesting its proficiency in capturing the underlying patterns in the data. Similarly, the ETR and xGBR models also showed a low RMSE of 0.091 eV (Table 2, entries 6(ii) and 8(ii) respectively). On the other hand, the GBR model gave an RMSE of 0.099 eV (Table 2, entry 7(ii)) for CO binding energy. Although RFR and ETR demonstrated superior performance in terms of RMSE values, our study uncovered a significant pattern wherein these models showed an inclination towards overfitting, particularly noticeable in the prediction of CO binding energies. Given the constraints of a small dataset, a large number of input features might have led to overfitting. This can be clearly observed by the inflated values from ML predictions (blue lines) as compared to the DFT values (orange line) shown in Fig. 3(e)–(g). In contrast, xGBR predicted values were closer to the DFT calculated values as shown in Fig. 3(h). The test RMSE value obtained for xGBR for CO binding (0.091 eV, Table 2, entry 8(ii)) was the lowest amongst all other models except RFR. Thus, xGBR was finally selected due to its ability to produce predictions that closely align with DFT calculated values. This choice was further supported by the model's capacity to mitigate inherent prediction biases in the dataset. Prior studies suggested that boosting algorithms, such as xGBR, are generally more effective at managing systematic prediction bias compared to bagging-based models like RFR and ETR.¹⁰⁸ The test RMSE value of 0.091 eV obtained using the xGBR model for predicting CO binding energy on (111)-terminated A₃B alloys in this study is much lower than those reported in the previous studies. For example, Li et al. obtained a RMSE value of 0.12 eV for CO binding energy prediction on (100)-terminated multi-metallic Cu catalysts by using an artificial neural network.⁷¹ In another study, the neural-network model trained with all available data sets of bimetallic catalysts predicted CO binding energy on Cu-based core–shell alloys (Cu₃B-A@Cu_ML) with a RMSE of 0.13 eV.¹⁰⁹ Zhong et al. by using the Random Forest Regression Algorithm also predicted CO binding energy on Cu based alloys with a RMSE of 0.1 eV.¹¹⁰

Fig. 3 Deviation of ML predicted CO binding energies from DFT calculated values for unseen data of (111)-terminated Cu₃M bimetallic alloys for (a) LR, (b) KNN, (c) SVR, (d) KRR, (e) RFR, (f) ETR, (g) GBR and (h) xGBR models. Error bars in the ML data represent standard deviation in the RMSE values obtained using RandomizedSearchCV. A very low value of standard deviation in some models (∼0.0089 to 0.0002) could not be represented in the error bars. Error bars in DFT data indicate the computational error (0.1 eV) in DFT simulations.

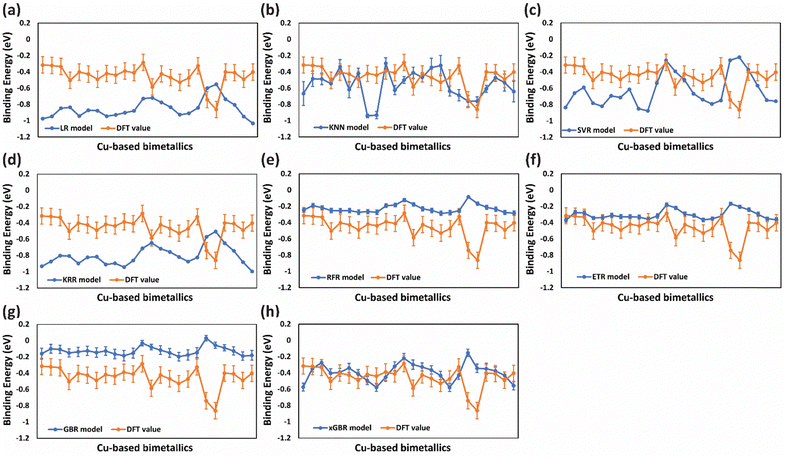
Similarly, for OH binding energy predictions, all models were found to overfit (Fig. 4(a)–(e)) except for ETR, GBR and xGBR as shown in Fig. 4(f)–(h). From Fig. 4(h), it is clear that xGBR model's predictions (blue lines) and DFT values (orange lines) are very close as compared to the other models. Moreover, xGBR gave the lowest RMSE value of 0.196 eV as shown in Table 2, entry 8(v). This highlights xGBR model's ability to deliver more consistent and dependable predictions, particularly when dealing with limited datasets. A similar RMSE value of 0.188 eV was obtained for predicting OH binding energy on (111)-terminated intermetallic (A₃B) and near-surface alloys by using deep learning algorithms integrated with the well-established d-band theory.⁶⁴ Furthermore, the RMSE values reported in this study using the xGBR model for predicting CO (0.091 eV) and OH (0.196 eV) binding energies on (111)-terminated A₃B bimetallic alloys are lower than the ones reported by Zheng et al. (0.22 eV for CO and 0.24 eV for OH).⁴⁴ The accuracy of the ML model was further evaluated using R² scores, as presented in Table 2. Higher R² scores, closer to 1, indicate better model performance. The xGBR model demonstrated higher R² scores (xGBR = 0.970) as compared to the other models tested (LR = 0.902, KNN = 0.781, SVR = 0.902, KRR = 0.933, RFR = 0.964, ETR = 0.965 and GBR = 0.956) as shown in Table 2, entries 1–7(iii)) for CO binding energies. Similarly, for OH binding energies the xGBR model was found to have the highest R² scores of 0.890 for OH binding energies as shown in Table 2, entry 8(vi). The R² score for CO binding energy predicted by the xGBR model (0.970) in this study is comparable to the one reported by Salomone et al. with the GBR model (0.970).¹¹¹

Fig. 4 Deviation of ML predicted OH binding energies from DFT calculated values of unseen data of (111)-terminated Cu₃M bimetallic alloys for (a) LR, (b) KNN, (c) SVR, (d) KRR, (e) RFR, (f) ETR, (g) GBR and (h) xGBR model. Error bars in the ML data represent standard deviation in the RMSE values obtained using RandomizedSearchCV. A very low value of standard deviation in some models (∼0.01 to 0.0002) could not be represented in the error bars. Error bars in DFT data indicate the computational error (0.1 eV) in DFT simulations.

Artificial Neural Networks (ANNs) inspired by the biological brain neural networks consist of multiple interconnected nodes that are loosely modelled on neurons.¹¹² Since they can also fit non-linear and complex data and are robust to noise and adaptive learning, they have proven to be predictive in solving various complex real-world problems. In this study, ANNs were tested with extensive parameter tuning, including layer configuration, neurons per layer and a range of learning rates. However, the test RMSE values of 0.387 and 0.406 eV were achieved for CO and OH molecule binding, which were higher as compared to tree-based ensemble models and even simple statistical models. This may be attributed to a very small data set, which might lead to poor performance of ANNs. Previous studies have also shown tree-based models to be best in predicting C and O binding energies on A₃B alloys.²²

A ML based study conducted by Zong et al. also found the xGBR model to be the best model in predicting the hydrogenolysis barrier of large hydrocarbons without the need for additional DFT features.¹¹³ In another study conducted by Praveen et al., the xGBR model in combination with a tree booster displayed the best performance for predicting the chemisorption energy of several gas-phase adsorbates on different metal facets.¹¹⁴ xGBR offers several advantages, which include high precision and speed, parallel processing abilities, effective handling of missing values, and high customizability.^115–117 A schematic illustration of the process flow for the xGBR model is shown in Fig. 5. All these advantages along with a lower RMSE value and a high R² score make xGBR the best choice in this study for predicting the descriptor binding energies. Thus, for further analysis only xGBR was considered.

Fig. 5 Representation of the xGBR tree algorithm.

For a small data set, like that used in the present study, choosing an optimum split ratio becomes very crucial. So, we tried different test/train ratios of 15/85, 20/80, 25/75, 30/70, and 50/50 and performed hyperparameter tuning for improving the RMSEs of these split ratios. As shown in Table 3 (columns (i) and (ii)), with an increase in the test/train ratio to 30/70 the test error decreases. However, a further increase in the ratio resulted in an increase in the error. This is because when the training data are small, the model may fail to capture essential patterns and will not be able to generalize well. And in cases where the testing data become small, one has to compromise the reliability of the predictions. In the present study, with a 70% training set, an optimum RMSE of 0.091 eV (Table 3, entry 4(ii)) was obtained for CO binding energy. Similar trends were observed for OH binding energy predictions, wherein, for the 30/70 test/train ratio, an RMSE value of 0.196 eV was obtained (Table 3, entry 4(iv)). Fig. 6 and 7 present the deviation of ML predicted CO and OH binding energy values from DFT calculated values respectively for different test/train ratios.

Table 3 Effect of the change of the test/train data ratio on training and testing errors for the xGBR model for predicting the binding energy of CO and OH on (111)-terminated A₃B bimetallic alloys

S. no.	Test/train split	For CO binding energy (eV)		For OH binding energy (eV)
		Train error	Test error	Train error	Test error
		(i)	(ii)	(iii)	(iv)
1	15%/85%	0.006	0.108	0.009	0.279
2	20%/80%	0.007	0.104	0.006	0.259
3	25%/75%	0.004	0.099	0.018	0.225
4	30%/70%	0.004	0.091	0.010	0.196
5	50%/50%	0.008	0.112	0.039	0.235

---

Fig. 6 The deviation of ML predicted CO binding energy using the xGBR model for (111)-terminated A₃B bimetallic alloys from DFT calculated values for train/test ratios of (a) 85/15, (b) 80/20, (c) 75/25, (d) 70/30 and (e) 50/50. The black and red dots signify the training data and the testing predicted data respectively.

Fig. 7 The deviation of ML predicted OH binding energy using the xGBR model for (111)-terminated A₃B bimetallic alloys from DFT calculated values for train/test ratios of (a) 85/15, (b) 80/20, (c) 75/25, (d) 70/30 and (e) 50/50. The black and red dots signify the training data and the testing predicted data respectively.

Analysis of computational time

A significant advantage of using ML over DFT calculations for the estimation of binding energy of adsorbates on the surface is in the reduction of computational resources and time. DFT simulations will need 10 to 11 hours of total CPU time cost for calculating one CO or OH binding energy on a 2 × 2 (111)-terminated A₃B alloy surface with four atomic layers on 20 cores of the Intel Xeon Cascade lake 8268 computing node. In contrast, ML predicts the same binding energy within 60 seconds of CPU time. Thus, the total CPU time cost of DFT is significantly higher compared to ML. Therefore, using DFT simulations to calculate the desired properties remains a bottleneck for computational research due to their high cost, and thus, machine learning models are used to make rapid predictions.

Feature importance for xGBR prediction

After developing the ML model, the most important step is to understand which features should be considered to determine the final binding energy (target variable). Initially, a total of 36 features were used to describe each bimetallic alloy for predicting the CO and OH binding energy on (111)-terminated Cu₃M bimetallic alloys. The Seaborn library from Python was employed to generate a correlation matrix, providing a visual representation of the relationships between features and the target variable. The correlation matrix scales from −1 to 1, where a positive value denotes positive correlations and a negative value indicates negative correlations as shown in Fig. 8. Features that are highly correlated with the target variables and correlated less with the other features are referred to as good features.^118,119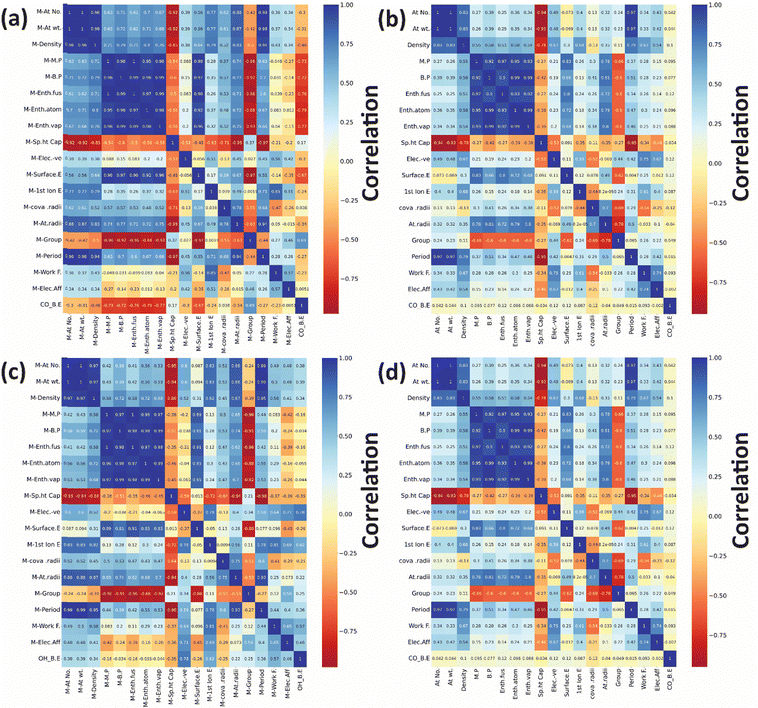

Fig. 8 Correlation plots for CO binding energy for: (a) “A” metal and (b) “B” metal and OH binding energy: (c) “A” metal and (d) “B” metal in (111)-terminated A₃B bimetallic alloys.

However, since the database is relatively small in the present study (less than 200 data points in the input database), a large number of input features may lead to overfitting. Thus, a separate analysis was performed to remove the least important features from the model so as to find the test error. The test error obtained for CO binding energy prediction with the xGBR model using 36 features was 0.091 eV (Table S2, entry 1, ESI†). Upon removing six highly correlated features the test error remained the same (Table S2, entry 2, ESI†). Upon reintroducing these six features as a single component using PCA, the error increased to 0.098 eV (Table S2, entry 3, ESI†). For the xGBR model built with the top 10 and top 20 features, the test error remained high (Table S2, entries 3 and 4, 0.096 and 0.093 eV respectively, ESI†), suggesting that the set of 36 features predicts the binding energy better. A similar observation was made by Shivam et al., wherein a set of 27 features were found to better predict the binding energy of O and the test error was observed to increase upon removing the features.²² This suggests that the less important features still carry meaningful and beneficial information, which helped in enhancing the model's robustness and accuracy. Furthermore, by using PCA on the reduced set of features (top 10 + 8 PCA components and top 20 + 5 PCA components) the model exhibited a further increase in RMSE (0.134 and 0.107 eV; Table S2, entries 6 and 7, ESI†). Similarly, the test error obtained for OH binding energy prediction with the xGBR model using 36 features was the least with the value of 0.196 eV (Table S3, entry 1, ESI†) as compared to the others mentioned in Table S3 (ESI†). Therefore, the model captures information better from individual features rather than from combined features (i.e. components). A similar analysis was performed for RFR and ETR, confirming that these models also leveraged information from less important features. It was observed that reducing the number of features led to a slight increase in RMSE as shown in Table S4 (ESI†), justifying the retention of all available features while managing the risk of overfitting. This analysis indicated that while some degree of overfitting was inevitable due to data limitations, it remained controlled across all models.

Fig. 9 shows the feature importance for predicting CO and OH binding energies with the xGBR model averaged over 25 000 trials. Notably, the surface energy of the main metal has the highest importance (Fig. 9(a)), followed by the main metal's melting point for CO binding energy on bimetallic alloys, which is consistent with the correlation matrix shown in Fig. 8(a). Similarly, for OH binding energy also, the surface energy of the main metal has the highest importance as shown in Fig. 9(b). This is because surface energies are intrinsically linked to the coordinative unsaturation of surface metal atoms. Typically, a higher surface energy system shows increased reactivity. On the other hand, the melting point refers to the energy required for breaking of a few bonds when an element goes from the solid state to the liquid state. Thus, stronger bonds result in a higher melting point, indicating that elements with a higher melting point may form alloys with higher binding energies. Salomone et al. also found surface energy as the most important feature for predicting CO binding energy on Cu-based alloys.¹¹¹ Similarly, Takigawa et al. also found surface energy as the most important feature in the ML prediction of C and CH binding energy over Cu-based alloys.⁴⁸

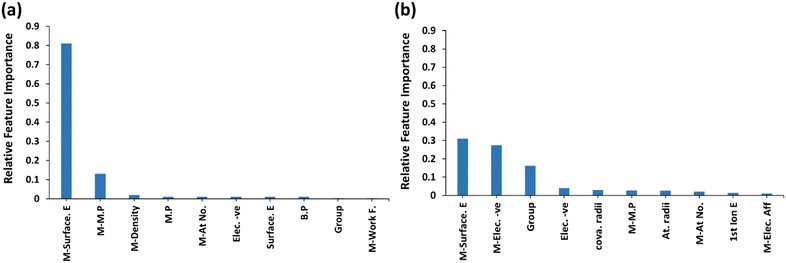Fig. 9 Feature importance plots for predicting: (a) CO and (b) OH binding energies using the xGBR model.

In addition to the main metal's surface energy, the main metal's electronegativity and guest metal's group were found to be important features for predicting OH binding energy on bimetallic alloy surfaces, as shown in Fig. 9(b). Features like electronegativity play a significant role in the ease of electron transfer between the surface metal atoms and the adsorbate, thereby influencing chemical bonding. The metal OH bonding is derived from the electronegativity of the elements. The binding energy decreases as we move from left to right in the periodic table due to higher electronegativity of elements towards the right.⁸³ The metal–oxygen binding energies also vary strongly with the group number⁸³ due to differential occupation of bonding δ-orbitals and antibonding π-orbitals. In general, the group of an element in the periodic table can influence its chemical property, which includes its tendency to form bonds with other elements. Elements from the same group have similar electronic configurations, leading to similar chemical properties. Therefore, the group number of an element can provide insights into the potential binding energy in an alloy. Ultimately, all the above-mentioned properties of alloys can directly or indirectly influence the binding energy of the alloy.

While ML models are often employed as data-driven black-box models, the feature importance in models offers an added advantage. It captures the underlying physics of the system, providing a deeper understanding of the model's predictions. This allows for a more comprehensive interpretation of the model beyond its predictive capabilities. Furthermore, plots of standard deviation for feature importance of CO and OH binding energies are shown in Fig. S1(a) and (b) (ESI†) respectively. These plots provide an estimate of the uncertainty or variability of the feature importance scores.¹²⁰ The standard deviation values for the highly important features like surface energy and electronegativity were also found to be low (approximately 0.04 eV), thus indicating the reliability of our model's predictions (Fig. S1(a) and (b), ESI†).

Validation of ML predictions

The CO and OH binding energies predicted in this study by xGBR model on unseen (111)-terminated Cu₃M bimetallic alloys are presented in Table S5 (ESI†). The model accuracy was further confirmed by DFT calculated CO and OH binding energies on a few (Cu₃Au, Cu₃Ga, Cu₃Zn and Cu₃Pd) Cu₃M alloy surfaces as shown in Table 4. The DFT methodology for the above calculations was adopted from the earlier study conducted by Zheng et al.⁴⁴ The mean absolute error (MAE) between the DFT calculated and ML predicted binding energies for CO on (111)-terminated Cu₃M surfaces (M-Au, Ga, Zn and Pd) was calculated as 0.03 eV (Table 4). Similarly, for OH binding energies on these Cu-based alloys, a MAE value of 0.02 eV was calculated. This low value for the errors tells that our predictions are very close to the DFT calculated values and confirms that the model is not simply memorizing patterns from the training data.

Table 4 DFT calculated CO and OH binding energies vs. ML predicted values by the xGBR model for (111)-terminated Cu₃M alloys

S. no.	Alloy	CO BE (DFT) (eV)	CO BE (ML predicted) (eV)	Deviation	OH BE (DFT) (eV)	OH BE (ML predicted) (eV)	Deviation
1	Cu3Au	−0.57	−0.56	−0.01	0.54	0.57	−0.03
2	Cu3Ga	−0.52	−0.58	0.06	0.19	0.20	−0.01
3	Cu3Zn	−0.49	−0.49	0	0.33	0.32	0.01
4	Cu3Pd	−0.48	−0.43	−0.05	0.46	0.43	0.03

---

To further assess the robustness of the model, additional validation tests were conducted using independent datasets obtained from Shivam et al.²² to predict C and O binding energy on AA-terminated A₃B type 211 surfaces. The xGBR model yielded reliable predictions on testing it with underrepresented alloy compositions (AA-terminated A₃B type 211 surface), which were not well represented in the training data. The train and test RMSE values of 0.0732 and 0.411 eV were obtained for C binding energy prediction as shown in Table S6 (ESI†), which were higher compared to 0.0003 and 0.340 eV obtained by Shivam et al.²² using the GBR model. In contrast, the xGBR model outperformed the results obtained by the previous GBR model for O binding energy predictions as shown in Table S6 (ESI†), wherein the test RMSE decreased from 0.310 to 0.289 eV although the train RMSE increased from 0.0003 to 0.0035 eV. The increase in train RMSE indicates that the xGBR model experienced less overfitting compared to the previous GBR model, which had a near-zero train RMSE (0.0003) and likely memorized the training data. Further improvements in the RMSE values of the xGBR model for C and O binding energy prediction can be expected from intensive hyperparameter tuning and feature selection through PCA. This demonstrates that the xGBR model provides reliable and trustworthy predictions, especially for alloys underrepresented in the dataset.

Furthermore, the model performance was observed to be better for CO (RMSE: 0.091 eV) with 156 data points, compared to OH (RMSE: 0.196 eV) with only 69 data points, highlighting the impact of the dataset size. However, the dataset size is not the only factor influencing model performance. When a switch was made from (111)-terminated A₃B type bimetallic alloys to AA-terminated A₃B alloys on the (211) surface and the target variable was also changed from CO to C and OH to O for additional validation tests using independent/unseen datasets, the xGBR model still delivered reasonable predictions (0.411 and 0.289 eV, Table S6, ESI†), particularly for O even with these substantial changes in the dataset. This demonstrates the flexibility of the xGBR model, which when appropriately tuned and explored further can perform well and yield reliable results even with limited data.

Overall, from this study xGBR turns out to be the best predictive model for CO and OH binding energies on Cu-based bimetallic alloys with the small available dataset. The high level of accuracy and robustness shown by the xGBR model will enable the high throughput screening of bimetallic alloys to accelerate the catalyst discovery for various catalytic reactions such as the reverse water gas shift reaction, CO or CO₂ reduction, methanol electro-oxidation, formic acid decomposition, etc.

Conclusion

In this work, we used different ML models to predict CO and OH binding energies on (111)-terminated Cu₃M bimetallic alloys. Readily available periodic properties of the transition metals were used as input features in the ML models. Among all the ML models used in this study, ensemble-based models like xGBR, GBR, RFR and, ETR performed better than the linear and kernel models. The xGBR model was found to be the best among the ensemble-based models because of low RMSE scores, high R² scores, precise predictions and reduced overfitting. Features like the main metal's surface energy and melting point played a major role in predicting the CO binding energies on the alloy surfaces. Similarly, for predicting the OH binding energies, features like the main metal's surface energy and electronegativity and guest metal's group exercised the maximum influence. The insights derived at the molecular level through these features enhance the significance of the ML model. The mean absolute error between the DFT calculated and ML predicted binding energies was very low, between 0.02 and 0.03 eV. Furthermore, these predicted descriptor binding energies can be used in the ab intio Micro Kinetic Modelling to calculate the turnover frequencies for various reactions. As the accessibility of alloy data from DFT calculations will expand, it is anticipated that the precision of ML models will correspondingly improve and will accelerate the catalyst discovery.

Data availability

The data supporting this article have been included as part of the ESI.† The codes and source data used for our results can be found at the Github link: https://github.com/Adipri1003/Machine-Learning-for-CO-and-OH-binding-energies-over-bimetallic-catalyst-surfaces.git.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

SG acknowledges seed grant (SG-23) from IIT Hyderabad and Start-up Research Grant (SRG/2022/000565) from the Science and Engineering Research Board (SERB) for financial support. SG and PD acknowledge the resources and support from PARAM Seva Computing Facility under the National Supercomputing Mission, Government of India and JICA funded Chemical Engineering Department Cluster at IIT Hyderabad. PD is grateful to the Ministry of Education, India for the Prime Minister Research Fellowship.

References

1. W. N. R. W. Isahak and A. Al-Amiery, Catalysts Driving Efficiency and Innovation in Thermal Reactions: A Comprehensive Review, Green Technol. Sustainability, 2024, 2(2), 100078–100090,  DOI:10.1016/j.grets.2024.100078.
2. I. V. Yentekakis and F. Dong, Grand Challenges for Catalytic Remediation in Environmental and Energy Applications Toward a Cleaner and Sustainable Future, Front. Environ. Chem., 2020, 1, 1–14,  DOI:10.3389/fenvc.2020.00005.
3. B. Cornils and W. A. Herrmann, Concepts in Homogeneous Catalysis: The Industrial View, J. Catal., 2003, 216(1–2), 23–31,  DOI:10.1016/S0021-9517(02)00128-8.
4. A. Rajeev, M. Balamurugan and M. Sankaralingam, Rational Design of First-Row Transition Metal Complexes as the Catalysts for Oxidation of Arenes: A Homogeneous Approach, ACS Catal., 2022, 12, 9953–9982,  DOI:10.1021/acscatal.2c01928.
5. M. Morimoto, T. Miura and M. Murakami, Rhodium-Catalyzed Dehydrogenative Borylation of Aliphatic Terminal Alkenes with Pinacolborane, Angew. Chem., 2015, 127(43), 12850–12854,  DOI:10.1002/ange.201506328.
6. Z. Wang and P. Hu, Some Attempts in the Rational Design of Heterogeneous Catalysts Using Density Functional Theory Calculations, Top. Catal., 2015, 58(10–11), 633–643,  DOI:10.1007/s11244-015-0406-9.
7. T. C. Bruice and S. J. Benkovic, Chemical Basis for Enzyme Catalysis, Biochemistry, 2000, 39(21), 6267–6274,  DOI:10.1021/bi0003689.
8. Z. Chen, Y. Yu, Y. Gao and Z. Zhu, Rational Design Strategies for Nanozymes, ACS Nano, 2023, 17(14), 13062–13080,  DOI:10.1021/acsnano.3c04378.
9. A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier Principle to a Predictive Theory of Transition-Metal Heterogeneous Catalysis, J. Catal., 2015, 328, 36–42,  DOI:10.1016/j.jcat.2014.12.033.
10. C. Costentin and J. M. Savéant, Heterogeneous Molecular Catalysis of Electrochemical Reactions: Volcano Plots and Catalytic Tafel Plots, ACS Appl. Mater. Interfaces, 2017, 9(23), 19894–19899,  DOI:10.1021/acsami.7b04349.
11. Z. J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Theory-Guided Design of Catalytic Materials Using Scaling Relationships and Reactivity Descriptors, Nat. Rev. Mater., 2019, 4(12), 792–804,  DOI:10.1038/s41578-019-0152-x.
12. C. F. Nwaokorie and M. M. Montemore, Alloy Catalyst Design beyond the Volcano Plot by Breaking Scaling Relations, J. Phys. Chem. C, 2022, 126(8), 3993–3999,  DOI:10.1021/acs.jpcc.1c10484.
13. M. Busch, M. D. Wodrich and C. Corminboeuf, Linear Scaling Relationships and Volcano Plots in Homogeneous Catalysis-Revisiting the Suzuki Reaction, Chem. Sci., 2015, 6(12), 6754–6761,  10.1039/c5sc02910d.
14. F. Jalid, T. S. Khan, F. Q. Mir and M. A. Haider, Understanding Trends in Hydrodeoxygenation Reactivity of Metal and Bimetallic Alloy Catalysts from Ethanol Reaction on Stepped Surface, J. Catal., 2017, 353, 265–273,  DOI:10.1016/j.jcat.2017.07.018.
15. D. Li, X. Ma, P. Su, S. Yang, Z. Jiang, Y. Li and Z. Jin, Effect of Phosphating on NiAl-LDH Layered Double Hydroxide Form S-Scheme Heterojunction for Photocatalytic Hydrogen Evolution, Mol. Catal., 2021, 516, 111990–112002,  DOI:10.1016/j.mcat.2021.111990.
16. G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K. R. Müller and O. A. Von Lilienfeld, Machine Learning of Molecular Electronic Properties in Chemical Compound Space, New J. Phys., 2013, 15, 095003–095019,  DOI:10.1088/1367-2630/15/9/095003.
17. K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. Von Lilienfeld, A. Tkatchenko and K. R. Müller, Assessment and Validation of Machine Learning Methods for Predicting Molecular Atomization Energies, J. Chem. Theory Comput., 2013, 9(8), 3404–3419,  DOI:10.1021/ct400195d.
18. D. Jia, H. Duan, S. Zhan, Y. Jin, B. Cheng and J. Li, Design and Development of Lubricating Material Database and Research on Performance Prediction Method of Machine Learning, Sci. Rep., 2019, 9(1), 20277,  DOI:10.1038/s41598-019-56776-2.
19. F. K. Wang and T. Mamo, Gradient Boosted Regression Model for the Degradation Analysis of Prismatic Cells, Comput. Ind. Eng., 2020, 144, 106494–106505,  DOI:10.1016/j.cie.2020.106494.
20. R. Gasper, H. Shi and A. Ramasubramaniam, Adsorption of CO on Low-Energy, Low-Symmetry Pt Nanoparticles: Energy Decomposition Analysis and Prediction via Machine-Learning Models, J. Phys. Chem. C, 2017, 121(10), 5612–5619,  DOI:10.1021/acs.jpcc.6b12800.
21. Z. Liu, W. Tian, Z. Cui and B. Liu, A Universal Microkinetic-Machine Learning Bimetallic Catalyst Screening Method for Steam Methane Reforming, Sep. Purif. Technol., 2023, 311, 123270–123282,  DOI:10.1016/j.seppur.2023.123270.
22. S. Saxena, T. S. Khan, F. Jalid, M. Ramteke and M. A. Haider, In Silico High Throughput Screening of Bimetallic and Single Atom Alloys Using Machine Learning and Ab Initio Microkinetic Modelling, J. Mater. Chem. A, 2020, 8(1), 107–123,  10.1039/c9ta07651d.
23. S. Wang, S. S. K. Kasarapu and P. T. Clough, High-Throughput Screening of Sulfur-Resistant Catalysts for Steam Methane Reforming Using Machine Learning and Microkinetic Modeling, ACS Omega, 2024, 9(10), 12184–12194,  DOI:10.1021/acsomega.4c00119.
24. A. Boddien, F. Gärtner, C. Federsel, P. Sponholz, D. Mellmann, R. Jackstell, H. Junge and M. Beller, CO₂-“Neutral” Hydrogen Storage Based on Bicarbonates and Formates, Angew. Chem., Int. Ed., 2011, 50(28), 6411–6414,  DOI:10.1002/anie.201101995.
25. M. Grasemann and G. Laurenczy, Formic Acid as a Hydrogen Source – Recent Developments and Future Trends, Energy Environ. Sci., 2012, 5(8), 8171–8181,  10.1039/c2ee21928j.
26. J. Davis and M. Barteau, Reactions of Carboxylic Acids on the Pd(111)–(2 × 2)O Surface: Multiple Roles of Surface Oxygen Atoms, Surf. Sci., 1991, 256(1–2), 50–66,  DOI:10.1016/0039-6028(91)91199-8.
27. F. Solymosi and I. Kov6cs, Adsorption and Reaction of HCOOH on K-Promoted Pd(100) Surfaces, Surf. Sci., 1991, 259(1–2), 95–108,  DOI:10.1016/0039-6028(91)90528-Z.
28. M. R. Columbia and P. A. Thlel, The Interaction of Formic Acid with Transition Metal Surfaces, Studied in Ultrahigh Vacuum, J. Electroanal. Chem., 1994, 369(1–2), 1–14,  DOI:10.1016/0022-0728(94)87077-2.
29. M. D. Marcinkowski, C. J. Murphy, M. L. Liriano, N. A. Wasio, F. R. Lucci and E. C. H. Sykes, Microscopic View of the Active Sites for Selective Dehydrogenation of Formic Acid on Cu(111), ACS Catal., 2015, 5(12), 7371–7378,  DOI:10.1021/acscatal.5b01994.
30. L. Lu, L. Shen, Y. Shi, T. Chen, G. Jiang, C. Ge, Y. Tang, Y. Chen and T. Lu, New Insights into Enhanced Electrocatalytic Performance of Carbon Supported Pd–Cu Catalyst for Formic Acid Oxidation, Electrochim. Acta, 2012, 85, 187–194,  DOI:10.1016/j.electacta.2012.08.113.
31. F. He, K. Li, G. Xie, Y. Wang, M. Jiao, H. Tang and Z. Wu, Understanding the Enhanced Catalytic Activity of Cu1@Pd3(111) in Formic Acid Dissociation, a Theoretical Perspective, J. Power Sources, 2016, 316, 8–16,  DOI:10.1016/j.jpowsour.2016.03.062.
32. J. S. Yoo, F. Abild-Pedersen, J. K. Nørskov and F. Studt, Theoretical Analysis of Transition-Metal Catalysts for Formic Acid Decomposition, ACS Catal., 2014, 4(4), 1226–1233,  DOI:10.1021/cs400664z.
33. M. Ren, Y. Zhou, F. Tao, Z. Zou, D. L. Akins and H. Yang, Controllable Modification of the Electronic Structure of Carbon-Supported Core–Shell Cu@pd Catalysts for Formic Acid Oxidation, J. Phys. Chem. C, 2014, 118(24), 12669–12675,  DOI:10.1021/jp5033417.
34. F. Studt, F. Abild-Pedersen, Q. Wu, A. D. Jensen, B. Temel, J. D. Grunwaldt and J. K. Norskov, CO Hydrogenation to Methanol on Cu–Ni Catalysts: Theory and Experiment, J. Catal., 2012, 293, 51–60,  DOI:10.1016/j.jcat.2012.06.004.
35. S. Wang, V. Petzold, V. Tripkovic, J. Kleis, J. G. Howalt, E. Skúlason, E. M. Fernández, B. Hvolbæk, G. Jones, A. Toftelund, H. Falsig, M. Björketun, F. Studt, F. Abild-Pedersen, J. Rossmeisl, J. K. Nørskov and T. Bligaard, Universal Transition State Scaling Relations for (de)Hydrogenation over Transition Metals, Phys. Chem. Chem. Phys., 2011, 13(46), 20760–20765,  10.1039/c1cp20547a.
36. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, How Copper Catalyzes the Electroreduction of Carbon Dioxide into Hydrocarbon Fuels, Energy Environ. Sci., 2010, 3(9), 1311–1315,  10.1039/c0ee00071j.
37. X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Understanding Trends in Electrochemical Carbon Dioxide Reduction Rates, Nat. Commun., 2017, 8,  DOI:10.1038/ncomms15438.
38. J. Wang, M. G. Sandoval, M. Couillard, E. A. González, P. V. Jasen, A. Juan, A. Weck and E. A. Baranova, Experimental and DFT Study of Electrochemical Promotion of Cu/ZnO Catalysts for the Reverse Water Gas Shift Reaction, ACS Sustainable Chem. Eng., 2024, 12(29), 11044–11055,  DOI:10.1021/acssuschemeng.4c04086.
39. E. Pahija, C. Panaritis, S. Gusarov, J. Shadbahr, F. Bensebaa, G. Patience and D. C. Boffito, Experimental and Computational Synergistic Design of Cu and Fe Catalysts for the Reverse Water–Gas Shift: A Review, ACS Catal., 2022, 12, 6887–6905,  DOI:10.1021/acscatal.2c01099.
40. P. Ferrin and M. Mavrikakis, Structure Sensitivity of Methanol Electrooxidation on Transition Metals, J. Am. Chem. Soc., 2009, 131(40), 14381–14389,  DOI:10.1021/ja904010u.
41. S. Sakong and A. Groß, The Importance of the Electrochemical Environment in the Electro-Oxidation of Methanol on Pt(111), ACS Catal., 2016, 6(8), 5575–5586,  DOI:10.1021/acscatal.6b00931.
42. L. Wang, S. A. Nitopi, E. Bertheussen, M. Orazov, C. G. Morales-Guio, X. Liu, D. C. Higgins, K. Chan, J. K. Nørskov, C. Hahn and T. F. Jaramillo, Electrochemical Carbon Monoxide Reduction on Polycrystalline Copper: Effects of Potential, Pressure, and PH on Selectivity toward Multicarbon and Oxygenated Products, ACS Catal., 2018, 8(8), 7445–7454,  DOI:10.1021/acscatal.8b01200.
43. J. Li, K. Chang, H. Zhang, M. He, W. A. Goddard, J. G. Chen, M. J. Cheng and Q. Lu, Effectively Increased Efficiency for Electroreduction of Carbon Monoxide Using Supported Polycrystalline Copper Powder Electrocatalysts, ACS Catal., 2019, 9(6), 4709–4718,  DOI:10.1021/acscatal.9b00099.
44. Z. Li, S. Wang, W. S. Chin, L. E. Achenie and H. Xin, High-Throughput Screening of Bimetallic Catalysts Enabled by Machine Learning, J. Mater. Chem. A, 2017, 5(46), 24131–24138,  10.1039/c7ta01812f.
45. Z. Yang and W. Gao, Applications of Machine Learning in Alloy Catalysts: Rational Selection and Future Development of Descriptors, Adv. Sci., 2022, 9(12), 2106043,  DOI:10.1002/advs.202106043.
46. M. Kim, B. C. Yeo, Y. Park, H. M. Lee, S. S. Han and D. Kim, Artificial Intelligence to Accelerate the Discovery of N₂ Electroreduction Catalysts, Chem. Mater., 2020, 32(2), 709–720,  DOI:10.1021/acs.chemmater.9b03686.
47. S. Back, J. Yoon, N. Tian, W. Zhong, K. Tran and Z. W. Ulissi, Convolutional Neural Network of Atomic Surface Structures to Predict Binding Energies for High-Throughput Screening of Catalysts, J. Phys. Chem. Lett., 2019, 10(15), 4401–4408,  DOI:10.1021/acs.jpclett.9b01428.
48. T. Toyao, K. Suzuki, S. Kikuchi, S. Takakusagi, K. I. Shimizu and I. Takigawa, Toward Effective Utilization of Methane: Machine Learning Prediction of Adsorption Energies on Metal Alloys, J. Phys. Chem. C, 2018, 122(15), 8315–8326,  DOI:10.1021/acs.jpcc.7b12670.
49. Y. Li and W. Guo, Machine-Learning Model for Predicting Phase Formations of High-Entropy Alloys, Phys. Rev. Mater., 2019, 3(9), 095005,  DOI:10.1103/PhysRevMaterials.3.095005.
50. A. Dasgupta, Y. Gao, S. R. Broderick, E. B. Pitman and K. Rajan, Machine Learning-Aided Identification of Single Atom Alloy Catalysts, J. Phys. Chem. C, 2020, 124(26), 14158–14166,  DOI:10.1021/acs.jpcc.0c01492.
51. Z. Lu, S. Yadav and C. V. Singh, Predicting Aggregation Energy for Single Atom Bimetallic Catalysts on Clean and O* Adsorbed Surfaces through Machine Learning Models, Catal. Sci. Technol., 2020, 10(1), 86–98,  10.1039/c9cy02070e.
52. B. M. Abraham, O. Piqué, M. A. Khan, F. Viñes, F. Illas and J. K. Singh, Machine Learning-Driven Discovery of Key Descriptors for CO₂ Activation over Two-Dimensional Transition Metal Carbides and Nitrides, ACS Appl. Mater. Interfaces, 2023, 15(25), 30117–30126,  DOI:10.1021/acsami.3c02821.
53. O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, High-Throughput Calculations of Catalytic Properties of Bimetallic Alloy Surfaces, Sci. Data, 2019, 6(1), 76,  DOI:10.1038/s41597-019-0080-z.
54. F. Jalid, T. S. Khan and M. A. Haider, In-Silico Screening of Pt-Based Bimetallic Alloy Catalysts Using Ab Initio Microkinetic Modeling for Non-Oxidative Dehydrogenation of Ethanol to Produce Acetaldehyde, MRS Commun., 2019, 9(1), 107–113,  DOI:10.1557/mrc.2019.6.
55. P. Zoontjens, G. Grochola, I. K. Snook and S. P. Russo, A Kinetic Monte Carlo Study of Pt on Au(111) with Applications to Bimetallic Catalysis, J. Phys.: Condens. Matter, 2011, 23(1), 015302–015313,  DOI:10.1088/0953-8984/23/1/015302.
56. Y. Xu, A. C. Lausche, S. Wang, T. S. Khan, F. Abild-Pedersen, F. Studt, J. K. Nørskov and T. Bligaard, In Silico Search for Novel Methane Steam Reforming Catalysts, New J. Phys., 2013, 15(12), 125021–125039,  DOI:10.1088/1367-2630/15/12/125021.
57. H. J. Li, A. C. Lausche, A. A. Peterson, H. A. Hansen, F. Studt and T. Bligaard, Using Microkinetic Analysis to Search for Novel Anhydrous Formaldehyde Production Catalysts, Surf. Sci., 2015, 641, 105–111,  DOI:10.1016/j.susc.2015.04.028.
58. B. Hammer and J. K. Nørskov, Theoretical Surface Science and Catalysis-Calculations and Concepts, 2000, vol. 45.
59. R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Data Descriptor: Surface Energies of Elemental Crystals, Sci. Data, 2016, 3, 160080–160093,  DOI:10.1038/sdata.2016.80.
60. R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Data Descriptor: Surface Energies of Elemental Crystals, Sci. Data, 2016, 3(1), 160080–160093,  DOI:10.1038/sdata.2016.80.
61. E. J. Ras, M. J. Louwerse, M. C. Mittelmeijer-Hazeleger and G. Rothenberg, Predicting Adsorption on Metals: Simple yet Effective Descriptors for Surface Catalysis, Phys. Chem. Chem. Phys., 2013, 15(12), 4436–4443,  10.1039/c3cp42965b.
62. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-Learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12(85), 2825–2830.
63. J. Bergstra, J. B. Ca and Y. B. Ca, Random Search for Hyper-Parameter Optimization Yoshua Bengio, J. Mach. Learn. Res., 2012, 13, 281–305,  DOI:10.5555/2188385.2188395.
64. S. H. Wang, H. S. Pillai, S. Wang, L. E. K. Achenie and H. Xin, Infusing Theory into Deep Learning for Interpretable Reactivity Prediction, Nat. Commun., 2021, 12(1), 5288,  DOI:10.1038/s41467-021-25639-8.
65. S. B. Bosch, S. Burhenne, D. Jacob and G. P. Henze, Sampling Based on Sobol’ Sequences for Monte Carlo Techniques Applied to Building Simulations, Proc. Building Simulation, 2011, 1816–1823,  DOI:10.26868/25222708.2011.1590.
66. M. Waskom, Seaborn: Statistical Data Visualization, J. Open Source Software, 2021, 6(60), 3021,  DOI:10.21105/joss.03021.
67. H. Hotelling, Analysis of a Complex of Statistical Variables into Principal Components, J. Educ. Psychol., 1933, 24(6), 417–441,  DOI:10.1037/h0071325.
68. M. T. Darby, M. Stamatakis, A. Michaelides and E. C. H. Sykes, Lonely Atoms with Special Gifts: Breaking Linear Scaling Relationships in Heterogeneous Catalysis with Single-Atom Alloys, J. Phys. Chem. Lett., 2018, 9(18), 5636–5646,  DOI:10.1021/acs.jpclett.8b01888.
69. S. Huang, C. Shen and V. Samarov, Processing, Microstructure, and Properties of Bimetallic Steel-Ni Alloy Powder HIP, Metals, 2024, 14(1), 118–139,  DOI:10.3390/met14010118.
70. J. Greeley, Theoretical Heterogeneous Catalysis: Scaling Relationships and Computational Catalyst Design, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635,  DOI:10.1146/annurev-chembioeng-080615-034413.
71. Z. Li, X. Ma and H. Xin, Feature Engineering of Machine-Learning Chemisorption Models for Catalyst Design, Catal. Today, 2017, 280, 232–238,  DOI:10.1016/j.cattod.2016.04.013.
72. P. Dhal and C. Azad, A Comprehensive Survey on Feature Selection in the Various Fields of Machine Learning, Appl. Intelligence, 2022, 52(4), 4543–4581,  DOI:10.1007/s10489-021-02550-9.
73. A. Rácz, D. Bajusz and K. Héberger, Effect of Dataset Size and Train/Test Split Ratios in Qsar/Qspr Multiclass Classification, Molecules, 2021, 26(4), 1111–1127,  DOI:10.3390/molecules26041111.
74. Y. Xu and R. Goodacre, On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning, J. Anal. Test, 2018, 2(3), 249–262,  DOI:10.1007/s41664-018-0068-2.
75. F. Akulich, H. Anahideh, M. Sheyyab and D. Ambre, Explainable Predictive Modeling for Limited Spectral Data, Chemom. Intell. Lab. Syst., 2022, 225, 104572–104592,  DOI:10.1016/j.chemolab.2022.104572.
76. J. W. Rocks and P. Mehta, Memorizing without Overfitting: Bias, Variance, and Interpolation in Overparameterized Models, Phys. Rev. Res., 2022, 4(1), 013201–013220,  DOI:10.1103/PhysRevResearch.4.013201.
77. D. Maulud and A. M. Abdulazeez, A Review on Linear Regression Comprehensive in Machine Learning, J. Appl. Sci. Technol. Trends, 2020, 1(2), 140–147,  DOI:10.38094/jastt1457.
78. J. Chen, K. de Hoogh, J. Gulliver, B. Hoffmann, O. Hertel, M. Ketzel, M. Bauwelinck, A. van Donkelaar, U. A. Hvidtfeldt, K. Katsouyanni, N. A. H. Janssen, R. V. Martin, E. Samoli, P. E. Schwartz, M. Stafoggia, T. Bellander, M. Strak, K. Wolf, D. Vienneau, R. Vermeulen, B. Brunekreef and G. Hoek, A Comparison of Linear Regression, Regularization, and Machine Learning Algorithms to Develop Europe-Wide Spatial Models of Fine Particles and Nitrogen Dioxide, Environ. Int., 2019, 130,  DOI:10.1016/j.envint.2019.104934.
79. M. B. Ferraro, R. Coppi, G. González Rodríguez and A. Colubi, A Linear Regression Model for Imprecise Response, Int. J. Approximate Reasoning, 2010, 51(7), 759–770,  DOI:10.1016/j.ijar.2010.04.003.
80. L. McClendon and N. Meghanathan, Using Machine Learning Algorithms to Analyze Crime Data, Mach. Learn. Appl.: Int. J., 2015, 2(1), 1–12,  DOI:10.5121/mlaij.2015.2101.
81. Y. Guan, D. Chaffart, G. Liu, Z. Tan, D. Zhang, Y. Wang, J. Li and L. Ricardez-Sandoval, Machine Learning in Solid Heterogeneous Catalysis: Recent Developments, Challenges and Perspectives, Chem. Eng. Sci., 2022, 248, 117224–117244,  DOI:10.1016/j.ces.2021.117224.
82. M. L. Zhang and Z. H. Zhou, ML-KNN: A Lazy Learning Approach to Multi-Label Learning, Pattern Recognit., 2007, 40(7), 2038–2048,  DOI:10.1016/j.patcog.2006.12.019.
83. N. S. Altman, An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression, Am. Stat., 1992, 46(3), 175–185,  DOI:10.1080/00031305.1992.10475879.
84. P. Anand, R. Rastogi and S. Chandra, A Class of New Support Vector Regression Models, Appl. Soft Comput. J., 2020, 94, 106446–106462,  DOI:10.1016/j.asoc.2020.106446.
85. Y. Zhang, Q. Wang, X. Chen, Y. Yan, R. Yang, Z. Liu and J. Fu, The Prediction of Spark-Ignition Engine Performance and Emissions Based on the SVR Algorithm, Processes, 2022, 10(2), 312–327,  DOI:10.3390/pr10020312.
86. A. J. Smola, B. Scholkopf and S. Scholkopf, A Tutorial on Support Vector Regression, Stat. Comput., 2004, 14, 199–222,  DOI:10.1023/B:STCO.0000035301.49549.88.
87. H. Drucker, C. J. C. Burges, L. Kaufman, A. Smola and V. Vapoik, Support Vector Regression Machines, Adv. Neural Inf. Process Syst., 1997, 28(7), 779–784.
88. H. Zhong, J. Wang, H. Jia, Y. Mu and S. Lv, Vector Field-Based Support Vector Regression for Building Energy Consumption Prediction, Appl. Energy, 2019, 242, 403–414,  DOI:10.1016/j.apenergy.2019.03.078.
89. G. C. Cawley, N. L. C. Talbot and O. Chapelle, Estimating Predictive Variances with Kernel Ridge Regression, Lecture Notes Comput. Sci., 2005, 3944, 56–77,  DOI:10.1007/11736790_5.
90. X. H. Wu and P. W. Zhao, Predicting Nuclear Masses with the Kernel Ridge Regression, Phys. Rev. C, 2020, 101(5), 051301–051307,  DOI:10.1103/PhysRevC.101.051301.
91. M. Maalouf and D. Homouz, Kernel Ridge Regression Using Truncated Newton Method, Knowl. Based Syst., 2014, 71, 339–344,  DOI:10.1016/j.knosys.2014.08.012.
92. K. P. Murphy, Machine Learning: A Probabilistic Perspective, MIT Press, 2012.
93. F. M. Al-Matarneh, FEM-Driven Machine Learning Approach for Characterizing Stress Magnitude, Peak Temperature and Weld Zone Deformation in Ultrasonic Welding of Metallic Multilayers: Application to Battery Cells, Modell. Simul. Mater. Sci. Eng., 2024, 32, 085009,  DOI:10.1088/1361-651X/ad8669.
94. S. An, W. Liu and S. Venkatesh, Fast Cross-Validation Algorithms for Least Squares Support Vector Machine and Kernel Ridge Regression, Pattern Recognit., 2007, 40(8), 2154–2162,  DOI:10.1016/j.patcog.2006.12.015.
95. S. An, W. Liu and S. Venkatesh, Face Recognition Using Kernel Ridge Regression, 2007 IEEE Conference on Computer Vision and Pattern Recognition, 2007 DOI:10.1109/CVPR.2007.383105.
96. M. Zhu, D. Philpotts and M. J. Stevenson, The Benefits of Tree-Based Models for Stock Selection, J. Asset Manage., 2012, 13(6), 437–448,  DOI:10.1057/jam.2012.17.
97. N. Asadi, J. Lin and A. P. De Vries, Runtime Optimizations for Tree-Based Machine Learning Models, IEEE Trans. Knowl. Data Eng., 2014, 26(9), 2281–2292,  DOI:10.1109/TKDE.2013.73.
98. J. M. Montgomery and S. Olivella, Tree-Based Models for Political Science Data, Am. J. Polym. Sci., 2018, 62(2), 1–16,  DOI:10.7910/DVN/8ZJBLI.
99. K. Fawagreh, M. M. Gaber and E. Elyan, Random Forests: From Early Developments to Recent Advancements, Syst. Sci. Control. Eng., 2014, 2(1), 602–609,  DOI:10.1080/21642583.2014.956265.
100. D. Chutia, D. K. Bhattacharyya, J. Sarma and P. N. L. Raju, An Effective Ensemble Classification Framework Using Random Forests and a Correlation Based Feature Selection Technique, Trans. GIS, 2017, 21(6), 1165–1178,  DOI:10.1111/tgis.12268.
101. A. Liaw and M. Wiener, Classification and Regression by RandomForest, Classification and Regression by Randomforest, 2002, vol. 2, pp. 18–22. https://CRAN.R-project.org/doc/Rnews/.
102. D. R. Cutler, T. C. Edwards, K. H. Beard, A. Cutler, K. T. Hess, J. Gibson and J. J. Lawler, Random Forests For Classification In Ecology, Ecology, 2007, 88(11), 2783–2792.
103. P. Geurts, D. Ernst and L. Wehenkel, Extremely Randomized Trees, Mach. Learn., 2006, 63(1), 3–42,  DOI:10.1007/s10994-006-6226-1.
104. G. Louppe, L. Wehenkel, A. Sutera and P. Geurts, Understanding Variable Importances in Forests of Randomized Trees, NIPS’13: Proceedings of the 27th International Conference on Neural Information Processing Systems, 2013, pp. 431–439 DOI:10.5555/2999611.2999660.
105. J. H. Friedman, Greedy Function Approximation: A Gradient Boosting Machine. The, Ann. Stat., 2001, 29(5), 1189–1232,  DOI:10.1214/aos/101320345.
106. T. Chen and C. Guestrin, XGBoost: A Scalable Tree Boosting System, Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, 2016, vol. 13–17, pp. 785–794 DOI:10.1145/2939672.2939785.
107. W. Li, Y. Yin, X. Quan and H. Zhang, Gene Expression Value Prediction Based on XGBoost Algorithm, Front. Genet., 2019, 10, 18452,  DOI:10.3389/fgene.2019.01077.
108. J. Ugirumurera, E. A. Bensen, J. Severino and J. Sanyal, Addressing Bias in Bagging and Boosting Regression Models, Sci. Rep., 2024, 14(1), 18452,  DOI:10.1038/s41598-024-68907-5.
109. X. Ma, Z. Li, L. E. K. Achenie and H. Xin, Machine-Learning-Augmented Chemisorption Model for CO₂ Electroreduction Catalyst Screening, J. Phys. Chem. Lett., 2015, 6(18), 3528–3533,  DOI:10.1021/acs.jpclett.5b01660.
110. M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C. T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C. S. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S. C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Accelerated Discovery of CO₂ Electrocatalysts Using Active Machine Learning, Nature, 2020, 581(7807), 178–183,  DOI:10.1038/s41586-020-2242-8.
111. M. Salomone, M. Re Fiorentin, F. Risplendi, F. Raffone, T. Sommer, M. García-Melchor and G. Cicero, Efficient Mapping of CO Adsorption on Cu1−xMx Bimetallic Alloys via Machine Learning, J. Mater. Chem. A, 2024, 12(23), 14148–14158,  10.1039/d3ta06915j.
112. W. S. Mcculloch, W. Lrerr and H. Pitts, A Logical Calculus of the Ideas Immanent in Nervous Activity, Bull. Math. Biophys., 1943, 5(4), 115–133,  DOI:10.1007/BF02478259.
113. X. Zong, T. Xie and D. G. Vlachos, Predicting Hydrogenolysis Reaction Barriers of Large Hydrocarbons on Metal Surfaces Using Machine Learning: Implications for Polymer Deconstruction, Appl. Catal., B, 2024, 353, 124070–124079,  DOI:10.1016/j.apcatb.2024.124070.
114. C. S. Praveen and A. Comas-Vives, Design of an Accurate Machine Learning Algorithm to Predict the Binding Energies of Several Adsorbates on Multiple Sites of Metal Surfaces, ChemCatChem, 2020, 12(18), 4611–4617,  DOI:10.1002/cctc.202000517.
115. M. Cheng, L. Zhong, Y. Ma, X. Wang, P. Li, Z. Wang and Y. Qi, A New Drought Monitoring Index on the Tibetan Plateau Based on Multisource Data and Machine Learning Methods, Remote Sens., 2023, 15(2), 512–529,  DOI:10.3390/rs15020512.
116. J. Ge, L. Zhao, Z. Yu, H. Liu, L. Zhang, X. Gong and H. Sun, Prediction of Greenhouse Tomato Crop Evapotranspiration Using XGBoost Machine Learning Model, Plants, 2022, 11(15), 1923–1940,  DOI:10.3390/plants11151923.
117. A. J. Zeleke, P. Palumbo, P. Tubertini, R. Miglio and L. Chiari, Comparison of Nine Machine Learning Regression Models in Predicting Hospital Length of Stay for Patients Admitted to a General Medicine Department, Inform. Med. Unlocked, 2024, 47, 101499–101510,  DOI:10.1016/j.imu.2024.101499.
118. L. Yu and H. Liu, Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution, Proceedings of the Twentieth International Conference on Machine Learning, 2003, pp. 856–863 DOI:10.5555/3041838.3041946.
119. I. Guyon and A. M. De, An Introduction to Variable and Feature Selection, J. Mach. Learn. Res., 2003, 3, 1157–1182,  DOI:10.5555/944919.944968.
120. B. H. Menze, B. M. Kelm, R. Masuch, U. Himmelreich, P. Bachert, W. Petrich and F. A. Hamprecht, A Comparison of Random Forest and Its Gini Importance with Standard Chemometric Methods for the Feature Selection and Classification of Spectral Data, BMC Bioinf., 2009, 10, 213–229,  DOI:10.1186/1471-2105-10-213.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04887c

‡ These authors contributed equally to this work.

---