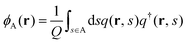Effect of architectural asymmetry of hyperbranched block copolymers on their phase boundaries†
Received
22nd December 2024
, Accepted 3rd March 2025
First published on 4th March 2025
Abstract
Asymmetric architecture of AB-type block copolymers can induce additional spontaneous curvature to the A/B interface, accordingly deflecting the phase boundaries. However, it is often difficult to determine or compare the asymmetric effects of different asymmetric architectures. In this work, we proposed to use the equivalent arm number nequ, which was originally defined as nequ = n/iĐ for ABn with unequal B-arms and iĐ being the intramolecular polydispersity of these B-arms, to quantify the asymmetric effect of various linear-hyperbranched copolymers. For each linear-hyperbranched copolymer, nequ is estimated by matching its phase boundaries on the side with expanded spherical phase region with those of ABn with unequal B-arms but tunable iĐ. Our results suggest that the addition of B-blocks at the further location from the A–B joint point has less influence on nequ, i.e. the asymmetric effect, because these B-blocks can access more space. For the linear-dendrimer copolymers, nequ changes from 2 to about 3.8 when the overall generation number of the copolymer increases from 2 to 5. In other words, the asymmetric effect of these linear-dendrimer copolymers is intermediate between those of AB2 and AB4 miktoarm star copolymers. In brief, nequ can effectively describe the asymmetric effect on the interfacial curvature of complex asymmetric architectures.
1 Introduction
Block copolymers can self-assemble into innumerable ordered structures when varying their composition and architectures,1–9 and thus have attracted abiding interest10–16 in many fields including functional nanomaterials and nanotechnology.17–20 AB diblock copolymers as the simplest block copolymer can form sphere, cylinder, network and lamellar structures as their composition changes from asymmetric to symmetric.21–30 If there are no other different properties between A and B blocks in the AB diblock, the phase diagram with respect to the composition (or the volume fraction of A-block, f) is symmetric.31 On both sides of the symmetric phase diagram, the spherical phase region is rather narrow and is mainly occupied by the body-centered cubic (BCC) phase. To expand the spherical region, an additional asymmetry factor needs to be introduced, such as the conformational asymmetry32–38 or architectural asymmetry.39–49 One of the common asymmetric architectures is ABn miktoarm star copolymers composed of a single A block connected with n B blocks.47,48,50–52 The multiple B blocks are more difficult to be stretched than the single A block, creating a tendency for the A/B interface to curve toward the A block. In other words, a curvature effect is caused by the branching architecture in addition to that arising from the compositional asymmetry. As a result, the phase diagram becomes asymmetric and is deflected to large volume fraction f of the A-block, of which the phase region of the A-sphere is expanded while that of the B-sphere is compressed. More importantly, the complex Frank–Kasper σ or A15 phase is stabilized with the expansion of the spherical region.42,47,53–55
Conformational asymmetry is related to the different intrinsic properties of flexibility, which can also be encoded into the asymmetry of the phase diagram. Almdal et al. proposed the ratio of Kuhn length bA/bB to describe the conformational asymmetry of the linear AB diblock by comparing the radius of gyration (Rg) of the linear A-block and B-block.32 The asymmetry parameter of the AB diblock was updated as ρAbA2/ρBbB2, where ρκ (κ = A or B) is the density of the κ-monomer.33,56 Soon after, Milner combined conformational asymmetry and architectural asymmetry into an asymmetry parameter, ε ≡ (nB/nA)(ρAbA2/ρBbB2)0.5, in an AB-type miktoarm star copolymer composed of nA A-arms and nB B-arms.50 This unified definition implies that the ratio of arm numbers and that of Kuhn lengths should have a similar effect on the phase behavior, which has been confirmed in subsequent experimental57–60 and theoretical studies.37,43,48
Besides the miktoarm star architectures, there are many other asymmetric architectures, and for some of them it is difficult to judge their degree of asymmetry (e.g. their deflection degree to the phase diagram). Some effort has been devoted to quantifying the asymmetry degrees of various complex AB-type block copolymers.44,51,61–63 For example, Fredrickson et al.44 attempted to calculate the asymmetry parameter of comblike/bottlebrush block copolymers by approximately computing the radius of gyration of the A and B blocks. Their asymmetry parameter can describe the deflection degree to the phase diagram for the comblike copolymers well, but not for the bottlebrush copolymers. In our previous work,51 we proposed the number of equivalent (or effective) arms (nequ) as an asymmetry parameter with reference to ABn miktoarm star copolymers of equal arms, and used it to quantify the deflection degree of the phase diagrams of ABn of unequal arms. We found that nequ can be simply expressed as nequ = n/iĐ, where iĐ represents the intramolecular polydispersity of the multiple arms. Our self-consistent field theory (SCFT) results demonstrate that various ABn of unequal arms with different n but with equal nequ exhibit very similar asymmetric phase diagrams, verifying that nequ is an efficient asymmetry parameter for measuring the effect of asymmetric architectures on the deflection of the phase diagrams. In line with Milner's description,50 we can combine conformational asymmetry with architectural asymmetry, then modify the equation for determining the equivalent ε (εequ) of linear-hyperbranched copolymers: εequ = nequ(ρAbA2/ρBbB2)0.5. For the linear-hyperbranched copolymers studied in this paper, we set ρA = ρB and bA = bB, thus nequ = εequ. The nequ(εequ) is mainly reflected in the change of spontaneous curvature for the AB-type copolymer, and the most prominent manifestation is its influence on the sphere/cylinder phase boundary. Therefore, in this work, we attempt to extend the concept of nequ to other asymmetric block copolymers to quantify their architectural asymmetry.
Hyperbranched copolymers including dendrimer-like have been extensively studied due to their unique architectures.42,46,64–78 Grason et al.42,46 proposed that the block copolymer composed of linear A-block and hyperbranched B-blocks exhibits a significantly amplified effect of spontaneous curvature toward the A-domain. As a result, the phase boundaries of these linear-hyperbranched copolymers are notably deflected to large volume fraction of the A-block (f), and the Frank–Kasper spherical A15 phase was predicted to be stable in the expanded region of the A-sphere.42,47 Although the architectures are notably asymmetric, it is still difficult to determine how large their asymmetry degrees are, for example by comparing them with those of ABn miktoarm star architectures. In this work, we will determine the equivalent arm number nequ by comparing the phase boundaries of various hyperbranched copolymers to those of different ABn with equal or unequal arms using SCFT. We first move the two B-arms of the equal-arm-AB4 or unequal-arm-AB4 architecture along the other two B-arms to obtain a series of linear-hyperbranched block copolymers (Fig. 1), thus determining their nequ. With the arm length ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the ideal linear-dendrimer architecture can be generated from AB4 when the two short B-arms are moved to the middle points of the other two B-arms, respectively. Then we propose a simple expression for nequ with respect to the tethering position, which can reasonably measure the asymmetry degrees of these different linear-hyperbranched copolymers.
2, the ideal linear-dendrimer architecture can be generated from AB4 when the two short B-arms are moved to the middle points of the other two B-arms, respectively. Then we propose a simple expression for nequ with respect to the tethering position, which can reasonably measure the asymmetry degrees of these different linear-hyperbranched copolymers.
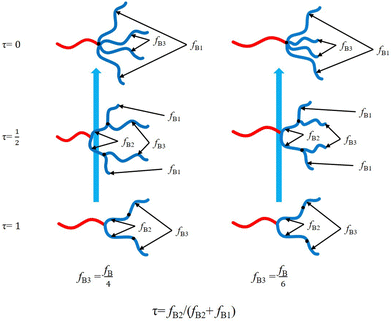 |
| | Fig. 1 Schematics of the linear-hyperbranched architectures generated from ABn with equal or unequal B arms. | |
2 Theory and method
We consider an incompressible melt of volume V consisting of nC chains of hyperbranched copolymers or ABn. To give prominence to the architectural effect on the self-assembly behavior, we simply assume that all segments have the same Kuhn length b and density ρ0. Each copolymer is composed of N segments in total, of which the A-block contains fN segments. Within the framework of SCFT for the Gaussian chain, the free energy functional per chain at temperature T is given by79,80| |  | (1) |
where kB is the Boltzmann constant. ϕκ(r) and wκ(r) (κ = A, B) are the volume-fraction function and the conjugate potential field of the κ-component, respectively. ξ(r) is a Lagrange multiplier used to enforce the incompressibility condition, ϕA(r) + ϕB(r) = 1. The quantity Q is the partition function of one single chain interacting with the mean fields of wκ(r) (κ = A, B), which is determined by| |  | (2) |
where q(r, s) and q†(r, s) are two conjugate propagator functions satisfying the modified diffusion equations| |  | (3) |
| |  | (4) |
where w(r, s) = wκ(r) when s belongs to the κ-block (κ = A, B). The values of q(r, s) or q†(r, s) at the free ends are set to 1 as the initial conditions. The spatial length is rescaled by the radius of gyration (Rg) of an unperturbed linear homopolymer chain with N segments,  . We considered that A and B segments have the same segment density (ρA = ρB) and length (bA = bB). The total number of segments in the A block and B blocks is given by fAN (fA = f) and fBN, respectively. Minimization of the free energy functional with respect to the volume-fraction functions and the mean fields leads to the following SCFT equations
. We considered that A and B segments have the same segment density (ρA = ρB) and length (bA = bB). The total number of segments in the A block and B blocks is given by fAN (fA = f) and fBN, respectively. Minimization of the free energy functional with respect to the volume-fraction functions and the mean fields leads to the following SCFT equations| | | wA(r) = χNϕB(r) + ξ(r) | (5) |
| | | wB(r) = χNϕA(r) + ξ(r) | (6) |
| | 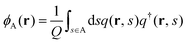 | (7) |
| |  | (8) |
We use the pseudospectral method81–83 to solve the modified diffusion equations, and implement the Anderson mixing iteration scheme84 to accelerate the converging process toward the equilibrium solution. We consider eight ordered phases, including face-centered cubic (FCC) spherical phase, body-centered cubic (BCC) spherical phase, Frank–Kasper σ/A15 spherical phase, hexagonal cylinder phase (C6), Fddd network phase (O70), double-gyroid network phase (G) and lamellar phase (L) (Fig. 2). It is necessary to mention that we do not consider the hexagonally close-packed (HCP) spherical phase because it is nearly degenerate with the FCC phase. The sizes of the unit cell (lx, ly and lz) are optimized by the variable cell algorithm.85–87 The chain contour is divided into pieces with Δs ≤ 0.005. The grid spacings Δx, Δy and Δz are chosen to be smaller than 0.15Rg by using a lattice of 64 × 64 × 64 for the three-dimensional phases except for a lattice of 256 × 256 × 128 for the σ phase and a lattice of 32 × 64 × 128 for the O70 phase. In addition, the pseudospectral method is accelerated using the crystallographic FFT to replace the normal FFT.88
 |
| | Fig. 2 Isosurface plots of the candidate ordered phases considered in the current study, including FCC, BCC, σ, A15, hexagonally arranged cylinders (C6), Fddd network (O70), double-gyroid (G) and lamellae (L). Larger and clearer figures and specific parameters are provided in the ESI.† | |
3 Results and discussion
We first consider a linear-hyperbranched architecture composed of a linear A-block connected with two generations of hyperbranched B-blocks. As shown in Fig. 1, this copolymer can be seen as an AB2 copolymer tethered by an additional B-block on each branching B-block. The tethering B-block with volume fraction of fB3 divides the branching B-block of AB2 into two sub-blocks denoted as B1 (with free end) and B2 (connected with A block) blocks with volume fractions fB1 and fB2, respectively. We introduce a variable τ = fB2/(fB2 + fB1) to characterize the tethering position of the B3-block. Accordingly, the linear-hyperbranched copolymer is reduced to AB2 with two equal B-arms at τ = 1 and AB4 with equal or unequal B-arms at τ = 0, respectively. The simple analysis implies that the asymmetry degree of this complex architecture should lie between those of AB2 and AB4 copolymers.
Besides the tethering position, another characteristic parameter is the ratio of B3-block. In this work, we consider two specific cases: fB3 = fB/4 and fB3 = fB/6. In the first case of fB3 = fB/4, the linear-hyperbranched architecture is reduced to AB4 of equal arms. In the other case of fB3 = fB/6, the architecture of the B-blocks becomes dendrimer-like at τ = 1/2.
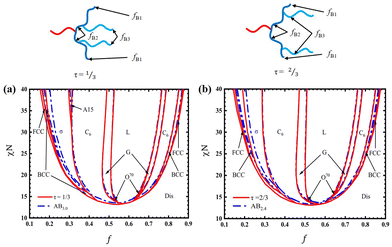
To demonstrate the change of the architecture on the asymmetry, we vary τ (i.e. the tethering position of B3-block) to gradually change the linear-hyperbranched architecture and construct the phase diagrams with respect to f and χN. Fig. 3 presents the phase diagrams of the linear-hyperbranched copolymer with fB3 = fB/4 for τ = 0, τ = 1/3, τ = 2/3 and τ = 1, respectively. At τ = 0, the copolymer is AB4 of equal arms, and thus its phase diagram is rather largely deflected to large f. Accordingly, the overall phase region of the A-sphere is expanded to range from f ≈ 0.172 to f ≈ 0.344 with a width of about Δf ≈ 0.172 at χN = 40, consisting of a wide window of Frank–Kasper σ-phase as well as a considerable window of A15-phase. As the two B3-blocks (two of B-arms) move away from the junction point to the tethering positions of τ = 1/3, the asymmetry of the phase diagram is noticeably reduced, accompanied by a narrowing of the A-spherical phase region. In particular, the width of the A15-phase window is decreased from Δf ≈ 0.041 at τ = 0 to Δf ≈ 0.018 at τ = 1/3. When the B3-blocks move to τ = 2/3, the asymmetry or deflection of the phase diagram is further decreased, leading to the absence of the A15-phase region. Finally, the architecture changes to AB2 at τ = 1, whose phase diagram is considerably less asymmetric than that of AB4 at τ = 0. The width of the A-spherical phase region at χN = 40 is narrowed to be Δf ≈ 0.127.
 |
| | Fig. 3 Phase diagrams for copolymers with (a) τ = 0, (b) τ = 1/3, (c) τ = 2/3, and (d) τ = 1. In all cases, fB3 = fB/4. | |
Qualitatively, the decrease in the asymmetry of the phase diagram with increasing τ can be explained by the change in the overall extension distance8 of the B-blocks from the A/B interface to the central area of the B-domain. Obviously, as the B3-blocks move from the junction point toward the free ends of the B1-blocks, the extension distance of the B-blocks increases, lowering the tendency of the B-blocks to locate outside the curvature. In other words, the effect of spontaneous curvature bending toward the A-domain is reduced with increasing τ, lowering the asymmetry of the phase diagram. In order to quantify the change in the asymmetry of the phase diagram with τ, we attempt to estimate the equivalent number of arms (nequ51) by comparing the phase boundaries of the linear-hyperbranched copolymer with those of ABn of unequal B arms. As the linear-hyperbranched architecture changes from AB4 to AB2 as τ increases from 0 to 1, its nequ should accordingly decrease from 4 to 2. Therefore, we choose n = 4 and consider four arms containing two equal long arms with a segment number of fBlN and two equal short arms with a segment number of fBsN. By tuning the relative lengths of the long and short arms of AB4, we can get any value of nequ = n/iĐ, where iĐ = 2(k2 + 1)/(k + 1)2 is the intramolecular polydispersity index51 of the four arms of AB4 with k = fBl/fBs. By minimizing the difference of the phase boundaries between the linear-hyperbranched copolymer with a given τ and AB4 of unequal arms with respect to nequ (or iĐ), we can obtain the value of nequ quantifying the asymmetry of the linear-hyperbranched copolymer.
When minimizing the difference of the phase boundaries in the phase diagrams with respect to f and χN between the linear-hyperbranched copolymer and the AB4 copolymer of unequal B arms with tunable nequ or iĐ, we find it difficult to make all the boundaries between them perfectly consistent. The main reason is that the asymmetric architecture affects the deflection of different phase boundaries in different degrees. Accordingly, we estimate nequ by mainly minimizing the sphere/cylinder, cylinder/gyroid and gyroid/lamella boundaries between the two copolymers in the region where A-blocks are located inside the curvature of the A/B interface, but not considering the sphere/disorder boundary. Fig. 4 presents the comparison of the phase diagrams between the linear-hyperbranched copolymer and the AB4 copolymer of unequal B arms with optimized nequ for τ = 1/3 and τ = 2/3. For τ = 1/3, the optimal nequ is estimated around 3.0. In Fig. 4(a), the left C6/G and G/L phase boundaries of the linear-hyperbranched copolymer with τ = 1/3 are nearly overlapped with those of AB4 with nequ = 3.0, and the σ/A15, σ/C6 and A15/C6 phase boundaries are also in good agreement with those of the latter. In contrast, the BCC/σ, BCC/FCC and FCC/disorder boundaries between the two copolymers are noticeably different. Another factor that should not be ignored is the difference in the equivalent segregation strength89 between the copolymers, which has a considerable influence on the order–disorder (ODT) transition boundaries.44,48 Nevertheless, the overall agreement of the phase boundaries between the two copolymers is acceptable. Therefore, it is a feasible approach to quantify the asymmetry of the phase diagram of the complex linear-hyperbranched copolymer using the equivalent number of arms defined by ABn of unequal B arms.
 |
| | Fig. 4 Phase diagrams of: (a) the linear-hyperbranched copolymer with fB3 = fB/4 for τ = 1/3 (red solid) and AB4 copolymer with nequ = 3.0 (simply denoted as AB3.0, blue dot-dashed lines); (b) the linear-hyperbranched copolymer with fB3 = fB/4 for τ = 2/3 (red solid) and AB4 copolymer with nequ = 2.4 (denoted as AB2.4, blue dot-dashed lines). The length percentages of the B-blocks of all considered samples are listed in Table 2. | |
In Table 1, we estimate the values of nequ for fB3 = fB/4 with τ = 0.1, 0.2, …, 0.9. Fig. 5(a) suggests that nequ decreases nonlinearly as τ increases from 0 to 1. Since many phase boundaries need to be determined using SCFT for the estimation of each nequ, the calculation is rather costly. To obtain the continuous value of nequ, it would be useful to find an expression for nequ as a function of τ. According to the changing trend, we choose the following concise equation to calculate nequ of linear-hyperbranched copolymers,
| | | nequ = nmin + Δn × (1 − τ)α, | (10) |
where Δ
n =
nmax −
nmin and
τ =
fB2/(
fB2 +
fB1). The copolymers with
nequ =
nmax = 4 and
nmin = 2 correspond to two limiting cases,
τ = 0 and
τ = 1, respectively.
α is a constant that quantifies the nonlinear relationship between
nequ and
τ. By fitting the data points in
Fig. 5(a) using the expression, we got
α ≈ 1.6. As
τ decreases from 1 to 0, the increasing of
nequ along the fitting curve with
α = 1.6 shown by the red solid lines in
Fig. 5(a) is accelerating, causing the value of
nequ on the curve to be smaller than the data points for
τ ≳ 0.5, then becomes larger than the data points for
τ ≲ 0.5. Overall, the fitting curve with
α = 1.6 is in good agreement with those data points.
Table 1 List of estimated nequ and calculated nequ for linear-hyperbranched copolymers with different τ
|
f
B3 = fB/4 |
|
τ
|
Estimated nequ |
n
equ with α = 1.6 |
| 0.1 |
3.63 |
3.69 |
| 0.2 |
3.32 |
3.40 |
| 0.3 |
3.06 |
3.13 |
| 0.4 |
2.84 |
2.88 |
| 0.5 |
2.65 |
2.66 |
| 0.6 |
2.50 |
2.46 |
| 0.7 |
2.36 |
2.29 |
| 0.8 |
2.24 |
2.15 |
| 0.9 |
2.13 |
2.05 |
|
f
B3 = fB/6 |
|
τ
|
Estimated nequ |
n
equ with α = 1.6 |
| 0.1 |
3.35 |
3.35 |
| 0.2 |
3.10 |
3.12 |
| 0.3 |
2.87 |
2.90 |
| 0.4 |
2.67 |
2.71 |
| 0.5 |
2.50 |
2.53 |
| 0.6 |
2.36 |
2.37 |
| 0.7 |
2.25 |
2.23 |
| 0.8 |
2.16 |
2.12 |
| 0.9 |
2.10 |
2.04 |
Table 2 List of fBi/fB for the considered linear-hyperbranched copolymers or ABn
| Copolymer |
f
B1/fB (%) |
f
B2/fB (%) |
f
B3/fB (%) |
f
B4/fB (%) |
|
τ = 1/3 |
16.7 |
8.3 |
25 |
— |
|
τ = 2/3 |
8.3 |
16.7 |
25 |
— |
| AB2.4 |
4.6 |
4.6 |
45.4 |
45.4 |
| AB3.0 |
10.6 |
10.6 |
39.4 |
39.4 |
| AB3.2 |
12.5 |
12.5 |
37.5 |
37.5 |
| AB3.3 |
13.5 |
13.5 |
36.5 |
36.5 |
| AB3.8 |
19.2 |
19.2 |
30.8 |
30.8 |
| AB3.9 |
21.0 |
21.0 |
29.0 |
29.0 |
 |
| | Fig. 5 Comparison of estimated nequ by matching the phase boundaries (filled squares) and calculated nequ using the expression of eqn (10) for linear-hyperbranched copolymers with different τ, α = 1.6 (red solid) for: (a) fB3 = fB/4; (b) fB3 = fB/6. | |
Similarly, we estimate the values of nequ by the matching approach for fB3 = fB/6 listed in Table 1. Using the expression in eqn (10) to fit these data points, we also obtain α ≈ 1.6. The fitting curve and the data points plotted in Fig. 5(b) show good agreement. These results demonstrate that nequ of the linear-hyperbranched copolymer with varying architectures can be roughly estimated using the expression of eqn (10). Note that the linear-hyperbranched copolymer with fB3 = fB/6 and τ = 0.5 becomes the three-generation linear-dendrimer architecture (i.e. g = 3) with equal B-blocks and its asymmetric effect on the spontaneous curvature can be roughly quantified by the nequ ≈ 2.5 intermediate between those of AB2 and AB3 copolymers.
To understand how the asymmetric effect of the linear-dendrimer copolymer on the spontaneous curvature or the phase boundaries changes with increasing g, we directly estimate nequ using the matching approach for g = 4 and g = 5, respectively. In Fig. 6(a), we calculated the sphere/cylinder/gyroid/lamella boundaries of AB4 with unequal arms in the range of 25 ≤ χN ≤ 40 as well as those of the linear-dendrimer copolymer with g = 4. For AB4, we consider two samples with nequ = 3.20 and nequ = 3.30. The comparison of the phase boundaries suggests that the phase boundaries of AB4 with nequ = 3.20 are in good agreement with those of the linear-dendrimer copolymer with g = 4, and are noticeably better than those of AB4 with nequ = 3.30. Accordingly, we quantify the asymmetric effect of the linear-dendrimer copolymer with g = 4 to be nequ ≈ 3.20. Similarly, we estimate nequ ≈ 3.80 for the linear-dendrimer copolymer with g = 5.
 |
| | Fig. 6 Partial phase boundaries of: (a) AB3.2 (red dot-dashed lines), AB3.3 (green dot-dashed lines), and the linear-dendrimer copolymer with g = 4 (solid lines); (b) AB3.8 (red dot-dashed lines), AB3.9 (green dot-dashed lines), and the linear-dendrimer copolymer with g = 5 (solid lines). The length percentages of the B-blocks for all considered ABn are listed in Table 2. | |
In Fig. 7(a), we plot the estimated nequ of the different linear-dendrimer copolymers with respect to g. When g = 2 increases to g = 3, the B-blocks at the outermost generation increase from 2 to 4, only raising n = 2 to nequ ≈ 2.5. In other words, the asymmetric effect of the linear-dendrimer copolymer with g = 3 is lower than that of AB3 with equal arms. When g = 3 changes to g = 4, eight B-blocks are added at the outmost generation, while nequ ≈ 2.5 increases to nequ ≈ 3.2. These results demonstrate that the addition of these B-blocks at the outer generation has less effect on the asymmetry. For the ABn copolymer, the packing of B-blocks nearby the A/B interface is very crowded, so it forces the interface to bend toward the A-block. The curved interface generates more space for the multiple B-blocks, thus reducing their stretching degree. In contrast, as the generation of the linear-dendrimer copolymer increases, B-blocks are added to the outermost generation while keeping the B-blocks directly joined with the single A-block unchanged. In particular, as these B-blocks move away from the A/B junction or the A/B curved interface, they can access expanding space and thus they have less effect on the curvature. Even for g = 5 with sixteen B-blocks at the outermost generation, its asymmetric effect on the phase diagram is still lower than that of AB4 with equal arms because of nequ ≈ 3.8.
 |
| | Fig. 7 (a) Variation of estimated nequ for different linear-dendrimer copolymers with g = 2, 3, 4 and 5; (b) comparison of the disorder/FCC/BCC/Frank–Kasper/C6/G/L phase boundaries of these different linear-dendrimer copolymers at χN = 40. | |
Previous works42,44,47,48,51 have shown that the architectural asymmetry of the block copolymer is commonly encoded into its phase diagram, leading to an expansion of the spherical phase region on one side and a compression on the opposite side. In the widened spherical region, complex Frank–Kasper phases tend to appear. Our previous work51 on asymmetric ABn copolymers with unequal B-arms demonstrated that the emergence of Frank–Kasper phases could be quantitatively indicated by the value of nequ. Specifically, the Frank–Kasper σ-phase appears when nequ ≳ 1.5, while the another Frank–Kasper A15-phase starts to emerge for nequ ≳ 2.5. To further confirm that such conclusions also hold for the linear-dendrimer copolymers, we calculated the disorder/FCC/BCC/Frank–Kasper/C6/G/L phase boundaries for the linear-dendrimer copolymers with g = 2, 3, 4, and 5 at χN = 40, as shown in Fig. 7(b). In the phase sequence of g = 3, there is a wide region of σ-phase but no A15 phase region due to nequ ≈ 2.5. For g = 4 with nequ ≈ 3.2 > 2.5, there exists a considerable region of A15-phase.
4 Conclusion
In summary, we have investigated the self-assembly behaviors of linear-hyperbranched copolymers using self-consistent field theory (SCFT). Firstly, we view the three-generation linear-hyperbranched copolymers as the derivatives of ABn with equal or unequal B-arms. Different linear-hyperbranched copolymers are generated by moving two B-blocks along the arms of AB2, and their equivalent arm numbers nequ are estimated by comparing their phase boundaries with those of ABn copolymers with unequal B-arms. The result of 2 ≤ nequ ≤ 4 suggests that their asymmetric effect on the spontaneous curvature or the deflection of phase boundaries, which is intermediate between those of AB2 and AB4 copolymers, is dependent on the tethering distance from the A/B junction point.
Then we turn to study the asymmetric effect of the linear-dendrimer copolymers composed of linear A-block as the first generation and equal B-block on the outer g − 1 generations. Note that the linear-dendrimer copolymer with g = 2 is AB2. For g = 3, 4 and 5, the equivalent arm numbers are estimated as nequ ≈ 2.5, 3.2 and 3.8, respectively. The changing tendency of nequ with g indicates that the addition of B-blocks at the outer generation has less effect on the spontaneous curvature because they are further from the A/B junction. The asymmetric effect of the linear-dendrimer copolymer quantified by the value of nequ is confirmed by the changing trend of these spherical phase regions. Specifically, the phase sequence of g = 3 contains Frank–Kasper σ-phase but no A15-phase because nequ ≈ 2.5 is close to the critical value of nequ for the emergence of A15. Since nequ increases to about 3.2 for g = 4, a noticeable region of A15 appears in the phase sequence. Our work provides a comprehensive understanding of the asymmetric effect on the phase boundaries for linear-hyperbranched copolymers.
Data availability
Isosurface plots and the corresponding parameters of the candidate ordered phases considered in the current study are available in the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 22333002, 21925301, 22203018, 22163006).
References
- F. S. Bates, M. A. Hillmyer, T. P. Lodge, C. M. Bates, K. T. Delaney and G. H. Fredrickson, Science, 2012, 336, 434–440 CrossRef CAS PubMed.
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098 CrossRef CAS.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 7641–7644 CrossRef CAS.
- H. Y. Hsueh, C. T. Yao and R. M. Ho, Chem. Soc. Rev., 2015, 44, 1974–2018 RSC.
- M. Stefik, S. Guldin, S. Vignolini, U. Wiesner and U. Steiner, Chem. Soc. Rev., 2015, 44, 5076–5091 RSC.
- M. Radjabian and V. Abetz, Prog. Polym. Sci., 2020, 102, 101219 CrossRef CAS.
- Z. W. Xu, Q. S. Dong and W. H. Li, Macromolecules, 2024, 57, 1869–1884 CrossRef CAS.
- F. Drolet and G. H. Fredrickson, Phys. Rev. Lett., 1999, 83, 4317–4320 CrossRef CAS.
- T. S. Bailey, C. M. Hardy, T. H. Epps and F. S. Bates, Macromolecules, 2002, 35, 7007–7017 CrossRef CAS.
- H. L. Deng, Y. C. Qiang, T. T. Zhang, W. H. Li and T. Yang, Nanoscale, 2016, 8, 15961–15969 RSC.
- T. H. Epps, E. W. Cochran, T. S. Bailey, R. S. Waletzko, C. M. Hardy and F. S. Bates, Macromolecules, 2004, 37, 8325–8341 CrossRef CAS.
- C. A. Tyler and D. C. Morse, Phys. Rev. Lett., 2005, 94, 208302 CrossRef PubMed.
- Z. W. Xu, Q. S. Dong, L. S. Zhang and W. H. Li, Nanoscale, 2022, 14, 15275–15280 RSC.
- C. H. Huang, Y. Y. Zhu and X. K. Man, Phys. Rep., 2021, 932, 1–36 CrossRef CAS.
- M. Müller, Prog. Polym. Sci., 2020, 101, 101198 CrossRef.
- E. Vargo, L. Ma, H. Li, Q. T. Zhang, J. Kwon, K. M. Evans, X. C. Tang, V. L. Tovmasyan, J. Jan, A. C. Arias, H. Destaillats, I. Kuzmenko, J. Ilavsky, W. R. Chen, W. Heller, R. O. Ritchie, Y. Liu and T. Xu, Nature, 2023, 623, 724–731 CrossRef CAS PubMed.
- T. Y. Tang, H. L. Wang, C. T. Yao, K. C. Yang, R. M. Ho and D. H. Tsai, Nanoscale, 2018, 10, 7352–7356 RSC.
- Y. W. Harn, S. Liang, S. L. Liu, Y. Yan, Z. W. Wang, J. Jiang, J. W. Zhang, Q. Li, Y. J. He, Z. L. Li, L. Zhu, H. P. Cheng and Z. Q. Lin, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–11 CrossRef PubMed.
- B. Wang, C. Wang, X. W. Yu, Y. Cao, L. F. Gao, C. P. Wu, Y. F. Yao, Z. Q. Lin and Z. G. Zou, Nat. Synth., 2022, 1, 138–146 CrossRef.
- H. Hasegawa, H. Tanaka, K. Yamasaki and T. Hashimoto, Macromolecules, 1987, 20, 1651–1662 CrossRef CAS.
- S. Foerster, A. K. Khandpur, J. Zhao, F. S. Bates, I. W. Hamley, A. J. Ryan and W. Bras, Macromolecules, 1994, 27, 6922–6935 CrossRef CAS.
- D. A. Hajduk, P. E. Harper, S. M. Gruner, C. C. Honeker, G. Kim, E. L. Thomas and L. J. Fetters, Macromolecules, 1994, 27, 4063–4075 CrossRef CAS.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660–2663 CrossRef CAS PubMed.
- A. K. Khandpur, S. Foerster, F. S. Bates, I. W. Hamley, A. J. Ryan, W. Bras, K. Almdal and K. Mortensen, Macromolecules, 1995, 28, 8796–8806 CrossRef CAS.
- D. Yamaguchi, T. Hashimoto, N. Y. Vaidya and C. D. Han, Macromolecules, 1999, 32, 7696–7699 CrossRef CAS.
- E. W. Cochran, C. J. Garcia-Cervera and G. H. Fredrickson, Macromolecules, 2006, 39, 4264 CrossRef CAS.
- Y. Y. Huang, J. Y. Hsu, H. L. Chen and T. Hashimoto, Macromolecules, 2007, 40, 406–409 CrossRef CAS.
- K. Kimishima, K. Saijo, T. Koga and T. Hashimoto, Macromolecules, 2013, 46, 9032–9044 CrossRef CAS.
- C. H. Lin, T. Higuchi, H. L. Chen, J. C. Tsai, H. Jinnai and T. Hashimoto, Macromolecules, 2018, 51, 4049–4058 CrossRef CAS.
- M. W. Matsen, Macromolecules, 2012, 45, 2161–2165 CrossRef CAS.
- K. Almdal, K. A. Koppi, F. S. Bates and K. Mortensen, Macromolecules, 1992, 25, 1743–1751 CrossRef CAS.
- J. D. Vavasour and M. D. Whitmore, Macromolecules, 1993, 26, 7070–7075 CrossRef CAS.
- F. S. Bates, M. F. Schulz, A. K. Khandpur, S. Foerster, J. H. Rosedale, K. Almdal and K. Mortensen, Faraday Discuss., 1994, 98, 7–18 RSC.
- M. W. Matsen and M. Schick, Macromolecules, 1994, 27, 4014–4015 CrossRef CAS.
- M. W. Matsen and F. S. Bates, J. Polym. Sci., Part B:Polym. Phys., 1997, 35, 945–952 CrossRef CAS.
- M. W. Bates, J. Lequieu, S. M. Barbon, R. M. Lewis, K. T. Delaney, A. Anastasaki, C. J. Hawker, G. H. Fredrickson and C. M. Bates, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13194–13199 CrossRef CAS PubMed.
- K. D. Dorfman, Macromolecules, 2021, 54, 10251–10270 CrossRef CAS.
- Y. C. Xu, W. H. Li, F. Qiu and Z. Q. Lin, Nanoscale, 2014, 6, 6844–6852 RSC.
- J. Park, S. Jang and J. K. Kim, J. Polym. Sci., Part B:Polym. Phys., 2015, 53, 1–21 CrossRef CAS.
- Y. C. Qiang, W. H. Li and A. C. Shi, ACS Macro Lett., 2020, 9, 668–673 CrossRef CAS PubMed.
- G. M. Grason and R. D. Kamien, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051801 CrossRef PubMed.
- W. Li and Y. X. Liu, J. Chem. Phys., 2021, 154, 014903 CrossRef CAS PubMed.
- D. L. Vigil, T. Quah, D. Sun, K. T. Delaney and G. H. Fredrickson, Macromolecules, 2022, 55, 4237–4244 CrossRef CAS.
- J. Lequieu, T. Koeper, K. T. Delaney and G. H. Fredrickson, Macromolecules, 2020, 53, 513–552 CrossRef CAS.
- G. M. Grason, B. A. DiDonna and R. D. Kamien, Phys. Rev. Lett., 2003, 91, 058304 CrossRef PubMed.
- G. M. Grason and R. D. Kamien, Macromolecules, 2004, 37, 7371–7380 CrossRef CAS.
- N. Xie, W. H. Li, F. Qiu and A. C. Shi, ACS Macro Lett., 2014, 3, 906–910 CrossRef CAS PubMed.
- Z. H. Gan, D. D. Zhou, Z. Ma, M. Xu, Z. Q. Xu, J. W. He, J. J. Zhou and X. H. Dong, J. Am. Chem. Soc., 2022, 145, 487–497 CrossRef PubMed.
- S. T. Milner, Macromolecules, 1994, 27, 2333–2335 CrossRef CAS.
- J. H. Shi, X. B. Huang and W. H. Li, Phys. Chem. Chem. Phys., 2023, 25, 20032–20041 RSC.
- X. Y. Feng, G. X. Liu, D. Guo, K. N. Lang, R. M. Zhang, J. H. Huang, Z. B. Su, Y. W. Li, M. J. Huang, T. Li and S. Z. D. Cheng, ACS Macro Lett., 2019, 8, 875–881 CrossRef CAS PubMed.
- S. Lee, M. J. Bluemle and F. S. Bates, Science, 2010, 330, 349–353 CrossRef CAS PubMed.
- Y. C. Liu, H. Y. Lei, Q. Y. Guo, X. Y. Liu, X. H. Li, Y. A. Wu, W. Y. Li, W. Zhang, G. X. Liu, X. Y. Yan and S. Z. D. Cheng, Chin. J. Polym. Sci., 2023, 41, 607–620 CrossRef CAS.
- X. Y. Yan, Y. C. Liu, X. Y. Liu, H. Y. Lei, X. H. Li, Y. C. Wang, W. Y. Li, Q. Y. Guo, M. J. Huang and S. Z. D. Cheng, Phys. Rev. Mater., 2023, 7, 120302 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Macromolecules, 1994, 27, 1065–1067 CrossRef CAS.
- M. W. Schulze, R. M. Lewis, J. H. Lettow, R. J. Hickey, T. M. Gillard, M. A. Hillmyer and F. S. Bates, Phys. Rev. Lett., 2017, 118, 207801 CrossRef PubMed.
- M. W. Bates, S. M. Barbon, A. E. Levi, R. M. Lewis, H. K. Beech, K. M. Vonk, C. Zhang, G. H. Fredrickson, C. J. Hawker and C. M. Bates, ACS Macro Lett., 2020, 9, 396–403 CrossRef CAS PubMed.
- S. M. Barbon, J. A. Song, D. Y. Chen, C. Zhang, J. Lequieu, K. T. Delaney, A. Anastasaki, M. Rolland, G. H. Fredrickson, M. W. Bates, C. M. Hawker and C. J. Bates, Macromolecules, 2020, 9, 1745–1752 CAS.
- Z. Ma, R. Tan, Z. H. Gan, D. D. Zhou, Y. D. Yang, W. Zhang and X.-H. Dong, Macromolecules, 2022, 55, 4331–4340 CrossRef CAS.
- E. B. Zhulina, S. S. Sheiko, A. V. Dobrynin and O. V. Borisov, Macromolecules, 2020, 53, 2582–2593 CrossRef CAS.
- Z. Ma, D. D. Zhou, M. Xu, Z. H. Gan, T. Y. Zheng, S. Wang, R. Tan and X.-H. Dong, Macromolecules, 2023, 56, 833–840 CrossRef CAS.
- R. J. Sánchez-Leija, J. A. Mysona, J. J. de Pablo and P. F. Nealey, Macromolecules, 2024, 57, 2019–2029 CrossRef PubMed.
- V. Percec, C. H. Ahn, G. Ungar, D. J. P. Yeardley, M. Moller and S. S. Sheiko, Nature, 1998, 391, 161–164 CrossRef CAS.
- B. K. Cho, A. Jain, S. M. Gruner and U. Wiesner, Science, 2004, 305, 1598–1601 CrossRef CAS PubMed.
- A. G. Marcos, T. M. Pusel, R. Thomann, T. Pakula, L. Okrasa, S. Geppert, W. Gronski and H. Frey, Macromolecules, 2006, 39, 971–977 CrossRef CAS.
- Y. W. Chung, J. K. Lee, W. C. Zin and B. K. Cho, J. Am. Chem. Soc., 2008, 130, 7139–7147 CrossRef CAS PubMed.
- W. M. Wan and C. Y. Pan, Macromolecules, 2008, 41, 5085–5088 CrossRef CAS.
- F. Wurm, H. Schüle and H. Frey, Macromolecules, 2008, 41, 9602–9611 CrossRef CAS.
- F. Wurm, J. Klos, H. J. Räder and H. Frey, J. Am. Chem. Soc., 2009, 131, 7954–7955 CrossRef CAS PubMed.
- A. M. Hofmann, F. Wurm, E. Hühn, T. Nawroth, P. Langguth and H. Frey, Biomacromolecules, 2010, 11, 568–574 CrossRef CAS PubMed.
- Y. Q. Xu, P. Xiang, Z. B. Ye and W. J. Wang, Macromolecules, 2010, 43, 8026–8038 CrossRef CAS.
- X. J. Zhang, J. A. Cheng, Q. R. Wang, Z. L. Zhong and R. X. Zhuo, Macromolecules, 2010, 43, 6671–6677 CrossRef CAS.
- C. Schüll, H. Rabbel, F. Schmid and H. Frey, Macromolecules, 2013, 46, 5823–5830 CrossRef.
- Y. Shi, X. S. Cao, S. J. Luo, X. F. Wang, R. W. Graff, D. Q. Hu, R. L. Guo and H. F. Gao, Macromolecules, 2016, 49, 4416–4422 CrossRef CAS.
- F. Li, M. X. Cao, Y. J. Feng, R. Q. Liang, X. W. Fu and M. J. Zhong, J. Am. Chem. Soc., 2019, 141, 794–799 CrossRef CAS PubMed.
- T. Jun, H. Park, S. Jeon, H. Ahn, W. D. Jang, B. Lee and D. Y. Ryu, Nanoscale, 2022, 14, 16936–16943 RSC.
- T. Jun, H. Park, J. Kim, W. Lee, H. Ahn, W. D. Jang, B. Lee and D. Ryu, Nanoscale, 2023, 15, 9069–9075 RSC.
- M. W. Matsen, J. Phys.: Condens. Matter, 2002, 14, R21–R47 CrossRef CAS.
-
G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, 2006 Search PubMed.
- G. Tzeremes, K. O. Rasmussen, T. Lookman and A. Saxena, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041806 CrossRef CAS PubMed.
- K. O. Rasmussen and G. Kalosakas, J. Polym. Sci., Part B:Polym. Phys., 2002, 40, 1777–1783 CrossRef CAS.
- P. Stasiak and M. W. Matsen, Eur. Phys. J. E:Soft Matter Biol. Phys., 2011, 34, 110 CrossRef CAS PubMed.
- R. B. Thompson, K. O. Rasmussen and T. Lookman, J. Chem. Phys., 2004, 120, 31–34 CrossRef CAS PubMed.
- C. A. Tyler and D. C. Morse, Macromolecules, 2003, 36, 8184–8188 CrossRef CAS.
- A. Arora, D. C. Morse, F. S. Bates and K. D. Dorfman, J. Chem. Phys., 2017, 146, 244902 CrossRef PubMed.
-
J. Qin, PhD thesis, The University of Minnesota, Minneapolis, USA, 2009 Search PubMed.
- Y. C. Qiang and W. H. Li, Macromolecules, 2020, 53, 9943–9952 CrossRef CAS.
- X. W. Ji and W. H. Li, Phys. Chem. Chem. Phys., 2020, 22, 17824–17832 RSC.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Qingshu
Dong
a,
Qingshu
Dong
 *a,
Tao
Yang
*a,
Tao
Yang
 b and
Weihua
Li
b and
Weihua
Li
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the ideal linear-dendrimer architecture can be generated from AB4 when the two short B-arms are moved to the middle points of the other two B-arms, respectively. Then we propose a simple expression for nequ with respect to the tethering position, which can reasonably measure the asymmetry degrees of these different linear-hyperbranched copolymers.
2, the ideal linear-dendrimer architecture can be generated from AB4 when the two short B-arms are moved to the middle points of the other two B-arms, respectively. Then we propose a simple expression for nequ with respect to the tethering position, which can reasonably measure the asymmetry degrees of these different linear-hyperbranched copolymers.




 . We considered that A and B segments have the same segment density (ρA = ρB) and length (bA = bB). The total number of segments in the A block and B blocks is given by fAN (fA = f) and fBN, respectively. Minimization of the free energy functional with respect to the volume-fraction functions and the mean fields leads to the following SCFT equations
. We considered that A and B segments have the same segment density (ρA = ρB) and length (bA = bB). The total number of segments in the A block and B blocks is given by fAN (fA = f) and fBN, respectively. Minimization of the free energy functional with respect to the volume-fraction functions and the mean fields leads to the following SCFT equations