Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spectral mechanisms of solid/liquid interfacial heat transfer in the presence of a meniscus†
Abdullah
El-Rifai
 *a,
Liudmyla
Klochko
*a,
Liudmyla
Klochko
 b,
Viktor
Mandrolko
b,
Viktor
Mandrolko
 c,
Sreehari
Perumanath
d,
David
Lacroix
c,
Sreehari
Perumanath
d,
David
Lacroix
 c,
Rohit
Pillai
*a and
Mykola
Isaiev
c,
Rohit
Pillai
*a and
Mykola
Isaiev
 *c
*c
aInstitute for Multiscale Thermofluids, University of Edinburgh, Edinburgh EH9 3FD, UK. E-mail: abdullah.elrifai@hotmail.com; r.pillai@ed.ac.uk
bUniversité de Lorraine, LORIA, Nancy F-54000, France
cUniversité de Lorraine, CNRS, LEMTA, Nancy F-54000, France. E-mail: mykola.isaiev@univ-lorraine.fr
dDepartment of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
First published on 1st May 2025
Abstract
In this study, we employ molecular simulations to investigate the enhancement in thermal conductance at the solid/liquid interface in the presence of a meniscus reported previously (Klochko et al., Phys. Chem. Chem. Phys., 2023, 25(4), 3298–3308). We vary the solid/liquid interaction strength at Lennard-Jones interfaces for both confined liquid and meniscus systems, finding that the presence of a meniscus yields an enhancement in the solid/liquid interfacial thermal conductance across all wettabilities. However, the magnitude of the enhancement is found to depend on the surface wettability, initially rising monotonously for low to moderate wettabilities, followed by a sharp rise between moderate and high wettabilities. The spectral decomposition of heat flux formalism was applied to understand the nature of this phenomenon further. By computing the in-plane and out-of-plane components of the heat fluxes within both the interfacial solid and liquid, we show that the initial monotonous rise in conductance enhancement predominantly stems from a rise in the coupling of out-of-plane vibrations within both the solid and the liquid. In contrast, the subsequent sharp rise at more wetting interfaces is linked to sharp increases in the utilization of the in-plane modes of the solid and liquid. These observations result from the interplay between the solid/liquid adhesive forces and the liquid/vapor interfacial tension. Our results can aid engineers in optimizing thermal transport at realistic interfaces, which is critical to designing effective cooling solutions for electronics, among other applications.
Introduction
The thermal transport across the region where the solid, liquid, and gas phases intersect, known as the “three-phase contact line” (TPCL), is key to phase-change processes,1,2 and impacts the performance of state-of-the-art two-phase cooling solutions for integrated circuits.3 Recently, for example, candidate cooling devices have been developed where high heat flux dissipation is achieved by inducing evaporation from menisci pinned within nanoporous membranes.4,5 Given the importance of the heat transfer at the TPCL in such devices, as well as its relevance to other practical applications such as scanning thermal microscopy,6–8 phase change materials,9,10 and photo-thermally induced bubble growth,11 gaining a better understanding of the energy transport at such interfaces is becoming increasingly important.Despite the nanoscale dimensions of the TPCL (shown to reach <30 nm experimentally12), several experimental and numerical studies have demonstrated that it plays a major role in evaporative heat transfer. Stephan and Busse13 found that half of the heat transferred within a grooved heat pipe evaporator occurred across the TPCLs of the liquid menisci. Ibrahem et al.14 studied the heat transfer characteristics at the TPCL of a liquid meniscus pinned in a microchannel, finding that the peak evaporative heat flux occurs at the TPCL. Kunkelmann et al.15 reported similar findings for advancing and receding menisci. Maroo and Chung16 simulated evaporation from nanoscale menisci, similarly reporting that the maximum evaporative heat flux occurs from the TPCL. Thus, to improve the rate of heat transfer in such systems, the energy transport at the TPCL must be better understood.
Numerous studies have reported that the overall heat transfer from evaporating TPCLs is impacted by the interfacial thermal conductance across the solid/liquid interface (Γ), which manifests as a temperature discontinuity at the interface (ΔT), and is related to the solid/liquid area of contact (Ac) and the heat transferred across this area (Q) via Γ = Q/AcΔT. Zhao et al.17 investigated evaporation processes in microchannels using kinetic theory, finding that Γ can reduce the peak evaporative heat flux from the TPCL by approximately 15%. Han et al.18 and Ma et al.19 studied thin-film evaporation using molecular dynamics (MD) simulations, finding that Γ can bottleneck evaporative heat transfer by up to 20% for regions of the TPCL where the liquid films become ultra-thin (<100 nm thick). Thus, a deeper understanding of Γ in the presence of the TPCL can help enhance the rate of evaporative heat transfer in such processes.
Klochko et al.20 investigated interfacial energy transport at the TPCL of a silicon/water interface for various surface wettabilities using a combination of MD and finite element method simulations. To understand how the presence of the TPCL influenced energy transport, they studied two distinct systems: (i) a system in which the silicon walls fully confined the water and thus had an absence of vapor, referred to as the “confined” system, and (ii) a system that contained TPCLs induced by pinning a water meniscus between two silicon walls, denoted as the “meniscus” system. In the confined system, the interfacial energy transport was determined by the total interfacial thermal conductance (G = Q/AΔT), where A is the cross-sectional area of the solid. In the meniscus system, there were comparatively fewer liquid atoms, which made a reduced area of contact with the solid (Ac) and led to a reduction in the total thermal conductance G of the interface. However, when computing the solid/liquid thermal conductance of the two systems Γ, Klochko et al.20 found that the presence of a meniscus led to a localized “enhancement” in Γ across all surface wettabilities, which is to say that greater heat is transported than expected once the reduction in contact area is accounted for. Note that this does not imply that the interface at a meniscus system transfers more thermal energy in total than the confined system. However, this localized enhancement is still unexpected and therefore noteworthy, and its origins have not yet been understood.
While studies on the enhancement of Γ at the TPCL are sparse, efforts have been made to uncover the origins of enhancements in Γ at solid/liquid interfaces through the analysis of the structural properties of the interfacial liquid. Shenogina et al.21 observed that Γ exhibits a linear relationship with the work of adhesion at self-assembled-monolayer/water interfaces; however, other studies have reported that this cannot be used as the sole predictor of Γ.22–24 Alexeev et al.25 reported a correlation between the peak interfacial density of the liquid and Γ at a graphene/water interface, but other studies have shown that this correlation does not always hold.24,26–31 Ramos-Alvarado et al.32 demonstrated a correlation between the density depletion length and Γ at a silicon/water interface, however this could not be successfully applied to other interfaces.28,31,33–35 Ma et al.26 demonstrated that the increase in Γ due to the presence of surface charges at a graphene/water interface was linked to a rise in the in-plane ordering of the interfacial liquid, but other studies have shown that this is not universally applicable.27,28,36 While structural properties have been partially successful in explaining increases in Γ, their lack of universality means other approaches must be sought to fully understand the origins of enhancements in Γ.
An alternative method to gain insights into enhancements in Γ revolves around deploying spectral techniques to directly probe the behavior of the interfacial atomic vibrations, the sole energy carriers across electrically non-conductive interfaces.37 In a number of studies, the enhancements in Γ were attributed to a change in the frequencies of the vibrations engaged in interfacial heat transfer, referred to as “utilized” modes. Qian et al.38 found that the rise in Γ with increasing surface wettability at a graphene/ionic–liquid interface was linked to a rise in the utilization of high-frequency modes within the interfacial solid. Ma et al.26 demonstrated that the enhancement in Γ yielded by an increase in the magnitude of surface charges at a graphene/water interface is similarly associated with greater high-frequency mode utilization in the interfacial solid. Qian et al.39 reported a comparable effect at graphene/ionic–liquid interfaces with increasing surface charge magnitude. In our previous work,40 we demonstrated that the exponential-to-linear regime cross-over that Γ experiences with increasing solid/liquid interaction strength (εSL) at LJ interfaces is related to an increase in the similarity of the frequencies of the utilized vibrations within the interfacial solid and liquid. The successful implementation of spectral techniques to understand enhancements in Γ at solid/liquid interfaces in these studies raises the following question for the TPCL system of interest here: does the presence of a TPCL similarly alter the frequencies of the vibrations utilized, and does that spectral variation enhance Γ?
In other studies, the increases in Γ at solid/liquid interfaces were also found to be linked to the orientation of the utilized vibrations with respect to the plane of the interface. Note that vibrational modes can be classified by orientation into: (i) in-plane (i.e. parallel to the interface), and (ii) out-of-plane (i.e. perpendicular to the interface) vibrations. Ramos-Alvarado and Kumar33 found that the rise in Γ with increasing wettability at silicon/water interfaces was linked to greater high-frequency mode utilization, as well as increased in-plane mode utilization in the solid. Gonzalez-Valle and Ramos-Alvarado35 reported similar findings at a silicon–carbide/water interface. Zhou et al.41 demonstrated that the rise in Γ induced by the presence of atomic defects at a graphene/hydrocarbon interface is similarly associated with greater in-plane mode utilization in the solid. These studies raise the second question about the TPCL-induced enhancement in Γ: does the presence of a TPCL influence the orientation of the vibrations utilized, and does that spectral variation enhance Γ?
Klochko et al.20 hypothesized that the enhancement in Γ in the presence of the TPCL stems from greater in-plane mode utilization in the interfacial solid; however, this hypothesis was not quantified using spectral techniques. In our previous work,40 the exponential-to-linear regime cross-over in Γ was explained by analyzing both the modes utilized within the solid to transmit energy to the liquid, as well as the modes within the liquid used to receive energy from the solid at a Lennard-Jones (LJ) interface. Therefore, in this work, the vibrations utilized within both the solid and liquid will be analyzed for the first time to understand the origin of the enhancement in Γ yielded by the presence of a TPCL at a simple LJ interface.
Methodology
System setup
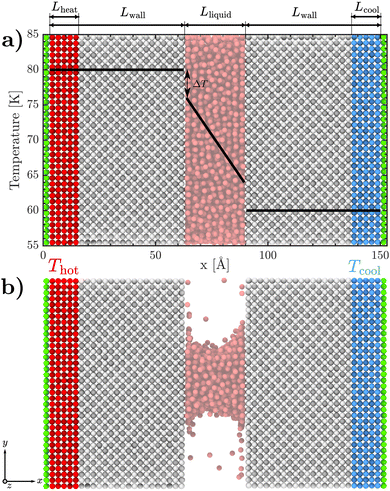
We conduct non-equilibrium MD simulations using LAMMPS42 to investigate the origin of the enhancement in interfacial energy transport at an LJ interface. We consider two systems: (i) a liquid fully confined between the walls of a nanochannel, referred to as the “confined” system (Fig. 1(a)), and (ii) a partially filled nanochannel comprising a meniscus, referred to as the “meniscus” system (Fig. 1(b)). The meniscus system was generated by removing the top and bottom 1/3rd of liquid atoms in the y-direction from the confined system. The confined system comprises 5157 liquid atoms, while the meniscus system comprises 1719 liquid atoms. The system geometry is identical for both the confined and meniscus systems. The nanochannel width is set to Lliquid ≈ 30 Å. The cross-sectional area of the domain Awall is set to 18 × 18 a2, where a = 5.304 Å is the lattice constant of the FCC solid. The [100] crystallographic planes of the walls are oriented along the direction of the heat flux. The wall thickness is set to Lwall = 12a. In both systems, each wall is composed of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 solid atoms. The domain is periodic in all dimensions except the x-direction, for which a ‘fixed’ boundary condition is used.
552 solid atoms. The domain is periodic in all dimensions except the x-direction, for which a ‘fixed’ boundary condition is used.
Systems are initially relaxed using an energy minimization step. Following this, simulations are initiated with an equilibration stage at 70 K under the NVT ensemble for 5 ns for both systems, with a timestep of 1 fs. In the case of the confined system, the pressure is controlled by applying a piston to the right wall to achieve the pressure corresponding to 1 atm. After the equilibration stage, the piston condition is removed, and the outermost green-colored solid layers at both ends of the simulation domain (see Fig. 1) are held rigid to maintain the specified pressure as well as avoid the displacement of the interfaces. The red-colored solid atoms in the left wall (tagged as Lheat in Fig. 1) are then set to Thot = 80 K, while the blue-colored atoms in the right wall (tagged as Lcool in Fig. 1) are set to Tcold = 60 K, using a Nosé–Hoover thermostat under the NVT ensemble. The solid atoms in the gray portions of both walls, all liquid atoms, and any vapor atoms are permitted to vibrate freely using the NVE ensemble. The system is thermalized under these conditions for 3 ns to ensure a steady state is reached. Afterwards, a data production run is conducted by running the simulation for an additional 10 ns, sampled every 1000 time steps.
All interatomic interactions are modeled using the LJ potential43 using a cut-off distance rcut = 8.5 Å. In line with prior studies on LJ interfaces,40,44,45 the liquid/liquid interaction strength is set to εLL = 10.3 meV, while the solid/solid interaction strength is set to εSS = 10εLL. For all interactions, the length scale in the LJ potential is kept at σ = 3.405 Å. All atomic masses m are set to 40.0 amu. To quantify the impact of the surface wettability on solid/liquid interfacial energy transport, the solid/liquid interaction strength εSL is varied directly in the range from 2.5 meV to 7.5 meV. The resulting wetting angles (θ) corresponding to all values of εSL were calculated from the density profiles similar to Isaiev et al.,46 and are presented in Fig. 2. MD snapshots of the resulting meniscus shape are illustrated in the insets. The range of values for εSL is chosen such that menisci of various curvatures are produced, with the transition from phobicity to philicity occurring around εSL ≈ 5 meV, as observed in Fig. 2. The maximum value of εSL is chosen so the meniscus does not thoroughly wet the surface. The interaction energies, temperatures, and system geometry are provided in LJ reduced units in Table S1 of the ESI.†
 | ||
| Fig. 2 The relationship between the cosine of the contact angle that the liquid makes with the surface (θ) and εSL. The insets depict the shape of the meniscus at various values of εSL. | ||
Calculation of the interfacial thermal conductance
The presence of thermostats at both ends of the domain which are 20 K apart produces a linearly varying temperature distribution within the domain (shown using black lines in Fig. 1(a)). The consequent interfacial temperature discontinuity at the solid/liquid interface (ΔT) can be calculated by extrapolating the best-fit line through the bulk liquid's temperature field to the interfacial solid in the left wall. The solid/liquid interfacial thermal conductance (Γ) is then computed using | (1) |
Spectral analysis of the interfacial thermal conductance
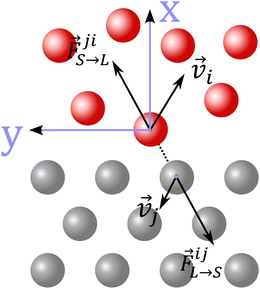
The spectral analysis of interfacial heat transfer can be conducted using the methodology developed by Sääskilahti et al.,44 and validated for liquids of varying wettability in our previous work.40 Through this, the spectral decomposition of heat flux within the interfacial solid q(ω)L→S can be computed, which quantifies the contributions of each vibration of frequency ω utilized within the solid to transmit energy to the liquid. It can be derived from the Fourier transform of the cross-correlation between the cumulative forces that all liquid atoms exert upon each solid atom and the velocities of the solid atoms via: | (2) |
 is the force acting on the j-th atom of the solid from the i-th atom of the liquid; and
is the force acting on the j-th atom of the solid from the i-th atom of the liquid; and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i and
i and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) j are the velocities of the i-th and j-th atom respectively, as illustrated in Fig. 3.
j are the velocities of the i-th and j-th atom respectively, as illustrated in Fig. 3.
The spectral decomposition of heat flux within the interfacial liquid q(ω)S→L, which instead quantifies the contributions of each vibration of frequency ω utilized within the liquid to receive energy from the solid, can be calculated using a similar approach. It can be derived from the Fourier transform of the cross-correlation between the cumulative forces that all solid atoms exert upon each liquid atom and the velocities of the liquid atoms via:
 | (3) |
 is the force acting on the i-th atom of the liquid from the j-th atom of the solid; and
is the force acting on the i-th atom of the liquid from the j-th atom of the solid; and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i and
i and ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) j are the velocities of the i-th and j-th atom respectively, similarly depicted in Fig. 3.
j are the velocities of the i-th and j-th atom respectively, similarly depicted in Fig. 3.
In order to consider the orientation of the vibrations, rather than merely their frequency, the directional components of the force and velocity vectors must be considered independently. The utilization of out-of-plane vibrations (q⊥L→S and q⊥S→L) is computed using the component of the forces and velocities vectors that is perpendicular to the interface, via:
 | (4) |
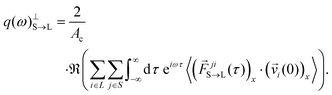 | (5) |
Similarly, the utilization of in-plane modes (q‖L→S and q‖S→L) is obtained from the components of the force and velocity vectors that are parallel to the interface, as follows:
 | (6) |
 | (7) |
From the separate components of the q(ω), the cumulative thermal conductance across the solid/liquid interface can be calculated for both in-plane and out-of-plane modes as follows:
 | (8) |
| Γ(ω)L→S,S→L = Γ(ω)⊥L→S,S→L + Γ(ω)‖L→S,S→L. | (9) |
In the computation of eqn (2)–(9), all solid and liquid atoms within the interaction cut-off distance rcut are considered.
Results & discussion
Effect of meniscus on Γ at various values of εSL
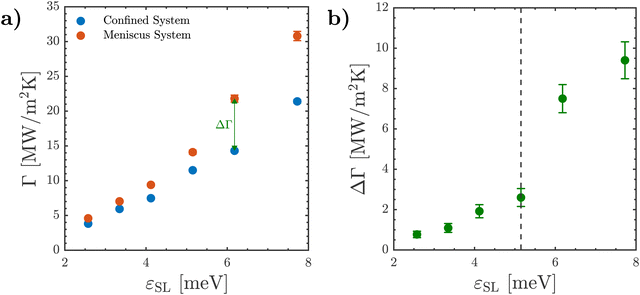
In Fig. 4(a), the variation of Γ with εSL is presented for the meniscus and confined systems as obtained through eqn (1). With rising εSL, Γ increases steadily for both systems. However, it can be observed that the magnitude of Γ in the meniscus system is larger than that of the confined system. This implies that the presence of a meniscus yields an enhancement in Γ across all values of εSL. This enhancement is denoted as ΔΓ = Γmeniscus − Γconfined, and is illustrated for the εSL ≈ 6 meV case in Fig. 4(a). To rule out the possibility that the observed enhancement in Γ is caused by system size effects, we conducted two additional simulations for confined and meniscus systems at εSL = 5 meV where the nanochannel width Lliquid was increased to ≈80 Å and the interaction cut-off distance rcut was increased to 13 Å. As shown in Table S2 of the ESI,† the presence of a meniscus leads to a notable enhancement in Γ, demonstrating that the reported enhancement in Γ is not related to the nanochannel width.Klochko et al.20 observed a similar enhancement in Γ caused by the presence of a meniscus at a realistic silicon/water interface. While such realistic interfaces possess complex interfacial forces (e.g. electrostatic interactions, hydrogen bonding) that influence interfacial structure,47–51 which consequently influences heat transfer,26,38,39 the simplified LJ system investigated in this study is capable of reproducing the enhancement in Γ reported at a realistic silicon/water interface. This makes it an ideal starting point in elucidating the spectral origins of the enhancement in Γ.
Next, ΔΓ is calculated for all values of εSL, as shown in Fig. 4(b). With increasing εSL, ΔΓ is seen to increase monotonously until εSL ≈ 5 meV. However, there is a discontinuity at εSL ≈ 5 meV, and it can be observed that ΔΓ experiences a sharp increase beyond this point. This indicates that, while the presence of a meniscus enhances Γ regardless of εSL, the magnitude of this enhancement is dependent on εSL. From Fig. 2, we know that the transition from phobicity to philicity occurs around εSL ≈ 5 meV. Therefore, the sharp rise in ΔΓ observed at this point coincides with a change in the characteristic curvature of the liquid/vapor interface, namely from concavity to convexity in the direction of the vapor. This raises the third question to be addressed in this work: why does the enhancement in Γ experience a sharp enhancement beyond εSL≈ 5 meV?
To answer the questions posed thus far, we will first assess whether the presence of a TPCL alters the frequencies of the utilized modes within both the interfacial solid and liquid, followed by an examination of the orientation of the utilized vibrations. This will be achieved by analyzing the spectral mechanisms of interfacial energy transport within the meniscus system, and comparing them to those within the benchmark confined system at each wettability.
Effect of meniscus on frequencies of utilized vibrations
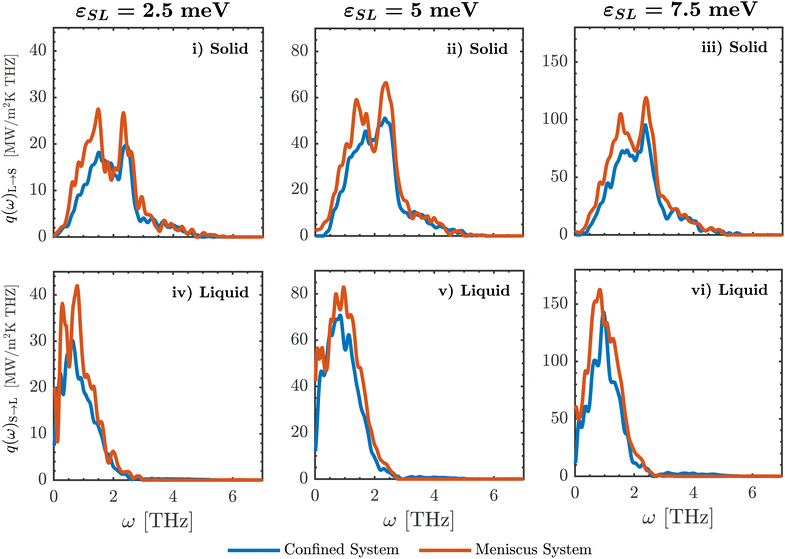
In Fig. 5, the q(ω)L→S and q(ω)S→L distributions are presented for the confined and meniscus systems at three values of εSL. It can be observed that the magnitudes of the q(ω)L→S and q(ω)S→L distributions differ greatly across the two systems, because the meniscus and confined systems possess significantly different magnitudes of Γ for the same value of εSL. Attempting to compare two distributions of vastly different magnitudes would obscure any differences between them. Therefore, the q(ω)L→S and q(ω)S→L distributions of the two systems are normalized by setting the area beneath their curves to unity to facilitate their comparison in the remainder of this section. First, the normalized q(ω)L→S distributions of the meniscus and confined systems will be compared, followed by their normalized q(ω)S→L distributions.To rule out the presence of potential size effects, the normalized q(ω)L→S and q(ω)S→L distributions in the confined system at εSL = 2.5–5 meV are compared to those at a much larger nanochannel, as reported in our previous work.40 As shown in Fig. S6 of the ESI,† the normalized q(ω)L→S and q(ω)S→L spectra are virtually identical across both nanochannels, implying the size of the nanochannel does not influence the spectral properties of interfacial energy transport.
Nonetheless, the enhancement in Γ due to the presence of a meniscus cannot be explained by a change in the frequencies of the vibrations utilized within the interfacial solid or liquid, and alternative mechanisms must be explored.
Effect of meniscus on orientation of utilized vibrations
Rather than merely comparing the overall spectral distributions of q(ω)L→S and q(ω)S→L, which probes whether the meniscus and confined systems utilize modes of different frequencies, these spectra can be further decomposed based on the orientation of the vibrations with respect to the plane of the interface.44 As stated previously, differences in the orientation of utilized modes have been observed in the literature,33,35,41 but this has not yet been studied at the TPCL. Thus, the next step is to analyze the contribution of the in-plane and out-of-plane modes towards the interfacial thermal conductance Γ.The spectral distributions q(ω)L→S and q(ω)S→L can be decomposed into their out-of-plane (q(ω)⊥L→S, q(ω)⊥S→L) and in-plane (q(ω)‖L→S, q(ω)‖S→L) components using eqn (6) and (7), as presented in Fig. S3 and S4 of the ESI.† However, this merely quantifies the contributions of each individual vibrational frequency ω towards interfacial energy transport. An alternative metric is the cumulative contribution of the entire range of vibrational frequencies towards Γ. This can be obtained by computing the “spectral accumulation” of each distribution, calculated via their cumulative integration with respect to ω, as presented in eqn (8). Using this calculation, the separate contributions of in-plane and out-of-plane modes towards the total energy transported in each system can be compared across the meniscus and confined systems. Note that, as we are now interested in comparing the actual energetic contributions of each vibrational orientation rather than merely their spectral distribution, the spectral accumulations will not be normalized. First, this analysis will be conducted in the interfacial solid, followed by the interfacial liquid.
The representative examples of the cumulative spectral distribution for the confined liquid and the meniscus case are presented in Fig. 7(a) and 8(a). It should be noted that both cumulative spectral distributions under higher frequencies are approximately equal to the thermal conductance calculated by the use of eqn (1): Γ = Γ(ω → ∞)L→S ≈ Γ(ω → ∞)S→L (see Fig. S5 in the ESI†). The discrepancy between the two is caused by the statistical error in computing the spectral decomposition of heat flux within both media, in line with prior studies.52
1. The leftmost panel (Fig. 7(a)(i)) illustrates the accumulations of the total Γ(ω)L→S distributions for both systems. The final value of each accumulation represents the actual magnitude of Γ of a given system, and the gap between the accumulations of the meniscus and confined systems represents the enhancement in Γ due to the meniscus ΔΓ, which are identical to the values first shown in Fig. 4.
2. The middle panel (Fig. 7(a)(ii)) shows the accumulations of the out-of-plane component of energy transport within the interfacial solid Γ(ω)⊥L→S for the two systems. Here, the gap between their accumulations represents the difference in the contributions of out-of-plane modes induced by the meniscus, denoted as ΔΓ⊥IS for the interfacial solid.
3. The rightmost panel (Fig. 7(a)(iii)) illustrates the accumulations of the in-plane component of heat transfer within the interfacial solid Γ(ω)‖L→S for the meniscus and confined systems. Conversely, the gap between these accumulations represents the difference in the contributions of in-plane modes due to the presence of a meniscus, denoted as ΔΓ‖IS for the interfacial solid.
Analyzing Fig. 7(a)(i)–(iii), significant differences can be observed between the spectral accumulations of Γ(ω)⊥L→S and Γ(ω)‖L→S across the confined and meniscus systems at the lowest value of εSL = 2.5 meV. Specifically, the meniscus is seen to yield a large increase in Γ(ω)⊥L→S, but a relatively smaller increase in Γ(ω)‖L→S.
By quantifying the magnitude of the gaps between the accumulations of Γ(ω)⊥L→S and Γ(ω)‖L→S for the meniscus and confined systems, ΔΓ can be effectively decomposed within the interfacial solid into its out-of-plane (ΔΓ(ω)⊥L→S) and in-plane (ΔΓ(ω)‖L→S) components. Fig. 7(b) plots these decomposed values within the solid at each value of εSL studied, as derived from their spectral accumulations. From this plot, two observations can be made:
1. ΔΓ(ω)⊥L→S is significantly larger than ΔΓ(ω)‖L→S across all magnitudes of εSL considered. Thus, the enhancement in Γ due to the presence of a meniscus coincides with the increase in the utilization of out-of-plane modes in the interfacial solid across all values of εSL studied.
2. When εSL < 5 meV, ΔΓ(ω)⊥L→S and ΔΓ(ω)‖L→S both increase monotonously. However, beyond εL→S > 5 meV, both ΔΓ(ω)⊥L→S and ΔΓ(ω)‖L→S rise sharply. This sharp increase in the utilization of the in-plane and out-of-plane modes of the solid coincides with the sharp enhancement in ΔΓ that occurs around εSL ≈ 5 meV, initially seen in Fig. 4(b).
Note that these differences arise from the transmitted spectra (i.e. within the interfacial solid); next, we evaluate the influence of the meniscus on the modes utilized to receive energy by the liquid.
Fig. 8(b) similarly depicts the decomposition of ΔΓ into its out-of-plane (ΔΓ(ω)⊥S→L) and in-plane (ΔΓ(ω)‖S→L) components within the liquid across the entire range of values for εSL studied. From this plot, four observations can be made:
1. When εSL = 2.5 meV, ΔΓ(ω)⊥S→L ≈ ΔΓ(ω)‖S→L. Thus, at this magnitude of εSL, the enhancement in Γ can be equally divided into the rise in the utilization of both out-of-plane and in-plane modes in the interfacial liquid, contrary to the interfacial solid (where the out-of-plane component dominated).
2. As εSL is increased to 5 meV, ΔΓ(ω)⊥S→L rises monotonously, while ΔΓ(ω)‖S→L remains roughly unchanged (the origin of the small dip at 5 meV is not fully understood, but does not impact the remainder of this discussion). Consequently, when εSL is in the range 2.5–5 meV, ΔΓ(ω)⊥S→L is notably larger than ΔΓ(ω)‖S→L, and the enhancement in Γ yielded by the meniscus coincides with an increase in the utilization of the out-of-plane modes of the liquid. This is in alignment with the interfacial solid in this range of values for εSL.
3. Upon further increasing εSL beyond 5 meV, ΔΓ(ω)‖S→L rises sharply, while ΔΓ(ω)⊥S→L increases to a lesser degree. Consequently, the difference between the two shrinks. As a result, at the highest value of εSL, the enhancement in Γ coincides with a rise in the utilization of both the in-plane and out-of-plane modes of the interfacial liquid, with the latter being more important.
4. The sharp increase in the utilization of the in-plane modes of the liquid ΔΓ(ω)‖S→L around εSL ≈ 5 meV coincides with the rise in ΔΓ that occurs around the same point, initially observed in Fig. 4(b).
From this set of spectral analyses, it is evident that the presence of a meniscus significantly impacts the orientation of the utilized modes within both the interfacial solid and liquid, which coincides with the observed enhancement in Γ. It is also evident that there are differences in spectral transmission between menisci for different εSL. These are discussed in the next section.
Connecting spectral mechanisms to the presence and curvature of the meniscus
The large variation in εSL leads to the formation of menisci of vastly different curvatures, as shown in Fig. 9(b)–(d). To understand the relationship between the spectral mechanisms described thus far and the curvature of the meniscus, the interfacial interactions between the three phases at the TPCL of each meniscus must first be examined. Following this, the role of the TPCL in inducing the spectral differences between the confined and meniscus systems will be described. Finally, the origins of the variation in these spectral differences induced by the change in the curvature of the TPCL will be discussed.FA = (1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)Fγ. θ)Fγ. | (10) |
Using eqn (10) and the wetting angles presented previously in Fig. 2, FA can be estimated for each value of εSL, as shown in Fig. 10. Thus, the balance between FA and Fγ with varying εSL gives rise to three distinct meniscus curvatures:
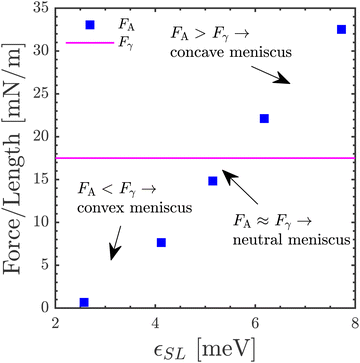 | ||
| Fig. 10 The variation of the length-averaged force of adhesion FA with the solid/liquid interaction strength εSL relative to the liquid/vapor interfacial tension Fγ. | ||
1. Convex meniscus: at the lowest value of εSL, it can be observed that the meniscus exhibits a pronounced convex shape, with a high curvature of the TPCLs it comprises, as illustrated in Fig. 9(b). This is caused by the magnitude of the interfacial tension Fγ exceeding the magnitude of the solid/liquid adhesive forces FA (i.e. FA < Fγ), as observed in Fig. 10. Due to these weak adhesion, the TPCL is not “pinned” to the surface and can move, leading to a high slip of the interfacial liquid.55
2. Neutral meniscus: as εSL is increased to 5 meV, the meniscus gradually reduces the curvature of its TPCLs, taking a neutral shape around εSL ≈ 5 meV, as shown in Fig. 9(c). In this case, the magnitude of the interfacial tension Fγ is roughly equal to that of the adhesive forces FA (i.e. FA ≈ Fγ), as seen in Fig. 10. As a result, the interfacial slip reduces, but is still non-negligible.56
3. Concave meniscus: as εSL is increased beyond 5 meV, the meniscus begins taking a concave shape, now increasing its curvature once again, as observed in Fig. 9(d). This is caused by the magnitude of FA exceeding that of Fγ (i.e. FA > Fγ), as shown in Fig. 10. Consequently, the TPCL becomes pinned, and the interfacial slip becomes negligible.56
In the liquid, Fig. 8(b) showed that the transition from a convex meniscus to a neutral one corresponds to a rise in the utilization of the out-of-plane modes of the liquid (ΔΓ(ω)⊥S→L), and an insignificant change in the utilization of its in-plane modes (ΔΓ(ω)‖S→L). Beyond εSL ≈ 5 meV, the utilization of the out-of-plane modes in the liquid continues to increase monotonously, while the utilization of its in-plane modes increases sharply. These enhancements between the confined and meniscus systems, as well as the dependence of these enhancements on the wettability of the surface, can be explained in the following way:
1. Solid:
(a) Increase in out-of-plane utilization (ΔΓ(ω)⊥L→S): it has been demonstrated that, at a solid/vapor interface, the out-of-plane modes within the solid are less hindered when compared to a solid/liquid interface, and are thus utilized to a larger degree.45 This is consistent with our observations where the utilization of these out-of-plane modes is increased for the meniscus systems where a vapor region is present, when compared to the confined system which is fully liquid.
(b) Variation of out-of-plane utilization with meniscus shape: with increasing εSL, the reduction in the curvature of the meniscus exposes the solid at the TPCL to a larger number of vapor atoms, and a correspondingly smaller number of liquid atoms. Thus, the mechanism in (a) above is drastically magnified upon the transition from a neutral meniscus to a concave one, due to the significant reduction in the number of liquid atoms adjacent to the solid atoms at the TPCL. This likely induces the sharp rise in the utilization of the out-of-plane modes beyond εSL ≈ 5 meV, previously observed in Fig. 7(b).
(c) Increase in in-plane utilization (ΔΓ(ω)‖L→S): the interplay between the adhesive forces FA and the interfacial tension Fγ localized on the solid atoms adjacent to the TPCL enables the solid to utilize its in-plane modes more effectively.
(d) Variation of in-plane utilization with meniscus shape: with increasing εSL, the resulting interfacial forces acting on the solid atoms of the TPCL increase steadily in magnitude,57 yielding the steady increase in the utilization of the in-plane modes of the solid observed in Fig. 7(b) for εSL < 5 meV.
2. Liquid:
(a) Increase in out-of-plane (ΔΓ(ω)⊥L→S) and in-plane (ΔΓ(ω)‖L→S) utilization: similar to the solid, the interplay between the adhesive forces FA and the interfacial tension Fγ localized on the liquid atoms in the TPCL acts as an additional dissipation mechanism for all received modes, facilitating their transmission from the solid into the liquid.
(b) Variation of out-of-plane utilization with meniscus shape: with increasing εSL, this mode dissipation is amplified, facilitating the transfer of the out-of-plane modes of the solid into out-of-plane modes within the liquid. This explains the rise in the utilization of the out-of-plane modes of the liquid observed in Fig. 8(b).
Conclusions
The impact of a meniscus on the solid/liquid interfacial thermal conductance (Γ) was studied at an LJ solid/liquid interface for various magnitudes of the solid/liquid interaction strength εSL. Across all values of εSL, the presence of a meniscus was found to yield a significant enhancement in Γ (ΔΓ). This enhancement was found to rise monotonously until εSL ≈ 5 meV, beyond which it increases sharply. To understand why the meniscus yields an enhancement in Γ, and why the magnitude of this enhancement rises sharply beyond εSL ≈ 5 meV, the spectral decomposition of heat flux formalism was used to probe the interfacial solid and liquid, respectively.The meniscus was shown to have negligible influence on the frequencies of the utilized vibrations in the interfacial solid or liquid. Instead, it was seen to influence the preferred orientation of the utilized vibrations. The monotonous enhancement in ΔΓ until εSL ≈ 5 meV coincided with an increase in the utilization of the out-of-plane vibrations engaged in heat transfer within both the interfacial solid and liquid. This was found to be caused by the interplay between adhesive forces and interfacial tension at the TPCL, which facilitates the utilization of out-of-plane modes in both media.
The sharp enhancement in ΔΓ beyond εSL ≈ 5 meV was found to be related to the sharp increases in the utilization of the in-plane vibrations within both the interfacial solid and liquid, accompanied by a sharp rise in the utilization of the out-of-plane modes of the solid. This was found to be related to the drastic reduction in the slip of the interfacial liquid upon the transition from a neutral meniscus to a concave one. These results elucidate heat transfer processes at the TPCL, which are particularly relevant to state-of-the-art two-phase evaporators for integrated circuit cooling, among other applications.
Data availability
The code for LAMMPS used to run the simulations in this study can be found at https://www.lammps.org with DOI https://doi.org/10.1016/j.cpc.2021.108171. The version of the code employed for this study is version lammps-15Jun2023.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported by ANR project “PROMENADE” no. ANR-23-CE50-0008. Molecular simulations were conducted using HPC resources from GENCI-TGCC and GENCI-IDRIS (no. A0150913052), as well as resources provided by the EXPLOR Center hosted by the University of Lorraine. S. P. thanks the Leverhulme Trust for the support provided through the Early Career Fellowship ECF-2021-137. R. P. is supported by the UKRI Frontier Guarantee Grant EP/Y036107/1.References
- P. A. Raghupathi and S. G. Kandlikar, Contact line region heat transfer mechanisms for an evaporating interface, Int. J. Heat Mass Transfer, 2016, 95, 296–306 CrossRef.
- P. A. Raghupathi and S. G. Kandlikar, Pool boiling enhancement through contact line augmentation, Appl. Phys. Lett., 2017, 110, 2014101 Search PubMed.
- K. Sefiane and A. Kosar, Prospects of heat transfer approaches to dissipate high heat fluxes: opportunities and challenges, Appl. Therm. Eng., 2022, 215, 118990 CrossRef.
- D. F. Hanks, Z. Lu, J. Sircar, T. R. Salamon, D. S. Antao, K. R. Bagnall, B. Barabadi and E. N. Wang, Nanoporous membrane device for ultra high heat flux thermal management, Microsyst. Nanoeng., 2018, 4, 1–10 CrossRef PubMed.
- D. F. Hanks, Z. Lu, J. Sircar, I. Kinefuchi, K. R. Bagnall, T. R. Salamon, D. S. Antao, B. Barabadi and E. N. Wang, High heat flux evaporation of low surface tension liquids from nanoporous membranes, ACS Appl. Mater. Interfaces, 2020, 12, 7232–7238 CrossRef PubMed.
- A. Assy, S. Lefèvre, P. O. Chapuis and S. Gomès, Analysis of heat transfer in the water meniscus at the tip-sample contact in scanning thermal microscopy, J. Phys. D: Appl. Phys., 2014, 47, 20–25 CrossRef.
- J. Bodzenta, A. Kamierczak-Bałata and K. Harris, Quantitative thermal measurement by the use of scanning thermal microscope and resistive thermal probes, J. Appl. Phys., 2020, 127, 031103 CrossRef.
- Y. Zhang, W. Zhu, F. Hui, M. Lanza, T. Borca-Tasciuc and M. Muñoz Rojo, A Review on Principles and Applications of Scanning Thermal Microscopy (SThM), Adv. Funct. Mater., 2020, 30, 1900892 CrossRef CAS.
- J. Qiu, D. Huo and Y. Xia, Phase-Change Materials for Controlled Release and Related Applications, Adv. Mater., 2020, 32, 1–21 Search PubMed.
- R. Jilte, A. Afzal and S. Panchal, A novel battery thermal management system using nano-enhanced phase change materials, Energy, 2021, 219, 119564 CrossRef CAS.
- X. Yan, J. Xu, Z. Meng, J. Xie and H. Wang, A New Mechanism of Light-Induced Bubble Growth to Propel Microbubble Piston Engine, Small, 2020, 16, 1–15 Search PubMed.
- M. Rivetti, T. Salez, M. Benzaquen, E. Raphaël and O. Bäumchen, Universal contact-line dynamics at the nanoscale, Soft Matter, 2015, 11, 9247–9253 RSC.
- P. C. Stephan and C. A. Busse, Analysis of the heat transfer coefficient of grooved heat pipe evaporator walls, Int. J. Heat Mass Transfer, 1992, 35, 383–391 CrossRef CAS.
- K. Ibrahem, M. F. Abd Rabbo, T. Gambaryan-Roisman and P. Stephan, Experimental investigation of evaporative heat transfer characteristics at the 3-phase contact line, Exp. Therm. Fluid Sci., 2010, 34, 1036–1041 CrossRef CAS.
- C. Kunkelmann, K. Ibrahem, N. Schweizer, S. Herbert, P. Stephan and T. Gambaryan-Roisman, The effect of three-phase contact line speed on local evaporative heat transfer: experimental and numerical investigations, Int. J. Heat Mass Transfer, 2012, 55, 1896–1904 CrossRef CAS.
- S. C. Maroo and J. N. Chung, Fundamental roles of nonevaporating film and ultrahigh heat flux associated with nanoscale meniscus evaporation in nucleate boiling, J. Heat Transfer, 2013, 135, 1–10 Search PubMed.
- J. J. Zhao, M. Huang, Q. Min, D. M. Christopher and Y. Y. Duan, Near-wall liquid layering, velocity slip, and solid–liquid interfacial thermal resistance for thin-film evaporation in microchannels, Nanoscale Microscale Thermophys. Eng., 2011, 15, 105–122 CrossRef CAS.
- H. Han, C. Schlawitschek, N. Katyal, P. Stephan, T. Gambaryan-Roisman, F. Leroy and F. Müller-Plathe, Solid–Liquid Interface Thermal Resistance Affects the Evaporation Rate of Droplets from a Surface: A Study of Perfluorohexane on Chromium Using Molecular Dynamics and Continuum Theory, Langmuir, 2017, 33, 5336–5343 CrossRef CAS PubMed.
- B. Ma, K. Guye, B. Dogruoz and D. Agonafer, Molecular dynamics simulations of thin-film evaporation: the influence of interfacial thermal resistance on a graphene-coated heated silicon substrate, Appl. Therm. Eng., 2021, 195, 117142 CrossRef CAS.
- L. Klochko, V. Mandrolko, G. Castanet, G. Pernot, F. Lemoine, K. Termentzidis, D. Lacroix and M. Isaiev, Molecular dynamics simulation of thermal transport across a solid/liquid interface created by a meniscus, Phys. Chem. Chem. Phys., 2023, 25, 3298–3308 RSC.
- N. Shenogina, R. Godawat, P. Keblinski and S. Garde, How wetting and adhesion affect thermal conductance of a range of hydrophobic to hydrophilic aqueous interfaces, Phys. Rev. Lett., 2009, 102, 1–4 CrossRef PubMed.
- S. Ge and M. Chen, Vibrational coupling and Kapitza resistance at a solid–liquid interface, Int. J. Thermophys., 2013, 34, 64–77 CrossRef CAS.
- J. A. Tomko, D. H. Olson, A. Giri, J. T. Gaskins, B. F. Donovan, S. M. O'Malley and P. E. Hopkins, Nanoscale Wetting and Energy Transmission at Solid/Liquid Interfaces, Langmuir, 2019, 35, 2106–2114 CrossRef CAS PubMed.
- C. U. Gonzalez-Valle and B. Ramos-Alvarado, Molecular Dynamics Simulations of Wettability, Thermal Transport, and Interfacial Liquid Structuring at the Nanoscale in Polar Solid–Liquid Interfaces, ACS Appl. Nano Mater., 2021, 4, 3821–3832 CrossRef CAS.
- D. Alexeev, J. Chen, J. H. Walther, K. P. Giapis, P. Angelikopoulos and P. Koumoutsakos, Kapitza Resistance between Few-Layer Graphene and Water: Liquid Layering Effects, Nano Lett., 2015, 15, 5744–5749 CrossRef CAS PubMed.
- Y. Ma, Z. Zhang, J. Chen, K. Sääskilahti, S. Volz and J. Chen, Ordered water layers by interfacial charge decoration leading to an ultra-low Kapitza resistance between graphene and water, Carbon, 2018, 135, 263–269 CrossRef CAS.
- X. Peng, P. Jiang, Y. Ouyang, S. Lu, W. Ren and J. Chen, Reducing Kapitza resistance between graphene/water interface via interfacial superlattice structure, Nanotechnology, 2022, 33, 035707 CrossRef CAS PubMed.
- S. Li, Y. Chen, J. Zhao, C. Wang and N. Wei, Atomic structure causing an obvious difference in thermal conductance at the Pd–H2O interface: a molecular dynamics simulation, Nanoscale, 2020, 12, 17870–17879 RSC.
- S. Alosious, S. K. Kannam, S. P. Sathian and B. D. Todd, Effects of Electrostatic Interactions on Kapitza Resistance in Hexagonal Boron Nitride-Water Interfaces, Langmuir, 2022, 38, 8783–8793 CrossRef CAS PubMed.
- H. Han, S. Mérabia and F. Müller-Plathe, Thermal Transport at Solid–Liquid Interfaces: High Pressure Facilitates Heat Flow through Nonlocal Liquid Structuring, J. Phys. Chem. Lett., 2017, 8, 1946–1951 CrossRef CAS PubMed.
- S. Li, Y. Chen, Z. Li, J. Zhao and N. Wei, Role of hydrogen bonds in thermal conductance at the graphene oxide-H2O interface, Int. J. Heat Mass Transfer, 2022, 183, 122125 CrossRef CAS.
- B. Ramos-Alvarado, S. Kumar and G. P. Peterson, Solid–Liquid Thermal Transport and Its Relationship with Wettability and the Interfacial Liquid Structure, J. Phys. Chem. Lett., 2016, 7, 3497–3501 CrossRef CAS PubMed.
- B. Ramos-Alvarado and S. Kumar, Spectral Analysis of the Heat Flow Across Crystalline and Amorphous Si–Water Interfaces, J. Phys. Chem. C, 2017, 121, 11380–11389 CrossRef CAS.
- C. U. Gonzalez-Valle, S. Kumar and B. Ramos-Alvarado, Thermal Transport across SiC-Water Interfaces, ACS Appl. Mater. Interfaces, 2018, 10, 29179–29186 CrossRef CAS PubMed.
- C. U. Gonzalez-Valle and B. Ramos-Alvarado, Spectral mapping of thermal transport across SiC–water interfaces, Int. J. Heat Mass Transfer, 2019, 131, 645–653 CrossRef CAS.
- A. Anandakrishnan, B. Ramos-Alvarado, S. K. Kannam and S. P. Sathian, Effects of interfacial molecular mobility on thermal boundary conductance at solid–liquid interface, J. Chem. Phys., 2023, 158, 094710 CrossRef CAS PubMed.
- J. Chen, X. Xu, J. Zhou and B. Li, Interfacial thermal resistance: past, present, and future, Rev. Mod. Phys., 2022, 94, 25002 CrossRef CAS.
- C. Qian, Y. Wang, H. He, F. Huo, N. Wei and S. Zhang, Lower Limit of Interfacial Thermal Resistance across the Interface between an Imidazolium Ionic Liquid and Solid Surface, J. Phys. Chem. C, 2018, 122, 22194–22200 CrossRef CAS.
- C. Qian, B. Ding, Z. Wu, W. Ding, F. Huo, H. He, N. Wei, Y. Wang and X. Zhang, Ultralow Thermal Resistance across the Solid–Ionic Liquid Interface Caused by the Charge-Induced Ordered Ionic Layer, Ind. Eng. Chem. Res., 2019, 58, 20109–20115 CrossRef CAS.
- A. El-Rifai, S. Perumanath, M. K. Borg and R. Pillai, Unraveling the Regimes of Interfacial Thermal Conductance at a Solid/Liquid Interface, J. Phys. Chem. C, 2024, 128, 8408–8417 CrossRef CAS PubMed.
- T. Zhou, H. K. Chilukoti, Z. Wu and F. Müller-Plathe, Effect of Defects on the Interfacial Thermal Conductance betweenn-Heneicosane in Solid and Liquid Phases and a Graphene Monolayer, J. Phys. Chem. C, 2021, 125, 14149–14162 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al., LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017 Search PubMed.
- K. Sääskilahti, J. Oksanen, J. Tulkki and S. Volz, Spectral mapping of heat transfer mechanisms at liquid–solid interfaces, Phys. Rev. E, 2016, 93, 1–8 CrossRef PubMed.
- A. Giri, J. L. Braun and P. E. Hopkins, Implications of interfacial bond strength on the spectral contributions to thermal boundary conductance across solid, liquid, and gas interfaces: a molecular dynamics study, J. Phys. Chem. C, 2016, 120, 24847–24856 CrossRef CAS.
- M. Isaiev, S. Burian, L. Bulavin, M. Gradeck, F. Lemoine and K. Termentzidis, Efficient tuning of potential parameters for liquid–solid interactions, Mol. Simul., 2016, 42, 910–915 CrossRef CAS.
- P. B. Miranda, L. Xu, Y. R. Shen and M. Salmeron, Icelike water monolayer adsorbed on mica at room temperature, Phys. Rev. Lett., 1998, 81, 5876–5879 CrossRef CAS.
- P. Geysermans, D. Gorse and V. Pontikis, Molecular dynamics study of the solid–liquid interface, J. Chem. Phys., 2000, 113, 6382–6389 CrossRef CAS.
- M. F. Reedijk, J. Arsic, F. F. Hollander, S. A. de Vries and E. Vlieg, Liquid Order at the Interface of KDP Crystals with Water: evidence for Icelike Layers, Phys. Rev. Lett., 2003, 90, 4 Search PubMed.
- Y. Kauffmann, S. H. Oh, C. T. Koch, A. Hashibon, C. Scheu, M. Rühle and W. D. Kaplan, Quantitative analysis of layering and in-plane structural ordering at an alumina–aluminum solid–liquid interface, Acta Mater., 2011, 59, 4378–4386 CrossRef CAS.
- S. A. Deshmukh and S. K. Sankaranarayanan, Atomic scale characterization of interfacial water near an oxide surface using molecular dynamics simulations, Phys. Chem. Chem. Phys., 2012, 14, 15593–15605 RSC.
- C. U. Gonzalez-Valle, L. E. Paniagua-Guerra and B. Ramos-Alvarado, Implications of the Interface Modeling Approach on the Heat Transfer across Graphite-Water Interfaces, J. Phys. Chem. C, 2019, 123, 22311–22323 CrossRef CAS.
- D. Zhou, M. Zeng, J. Mi and C. Zhong, Theoretical study of phase transition, surface tension, and nucleation rate predictions for argon, J. Phys. Chem. B, 2011, 115, 57–63 CrossRef CAS PubMed.
- J. Israelachvili, Intermolecular and Surface Forces, 2011 Search PubMed.
- X. Geng, M. Yu, W. Zhang, Q. Liu, X. Yu and Y. Lu, Slip length and structure of liquid water flowing past atomistic smooth charged walls, Sci. Rep., 2019, 9, 18957 CrossRef CAS PubMed.
- V. Mandrolko, G. Castanet, S. Burian, Y. Grosu, L. Klochko, D. Lacroix and M. Isaiev, Features of the contact angle hysteresis at the nanoscale: a molecular dynamics insight, Phys. Fluids, 2024, 36, 052012 CrossRef CAS.
- J. Fan, J. De Coninck, H. Wu and F. Wang, Microscopic Origin of Capillary Force Balance at Contact Line, Phys. Rev. Lett., 2020, 124, 125502 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04768k |
| This journal is © the Owner Societies 2025 |