Host–guest geometry in paramagnetic cavitands elucidated by ¹⁹F electron-nuclear double resonance

Abstract

Elucidating structural information of supramolecular host–guest systems is pivotal for understanding molecular recognition and designing functional materials. This study explores the binding modes of fluorinated benzylamine guests in cyclodextrin-based paramagnetic cavitands, employing Gd(III)-capped cyclodextrins (Gd-α-CD and Gd-β-CD, comprising six and seven glucopyranoside units, respectively) and high-field ¹⁹F electron-nuclear double resonance (ENDOR). The ¹⁹F ENDOR spectra revealed distinct behaviors based on the fluorine position and cyclodextrin cavity size. For para-fluorinated benzylamine guests, Gd-β-CD displayed a bimodal distribution of Gd–F distances, corresponding to two distinct binding modes, whereas Gd-α-CD exhibited a single binding mode. In contrast, meta-fluorinated benzylamines demonstrated a single binding mode for both Gd-α-CD and Gd-β-CD, underscoring the influence of cavity size and fluorine substitution in the guest on binding specificity. ENDOR measurements performed at the EPR central transition of Gd(III) are generally expected to yield Gd–F distances without orientation-specific details. Surprisingly, in Gd-CDs systems, an unexpected orientation selectivity was observed, enabling the extraction of both Gd–F distances and orientation of the guest molecule relative to the cavitand's Gd(III) zero-field splitting (ZFS) tensor. This two-faceted capability of ¹⁹F-ENDOR allows for determining host–guest complexation geometry and provides insights into ZFS orientation within the cavitand structure.

---

Introduction

Supramolecular host–guest chemistry involves the interaction between two or more molecules, where one (the host) provides a suitable environment to accommodate the other (the guest) through non-covalent interactions. Determining structural parameters in host–guest supramolecular systems is paramount for advancing the understanding of molecular recognition, self-assembly, and the design of functional materials.^1–3 Various techniques, including X-ray crystallography,^4–6 NMR spectroscopy,^7,8 and computational modeling,^9,10 have been employed routinely to probe these structural aspects. However, challenges remain in obtaining precise structural details, especially for systems that are flexible, dynamic or do not readily crystallize. Current methods may struggle with resolving transient states and weak interactions. These limitations call for developing new analytical tools that can accurately extract structural information and enable additional insights into the behavior of host–guest systems. Recently, a new approach for studying supramolecular host–guest exchange kinetics called guest exchange saturation transfer (GEST) was proposed. It employs the CEST (chemical exchange saturation transfer) principles along with the attachment of a paramagnetic lanthanide to the host (para-GEST) for studying ¹⁹F-labeled guest molecules that exchange between their inner-cavitand complex states and their free state in the solution.^11–14 Recently, such a system enabled multiplexed information encoding and multicolor displays of supramolecular systems in MRI without needing a light source. This was based on cyclodextrins functionalization with different lanthanides and various fluorine-containing guests, giving different frequency shifts that are translated to different colors.¹⁴

The application of para-GEST to investigate host–guest systems of lanthanide-capped α-cyclodextrin (Ln-α-CD) or Ln-β-CD hosts^14,15 with fluorobenzylamine (FBA) guests reported that the guest exists in at least two distinct states when accommodated within Ln-β-CD but only one in Ln-α-CD. Nevertheless, the structural basis for the two distinct populations allowed by the larger cavitand Ln-β-CD, remained unknown. Here, we present a new application of ¹⁹F electron-nuclear double resonance (ENDOR) aimed at the structural elucidation of these cyclodextrin-based host–guest systems, the chemical structures of which are shown in Fig. 1. We show that by applying ¹⁹F ENDOR and choosing Gd(III) as the paramagnetic lanthanide to form the paramagnetic cavitands Gd-α-CD and Gd-β-CD (Fig. 1A), it is possible to obtain the missing structural information.

Fig. 1 (A) Schematic drawing of the host–guest complexes studied and the chemical structures of CD hosts. The dotted lines represent potential complexation of the Gd(III). (B) Chemical structures of studied guests: 4-FBA, 4-CF₃BA, 3-FBA, and 3,5-diFBA.

¹⁹F ENDOR is an emerging effective tool for structural studies of biomacromolecules. It involves a spin label attached to the molecule of interest, and the distance between this spin label and a ¹⁹F nucleus on an amino-acid residue is measured.¹⁶ The use of ¹⁹F nuclei offers high sensitivity due to its high gyromagnetic ratio, approaching that of ¹H, and excellent selectivity, as ¹⁹F nuclei are absent in biomolecules, unlike the widely abundant ¹H nuclei. To date, a range of potential spin labels for ¹⁹F ENDOR distance determination has been suggested, including nitroxide^16–19 and trityl^20,21 spin labels, intrinsic tyrosyl radicals,²² as well as Gd(III)^23–25 and Cu(II)²⁶ complexes. These spin labels were used to explore the structural aspects of nucleic acids and proteins. The performance of various labels was also compared.²⁷ Gd(III) based spin labels have also been demonstrated to study structural details of proteins in cells.²⁴

The application of the ¹⁹F ENDOR technique is natural for the present system, as both the paramagnetic ion incorporated into the host structure and one or more fluorine atoms in the guest structure are intrinsic and no spin labeling is required. Therefore, data interpretation is more straightforward, as it does not involve factoring in possible structural changes resulting from the introduction of the spin label. In addition, this method allows studying host–guest systems with low binding constants as it is “blind” to the free guest which can be added in large excess without interfering with the analysis. For example, a 10 mM background concentration of the non-bound guest, taken in 50-fold excess to Gd(III), results in the average distance between Gd(III) and F of approximately 3 nm, which results in negligible matrix ENDOR signal as compared to the bound guest.

The two techniques, namely, ¹⁹F ENDOR and para-GEST NMR, should be considered complementary rather than competing. Both measurements are performed in comparable complex concentrations,¹⁵ and are sensitive to different binding modes of the guest. However, ENDOR is performed in the frozen state and provides additional geometrical information on the host–guest complexation, whereas para-GEST measurements are performed at ambient temperatures and can be used to obtain information on the host–guest complexation kinetics.

Gd(III) ion has 7 unpaired electrons with an electron spin of S = 7/2 and a relatively small zero-field splitting (ZFS). Accordingly, at a high magnetic field and low temperature (frozen solutions), its EPR spectrum comprises a relatively narrow peak, corresponding to the central |−1/2〉 ↔ |+1/2〉 transition (CT), superimposed on a broad, usually featureless background corresponding to all other transitions. The CT yields a narrow spectrum because its width depends on the ZFS only to second order, i.e. it is proportional to D²/ν₀, where D is the ZFS axial component, and ν₀ is the spectrometer frequency.²⁸ Gd(III) complexes in frozen solutions usually feature large distributions of the D and E parameters of ZFS, with E/D denoting the deviation from axial symmetry, and the distribution of the orientations of ZFS tensors within the individual complexes.^29,30 These broad distributions are expected to eliminate the so-called orientation selection effect, particularly for the CT. This implies that in pulse EPR experiments, setting the magnetic field anywhere within the CT would excite all possible orientations of Gd(III) complexes with respect to the magnetic field, also for a limited excitation bandwidth of 30–50 MHz.^23,24,27,31 There are some exceptions of Gd(III) spin labels, which featured a large ZFS with a broad CT, that exhibited a subtle ¹H orientation selection. The spectra were difficult to analyze due to the many protons present.³² In contrast, we observed strong orientation selection in the ¹⁹F ENDOR of the studied CD systems. In other words, selective excitation of particular molecular orientations of the Gd(III) chelates is also possible for the CT. This, in turn, provides valuable insights into the ZFS orientation within the molecule – information that has been challenging to obtain experimentally so far.

We begin our study with meta-substituted benzylamine guests in both hosts and para-substituted guests in Gd-α-CD, exhibiting only one population of ¹⁹F–Gd(III) distances. Using these results, we establish the data analysis approach for orientation selection in Gd(III). Then, we describe para-substituted guests in Gd-β-CD, which exhibit two populations of ¹⁹F–Gd(III) distances. We conclude by determining the position and orientation of the fluorinated guests within the two types of CD cages, as derived from the ENDOR data and the orientation of the ZFS principal axes system in the host structure.

Theoretical background

The spin Hamiltonian describing Gd(III) is given by:³³where the first term corresponds to the Zeeman interaction and the other two describe the zero field splitting (ZFS). D is the axial component of the ZFS tensor, and E represents its rhombicity. In the standard convention, the components of the ZFS tensor are given by:³³

Conventionally, the principal components of ZFS principal components are defined as follows:

|D_X| ≤ |D_Y| ≤ |D_Z| (3)

In the presence of a broad distribution of ZFS parameters, reordering the assignment of ZFS principal values according to eqn (5) for each distribution component might lead to different orientations of ZFS axes in the molecular frame. To avoid this, in the present work, D and E are assumed to be formal parameters having independent Gaussian distributions. Then, the ZFS principal components are calculated from D and E using eqn (2), and even if expression (3) is not fulfilled, no reordering of the ZFS axes is performed. In eqn (1) the terms corresponding to the hyperfine interaction are omitted because their contribution is small, and does not influence the EPR spectrum shape.

The ENDOR resonance frequencies for the allowed NMR transitions (|Δm_I| = 1) are given by:³⁴

ν(β,m_S) = ν_I − m_S·a(β) (4)

where a is the hyperfine coupling and β is the angle between the magnetic field direction and the vector connecting the Gd(III) ion and the ¹⁹F nucleus. As we deal with long Gd–F distances in non-conjugated systems, the hyperfine coupling can be assumed to be purely dipolar according to:where μ₀ is vacuum magnetic permeability, g_e and g_n are electron and nuclear g-values, μ_B and μ_N are Bohr magneton and nuclear magneton, respectively, h is the Planck constant, and r is the Gd–F distance.

The geometrical conventions used in the present work are illustrated in Scheme 1. Here, Gd and F represent the corresponding atoms, the black solid lines correspond to the principal axes of the ZFS tensor, the red arrow shows the direction of the external magnetic field, and the green arrow connects the Gd and F atoms, and represents the radius-vector of the electron-nuclear dipolar interaction. The Euler angles (φ₀, θ₀, 0) give the orientation of the magnetic field in the ZFS frame, and so are the angles (γ, ρ, 0) for the electron-nuclear dipolar interaction (Gd–F) frame. θ₀ and γ are the polar angles and φ₀ and ρ are the azimuthal angles.

Scheme 1 Definitions of angles used in this work. D_X, D_Y and D_Z are the principal axes of the (molecular) ZFS frame, B₀ is the direction of the spectrometer's magnetic field, and the green arrow is the direction of Gd–F vector in the molecular frame.

Pulse ENDOR measurements are carried out by setting the magnetic field to a position within the EPR spectrum and applying the relevant pulse sequence. The anisotropic line shape of the EPR spectra determines the range of θ₀ and φ₀ angles that contribute to the ENDOR spectrum at a particular magnetic field. The contributing orientations of the Gd–F vectors with respect to the external magnetic field are given by:

cos β = cos ρ sin γ cos φ₀ sin θ₀ + sin ρ sin γ sin φ₀ sin θ₀ + cos γ cos θ₀ (6)

Without orientation selection, all possible θ₀ and φ₀ values contribute equally, generating the classical ENDOR powder patterns. The angle β determines the apparent hyperfine splitting according to eqn (5), which, in turn, gives the resonant ENDOR frequencies according to eqn (4). The intensities of the Mims ENDOR spectra depend on the hyperfine interaction and the experimentally chosen delay τ between the first two pulses in the pulse sequence (see Experimental details), according to the well-known expression:³⁵

F_ENDOR ∝ sin²[π·a(β)τ] (7)

where F_ENDOR is proportional to the ENDOR spectrum intensity.

Materials and methods

Sample preparation

The syntheses of the functionalized cyclodextrin Gd(III) containing cavitands and their host–guest complexes were carried out as described previously.¹⁵ The host–guest complexes were prepared in D₂O – glycerol-d₈ solution at 50× excess of guest molecules at a final host concentration of 260 μM. For this, the D₂O solutions containing calculated amounts of the host and the guest were combined, and the resulting mixture was stirred overnight at room temperature and then filtered. Glycerol-d₈ (25–30% v/v) was added, and the solutions were placed into 0.60 mm I. D. fused silica capillaries sealed with crytoseal.

Spectroscopic measurements

Pulsed EPR and ENDOR measurements were performed using two pulsed home-built W-band EPR spectrometers equipped with cylindrical TE₀₁₁ cavities and Helmholtz radiofrequency (RF) coils, as described earlier.³⁶ The first spectrometer (referred to as 1) has a solenoid superconducting magnet (Cryomagnetics, Inc.), a 3 W pulsed microwave power amplifier (QPP95013530, Quinstar), and a pulsed 2 kW RF amplifier (BT02000-GammaS, TOMCO). The second spectrometer (referred to as 2) has a 0–5 T cryogen-free magnet with an integrated variable temperature unit and 300 mT sweep coil (J3678, Cryogenic Ltd),³⁷ and is equipped with a 2 W pulsed microwave power amplifier (QPP95023330-ZW1, Quinstar) and a 1 kW RF amplifier (3446 Herley-AMT). Identical sample tubes were used in both spectrometers.

Echo-detected electron paramagnetic resonance (ED-EPR) spectra were recorded at 10 K using the Hahn echo (π/2 − τ − π − τ − echo) sequence. Mims ENDOR spectra were recorded at 10–11 K using the sequence π/2 − τ − π/2 − T(π_RF) − π/2 − τ − echo − [τ₂ − π − τ₂ − echo]_n with a four-step phase cycle and a Carr–Purcell–Meiboom–Gill (CPMG) detection train at the end to enhance the signal-to-noise ratio.³⁸ We used three to five CPMG echoes with τ₂ = 600 ns for detection. Each echo was integrated over a 20 ns window, optimized for the best signal-to-noise ratio. Random sampling of RF was employed,³⁹ with 5–10 shots acquired per frequency point in each scan. Microwave power was adjusted to result in a π pulse of 28–32 ns, using the Rabi nutation sequence, t_nut − t_wait − π/2 − τ − π − τ − echo (t_nut was varied; t_wait was chosen such as to let for the decay of the transverse magnetization). RF power was adjusted to yield the desired π_RF pulse length, using a Rabi nutation sequence π/2 − τ − π/2 − T(t_RF) − π/2 − τ − echo, with a constant mixing time T of 100 μs and varying RF pulse length, t_RF. The RF pulse length was set to be 35–50 μs. The mixing time T in the Mims ENDOR experiment was set to be 2–5 μs longer than the RF pulse length.

Simulations of ED EPR and ENDOR spectra

ED-EPR spectral simulations were carried out using a previously published approach and home-written software based on the spin Hamiltonian given by eqn (1).²⁵

The Boltzmann population of the electron spin levels at T = 4.5 K and B₀ = 3.4 T was taken into account, and the flip angle correction was implemented to compensate for the different nutation frequencies of the different electron spin transitions as described previously.²⁵ For the ED-EPR spectral simulations, uncorrelated Gaussian distributions of the ZFS parameters D and E were assumed, with the probability densities given by

where D₀ and E₀ are the distribution centers and ΔD and ΔE are distribution widths, and no further reassignment of the ZFS indices (X, Y, Z) was performed. Simulations were also carried out under the assumption of Gaussian distributions of D and E/D. This way of parametrization results in a correlation of the distributions of D and E. It yielded an equally good description of the ED-EPR spectra but failed to reproduce the observed ENDOR spectra in the presence of orientation selection. The low-temperature and the high-field allows determining the absolute signs of D and E because of the substantial difference in electron spin level populations.

The ENDOR spectral simulations were carried out in two steps. First, the ED-EPR spectrum was simulated using the above-described approaches, and for each magnetic field at which ENDOR spectra were recorded, the excitation probability of each of the orientations (θ₀,φ₀) was determined. For the sake of simplicity, the bandwidth of the ENDOR MW pulses was assumed to be infinitely small. Then, these probabilities were used to calculate the powder patterns of ENDOR spectra using eqn (4)–(7). The ENDOR spectra measured at different fields were jointly simulated and the fit parameters were: the hyperfine splitting constant, |a_⊥|, ENDOR line width parameters, and the angles γ and ρ that define the orientation of Gd–F axis in the ZFS reference frame (Scheme 1). The ENDOR line shape was assumed Lorentzian, with the shape of the individual line given by:

where Δν is the frequency offset, and Δ_L is the line width.

The optimal fit values of the varied parameters were found using the nonlinear least-squares algorithm NL2SOL, and the errors were estimated from the corresponding correlation matrices.⁴⁰

Because of the orthorhombic symmetry of the ZFS tensor, the angles ±θ₀, ±φ₀, as well as 90° ± θ₀, 90° ± φ₀ cannot be distinguished, and the same holds for the angles ±ρ, ±γ and 90° ± ρ, 90° ± γ. Thus, for consistency, the angles are listed in the interval from 0 to 90°.

Results

ED EPR spectra

The W-band echo-detected EPR (ED-EPR) spectra of Gd-α-CD and Gd-β-CD in the absence of a guest and with several fluorinated benzylamine derivatives (4-CF₃BA, 4-FBA, 3,5-diFBA, 3-FBA), are presented in Fig. 2. The spectra are characteristic of Gd(III) at a high magnetic field and Fig. 2A and B focus on the CT, revealing asymmetric shoulders both for Gd-α-CD and Gd-β-CD. The spectra of the two cages are generally similar, with that of Gd-β-CD having a slightly wider CT, as shown by the comparison between the CT of the two hosts with 3-FBA in Fig. 2C. Interestingly, the spectra of the empty hosts have the same features as those with the guests, indicating that this line shape does not originate from host–guest interactions, but is an inherent property of the ZFS of the capping Gd(III).

Fig. 2 (A) and (B) ED-EPR spectra (10 K) of the CT region of (A) Gd-α-CD and (B) Gd-β-CD with various guests as indicated on each panel. (C) Comparison of the ED-EPR spectra of Gd-α-CD and Gd-β-CD with 3-FBA. (D) Full range spectra of 4-CF₃BA/Gd-α-CD (upper panel) and 3-FBA/Gd-β-CD (lower panel), measured at 4.5 K. Black lines – experimental spectra, red lines – simulation, colored lines show the contributions of individual electron spin transitions to the overall spectrum. Simulation parameters are listed in Table 1.

The spectra of 4-CF₃BA/Gd-α-CD and 3-FBA/Gd-β-CD were chosen as representative of Gd(III) in α- and β-CD hosts and wide magnetic field range ED-EPR spectra, measured at 4.5 K, are shown in Fig. 2D. The low temperature was chosen to enhance the contributions of transitions other than the CT. These were simulated to extract the distributions of D and E, which are listed in Table 1. The distributions consist of two components; the first, comprising 25–30% of the population, is characterized by D and E with relatively broad Gaussian distributions. As shown previously,⁴¹ by reordering the axes of the ZFS tensor to fulfil eqn (3), this distribution can be reformulated in an alternative way that is close to that described by Raitsimring et al.⁴² This broad distribution of ZFS values is characteristic of widely used MRI agents and Gd(III) containing spin labels. The centers of both the D and E distributions are significantly larger for Gd-β-CD. The second contribution, which corresponds to the majority (70–75%) of the complexes, is similar for both Gd-α-CD and Gd-β-CD, and is characterized by a broader distribution of D values and a relatively narrow distribution of E values. This part of the ZFS parameters distribution is responsible for the apparent shoulders in the full-range ED-EPR spectra observed in Fig. 2D. This contrasts the ED-EPR spectra of Gd(III) with cyclene chelates, such as DOTA or DO3A, which exhibit featureless backgrounds.²⁹ This relatively narrow distribution of E can result from the binding to the CD scaffold, leading to a more restricted Gd(III) coordination sphere structure.

Table 1 Gaussian distributions of D and E obtained from simulations of the ED-EPR spectra of Gd-α-CD and Gd-β-CD

Distribution	Center, D0 (E0), MHz	Width, ΔD (ΔE), MHz	Relative fraction
4-CF3BA/Gd-α-CD
D 1	1210 ± 70	570 ± 100	(32 ± 10)%
E 1	675 ± 50	590 ± 60
D 2	−1560 ± 30	1010 ± 40	(68 ± 10)%
E 2	−460 ± 10	0 ± 200
3-FBA/Gd-β-CD
D 1	1600 ± 100	500 ± 100	(24 ± 3)%
E 1	930 ± 200	300 ± 30
D 2	−1550 ± 40	900 ± 80	(76 ± 3)%
E 2	−522 ± 10	0 ± 200

---

¹⁹F Mims ENDOR measurements.
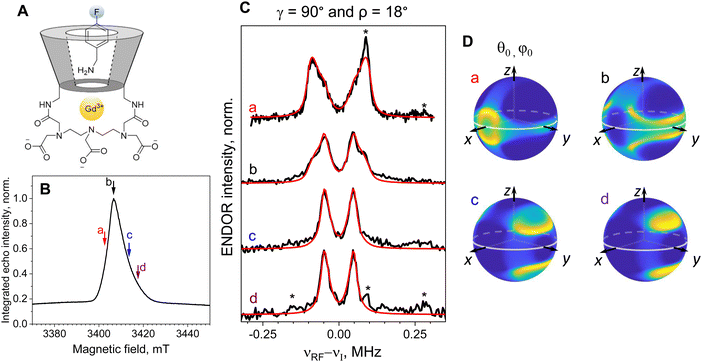
3-FBA,4-FBA,4-CF₃BA/Gd-α-CD, 3-FBA,3,5-diFBA/Gd-β-CD: data analysis in the presence of orientation selection. The relatively broad CT (Fig. S1, ESI†) allowed recording ENDOR spectra at different magnetic fields within the CT as shown for 3-FBA/Gd-β-CD (Fig. 3A and B) and the spectra reveal clear orientation selection effects (Fig. 3C). Measurements at positions a and c, yielded doublets with distinct splittings of 255 kHz and 140 kHz, respectively, and at the position b, a superposition of the two splittings was observed (Fig. 3C). The approximate two-fold relation between the splittings observed at different fields suggests that they correspond to a_⊥ (β = 90°) and a_‖ (β = 0°), respectively. Namely, excitation at position a selects Gd–F vectors parallel to the external magnetic field, B₀, whereas excitation at position c selects mostly Gd–F vectors perpendicular to B₀.

Fig. 3 (A) A schematic illustration of 3-FBA/Gd-β-CD. (B) The central transition region of the corresponding ED-EPR spectrum (10 K), with the positions at which ENDOR spectra were recorded. (C) Experimental ¹⁹F Mims ENDOR spectra recorded at −4 mT (a), 0 mT (b) and +11 mT (c) (black) and their simulations (in red); dashed vertical lines correspond to the two observed splittings, a_⊥ and a_‖. The angles γ and ρ, determined from the simulation are indicated above the panel. (D) Heat plots showing the selected orientations θ₀, φ₀ at field positions a, b, and c. An inter-pulse delay τ = 1 μs was used in the Mims sequence.

The assignment of the two doublets to a_‖ and a_⊥ was further corroborated by the ENDOR spectrum measured outside the CT at position d. A single distance should give rise to ENDOR peaks at positions , , 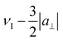, , , , and (see eqn (4)), precisely as observed in the experiment (Fig. 4). The fact that ENDOR peaks corresponding to the parallel and perpendicular orientations of Gd–F vector for Gd(III) |m_S| ≠ 1/2 are situated further away from the Larmor frequency compared to the CT was previously utilized to enhance the resolution and increase the distances accessible by Gd–¹⁹F ENDOR distance measurements.²⁵

Fig. 4 The ¹⁹F-ENDOR spectrum of 3-FBA/Gd-β-CD, recorded 8 K and at field position d (see Fig. 3B). Singularities corresponding to parallel and perpendicular orientations of the corresponding m_S → m_S + 1 transitions are shown with dashed lines. Simulation with parameters given in Table 2 are shown in brown.

The peaks observed in Fig. 4 correspond to m_S in the range of −7/2 to −1/2, (eqn (4)), the signals with positive m_S are not observed because the corresponding electron spin levels are poorly populated at 8 K.

To account quantitatively for the observed orientation selection, we carried out spectral simulations. Briefly, we used the simulations of the ED-EPR spectrum to determine the orientations θ₀ and φ₀ of the magnetic field B₀ relative to the molecular ZFS frame that are preferentially excited by the MW pulses at each field position (shown as heat plots in Fig. 3D, see Scheme 1 for angle definitions) and used them to calculate the ENDOR spectra. The best-fit simulations for positions a–c are shown in Fig. 3C, and the parameters are given in Table 2. The determined γ and ρ angles mean that the Gd–F vector makes an angle of 29° with the D_X axis. To the best of our knowledge, this is the first time that there was sufficient experimental data to determine the orientation of the ZFS in a Gd(III) complex relative to a known structural feature in a frozen solution. The same approach can be used to simulate the spectrum recorded off the CT (Fig. 4, brown line); in this case, all electron spin transitions other than CT were taken into account, and their relative contributions were determined from the simulations of the ED-EPR spectra. The simulation agrees with the experiment, and the set of optimal parameters found is close to those obtained from the CT spectra (Table 2).

Table 2 Summary of Gd–F hyperfine couplings and distances for all guests and hosts studied. For each guest, the first row corresponds to simulation of the field dependent ENDOR spectra with orientation selection, and the second row corresponds to simulation of a single ENDOR spectrum recorded at the position of the maximum of the CT, neglecting orientation selection. Δ_L – Lorentzian ENDOR linewidth used for the simulation

Guest	|a⊥|, kHz Gd-α-CD	r, Å Gd-α-CD	Δ L, kHz Gd-α-CD	γ, ρ, deg Gd-α-CD	|a⊥|, kHz Gd-β-CD	r, Å Gd-β-CD	Δ L, kHz Gd-β-CD	γ, ρ, deg. Gd-β-CD
a Obtained from simulations of field-dependent ENDOR spectra with the explicit account of orientation selection. b Obtained from simulation of a single ENDOR spectrum recorded at the position of the maximum of the CT. c Obtained from simulation of an ENDOR spectrum recorded at the field position off CT (position d in Fig. 3B). d No orientation selection is assumed for short-distance admixture. e Obtained from simulation of a series of ENDOR spectra recorded at the position of the maximum of the CT at various values of inter-pulse delay τ (see Fig. S7, ESI).
4-FBA	102^a	9.0^a	14	90 ± 8, 18 ± 3
	107^b (95%)	8.8^b (95%)	27		118^b (75%)	8.6^b (75%)	21
	573^b (5%)	5.1^b (5%)	36		575^b (25%)	5.1^b (25%)	87
4-CF3 FBA	85^a (95%)	9.6^a (95%)	19	68 ± 16, 24 ± 10
	210^a (5%)	7.1^a (5%)	74	Isotropic^d
	122^b (97%)	8.5^b (97%)	41		93^b (80%)	9.3 (80%)	29
	374^b (3%)	5.8^b (3%)	27		374^b (20%)	5.8 (20%)	64
3-FBA	138^a	8.1	15	73 ± 6, 23 ± 4	155^a	7.8	21	73 ± 5, 24 ± 3
					146^c	8.0	40	74 ± 4, 42 ± 5
	147^b	8.0	34		160^b	7.8	27
3,5-diFBA					157^a	7.8	28	75 ± 5, 26 ± 3
	148^b	8.0	23		160^b	7.8	32
	140^e	8.1	21

---

The ENDOR spectra of 3,5-diFBA/Gd-β-CD were very similar to those of 3-FBA/Gd-β-CD, as illustrated in Fig. S2 (ESI†). As expected, simulations (Fig. S3, ESI†) yielded parameters very close to those obtained for 3-FBA as listed in Table 2 and the differences are within experimental error. Similar fits could be generated with γ ≈ 60° and ρ ≈ 17°; however, these angles do not explain the identical ENDOR spectra of 3-FBA and 3,5-diFBA (see Discussion). The orientation selection behavior described above is not exclusive to Gd-β-CD. We observed it also for 3-FBA/Gd-α-CD (Fig. S4, ESI,†Table 2) and 4-FBA/Gd-α-CD as illustrated in Fig. 5. Here, because the ZFS is smaller, some detectable contributions of electron spin transitions other than the CT are excited (e.g., |−3/2〉 ↔ |−1/2〉), which leads to the appearance of the additional peaks at and in ENDOR spectra recorded at positions a and d, and the asymmetric enhancement of the peak corresponding to in the spectrum recorded at position a (Fig. 5C). Otherwise, these spectra demonstrate a similar behavior to the described above. They can be simulated similarly, and the parameters obtained are listed in Table 2. Here, the Gd–F vector seems to be even closer to the D_X axis than for the 3-FBA and 3,5-FBA guests and it lies in the D_X–D_Y plane.

Fig. 5 (A) A schematic illustration of 4-FBA/Gd-α-CD. (B) The central transition region of the ED-EPR spectrum (10 K), with the positions at which ENDOR spectra were recorded. (C) Experimental ¹⁹F Mims ENDOR spectra recorded at −4 mT (a), 0 mT (b), +7 mT (c) and +11 mT (d) (black) and their simulations (in red). Asterisks indicate contributions in the ENDOR spectra from the excitation of non-CT electron spin manifolds. (D) Heat plots showing the selected orientations θ₀, φ₀ at a–d. The inter-pulse delay τ = 2 μs was used in the Mims sequence.

The orientation selection ENDOR spectra of 4-CF₃BA/Gd-α-CD are shown in (Fig. S5, ESI†). In this case, the spectra are superimposed on a broad background, which could be accounted for as an admixture of a small population (∼5%) with a shorter Gd–F distance (7 Å), and all simulation parameters are listed in Table 2.

4-FBA,CF₃BA/Gd-β-CD, 3,5-diFBA/Gd-α-CD: data analysis neglecting orientation selection. While the orientation selection can reveal geometrical details, it requires simulations of the ED-EPR spectra and joint simulations of a set of ENDOR spectra with more fitting parameters, as discussed above. When there are several binding modes of the guest having different Gd–F distances or broad Gd–F distance distributions, the experimental spectra may not contain sufficiently resolved features to determine all the geometrical parameters. In this case, orientation selection analysis is impractical. Our analysis of the presented examples above shows that measurements at the maximum of the CT peak led to the excitation of many different orientations of B₀, and the resulting ENDOR spectrum is close to the powder pattern where all possible orientations of the Gd–F vector with respect to B₀ contribute. Therefore, the spectra recorded at this position can be simulated neglecting orientation selection effects. This is illustrated in Fig. S6 (ESI†) for 3-FBA, 3,5-diFBA/Gd-β-CD, where the two approaches of spectral simulations are compared. In the first one, the field-dependent ENDOR spectra are jointly simulated with orientation selection. In the second one, only the spectrum recorded at the maximum of the CT is simulated, neglecting orientation selection effects. While the latter produced a somewhat worse fit, the Gd–F distances obtained were essentially the same, considering the experimental error. This justifies using a single ENDOR spectrum recorded at the maximum of the Gd(III) CT to extract Gd–F distances. The reliability of this approach can be further strengthened by recording ENDOR spectra with a set of different values of the inter-pulse delay, τ, and then simulating them jointly (Fig. S7, ESI†). The behavior of 3-FBA, 3,5-diFBA/Gd-α-CD was similar to that of Gd-β-CD as shown in Fig. 6A, presenting ¹⁹F doublet splittings of around 0.135 MHz and two clear shoulders with a splitting of ∼0.25 MHz assigned to |a_⊥| and |a_‖|. Simulations carried out as described above are shown in Fig. S8 (ESI†), and the best-fit parameters are given in Table 2. Notably, the line widths obtained from simulation neglecting orientation selection are systematically larger than those obtained with orientation selection. In the former case, the larger line width compensates for inaccuracies from neglecting orientation selection.

Fig. 6 ¹⁹F Mims ENDOR spectra of Gd-α-CD (black) and Gd-β-CD (red) with (A) 3-FBA (top) and 3,5-diFBA (bottom) and (B) 4-FBA (top) and 4CF₃-BA (bottom). The inter-pulse delay τ = 1 μs was used in the Mims sequence. a_⊥ and a_‖ in panel (A) reflect the perpendicular and parallel singularities of the powder pattern, and a_1,⊥ and a_2,⊥ in panel (B) correspond to splittings due to different electron-nuclear distances.

The spectra of 4-FBA in both hosts (Fig. 6B, top) recorded at the peak of the CT feature a doublet with a splitting of 0.11–0.12 MHz. An additional doublet with broader lines and a splitting of ∼0.6 MHz appears for Gd-β-CD only, confirming the presence of two 4-FBA/Gd-β-CD populations,¹⁵ with Gd–F distances of 8.5–8.8 Å and 5.1 Å derived from the ¹⁹F doublet splitting. We observed the same behavior for 4-CF₃BA, where a doublet with a splitting of 0.12 MHz appeared for both Gd-α-CD and Gd-β-CD, with an additional doublet for Gd-β-CD with a 0.36 MHz splitting (Fig. 6B, bottom), corresponding to distances of 9.3 Å and 5.8 Å respectively. Simulation of these spectra was carried out neglecting orientation selection (Fig. S9, ESI†), yielding a population of 20–25% for the short distance. The relative intensity of this doublet in the spectrum seems much larger, and this is a manifestation of the dramatic growth of the Mims ENDOR efficiency with 1/r⁶.²³ For 4-CF₃BA,4-FBA/Gd-α-CD, the broad background at the wings of the ENDOR spectra revealed the presence of 3–5% complexes with short Gd–F distances. To increase the stability of fit in the presence of such a minor contribution of shorter distance, the short distance was assumed to be the same for the α- and β-host. The line widths obtained for the minor short-distance components of the spectra are notably larger than those for the longer-distance components. A plausible reason for this is that in this range of electron-nuclear distances, even the slightest variations of distance due to conformational freedom of the guest result in a significant change of the hyperfine splitting, proportional to 1/r³.

Discussion

We summarize the experimental observations as follows (see Table 2): (i) The guests 3-FBA and 3,5-diFBA exhibited the same spectral behavior in both hosts, revealing the same single binding mode. Furthermore, the Gd(III)–F distances for ¹⁹F in positions 3 and 5 are the same, implying their symmetry about the axis that connects the Gd(III) and the para position in the benzyl ring, such that a rotation or a 180° flip about the C₁–C₇ axis (see Fig. 7) does not alter the ENDOR spectra. (ii) The behavior of 4-FBA and 4-CF₃BA clearly differs between Gd-α-CD and Gd-β-CD. In both cases, two populations are observed, a major one consistent with Gd(III)–F distances of the other two guests and a minor one with a shorter distance that indicates a very different position in the host. While for Gd-β-CD, this population is significant, 20–25%, for Gd-α-CD, it is only 3–5%.

Fig. 7 (A) Gd(III) coordination scheme with 3- and 4-FBA in the host–guest complex. The blue arrows designate the ZFS principal axes, and the dashed lines outline the plane of the guest's phenyl ring. Angles ρ, γ, corresponding to the 4-FBA guest, are added for illustration. (B) A structure of 4-FBA/Gd-α-CD that is consistent with geometrical findings inferred from ¹⁹F ENDOR measurements. Carbon atoms are shown in dark-gray on the CD backbone of the host, in green on the DTPA bridge of the host, and cyan on the structure of the guest. The gray plane corresponds to the plane where the D_Y and D_Z axes of Gd(III) ZFS tensor are situated. Two panels correspond to two mutually orthogonal viewpoints. PyMOL software (https://www.pymol.org/) was used for preparing the figure.

The position of the guest in the host

Analysis of the Gd–¹⁹F distances derived from the ENDOR measurements allowed us to position the guest within the host. It revealed that the amine group is close to Gd(III) as shown in Fig. 3A and 5A, and as suggested earlier based on NMR data.¹⁵ In Fig. 7A we show the structure of the guest molecule with two F atoms in 3- (m, meta) or 4- (p, para) position, including the Gd(III) ion position. Placing the Gd(III) ion on the C₁–C₄ axis with a Gd–N distance of 2.7 Å⁴³ results in a Gd–F distances of r(Gd–p-F) = 9.1 Å, r(Gd–m-F) = 8.2 Å and a p-F–Gd–m-F angle of 17°. This gives a remarkable agreement with the experimental values of 9.0 Å, 8.0 Å and 18°, respectively. For 4-CF₃BA this structure gives r(Gd–F) = 9.9 Å, which, again, agrees well with the experimental distance of 9.6 Å. The picture outlined above is summarized in the assembly structure shown in Fig. 7B. Here, we used the previously published DFT-calculated model of Dy-α-CD¹⁵ as an analog for Gd-α-CD. We place the 4-FBA guest based on the experimental parameters for the Gd-guest geometry, as discussed and shown in Fig. 7A.

Interestingly, for all studied guests, the distances of the major populations tend to be slightly shorter for the 7-member ring (Gd-β-CD), indicating a somewhat shorter Gd(III)–N distance, implying that the guest is located deeper in the host cavity, afforded by the wider cavity. Provided that the interaction between the lanthanide and the nitrogen-centered ligands is predominantly electrostatic,⁴⁴ this indicates a stronger Gd–N complexation in the case of Gd-β-CD.

Next, we address the minor population observed for 4-FBA,4-CF₃BA/Gd-β-CD, which features a short distance of ∼5–6 Å. According to the literature data on CD structures and DFT calculations of the empty complexes under study,¹⁵ the diameter of β-CD is 6.0–6.5 Å, that of α-CD is 4.7–5.3 Å,⁴⁵ and the cavity height of the functionalized CD is ∼5 Å. The length of 4-CF₃BA, the longest guest, is ∼8 Å; therefore, a highly tilted orientation of the guest with a Gd(III)–F distance of ∼5 Å seems plausible for β-CD but not for α-CD. Such a tilted guest arrangement is consistent with a longer Gd–F distance of the minor population for 4-CF₃BA than that for 4-FBA.

A remaining question is why the tilted orientation is not observed for 3-FBA and 3,5-diFBA/Gd-β-CD, which should be possible based on space considerations. Here, we speculate that hydrogen bonding and electrostatic interaction between the fluorine and the host stabilize the structure given in Fig. 7. In addition, the thermodynamics of guest–host complexation also includes excluding water molecules from the host cavity, which is associated with the increase of enthalpy and decrease in entropy of the whole system.⁴⁶ A combination of these factors may underlie the experimentally observed bimodal complexation of para-substituted guests, instead of a single-mode complexation of the meta-substituted ones.

The ZFS orientation in the complex

The angles obtained from ¹⁹F ENDOR simulations indicate that the C₁–C₄–Gd axis lies in the D_X–D_Y plane of the ZFS, making an angle ρ of ∼18–29° with the D_X axis. The plane of the guest's phenyl ring (outlined by dashed lines in Fig. 7A) is perpendicular to the D_X–D_Y plane of the ZFS and comprises the D_Z axis. Such a geometry is based on the fact that the ¹⁹F ENDOR spectra for 3-FBA and 3,5-diFBA guests are the same.

Aligning the D_X axis along the line connecting the Gd atom in the host with the nitrogen atom in the guest leaves the remaining ZFS axes, D_Y and D_Z, within the gray plane shown in Fig. 7B. Several oxygen atoms in the first coordination sphere of the Gd(III) ion are located in the vicinity of this plane and are likely to determine the ligand field geometry. In other words, the orientation of the D_Y–D_Z plane is determined by the ligand atoms in the CD cage structure and positions the direction of the D_X axis close to Gd(III)–N bond. Interestingly, the ED-EPR lineshape in the absence and in the presence of the guest are the same. This indicates that the coordination of the guest does not affect the ZFS within the available resolution although the Gd(III) coordination sphere is somewhat different (Fig. 2A and B). In the absence of guest, the Gd(III) is presumably coordinated to a D₂O molecule inside the CD cavity. In addition, the shapes of EPR spectra of Gd-β-CD are closely similar for all studied guests. Therefore, it is unlikely that the various complexation modes observed only for para-substituted guests modify the ZFS.

Thus, the ENDOR data converge to form a coherent picture of the Gd(III) ion coordination with the guest molecules in the CD cavity with the assignment of ZFS principal axes orientation with respect to the guest molecule. The pronounced orientation selection observed for the CT is probably due to the broader spectrum of the CT (large ZFS) and the smaller ZFS distributions owing to a better defined orientation of ligands surrounding the Gd ion. We previously observed an appreciable orientation selectivity in the ENDOR spectra of Gd(III) spin labels while performing the measurements at the electron spin transition (|−7/2〉 ↔ |−5/2〉), while no such effect was observed in this case at the narrow CT.²⁵

Importantly, the orientation-selective ¹⁹F ENDOR data may be used to determine experimentally the position of the Gd(III) ZFS principal axes in the molecular system, which so far has been only addressed theoretically,³⁰ and provide the experimental basis to verify theoretical predictions. If, in turn, the geometry of the ZFS axes in Gd(III) complexes can be reliably quantified theoretically, this information may be used to derive the orientation of Gd–F vector in biomolecules and materials of interest.

Conclusions

In this work, we implemented ¹⁹F ENDOR methodology to study supramolecular host–guest complexes, characterized by non-covalent interactions. This approach allowed us to quantitively determine the location of the guest in the cavity of metallo-cyclodextrins hosts and resolve bimodal complexation behavior for para-substituted guests in Gd-β-CD with a quantitative estimation of the associated relative populations.

The unexpected observation of orientation selection behavior for the ENDOR spectra recorded at the central transition of Gd(III) and quantitative joint simulation of EPR and ENDOR spectra of these complexes provided valuable information about the complexation geometry. Moreover, the approaches developed here secure a more quantitative understanding of the orientation of the ZFS tensor in Gd(III) chelates and thus provide a handle to fully access the information contained in Gd(III)–¹⁹F ENDOR spectra. Such information can also be obtained from low-temperature measurements outside the CT, but at the expense of SNR.

This work advances the applicability of magnetic resonance for structural characterization of bound states in systems undergoing chemical exchange between bound and free states with low binding constants in solution.

Data availability

Programs used for spectral simulations along with the data and simulation results for this manuscript can be accessed at https://sourceforge.net/projects/mimsgd/.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was funded by the National Science Foundation USA-Israel Science Foundation program through BSF 2021617 (to DG) and was made possible, in part, by support from the Helen and Martin Kimmel Institute for Magnetic Resonance Research and the historic generosity of the Harold Perlman Family (DG). The Israel Science Foundation (grant 1329/20 to A. B.-S.), and the Minerva Science Foundation (A. B.-S.) also supported this research. A. B.-S. heads the Clore Institute for High-Field Magnetic Resonance Imaging and Spectroscopy, whose support is also acknowledged.

References

1. F. Biedermann, W. M. Nau and H.-J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171.
2. Z. He, W. Jiang and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 779–789.
3. J. H. Jordan and B. C. Gibb, Chem. Soc. Rev., 2015, 44, 547–585.
4. Q.-Q. Wang, V. W. Day and K. Bowman-James, J. Am. Chem. Soc., 2013, 135, 392–399.
5. T. K. Ronson, W. Meng and J. R. Nitschke, J. Am. Chem. Soc., 2017, 139, 9698–9707.
6. J. Kim, I.-S. Jung, S.-Y. Kim, E. Lee, J.-K. Kang, S. Sakamoto, K. Yamaguchi and K. Kim, J. Am. Chem. Soc., 2000, 122, 540–541.
7. L. Avram and Y. Cohen, J. Am. Chem. Soc., 2004, 126, 11556–11563.
8. A. Swartjes, P. B. White, M. Lammertink, J. A. A. W. Elemans and R. J. M. Nolte, Angew. Chem., Int. Ed., 2021, 60, 1254–1262.
9. K. I. Assaf, M. Florea, J. Antony, N. M. Henriksen, J. Yin, A. Hansen, Z.-W. Qu, R. Sure, D. Klapstein, M. K. Gilson, S. Grimme and W. M. Nau, J. Phys. Chem. B, 2017, 121, 11144–11162.
10. S. Moghaddam, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2009, 131, 4012–4021.
11. L. Avram, M. A. Iron and A. Bar-Shir, Chem. Sci., 2016, 7, 6905–6909.
12. L. Avram, A. D. Wishard, B. C. Gibb and A. Bar-Shir, Angew. Chem., Int. Ed., 2017, 56, 15314–15318.
13. L. Avram and A. Bar-Shir, Org. Chem. Front., 2019, 6, 1503–1512.
14. E. Goren, L. Avram and A. Bar-Shir, Nat. Commun., 2021, 12, 3072.
15. E. Goren, M. A. Iron, Y. Diskin-Posner, A. Falkovich, L. Avram and A. Bar-Shir, Chem. Sci., 2023, 14, 11351–11358.
16. A. Meyer, S. Dechert, S. Dey, C. Höbartner and M. Bennati, Angew. Chem., Int. Ed., 2020, 59, 373–379.
17. A. Kehl, M. Hiller, F. Hecker, I. Tkach, S. Dechert, M. Bennati and A. Meyer, J. Magn. Reson., 2021, 333, 107091.
18. H. Wiechers, A. Kehl, M. Hiller, B. Eltzner, S. F. Huckemann, A. Meyer, I. Tkach, M. Bennati and Y. Pokern, J. Magn. Reson., 2023, 353, 107491.
19. M. Gauger, M. Heinz, A.-L. J. Halbritter, L. S. Stelzl, N. Erlenbach, G. Hummer, S. T. Sigurdsson and T. F. Prisner, Angew. Chem., Int. Ed., 2024, e202402498.
20. N. B. Asanbaeva, A. A. Sukhanov, A. A. Diveikina, O. Y. Rogozhnikova, D. V. Trukhin, V. M. Tormyshev, A. S. Chubarov, A. G. Maryasov, A. M. Genaev, A. V. Shernyukov, G. E. Salnikov, A. A. Lomzov, D. V. Pyshnyi and E. G. Bagryanskaya, Phys. Chem. Chem. Phys., 2022, 24, 5982–6001.
21. N. B. Asanbaeva, D. S. Novopashina, O. Y. Rogozhnikova, V. M. Tormyshev, A. Kehl, A. A. Sukhanov, A. V. Shernyukov, A. M. Genaev, A. A. Lomzov, M. Bennati, A. Meyer and E. G. Bagryanskaya, Phys. Chem. Chem. Phys., 2023, 25, 23454–23466.
22. A. Meyer, A. Kehl, C. Cui, F. A. K. Reichardt, F. Hecker, L.-M. Funk, M. K. Ghosh, K.-T. Pan, H. Urlaub, K. Tittmann, J. Stubbe and M. Bennati, J. Am. Chem. Soc., 2022, 144, 11270–11282.
23. M. Judd, E. H. Abdelkader, M. Qi, J. R. Harmer, T. Huber, A. Godt, A. Savitsky, G. Otting and N. Cox, Phys. Chem. Chem. Phys., 2022, 24, 25214–25226.
24. M. Seal, W. Zhu, A. Dalaloyan, A. Feintuch, A. Bogdanov, V. Frydman, X.-C. Su, A. M. Gronenborn and D. Goldfarb, Angew. Chem., Int. Ed., 2023, 62, e202218780.
25. A. Bogdanov, V. Frydman, M. Seal, L. Rapatskiy, A. Schnegg, W. Zhu, M. Iron, A. M. Gronenborn and D. Goldfarb, J. Am. Chem. Soc., 2024, 146, 6157–6167.
26. S. L. Schumann, S. Kotnig, Y. Kutin, M. Drosou, L. Stratmann, Y. Streltsova, A. Schnegg, D. Pantazis, G. Clever and M. Kasanmascheff, Chem. – Eur. J., 2023, 29, e202302527.
27. A. Bogdanov, L. Gao, A. Dalaloyan, W. Zhu, M. Seal, X.-C. Su, V. Frydman, Y. Liu, A. M. Gronenborn and D. Goldfarb, Phys. Chem. Chem. Phys., 2024, 26, 26921–26932.
28. E. Meirovitch and R. Poupko, J. Phys. Chem., 1978, 82, 1920–1925.
29. A. M. Raitsimring, A. V. Astashkin and P. Caravan, High Resolution EPR: Applications to Metalloenzymes and Metals in Medicine, 2009, pp. 581–621.
30. S. Khan, R. Pollet, R. Vuilleumier, J. Kowalewski and M. Odelius, J. Chem. Phys., 2017, 147, 244306.
31. H. K. Pyle, M. Judd, A. Barancewicz, A. J. Mayer, N. Cox, S. A. Kondrat and S. J. Butler, Inorg. Chem., 2024, 63, 20726.
32. G. Prokopiou, M. D. Lee, A. Collauto, E. H. Abdelkader, T. Bahrenberg, A. Feintuch, M. Ramirez-Cohen, J. Clayton, J. D. Swarbrick, B. Graham, G. Otting and D. Goldfarb, Inorg. Chem., 2018, 57, 5048–5059.
33. J. Telser, in EPR Spectroscopy: fundamentals and methods, ed. D. Goldfarb and S. Stoll, 2017, pp. 207–234.
34. M. Horitani, A. R. Offenbacher, C. A. M. Carr, T. Yu, V. Hoeke, G. E. Cutsail, III, S. Hammes-Schiffer, J. P. Klinman and B. M. Hoffman, J. Am. Chem. Soc., 2017, 139, 1984–1997.
35. C. Gemperle and A. Schweiger, Chem. Rev., 1991, 91, 1481–1505.
36. I. Gromov, V. Krymov, P. Manikandan, D. Arieli and D. Goldfarb, J. Magn. Reson., 1999, 139, 8–17.
37. A. Feintuch, D. Shimon, Y. Hovav, D. Banerjee, I. Kaminker, Y. Lipkin, K. Zibzener, B. Epel, S. Vega and D. Goldfarb, J. Magn. Reson., 2011, 209, 136–141.
38. F. Mentink-Vigier, A. Collauto, A. Feintuch, I. Kaminker, V. Tarle and D. Goldfarb, J. Magn. Reson., 2013, 236, 117–125.
39. B. Epel, D. Arieli, D. Baute and D. Goldfarb, J. Magn. Reson., 2003, 164, 78–83.
40. J. E. Dennis, D. M. Gay and R. E. Walsh, ACM Trans. Math. Software, 1981, 7, 348–368.
41. J. A. Clayton, K. Keller, M. Qi, J. Wegner, V. Koch, H. Hintz, A. Godt, S. Han, G. Jeschke, M. S. Sherwin and M. Yulikov, Phys. Chem. Chem. Phys., 2018, 20, 10470–10492.
42. A. M. Raitsimring, A. V. Astashkin, O. G. Poluektov and P. Caravan, Appl. Magn. Reson., 2005, 28, 281–295.
43. P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Chem. Rev., 1999, 99, 2293–2352.
44. J. H. Forsberg, Coord. Chem. Rev., 1973, 10, 195–226.
45. E. M. M. Del Valle, Process Biochem., 2004, 39, 1033–1046.
46. A. A. Sandilya, U. Natarajan and M. H. Priya, ACS Omega, 2020, 5, 25655–25667.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental and simulation details, additional figures. See DOI: https://doi.org/10.1039/d4cp04734f

‡ These authors contributed equally to this work.

§ Current address: Department of Education, Indian Institute of Technology, Kharagpur 721302, WB, India.

---