Crack control in dried ferro-colloidal droplets: effect of particle aspect-ratio and magnetic field orientations

Abstract

Crack formation in dried colloidal films is a common phenomenon encountered in diverse fields, from coatings and materials science to biological and environmental applications. Understanding the mechanisms behind crack patterns and their dependency on external factors is crucial for tailoring deposit structures. In this study, we investigate the impact of an externally directed magnetic field on the crack morphology and self-assembly in dried deposits composed of anisotropically shaped ferro-colloidal particles of varying sizes. Employing a sessile drop configuration, distinct crack patterns are observed in ring-like deposits as the magnetic field is applied in parallel, perpendicular, and oblique orientations. Notably, crack propagation in the oblique field direction transitions from wavy to helical-shaped patterns depending on the size of the nanoparticles, in contrast to the patterns seen in parallel and perpendicular fields. Our findings demonstrate that ferro-colloids align with the magnetic moment along the tensile stress direction, particularly at the edges of the deposits where cracks propagate. The particle orientation and self-assembly in the deposits were controlled by the interaction of hydrodynamic and magnetic forces, with force calculations revealing that this interaction strongly depends on particle size and field angle. This interaction leads to crack alignment along the particle's long axes, emphasizing the influence of the magnetic field on the deposit's structural integrity. Additionally, ferro-colloid concentration significantly impacts crack density, with higher concentrations promoting the development of prominent cracks at the rim edges of the deposits. By leveraging the interplay between magnetic interactions and evaporation dynamics, we can develop novel strategies for manipulating nanoscale structures for advanced technology.

---

1 Introduction

Cracks in colloidal particle films have been extensively investigated and recognized as a prevalent phenomenon in colloidal systems.^1,2 During the drying of colloidal dispersions, colloidal particles are progressively drawn together, ultimately forming a continuous film as the suspending medium evaporates. Following this, the film undergoes additional shrinkage due to the increased capillary and van der Waals forces acting between the particles.³ As these forces intensify, stress accumulates within the film, leading to the nucleation and propagation of cracks.^4,5 The energy released during crack formation has been quantitatively determined to match the energy required to generate new surfaces along the crack edges.⁶ The occurrence of particulate fractures is understood to compromise the mechanical integrity and durability of the coatings,⁴ which is critical in applications such as drug delivery,⁷ biosensing,⁸ photonics,⁹ microfluidic devices,⁵ microelectronics,¹⁰ and the self-assembly of defect-free layers of micro- and nanoparticles.¹¹ Crack dynamics in colloidal films are influenced by a range of factors, including particle shape and size,¹² particle concentration,¹³ the presence of additional components in the dispersion,¹⁴ and external stimuli such as temperature variations or applied electric and magnetic fields.¹⁵ Studies on the evaporation behavior of colloidal suspensions on different substrate surfaces have unraveled various phenomena, including the coffee-ring effect and the self-assembly processes of nanoparticles during droplet drying.¹⁶ While much of the earlier research has focused on spherical particles, providing insights into particle deposition patterns and structural evolution during evaporation,^17,18 the introduction of non-spherical, anisotropic particles has added new complexities to these systems.¹⁹ The shape anisotropy of such particles introduces directional dependencies in particle orientation and assembly, significantly affecting the final morphology of the deposited film. Moreover, diverse crack morphologies, such as circular, radial, spiral, and wavy patterns, have been experimentally observed in particulate films, with their formation dependent on the specific drying conditions.^2,20 In recent years, the integration of external stimuli into this research paradigm has opened up new dimensions of control and manipulation.

Ferro-colloids, characterized by magnetic nanoparticles suspended in a carrier fluid, present an extraordinary opportunity to investigate the intricate relationship between magnetic forces and evaporative dynamics.²¹ The behavior of such colloidal systems under evaporation, particularly when containing magnetic nanoparticles, has been extensively studied using diverse magnetic field configurations, including permanent magnets, ring magnets, and electromagnets.^22,23 Evaporation studies, particularly of magnetic particle-laden droplets, demonstrate how external fields, both electric²⁴ and magnetic²⁵ affect crack formation in colloidal films. These interactions play a significant role in modulating the drying patterns and have led to new insights into how evaporation can be controlled to achieve desirable deposition outcomes. In ferrofluids, the dynamic response to magnetic fields has been extensively studied, particularly in microfluidic applications where uniform and non-uniform magnetic fields manipulate the fluid flow and particle alignment.²⁶ The addition of anisotropic particles, such as ellipsoids, further complicates the system, as these particles exhibit unique hydrodynamic and magnetic properties.²³ The breakage of rotational symmetry in ellipsoidal particles introduces anisotropic forces that alter their orientation and arrangement during evaporation.^27,28 When exposed to external magnetic fields, these particles exhibit complex reorientation and self-assembly behaviors, with the directionality of the field playing a crucial role.²⁹ This convergence of anisotropic particle shape, hydrodynamics, and magnetism opens a fascinating window into colloidal science, where the interplay of forces can be finely tuned to control the particle arrangement and deposition patterns.

This study investigates the mechanisms of crack formation during the drying of ferro-colloid droplets containing particles with varying aspect ratios, subjected to a directed magnetic field. Our experiments focus on droplets composed of hematite ellipsoids, revealing that the size-dependent magnetic properties of the particles strongly influence the crack patterns in the dried deposits. The combined effects of hydrodynamic forces and magnetic force, particularly as modulated by the orientation of the applied magnetic field, govern the alignment of ellipsoidal particles during self-assembly. In addition, particle concentration plays a critical role, particularly in the ring regions, where higher concentrations lead to denser and enhanced crack development. These results emphasize how particle shape, size, concentration, and magnetic field orientation collectively determine the crack propagation and final arrangement in the dried deposits.

2 Experimental method

Ellipsoidal hematite particles were synthesized via the forced hydrolysis of Fe⁺³ with urea.³⁰ A mixture of 9.24 g Fe(ClO₄)₃ (Sigma-Aldrich, India) and 1.2 g of urea (Merck, India) was dissolved in 200 mL of Milli-Q water (18.2 MΩ cm) and transferred to a clean 250 mL Pyrex bottle. To control the particle size, NaH₂PO₄ (Merck, India) was introduced into the solution. The sealed bottle was incubated in a preheated oven at 100 °C for 24 hours. After the reaction, the product was centrifuged at 6000 rpm for 30 minutes and washed repeatedly with deionized water until the supernatant pH matched Milli-Q water. The final ellipsoidal hematite particles were resuspended in Milli-Q water for further use. The aspect ratio of the synthesized particles was accurately measured using field-emission scanning electron microscopy (FE-SEM, JEOL). To proceed with the subsequent experiments, nanoparticles with 4 different ellipsoidal sizes and a fixed concentration of 2 wt% were prepared. These suspensions underwent centrifugation and ultrasonic treatment for 15 minutes to ensure thorough mixing of the particles. In preparation for the drying droplet experiments, glass slides underwent a rigorous cleaning procedure. First, they were immersed in piranha solution (3 : 1 volume ratio of H₂SO₄ to H₂O₂) for 5 minutes to remove organic contaminants. Afterward, the slides were cleaned using a 0.3 wt% labolene (soap) solution for 10 minutes to eliminate any remaining residues, followed by a 5-minute rinse with ethanol to further clean the surface and remove soap traces. Finally, the slides were rinsed multiple times with deionized water to ensure complete removal of any chemical residues, making them ready for the experiments.

A 1 μL droplet of the nanoparticle suspension was deposited onto the cleaned glass substrate using a micro-pipette and allowed to evaporate in the presence of an external magnetic field. The magnetic field was generated by an electromagnetic setup (Raman Scientific Instrument) and the drying was conducted under controlled ambient conditions at a temperature of 23 ± 2 °C and relative humidity (RH) of 40 ± 5%. The experimental arrangement is depicted in Fig. 1, showing a rotating electromagnet mounted on a circular board with a pole-to-pole distance of 30 mm. The electromagnet was oriented along the z-axis, while the droplet remained stationary in the x–y plane. Experiments were performed under three different magnetic field orientations: parallel to the substrate (H_parallel = 0°), perpendicular to the substrate (H_perp = 90°), and at an oblique inclination (H_canted = 40° ± 2°). The strength of the applied magnetic field was maintained at 2000 G, directed from the north to the south pole, and was continuously monitored using a digital Gaussmeter (Raman Scientific Instrument). The dried droplet deposition patterns were analyzed using a (Nikon LV100ND) optical microscope at 10× and 20× magnifications.

Fig. 1 Experimental setup schematic depicting a sessile drop undergoing evaporation between the pole pieces of an electromagnet, with the magnetic field direction denoted as H⃑.

3 Results and discussion

3.1 Characterisation of hematite particles

The aspect ratio (Ω) of hematite ellipsoids, representing the ratio of the major axis length to the minor axis length, was determined as 1.2 ± 0.31, 2.9 ± 0.26, 4.8 ± 0.34, and 7.1 ± 0.17 based on SEM images corresponding to Ω₁, Ω₃, Ω₅ and Ω₇ as shown in Fig. 2(a) and (b). The corresponding magnetic properties of hematite ellipsoids were investigated by observing the magnetic moment (M) variation with the applied magnetic field (H) at 300 K for all samples shown in Fig. 2(c). The observations reveal hysteresis loops with coercive fields (H_c) of approximately 508, 306, 422, and 456 G for Ω₁, Ω₃, Ω₅, and Ω₇, respectively. The non-zero coercivity confirms the ferromagnetic behaviour of hematite ellipsoids, consistent with established literature.³¹ The calculated value of magnetic susceptibility, magnetization saturation, viscosity, surface tension and zeta potential of ferro-colloids have been reported in Table 1. These properties provide insight into both the collective behavior of the suspension and the intrinsic characteristics of colloidal particles. The data highlight the influence of magnetic properties on particle interactions, emphasizing the critical role of particle shape and size in field-assisted assembly processes.³² This underscores the interplay between magnetic attributes and the physicochemical properties of the system.

Fig. 2 (a) FE-SEM images of hematite nanoparticles of different shapes. (b) Dimensional measurement of anisotropic-shaped particles with aspect ratios of 1, 3, 5, and 7 denoted by Ω₁, Ω₃, Ω₅ and Ω₇, respectively. (c) The magnetization curve illustrates the magnetic behavior of hematite particles with different aspect ratios/sizes measured at 300 K.

Table 1 Properties of ferro-colloids in the 2 wt% suspension

Particulars	Ω 1	Ω 3	Ω 5	Ω 7
Magnetic susceptibility (χ)	4.3 × 10^−5	1.4 × 10^−4	9.1 × 10^−5	6.1 × 10^−5
Saturation magnetization (Ms)	1.9 A m^2	2.4 A m^2	1.8 A m^2	1.5 A m^2
Viscosity (η)	0.0038 Pa s	0.0015 Pa s	0.0014 Pa s	0.0016 Pa s
Surface tension (γl)	64.06 nN m^−1	60.26 nN m^−1	56.47 nN m^−1	62.59 nN m^−1
Zeta potential (ϕp)	49 mV	28 mV	38 mV	24 mV

---

3.2 Deposition morphology in the absence/presence of external fields

In the absence of a magnetic field, anisotropic particle-containing droplets exhibit distinct deposition patterns based on particle shape, as shown in Fig. 3. Spheroids (Ω₁) create radial crack patterns as they aggregate symmetrically around the droplet's centre; their isotropic properties facilitate uniform contraction during evaporation, leading to evenly spaced cracks radiating outward.¹⁶ In contrast, ellipsoidal particles (Ω₃, Ω₅, Ω₇) form annular crack patterns due to their anisotropic nature, which causes them to align along specific axes, i.e., major-axes. As the droplet dries, these elongated particles generate localized stresses along the minor axes that promote concentric cracking, resulting in a layered appearance.²⁰ This localized stress along the minor axes leads to the formation of concentric rings, with the stress being most concentrated at the edges and progressively dissipating toward the centre. Thus, the differences in particle shape significantly influence the stress distribution and the subsequent cracking patterns during evaporation. The differences in particle shape significantly influence the stress distribution and subsequent cracking patterns during evaporation. In both the presence and absence of a magnetic field, spherical particles in dried deposition exhibit similar morphological characteristics, primarily forming radial crack patterns, as shown in Fig. 4(a). Without a magnetic field, the isotropic nature of the spherical particles allows them to distribute uniformly as the droplet evaporates, leading to the development of cracks that radiate outward from the center due to uniform stress distribution.¹⁶ In the presence of a magnetic field in all directions, while the particles may experience some alignment along the field lines, the overall deposition morphology remains similar (Fig. 4(b)). The magnetic interactions may enhance local ordering but do not fundamentally alter the radial nature of the cracks formed. Up to 2000 G, the cracks remain unchanged, with particles aligning along the field lines, while at higher field strengths, particle alignment is more pronounced, enhancing local ordering without affecting the overall radial nature of the cracks.

Fig. 3 Desiccation patterns of dried droplets containing anisotropically-shaped nanoparticles with varying aspect ratios: (a) Ω₁, (b) Ω₃, (c) Ω₅, and (d) Ω₇ in the absence of an external magnetic field. Fig. S1 in the ESI† shows magnified images for better visualization.

Fig. 4 Deposition morphologies illustrating the arrangement of spheroidal particles (Ω₁) and crack propagation at the ring of the deposit in the (a) absence and (b) presence of an external magnetic field.

3.3 Self-assembly of ellipsoidal particles with an external magnetic field

During the evaporation process of a sessile drop influenced by a magnetic field, particle orientation near the contact line was determined by both fluid flow direction and magnetic field orientation. Ellipsoids generally align with their major axis parallel to the solvent flow direction, i.e., radially outward.⁶ Simultaneously, the magnetic field aligns the ellipsoids with their minor axis along the field direction, as the magnetic moment is confined to the minor axis due to the Fe⁺³ spins located in the basal plane of the hematite.³¹ The orientation of particles at the contact line was decided by the relative strength of magnetic particles in the evaporating fluid and the external magnetic field. It was established that for ellipsoidal magnetic particles, the superimposition of hydrodynamic and magnetic characteristics influences the deposition patterns of the particle.^28,33

3.3.1 Electromagnet parallel to the substrate. As shown in Fig. 5(a), sessile droplets containing hematite ellipsoids undergo evaporation under the influence of external magnetic fields aligned parallel to the substrate, featuring varying particle sizes. The resulting crack morphology exhibits linearity, following the chord of the coffee ring formed in the particulate deposit, a consistent observation across all cases. However, enhancement of crack width occurs in the reverse order of the ellipsoidal aspect ratio. This phenomenon was accompanied by the assembly of particles (with a major axis) in a perpendicular direction to the field, facilitated by the orientation of the magnetic moment of particles parallel to the applied magnetic field.^31,32 The crack width was maximum for Ω₃ and lowest for Ω₇, as shown in Fig. 5(b). Additionally, the optical figures presented illustrate distinct regions: the exterior corresponds to the area outside the coffee-ring particulate deposit, while the interior designates the space within the deposit. The majority of ellipsoids were deposited in the annular region, contributing to the observed crack patterns due to stress build-up at the end of the evaporation.³⁴

Fig. 5 (a) Schematic displaying the experimental setup with the magnet oriented parallel to the sessile droplet along the x-axis and the creation of the resulting deposition patterns. (b) FE-SEM and optical images illustrate the particle alignment and fracture direction during the deposition of various aspect ratios of 3, 5, and 7, respectively. For better observation of the deposition pattern, refer to Fig. S2–S4 in the ESI.†

3.3.2 Electromagnet perpendicular to the substrate. In the schematic of Fig. 6(a), the application of a magnetic field in a perpendicular direction results in the formation of a coffee ring, but with a distinctive alteration in the crack pattern exhibiting concentric rings like depositions. This phenomenon can be explained by the continuous evaporation of fluid from the drop surface during sessile drop evaporation, where the maximum evaporative flux occurs at the three-phase contact line.³⁵ The nonuniform evaporative flux, combined with the external magnetic field applied perpendicular to the surface, induces a more rapid outward radial flow of the particles towards the contact line of the drop.¹⁹ This radial flow, coupled with the effective force applied to the particle, determines the deposition pattern of the ferrofluid. The resulting interaction forces accumulate stress in the gel region during the final stages of evaporation, initiating cracks in the circular formation. FE-SEM images of Fig. 6(b) demonstrate that the cracks align along the periphery of the drop, tracing the direction of the major axis of the ellipsoidal particles. The crack width was observed to intensify for smaller particles (Ω₃) as compared to the larger particles. Despite particle alignment in the direction of the crack, the assembly was more regular for Ω₇ due to its higher restraining effect attributed to a large amount of force applied to these particles.

Fig. 6 (a) Schematic of the experimental setup where a magnet aligns perpendicularly (along the z-axis) to the sessile droplet situated within the x−y plane with the resulting deposition pattern formation after drying. (b) Optical and FE-SEM images of the deposition of different aspect ratios (3, 5 and 7) with the crack propagation and particle alignment. For enhanced clarity, magnified optical images are provided in Fig. S5–S7 of the ESI.†

3.3.3 Electromagnet at the canted direction to the substrate. In the presence of an oblique magnetic field, the evaporation of ferrofluids generates distinctive and intricate crack patterns in the dried deposition, shaped by both the external field and the inherent properties of the colloidal particles. As shown in Fig. 7(a), the experimental setup highlights the evolution of these cracks at the canted direction of the external field. The images in Fig. 7(b) reveal that cracks along the y-axis are more pronounced, dense, and randomly oriented compared to those along the x-axis, where they exhibit more circular and organized structures. This variation in crack morphology is primarily attributed to the shape anisotropy and long-range ordering of the ellipsoidal particles, which lead to preferential crack propagation along directions where less energy is required for the crack to advance.²³ When the magnetic field is neither perfectly parallel nor perpendicular to the surface of the drying droplet, the morphology of the cracks transitions from helical or hook-like formations to circular patterns, depending on the local influence of the magnetic field at various regions of the deposit. The observed transition highlights the role of the canted magnetic field in modulating the stress for crack propagation, effectively guiding cracks along preferential pathways dictated by the field orientation.¹⁵ For instance, in the case of Ω₃ particles, wavy crack patterns appear at the top and bottom of the droplet. The application of magnetic forces to these particles’ magnetic moment induces greater deviations in particle alignment, causing significant disruptions in the overall crack structure. As particle size increases, as observed with Ω₅ and Ω₇ particles, spiral-shaped cracks become more pronounced along the y-axis, intensifying with particle size. Additionally, the width of the helical cracks expands with increasing particle elongation. This phenomenon arises from a reduced packing efficiency within the self-assembled deposits, as elongated particles encounter steric hindrances that restrict their arrangement into tightly packed structures. The resulting lower packing density creates more noticeable voids between particles at Ω₇, disrupting the uniformity of the assembled network and giving rise to wider and less defined crack patterns in systems containing larger and more anisotropic particles. Thus, the deposition pattern of a particle gets intricately linked to the forces it experiences, which can be controlled by its orientation and the particle's magnetic moments in the external magnetic field and the ambient flow field.

Fig. 7 (a) Schematic of the experimental setup showing the creation of the deposition pattern after drying, with magnets positioned at an oblique direction that is neither parallel nor perpendicular to the sessile droplet located within the xy plane. (b) FE-SEM and optical images show the deposition of various aspect ratios (3, 5, and 7) along with particle alignment and crack propagation along different deposit sites. Magnified optical images are presented in Fig. S8–S10 within the ESI† for enhanced detail and visualization.

3.4 Interplay of forces in fluid governing deposition pattern evolution

It is thus observed that the drying patterns of ferrofluid droplets are significantly influenced by both the direction and intensity of the external magnetic field. Crack propagation in the film is primarily governed by the balance between surface tension and the resistance experienced by the particles during drying.³⁶ Additionally, the final particle deposition is directly related to the magnetic forces acting on the particles under a directional magnetic field. Fig. 8 illustrates the forces (F) acting on a particle within the droplet as a function of the magnetic force (F_m) and hydrodynamic force (F_h). The total force on a particle can be expressed by the equation:

F = F_m cos ϕ_m + F_h (1)

where cos ϕ_m is the horizontal component of the magnetic field in the x–y plane, and F_h was estimated based on Stokes’ law, assuming a low Reynolds number regime where viscous effects dominate.²² This force experienced by a particle of hydrodynamic radius r_h ∼ b (semimajor-axis) moving with velocity v in a fluid of viscosity η is given by F_h = 6πηr_hv. The effective magnetic force acting on a particle during drying under an applied magnetic field, H⃑ is given by F_m = μ₀V_pχ(H_p∇H),³⁷ where H_p represents the magnetic field associated with the particle's magnetic moment, which aligns along its minor axis, χ is the magnetic susceptibility of the ferro-colloid, and V_p is the volume of the particle. Since forces are vectorial quantities, both magnitude and direction influence the resulting deposition patterns. The hydrodynamic and magnetic forces act at different orientations, contributing to the alignment and distribution of particles. As illustrated in Fig. 8, the total maximum forces, on the order of 10⁻¹³ N, increase with particle size, leading to enhanced alignment in the particles. Larger particles experience stronger magnetic torques, leading to more pronounced alignment along the field direction. Additionally, hydrodynamic interactions vary with particle size, as larger particles experience greater drag forces, modifying their motion within the evaporating droplet. For H_parallel, the forces reach a maximum of 5.7× 10⁻¹³ N for Ω₇. These magnetic forces influence particle orientation by aligning the magnetic moments along the field direction, resulting in a linear arrangement of particles and cracks in the deposit. The hydrodynamic force, although lower in magnitude compared to the magnetic force in the present study, plays a role in the local mobility of the particles before deposition. As evaporation progresses, competition between hydrodynamic drag and magnetic attraction dictates the final alignment. Additionally, the influence of electrostatic forces was considered negligible as it is of the order of 10⁻²⁰ N, though a detailed zeta potential analysis could provide further insight into potential electrostatic interactions. For instance, the Ω₇ particles show intensified crack patterns across all directions of the magnetic field, with applied forces ranging from 2 × 10⁻¹³ to 5.7× 10⁻¹³ N. The increase in force with particle size leads to significant deviations in their alignment, contributing to distinctive crack patterns and particle alignment. In cases where particles aggregate unevenly, certain regions experience elevated stress, leading to more pronounced cracks. These stressed areas are prone to forming complex crack structures, such as hook-shaped or spiral cracks, driven by the uneven force distribution within the droplet.^38,39 This highlights the complex relationship between magnetic field orientation, particle arrangement, and evaporation dynamics in shaping the final deposition patterns in ferrofluid films.

Fig. 8 Total forces for the various particle sizes (Ω₃, Ω₅, and Ω₇) in dependence on the direction of the magnetic field acting on the sessile droplet during evaporation.

3.5 Effect of variation in concentration in the crack propagation

As the concentration of particles of Ω₇ in a droplet increases from 0.5 wt% to 5 wt% under the influence of a magnetic field, as shown in Fig. 9, the crack patterns exhibit distinct variations. At a concentration of 0.5 wt%, radial cracks emerge, directed towards the rim. As the concentration increases to 2 wt%, the stronger magnetic forces facilitate greater alignment of particles, particularly in H_parallel. This alignment results in more organized crack patterns, with elongated and interconnected cracks. At the highest concentration of 5 wt%, crack propagation is constrained, leading to wider and complex fracture networks. For H_perp, crack propagation becomes less complex, resulting in an annular crack pattern similar to deposition obtained without a magnetic field. Additionally, when particles are canted relative to the magnetic field, H_canted, the cracks display intricate patterns that suggest a hybrid influence of both parallel and perpendicular alignments, resulting in slanted/tilted crack patterns containing helical-shaped cracks at the nanoscale.

Fig. 9 Optical images illustrating crack propagation at the rim on the top side of the deposit as a function of varying concentrations of Ω₇ ferro-colloid suspension in the absence and presence of an external magnetic field.

Fig. 10 provides insights into the crack density that offers valuable information about the behaviour of the dried deposits. Crack density, determined as the total number of cracks per unit rim area in the ring pattern of micrometre-scale deposit films, exhibits a pronounced decreasing trend with increasing ferro-colloid concentrations of Ω₇. At lower concentrations of 0.5 and 1 wt%, the crack density is within the order of 10⁻⁴, whereas higher concentrations of 2 and 5 wt% exhibit a significant reduction to the order of 10⁻⁵. This decline correlates with an increase in rim width as the ferro-colloidal concentration rises. The measurement demonstrates that the canted magnetic field direction (H_canted) plays a crucial role in influencing crack density, especially at higher concentrations (2 and 5 wt%). In this orientation, the combination of reduced crack numbers and increased rim width enhances particle alignment and densification, resulting in slightly lower crack densities compared to those observed in parallel or perpendicular magnetic field orientations. However, in the absence of a magnetic field, the crack density increases comparatively for higher-concentration deposits totally depending on the capillary stress that induced cracking.¹⁶ Thus, increasing particle concentration not only intensifies the magnetic interactions but also transitions the crack propagation from simple radial patterns to complex networks that are heavily influenced by the magnetic field orientation. These preferential outcomes of ellipsoidal ferro-colloid deposition, influenced by an oriented magnetic field, exhibit promise for applications in field-driven self-assembly and the development of advanced coatings.

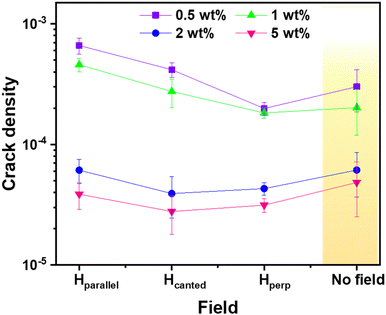Fig. 10 Crack density measurement for varying concentrations of Ω₇ deposits at different magnetic field orientations.

4 Conclusions

In conclusion, our study explores crack formation mechanisms during the drying of ferro-colloid droplets with ellipsoidal particles of varying aspect ratios (Ω = 1, 3, 5, 7) under a directed magnetic field. The findings demonstrate that crack patterns and particle alignment are significantly affected by the direction of the particles magnetic moments and the applied magnetic field, resulting in a combination of circular, wavy, and helical-shaped cracks in the deposit patterns. This observed behavior was driven by the interplay of magnetic and hydrodynamic forces, whose combined effects varied with particle size and the angle of the magnetic field, establishing a complex relationship that governs particle distribution and orientation during self-assembly. Furthermore, the concentration of the particle suspension influenced crack propagation. Higher particle concentrations amplified the development of helical cracks, highlighting the role of particle anisotropy and concentration in directing self-assembly. This simple technique can be useful in controlled deposition, and crack patterns under the influence of external stimuli can give further insight for applications in materials science, surface engineering, and nanotechnology.

Data availability

The data generated or analyzed during this study are included in this article. Furthermore, the datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge support from the Central Research Facility (CRF) of Indian Institute of Technology (IIT) Ropar. DR and SS also thank the Institute Instrumentation Centre, IIT Roorkee, for VSM measurements. DR is thankful for financial support through a research fellowship from the University Grants Commission (UGC), Government of India.

References

1. P. Xu, A. S. Mujumdar and B. Yu, Drying Technol., 2009, 27, 636–652.
2. A. F. Routh, Rep. Prog. Phys., 2013, 76, 046603.
3. U. U. Ghosh, M. Chakraborty, A. B. Bhandari, S. Chakraborty and S. DasGupta, Langmuir, 2015, 31, 6001–6010.
4. E. R. Dufresne, E. I. Corwin, N. A. Greenblatt, J. Ashmore, D. Y. Wang, A. D. Dinsmore, J. X. Cheng, X. S. Xie, J. W. Hutchinson and D. A. Weitz, Phys. Rev. Lett., 2003, 91, 224501.
5. W. Han, B. Li and Z. Lin, ACS Nano, 2013, 7, 6079–6085.
6. W. P. Lee and A. F. Routh, Langmuir, 2004, 20, 9885–9888.
7. O. D. Velev and E. W. Kaler, Adv. Mater., 2000, 12, 531–534.
8. D. Brutin, B. Sobac, B. Loquet and J. Sampol, J. Fluid Mech., 2011, 667, 85–95.
9. A. Stein and R. C. Schroden, Curr. Opin. Solid State Mater. Sci., 2001, 3, 553–564.
10. H. O. Jacobs and G. M. Whitesides, Science, 2001, 291, 1763–1766.
11. H. Zargartalebi, S. H. Hejazi and A. Sanati-Nezhad, Nat. Commun., 2022, 13, 3085.
12. A. Lassoued, B. Dkhil, A. Gadri and S. Ammar, Results Phys., 2017, 7, 3007–3015.
13. J. Y. Kim, K. Cho, S. A. Ryu, S. Y. Kim and B. M. Weon, Sci. Rep., 2015, 5, 13166.
14. D. Rani, D. Lohani, M. G. Basavaraj, D. K. Satapathy and S. Sarkar, Langmuir, 2024, 40, 20323.
15. L. Pauchard, F. Elias, P. Boltenhagen, A. Cebers and J. C. Bacri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 021402.
16. D. Rani and S. Sarkar, Eur. Phys. J. E: Soft Matter Biol. Phys., 2023, 46, 113.
17. R. D. Deegan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 475–485.
18. H. Hu and R. G. Larson, Langmuir, 2005, 21, 3963–3971.
19. P. J. Yunker, M. A. Lohr, T. Still, A. Borodin, D. J. Durian and A. G. Yodh, Phys. Rev. Lett., 2013, 110, 035501.
20. D. Rani, S. K. Saroj and S. Sarkar, Colloids Surf., A, 2025, 708, 135851.
21. C. Scherer and A. M. F. Neto, Braz. J. Phys., 2005, 35, 718–727.
22. S. K. Saroj and P. K. Panigrahi, Colloids Surf., A, 2019, 580, 123672.
23. H. Lama, V. R. Dugyala, M. G. Basavaraj and D. K. Satapathy, Phys. Rev. E, 2016, 94, 012618.
24. T. Khatun, M. D. Choudhury, T. Dutta and S. Tarafdar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 016114.
25. U. Banerjee and A. K. Sen, Soft Matter, 2018, 14, 2915–2922.
26. M. A. Bijarchi and M. B. Shafii, Langmuir, 2020, 36, 7724–7740.
27. P. Schiller, S. Krüger, M. Wahab and H. J. Mögel, Langmuir, 2011, 27, 10429–10437.
28. M. M. Tavakol, O. Abouali, M. Yaghoubi and G. Ahmadi, Int. J. Multiphase Flow, 2015, 75, 54–67.
29. M. Jadav, R. J. Patel and R. V. Mehta, J. Appl. Phys., 2017, 122, 12553.
30. M. Ocaña, M. P. Morales and C. J. Serna, J. Colloid Interface Sci., 1999, 212, 317–323.
31. M. Reufer, H. Dietsch, U. Gasser, B. Grobety, A. M. Hirt, V. K. Malik and P. Schurtenberger, J. Phys.: Condens. Matter, 2011, 23, 065102.
32. A. Pal, C. A. D. Filippo, T. Ito, M. A. Kamal, A. V. Petukhov, C. D. Michele and P. Schurtenberger, ACS Nano, 2022, 16, 2558–2568.
33. D. Hoffelner, M. Kundt, A. M. Schmidt, E. Kentzinger, P. Bender and S. Disch, Faraday Discuss., 2015, 181, 449–461.
34. M. S. Tirumkudulu and W. B. Russel, Langmuir, 2005, 21, 4938–4948.
35. D. O. Kim, M. Pack, H. Hu, H. Kim and Y. Sun, Langmuir, 2016, 32, 11899–11906.
36. Z. Liu, J. Zhou, Y. Li, X. Zhuo, X. Shi and D. Jing, Fundam. Res., 2022, 2, 222–229.
37. J. A. Stratton, Electromagnetic Theory, John Wiley & Sons, Inc., illustrated, reprint, reissue edn, 2007, pp. 1–640.
38. S. Kumar, H. Kumar, M. G. Basavaraj and D. K. Satapathy, Colloids Surf., A, 2022, 641, 128579.
39. E. Keita, Materials, 2021, 14, 5120.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04667f

---