 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient state-interaction approach for the g-matrix analysis in high-spin molecules†
Antonio
Cebreiro-Gallardo
 ab and
David
Casanova
ab and
David
Casanova
 *ac
*ac
aDonostia International Physics Center (DIPC), 20018 Donostia, Euskadi, Spain. E-mail: david.casanova@dipc.org
bPolimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila, Kimika Fakultatea, Euskal Herriko Unibertsitatea (UPV/EHU), PK 1072, 20080 Donostia, Euskadi, Spain
cIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Euskadi, Spain
First published on 14th March 2025
Abstract
We present an efficient state-interaction approach for evaluating g-shifts in high-spin molecular systems. Using a spin–orbit-coupled effective Hamiltonian with a restricted active space configuration interaction wavefunction, this method captures key excited-state contributions to g-shifts without requiring large orbital spaces, maintaining computational efficiency. Additionally, we introduce a property-driven algorithm to automatically select relevant orbitals, optimizing the active space selection. Application to diatomic and conjugated organic molecules demonstrates accuracy comparable to advanced methods, providing detailed insight into the origins of g-shifts. This methodology offers a flexible, efficient tool for exploring magnetic properties in complex molecules.
1 Introduction
The understanding and prediction of magnetic properties in high-spin molecules are crucial for advancing applications in catalysis, magnetic materials, and biochemical processes.1–7 High-spin, open-shell systems—characterized by an unpaired number of electrons and distinct populations of α and β electrons in their outer orbitals—are found across many fields, including organic synthesis, organometallic catalysis, and materials science.8 These reactive species are often studied using electron paramagnetic resonance (EPR) or electron spin resonance (ESR) spectroscopy, techniques that provide insights into molecular geometry and electronic configuration by probing interactions between unpaired electrons and external magnetic fields. Central to EPR analysis is the g-matrix, which defines the Zeeman splitting of spin states in an applied magnetic field, offering a window into the electronic structure and local environment of these molecules.9,10The g-matrix encodes the effects of relativistic interactions, including contributions from spin–orbit coupling (SOC) and the electronic structure of the molecule, which collectively influence the response of electronic spins to an external magnetic field. Accurate determination of g-values is crucial for effectively characterizing complex systems. In the past, g-matrix calculations relied on semiempirical methods limited to simplified models, with limited validity across system types. Since the 1990s, ab initio approaches, such as density functional theory (DFT) and wavefunction theory (WFT), have been increasingly applied to open-shell systems.11,12 DFT methods typically treat the magnetic field perturbatively and offer efficiency, though they often depend heavily on functional choice and tend to underestimate g-values in transition-metal complexes.9,13,14 In contrast, WFT methods can potentially handle high-spin states and transition metals with great accuracy by incorporating extensive electron correlation and relativistic effects, though at a higher computational cost.
Early work in WFT calculations at the Hartree–Fock (HF) level paved the way for increasingly sophisticated approaches in computing g-matrix parameters.15–19 This initial work facilitated the extension of g-matrix calculations to post-HF methods, such as coupled-cluster (CC) response theory,20,21 equations-of-motion coupled-cluster (EOM-CC),22 and multi-configuration techniques including complete active space self-consistent field (CASSCF)23–25 and restricted active space configuration interaction (RASCI).22 These methods enable a targeted treatment of specific orbital spaces and capture essential electron correlation effects. Recent advancements, such as combining CASSCF with second-order perturbation theory (CASPT2), have shown that sum-over-states (SOS) techniques, when paired with high-quality wavefunctions, can produce reliable g-values for complex transition-metal systems.26,27 Multi-reference configuration interaction (MR-CI) methods have similarly improved g-matrix accuracy by expanding state interactions through SOS formulations.28 However, due to their computational intensity, MR-CI methods often become impractical for medium to large molecular systems.
Despite these advances, challenges remain, however, for high-spin systems with multiplicities beyond S = 3/2, where zero-field splitting effects might become significant and are challenging to capture using traditional DFT or low-level WFT approaches.29 Addressing these systems requires sophisticated treatments of both dynamic correlation and SOC, particularly for heavy-element complexes where scalar-relativistic approximations are insufficient. For these cases, dynamic correlation and state-interaction approaches, capable of capturing spin-dependent interactions more comprehensively, are critical for accurately calculating the g-matrix. Consequently, as far as we are aware, few studies have attempted to evaluate the g-matrix computationally in high-spin molecules.29–31
In this study, we aim to advance g-matrix calculations in high-spin molecules by leveraging the advantages of state-interaction approaches. Unlike traditional response theory-based methods, state-interaction techniques allow for a more detailed decomposition of g-matrix shifts, offering unique insights into the underlying mechanisms. Specifically, they provide a granular analysis of contributions from SOCs and transitions to excited states, making it possible to disentangle how each factor influences magnetic behavior. This capability is especially beneficial for high-spin compounds, where understanding the precise contributions from SOCs and excitation energies is critical for accurate magnetic property predictions. By applying these methods across a series of systems with diverse electronic and SOC characteristics, we aim to refine computational strategies for g-matrix determinations, enhancing our understanding of the molecular factors driving magnetic properties in complex high-spin systems.
2 Theoretical background
2.1 Mapping between Zeeman and pseudospin Hamiltonians
Parametrization of the interaction between a high-spin molecular electronic state with an external magnetic field is typically done either by evaluating second order derivatives of the Zeeman splitting11,32 or by mapping the real Zeeman Hamiltonian (eqn (1)) to an effective spin (or pseudospin) Hamiltonian (eqn (2)).26,31,33| HZeeman = βeBt(L + geS) | (1) |
![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) spin = βeBtg spin = βeBtg![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) | (2) |
![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) is a pseudospin vector operator and the 3 × 3 matrix g contains the strength and anisotropy of the Zeeman splitting.
is a pseudospin vector operator and the 3 × 3 matrix g contains the strength and anisotropy of the Zeeman splitting.
In the present work, we map the ![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) spin to the Zeeman Hamiltonian expressed in the basis of electronic states belonging to the target multiplet of dimension M. Therefore, equating eqn (1) and (2) in the matrix representation of the pseudospin, S and L operators results in:
spin to the Zeeman Hamiltonian expressed in the basis of electronic states belonging to the target multiplet of dimension M. Therefore, equating eqn (1) and (2) in the matrix representation of the pseudospin, S and L operators results in:
 | (3) |
Importantly, these multiplet states are obtained following a state-interaction approach22 through the diagonalization of a SOC-dressed effective Hamiltonian (eqn (4)),
| HeffIJ = EIδIJ + HSOIJ | (4) |
Extraction of the terms of the g-matrix is pursued by applying the projection technique introduced by Tatchen and coworkers,31 which involves the projection of eqn (3) to individual components of the pseudospin, ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) i, i = X,Y,Z,
i, i = X,Y,Z,
 | (5) |
gzZ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) Z = Jz Z = Jz | (6) |
gyY![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) Y + gyZ Y + gyZ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) Z = Jy Z = Jy | (7) |
gxX![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) X + gxY X + gxY![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) Y + gxZ Y + gxZ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) Z = Jx Z = Jx | (8) |
Details of the use of eqn (5)–(8) and the procedure to obtain the principal values of the g-matrix can be found elsewhere.31
2.2 Nonrelativistic wavefunction
Finally, selecting an appropriate electronic structure method to approximate the eigenstates of the nonrelativistic Hamiltonian and construct Heff is crucial. For this purpose, we employ the RASCI method.34,35 In RASCI, the electronic wavefunctions are generated by applying an excitation operator to a reference configuration, typically a Hartree–Fock determinant. In RASCI, the molecular orbital space is divided into three subspaces: RAS1, RAS2, and RAS3. The RAS2 subspace contains the key orbitals and electrons necessary to describe the ground and low-lying excited states of the molecule. RAS1 corresponds to the doubly occupied orbitals below the RAS2 space, while RAS3 represents the virtual orbitals above RAS2. The excitation operator acting on the reference configuration is expressed as:![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) = = ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 0 + 0 + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) h + h + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) p + p + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) hp + hp + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2h + 2h + ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 2p + … 2p + … | (9) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 0 accounts for all possible configurations of electrons within RAS2, while the remaining terms describe configurations involving an increasing number of holes (h) in RAS1 and particles (p) in RAS3. This framework allows for a natural and flexible description of the ground and low-lying states with different spin multiplicities, making it especially suitable for strongly correlated systems such as open-shell molecules or systems with near-degenerate states. The accuracy and computational efficiency of the RASCI wavefunction are determined by the size of the RAS2 space and the truncation of the excitation operator in eqn (9).
0 accounts for all possible configurations of electrons within RAS2, while the remaining terms describe configurations involving an increasing number of holes (h) in RAS1 and particles (p) in RAS3. This framework allows for a natural and flexible description of the ground and low-lying states with different spin multiplicities, making it especially suitable for strongly correlated systems such as open-shell molecules or systems with near-degenerate states. The accuracy and computational efficiency of the RASCI wavefunction are determined by the size of the RAS2 space and the truncation of the excitation operator in eqn (9).
For the feasible application of RASCI in the calculation of g-shifts within the state-interaction framework, it is essential that the wavefunction accurately captures those nonrelativistic states contributing to the target electron spin multiplet while maintaining a moderate computational cost. Therefore, we chose a minimal RAS2 space, designed to describe the target spin multiplet M (where M = 2S + 1), using M − 1 electrons in M − 1 orbitals. Additionally, we truncate the excitation operator to include only the first three terms on the right-hand side of eqn (9). We expect that including hole and particle excitations will efficiently account for the influence of the full set of molecular orbitals, allowing us to construct large effective Hamiltonians, i.e., considering a wide range of excitations, without a significant increase in computational cost. The computational efficiency of the proposed method stems from employing a compact RAS2 space and truncating the excitation operator in eqn (9). As a result, the computational cost scales linearly with the size of the molecule and the basis set. This streamlined approach, which balances accuracy and efficiency, is more challenging to achieve in other multiconfigurational methods such as CASSCF.
Additionally, to optimize the RASCI wavefunction for calculating the g-matrix, we have developed an automated scheme to enhance the RAS2 space by identifying the most important states contributing to the shifts in the g-matrix relative to the free-electron spin (g = geI + Δg). Starting from a minimal RAS2 space, we expand it by incorporating relevant orbitals from RAS1 and/or RAS3. This is guided by the perturbative sum-over-states expression for evaluating the Zeeman/spin–orbit contributions to the Δg elements:13,36
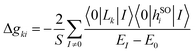 | (10) |
 | (11) |
 | (12) |
3 Computational procedure
Calculations for the triplet states of diatomic molecules O2, S2, NH, NF, NCl, and NBr were conducted using experimental bond lengths.40 For the remaining high-spin diatomic molecules, geometries were optimized using DFT with the BP86 exchange–correlation functional.29 Molecular coordinates for the conjugated cyclic organic compounds, optimized at the B3LYP level and discussed in Section 4.2, were taken from ref. 31. Additionally, triplet state geometries of linear acenes, ranging from anthracene to hexacene, were optimized using the M06-2X energy functional41 (ESI†).The choice of molecular orbitals for constructing RASCI wavefunctions is a critical factor. In this study, RASCI calculations have been performed using the high-spin ROHF wavefunction corresponding to the target state as the reference configuration. Details of the employed RAS2 spaces are indicated in Section 4 and in the ESI† (in particular those following the g-driven automatic strategy in eqn (11)). Unless otherwise specified, the RASCI calculations utilize the full set of occupied and virtual orbitals, with no frozen orbitals. The only exception is for polyatomic conjugated organic molecules, where the 1s core electrons of carbon, oxygen, and nitrogen atoms were frozen, meaning they were excluded from the RAS1 orbital space. Second-order perturbative corrections to RASCI excitation energies, i.e., RASCI(2),42 of diatomic molecules in Table S2 (ESI†) have been computed with the Davidson–Kapuy partition of the Hamiltonian.
Spin–orbit interactions have been introduced by means of the Breit–Pauli spin–orbit Hamiltonian,43,44 with a mean-field treatment of the two-electron terms,45 following a recent implementation.46 Scalar relativistic effects were not incorporated in the RASCI calculations.
Accurate calculation of g-matrix parameters necessitates the use of, at least, triple-ζ sets to give reliable results20 and the inclusion of polarization functions to address the gauge dependence problem.17 Consequently, the def2-TZVP basis set was employed for all g-shift calculations. Gauge dependency arises in g-matrix calculations due to the origin dependence of the angular momentum operator for finite basis sets. It is usually treated with gauge including atomic orbitals47 or the selection of the center of electronic charge as the gauge origin,48 being the latter a simple and effective way to treat this dependence. In our case, the gauge origin is placed at the center of nuclear charge, which, in non-ionic systems, appears to provide a reasonable approximation to the electronic charge center.26,33 Unless indicated, all g-values are reported as g-shifts (Δg) in parts per thousand (ppt). As indicated by eqn (5), within the state-interaction framework, the sign of the g-shift parameters is governed by the signs of the SOC and orbital angular momentum contributions. While a detailed exploration of this topic is beyond the scope of this work, the origin and uniqueness of the g-matrix sign are thoroughly discussed in the existing literature.49–53
Electronic structure calculations have been carried out using a developers version of Q-Chem 6.0.54 CP-DFT calculations have been performed with ORCA 6.0.55–58 Evaluation of the g-matrix parameters was carried out with in-house codes integrated within the PyQChem interface.59
4 Results and discussion
In the following, we apply our state-interaction approach to evaluate the g-matrix in a range of high-spin molecular species. Specifically, we assess the performance of RASCI in calculating g-shifts for diatomic molecules with high-spin ground states, as well as for spin-triplet states in conjugated polycyclic organic molecules.4.1 Diatomic molecules
We begin our analysis by evaluating the impact of using a g-driven selected RAS2 orbital space (g-RAS2) and investigating the dependence of the results on the number of states included in the effective Hamiltonian. To this end, we consider a small set of diatomic molecules with a triplet ground state: O2, S2, NH, NF, NCl, and NBr. Table 1 presents the g-tensor shifts computed using various RASCI state-interaction approaches for the selected ground-state spin-triplet diatomic molecules. The results are compared with experimental data and theoretical values obtained from MRSOCI,31 coupled-perturbed CASSCF (CP-CASSCF)25 and BP8629 calculations, all of which also utilize a mean-field approximation to the full Breit–Pauli operator. RASCI and MRSOCI computations were performed using experimental bond lengths,40 while CP-CASSCF and BP86 values were obtained at geometries optimized with the BP86 exchange–correlation functional.29 Our focus is on the doubly degenerate g-tensor component perpendicular to the molecular axis (Δg⊥), which is typically reported in experiments. The parallel component is symmetry-forbidden in homonuclear diatomic molecules,60 and tends to be small in heteronuclear diatomic compounds.| Molecule | min-RAS2[3] | min-RAS2[100] | g-RAS2[3] | g-RAS2[100] | MRSOCI | CP-CASSCF | BP86 | Exp. |
|---|---|---|---|---|---|---|---|---|
| O2 | 2.8 | 2.8 | 2.9 | 2.9 | 2.7 | 2.9 | 3.1 | 2.9 |
| S2 | 11.2 | 11.8 | 11.8 | 12.5 | 12.9 | 13.0 | 12.1 | 14.5 |
| NH | 1.4 | 1.4 | 1.4 | 1.4 | 1.3 | 1.2 | 1.5 | 1.7 |
| NF | 0.9 | 1.0 | 1.2 | 1.3 | 1.8 | 1.7 | 2.0 | 2.0 |
| NCl | 3.2 | 3.4 | 3.8 | 4.0 | 4.8 | 4.4 | 5.0 | 5.4 |
| NBr | 11.0 | 11.1 | 14.0 | 13.1 | 16.4 | 14.6 | 21.8 | 19.3 |
The homoatomic molecules O2 and S2 belong to the D∞h point group, with a triplet ground state X3Σg− characterized by two unpaired electrons in the degenerate  orbitals. Consistent with symmetry selection rules, the primary contribution to Δg⊥ arises from the interaction between the ground state and the lowest two-fold degenerate 3Πg excited states. The RASCI-computed g-shifts for O2 show excellent agreement with experimental results, while the computed shifts for S2 are slightly lower than experimental values. In O2, only the lowest doubly-degenerated 3Πg state significantly contributes to Δg⊥, as convergence is achieved with just three states (X3Σg− and 13Πg). Increasing the number of states in the effective Hamiltonian does not alter the results, as confirmed by the individual state contributions shown in Fig. 3. In contrast, expanding the RAS2 space by including additional orbitals to better describe the X3Σg− and 13Πg states using the g-driven RAS2 expansion technique leads to a slight improvement in the computed values. Starting with the minimal RAS2 orbital space required to describe the ground state triplet, consisting of two electrons in the two π-orbitals (min-RAS2), we employ the g-driven RAS2 expansion technique to automatically generate an improved fully correlated orbital space (Fig. 1). In this case, the primary contributions to Δg⊥ (in the x- and y-directions) arise from
orbitals. Consistent with symmetry selection rules, the primary contribution to Δg⊥ arises from the interaction between the ground state and the lowest two-fold degenerate 3Πg excited states. The RASCI-computed g-shifts for O2 show excellent agreement with experimental results, while the computed shifts for S2 are slightly lower than experimental values. In O2, only the lowest doubly-degenerated 3Πg state significantly contributes to Δg⊥, as convergence is achieved with just three states (X3Σg− and 13Πg). Increasing the number of states in the effective Hamiltonian does not alter the results, as confirmed by the individual state contributions shown in Fig. 3. In contrast, expanding the RAS2 space by including additional orbitals to better describe the X3Σg− and 13Πg states using the g-driven RAS2 expansion technique leads to a slight improvement in the computed values. Starting with the minimal RAS2 orbital space required to describe the ground state triplet, consisting of two electrons in the two π-orbitals (min-RAS2), we employ the g-driven RAS2 expansion technique to automatically generate an improved fully correlated orbital space (Fig. 1). In this case, the primary contributions to Δg⊥ (in the x- and y-directions) arise from  excitations. Consequently, the g-driven RAS2 space is extended to include four electrons within the
excitations. Consequently, the g-driven RAS2 space is extended to include four electrons within the  , and σpz orbitals.
, and σpz orbitals.
 | ||
| Fig. 1 Scheme of the g-driven RAS2 expansion technique in O2, using (2,2) active space in min-RAS2 and increasing it to (4,3) in g-RAS2. | ||
The magnitude of Δg⊥ in S2 is significantly larger than in O2, due to the stronger SOC arising from the higher atomic number of sulfur. The minimal RASCI approach, which uses a three-state Hamiltonian and a restricted RAS2 space (two electrons in the  orbitals), underestimates the experimental value by 23%. However, increasing the size of the RAS2 space and including additional electronic states in the effective Hamiltonian substantially improves the accuracy, yielding results comparable to those from MRSOCI and CP-CASSCF calculations.
orbitals), underestimates the experimental value by 23%. However, increasing the size of the RAS2 space and including additional electronic states in the effective Hamiltonian substantially improves the accuracy, yielding results comparable to those from MRSOCI and CP-CASSCF calculations.
Heteroatomic molecules NH, NF, NCl, and NBr belong to the C∞v point group and have a X3Σ− spin-triplet ground state. Deviations from the free-electron Landé factor in the direction perpendicular to the molecular bond axis are induced by SOC with the doubly degenerate 3Π state. RASCI-computed g-shifts follow the experimental trend along the NX series (H ∼ F < Cl < Br), but systematically underestimate the magnitude of the Δg⊥ values. Similar to the case of S2, both the expansion of the RAS2 space and the inclusion of more electronic states in the SOC-dressed Hamiltonian in general lead to improved results compared to the minimal scheme (RAS2 with two electrons in two orbitals and a three-state SOC Hamiltonian). The expansion of the RAS2 space, however, has a more significant impact. The absolute error in the RASCI-predicted Δg⊥ increases with the atomic number of X, likely due to inaccuracies in the computed excitation energies and/or SOCs, and possibly to the increasing influence of scalar relativistic effects.
To further investigate the parameters determining the magnitude of the g-values in nitrogen monohalides, we analyze the excitation energies and SOCCs between the ground-state triplet and the excited triplet state 3Π that primarily contribute to Δg⊥ (Table 2). The increase in the computed g-shifts is driven by the simultaneous decrease in excitation energies and the increase in SOCs with the atomic number of the halogen atom. The RASCI excitation energies are generally lower than those obtained from TDDFT using the B3LYP functional and from equation-of-motion coupled-cluster singles and doubles (EOM-CCSD). This suggests that inaccuracies in the relative energies of triplet–triplet states are unlikely to be the primary cause of the systematic underestimation of g-shifts. Table 2 also presents g-matrix parameters obtained by considering only the one-electron part of the BP Hamiltonian (Δg⊥1). A comparison of the total g-shifts reveals a decreasing two-electron contribution along the NF, NCl, and NBr series, consistent with the linear dependence of the one-electron SOC term on the atomic number Z. Since the two-electron SOC terms partially cancel the one-electron contribution,61 Δg⊥1 is consistently larger than the full Δg⊥. Excluding the two-electron SOC terms yields g-values that are closer to the experimental results, likely due to a fortuitous cancellation of errors.
| Molecule | ΔE | SOCC | Δg⊥1 | Δg⊥ | ||
|---|---|---|---|---|---|---|
| B3LYP | EOM-CCSD | RASCI | ||||
| NF | 7.70 | 7.07 | 7.13 | 56 | 1.9 | 1.2 |
| NCl | 5.52 | 5.10 | 5.04 | 102 | 5.2 | 3.8 |
| NBr | 4.89 | 4.50 | 4.35 | 315 | 16.2 | 14.0 |
We next extend our study to a broader set of diatomic molecules with high-spin ground states (S = 3, 4, 6, 7, and 12). Table 3 presents the RASCI g-shifts obtained using a high-spin ROHF reference configuration, a g-driven RAS2 space and incorporating 30 electronic states in the SOC-dressed Hamiltonian. These results are compared to BP86 calculations29 and experimental measurements. The excitation energies and the percentage of each configuration in each excited state using the min-RAS2, and the g-RAS2 approach with and without hole and particle configurations, are provided in the ESI† (Tables S2 and S3). Excluding hole and particle configurations systematically results in blue-shifted excitation energies, leading to reduced g-shifts. Furthermore, while min-RAS2 states predominantly exhibit contributions from hole and particle configurations, g-RAS2 states are mainly characterized by active configurations.
| Molecule | 2S + 1 | g-RAS2[30] | BP86 | Exp. |
|---|---|---|---|---|
| O2 | 3 | 2.9 (0) | 3.1 (7) | 2.9 |
| S2 | 3 | 13.9 (4) | 12.1 (17) | 14.5 |
| SeO | 3 | 15.1 (54) | 17.9 (45) | 32.7 |
| NH | 3 | 1.4 (18) | 1.5 (12) | 1.7 |
| NF | 3 | 1.2 (40) | 2.0 (0) | 2.0 |
| NCl | 3 | 4.0 (26) | 5.0 (7) | 5.4 |
| NBr | 3 | 14.3 (26) | 21.8 (13) | 19.3 |
| NI | 3 | 1.8 (94) | 38.9 (25) | 31.0 |
| Ge2+ | 4 | −39.4 (38) | −49.2 (22) | −63.2 |
| GaAs+ | 4 | −13.8 (189) | −20.3 (351) | −4.5 |
| V2+ | 4 | −54.7 (17) | −11.3 (76) | −46.3 |
| CrH | 6 | −1.5 (44) | −4.6 (270) | 2.7 |
| CrF | 6 | −1.1 (15) | −11.0 (746) | −1.3 |
| MnO | 6 | −3.2 (56) | 2.5 (134) | −7.3 |
| MnS | 6 | 2.4 (64) | 10.2 (52) | 6.7 |
| MnH | 7 | −1.9 (46) | −2.0 (54) | −1.3 |
| MnF | 7 | −1.0 (23) | 0.1 (108) | −1.3 |
| MnCl | 7 | −1.8 (75) | 0.9 (112) | −7.3 |
| MnBr | 7 | −3.3 (65) | 5.1 (155) | −9.3 |
| MnI | 7 | −2.4 (74) | 10.7 (215) | −9.3 |
| Mn2+ | 12 | −0.7 (79) | 2.0 (161) | −3.3 |
In general, the RASCI errors are comparable to those obtained with BP86. However, an interesting trend emerges: for molecules with a triplet-spin ground state, the DFT errors are smaller than those from RASCI. Conversely, for higher-spin ground states (S ≥ 6), the RASCI results show better agreement with experimental data. This discrepancy may be attributed to the known limitations of KS-DFT functionals in accurately describing systems with near-degenerate ground states, whereas the optimized active space in our RASCI calculations helps capture these effects more effectively.
Certain systems exhibit significant deviations from the reference experimental values. Notably, for SeO, both RASCI and BP86 substantially underestimate Δg⊥. Similar underestimations have been reported using the VWN local density approximation, the RPBE gradient-corrected functional,29 and the PBE functional implemented with the effective potential method.30
The underestimation is even more pronounced in the case of NI, although the BP86 value slightly exceeds the experimental shift. Notably, the BP86 calculations by Patchkovskii and Ziegler29 utilized Slater-type orbitals and incorporated scalar relativistic effects via relativistic frozen core potentials and the first-order Pauli Hamiltonian. To investigate the origin of this discrepancy, we performed additional CP-DFT/BP86 calculations. Using the same atomic basis set as in our RASCI computations (def2-TZVP), CP-DFT/BP86 yields a significant underestimation of Δg⊥ (1.9 ppt). However, the value increases substantially to 35.2 ppt when the ANO-RCC basis set is employed.62 Analysis of the contributions to Δg reveals that this increase arises from the cross term between the orbital Zeeman and spin–orbit coupling interactions,63 a contribution also captured in our approach. These results underscore the crucial role of the basis set in accurately calculating g-shifts, particularly for molecules containing heavy elements such as iodine.
In GaAs+, the ground state X4Σ− exhibits the strongest spin–orbit interaction with the doubly degenerate 4Π state, which have an excitation energy of 3.42 eV. Considering only these three states (g-RAS2[3]) yields Δg⊥ = −9.6 ppt. Replacing the g-RAS2 computed energy (3.42 eV) with the CASSCF energy reported by Balasubramanian (6.46 eV)64 in the 3-state effective SOC-dressed Hamiltonian reduces the shift to Δg⊥ = −5.1 ppt. This indicates that the overestimation of the g-shift in this case arises primarily from an underestimation of the quartet-quartet excitation energy.
4.2 Conjugated cyclic organic molecules
We next apply our methodology to the characterization of g-parameters in the lowest triplet state of neutral organic conjugated molecules. In these larger systems, the increased density of electronic states compared to diatomic molecules means that higher-energy or multiple excited states can significantly influence the interaction between electronic spins and an external magnetic field. To begin, we analyze three conjugated carbonyl compounds: 1,4-benzoquinone (also known as p-benzoquinone), benzophenone, and fluorenone. These molecules feature low-lying ππ* and nπ* states with significant SOCs, in agreement with the El-Sayed rules.65 Following this, we explore the triplet state of the simplest polycyclic aromatic hydrocarbon, naphthalene, and examine the effects of nitrogen substitution in quinoline. The computed g-values are presented in Table 4, alongside DFT/MRSOCI results31 and experimental data, when available, for comparison.| Molecule | min-RAS2[30] | g-RAS2[30] | min-RAS2[500] | DFT/MRSOCI | Exp.a | |
|---|---|---|---|---|---|---|
| a Experimental values for benzophenone (ref. 66 and 67), benzoquinone (ref. 68), naphthalene and in quinoline (ref. 69). | ||||||
| p-Benzoquinone | Δgxx | 3.01 | 3.08 | 2.83 | 2.38 | 2.18 |
| Δgyy | 0.10 | 0.16 | 0.64 | 0.55 | 1.18 | |
| Δgzz | 12.69 | 10.83 | 12.46 | 44.40 | 7.62 | |
| Benzophenone | Δgxx | 3.08 | 3.04 | 3.04 | 2.73 | −0.22, −2.92 |
| Δgyy | 0.16 | 0.13 | 0.55 | 0.31 | −1.42, −3.32 | |
| Δgzz | 12.30 | 9.75 | 12.25 | 12.10 | 8.28, 7.38 | |
| Fluorenone | Δgxx | 0.01 | 0.01 | 0.01 | 0.01 | — |
| Δgyy | 0.04 | 0.29 | 0.66 | 0.94 | — | |
| Δgzz | 0.40 | 1.29 | 0.79 | 2.30 | — | |
| Naphthalene | Δgxx | 0.09 | 0.48 | 0.40 | 0.21 | 0.68 |
| Δgyy | 0.01 | 0.08 | 0.45 | 0.29 | 0.68 | |
| Δgzz | 0.03 | 0.02 | 0.03 | 0.03 | 0.58 | |
| Quinoline | Δgxx | 0.28 | 0.25 | 0.51 | 1.23 | 1.68 |
| Δgyy | 0.16 | 0.01 | 0.45 | 0.41 | 0.58 | |
| Δgzz | 0.01 | 0.01 | 0.01 | 0.02 | −0.42 | |
The ground-state singlet of p-benzoquinone exhibits an optimized geometry that belongs to the D2h symmetry point group. Upon geometry optimization on the lowest triplet state PES, the molecule retains its planarity but reduces its symmetry to C2v due to a pseudo-Jahn–Teller distortion involving several nearly degenerate electronic states.70 At the PES minimum, the T1 state belongs to the 3A2 irreducible representation and exhibits a nπ* character (Fig. S2, ESI†).71 The strongest component of the g-matrix, both experimentally observed and computationally predicted, lies along the two carbonyls bond axis (Δgzz). RASCI calculations for the gzz shift, using the minimal RAS2 space, slightly overestimate the experimental value,68 and the shift remains nearly invariant as the number of states is increased. The relatively large Δgzz arises from the coupling of T1 with low-lying ππ* triplet states (Fig. S2 and Section 2.2 in the ESI†). Modifying the RAS2 space via the g-driven procedure improves the description of these critical states, resulting in better agreement with experimental data. Notably, the RASCI calculations do not suffer from the large overestimation of Δgzz observed in DFT/MRSOCI calculations. This discrepancy may be attributed to the underestimation of energy gaps to low-lying 3ππ* states in DFT/MRSOCI, which artificially amplifies the g-shift. The primary contribution to the xx-component of the g-matrix arises from a 3B2 (σπ*) state (Section 2.2 in the ESI†). RASCI calculations using the minimal RAS2 space overestimate the experimental Δgxx value. Increasing the size of the RAS2 space via the g-driven procedure does not significantly improve the results, and only a slight reduction in the overestimation is observed when a large number of states are included in the effective Hamiltonian. Similarly, the best results for Δgyy are obtained when a large number of states are included in the state-interaction scheme.
The T1 state of benzophenone adopts a non-planar structure with C2 symmetry, which can be attributed to an out-of-plane bending distortion caused by the pseudo-Jahn–Teller effect. This distortion arises from the interaction between the lowest 3nπ* state and a low-lying 3ππ* state.31 Our RASCI calculations identify the lowest triplet state as belonging to the A2 irreducible representation, with a strong nπ* character, consistent with the experimental assignment.72 The performance of different RASCI approaches in evaluating g-shifts is similar to that observed in p-benzoquinone. The g-shift along the carbonyl bond axis (Δgzz), arising from the interaction between the (nπ*) T1 state and low-lying 3ππ* states, improves with an expansion of the g-driven RAS2 space. On the other hand, Δgyy is more sensitive to the size of the effective SOC-dressed Hamiltonian (Section 2.2 in the ESI†).
Fluorenone belongs to the C2v point group, with the T1 state corresponding to the 3B1 irreducible representation and having a ππ* character, as confirmed by experimental results.73 In RASCI calculations, the main g-shift, Δgzz, occurs along the carbonyl bond axis and arises from the interaction of the ground state with the 13B2 state (nπ*, ΔE = 3.02 eV, SOCC = 44 cm−1). The Δgyy component results from interactions with high-energy 3A2 states (σπ*), such as the 173A2 state, with ΔE = 10.32 eV and SOCC = 22 cm−1.
The optimized geometry of naphthalene on the T1 potential energy surface retains the D2h symmetry of the ground-state singlet. At its energy minimum, the lowest triplet state exhibits a pristine ππ* character and belongs to the B2u irrep. Compared to the three conjugated ketone molecules studied, the absence of heteroatom lone pairs (n) in naphthalene results in g-values that are closer to the free-electron value, in agreement with the El-Sayed rules.65 In-plane g-shifts (Δgxx and Δgyy) arise from the coupling of T1 with 3B1u and 3Au states, respectively, both of which have σπ* or πσ* character. The computed g-shifts underestimate experimental values, consistent with previous MRSOCI calculations by Tatchen et al.,31 who suggested that this discrepancy could stem from the absence of first-order corrections (relativistic mass correction to the spin-Zeeman interaction, and the one- and two-electron spin–orbit Zeeman gauge corrections). However, our results indicate that, to achieve Δgxx and Δgyy values closer to experimental measurements within a state-interaction framework, a large number of excited states must be included in the effective Hamiltonian (eqn (4)), as demonstrated by calculations using a minimal RAS2 space (2 electrons in 2 orbitals) and 500 states. Conversely, RASCI calculations with various RAS2 spaces, even when including many excited states, underestimate the g-shift along the axis normal to the molecular plane. The primary contributions to Δgzz originate from low-lying 3ππ* states. We tentatively attribute this discrepancy to limitations in the chosen wavefunction method, particularly the lack of dynamic correlation in RASCI with hole and particle excitations, as recently discussed in the computation of g-parameters for spin-doublet molecules.22 This deficiency likely leads to overly large energy gaps between the T1 state and other excited 3ππ* states. For instance, the energy gap between the lowest triplet state and the 3ππ* state that predominantly contributes to Δgzz, identified as 13B3u, is 1.98 eV when computed at the TDDFT/B3LYP level, significantly smaller than the RASCI value of 2.87 eV. However, substituting the RASCI energy with the B3LYP value in the g-RAS2[30] SOC-dressed effective Hamiltonian results in only a slight increase in the magnitude of the g-shift (Δgzz = 0.031 ppt). This minor adjustment does not fully account for the discrepancy with the experimental value, suggesting other factors may also contribute to the observed differences. Furthermore, it has been suggested that the mean-field approximation to the two-electron term in the Breit–Pauli Hamiltonian is inadequate for accurately describing SOCs between ππ* states.74
Quinoline in its lowest triplet state adopts a planar structure with Cs symmetry. Similar to naphthalene, it exhibits a ππ* character, though with a slightly distorted distribution of the two unpaired electrons, as observed in Fig. 2. The results obtained using various RASCI methods exhibit a performance comparable to that for naphthalene. As with naphthalene, accurately reproducing the magnitude of the g-shifts within the molecular plane requires the inclusion of high-lying triplet states with σπ* and πσ* character. However, the presence of a nitrogen atom in the quinoline backbone significantly increases the experimentally observed Δgxx compared to naphthalene. This trend is only partially captured by the RASCI calculations (min-RAS2[500]). This discrepancy can be attributed to the overestimation of the energy gap between the T1 state and higher-energy contributing triplets. In RASCI, the lowest triplet state with notable σπ* character and a sizable spin–orbit coupling constant (SOCC) of 8.2 cm−1 is calculated at an energy gap of 7.3 eV, while in DFT/MRSOCI, the first triplet above T1 appears at 1.3 eV with a larger SOCC of 10 cm−1.
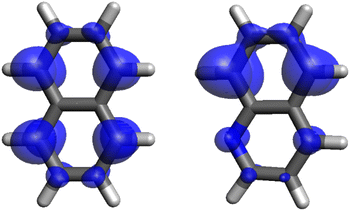 | ||
| Fig. 2 Electron spin density distributions for the T1 state of naphthalene (left) and quinoline (right). Isosurface value: 0.005 Bohr−3. | ||
Benzophenone and p-benzoquinone exhibit their most significant contributions to the g-parameters in two states that are energetically closer to the ground state. As a result, an optimal description of these states, and consequently the g-shift, is achieved using the refined active space defined without requiring a large effective Hamiltonian. In contrast, fluorenone, naphthalene, and quinoline do not show a single dominant transition but rather a multitude of transitions that collectively influence Δg. For these molecules, the best description of the g-shift is attained within the initial active space, utilizing a larger number of states. Fig. 3 illustrates these transitions for benzophenone, naphthalene, and quinoline.
 | ||
| Fig. 3 Absolute values of the Δg components in two-state SOC-dressed Hamiltonians, the ground and a single excited state (# roots in the x-axis) for O2, benzophenone, naphthalene and quinoline. | ||
4.3 Linear acenes
Finally, we examine the performance of our approach in calculating g-values for linear acenes. This allows us to determine whether the trends observed in naphthalene extend to other polyaromatic hydrocarbons and to analyze the dependence of g-values on molecular size across the series from naphthalene to hexacene. Table 5 presents the g-tensor shifts for linear [n]acenes with n = 2–6, calculated using various RASCI approaches. We employed three orbital space configurations: a complete active space CI with 8 electrons in the 8 frontier π-orbitals (without additional hole or particle contributions), the minimal RAS2 space selection (2 electrons in 2 orbitals), and the system specific g-driven expanded RAS2 space. No comparable experimental or theoretical data is available, as studies on these molecules have focused only on their ionic structures.75–78 Results are also compared with CPKS BP86 calculations,63 which were performed variationally using a non-relativistic Hamiltonian. Scalar relativistic effects were not included, and the same basis set was used for consistency. For clarity, unlike previous sections, values in Table 5 are presented in part per million (ppm).| n | π-CASCI[30] | min-RAS2[30] | g-RAS2[30]a | min-RAS2[500] | BP86 | |
|---|---|---|---|---|---|---|
| a Details on the RAS2 space given in the ESI. | ||||||
| 2 | Δgxx | 1 | 192 | 25 | 475 | 664 |
| Δgyy | −1 | 159 | −3 | 430 | 563 | |
| Δgzz | 18 | 14 | 20 | 14 | −56 | |
| 3 | Δgxx | 0 | 145 | 13 | 445 | 665 |
| Δgyy | 0 | 122 | 6 | 409 | 560 | |
| Δgzz | 17 | 12 | 8 | 13 | −41 | |
| 4 | Δgxx | 0 | 8 | 1 | 449 | 672 |
| Δgyy | 0 | −20 | −1 | 383 | 561 | |
| Δgzz | 22 | 17 | 11 | 22 | −31 | |
| 5 | Δgxx | 0 | 84 | 2 | 425 | 677 |
| Δgyy | 0 | 89 | 2 | 406 | 545 | |
| Δgzz | 18 | 11 | 9 | 15 | −26 | |
| 6 | Δgxx | 0 | 6 | 1 | 508 | 686 |
| Δgyy | 0 | −14 | −0 | 382 | 541 | |
| Δgzz | 19 | 12 | 1 | 17 | −24 | |
The DFT-computed g-shifts of naphthalene in the molecular plane, Δgxx (short molecular axis) and Δgyy (long molecular axis), show good agreement with experimental values (Table 4). Therefore, BP86 values for Δgxx and Δgyy will be used as reference points for evaluating our RASCI calculations in the remaining [n]acenes in the triplet state. Conversely, the DFT result for Δgzz in naphthalene has an opposite sign to the experimental value and is an order of magnitude smaller.
As discussed for naphthalene, the g-shift component perpendicular to the molecular plane (Δgzz) is primarily influenced by interactions between T1 and other low-lying 3ππ* nonrelativistic states. Consequently, the CASCI values obtained with an active space limited to π-orbitals cannot be enhanced through the g-driven automatic orbital selection strategy or by expanding the effective Hamiltonian. The requirement to include states with σπ* and πσ* character to achieve significant xx and yy shifts becomes evident in the vanishing CASCI values and the results from a minimal RAS2 space (min-RAS2[30] and min-RAS2[500] in Table 5). To fully capture these contributions, a broad manifold of excited states is essential. Additionally, the convergence of the state-interaction approach may necessitate an even larger number of excited states as molecular size increases (Fig. S13, ESI†), owing to the higher density of states.
Notably, the difference between Δgxx and Δgyy relative to BP86 shifts grows with the increasing number of six-membered rings. Specifically, Δgxx increases with the length of the molecules, while Δgyy remains relatively constant across the series. This trend aligns with the expected rise in anisotropy between the x and y directions as the molecular length increases. The RASCI method, using a minimal RAS2 space and a large-dimension state interaction scheme, yields in-plane g-shifts of similar magnitude to those obtained with DFT. However, it does not capture the increasing anisotropy between the short and long molecular axes with the molecular size.
5 Conclusions
We have developed a general methodology for efficiently evaluating g-shifts in molecular systems with any spin multiplicity, leveraging a state-interaction approach to construct a SOC-dressed (effective) Hamiltonian from nonrelativistic states obtained with the RASCI wavefunction. Our method incorporates both hole and particle configurations, allowing for a focused analysis of excited-state contributions to the g-matrix. By circumventing the need for extensive complete active spaces, this approach maintains computational efficiency while achieving accurate results. Importantly, our method enables a detailed dissection of g-shifts by analyzing the couplings between target nonrelativistic spin multiplets in terms of excitation energies, SOC effects, and transition angular moments.Overall, our strategy has proven to be a viable approach for evaluating and characterizing g-shifts. Our results for a range of diatomic molecules show very good agreement with both high-accuracy methods and experimental data, demonstrating the effectiveness of our approach. In these systems, g-values depend on contributions from a limited set of excited states, simplifying their computational characterization. Larger molecules, such as conjugated organic compounds, however, often feature numerous low-lying electronic excited states with significant spin–orbit interactions with the ground state, and a broader set of excited states might substantially contribute to the overall g-shifts. In these cases, the methodology benefits from larger effective Hamiltonians, as the g-shifts are the cumulative result of numerous contributions. We observed that discrepancies in accuracy of g-values of conjugated organic molecules in the T1 state may arise from errors in the computed energy gaps between nonrelativistic states and from variations in SOC magnitudes. For instance, the underestimation of Δg in some molecules primarily stems from overestimated energy gaps between the lowest triplet state and 3ππ* excited states.
While various strategies and algorithms have been developed for automatic active-orbital-space selection in multi-configurational wavefunctions, this work, to the best of our knowledge, represents the first instance of a property-driven automatic approach for constructing an active orbital space tailored for magnetic property calculations. This selection targets those orbitals critical for capturing the dominant contributions to the Δg values, further reducing computational demands. The RASCI framework is particularly well-suited to this approach, as it enables the exploration of orbitals' impact on electronic properties through hole and particle excitations beyond the RAS2 space. This property-driven scheme holds promise for extension to other electronic properties, an area we are actively investigating in our lab.
Author contributions
A. C.-G. and D. C. jointly conceived and designed the project and developed the computational methodologies. A. C.-G. conducted the calculations and performed data analysis. Both authors collaborated in drafting and revising the manuscript, providing critical insights and edits throughout the writing process.Data availability
The data that supports the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from MICIU/AEI/10.13039/501100011033 (projects PID2022-136231NB-I00 and PRE2020-094317) and by FEDER, UE, the Gipuzkoa Provincial Council (project QUAN-000021-01), the European Union (project NextGenerationEU/PRTR-C17.I1), as well as by the IKUR Strategy under the collaboration agreement between Ikerbasque Foundation and DIPC on behalf of the Department of Education of the Basque Government. The authors are thankful for the technical and human support provided by the Donostia International Physics Center (DIPC) Computer Center. D. C. is thankful for financial support from IKERBASQUE (Basque Foundation for Science).Notes and references
- Transition Metal and Rare Earth Compounds: Excited States, Transitions, Interactions I, ed. H. Yersin, Springer-Verlag, 2004 Search PubMed.
- F. Neese, J. Chem. Phys., 2009, 132, 034105 Search PubMed.
- J. K. McCusker, Acc. Chem. Res., 2003, 36, 876–887 CrossRef CAS PubMed.
- A. Bencini and D. Gatteschi, EPR of Exchange Coupled Systems, Springer-Verlag, 1990 Search PubMed.
- E. I. Solomon, U. M. Sundaram and T. E. Machonkin, Chem. Rev., 1996, 96, 2563–2605 CrossRef CAS PubMed.
- G. Morra, G. Colombo and M. Meli, Biochemistry, 2012, 51, 1957–1972 Search PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- A. I. Krylov, Rev. Comput. Chem., 2017, 30, 151–224 CAS.
- F. Neese and E. I. Solomon, Magnetism: Molecules to Materials IV: Nanosized Magnetic Materials, 2001, pp. 345–466 Search PubMed.
- G. H. Lushington, J. Phys. Chem. A, 2000, 104, 2969–2974 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem. A, 1997, 101, 3388–3399 CrossRef CAS.
- E. van Lenthe, P. E. Wormer and A. van der Avoird, J. Chem. Phys., 1997, 107, 2488–2498 CrossRef CAS.
- S. K. Singh, M. Atanasov and F. Neese, J. Chem. Theory Comput., 2018, 14, 4662–4677 CrossRef CAS PubMed.
- O. L. Malkina, J. Vaara, B. Schimmelpfennig, M. Munzarová, V. G. Malkin and M. Kaupp, J. Am. Chem. Soc., 2000, 122, 9206–9218 CrossRef CAS.
- D. Moores and R. McWeeny, Mol. Phys., 1973, 26, 1337–1350 Search PubMed.
- G. Lushington, P. Bündgen and F. Grein, Int. J. Quantum Chem., 1995, 55, 377–392 CrossRef CAS.
- G. Lushington and F. Grein, Int. J. Quantum Chem., 1996, 60, 1679–1684 CrossRef.
- G. H. Lushington and F. Grein, Theor. Chim. Acta, 1996, 93, 259–267 CAS.
- M. Engström, O. Vahtras and H. Ågren, Chem. Phys., 1999, 243, 263–271 CrossRef.
- J. Gauss, M. Kallay and F. Neese, J. Phys. Chem. A, 2009, 113, 11541–11549 CrossRef CAS PubMed.
- A. Perera, J. Gauss, P. Verma and J. A. Morales, J. Chem. Phys., 2017, 146, 164104 CrossRef PubMed.
- S. Kähler, A. Cebreiro-Gallardo, P. Pokhilko, D. Casanova and A. I. Krylov, J. Phys. Chem. A, 2023, 127, 8459–8472 CrossRef PubMed.
- O. Vahtras, B. Minaev and H. Ågren, Chem. Phys. Lett., 1997, 281, 186–192 CrossRef CAS.
- O. Vahtras, M. Engström and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 351, 424–430 CrossRef CAS.
- T. N. Lan, J. Chalupský and T. Yanai, Mol. Phys., 2015, 113, 1750–1767 CrossRef CAS.
- S. Vancoillie, P.-Å. Malmqvist and K. Pierloot, ChemPhysChem, 2007, 8, 1803–1815 CrossRef CAS PubMed.
- S. Vancoillie and K. Pierloot, J. Phys. Chem. A, 2008, 112, 4011–4019 CrossRef CAS PubMed.
- G. Lushington and F. Grein, Theor. Chim. Acta, 1996, 93, 259–267 CAS.
- S. Patchkovskii and T. Ziegler, J. Phys. Chem. A, 2001, 105, 5490–5497 CrossRef CAS.
- A. Van Yperen-De Deyne, E. Pauwels, V. Van Speybroeck and M. Waroquier, Phys. Chem. Chem. Phys., 2012, 14, 10690–10704 RSC.
- J. Tatchen, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2009, 130, 154106 CrossRef PubMed.
- D. Jayatilaka, J. Chem. Phys., 1998, 108, 7587–7594 CrossRef CAS.
- H. Bolvin, ChemPhysChem, 2006, 7, 1575–1589 CrossRef CAS PubMed.
- D. Casanova and M. Head-Gordon, Phys. Chem. Chem. Phys., 2009, 11, 9779–9790 RSC.
- D. Casanova, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1561 CAS.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- E. Epifanovsky, K. Klein, S. Stopkowicz, J. Gauss and A. I. Krylov, J. Chem. Phys., 2015, 143, 064102 CrossRef PubMed.
- B. Huron, J. Malrieu and P. Rancurel, J. Chem. Phys., 1973, 58, 5745–5759 CrossRef CAS.
- F. Neese, Magn. Reson. Chem., 2004, 42, S187–S198 CrossRef CAS PubMed.
- K. Huber, Molecular spectra and molecular structure: IV. Constants of diatomic molecules, Springer Science & Business Media, 2013 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- D. Casanova, J. Chem. Phys., 2014, 140, 144111 CrossRef PubMed.
- W. Pauli, Z. Phys., 1927, 43, 601–623 CrossRef CAS.
- H. A. Bethe and E. E. Salpeter, Quantum mechanics of one and two electron atoms, Plenum, New York, 1977 Search PubMed.
- C. M. Marian, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- A. Carreras, H. Jiang, P. Pokhilko, A. I. Krylov, P. M. Zimmerman and D. Casanova, J. Chem. Phys., 2020, 153, 214107 CrossRef CAS PubMed.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- A. Luzanov, E. Babich and V. Ivanov, J. Mol. Struct., 1994, 311, 211–220 CrossRef.
- M. Pryce, Phys. Rev. Lett., 1959, 3, 375 CrossRef CAS.
- A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, OUPOxford, 2012, ch. 3, pp. 133–216 Search PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- L. F. Chibotaru, Adv. Chem. Phys., 2013, 153, 397–519 CrossRef CAS.
- S. Komorovsky, arXiv, 2023, preprint, arXiv:2305.06778 DOI:10.48550/arXiv.2305.06778.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- F. Neese, J. Comput. Chem., 2023, 44, 381–396 Search PubMed.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- A. Carreras, PyQchem: a python interface for Q-Chem, https://github.com/abelcarreras/PyQchem, 2019 Search PubMed.
- W. J. Weltner, Magnetic Atoms and Molecules, Dover Publications, New York, 1983 Search PubMed.
- D. G. Fedorov and M. S. Gordon, J. Chem. Phys., 2000, 112, 5611–5623 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2001, 115, 11080–11096 CrossRef CAS.
- K. Balasubramanian, J. Chem. Phys., 1987, 86, 3410–3413 CrossRef CAS.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- J. A. Mucha and D. W. Pratt, J. Chem. Phys., 1977, 66, 5339–5355 CrossRef CAS.
- M. Sharnoff and E. B. Iturbe, J. Chem. Phys., 1975, 62, 145–156 CrossRef CAS.
- J. H. Lichtenbelt, J. G. Fremeyer, H. Veenvliet and D. A. Wiersma, Chem. Phys., 1975, 10, 107–115 CrossRef CAS.
- C. A. Hutchison Jr and B. W. Mangum, J. Chem. Phys., 1961, 34, 908–922 CrossRef.
- K. Nakatani, H. Sato and R. Fukuda, Chem. Phys. Lett., 2020, 741, 137072 CrossRef CAS.
- M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VCH, 1995 Search PubMed.
- S. Dym, R. M. Hochstrasser and M. Schafer, J. Chem. Phys., 1968, 48, 646–652 CrossRef CAS.
- L. J. Andrews, A. Deroulede and H. Linschitz, J. Phys. Chem., 1978, 82, 2304–2309 CrossRef CAS.
- O. Vahtras, M. Engström and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 351, 424–430 CrossRef CAS.
- A. Stone, Mol. Phys., 1964, 7, 311–316 CrossRef CAS.
- R. Biehl, M. Plato and K. Möbius, Mol. Phys., 1978, 35, 985–996 CrossRef CAS.
- G. Owen and G. Vincow, J. Chem. Phys., 1971, 54, 368–375 Search PubMed.
- D. Fassaert and E. De Boer, Mol. Phys., 1971, 21, 485–496 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04511d |
| This journal is © the Owner Societies 2025 |
