Multidimensional quantum Fourier transform for nanosheet material evaluation by electron microscopy: a case of 2D pattern processing

Abstract

A method of quantum Fourier transform for multidimensional inputs of any periodicity was newly developed and conducted first-approximated simulations of the selected area electron diffraction patterns for the evaluation of nanosheet materials.

---

Nanosheet materials have attracted attention recently for use in various chemical applications.^1,2 The physicochemical properties of nanosheet materials differ drastically depending on their thickness.¹ For this reason, thickness-controlled synthesis and layer number identification of nanosheet materials are crucially important to tailor their various characteristics.³ Transmission electron microscopy (TEM) observation is a promising means of identifying the layer number. Both transmission images and SAED patterns are obtained from TEM observations. In fact, simulations of the SAED pattern of nanosheet materials using next-generation computing are promising. To explore the application of multidimensional QFT (Quantum Fourier Transform) and to characterise the available inputs further, the approximated SAED patterns of CeO₂ nanosheets were simulated using QFT in this work. CeO₂ is a versatile material,⁴ and moreover, a large number of oxygen vacancies and high ion conductivity, which are important properties for catalysis applications, are observed in its nanosheet materials.^5,6

The development of quantum algorithms with widely diverse applications is essential for leveraging quantum computing for solving various problems, and for the development of quantum hardware.⁷ In terms of computational methods, quantum computers differ entirely from classical computers because of the behaviour of the unit of information: the bit. Utilising the properties of the quantum bit achieves exponential speedup in some instances (quantum advantage). Broadening the scope of applications for algorithms with the quantum advantage grows solvable problems in a realistic time. QFT,⁸ a quantum algorithm with proven quantum advantage, implements discrete Fourier transform in classical computing in a quantum computer. Discrete FT in chemistry is an established method used for spectrum processing.^9–12 In addition, QFT is a subroutine for diverse quantum algorithms such as quantum state estimation,^13,14 solving simultaneous equations,¹⁵ numerical integration,¹⁶ and prime factorisation.¹⁷ Consequently, diversifying the applications of QFT plays an important role from the viewpoints of application in discrete FT and enrichment of quantum algorithms.

Earlier reports have described that QFT, with some modification, is applicable to various input data.^15,16 Pfeffer reported the development of a quantum circuit of QFT for multidimensional input; also, a two-dimensional QFT was performed on an IBM quantum computer.¹⁸ According to Camps et al., an analysis of QFT by tensor decompositions extended quantum operators and quantum circuits of QFT into radix-d operators and circuits, where d is an arbitrary natural number. However, the general input shape of QFT is radix-2 because a typical quantum bit is expected to represent two values.¹⁹ However, this earlier research considered some prerequisites: one study included an assumption of input equally sized along every dimension;¹⁸ the other study included necessary hardware, where a quantum bit represents d different values although the general input shape of QFT is radix-2 because a typical quantum bit is expected to represent two values, ¹⁹ to realise the proposed operations.¹⁶ Therefore, robust modification with no assumption of multidimensional QFT for arbitrary input shape, increasing the applications of QFT, remains elusive.

Here, we have developed a robust QFT method for arbitrary input shape on a general quantum computer system through simulations of SAED patterns approximated by QFT of the electron density of the sample. The electron densities were converted to inputs of each FT, as presented in Fig. 1. An interpretation of the quantum circuit of the multidimensional QFT indicated that the multidimensional QFT can be performed even using inputs not equally separated along the dimensions. Moreover, multiplying a window function by an input enables us to obtain an accurate ratio of intensities for inputs possessing a repeating unit, not a divisor of 2ⁿ, the input length of QFT.

Fig. 1 Procedure for input generation.

A quantum circuit represents quantum operations acting on each quantum bit at a quantum algorithm. A quantum circuit of two-dimensional QFT is presented as an example. Also, the requirements for inputs in multidimensional QFT algorithms are elucidated. Quantum operations at multidimensional QFT algorithms were derived as presented in Note S1 of the ESI.† A quantum circuit for 2³ × 2³ shaped input is portrayed in Fig. 2. A box and line between two bits respectively represent quantum operations based on a quantum state and two quantum states. In Fig. 2, q₀ to q₂ and q₃ to q₅ respectively correspond to the index along the x-direction and y-direction. No operation exists between bits of the x-index and y-index, indicating that the x and y directions are independent in terms of quantum operations at two-dimensional QFT. This independence between directions was general for arbitrary dimensional QFT (Note S1 and Fig. S3 in ESI†). Therefore, the multidimensional QFT acts on all input shapes realised by quantum computers to be used because the input length along a direction, whether long or short, does not affect the other input direction. Also, multidimensional QFT features provide lower computational complexity (quantum supremacy) than discrete Fourier transform in classical computing, discrete FT, and fast Fourier transform (FFT), which conduct radix-2 discrete FT with low computational complexity (Fig. S4, ESI†).

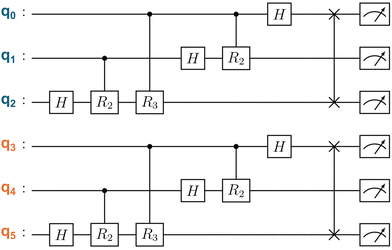Fig. 2 Quantum circuit of 2-dimensional QFT for 2³ × 2³ shaped input. Blue and orange letters correspond to bits along the x- and y-dimension. Vertical lines and boxes represent quantum operations.

The multidimensional QFT was applied to the SAED simulation of a nanosheet material. A CeO₂ nanosheet exposing the (100) surface was selected as a model. Because CeO₂(100) has 2 × 2 of x–y periodicity, each Fourier transform (i.e., discrete FT, FFT, and QFT) was performed for 2ⁿ × 2^m shaped input that kept its x–y period, where the shape of the input corresponds to the x–y size of the nanosheet material considered. Details of the SAED simulations and analysis implementation in this article were presented respectively in the ESI,† and https://github.com/Hiroshi3pei/2DQFTforSAED.

Because FFT and QFT are performed under the assumption that their input repeats periodically, they give the same SAED pattern as discrete FT as long as the period of the input is the same as that of the nanosheet surface (Fig. 3). For cases with different periods of input and nanosheet surface, a comparison of QFT for input and discrete FT for the period of the nanosheet surface is provided in the following paragraphs. Identical SAED patterns obtained from discrete FT and QFT indicate that the multidimensional QFT works correctly with rectangular input. Although QFT with input equally sized along every dimension has been discussed in earlier work,¹⁵ the present report describes, for the first time, that the multidimensional QFT operates for inputs with various aspect ratios. Furthermore, both discrete FT and QFT gave the same SAED pattern when the input size was varied (Fig. S6 in ESI†). Additionally, the intensity ratio of I(0, 2) to I(0, 0), corresponding to the direct beam for 2³ × 2² shaped input, was unique for each number of layers of the CeO₂ nanosheet exposing the (100) surface, where I(x, y) represents the intensity ratio at position (x, y) (Fig. S7 in ESI†). However, the intensity ratio of I(4, 2) to I(0, 0) was irrespective of the number of layers (Fig. S7 in ESI†). The layers of the synthesised nanosheet materials can be quantified within the accuracy of spot intensity measurements by comparing QFT results without the approximation of scattering media described in the ESI,† to the intensity ratio of the measured spot, which gives a unique intensity. As described in the ESI,† this SAED simulation assumed the kinematical diffraction condition besides approximation of scattering and the direction of the electron beam. Various criteria have been proposed for limiting the specimen thickness to adopt kinematic diffraction.²⁰ Therefore, in practice, the balance between the limitation of the kinematical diffraction and the accuracy of spot intensity measurement determines the maximum number of identifiable layers of the nanosheet material.

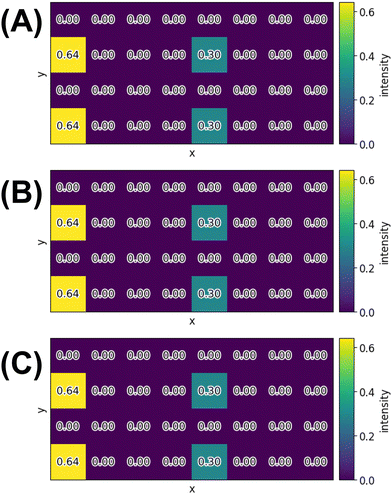Fig. 3 SAED patterns for a 2³ × 2² shaped one layered CeO₂(100) surface derived from (A) discrete FT, (B) FFT and (C) QFT. The values are intensities in the heat map.

We applied QFT for a nanosheet material with 2ⁿ × 2^m periodicity, CeO₂(100), as presented in Fig. 3. In general, a quantum bit represents binary values. Because the expressed values from quantum bits are assigned to the corresponding index of an input in the (multidimensional) QFT algorithm, the applicability of QFT to inputs with a shape unable to be represented by 2ⁿ × 2^m is nontrivial. Then, to elucidate the available input shape for multidimensional QFT, each FT was performed to the CeO₂ nanosheet exposing a (111) surface, having 3 × 3 x–y periodicity derived from stacking along the z-direction, as a model (Fig. S9 in ESI†). First, the results of discrete FT and QFT for 18 × 9 shaped inputs were compared (Fig. 4). Because general QFT received only 2ⁿ × 2^m shaped input, the 18 × 9 sized surface was cut out into a 2⁴ × 2³ shaped surfaces. The part of the QFT results corresponding to the diffraction spots expanded, although that of QFT in Fig. 2 and that of discrete FT for 18 × 9 shaped inputs were located in single points (Fig. 4). This correspondent part is the spectral leakage attributable to censoring in the middle of the period in the inputs. From the spectral leakage, the SAED spots of QFT results at single points in the discrete FT results were broadened and weakened at approximately the same positions. The ratios between the intensity of indices corresponding to a diffraction spot and the direct beam were found to be 0.595 and 0.338, respectively, by discrete FT and QFT. Because the layer number identification of nanosheet materials by SAED simulation requires accurate simulations of intensity to diversify the applications of QFT, some methods to obtain accurate intensities should be developed even when the inputs are censored in the middle of a period.

Fig. 4 Comparison between (A) discrete FT for 18 × 9 shaped input and (B) QFT for 2⁴ × 2³ shaped inputs, for mono-layered CeO₂(111).

Pretreatments for the inputs were conducted to cancel out the decrease in the intensities of the spots by the spectral leakage. The error of the results between the QFT for inputs censored in the middle of a period with various pretreatments and the discrete FT for inputs without spectral leakage is portrayed in Fig. 5(A). The same errors were encountered irrespective of the input sizes in the case of the QFT for inputs with no pretreatment. These results indicate that the QFT result cannot be improved by reducing the ratio of the censored periodic portion to the full periodic portion by changing the input size. The flat top function, a kind of window function, is suitable for acquiring the accurate intensity of the Fourier transform result. Only a negligible error was found between the results of QFT for censored inputs multiplied by the flat top function and discrete FT for inputs without spectral leakage in Fig. 5(A). These results suggest that the combination of the multidimensional QFT and the flat top function can analyse accurate spot intensities in SAED patterns robustly, even though the periodicity of inputs is beyond the expressive power of the quantum computer. Additionally, in the case where the inputs in Fig. 5 are used as their inputs, the results of discrete FT, FFT, and QFT produced the same SAED pattern (Fig. S11 in ESI†). It is noteworthy that the intensities themselves are not the same in discrete FT and QFT, but the ratios of the two intensities are the same in them because (1) the locations of the SAED spots are broadened, (2) the intensities of the SAED spots are maintained by the flat top functions, and (3) the outputs of quantum computers are normalised to 1 as a probability. Zero padding was used as a pretreatment method for comparison. The zero padding converts the values of the censored periodic portion into 0. This method is used to reshape the input size to a power of two in FFT. From Fig. 5(A), the application of zero padding to QFT reduced errors to discrete FT for inputs without spectral leakage in the case of small input. However, the error, asymptotic to the results of QFT for censored inputs without pretreatment, and the zero-padding, led to larger errors than the flat top function in all regions. Moreover, applying the zero padding and the flat top function to avoid censoring the periodicity of input did not reduce the error (Fig. 5(B)). Therefore, we summarise that applying only the flat top function is the most robust pretreatment to obtain peak intensities. The QFT with the input treated using the flat top function yielded a series of intensity ratios. The intensity ratios were unique for each nanosheet layer number, except for the number of layers in multiples of 3 (Fig. S12 in ESI†). For several layers in multiples of 3, the number of layers is not identified independently of the accuracy of spot intensity measurement because CeO₂(111) has three-stacking periodicity along the z-direction. By contrast, CeO₂(100) has no stacking periodicity along the z-direction derived from thermodynamically induced oxygen vacancies on the topmost and undermost layers. It gives a unique intensity ratio in all regions. Furthermore, the QFT with inputs pre-treated by the flat top function gives an identical intensity ratio to that of discrete FT, which enables us to compare it to the peak intensities measured during experimentation if more accurate approximation to the scattering medium is used (Fig. S13, ESI†).

Fig. 5 Effects of pretreatments for input on error in intensity ratio. Intensity ratio in ([2ⁿ⁺¹/3], [2ⁿ/3]) to (0, 0) with (A) single pretreatment and (B) composite pretreatments. The input shapes and spot locations for the QFT results are listed in Table S1 in ESI.† The discrete FT result in the case of 18 × 9 shaped input is used as the reference value because the same results are given by discrete FT for inputs having the same periodicity.

In conclusion, we established a method by which multidimensional QFT is applied to inputs with arbitrary periodicity and simulated SAED patterns using the method. Specifically, the utilisation of inter-dimensional independence of QFT and a flat top function leads to QFT acquisition of intensities at any position accurately and robustly for any periodic structure input. These findings indicate that the QFT can substitute for discrete FT with low computational complexity for various purposes. Hence, the results reported in this article can be applied to not only materials having the same periodicity of CeO₂ nanosheets, but also other materials which have the same periodic structure. Moreover, this method is believed to expand the range of quantisable software because the Fourier transform corresponds to an expansion of the basis in a framework on the theory of statistical thermodynamics:²¹ quantum machine learning for chemistry through embedding information of statistical thermodynamics to quantum states.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors have no conflict to declare.

Acknowledgements

This work was partially funded by JSPS KAKENHI Grant Number JP24KJ2090 and by JST SPRING Grant Number B2R101263201.

Notes and references

1. Y. Song, B. Xu, T. Liao, J. Guo, Y. Wu and Z. Sun, Small, 2021, 17, 2002240.
2. T. G. Novak, J. Kim, P. A. DeSario and S. Jeon, Nanoscale Adv., 2021, 3, 5166–5182.
3. R. J. Wu, M. L. Odlyzko and K. A. Mkhoyan, Ultramicroscopy, 2014, 147, 8–20.
4. T. Montini, M. Michele Melchionn, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116(10), 5987–6041.
5. F. Dong, X. Liang, Z. Zhang, H. Yin, D. Wang, J. Li and Y. Li, Adv. Matter., 2024, 36, 2401055.
6. S. Paydar, B. Zhu, J. Shi, N. Akbar, Q. A. Islam, S. Yun, A. Muhammad, M. H. Paydar and Y. Wu, Ceram. Int., 2023, 49, 9138–9146.
7. Y. Alexeev, D. Bacon, K. R. Brown, R. Calderbank, L. D. Carr, F. T. Chong, B. DeMarco, D. Englund, E. Farhi, B. Fefferman, A. V. Gorshkov, A. Houck, J. Kim, S. Kimmel, M. Lange, S. Lloyd, M. D. Lukin, D. Maslov, P. Maunz, C. Monroe, J. Preskill, M. Roetteler, M. J. Savage and J. Thompson, PRX Quantum, 2021, 2, 017001.
8. D. Coppersmith, arXiv, preprint, arXiv:quant-ph/0201067, 2002 DOI:10.48550/arXiv.quant-ph/0201067.
9. Y. Qi, P. Fu and D. A. Volmer, Mass Spectrom. Rev., 2022, 41, 647.
10. E. Collini, J. Phys. Chem. C, 2021, 125, 13096.
11. M. O. Guerrero-Pérez and G. S. Patience, Can. J. Chem. Eng., 2020, 98, 25.
12. R. R. Ernst, Angew. Chem., Int. Ed. Engl., 1992, 31, 805.
13. A. Y. Kitaev, arXiv, preprint, arXiv:quant-ph/9511026, 1995 DOI:10.48550/arXiv.quant-ph/9511026.
14. G. Brassard, P. Høyer, M. Mosca and A. Tapp, Contemp. Math., 2002, 305, 53.
15. A. W. Harrow, A. Hassidim and S. Lloyd, Phys. Rev. Lett., 2009, 103, 150502.
16. D. S. Abrams and C. P. Williams, arXiv, preprint, arXiv:quant-ph/9908083, 1999 DOI:10.48550/arXiv.quant-ph/9908083.
17. P. W. Shor, Proceedings 35th Annual Symposium on Foundations of Computer Science, Santa Fe, 1994, pp. 124–134.
18. P. Pfeffer, arXiv, preprint, arXiv:2301.13835, 2023 DOI:10.48550/arXiv.2301.13835.
19. D. Camps, R. V. Beeumen and C. Yang, Numer. Linear Algebra Appl., 2021, 28, e2331.
20. A.-C. Gaillot, V. A. Drits, D. R. Veblen and B. Lanson, Phys. Chem. Miner., 2011, 38, 435–448.
21. J. M. Sanchez, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 224202.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04399e

---