pH control of the reaction mechanism: interactions of the Au(I)-NHC complex with thioredoxin reductase (modeled by cysteine and selenocysteine); ab initio and DFT calculations

Abstract

Interactions of Cys and Sec amino acids with a simple model of the Au(I)-NHC complex were explored using DFT functionals and post-HF methods. In addition to the conventional quantum chemical description with the NVT canonical ensemble, a transformation to the grand-canonical ensemble was performed. This approach allowed for the consideration of chemical species with different numbers of protons and the evaluation of reactions at constant pH. For this purpose, a new thermodynamic state function, the Gibbs-Alberty free energy (ΔGA⁰), was introduced, with the proton chemical potential as the natural variable, and applied to Cys/Sec-Au(I)NHC interactions. Having determined all the necessary pK_a values, the pH-dependent equilibrium constant was expressed for both Cys and Sec coordination to the gold(I) complex. The dependences of ΔGA⁰(Cys) and ΔGA⁰(Sec) as functions of varying pH demonstrated a clear preference for Sec coordination under acidic and neutral conditions, which shifted near pH ≈ 8, where Cys coordination became thermodynamically more stable.

---

Introduction

The thioredoxin system plays a key role in controlling the overall intracellular redox balance in cells. It is basically composed of the small redox protein thioredoxin (Trx), nicotinamide adenine dinucleotide phosphate in its reduced form (NADPH), and thioredoxin reductase (TrxR), a large homodimeric selenoenzyme that regulates the redox state of thioredoxin. Its mechanism of action is clearly summarized in the study by Sun et al.¹ Crystallographic data and the 3D structure of mammalian thioredoxin reductase were solved by Sandalova et al.^2,3 The active center of the reductase is located in a small cavity near the C-terminus of the enzyme. Details of the mechanism of selenoenzyme inhibition are still under investigation in several laboratories.^4,5 Nevertheless, the thioredoxin system is now clearly recognized as an effective “druggable” target for the development of new anticancer drugs.^6–8 Accordingly, a number of established anticancer agents have been retrospectively found to be potent inhibitors of thioredoxin reductases and to induce severe oxidative stress. Previously, a variety of gold compounds, either gold(I) or gold(III), have been reported to exhibit outstanding antitumor properties, forming a promising class of experimental anticancer agents.^9–11 In the study by Serratrice et al.,¹² it is noted that similar cytotoxic properties were observed in parent gold(III) complexes as in the corresponding gold(I) complexes, which suggests that gold(III) may be reduced to gold(I) in the cellular environment. On the other hand, the same laboratory discovered that certain gold(III) complexes remain in the +3 oxidation state when in adduct form with proteins.¹³ An extended set of small molecules, which can serve as inhibitors of TrxR, were reported by Cai et al.¹⁴ In their study, besides Au, Pt, and Ru metallocomplexes, sulphur, selenium and tellurium-containing compounds were also examined.

The biological target of the metallodrugs is believed to be the small cavity near the C-terminus of thioredoxin reductase. The active center can be effectively blocked by transition metal complexes. Specifically, Au(I) complexes were found to have a high affinity for this site⁵ and have been recognized as a promising candidate for a new class of anticancer drugs for some time.¹⁰ Au(I) phosphine complexes were one of the first compounds to be examined, and it was demonstrated that they inhibit the activities of both thioredoxin and thioredoxin reductase.¹⁵ The inhibition was found to be more pronounced in breast cancer cells. Later, the same group also confirmed that Au(I) complexes with N-heterocyclic carbene (NHC) ligands can serve as anticancer drugs by attacking mitochondrial enzymes.¹⁶ In their study, several derivatives with methyl, i-propyl, n-butyl and t-butyl modifications of the imidazole ring were explored. By tuning the ligand exchange reactions at the Au(I) center, the authors designed lipophilic and cationic Au(I) complexes that selectively induce apoptosis in cancer cells but not in normal cells and allow selective targeting of mitochondrial selenoproteins. The activity of Au(I) complexes with NHC ligands and analogous Ag(I) complexes were compared with cisplatin, revealing similar antitumor IC₅₀ parameters.¹⁷

Recently, Au(I) complexes with modified NHC were found to be more active against both colon and breast cancer cells in comparison with cisplatin or auranofin.¹⁸ Particularly, dinuclear Au(I) phosphano-complexes have significantly lower IC₅₀ for colorectal and breast cancer, as reported by Sulaiman et al.¹⁹ and Abogosh et al.²⁰ New thiolate gold(I) complexes that inhibit the proliferation of different human cancer cells were reported by Abas et al.,²¹ showing higher cytotoxic activity than cisplatin. Strong antiproliferative effects of Au(I) complexes with NHC ligands were found also in another study exploring lung, colon, and breast tumors.²²

A complementary computational QM/MM study of the reduction of the disulphide bridge in the Trx structure (PDB ID 1EP7) was published by Rickard et al.²³ The interaction of an auranofin model with the tetrapeptide sequence of TrxR was studied based on DFT by Howell.²⁴ A higher gold activity at the selenium site in comparison with the sulphur of cysteine was confirmed. Recently, Delgado calculated the standard Au³⁺/Au⁺ reduction potentials of the Au(III) complexes in connection with anticancer treatment.²⁵ They came to the conclusion that the CAM-B3LYP functional in combination with SMD solvation is superior to other examined computational models. Recently, another DFT study of some other modified Au(I)-NHC complexes with ethylselenolate was published.²⁶

In this study, we have determined the thermodynamic and kinetic parameters for the substitution reaction of a simple chloro(imidazol-2-ylidene)gold(I) model complex, which is denoted as Au(I)-NHC. Modeling its binding to TrxR, the substitution reaction of the Au(I)-NCH complex with cysteine (Cys) and selenocysteine (Sec) amino acids was explored by combining various QM and DFT levels with D-PCM/sUAKS solvation single-point calculations. One of the most important parts of this study is the determination of the binding preference of the gold complex to the selenium and sulphur sites via the key sequence of TrxR in a pH-dependent manner. The Sec and Cys amino acids were regarded as models of the active tetrapeptide redox center (Gly-Sec-Cys-Gly) in the C-terminus of TrxR. Therefore, a new Legendre transformation of Gibbs free energy to the grand canonical ensemble regarding proton chemical potential was performed to evaluate Gibbs-Alberty free energy, which demonstrated differences in complexation energies between gold and selenium or gold and sulphur depending on the pH of the environment.

Computational tools

All the explored molecules (amino acids, gold complexes, and supermolecular systems) were optimized using the DFT method. Two levels were chosen for determining the reaction coordinate; the B3LYP functional^27–30 was combined with (a) the double zeta quality basis set (6-31+G(d)) and Stuttgart–Dresden effective core potentials with corresponding pseudoorbitals (Opt/D level) or (b) the triple-zeta basis set (6-311++G(2df,2pd)) and the same quality of pseudoorbitals (with 2fg-polarization and diffuse functions extension; Opt/T level), as discussed in our previous papers.^31–33 The corresponding set of pseudoorbitals³⁴ for the Au, S, Cl, and Se atoms are summarized in the ESI.† Both optimization levels (a) and (b) were processed with the same COSMO solvation model³⁵ using UFF cavities and van der Waals atomic radius of 1.10. At the same levels, frequency analyses were performed to check the characteristics of the calculated stationary points on the potential energy surface (minima or transition states (TS)) of the explored molecular systems and to quantify the nuclear degrees of freedom. During the final evaluation of Gibbs free energy in the water solution, the entropy contributions of the translational and rotational degrees of freedom were corrected as suggested by Wertz³⁶ and Goddard:³⁷

S^trans+rat_liq = (S^trans_gas + S^rot_gas − 14.3) × 0.54 + 8.0 (1)

These corrections originate from the fact that the translational and rotational degrees of freedom are visibly reduced in the liquid phase in comparison with the gas phase. More details can be found in ESI,† – part 2. In this way, the estimated Gibbs free energy profiles of the searched reaction were determined. The higher optimization model Opt/T was used since it is computationally suitable for these small molecules and can provide more accurate results. Later, the differences between models Opt/D and Opt/T can be utilized for error estimation for more extended systems when no better choice (than the Opt/D model) is possible, which is expected in our next studies on this topic. QM study and QM/MM approach using tetrapeptide were employed to analyze the complete TrxR monomeric unit interacting with this Au(I)-NHC model complex. In order to compare the accuracy of the optimization processes, the geometries (selected bond lengths), AIM (bond) critical points, and energetical relations were compared.

The thermodynamic and kinetic parameters of the reaction were determined at several computational levels for stationary points optimized at both Opt/D and Opt/T levels using more accurate single-point calculations (SP). They differed in terms of the basis sets, implicit solvation models employed or the evaluation of electronic structures using only DFT or post-HF methods.

(I) DP-models (SP with D-PCM): since the pH-dependent thermodynamic model had to be used (refer to the text below), the first choice was a recently developed model for the reliable determination of pK_a values of amino acids, peptides, and proteins. The SP energies were evaluated at the DFT/6-311++G(2df,2pd)/D-PCM/scaled-UAKS computational level,^38,39 as described in our previous papers.^40–42 Two functionals were employed: B3LYP because of continuity and M06-2X, which provides better agreement between the calculated and experimental pK_a values.⁴³ These functionals were further complemented with Grimme's D3 empirical dispersion and Becke–Johnson (BJ) dumping functions for the B3LYP functional. The D-PCM solvation model with scaled-UAKS cavities was found recently as one of the best options for the simulation of the water solution for pK_a evaluation.⁴³ Cavity rescaling was performed based on the actual NBO charges^44,45 and the original UAKS cavities, as suggested by Tomasi⁴⁶ and Barone,⁴⁷ and extended by Orozco and Luque.^48,49 The atomic radii R_X were linearly scaled using partial charge (q^NBO_X,actual) of the actual atomic groups X (thiol, chloride, and carboxyl oxygens) in the examined molecule relative to the change of its partial charge (q^NBO_X,prot − q^NBO_X,dep) in the reference molecules with protonated and deprotonated group X.^{34,40–42,50} This can be expressed by the formula:

where the scaling factors γ and the radii R⁰_X from the original UAKS model are utilized.^48,49 Using partial charges instead of formal charges leads to smooth and more consistent results. The reference molecules suggested in the original UAKS approach were chosen for the determination of partial charges on the given groups X in the deprotonated q^NBO_X,dep and protonated form q^NBO_X,prot.⁴⁸ Besides electrostatic solvation energy, non-electrostatic (repulsion, dispersion, and cavitation) terms were also included in the total Gibbs free energy of the explored system. This model was applied for both optimal geometries obtained at the Opt/D and Opt/T levels and are labeled as DP/D (DP_B3/D and DP_M06/D) and DP/T (only for B3LYP) hereafter, respectively.

(IIa) CP/T model (SP with C-PCM): for comparison, the geometries from double-zeta optimization Opt/D were further employed in the same SP calculations at the B3LYP-GD3BJ/6-311++G(2df,2pd) level using COSMO solvation model along with Klamt cavities.

(IIb) CP/Q model: analogous to the extension from DP/D to CP/T, the B3LYP-GD3BJ computational level was considered for model Opt/T, where energy profiles are determined in combination with the quadruple-zeta basis set aug-cc-pVQZ for H, C, N, O atoms,^51,52 S and Cl atoms⁵³ and consistent with aug-cc-pVQZ-PP for the Se⁵⁴ and Au^55,56 atoms taken from Basis Set Exchange.^57–59 This computational level was also supplemented with the COSMO/Klamt solvation model.

In order to demonstrate the accuracy of the previous computational levels, the last pair of computational models were evaluated based on CCSD(T) calculations for the structures obtained only using the Opt/T optimization model.

(IIIa) MP2/D and CC/D model: the reaction profile was evaluated at the (CCSD(T)/6-31+G(d))/D-PCM/scaled-UAKS level of theory.

(IIIb) MP2/T, CC/T, and CC/Te models: the CCSD(T)/6-311++G(2df,2pd)/D-PCM/scaled-UAKS level (signed as CC/T) was determined only for the deprotonated branch of the reaction scheme. Since these calculations are extremely processing-intensive, the protonated species were evaluated only using the MP2/6-311++G(2df,2pd) computational level to save computational time, and the higher level of correlation contributions were estimated based on the below formula:^60,61

ΔE_CCSD(T)/TZP = ΔE_MP2/TZP + [ΔE_CCSD(T)/DZP − ΔE_MP2/DZP] (3)

to conserve some sense correlation effects from the lower basis set to the higher basis set calculations. In all the CCSD(T) calculations, the D-PCM/scaled-UAKS solvation model was used (labeled as CC/Te).

All the above-mentioned SP calculations were also complemented with Wertz's corrections of the liquid environment from the corresponding level of optimization. The electronic properties during the process were further investigated using NBO and QTAIM for geometries using the optimization model Opt/D.

All the necessary pK_a values were determined at the DP/D level (both M06-2X and B3LYP) and also compared with values obtained at the DP/T and post Hartree–Fock levels according to the formula:

pK_a = ΔG⁰/(2.303RT) (4)

considering reaction Gibbs free energy ΔG⁰ for the deprotonation reaction:

HA + H₂O → H₃O⁺ + A⁻ (5)

R and T represent the Avogadro constant and temperature at which deprotonation occurs. In addition, the correction term −log[H₂O] = −1.74 of the standard state of bulk water was used. Further details can be found in ref. 62.

Results and discussion

Protonation states of the reactants and products – pK_a evaluation

Modeling of the substitution reaction in which the chloro ligand of the Au(I)-NHC complex is replaced by Cys or Sec amino acid (Scheme 1) was investigated using different protonation states of the reactants and products under different pH conditions. Several protonated forms of the acidic and basic functional groups, namely carboxyl, thiol/selenol, and amino groups in Cys/Sec, the imidazole group in Au(I)-NHC complex, and their adducts, were considered. For each protonation state, several local minima were compared to identify the global minima at both Opt/D and Opt/T optimization levels. This step is crucial to obtain correct pK_a values and energy differences between the stationary points on the energy profiles.

Scheme 1 Coordination reaction of the gold(I) complex with Cys/Sec amino acid.

It is generally known (e.g. ref. 43 and its citations) that most of the directly applied PCM models are not able to match the experimental pK_a values with sufficient accuracy.^63–65 Hence, in our previous series of papers, we suggested a general strategy to determine pK_a (usually within one log unit) based on the D-PCM model with scaled UAKS cavities, corresponding to the DP models employed in this study.^40–42,50 In this way, SP energy was evaluated with both B3LYP (DP_B3/D model) and M06-2X functionals (DP_M06/D) for geometries obtained at the Opt/D level, and for structures optimized at the Opt/T level, only the B3LYP functional (DP/T) was used. The pK_a values of the relevant (de)protonated states of both isolated reactants and products were calculated according to eqn (4) and are summarized in Table 1. The DP_M06/D values were reasonably close to measured data^66,67 (RMSD difference ca. 2.2 log units). Overestimated pK_a values were particularly obtained for the most basic values (deprotonation of amino groups). For such negative ionic states (−2e), simple linear cavity scaling is probably not appropriate. pK_a evaluation with more extended basis sets usually leads to lower accuracy since the UAKS model is optimized for DFT calculations with the double-zeta basis set similarly to other implicit solvation models. Similarly, a higher level of theory (post Hartree–Fock methods) does not lead to more accurate pK_a predictions, and similarly, a larger basis set further deteriorates the results.⁴³ Basically, the main reason is that all cavity parameters were fitted to the DFT double-zeta methods. It should be noted that K_a values are exponentially dependent on free energies. Therefore, even a small change makes a visible difference in the value of the equilibrium constant.

Table 1 pK_a values from selected levels of calculations, including the nuclear degrees of freedom using the Wertz correction. Plot of calculated vs. experimental values, along with fits for all the methods used, is provided in ESI – Part 1

	DP_B3/D	DP_M06/D	DP/T	MP2/D	CC/D	MP2/T	CCe/T	Exp.^66,67
a Cys(COO) refers to the deprotonation of the carboxyl group, Cys(S) to the subsequent deprotonation of the thiol group, and Cys(NH2) to the third deprotonation on the NH2 group (e.g., an anion with a charge of −2e). This analogy applies to all other systems with amino acids. b (Fourth) deprotonation occurs on the imidazole ring, (NHC)^−.
Cys(COO)^a	3.5	2.8	4.3	0.7	1.7	3.0	4.0	1.9
Cys(S)	11.5	8.3	11.7	11.6	12.9	12.6	13.8	8.3
Cys(NH2)	15.8	13.5	15.7	16.1	15.9	15.4	15.3	10.7
Sec(COO)	3.0	2.4	3.6	0.7	1.7	2.7	3.8	1.9
Sec(Se)	8.0	6.4	8.3	7.4	8.9	9.2	10.6	5.7
Sec(NH2)	14.4	13.3	15.1	16.0	15.9	15.3	15.2	10.0
Au-NHC	18.6	16.1	18.0	15.9	17.6	16.0	17.8
Au-NHC-Cys(S)	0.1	−2.9	0.8	−2.1	−0.5	−1.6	0.0
Au-NHC-Cys(COO)	2.3	1.2	2.2	−0.8	0.1	1.5	2.4
Au-NHC-Cys(NH2)	8.7	5.8	9.1	8.0	7.9	7.5	7.5
Au-(NHC)^−-Cys^b	26.4	23.5	17.6	23.9	25.5	24.2	25.8
Au-NHC-Sec(Se)	−6.4	−9.6	−2.3	−9.6	−7.5	−8.9	−6.8
Au-NHC-Sec(COO)	2.4	−0.9	2.4	−0.1	0.8	2.0	2.9
Au-NHC-Sec(NH2)	12.1	9.4	11.6	11.5	11.5	11.0	11.0
Au-(NHC)^−-Sec^b	21.8	19.5	16.2	19.5	21.1	20.2	21.8
HCl	−7.6	−10.1	−6.1	−7.9	−6.3	−0.2	−0.6	−7.0
Kw	16.0	16.9	16.8	13.6	15.4	16.9	17.7	14.0
RMSD	2.9	2.2	3.3	3.2	3.5	4.1	4.5

---

Besides amino acid functional groups, the pK_a of the N-coordinated hydrogen atoms of the Au(I)-NHC complex were also explored for the sake of completeness. Nevertheless, it was confirmed that the Au(I)-NHC hydrogens (better naming than protons) have pK_a values in a very high basic range, definitely above 14, as seen in Table 1. Such a high value also corresponds with the fact that in the experiments, these hydrogens in the complexes are replaced by some bulky organic ligands, which are not cleaved during the coordination of the Au(I)-NHC complex to the active site in the vicinity of the TrxR C-terminus.

Energetics of the interaction of Au(I)-NHC complex with Cys and Sec amino acids

Initially, the substitution reactions were investigated by assuming the standard canonical ensemble. Based on the experimental pK_a values of 8.3 for thiol in Cys and 5.7 for selenol in Sec, both protonation states of the mentioned groups were considered and hence, both deprotonated and protonated branches were included in the calculations, that is, the reactants containing thiol or selenol and thiolate or selenolate anion, respectively. In the product complexes of the protonated branch, no proton is bound to the S or Se atom. This proton is moved to the nearest oxygen of the amino acid according to the calculated pK_a values (Table 1) so that both the carboxyl and amino groups are protonated (NH₃⁺). In total, we considered two reaction branches for each amino acid, which can further differ in their reaction mechanism.

After optimizing the isolated species (all necessary forms of Cys and Sec, as well as the Au(I)-NHC complex), several different H-bonded associates of the Cys/Sec amino acid with the Au(I) complex were searched to identify the optimal reactant supermolecules that may serve as a starting point for the determination of activation barriers. Similarly, in products, stable supermolecular forms in which Au–S/Au–Se coordination is associated with the released chloride particle were examined (Scheme 1). A reaction energy profile is only complete with the determination of the transition state (TS) structures. In the case of the deprotonated branch, a single-step reaction mechanism exists, with a TS structure characterized by one negative vibration mode corresponding to the asymmetric stretching of the Au–Cl and Au–S(Se) bonds. When the thiol (–SH) and selenol (–SeH) groups are present in the protonated branch, two different mechanisms can be distinguished: a two-step reaction mechanism where the proton is first transferred from the S/Se site to one of the electronegative oxygen atoms of the carboxyl group and subsequent coordination of the metallo-complex to the S/Se atom or a single-step mechanism where both processes occur simultaneously.

All the various SP methods described in Computational Tools were applied for the determination of the reaction energy profiles, and the obtained activation and reaction free energies are summarized in Table 2. Although the energies determined for the dissociation constants at the CC/T level are not comparable with the experimental data (Table 1), it is still assumed that the Gibbs free reaction energies evaluated at this level represent the most accurate approximation. However, these calculations are extremely demanding. Therefore, such calculations were only performed for the deprotonated branch, which contains a smaller set of molecules. For all protonated systems, the corresponding energies were estimated based on (eqn (3)), allowing the supplementation of the relatively modest calculations at the MP2/TZP level by energy corrections beyond the second order of the perturbation theory, i.e. differences between the CCSD(T) and MP2 values received at the cheaper CCSD(T)/DZP level, as used frequently before.^{31,32,60,61,68} The quality of these estimations was assessed by comparison with the reaction and activation energies of the deprotonated branch. Since the estimation is relatively plausible, with the maximal difference lower than 0.3 kcal mol⁻¹ (Table 2; last two columns), the estimated Gibbs free energies were considered as references for both reaction branches for the sake of consistency.

Table 2 Gibbs free energies for stationary structures from individual reaction coordinates (in kcal mol⁻¹), with the reactant supermolecules taken as the zero-reference level. R represents reactants, P represents products, I represents intermediates, TS represents the transition state (single-step without any number, with 1 and 2 distinguishing the points in a two-step mechanism)

	Opt/D	DP_B3/D	DP_M06/D	CP/T	Opt/T	DP/T	CP/Q	MP2/D	CC/D	MP2/T	CCe/T	CC/T
Cysteine
R	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TS	6.9	11.6	10.4	8.1	8.1	12.0	8.4	12.9	12.2	13.8	13.2	13.1
P	−15.2	−13.3	−13.4	−13.4	−13.6	−14.5	−13.9	−13.8	−13.0	−13.8	−13.2	−13.0
R	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TS1	10.5	12.3	13.9	8.5	9.2	8.8	10.0	14.4	16.2	10.4	12.1
I	10.2	11.7	10.3	7.6	6.6	7.5	9.2	13.6	13.7	9.6	10.5
TS2	22.2	15.5	12.5	17.7	19.4	11.9	19.5	19.2	18.9	16.0	15.5
TS	11.8	9.4	9.8	11.8	12.1	8.4	12.5	9.6	9.9	8.5	8.0
P	−2.2	−6.8	−6.3	−4.0	−4.6	−8.4	−4.8	−4.9	−3.2	−7.1	−5.4
Selenocysteine
R	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TS	6.5	11.0	8.7	7.9	7.1	11.1	7.4	9.4	8.2	10.8	10.5	10.2
P	−14.7	−15.6	−14.0	−14.6	−14.8	−15.7	−14.7	−14.5	−13.6	−14.6	−13.7	−13.8
R	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TS1	11.4	9.5	12.5	11.1	10.5	10.9	10.1	14.1	16.0	11.9	13.7
I	8.0	6.2	6.7	7.2	5.5	7.4	5.9	10.5	10.7	9.0	10.0
TS2	19.5	10.5	13.6	17.0	17.7	10.8	16.3	15.1	15.0	13.4	13.3
TS	10.1	8.3	11.2	11.9	9.0	7.5	9.6	7.6	7.6	7.4	7.4
P	−6.4	−11.6	−10.4	−6.8	−7.8	−10.5	−8.9	−8.9	−7.2	−10.8	−9.1
RMSD	3.7	2.3	2.0	3.1	3.3	2.3	3.0	1.6	2.2	1.1		0.2

---

The determined reaction energy profiles (Fig. 1) show that both reaction branches preferentially pass through a single activation barrier. In all explored computational models, their heights were higher in Cys-involving reactions than the Sec counterparts, despite small energy differences in the case of the deprotonated TS structures obtained at computational levels utilizing the double zeta basis set (xxx/D models in Table 2), where the differences were often below 1 kcal mol⁻¹. Considering the two-step reaction mechanism in the protonated branch, the first activation barrier (TS1) corresponding to proton transfer to the carboxyl oxygen is usually lower in energy than the second activation barrier (TS2), which is connected to the replacement of the chloro ligand by the formation of a coordination bond between the S/Se site and Au(I). It can be concluded that at least the TS energies of the second barriers are visibly higher in complexes with Cys than those containing Sec (Table 2). Nevertheless, as mentioned above, the single-step reaction mechanism is associated with visibly lower activation barriers. Another important conclusion based on the comparison of the TS energies of deprotonated and protonated branches is that the activation barriers in the protonated branches are usually predicted to be lower than the barriers connected with the deprotonated forms. The activation barriers reported by Tolbatov et al.²⁶ are in good accordance with our results; nevertheless, their reaction energies are not comparable to our calculated values, which indicates an endoergic reaction since energy is used for the interaction of ethylselenolate with quite a different gold(I) complex via a more complex reaction mechanism.

Fig. 1 Reaction energy profile for coordination of the Au(I)-NHC model complex to Cys (blue lines) and Sec (red lines). Solid lines represent reactions in deprotonated forms, while dashed lines represent reactions in protonated forms (simulating more acidic solutions). The upper structures display stationary points of the two-step reaction mechanism for the interaction of the gold complex with selenocysteine, and the lower structures show the interaction with the deprotonated cysteine amino acid.

As indicated by the reaction Gibbs free energies, the reactions with Sec are generally slightly more exergonic than those with Cys. This higher exoergicity is more clearly seen in the case of protonated systems, where the difference is generally more than 3 kcal mol⁻¹. A substantially smaller energy difference is observed for deprotonated amino acids, with an exoergicity difference of less than 1 kcal mol⁻¹. Notably, the deprotonated reaction branches exhibit visibly higher exergonic characteristics in comparison with the protonated branches also partially due to the protonation of carboxyl oxygen in the course of the substitution reaction.

Kinetic aspects

By applying Eyring's transition state theory to the determined reaction energy profiles, the estimated reaction rates were obtained. In the case of the single-step mechanism, where the system needs to undergo only over one TS, the estimation of rate constants is simple according to the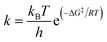 formula, where ΔG^‡ corresponds to the Gibbs free activation barrier; k_B, R, and h are the Boltzmann, universal gas, and Planck constants, respectively, and all rate constants are determined at temperature T = 298 K. For the two-step mechanism with rate constants k₁ and k₂ for the forward steps and k₋₁ and k₋₂ for the pertinent reverse reactions, the total rate constant can be derived based on the steady-state intermediate I, i.e. d[I]/dt ≈ 0 and supposing k₁ ≪ k₋₁, k₂ ≫ k₋₂, which leads to the total rate constant⁶⁹ (ESI,† part 3):The results of the deprotonated branch are tabulated in the upper part of Table 3 and total k_tot together with the partial rate constants k₁, k₋₁, k₂, and k₋₂ for the protonated branch are given in the lower part. They show that all the computational levels predict faster reaction rates for Sec than for Cys in the case of the single-step mechanism in both branches, with the exception of only CP/T for the protonated branch. Based on the total rate constants, the same conclusion is also valid for the two-step mechanism, for which it can be seen that the conditions for the steady-state intermediate are fulfilled, and the estimation of the total rate constant is sufficiently justified. The total rate constants also confirm a significant preference (faster occurrence) for the one-step mechanism in comparison with the two-step reaction mechanism as it ensues from the activation barriers. An important finding is that the substitution reactions of amino acids with a protonated S/Se site are visibly faster than those of the deprotonated sites. This means that the reaction will be faster in acidic solutions than in a basic environment. Nevertheless, according to the relatively large values of all the rate constants, it is evident that the reaction rate is still quite fast from the human perspective (even at millimolar concentrations, it should be complete in the sub-second scale).

Table 3 Rate constants for the formation of the Au(I)-NHC complex with Cys or Sec. Rate constants k₁, and k₂ correspond to the forward reactions, while k₋₁, and k₋₂ correspond to the reverse reactions in the two-step mechanism. k_tot represents the overall rate constant for this mechanism, obtained according to (eqn (6))

	Opt/D	DP_B3/D	DP_M06/D	CP/T	Opt/T	DP_B3/T	CP/Q	MP2/D	CC/D	MP2/T	CCe/T
Deprotonated branch – one-step mechanism
k(Cys)	5.1 × 10^7	2.1 × 10^4	1.5 × 10^5	7.6 × 10^6	7.1 × 10^6	9.6 × 10^3	4.4 × 10^6	2.1 × 10^3	6.9 × 10^3	4.9 × 10^2	1.6 × 10^3
k(Sec)	1.0 × 10^8	5.0 × 10^4	2.7 × 10^6	9.2 × 10^6	4.0 × 10^7	3.3 × 10^5	2.3 × 10^7	8.1 × 10^5	6.5 × 10^6	7.8 × 10^4	2.0 × 10^5
Protonated branch – one-step mechanism
k(Cys)	1.4 × 10^4	8.3 × 10^5	1.5 × 10^4	8.0 × 10^4	7.9 × 10^3	4.5 × 10^6	3.9 × 10^3	5.7 × 10^5	3.4 × 10^5	3.8 × 10^6	8.9 × 10^6
k(Sec)	2.6 × 10^5	4.7 × 10^6	3.6 × 10^4	1.2 × 10^4	1.4 × 10^6	2.1 × 10^7	6.0 × 10^5	1.6 × 10^7	1.6 × 10^7	2.5 × 10^7	2.4 × 10^7
Protonated branch – two-step mechanism
k 1(Cys)	1.2 × 10^5	6.1 × 10^3	4.0 × 10^2	3.5 × 10^6	1.1 × 10^6	2.1 × 10^6	2.7 × 10^5	1.7 × 10^2	7.6 × 10	1.4 × 10^5	8.2 × 10^3
k −1(Cys)	3.5 × 10^12	2.4 × 10^12	1.5 × 10^10	1.2 × 10^12	7.2 × 10^10	7.1 × 10^11	1.5 × 10^12	1.7 × 10^12	8.8 × 10^10	1.6 × 10^12	4.1 × 10^11
k 2(Cys)	9.7 × 10^3	1.0 × 10^10	1.6 × 10^11	2.2 × 10^5	2.3 × 10^3	4.0 × 10^9	1.8 × 10^5	1.9 × 10^9	7.2 × 10^10	1.3 × 10^8	1.3 × 10^9
k −2(Cys)	7.4 × 10^−6	3.7 × 10^3	1.1 × 10^−1	6.6 × 10^−4	1.6 × 10^−5	7.6 × 10^−3	6.2 × 10^−7	1.4 × 10^−5	4.1 × 10^−4	1.2 × 10^−2	2.9 × 10^−3
k tot(Cys)	3.3 × 10^−4	2.6 × 10^1	3.7 × 10^2	6.1 × 10^−1	3.6 × 10^−2	1.2 × 10^4	3.2 × 10^−2	1.9 × 10^−1	3.5 × 10	1.2 × 10^1	2.5 × 10^1
k 1(Sec)	2.6 × 10^4	6.4 × 10^5	4.1 × 10^3	4.5 × 10^4	1.3 × 10^5	6.4 × 10^4	2.2 × 10^5	2.7 × 10^2	1.1 × 10^1	1.2 × 10^4	5.2 × 10^2
k −1(Sec)	1.8 × 10^10	2.1 × 10^10	3.4 × 10^8	8.5 × 10^9	1.0 × 10^9	1.8 × 10^10	4.4 × 10^9	1.4 × 10^10	7.8 × 10^8	4.4 × 10^10	1.1 × 10^10
k 2(Sec)	2.3 × 10^4	4.0 × 10^9	5.8 × 10^7	3.7 × 10^5	6.8 × 10^3	2.3 × 10^10	1.2 × 10^17	3.0 × 10^9	4.7 × 10^9	3.6 × 10^9	2.3 × 10^10
k −2(Sec)	7.2 × 10^−7	4.9 × 10^1	1.6 × 10^−5	1.8 × 10^−5	3.2 × 10^−7	1.6 × 10^−3	2.1 × 10^−6	1.6 × 10^−5	3.3 × 10^−4	1.1 × 10^−5	2.4 × 10^−4
k tot(Sec)	3.3 × 10^−2	1.0 × 10^5	6.1 × 10^2	1.9 × 10	9.1 × 10^−1	3.6 × 10^4	2.2 × 10^5	4.7 × 10^1	9.2 × 10	8.8 × 10^2	3.5 × 10^2

---

Transformation to the grand-canonical ensemble

Up to now, we have regarded the explored reaction in the framework of the standard canonical ensemble. Nevertheless, when biochemical or biophysical processes are studied, often a constant pH environment must be considered. Therefore, Legendre's transformation of Gibbs free energy to the grand-canonical description was considered by introducing a new thermodynamic state function, namely Gibbs-Alberty free energy (GA):^70–73where the first sum basically indicates all non-polar molecules, while the second summation deals with the polar or ionic species, which can differ by the number of active protons. Contrary to Gibbs energy, where pressure, temperature, and molar concentrations are the intrinsic variables, the newly introduced thermodynamical potential (Gibbs-Alberty free energy) is a function of pressure, temperature, and chemical potentials, in our case proton chemical potentials, as defined elsewhere.^{41,42,50,74,75} In this way, the reactions cannot proceed to the standard chemical equilibrium, i.e. till the concentration of the individual species is constant (dn_i = 0) but till the change in chemical potential is zero (dμ_i = 0). In our case, this means that the proton chemical potentials of the individual species active in the explored chemical reaction are important. Actually, the change in protonation state is the controlling element for varying the pH of the solution. An illustrative case is the proton chemical potential of water, which is defined as:Similarly, the proton chemical potentials of all species from Scheme 1 were evaluated and combined to give the grand-canonical equilibrium constant:where f(pH) is defined based on the corresponding proton chemical potentials:Labeling of the individual deprotonation states is given in Table 1. As mentioned above, ΔGA⁰ is a function of the chemical potential. This means that this new grand-canonical thermodynamic potential is the only possibility (under constant p and T) to evaluate the pH dependence of the reaction energy. One basic shortcoming is the fact that all the required pK_a must be known. Nevertheless, when only a short pH range is explored, the expression in eqn (10) can be drastically reduced. For example, for energy determination in the pH range 6–8, the following reduction can be obtained:since all the other forms that differ in protonation state will contribute only very marginally.

If different protonated forms of some reactant or product are used in the first part of K′, then the f(pH) part has to be modified correspondingly i.e., the proton chemical potential of that concrete form must be used. When the water would be a part of the reaction and we decide to use [OH⁻] instead, then its proton chemical potential must be considered too and the f(pH) function must be modified correspondingly.

In our case, for the fully protonated form of Cys(COOH), the second term in the denominator will be based on the following proton chemical potential:The value of K′ is fully independent on the choice of particular forms of reactants and products considered in the evaluation of (eqn (10)) supposing that all the reaction energies and pK_a calculations are performed at the same computational level. Finally, it should be mentioned that species with negative or very high pK_a (say over 14) can be omitted from (eqn (10)) since their contribution is negligible if the explored pH range is e.g., between 2 and 12. In our case, for instance, the term since pK_a(HCl) ≈ −10.1 (at the M06-2X level) or with pK_a(Au(I)-NHC) = 16.1 log units. Finally, the pH-dependent Gibbs-Alberty free reaction energy (ΔGA⁰) is obtained from the equilibrium constant K′ based on van’t Hoff reaction isotherm:

ΔGA⁰ = −RT·ln(K′). (14)

For a detailed analysis of ΔGA⁰, it is worth focusing on the behavior of the proton chemical potentials of the individual species. For further insights into the variation of ΔGA⁰ free energy as a function of pH, plots of the proton chemical potential of neutral molecules Cys, and Sec versus pH were drawn for both isolated amino acids as well as coordinated to the Au(I)-NHC complex, as presented in Fig. 2, based on the M06-2X/6-31+G(d)/D-PCM/sUAKS computational model.

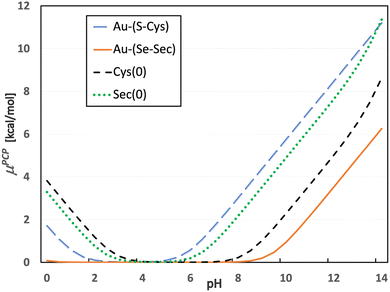Fig. 2 Proton chemical potential of selected neutral molecules occurring along the reaction coordinate.

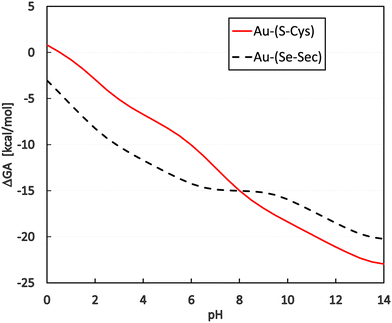
By applying this to the grand-canonical model together with all the necessary pK_a values, the pH-dependent equilibrium constant K′ was determined according to eqn (9) and (10)). Consequently, pH dependence of the Gibbs-Alberty free reaction energy (ΔGA⁰) was evaluated using (eqn (14)) for both reactions with Cys and Sec, as plotted in Fig. 3. A detailed inspection of Fig. 2 demonstrates that the changes in the slopes of both curves in Fig. 3 are associated with changes in the protonation states of the given reactant or product molecules depicted in Fig. 2. The other reactant (Au(I)-NHC) or product (Cl⁻) species do not contribute to any slope change since their pK_a values are out of the explored range (discussion in the previous paragraph).

Fig. 3 Dependence of the reaction Gibbs-Alberty free energy (in kcal mol⁻¹) on the pH of the solution. Coordination energy of Cys is represented by the black dashed line, and that of Sec by the red solid line.

Regarding the presence of these two amino acids in the reduction center at the C-terminus of TrxR (…Ser-Gly-Cys-Sec-Gly), the preference for gold(I) coordination to one or the other amino acid is important for a deeper understanding of the possible reaction mechanism of metal coordination at this active site for blocking the natural enzyme function. From the plot in Fig. 3, it can be seen that for pH lower than 8, preferential coordination to the Se site of Sec occurs, while in more basic solutions, the S site of Cys is used for coordination. However, tangible consequences of this preference on the practical behavior of the enzyme must be proven by additional in vitro or in vivo experimental studies focused on this particular aspect.

Conclusions

In this work, substitution reactions of the model Au(I)-NHC complex with Cys and/or Sec amino acid are studied. The B3LYP and M06-2X functionals are used together with post-HF (MP2 and CCSD(T)) methods and are combined with double- to quadruple-zeta basis sets. These computational levels are complemented by the D-PCM/sUAKS or C-PCM/Klamt implicit solvation model for the determination of pK_a values and reaction energy profiles. The explored reaction is predicted to be exoergic for both protonated and deprotonated S/Se sites based on all applied computational models. Nevertheless, the deprotonated branch gives a more pronounced energy release (is more exergonic) in comparison with the protonated branch. Moreover, the energetic preference for Sec in the framework of the canonical ensemble is noticeable and visibly more distinguished in the protonated branch. Regarding activation barriers, higher energies are obtained for the transition states in Cys reactions in a majority of the computational approaches in the single-step (preferable) reaction mechanism for both protonated and deprotonated branches, with more visible differences in the deprotonated branch. These conclusions are also reflected in rate constant values estimated using Eyring's transition state theory, indicating a relatively fast course of substitution reactions. For the deprotonated branch, the reaction course predicted at micromolar concentrations was still within the sub-second timescale.

In the second part of the study, Legendre transformation from the canonical to the grand-canonical ensemble was performed, leading to the determination of equilibrium constants K′ depending on the acidity of the solution. Such calculations require pK_a evaluation of the functional groups in the vicinity of the pH range of interest. In accordance with our previous study, these values for known systems (Cys, Sec, HCl, and water) were reproduced with reasonable accuracy at the M06-2X/6-31+G(d)/D-PCM/sUAKS level and were even comparable with the post-HF methods (MP2 and CCSD(T)). From the transformed equilibrium constants K′, the Gibbs-Alberty free energies were subsequently evaluated for the interactions of Cys and Sec with the Au(I) complex in solutions of different pH. By comparing the course of both Cys and Sec energy curves, there is an evident preference for Sec coordination to the gold complex in acidic and neutral solutions, while in a basic environment (with pH > 8), the formation of Au-(S-Cys) is more exergonic. This result should be considered from the perspective of the TrxR enzyme in which both amino acids are in close proximity. Accordingly, different coordination sites can be controlled by changing the pH in the cellular environment.

As for the newly introduced thermodynamic potential, when the studied chemical process involves each reactant and product only in a single form (considering protonation) e.g., water at pH = 7 and the concentrations of the other protonation states (OH⁻ and H₃O⁺) can be neglected, then using both the standard canonical method and this new grand-canonical approach will give the same results (ΔGA⁰ = ΔG⁰). However, when more than one protonated form is present in a system (e.g., cysteine at pH = 8.3 will have an equal number of protonated and deprotonated forms of the thio-group), then no option other than the grand-canonical approach should be used. The only disadvantage is that all the required pK_a values have to be known.

Data availability

All necessary data are presented in the form of tables and figures. ESI,† including the optimized basis sets, is provided by the authors. The programs used in the study are clearly specified and openly available. Additional information can be obtained upon request from the corresponding author.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the Grant Agency of the Czech Republic (no. 23-06909S) for supporting this project. We also highly appreciate the generous access to the computing facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the program “Projects of Large Infrastructure for Research, Development, and Innovations” (LM2010005).

References

1. Q.-A. Sun, L. Kirnarsky, S. Sherman and V. N. Gladyshev, Selenoprotein oxidoreductase with specificity for thioredoxin and glutathione systems, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 3673–3678.
2. T. Sandalova, L. Zhong, Y. Lindqvist, A. Holmgren and G. Schneider, Three-dimensional structure of a mammalian thioredoxin reductase: implications for mechanism and evolution of a selenocysteine-dependent enzyme, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 9533–9538.
3. Q. Cheng, T. Sandalova, Y. Lindqvist and E. S. Arnér, Crystal structure and catalysis of the selenoprotein thioredoxin reductase 1, J. Biol. Chem., 2009, 284, 3998–4008.
4. A. Bindoli, M. P. Rigobello, G. Scutari, C. Gabbiani, A. Casini and L. Messori, Thioredoxin reductase: a target for gold compounds acting as potential anticancer drugs, Coord. Chem. Rev., 2009, 253(11–12), 1692–1707,  DOI:10.1016/j.ccr.2009.02.026.
5. O. Rackham, S. N. Nichols, P. J. Leedman, S. N. Berners-Price and A. Filipovska, A gold(I) phosphine complex selectively induces apoptosis in breast cancer cells: implications for anticancer therapeutics targeted to mitochondria, Biochem. Pharmacol., 2007, 74, 992–1002.
6. M. Coronnello, E. Mini, B. Caciagli, M. A. Cinellu, A. Bindoli, C. Gabbiani and L. Messori, Mechanisms of cytotoxicity of selected organogold(III) compounds, J. Med. Chem., 2005, 48(21), 6761–6765,  DOI:10.1021/jm050493o.
7. C. Gabbiani, G. Mastrobuoni, F. Sorrentino, B. Dani, M. P. Rigobello, A. Bindoli, M. A. Cinellu, G. Pieraccini, L. Messori and A. Casini, Thioredoxin reductase, an emerging target for anticancer metallodrugs. Enzyme inhibition by cytotoxic gold(III) compounds studied with combined mass spectrometry and biochemical assays, MedChemComm, 2011, 2(1), 50–54,  10.1039/c0md00181c.
8. M. J. McKeage, Gold opens mitochondrial pathways to apoptosis, Br. J. Pharmacol., 2002, 136(8), 1081–1082,  DOI:10.1038/sj.bjp.0704822.
9. S. Urig, K. Fritz-Wolf, R. Reau, C. Herold-Mende, K. Toth, E. Davioud-Charvet and K. Becker, Undressing of phosphine gold(I) complexes as irreversible inhibitors of human disulfide reductases, Angew. Chem., Int. Ed., 2006, 45(12), 1881–1886,  DOI:10.1002/anie.200502756.
10. M. P. Rigobello, L. Messori, G. Marcon, M. A. Cinellu, M. Bragadin, A. Folda, G. Scutari and A. Bindoli, Gold complexes inhibit mitochondrial thioredoxin reductase: consequences on mitochondrial functions, J. Inorg. Biochem., 2004, 98(10), 1634–1641,  DOI:10.1016/j.jinorgbio.2004.04.020.
11. M. Deponte, S. Urig, L. D. Arscott, K. F. Wolf, R. Reau, C. Herold-Mende, S. Koncarevic, M. Meyer, E. Davioud-Charvet and D. P. Ballou, et al., Mechanistic studies on a novel, highly potent gold-phosphole inhibitor of human glutathione reductase, J. Biol. Chem., 2005, 280(21), 20628–20637,  DOI:10.1074/jbc.M412519200.
12. M. Serratrice, M. A. Cinellu, L. Maiore, M. Pilo, A. Zucca, C. Gabbiani, A. Guerri, I. Landini, S. Nobili and E. Mini, et al., Synthesis, Structural Characterization, Solution Behavior, and in Vitro Antiproliferative Properties of a Series of Gold Complexes with 2-(2′-Pyridyl)benzimidazole as Ligand: Comparisons of Gold(III) versus Gold(I) and Mononuclear versus Binuclear Derivatives, Inorg. Chem., 2012, 51, 3161–3171.
13. L. Maiore, M. A. Cinellu, S. Nobili, I. Landini, E. Mini, C. Gabbiani and L. Messori, Gold(III) complexes with 2-substituted pyridines as experimental anticancer agents: solution behavior, reactions with model proteins, antiproliferative properties, J. Inorg. Biochem., 2012, 108, 123–127.
14. W. Cai, L. Zhang, Y. Song, B. Wang, B. Zhang, X. Cui, G. Hu, Y. Liu, J. Wu and J. Fang, Small molecule inhibitors of mammalian thioredoxin reductase, Free Radical Biol. Med., 2012, 52, 257–265.
15. V. Gandin, A. P. Fernandes, M. P. Rigobello, B. Dani, F. Sorrentino, F. Tisato, M. Bjornstedt, A. Bindoli, A. Sturaro and R. Rella, et al., Cancer cell death induced by phosphine gold(I) compounds targeting thioredoxin reductase, Biochem. Pharmacol., 2010, 79(2), 90–101,  DOI:10.1016/j.bcp.2009.07.023.
16. J. L. Hickey, R. A. Ruhayel, P. J. Barnard, M. V. Baker, S. J. Berners-Price and A. Filipovska, Mitochondria-targeted chemotherapeutics: the rational design of gold(I) N-heterocyclic carbene complexes that are selectively toxic to cancer cells and target protein selenols in preference to thiols, J. Am. Chem. Soc., 2008, 130(38), 12570–12571,  DOI:10.1021/ja804027j.
17. T. J. Siciliano, M. C. Deblock, K. M. Hindi, S. Durmus, M. J. Panzner, C. A. Tessier and W. J. Youngs, Synthesis and anticancer properties of gold(I) and silver(I) N-heterocyclic carbene complexes, J. Organomet. Chem., 2011, 696, 1066e1071.
18. D. Curran, H. Muller-Bunz, S. I. Bar, R. Schobert, X. M. Zhu and M. Tacke, Novel Anticancer NHC*-Gold(I) Complexes Inspired by Lepidiline A, Molecules, 2020, 25(15), 3474–3490,  DOI:10.3390/molecules25153474.
19. A. A. A. Sulaiman, S. Ahmad, S. M. Hashimi, A. I. Alqosaibi, A. M. P. Peedikakkal, A. Alhoshani, N. B. Alsaleh and A. A. Isab, Novel dinuclear gold(I) complexes containing bis(diphenylphosphano)alkanes and (biphenyl-2-yl)(di-tert-butyl)phosphane: synthesis, structural characterization and anticancer activity, New J. Chem., 2022, 46(35), 16821–16831,  10.1039/d2nj01680j.
20. A. K. Abogosh, M. K. Alghanem, S. Ahmad, A. Al-Asmari, H. M. A. Sobeai, A. A. A. Sulaiman, M. Fettouhi, S. A. Popoola, A. Alhoshani and A. A. Isab, A novel cyclic dinuclear gold(I) complex induces anticancer activity via an oxidative stress-mediated intrinsic apoptotic pathway in MDA-MB-231 cancer cells, Dalton Trans., 2022, 51(7), 2760–2769,  10.1039/d1dt03546k.
21. E. Abas, R. Pena-Martinez, D. Aguirre-Ramírez, A. Rodriguez-Dieguez, M. Laguna and L. Gras, New selective thiolate gold(I) complexes inhibitthe proliferation of different human cancer cellsand induce apoptosis in primary cultures of mousecolon tumors, Dalton Trans., 2020, 49, 1915–1927.
22. M. S. Filho, T. Scattolin, P. Dao, N. V. Tzouras, R. Benhida, M. Saab, C. Van Hecke, P. Lippmann, A. R. Martin and I. Ott, et al., Straightforward synthetic route to gold(I)-thiolato glycoconjugate complexes bearing NHC ligands (NHC = N-heterocyclic carbene) and their promising anticancer activity, New J. Chem., 2021, 45, 9995–10001.
23. G. A. Rickard, J. Berges, C. Houee-Levin and A. Rauk, Ab Initio and QM/MM Study of Electron Addition on the Disulfide Bond in Thioredoxin, J. Phys. Chem. B, 2008, 112, 5774–5787.
24. J. A. S. Howell, DFT investigation of the interaction between gold(I) complexes and the active site of thioredoxin reductase, J. Organomet. Chem., 2009, 694(6), 868–873,  DOI:10.1016/j.jorganchem.2008.10.029.
25. G. Y. S. Delgado, D. Paschoal and H. F. Dos Santos, Predicting standard reduction potential for anticancer Au(III)-complexes: a DFT study, Comput. Theor. Chem., 2017, 1108, 86–92,  DOI:10.1016/j.comptc.2017.03.027.
26. I. Tolbatov, P. Umari and A. Marrone, Mechanism of Action of Antitumor Au(I) N-Heterocyclic Carbene Complexes: A Computational Insight on the Targeting of TrxR Selenocysteine, Int. J. Mol. Sci., 2024, 25, 2625–2635,  DOI:10.3390/ijms25052625.
27. A. D. Becke, Density Functional thermochemistry. III. The role of exact exchange, J. Phys. Chem., 1993, 98, 5648–5652.
28. C. Lee, W. Yang and R. G. Parr, Development of the Cole-Salvetti correlation energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculations of vibrational absorption and circular-dichroism spectra using density-functional force-fields, J. Phys. Chem., 1994, 98(45), 11623–11627,  DOI:10.1021/j100096a001.
30. S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin-density calculations – a critical analysis, Can. J. Phys, 1980, 58(8), 1200–1211.
31. J. V. Burda, M. Zeizinger, J. Sponer and J. Leszczynski, Hydration of cis- and trans-platin: a pseudopotential treatment in the frame of a G3-type theory for platinum complexes, J. Chem. Phys., 2000, 113(6), 2224–2232.
32. M. Zeizinger, J. V. Burda, J. Šponer, V. Kapsa and J. Leszczynski, A Systematic ab Initio Study of the Hydration of Selected Palladium Square-Planar Complexes. A Comparison with Platinum Analogues, J. Phys. Chem. A, 2001, 105(34), 8086–8092.
33. T. Zimmermann, M. Zeizinger and J. V. Burda, Cisplatin Interaction with Cysteine and Methionine; theoretical DFT study, J. Inorg. Biochem., 2005, 99, 2184–2196.
34. T. Zimmermann, Z. Chval and J. V. Burda, Cisplatin Interaction with Cysteine and Methionine in Aqueous Solution: Computational DFT/PCM Study, J. Phys. Chem. B, 2009, 113(10), 3139–3150,  DOI:10.1021/jp807645x.
35. A. Klamt and G. Schuurmann, Cosmo – a New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient, J. Chem. Soc., Perkin Trans. 2, 1993,(5), 799–805.
36. D. H. Wertz, Relationship between the Gas-Phase Entropies of Molecules and Their Entropies of Solvation in Water and 1-Octanol, J. Am. Chem. Soc., 1980, 102, 5316–5322.
37. M.-J. Cheng, R. J. Nielsen and W. A. Goddard III, Chem. Commun., 2014, 50, 10994.
38. F. Šebesta and J. V. Burda, Side Reactions with an Equilibrium Constraint: Detailed Mechanism of the Substitution Reaction of Tetraplatin with dGMP as a Starting Step of the Pt(IV) Reduction Process, J. Phys. Chem. B, 2017, 121, 4400–4413.
39. F. Šebesta and J. V. Burda, Interactions of Ascorbic Acid with Satraplatin and Its Trans Analog JM576; DFT Computational Study, Eur. J. Inorg. Chem., 2018, 1481–1491,  DOI:10.1002/ejic.201701334.
40. T. Zimmermann and J. V. Burda, Charge-scaled cavities in polarizable continuum model: determination of acid dissociation constants for platinum-amino acid complexes, J. Chem. Phys., 2009, 131, 135101.
41. T. Zimmermann and J. V. Burda, Reaction of cisplatin with cysteine and methionine at constant pH, Dalton Trans., 2010, 39, 1295–1301.
42. T. Zimmermann, J. Leszczynski and J. V. Burda, Activation of the cisplatin and transplatin complexes in solution with constant pH and concentration of chloride anions; quantum chemical study, J. Mol. Model., 2011, 17, 2385–2393.
43. F. Šebesta, Ž. Sovová and J. V. Burda, Determination of Amino Acids’ pK_a: Importance of Cavity Scaling within Implicit Solvation Models and Choice of DFT Functionals, J. Phys. Chem. B, 2024, 128(7), 1627–1637,  DOI:10.1021/acs.jpcb.3c07007.
44. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83(2), 735–746.
45. NBO v 5.9 Program, University of Wisconsin, Madison, Wisconsin 53706: Wisconsin, 2001, https://www.chem.wisc.edu/~nbo5 (accessed).
46. G. Schüürmann, M. Cossi, V. Barone and J. Tomasi, Prediction of the pK_a of carboxylic acids using the ab initio continuum-solvation model PCM-UAHF, J. Phys. Chem. A, 1998, 102(33), 6706–6712.
47. V. Barone, M. Cossi and J. Tomasi, A new definition of cavities for the computation of solvation free energies by the polarizable continuum model, J. Chem. Phys., 1997, 107(8), 3210–3221.
48. C. Curutchet, A. Bidon-Chanal, I. Soteras, M. Orozco and F. J. Luque, MST Continuum Study of the Hydration Free Energies of Monovalent Ionic Species, J. Phys. Chem. B, 2005, 109(8), 3565–3574.
49. M. Orozco and F. J. Luque, Optimization of the cavity size for ab initio MST-SCRF calculations of monovalent ions, Chem. Phys., 1994, 182, 237–248.
50. T. Zimmermann, F. Šebesta and J. B. Burda, A new grand-canonical potential for the thermodynamic description of the reactions in solutions with constant pH, J. Mol. Liq., 2021, 335, 115979.
51. T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023.
52. R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron-Affinities Of The 1st-Row Atoms Revisited – Systematic Basis-Sets And Wave-Functions, J. Chem. Phys., 1992, 96(9), 6796–6806,  DOI:10.1063/1.462569.
53. D. E. Woon and T. H. Dunning, Gaussian-basis sets for use incorrelated molecular calculations.3. The atoms Aluminium through Argon, J. Chem. Phys., 1993, 98(2), 1358–1371,  DOI:10.1063/1.464303.
54. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the 4d elements Y-Pd, J. Chem. Phys., 2007, 126, 124101,  DOI:10.1063/1.2647019.
55. K. A. Peterson and C. Puzzarini, Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements, Theor. Chem. Acc., 2005, 114, 283–296,  DOI:10.1007/s00214-005-0681-9.
56. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Energy-consistent pseudopotentials for group 11 and 12 atoms: adjustment to multi-configuration Dirac-Hartree-Fock data, J. Chem. Phys., 2005, 311, 227–244,  DOI:10.1016/j.chemphys.2004.10.005.
57. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community, J. Chem. Inf. Model., 2019, 59, 4814–4820.
58. D. Feller, The role of databases in support of computational chemistry calculations, J. Comput. Chem., 1996, 17, 1571–1586.
59. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, Basis Set Exchange: A Community Database for Computational Sciences, J. Chem. Inf. Model., 2007, 47, 1045–1052,  DOI:10.1021/ci600510j.
60. M. Urban, I. Černušák, V. Kello and J. Noga, Electron Correlation in Molecules, in Methods in Computational Chem, ed. S. Wilson, Plenum Press, 1987, vol. 1.
61. P. Jurecka and P. Hobza, On the convergence of the (dE(CCSD(T))–dE(MP2)) term for complexes with multiple H-bonds, Chem. Phys. Lett., 2002, 365(1), 89–94.
62. V. S. Bryantsev, M. S. Diallo and W. A. Goddard Iii, Calculation of Solvation Free Energies of Charged Solutes Using Mixed Cluster/Continuum Models, J. Phys. Chem. B, 2008, 112(32), 9709–9719,  DOI:10.1021/jp802665d.
63. M. Gupta, E. F. da Silva and H. F. Svendsen, Explicit Solvation Shell Model and Continuum Solvation Models for Solvation Energy and pK_a Determination of Amino Acids, J. Chem. Theor. Comput., 2013, 9(11), 5021–5037.
64. R. Casasnovas, D. Fernández, J. Ortega-Castro, J. Frau, J. Donoso and F. Muñoz, Avoiding gas-phase calculations in theoretical pK_a predictions, Theor. Chem. Acc., 2011, 130(1), 1–13.
65. S. Sastre, R. Casasnovas, F. Muñoz and J. Frau, Isodesmic reaction for accurate theoretical pK_a calculations of amino acids and peptides, Phys. Chem. Chem. Phys., 2016, 18(16), 11202–11212.
66. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 88th edn, 2007, vol. 7-1 Properties of Amino Acids, p. 2640.
67. R. E. Huber and R. S. Criddle, Comparison of the Chemical Properties of Selenocysteine and Selenocystine with Their Sulfur Analogs, Arch. Biochem. Biophys., 1967, 122, 164–173.
68. J. V. Burda, Z. Futera and Z. Chval, Exploration of various electronic properties along the reaction coordinate for hydration of Pt(II) and Ru(II) complexes; the CCSD, MPx, and DFT computational study, J. Mol. Model., 2013, 19(12), 5245–5255,  DOI:10.1007/s00894-013-1994-6.
69. J. R. Murdoch, What is the rate-limiting step of a multistep reaction?, J. Chem. Educ., 1981, 58(1), 32,  DOI:10.1021/ed058p32.
70. R. A. Alberty, Effect of Ph and Metal Ion Concentration on Equilibrium Hydrolysis of Adenosine Triphosphate to Adenosine Diphosphate, J. Biol. Chem., 1968, 243(7), 1338–1343.
71. R. A. Alberty and I. Oppenheim, Fundamental equation for systems in chemical equilibrium, J. Chem. Phys., 1988, 89(6), 3689–3693.
72. R. A. Alberty, Biochemical thermodynamics, Biochem. Biophys. Acta, 1994, 1207, 1–11.
73. R. A. Alberty, Use of Legendre transforms in chemical thermodynamics – (IUPAC Technical Report), Pure Appl. Chem., 2001, 73(8), 1349–1380.
74. F. Šebesta, J. Šebera, V. Sychrovsky, Y. Tanaka and J. V. Burda, QM and QM/MM umbrella sampling MD study of the formation of Hg(II)–thymine bond: Model for evaluation of the reaction energy profiles in solutions with constant pH, J. Comput. Chem., 2020, 41, 1509–1520.
75. L. Michera, M. Nekardova and J. V. Burda, Reactions of cisplatin and glycine in solution with constant pH: a computational study, Phys. Chem. Chem. Phys., 2012, 14, 12571–12579.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04386c

---