Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The physics of defect chemistry and the chemistry of defect physics
Andreas
Klein
 * and
Denis
Sudarikov
* and
Denis
Sudarikov

Technical University of Darmstadt, Electronic Structure of Materials, Darmstadt, Germany. E-mail: aklein@esm.tu-darmstadt.de
First published on 12th March 2025
Abstract
Defect chemistry is the classical approach to evaluate point-defect concentrations in solids depending on the chemical activity of the (n − 1) of n constituents by evaluating the mass action laws of a number of defect reactions conserving species, lattice sites, and charge. In an alternative approach, formation energies of individual defects can be calculated to determine the dependence on the Fermi level and on the chemical potentials of the reservoirs. This contribution provides the quantitative relationship between the two approaches, offering the opportunity to compare calculated defect formation energies with experimentally determined quantities. As an example, the application of the two approaches to the comparison of electronic and ionic compensation of doping and the influence of the band edge energies on it is given. This example demonstrates that the Gibbs energy of reduction and oxidation are essentially aligning the energy axis of ionic defects relative to that of electronic defects. In conjunction with the dependence of the valence band maximum and conduction band minimum energies on material composition, this offers the opportunity to tune the preference for electronic, ionic or mixed compensation of doping by two independent quantities.
1 Introduction
Point defects affect almost every material property, particularly those of ionic solids.1 Understanding their influence and controlling their concentrations is a central issue of materials science. Traditionally, the thermodynamics and kinetics of defects in solids are described by defect chemistry, which has become a separate discipline in physical chemistry.2–4 The comparison of defect models with experiments is indispensable for obtaining a quantitative description of defect concentrations. However, the considerable complexity of some ionic solids with plenty of different defect species does not always allow for a unique solution of the involved set of equations. Therefore, research on defect properties is still ongoing even for well-studied materials, such as BaTiO3.5–15 With the progress of first-principles electronic structure calculations, a new approach was revealed in the late 20th century,16,17 which is becoming increasingly important with further refinement of the techniques.18 The approach, which is termed the physical approach in this contribution, is based on the comparison of total energies of supercells with and without defects. Thereby it provides the formation energy of a single isolated defect, which experimentally is not accessible. Apart from the approximations required to perform the calculations, no assumptions about the presence of other defects and no experimental inputs are necessary. While defect chemistry provides defect concentrations depending on the chemical activity in so-called Brouwer diagrams, the physical approach provides independent Gibbs formation energies for every defect, which are typically plotted as a function of the electron chemical potential (the Fermi level) for selected chemical boundary conditions. It has already been emphasized that the chemical and the physical descriptions of defect properties are equivalent,19,20 but a quantitative relationship allowing for a comparison of the two approaches is still lacking.This article will first provide a brief introduction to the two approaches for describing defect properties, restricted to the simple case of dilute, non-interacting defects and to a situation with only four different native defect species, an ionic acceptor and an ionic donor species and free electrons and holes in the conduction and valence bands. The defect reactions and their relationship to defect formation energies will be exemplified using the example of Schottky disorder (cation and anion vacancies as native defect species), but are equally valid for any other kind of disorder. This simplified scenario is sufficient to provide a quantitative relationship between equilibrium constants of defect reactions and calculated defect formation energies, which remain valid if the complexity is increased, for example by including valence changes of the ionic defects, trapped electronic carriers, and charged dopants. The influence of the latter is specifically elaborated for the important competition between ionic and electronic compensation of doping, which determines the nature of conductivity (ionic, electronic, or mixed). The scenario will also be used to highlight differences and synergies of the two descriptions of defect properties.
2 Defect chemistry
Defect chemistry is the traditional approach used to describe the dependence of defect concentrations on thermodynamic variables.2,3 The chemical boundary conditions include the temperature T and the activities of the involved components ai, where the activities are related to the chemical potentials μivia:μi = μ0i + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ai ai | (1) |
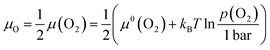 | (2) |
Together with the tabulated values for the standard chemical of molecular oxygen, μ0(O2) (equivalent to the standard molar Gibbs energy of oxygen, ΔG0m(O2), see e.g. ref. 22), the relationship between the chemical potential and the partial pressure of oxygen is obtained from eqn (2). Data for 300, 600 and 1000 K are shown in Fig. 1. The significant influence of temperature is evident from the calculation.
 | ||
| Fig. 1 Relationship between the oxygen chemical potential and the oxygen partial pressure as calculated from eqn (2) using data for the standard Gibbs energy of molecular oxygen22 (100 kJ mol−1 = 1.0364 eV ≈ 1 eV). The insert depicts the standard molar Gibbs energy of molecular oxygen, G0m(O2) = μ0 (data taken from ref. 22). | ||
Defect concentrations are obtained by evaluating the defect reactions specific to the material. When only charged intrinsic defects are assumed and defect association is neglected, the relevant ionic defects in a binary compound MXz are the metal and anion vacancies, vM and vX, and interstitials, Mi and Xi, respectively (we use lowercase “v” and “i” for vacancies and interstitials for clarity1). In most cases, only two ionic defects are important. The resulting different disorders are of Schottky (S: vM & vX), Frenkel (F: vM & Mi), anti-Schottky (![[S with combining macron]](https://www.rsc.org/images/entities/char_0053_0304.gif) : Mi and Xi), or anti-Frenkel (
: Mi and Xi), or anti-Frenkel (![[F with combining macron]](https://www.rsc.org/images/entities/char_0046_0304.gif) : vX & Xi) type. The different types of disorder are independent but connected to each other by F +
: vX & Xi) type. The different types of disorder are independent but connected to each other by F + ![[F with combining macron]](https://www.rsc.org/images/entities/char_0046_0304.gif) − S =
− S = ![[S with combining macron]](https://www.rsc.org/images/entities/char_0053_0304.gif) . This contribution will restrict the comparison between the chemical and physical approaches for describing properties to the example of Schottky disorder, but it is equally valid for any kind of ionic disorder. For an oxide with composition MO, the ionic equilibrium for Schottky disorder is determined by transferring a metal and an oxygen species to the surface of the material, which is described using the following reaction:
. This contribution will restrict the comparison between the chemical and physical approaches for describing properties to the example of Schottky disorder, but it is equally valid for any kind of ionic disorder. For an oxide with composition MO, the ionic equilibrium for Schottky disorder is determined by transferring a metal and an oxygen species to the surface of the material, which is described using the following reaction:
 | (3) |
with the mass action law:
 | (4) |
 ,
,  .
.
In addition to the ionic defects, electronic disorder is related to the excitation of electrons from the valence band into the conduction band, thereby generating an electron in the conduction band and a hole in the valence band according to:
| nil ⇌ e′ + h˙ | (5) |
with the mass action law:
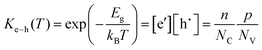 | (6) |
Here, the band gap of the material, Eg, is the free energy of formation of the electron–hole pair, n and p are the concentrations of free (non-trapped) electrons and holes, and NC and NV are the effective density of states in the conduction and valence band for non-degenerate semiconductors with parabolic band dispersion. The link connecting electronic and ionic disorder to each other (see the section on ionic vs. electronic compensation for an explanation) and to the oxygen partial pressure is the reduction (or oxidation) reaction of the sample. For example, the reduction of an oxide may proceed according to:
 | (7) |
The mass action law related to this reduction is
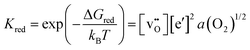 | (8) |
Instead of the reduction reaction, it is sometimes more convenient to consider the oxidation reaction. To be consistent with the discussion below, we express the oxidation reaction for Schottky disorder as:
 | (9) |
 | (10) |
The significance of the distinction between the reduction and oxidation reaction will become evident during the discussion of the influence of the band edge energies.
Eqn (3)–(8) include only doubly charged oxygen and metal vacancies. In principle, also singly charged and neutral vacancies may be present. For every added defect species, an additional reaction is required. For differently charged ionic defects, these would be the ionization reactions,3 which are omitted here for clarity. Eventually, the defect concentrations for a compound MO with Schottky and electronic disorder are obtained from the Gibbs energies of Schottky disorder and of the reduction reaction by solving the set of the three mass action laws, eqn (4), (6) and (8) (or (10)), in conjunction with the charge neutrality condition. The latter is given for Schottky disorder with the concentrations (per volume) of doubly charged metal and oxygen vacancies, 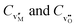 , by:
, by:
 | (11) |
For the charge neutrality condition, concentrations of defects have to be used instead of the site fractions as the number of potential defect sites can differ for defects, for example, the concentration of potential defect sites for oxygen vacancies is the concentration of oxygen lattice sites, while that of the electronic defects is the effective density of states, NC and NV, which is about three orders of magnitude lower than that of the lattice sites.
One possible practical solution to the set of equations is obtained by calculating the concentrations of all defects depending on the concentrations of, for example, oxygen vacancies for a given set of oxygen partial pressure and equilibrium constants K of the three reactions. For the given example it is convenient to start with eqn (4) to obtain the metal vacancy concentration as a function of oxygen vacancy concentration. Eqn (8) then provides the electron concentration, and eqn (6) the hole concentration as a function of  . With the dependence of all defect concentrations on
. With the dependence of all defect concentrations on  in the form
in the form 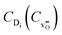 , the equilibrium oxygen vacancy concentration,
, the equilibrium oxygen vacancy concentration, 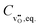 , is obtained by directly solving the charge neutrality equation, eqn (11). Eventually, all equilibrium defect concentrations are obtained from the equilibrium oxygen vacancy concentration,
, is obtained by directly solving the charge neutrality equation, eqn (11). Eventually, all equilibrium defect concentrations are obtained from the equilibrium oxygen vacancy concentration,  . Doing the calculation with a variation of the oxygen partial pressure finally reveals the Brouwer diagram, i.e. the concentrations of all defects depending on oxygen partial pressure. An example of this kind of diagram is presented in Fig. 2(a).
. Doing the calculation with a variation of the oxygen partial pressure finally reveals the Brouwer diagram, i.e. the concentrations of all defects depending on oxygen partial pressure. An example of this kind of diagram is presented in Fig. 2(a).
3 The physical approach
An alternative way to obtain defect concentrations in materials starts with the Gibbs formation energies of individual defects. These can be calculated by means of density functional theory (DFT) as a function of the chemical potential of the constituents and of the Fermi level.16–18 The Gibbs formation energies are obtained by comparing the total energies of a supercell with and without a defect. Addition or removal of an atom to the supercell changes its energy by the chemical potential of that atom, which is determined by the external conditions. The range of possible chemical potentials is restricted by the boundary phases. In the case of a binary metal oxide with composition MO and pure metal and oxygen as boundary phases, most oxidizing conditions are given by μO = 0 eV and most reducing ones by μM = 0 eV. As μMO = μO + μM, where μMO is the standard molar formation energy of the MO compound, the reduced limit is given by μO = μMO. Between the oxidized and the reduced limit, the defect formation energies depend linearly on the chemical potential. Therefore, only one chemical potential needs to be specified for binary compounds. The chemical boundary conditions for a compound containing n species requires the specification of (n − 1) chemical potentials. For SrTiO3, as an example, one needs to specify the activity of either Sr, Ti, SrO, or TiO2 in addition to that of oxygen. For binary metal oxides, one can also express the boundary conditions in terms of the experimentally controlled oxygen partial pressure, which is related to the oxygen potential viaeqn (2). However, the use of chemical potentials to describe thermodynamic stability is more straightforward and is therefore commonly used. Where possible, both scales are included in the diagrams in this contribution, but it is emphasized that the connection between μO and p(O2) is strongly dependent on temperature as illustrated in Fig. 1.The charge state of the defect is accounted for by adding either positive or negative background charges. As for atoms, addition or removal of an electron from the supercell changes its energy by the chemical potential of the electron μe. In summary, the defect formation energy ΔGqD of a defect in charge state q can be written as:17
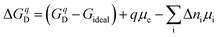 | (12) |
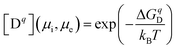 | (13) |
It is mentioned that the DFT calculations reveal formation energies of the supercells at zero Kelvin, HD(0 K). The temperature dependence of the enthalpy and entropy contribution to the Gibbs formation energy of defects are not included. It is also mentioned that additional posteriori corrections to eqn (12) are required, for example, to account for effects related to the small size of the supercells. These corrections do not affect the dependence of ΔGqD on the chemical potentials and the Fermi level. Details for the corrections can be found, for example, in ref. 18.
According to eqn (12), the Gibbs formation energies of charged defects depend linearly on the Fermi energy. This can be rationalized as the electrons added or removed from a defect have an energy corresponding to the (electro)chemical potential of the electrons, which is called the Fermi level.20 Following eqn (12), it is sufficient to calculate the defect formation energy in a given charge state at any value of the Fermi level and chemical potential. To display the result of the calculation, the defect formation energies are typically plotted as a function of the Fermi level for the most oxidizing and most reducing conditions. An example for a simple hypothetical binary metal oxide MO with Schottky disorder is given in Fig. 2(b). Only doubly charged states of the metal and oxygen vacancies are considered for clarity.
Practically, the equilibrium defect concentrations are obtained by calculating the defect concentrations as a function of the Fermi level using the defect formation energies for a given chemical potential of oxygen. The equilibrium Fermi level is then determined by solving the charge neutrality eqn (11) and used to obtain the equilibrium defect concentrations. Repeating the calculations for the allowed range of oxygen chemical potentials finally results in the Brouwer diagram. The formation energies given in Fig. 2(b) reveal defect concentrations at 1000 °C identical to those displayed in Fig. 2(a).
4 Connecting the two approaches
The two approaches for finding defect concentrations are equivalent as they provide identical defect concentrations for an appropriately selected set of parameters. In order to put this equivalence on a mathematical basis, it is necessary to relate the quantities required for calculating the concentrations using the defect chemistry approach to the defect formation energies used in the physical approach. For the example used above, the relationship has to be identified for the reaction free energies of the Schottky and the reduction reaction. The third quantity, the band gap, is directly used in both approaches. The relationship for the Schottky reaction is easily identified, as the free energy of the Schottky pair formation is equivalent to the sum of the formation energies of the charged metal and oxygen vacancies for the metal oxide MO with a divalent metal (see eqn (3)): | (14) |
Although the Gibbs formation energies of the metal and oxygen vacancies both depend on the chemical potentials and on the Fermi level, the sum of the two does not. Whenever the Gibbs formation energy of one of the two defects is changing with EF or μO, the formation energy of the other defect is changing by the same amount in the opposite direction. The first is the case due to the opposite charge state of the metal and oxygen vacancy in eqn (12) and the second is the case as the chemical potential of the oxygen and the metal in the last term of eqn (12) are connected by:
| μ(O) + μ(M) = μ(MO) | (15) |
The relationship for the free reaction energy of the reduction can be obtained via the mass action law for the reduction reaction (8). In this equation, the site fraction for oxygen vacancies,  , which is a function of the Fermi level and the oxygen chemical potential, is replaced by
, which is a function of the Fermi level and the oxygen chemical potential, is replaced by 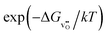 , that for electrons, [e′], which is a function of the Fermi level, by exp(−(ECB − EF)/kT), and the oxygen partial pressure by using the expression given in eqn (2). This leads to:
, that for electrons, [e′], which is a function of the Fermi level, by exp(−(ECB − EF)/kT), and the oxygen partial pressure by using the expression given in eqn (2). This leads to:
 | (16) |
Taking the logarithm of (16) and multiplying the result by kBT reveals:
 | (17) |
This equation is valid for any combination of EF and μO. It is convenient to evaluate eqn (17) for μO = 0 eV (oxygen-rich limit) and EF = ECB (Fermi level at the conduction band minimum), resulting in:
 | (18) |
While ΔGred can be obtained from experiment (for BaTiO3 see e.g., ref. 7 and references therein),  is only accessible from computations (for BaTiO3 see, e.g., ref. 11, 15, and 23). Therefore, eqn (18) directly offers the opportunity to compare calculated defect formation energies with experimentally derived quantities, which is not possible otherwise. The difference between ΔGred and
is only accessible from computations (for BaTiO3 see, e.g., ref. 11, 15, and 23). Therefore, eqn (18) directly offers the opportunity to compare calculated defect formation energies with experimentally derived quantities, which is not possible otherwise. The difference between ΔGred and  is given by
is given by  , which is a function of temperature. The oxygen chemical potential can be obtained from thermodynamic data22 and can be up to several electronvolts as illustrated by the insert in Fig. 1. For given formation energies of the cation and anion vacancies, eqn (14) and (18) provide the quantitative relationship to calculate the free energies and equilibrium reaction constants for Schottky disorder and the reduction reaction. For the example given in Fig. 2, the sum of the formation energies of the metal and oxygen vacancy is 2.5 eV at any value of the Fermi energy and oxygen chemical potential. The formation energy of the oxygen vacancy at the conduction band minimum (EF = ECB) under oxidizing conditions (μO = 0 eV is 6.2 eV, extrapolation of the red dashed line to E = ECB in Fig. 2(b)). To obtain the free reduction energy, the standard molar free formation energy of oxygen molecules, μ0(O2) at 1273 K, is required. This is obtained from thermodynamic reference data22 as −287.67 kJ mol−1 = −2.98 eV, resulting in ΔGred = 6.2 − 1.5 = 4.7 eV, which is used to calculate the Brouwer diagram in Fig. 2(a). The value of μ0(O2) can also be obtained by extrapolating the respective curve in Fig. 1 to μO = 0 and then evaluating eqn (2).
, which is a function of temperature. The oxygen chemical potential can be obtained from thermodynamic data22 and can be up to several electronvolts as illustrated by the insert in Fig. 1. For given formation energies of the cation and anion vacancies, eqn (14) and (18) provide the quantitative relationship to calculate the free energies and equilibrium reaction constants for Schottky disorder and the reduction reaction. For the example given in Fig. 2, the sum of the formation energies of the metal and oxygen vacancy is 2.5 eV at any value of the Fermi energy and oxygen chemical potential. The formation energy of the oxygen vacancy at the conduction band minimum (EF = ECB) under oxidizing conditions (μO = 0 eV is 6.2 eV, extrapolation of the red dashed line to E = ECB in Fig. 2(b)). To obtain the free reduction energy, the standard molar free formation energy of oxygen molecules, μ0(O2) at 1273 K, is required. This is obtained from thermodynamic reference data22 as −287.67 kJ mol−1 = −2.98 eV, resulting in ΔGred = 6.2 − 1.5 = 4.7 eV, which is used to calculate the Brouwer diagram in Fig. 2(a). The value of μ0(O2) can also be obtained by extrapolating the respective curve in Fig. 1 to μO = 0 and then evaluating eqn (2).
The connection between the formation energy of the metal vacancy and the Gibbs energy of the oxidation can be obtained in the same manner as that for the reduction (eqn (16)) as:
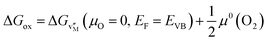 | (19) |
The free reaction energy of the oxidation, ΔGox, is connected to that of the reduction, ΔGred, the Schottky pair, ΔGS, and the electron–hole pair, ΔGe–h = Eg, via:
| ΔGox = ΔGS + 2·Eg − ΔGred | (20) |
The relationship between Brouwer diagrams and Gibbs energies of the formation of metal and oxygen vacancies of a binary metal oxide MO with Schottky disorder for three different values of the Gibbs energy of reduction is illustrated in Fig. 3. Three scenarios with identical Gibbs energy for Schottky disorder (ΔGS = 4.5 eV) and identical band gaps (Eg = 2.7 eV) but different Gibbs energies of reduction are compared. The scenario in the middle column of Fig. 3 is identical to the one depicted in Fig. 2. In the left and right columns, the Gibbs energy of reduction is changed by ±1.3 eV. Lowering (left column) and raising (right column) the Gibbs energy of reduction shifts the Brouwer diagram towards higher and lower oxygen activity, respectively.
The Gibbs formation energies of metal and cation vacancies representing the three scenarios are given below the respective Brouwer diagrams. As expressed by eqn (18), lowering the Gibbs energy of reduction lowers the Gibbs formation energy of the oxygen vacancy by the same amount for both oxidizing and reducing conditions (dashed and solid red lines). As the Gibbs energy for Schottky disorder is the same in all three scenarios, the changes of the Gibbs formation energy of the metal vacancy are opposite to those of the oxygen vacancy. This leads to an apparent shift of the formation energies on the energy axis, which amounts to half of the change in the Gibbs energy of reduction due to the double charge of the defects considered.
5 Ionic vs. electronic compensation
One of the major differences between materials is whether they react on doping by the formation of electronic, ionic or both charge carriers. Due to the charge neutrality requirement, a positively charged donor added to a material, for example by substituting Sr2+ in SrTiO3 by La3+, can be compensated either by an intrinsic acceptor, such as a metal vacancy, or by an electron in the conduction band.24 A negatively charged acceptor can be compensated by an intrinsic donor, such as an oxygen vacancy, or by a hole in the valence band. Electronic compensation is desirable for semiconducting properties, pure ionic conduction for electrolytes in batteries and fuel cells and mixed ionic-electronic conduction for electrode materials and gas permeation membranes. For semiconductors, particularly those with larger energy gaps, it has been known for many years that electronic carrier concentrations are limited by self-compensation, which is the same as the formation of ionic lattice defects upon increasing the dopant concentration.25,26The difference between ionic and electronic compensation is directly related to the formation energies of the ionic defects.20,27,28 Donor or acceptor doping adds or removes electrons from the host material, which raises or lowers the Fermi level, respectively. As illustrated in Fig. 2 and in the lower row of Fig. 3, raising the Fermi level will lower the Gibbs formation energy of the intrinsic acceptor (metal vacancy), while lowering the Fermi level will reduce the formation energy of the intrinsic donor (oxygen vacancy). Eventually, the formation energies may become zero or even negative. Negative formation energies correspond to a thermodynamic instability. If the Gibbs formation energies of defects are negative, the material can gain energy unlimited by the formation of defects with an equilibrium defect concentration being higher than the concentration of potential defect sites ([…] > 1). If not kinetically limited, the decrease in the formation energy towards zero will result in the formation of a high concentration of ionic defects. These prevent the Fermi level from shifting further. Using this picture, ionic compensation will occur if the Gibbs energy of the formation of the ionic defect becomes zero before the Fermi level reaches either the conduction band minimum upon donor doping or the valence band maximum upon acceptor doping. Electronic compensation corresponds to the formation of electrons or holes, which appears if the Fermi level approaches the conduction or valence band, respectively. The limits of the Fermi level for the different conditions are indicated in the bottom row of Fig. 3 by red arrows for acceptor doping and by blue arrows for donor doping. The limits are depending on the chemical boundary conditions, i.e. the oxygen partial pressure in the present scenario. Based on this description, the occurrence of ionic compensation can be clearly identified. For ΔGred = 3.4 eV, for example, oxidizing conditions lead to ionic compensation for both donor and acceptor doping, while reducing conditions lead to ionic compensation for acceptor doping and to electronic compensation for donor doping. The respective compensation mechanisms are indicated in the graphs in the upper row of Fig. 3.
The relationship between the Gibbs energy of reduction, i.e. the Gibbs formation energy of the oxygen vacancy, and the charge compensation for the case of donor doping is illustrated in Fig. 4. For the calculation, the concentration of singly positively charged donors is included in the charge neutrality eqn (11) when determining the equilibrium concentrations. For simplicity, a shallow donor with a valence independent of the Fermi level is used. For donor doping, charge compensation can be either by electrons or, for the case of Schottky disorder, the metal vacancy. To illustrate the effect, Gibbs energies for Schottky disorder of ΔGS = −3.2 eV and for reduction of ΔGred = −5.4 eV and a band gap of Eg = 3.0 eV are used for the calculation of defect concentrations as a function of donor concentration. The Brouwer diagram for the undoped material is again symmetric, while adding 1018 cm−3 donors leads to an increase of the concentration of metal vacancies  for oxygen chemical potentials μO > −3 eV. The dependence of defect concentrations on doping concentrations for μO > −3 eV (case (1) in Fig. 4) are displayed in the lower left graph of Fig. 4. For all doping concentrations, the metal vacancy remains the dominant compensating defect.
for oxygen chemical potentials μO > −3 eV. The dependence of defect concentrations on doping concentrations for μO > −3 eV (case (1) in Fig. 4) are displayed in the lower left graph of Fig. 4. For all doping concentrations, the metal vacancy remains the dominant compensating defect.
The situation is changing with decreasing oxygen activity. For μO = −3.7 eV, case (2) in Fig. 4, electrons are the dominant compensating defect for donor concentrations up to ND ≈ 3 × 1018 cm−3. For higher ND, metal vacancies dominate. In this situation, which corresponds to a mixed compensation, the formation energy of the metal vacancy vanishes exactly at the conduction band minimum (see the upper right graph in Fig. 4). For even more reducing conditions, case (3) in Fig. 4, electronic compensation is dominating for the whole range of donor concentration. Fig. 4 illustrates the change in compensation mechanism for donor doping and its relationship to the formation energy of the metal vacancies and the conduction band minimum. In none of the cases illustrated in Fig. 4 is saturation of the electron carrier concentration with increasing doping concentration observed. This kind of saturation is expected as the Fermi level cannot increase beyond the energy, at which the formation energy of the cation vacancy vanishes. The saturation will occur but at much higher doping concentrations. These are not included in Fig. 4 as the approximation of dilute defect concentrations is not valid in this case. The case of acceptor doping and its relationship to the formation energy of the oxygen vacancy and the valence band maximum can be demonstrated analogously for oxygen chemical potentials of μO = −1.5…0 eV.
The examples illustrate that the preference for electronic or ionic compensation is determined by the defect formation energy of the ionic defects. Comparing the magnitudes of the formation energy of the ionic defects, e.g. Schottky disorder, and the electronic defects is not sufficient. In order to reveal the compensation mechanism, it is necessary to plot the formation energy of the ionic defects on the same energy axis as the formation energies of the electronic defects as in Fig. 2(b). Keeping the formation energy of the electronic defects fixed by fixing the energies of the band edges, it is the energy of the reduction (or oxidation) reaction, which shifts the formation energy of the ionic defects relative to the electronic ones as illustrated by the top graphs in Fig. 3. As the plots with the formation energy directly reveal the preferred compensation mechanism, the representation of the defect properties in the physical picture is more intuitive in this case.
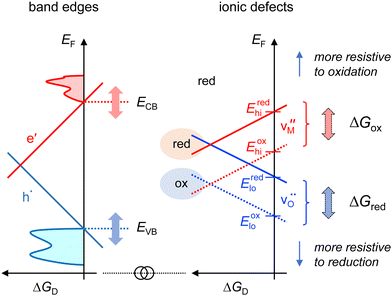
6 Influence of the band edges
The previous section has illustrated how the Gibbs energy of the reduction or oxidation reaction aligns the dependence of the formation energy of ionic defects with those of the electronic defects. This alignment is displayed explicitly in Fig. 5, which is an extended representation of Fig. 2(b). The formation energies of the ionic defects and those of the electronic defects can both be displayed depending on the Fermi level, EF. As the Fermi level is the same for all defects, the two energy axis are identical as indicated at the bottom of the graph. The alignment of the energy axes holds not only for electronic and ionic defects, but for any charged defect in the material.20 Other defects of relevance are, for example, the different charge states of the ionic defects, which introduce charge transition levels independent of the chemical activity. Other defects are related to valence changes of the host species, which correspond to trapping of electrons or holes on cationic or anionic sites, for example ,
,  , and
, and 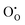 . Defect reactions such as
. Defect reactions such as  have been used, for example, to describe the energy gaps in Fe2O3 or La(Sr)FeO3−x.29,30 Moreover, the dependence of the formation energies of charged dopants on the Fermi level is related to the solubility of the dopants.20,31 Another relation to the dependence of defect charge states on the Fermi level is the phenomenon of exsolution.32 Therefore, using the Fermi level as a common energy axis constitutes a unique opportunity for a comprehensive description of defect formation, forming the basis for the recently proposed concept of Fermi level engineering.20
have been used, for example, to describe the energy gaps in Fe2O3 or La(Sr)FeO3−x.29,30 Moreover, the dependence of the formation energies of charged dopants on the Fermi level is related to the solubility of the dopants.20,31 Another relation to the dependence of defect charge states on the Fermi level is the phenomenon of exsolution.32 Therefore, using the Fermi level as a common energy axis constitutes a unique opportunity for a comprehensive description of defect formation, forming the basis for the recently proposed concept of Fermi level engineering.20
As discussed in the previous section, the preference for electronic or ionic compensation is determined by the energies, at which the formation energies of the respective defects vanish. The preference can hence be changed either by moving the formation energies of the ionic defects or by moving the formation energies of the electronic defects on the common energy axis. In principle, the two effects can be considered independently. The discussion will start with the variation of the ionic defects.
According to eqn (18) and (19), the Gibbs energies of reduction and oxidation, ΔGred and ΔGox, affect the formation energy of the oxygen and metal vacancies as illustrated at the right in Fig. 5. The effect of ΔGred and ΔGox on the formation energies has to be added to the difference between oxidizing (high p(O2)) and reducing environments (low p(O2)). For a fixed formation energy of Schottky disorder, as exemplified in Fig. 2, 3 and 5, the formation energy of the metal and oxygen vacancies are inversely affected by changes of ΔGred and ΔGox if the metal has a valency of +II. For materials with different stoichiometry, such as M2O, M2O3, etc., the change of the formation energy of the cation vacancy has a different magnitude than that of the oxygen vacancy.
If a material is more resistive to reduction, the Gibbs energy of reduction increases and that of the formation of oxygen vacancies (blue lines in Fig. 5) increases accordingly. Consequently, the lower limit of the Fermi level, labelled Eredlo and Eoxlo in Fig. 5 moves downwards on the energy axis. If a material is more resistive to oxidation, the upper limits of the Fermi level, labelled Eredhi and Eoxhi in Fig. 5, move upwards on the energy axis. With the labels for the upper and lower limits of the Fermi level in Fig. 5, the condition for electronic and ionic compensation of acceptor and donor doping, which are the essence of the practical doping principles of semiconductors,33 can be expressed as:
 | (21) |
The distinction between electronic and ionic compensation according to eqn (21) also includes the variation between oxidizing and reducing conditions. For example, donor-doped SrTiO3 exhibits electronic compensation under reducing but ionic compensation under oxidizing conditions.24 In the context of Fig. 5, this can be expressed by Eredhi > ECB > Eoxhi.
In addition to changing the preference for electronic or ionic compensation by changing the Gibbs energies of reduction and oxidation, the preference is also changed when the formation energies of the ionic defects is kept constant on the common energy axis but the formation energies of the electronic defects are shifted in energy as illustrated on the left side of Fig. 5. The latter are determined by the position of the band edges. By definition, the formation energy of electrons will be zero at ECB and that of holes will be zero at EVB. Therefore, moving the position of the band edges up or down as indicated on the left side of Fig. 5 can be used to change the preference for ionic or electronic compensation. This dependence of the charge compensation mechanism on the band edge energies is well known in semiconductor physics and explains the different dopability of materials, i.e., the achievable electronic carrier concentration upon donor or acceptor doping.25–27,33–39
It is also well-known that the energies of the valence band maximum and conduction band minimum can vary quite substantially between materials. The valence band maximum energy, for example, is affected by the choice of the anion due to the energy of the p-orbitals,37,40 but also by cationic contributions to the valence band density of states. Such cationic contributions are present for transition metal compounds with shallow d orbitals, e.g. Cu, or partially, e.g. Fe, but also for compounds containing heavier ions with filled s-orbitals, such as Pb2+, Sn2+ or Bi3+.36,37,41–43 These contributions result in an upward shift in the valence band maximum, which is favorable for electronic compensation by holes. In fact, room temperature p-type electronic conduction by holes is exclusively found in materials with a high valence band maximum energy originating from such cation orbital contributions to the valence band.27,44–48 Further discussion of the factors determining the energy band alignment of materials can be found, for example, in ref. 36, 37, and 43.
7 Summary and perspective
Point defects are fundamental ingredients of materials, particularly in ionic solids, which affect a wide range of properties. Understanding and controlling the concentration of point defects is of key importance. There are two approaches to describe defect concentrations: defect chemistry and the calculation of defect formation energies by ab initio methods. While the equivalency of both approaches is evident and has been explicitly reported previously,19,20 a direct quantitative relationship between the equilibrium constants of the defect reactions used in defect chemistry and the formation energies of ionic defects has been presented here for the first time. For example, the Gibbs energy of reduction has been related to the Gibbs energy of the formation of oxygen vacancies (eqn (18)), revealing that the two are not equivalent. The provided quantitative relationship between defect chemistry and the physical approach is essential for a direct comparison of both approaches and enables a combined application with potential synergetic effects. For example, the quantitative relationship allows us to compare experimental values derived from defect chemical experiments with the calculated formation energies, which cannot be determined directly from experiments. This may help, for example, to identify potential quantitative uncertainties in defect calculations.The competition between ionic and electronic compensation decides if a material becomes an ionic conductor (or an insulator if the ionic defects are not mobile), an electronic (semi)conductor, or a mixed ionic-electronic conductor. The prevailing compensation mechanism can directly be extracted from the dependence of the defect formation energies on the Fermi level in the physical approach. In contrast, the equilibrium constants of the defect reactions do not provide a direct connection to the compensation mechanism. A simple comparison of the Gibbs energies of ionic and electronic disorder is not sufficient. This is not only the case because the charge states of ionic and electronic defects are different. More importantly, it is necessary to connect the Fermi level dependence of the formation energies of electronic and ionic defects on a common energy axis in order to extract the prevailing compensation mechanism for donor and acceptor doping. It has been demonstrated that the connection of the energy axes of ionic and electronic defects is directly provided by the Gibbs energy of reduction and oxidation. While the latter two are connected in a specific material by its ionic disorder and the band gap (eqn (20)), they can, in principle, be tuned independently by material composition. In addition to tuning the Gibbs energies of reduction and oxidation, the prevalent charge compensation mechanism is affected by the valence band maximum and conduction band minimum energies. A high valence band maximum favors electronic compensation for acceptor doping and a low conduction band minimum favors electronic compensation for donor doping. The energies of the band edges also depend on material composition.
As the band edge energies and the Gibbs energies of reduction and oxidation both depend on the material composition, it would, perspectively, be interesting to figure out if the two dependencies are connected or independent. To our knowledge, no direct connection between the band edge energies and the Gibbs energies of reduction/oxidation has been established. It is unclear whether this kind of relationship is physically reasonable at all but it is interesting to note that Cu-containing materials, which exhibit a significantly higher valence band maximum than comparable compounds without shallow occupied d-states,37,43 typically show a high concentration of Cu vacancies,49,50 indicating that they are easy to oxidize. This indicates that it may not be possible to tune the electronic and ionic disorder independently, which would considerably reduce the degree of freedom in the design of materials with the desired electrical properties. It would therefore be important to evaluate whether such a fundamental connection exists or not.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The presented work has been performed in the framework of the collaborative research centre FLAIR (Fermi level engineering applied to oxide electroceramics), which is funded by the German Research Foundation (DFG), project-ID 463184206 – SFB 1548. Helpful comments by R. A. De Souza and K. Albe are gratefully acknowledged.Notes and references
- R. A. De Souza and G. Harrington, Nat. Mater., 2023, 22, 794–797 CrossRef CAS PubMed.
- F. A. Kröger, The chemistry of imperfect crystals, North-Holland, Amsterdam, 1964 Search PubMed.
- J. Maier, Physical Chemistry of Ionic Materials, Wiley-VCH, Weinheim, 2004 Search PubMed.
- D. M. Smyth, The defect chemistry of metal oxides, Oxford University Press, Oxford, 2000 Search PubMed.
- F. D. Morrison, A. M. Coats, D. C. Sinclair and A. R. West, J. Electroceram., 2001, 6, 219–232 CrossRef CAS.
- D. M. Smyth, J. Electroceram., 2002, 9, 179–186 CrossRef CAS.
- H.-I. Yoo, C.-R. Song and D.-K. Lee, J. Electroceram., 2002, 8, 5–36 CrossRef CAS.
- D. M. Smyth, J. Electroceram., 2003, 11, 89–100 CrossRef CAS.
- S. Lee, C. A. Randall and Z.-K. Liu, J. Am. Ceram. Soc., 2008, 91, 1748–1752 CrossRef CAS.
- S. Lee, C. A. Randall and Z.-K. Liu, J. Am. Ceram. Soc., 2008, 91, 1753–1761 CrossRef CAS.
- J. N. Baker, P. C. Bowes, J. S. Harris and D. L. Irving, J. Appl. Phys., 2018, 124, 114101 CrossRef.
- P. C. Bowes, J. N. Baker and D. L. Irving, Phys. Rev. Mater., 2020, 4, 084601 CrossRef CAS.
- P. C. Bowes, G. H. Ryu, J. N. Baker, E. C. Dickey and D. L. Irving, J. Am. Ceram. Soc., 2021, 104, 5859–5872 CrossRef CAS.
- G. H. Ryu, P. C. Bowes, J. R. McGarrahan, D. L. Irving and E. C. Dickey, J. Am. Ceram. Soc., 2022, 105, 292–298 CrossRef CAS.
- T. Kanagawa, D. Hirai and S. Hirose, J. Appl. Phys., 2024, 136, 034103 CrossRef CAS.
- G. X. Qian, R. M. Martin and D. J. Chadi, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 7649–7663 CrossRef CAS PubMed.
- S. B. Zhang and J. E. Northrup, Phys. Rev. Lett., 1991, 67, 2339–2342 CrossRef CAS PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- S. Anand, M. Y. Toriyama, C. Wolverton, S. M. Haile and G. J. Snyder, Acc. Mater. Res., 2022, 3, 685–696 CrossRef CAS.
- A. Klein, K. Albe, N. Bein, O. Clemens, K. A. Creutz, P. Erhart, M. Frericks, E. Ghorbani, J. P. Hofmann, B. Huang, B. Kaiser, U. Kolb, J. Koruza, C. Kübel, K. N. S. Lohaus, J. Rödel, J. Rohrer, W. Rheinheimer, R. A. De Souza, V. Streibel, A. Weidenkaff, M. Widenmeyer, B.-X. Xu and H. Zhang, J. Electroceram., 2023, 51, 147–177 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- https://janaf.nist.gov/, NIST-JANAF Thermochemical Tables.
- P. Erhart and K. Albe, J. Appl. Phys., 2007, 102, 084111 CrossRef.
- R. Meyer, A. F. Zurhelle, R. A. D. Souza, R. Waser and F. Gunkel, Phys. Rev. B, 2016, 94, 115408 CrossRef.
- W. Walukiewicz, Phys. B, 2001, 302–303, 123–134 CrossRef.
- S. B. Zhang, S.-H. Wei and A. Zunger, J. Appl. Phys., 1998, 83, 3192–3196 CrossRef CAS.
- S. B. Zhang, S.-H. Wei and A. Zunger, Phys. Rev. Lett., 2000, 84, 1232 CrossRef CAS PubMed.
- A. Klein, J. Am. Ceram. Soc., 2016, 99, 369–387 CrossRef CAS.
- J. B. Goodenough, Prog. Solid State Chem., 1971, 5, 145–399 CrossRef CAS.
- J. Mizusaki, T. Sasamoto, W. R. Cannon and H. K. Bowen, J. Am. Ceram. Soc., 1983, 66, 247–252 CrossRef CAS.
- M. V. Frischbier, H. F. Wardenga, M. Weidner, O. Bierwagen, J. Jia, Y. Shigesato and A. Klein, Thin Solid Films, 2016, 614, 62–68 CrossRef CAS.
- A. Bonkowski, M. J. Wolf, J. Wu, S. C. Parker, A. Klein and R. A. De Souza, J. Am. Chem. Soc., 2024, 146, 23012–23021 CrossRef CAS PubMed.
- A. Zunger, Appl. Phys. Lett., 2003, 83, 57–59 CrossRef CAS.
- S. Lany, J. Osorio-Guillén and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 241203 CrossRef.
- J. Robertson and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075205 CrossRef.
- A. Klein, Applications of X-ray photoelectron spectroscopy to catalytic studies, World Scientific, 2023, pp. 193–230 Search PubMed.
- A. Klein, J. Phys.: Condens. Matter, 2015, 27, 134201 CrossRef PubMed.
- Photoelectrochemical Hydrogen Production, ed. R. van de Krol and M. Grätzel, Springer, Boston, MA, 2012 Search PubMed.
- C. G. Van de Walle and J. Neugebauer, Nature, 2003, 423, 626–628 CrossRef CAS PubMed.
- W. A. Harrison, Electronic structure and the properties of solids, Dover Publications, New York, 1989 Search PubMed.
- R. Schafranek, S. Li, C. Chen, W. Wu and A. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045317 CrossRef.
- S. Li, J. Morasch, A. Klein, C. Chirila, L. Pintilie, L. Jia, K. Ellmer, M. Naderer, K. Reichmann, M. Gröting and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045428 Search PubMed.
- S. Li, F. Chen, R. Schafranek, T. J. M. Bayer, K. Rachut, A. Fuchs, S. Siol, M. Weidner, M. Hohmann, V. Pfeifer, J. Morasch, C. Ghinea, E. Arveux, R. Günzler, J. Gassmann, C. Körber, Y. Gassenbauer, F. Säuberlich, G. V. Rao, S. Payan, M. Maglione, C. Chirila, L. Pintilie, L. Jia, K. Ellmer, M. Naderer, K. Reichmann, U. Böttger, S. Schmelzer, R. C. Frunza, H. Uršič, B. Malič, W.-B. Wu, P. Erhart and A. Klein, Phys. Status Solidi RRL, 2014, 8, 571–576 CrossRef CAS.
- H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, Nature, 1997, 389, 939–942 CrossRef CAS.
- H. Yanagi, T. Hase, S. Ibuki, K. Ueda and H. Hosono, Appl. Phys. Lett., 2001, 78, 1583–1585 CrossRef CAS.
- Y. Ogo, H. Hiramatsu, K. Nomura, H. Yanagi, T. Kamiya, M. Hirano and H. Hosono, Appl. Phys. Lett., 2008, 93, 032113 CrossRef.
- B. K. Meyer, A. Polity, D. Reppin, M. Becker, P. Hering, P. J. Klar, T. Sander, C. Reindl, J. Benz, M. Eickhoff, C. Heiliger, M. Heinemann, J. Bläsing, A. Krost, S. Shokovets, C. Müller and C. Ronning, Phys. Status Solidi B, 2012, 249, 1487–1509 CrossRef CAS.
- G. Hautier, A. Miglio, G. Ceder, G.-M. Rignanese and X. Gonze, Nat. Commun., 2013, 4, 2292 CrossRef PubMed.
- H. Raebiger, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 045209 Search PubMed.
- Y.-J. Zhao, C. Persson, S. Lany and A. Zunger, Appl. Phys. Lett., 2004, 85, 5860–5862 CrossRef CAS.
| This journal is © the Owner Societies 2025 |