Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gas-phase, conformer-specific infrared spectra of 3-chlorophenol and 3-fluorophenol†
Olga A.
Duda
 a,
Gerrit C.
Groenenboom
a,
Gerrit C.
Groenenboom
 b,
Daniel A.
Horke
b,
Daniel A.
Horke
 b and
Joost M.
Bakker
b and
Joost M.
Bakker
 *a
*a
aInstitute for Molecules and Materials, HFML-FELIX Laboratory, Radboud University, Toernooiveld 7, 6525 ED Nijmegen, The Netherlands. E-mail: joost.bakker@ru.nl
bInstitute for Molecules and Materials, Radboud University, Heijendaalseweg 135, 6525 AJ Nijmegen, The Netherlands
First published on 20th February 2025
Abstract
Conformational isomerism of phenol derivatives has been a subject of extensive spectroscopic study. Combining the capabilities of the widely tuneable infrared free-electron laser FELIX with molecular beam technologies allows for revisiting existing data and gaining additional insights into far-IR spectroscopy of halogenated phenols. Here we present conformer-resolved infrared spectra of the syn and anti conformers of 3-chlorophenol and 3-fluorophenol recorded via IR-UV ion-dip spectroscopy. The experimental work is complemented by density functional theory calculations to aid in assignment of the observed bands. The experimental spectra for the two conformers of each molecule show overall a great similarity, but also include some distinct conformer-specific bands in the spectral range investigated. Our spectra confirm previously reported OH torsional mode frequencies for the syn and anti conformers of 3-chlorophenol (3CP) at 315 cm−1, (Manocha et al., J. Phys. Chem., 1973, 77, 2094) but reverse their assignment of the 311 and 319 cm−1 bands for 3-fluorophenol. 1D torsional mode calculations were performed for 3CP to help assign possible OH torsion overtones.
1 Introduction
Conformational isomerism plays a key role in numerous aspects of chemistry. In a variety of reactions the conformation of reagents determines their reactivity and intermediates, as well as influences the identity of the products formed.1–3 In biological systems, conformation plays a crucial role in enzyme activity ranging from biosynthesis to protein activity regulation.4,5 Furthermore, conformational preferences and switching are subjects of interest in macrocyclic and organometallic chemistry due to their potential synthetic and medicinal applications.6–8To understand this class of reactions on a fundamental level, ortho- and meta-monosubstituted phenol derivatives are widely studied. Substitution of the hydrogen atom at the meta (3) or ortho (2) position of phenol leads to syn–anti conformational isomerism where the hydroxyl group either points towards (syn) or away (anti) from the heteroatom substituent (Fig. 1). Gas-phase spectroscopic studies allow for a detailed insight into the structural and energetic differences without the additional level of complexity arising from the solvent contribution.9,10 Moreover, short-pulse laser systems in conjunction with conformer-specific detection schemes could allow for highly controlled experiments studying the dynamics of interconversion reactions.11
 | ||
| Fig. 1 Structures of anti and syn 3-chlorophenol (3CP) optimised at the B3LYP/def2-TZVP level of theory. The exact xyz coordinates for the optimised structures of both 3CP and 3-fluorophenol (3FP) can be found in the ESI.† | ||
The simplest of such systems, halogenated phenols, have attracted considerable spectroscopic attention, with a number of studies focusing on 3-fluorophenol (3FP),12–18 and 3-chlorophenol (3CP).12,13,19–22 Among these, Manocha et al. observed a separation of the OH torsional band in the vapour phase IR absorption spectrum of 3FP, but only a single band for 3CP.12 This suggests that the frequency of the torsional mode of 3FP is conformer-specific. For 3CP the frequencies could be near-degenerate, or the population of one of the conformers strongly dominated under the experimental conditions. In the cold environment of a molecular beam, where significantly higher resolutions are achieved, such relative populations can be inferred from the intensities of the origin bands in (1 + 1) UV resonance-enhanced multiphoton ionization (REMPI) spectra. Roughly equal populations of the two 3FP conformers were reported,13,14 strengthening the suggestion of a conformer-specific frequency of the torsional mode. Similarly, roughly equal intensities of the syn and anti origin bands were reported for 3CP,19,23 pointing to near-degeneracy of the torsional frequencies.
The OH torsional modes are of particular interest as, in theory, the two conformers of 3-substituted halophenols could be interconverted by a 180° rotation of the hydroxyl group. However, since the frequencies of these modes are found around 300 cm−1, they prove challenging to study using traditional tabletop IR lasers.24 The far-IR range of the electromagnetic spectrum can readily be accessed with an infrared free-electron laser, such as FELIX.25
The low conformational isomerization barrier makes 3FP and 3CP ideal candidate systems for dynamics experiments aimed at directly observing isomerization. Here, interconversion would be triggered by laser excitation of one conformer, and the interconversion processes followed by selectively probing the nascent population of the other conformation. In this light, recent experiments by Lopes Jesus et al. are of interest.17 They reported the infrared signatures of conformational changes induced in 3FP isolated in argon and nitrogen matrices by non-conformer-specific, broadband IR irradiation. For more controlled experiments aimed at studying interconversion, it is imperative to have detailed information on the conformer-specific vibrational modes. Gas-phase IR-UV ion-dip spectroscopy, first introduced by Page et al.,26 allows to record conformer-specific infrared spectra by virtue of subtle differences in the conformers' REMPI spectra.27–29 In this way, differences in conformer-sensitive vibrational modes can be detected unambiguously. This technique could also confirm the previous assignments of the REMPI spectra to the different conformers.
Here, we present IR-UV ion-dip spectra for the syn- and anti-conformers of 3CP and 3FP. They are recorded employing the FELIX free-electron laser in the 230–1750 cm−1 (3CP) and 270–1750 cm−1 (3FP) spectral ranges. The spectra observed are complemented by Density Functional Theory (DFT) calculations to assign the vibrational bands. A particular focus is placed on finding the OH torsional mode as it is the coordinate along which conformational interconversion is likely to take place.
2 Methods
3CP and 3FP (99% purity, Sigma Aldrich) were heated to 60–75 °C and seeded into Ar carrier gas at a stagnation pressure of 1–3 bar. The gas mixture was expanded into vacuum (1 × 10−7 mbar background pressure, 5 × 10−6 mbar when operational) through a pulsed General Valve, with the nozzle held at 10 °C above the sample temperature to prevent condensation. The molecular beam formed was collimated using a 2 mm diameter skimmer (Beam Dynamics, Inc.) upon entering a differentially pumped vacuum chamber. Here, it was illuminated by counter-propagating IR light produced by the free-electron laser FELIX.25 The package of molecules illuminated was then allowed to propagate several tens of μs until it reached the extraction region of a reflectron time-of-flight mass spectrometer (TOF-MS) (Jordan TOF Products, Inc.), where it was intersected by the frequency-doubled output of an Nd:YAG-pumped dye laser (Lioptec LiopStar, Coumarin 153 dye, ∼1 mJ per pulse). All ions formed were mass-separated by the reflectron TOF-MS and detected using a microchannel plate. The UV laser was tuned to the 0–0 transitions (S1 ← S0) of the syn- and anti-conformers of 3CP (35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783, 35
783, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 902 cm−1) and 3FP (36
902 cm−1) and 3FP (36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 632, 36
632, 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839 cm−1)13,14 producing a constant ion signal. When the IR laser was in resonance with an IR-active vibrational mode of the species of interest, depopulation of the vibrational ground state in the electronic ground state occurred. This, in turn, led to depletion in the ion signal. The experiment was run at twice the FELIX repetition rate of 5 Hz, enabling the recording of reference mass spectra to compensate for long-term source fluctuations. The spectra presented were constructed using the depletion yield, defined as the logarithmic ratio of the ion intensity without and with IR irradiation, and normalized by the macropulse energy. The spectra presented for 3CP are isotope-selected for the more abundant 35Cl-substituted isotopomer by virtue of employing mass spectrometry for detection.
839 cm−1)13,14 producing a constant ion signal. When the IR laser was in resonance with an IR-active vibrational mode of the species of interest, depopulation of the vibrational ground state in the electronic ground state occurred. This, in turn, led to depletion in the ion signal. The experiment was run at twice the FELIX repetition rate of 5 Hz, enabling the recording of reference mass spectra to compensate for long-term source fluctuations. The spectra presented were constructed using the depletion yield, defined as the logarithmic ratio of the ion intensity without and with IR irradiation, and normalized by the macropulse energy. The spectra presented for 3CP are isotope-selected for the more abundant 35Cl-substituted isotopomer by virtue of employing mass spectrometry for detection.
The FELIX light is formed in a 10 μs pulse train (macropulse) consisting of 1-ns spaced picosecond pulses (micropulses). Macropulse energies used ranged from ∼70 mJ per pulse in the 1800 cm−1 region to ∼20 mJ around 300 cm−1. The laser is near-transform-limited and tuned to a spectral bandwidth of 0.4% full-width at half-maximum (FWHM) of the central frequency. The IR wavelength was calibrated using a grating spectrometer.
DFT calculations were performed using the Gaussian 16 suite30 with the B3LYP functional31 and the def2-TZVP basis set.32 For the optimized structures, harmonic frequencies were calculated to ensure true minima, as well as to compare to the experimental spectra. For the latter purpose, the calculated harmonic frequencies are scaled by an empirical factor of 0.985 to compensate for anharmonicities.33 The scaled stick spectra were subsequently convolved with a Gaussian lineshape function with a 0.4% FWHM, mimicking the FELIX spectral bandwidth. All harmonic frequency values used in this work are scaled values. Because low-frequency vibrations of phenol derivatives exhibit a significant degree of anharmonicity,10,24 additional anharmonic frequency calculations were carried out utilizing the Rayleigh–Schrödinger perturbation theory.34 To identify possible overtones of the torsional modes of 3CP, the torsional coordinate was scanned using Gaussian IRC keyword. The first order nature of the transition state was ensured by calculating harmonic frequencies and finding a single imaginary frequency. The resulting potential was used to calculate the torsional vibrational wavefunctions and frequencies.
3 Results and discussion
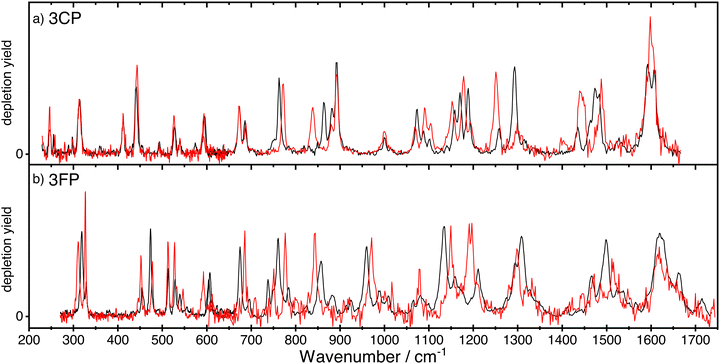
The spectra of anti- and syn-3CP and 3FP are shown together, respectively, in panel (a) and (b) of Fig. 2, allowing for a direct comparison. The depletions observed and the signal-to-noise of the spectrum for syn-3FP in the higher frequency range are significantly lower than those for anti-3FP. To aid the comparison, the syn-3FP spectrum is vertically scaled in the 700–1700 cm−1 range. We speculate that this part of the spectrum is recorded with a smaller spatial overlap, because the calculated spectra (discussed in Sections 3.1 and 3.2) suggest no large differences between intensities. The unscaled syn-3FP spectrum is shown in Fig. 2 of the ESI.† The 3CP spectra are presented without scaling.All spectra for 3CP and 3FP exhibit numerous distinct bands, with the spectral bandwidth progressively growing with increasing wavenumber, reflecting the FELIX spectral bandwidth. Although IR ion-dip spectroscopy is widely assumed to be a single-photon technique, we cannot rule out multiple photon absorption, especially for some of the stronger bands that may suffer from saturation and additional (power) broadening. Differences in both position and intensity are observed between the two conformers in the case of 3FP across the entire spectral range. In contrast, below 700 cm−1 the spectra of the 3CP conformers are near identical with marked differences becoming significant in the higher frequency range.
3.1 Spectroscopy of 3-chlorophenol
Fig. 3 shows the conformer-specific infrared spectra recorded for anti- (panel a) and syn-3CP (panel c). Each experimental spectrum is compared to a DFT-calculated spectrum in the harmonic approximation in panels (b) and (d). Overall, the harmonic calculated spectra are in good agreement with the experimental spectrum of syn- and anti-3CP, even to the extent that most differences between the experimental spectra for each conformer are faithfully reproduced. Below, we globally discuss the assignments of the bands in the experimental spectra, with a special focus on where the two experimental spectra differ. A detailed assignment of all bands is found in Table 1. The in-text discussion uses an anti/syn convention when stating the mode frequencies. | ||
| Fig. 3 The experimental (a) and (c) and simulated (b) and (d) spectra of anti- and syn-3CP, respectively. In panels (b) and (d), the blue line represents the scaled harmonic spectrum. | ||
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp) and calculated (
exp) and calculated (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DFT) band frequencies in cm−1 in the IR-UV ion dip spectrum of 3-chlorophenol and their assignments. For vibrations which are analogous to phenol normal modes, Varsanyi notation is used.35 Abbreviations: oop = out-of-plane, ip = in-plane, def = deformation, disp = displacement, str = stretch, τ = torsion
DFT) band frequencies in cm−1 in the IR-UV ion dip spectrum of 3-chlorophenol and their assignments. For vibrations which are analogous to phenol normal modes, Varsanyi notation is used.35 Abbreviations: oop = out-of-plane, ip = in-plane, def = deformation, disp = displacement, str = stretch, τ = torsion
| anti-3CP | syn-3CP | Mode description | ||
|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp
exp
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DFT
DFT
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp
exp
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DFT
DFT
|
|
| 229 | 228 | 228 | 228 | ν 10b |
| 247 | 245 | 246 | 244 | C–O, C–Cl bend |
| 315 | 339 | 315 | 338 | τ OH |
| 412 | 404 | 412 | 404 | C–Cl str |
| 442 | 439 | 444 | 442 | ip O–C–C bend |
| 455 | 449 | — | 446 | ν 16a |
| 493 | 490 | 496 | 488 | Overtone of 247/246 |
| 528 | 530 | 529 | 531 | ν 6a |
| 540 | 568 | 541 | 567 | oop bend |
| 574 | 584 | — | 582 | oop ring bend, C–C twist |
| 595 | — | 598 | — | τ OH 2 |
| 672 | 680 | 672 | 683 | ν 4 |
| 686 | 687 | 688 | 690 | ν 6b |
| 763 | 766 | 773 | 777 | oop C–H bend |
| 863 | — | 839 | — | τ OH 3 |
| 881 | 878 | 879 | 884 | oop C–H bend |
| 893 | 887 | 893 | 885 | Ring def, C–Cl str |
| 1000 | 1000 | 1000 | 1000 | ν 12 |
| 1072 | 1075 | 1070 | 1073 | Ring def, C–Cl disp |
| 1088 | 1095 | 1090 | 1096 | C–H bend |
| 1102 | — | 1104 | — | Combination 686 + 412 |
| 1158 | 1167 | 1152 | 1165 | C–H bend (all) |
| 1170 | 1176 | 1178 | 1175 | C–H bend (C4, C5, C6) |
| 1189 | — | 1192 | — | ? |
| 1257 | 1260 | 1251 | 1258 | ν 13 |
| 1293 | 1308 | 1299 | 1322 | ip C–H bend, O–H bend |
| 1315 | 1325 | 1310 | — | ip C–H bend |
| 1474 | 1471 | 1442 | 1454 | ip C–H bend, ring def |
| 1484 | 1489 | 1488 | 1500 | ip C–H bend |
| 1592 | 1603 | — | 1603 | C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C ring str C ring str |
| 1606 | 1615 | 1598 | 1617 | C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C ring str C ring str |
| 6.9 | 8.6 | Mean absolute deviation | ||
Up to 800 cm−1, the spectrum of both conformers is populated by bands corresponding to both in-plane and out-of-plane bending vibrations. Above 800 cm−1, the spectrum is dominated by in-plane modes primarily involving C–H bending, while the highest energy bands correspond to C–C and C–O stretching modes.
In the low-frequency range, we immediately find the largest mismatch between theory and experiment in a very intense predicted band for the OH torsional (τOH) mode. Given the good match between other experimental and calculated modes, this predicted band must be assigned to the experimental band observed at 315 cm−1 for both conformers. This experimental value is in good agreement with literature values.12 The mismatch in both frequency and intensity also mirrors observations for τOH in other jet-cooled phenol derivatives.24
Although the only structural difference between the two conformers is the orientation of the hydroxyl group, several bands across the whole spectrum exhibit conformer-specific frequencies. The lowest frequency mode differing significantly between the two conformers is an out-of-plane C–H bending mode observed at 763/773 cm−1. An even more dramatic difference of 24 cm−1 is observed for the band at 863/839, cm−1, a vibration mainly involving out-of-plane bending of the C(2)–H group. Further to the blue, another major difference involves the band pairs at 1257/1251 and 1293/1299 cm−1. Experimentally, anti-3CP shows a doublet of bands (1257/1293 cm−1) with the high-frequency partner the most intense; for syn-3CP (1251/1299 cm−1) the intensity distribution is reversed. The computations accurately predict these intensity patterns. In both cases, the lower frequency mode has predominantly a C–O stretching character, which matches very well the frequency of the analogous ν13 mode of phenol.36,37 Finally, in the 1400–1500 cm−1 range, the anti conformer spectrum shows an intense band at 1474 cm−1 and a weaker one at 1435 cm−1. In contrast, the syn-spectrum shows two bands of similar intensities at 1488 and 1442 cm−1, respectively. The computations predict two closely spaced bands for anti-3CP, (at 1481 and 1464 cm−1) that combine into a single band at 1481 cm−1, whereas syn-3CP displays two bands at 1492 and 1447 cm−1, respectively.
While the symmetry reduction by halogenation prevents one from making an ‘elegant’ symmetry-based assignment for the majority of the vibrational modes, several vibrations show close similarity to the well-characterized phenol modes (for an overview of the relevant frequencies please see ESI†).36,37 The 229/228 cm−1 mode is an analogue of the phenol ν10b mode,35 an out-of-plane ring deformation. The 455/455 cm−1 vibration can be thought of as a phenol ν16a mode analogue, also an out-of-plane displacement. The phenol ν6a and ν6b modes, in-plane ring deformations, are found at 528/529 and 686/688 cm−1. The ν4 analogue, a concerted out-of-plane motion of the hydrogen atoms at positions 2, 4, and 6, is observed at 672 cm−1 for both conformers. The bands observed at 1000 cm−1 for both conformers can readily be assigned to ‘ring breathing’ modes, at a near-identical frequency as is observed for phenol.36,37
Two bands of particular interest for the halogen substitution are the ones observed at 412/412 and 891/893 cm−1. DFT predicts modes at 402/402 cm−1 and 882/881 cm−1 both involving a significant C–Cl stretch contribution, with the higher frequency mode having a significant ring-breathing character. The ring-breathing deformation is not unlike that resulting from coupling of the C–Cl motion with a skeletal vibration, which was shown to give rise to two C–Cl stretching bands in chlorinated benzene derivatives.35 This observation is supported by the considerable red-shift of the C–Cl stretch with respect to its usual frequency.38,39
Out of the vibrations showing a close resemblance to the phenol modes, the ν16a and ν6b analogues show significant blue shifts with respect to the phenol bands of 41 and 68/70 cm−1, respectively. In contrast, the ν10b and ν6a analogues exhibit an only negligible blue shift of 2–4 cm−1, which is well within the spectral bandwidth of FELIX.37 Inspection of the displacement vectors suggests that highly delocalised vibrations show limited influence of chlorine substitution, unless the C–Cl bond is involved explicitly or the motion of the other atoms is perturbed by the Cl presence. For the ν16a mode, a marked difference between the phenol mode and the 3CP analogue is the lack of Cl participation in the vibration, which otherwise involves a significant contribution from the C3 substituent (hydrogen) in phenol. In the ν6b analogue, a strong C–Cl stretching motion accompanies the ring deformation. Conversely, in phenol, ν10b has participation of C3, but in 3CP the Cl is not involved. A similar observation can be made for the ν6a mode where significant delocalisation of the vibration prevails over the local effect of chlorine substitution.
The highest frequency bands observed in the experimental spectra around 1600 cm−1 can be assigned to C–C ring stretching modes. Although only experimentally resolved for the anti conformer, for both species the calculations predict two such modes, differing only by the specific C–C bond involved.
Not all bands, however, can be assigned purely based on the results of the harmonic calculations. We note an intriguing progression of bands at 595/598, 863/839 and 1189/1192 cm−1 for anti- and syn-3CP, which have no DFT counterpart in the harmonic approximation. We speculate that these bands could be the overtones of the OH torsional mode, for which the fundamental was observed at 315 cm−1. It is well-known that such modes are strongly anharmonic.24 Anharmonic calculations (Fig. S3 of the ESI†) place τOH at 328/311 cm−1 and its first overtone at 629/606 cm−1. Based on these calculated frequencies of the fundamental and the first overtone, we can extract an anharmonicity parameter and estimate the frequencies of the higher order overtones, yielding the second and third overtone frequencies of 903/885 and 1150/1148 cm−1. Using the experimental values in place of the DFT-derived ones gives 840/849 for the second overtone, and 1050/1068 for the third one. However, since these estimated values do not match closely with the experimental results, we decided to perform additional calculations. To simultaneously describe the OH torsional modes for both conformers, a 1-dimensional torsional model was constructed using the moment of inertia calculated by Manocha et al.12 This torsional model places the OH torsion fundamental and its overtones at 312/315, 600/606, 862/856, and 1111/1191 cm−1. While not in perfect agreement with the observed frequencies, these results support our tentative assignment of the second overtone bands. It is important to note, however, that the wavefunctions for the higher vibrational states are highly delocalised (shown in Fig. S5, ESI†) and thus the syn and anti labels do not perfectly reflect the geometries of the molecules involved. Another possibility for the assignment of those modes would be combination bands. For the 1189/1192 band, the only contenders based on a frequency match are combination mode calculated at 1189/1193 cm−1 (Fig. S3, ESI†). While the intensity of the calculated 1193 cm−1 is appreciable, the intensity of the 1189 cm−1 band is near-negligible. As such, we choose to refrain from assigning that peak.
3.2 Spectroscopy of 3-fluorophenol
Fig. 4 shows the conformer-specific infrared spectra recorded for anti- (panel a) and syn-3FP (panel c). Each experimental spectrum is compared to a DFT-calculated spectrum (panels b and d).Overall, the harmonic calculated spectra are again in good agreement with the experiments, with the intensities and band positions being accurately reproduced. Similar to 3CP, an exception is formed by the OH torsional mode, for which the frequency is overestimated by the harmonic calculations. A detailed assignment of the observed vibrational bands is presented in Table 2, while a general discussion is presented below. The anti/syn convention used while discussing the band line positions for 3CP is used here as well.
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp) and calculated (
exp) and calculated (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DFT) band frequencies in cm−1 in the IR-UV ion dip spectra of 3FP and their assignments. For vibrations which are analogous to phenol normal modes, Varsanyi notation is used.35 Abbreviations: oop = out-of-plane, ip = in-plane, def = deformation, str = stretch, τ = torsion, exp = experimental
DFT) band frequencies in cm−1 in the IR-UV ion dip spectra of 3FP and their assignments. For vibrations which are analogous to phenol normal modes, Varsanyi notation is used.35 Abbreviations: oop = out-of-plane, ip = in-plane, def = deformation, str = stretch, τ = torsion, exp = experimental
| anti-3FP | syn-3FP | Mode description | ||
|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp
exp
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DFT
DFT
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exp
exp
|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) DFT
DFT
|
|
| 319 | 345 | 311 | 337 | τ OH |
| 329 | 325 | 327 | 325 | C–O, C–F bend |
| 454 | 456 | 452 | 457 | ν 16a |
| 473 | 471 | 478 | 477 | C–O, C–F bend |
| 514 | 513 | 513 | 514 | ν 6b |
| 529 | 529 | 528 | 531 | ν 6a |
| 539 | — | 547 | — | τ OH (exp) + 223/223(DFT) |
| 607 | — | 593 | — | τ OH 2 |
| 675 | 673 | 686 | 680 | ν 4 |
| 738 | 742 | 751 | 744 | Ring def, C–F str |
| 761 | 756 | 777 | 768 | oop C–H bend |
| 785 | — | — | — | τ OH + 473 |
| 857 | 861 | 844 | 836 | ν 17b |
| 925 | 924 | — | — | oop C–H bend |
| 959 | 959 | 971 | 959 | Ring def, C–O str |
| 989 | — | — | — | τ OH 3 |
| 1008 | 1006 | 1016 | 1006 | ν 12 |
| 1080 | 1082 | 1078 | 1076 | ip C–H bend (C4 and C6) |
| 1134 | 1131 | 1149 | 1142 | ip C–H bend, C–O, C–F str |
| 1160 | 1164 | — | 1166 | ip C–H, O–H bend |
| 1211 | 1198 | 1195 | 1177 | ip C–H, O–H bend, C–F str |
| 1295 | 1288 | 1298 | 1288 | ν 13 |
| 1308 | 1307 | 1328 | 1331 | ip C–H bend, C–O str |
| 1466 | 1492 | 1472 | 1472 | H–O–C bend |
| 1500 | 1500 | 1512 | 1513 | Ring def, O–H bend |
| 1620 | 1628 | 1619 | 1618 | C–C stretch |
| 1662 | — | — | — | Combination ν16a + 1211 |
| 1715 | — | — | — | ν 17b 2 |
| 5.3 | 6.7 | Mean absolute deviation | ||
Within the investigated spectral range, the lowest frequency bands are the doublet features observed at 319 and 329 cm−1 for anti-3FP and at 311 and 327 cm−1 for syn-3FP, respectively. The calculations yield an in-plane C–O, C–F bending mode at 325 cm−1 for both conformers, matching the higher-frequency components of the observed features. This suggests that the lower-frequency components correspond to the OH torsional mode, in line with the assignments by Manocha et al.,12 but crucially reversing them. Manocha et al. made no use of an conformer-specific detection scheme and observed the bands at 311 and 319 cm−1 simultaneously. Their stability-based argument to assign the 319 cm−1 band to the anti conformer is here disproven with the IR-UV ion-dip experiments. The assignment of the UV spectra, originally based on dispersed fluorescence,13,14 is confirmed by the good agreement of the vast majority of frequencies in our IR spectra with the results of the DFT calculations. Consequently, we assign the 319 cm−1 band to τOH of the anti conformer and the 311 cm−1 band to its syn counterpart. The assignment is further strengthened by the positions of the assigned overtones at 607/593 cm−1, and 989/921 cm−1.
A total of twelve vibrations show a frequency difference of 8 cm−1 or more between the two conformers, against only five such vibrations identified for 3CP. A significant number of these, particularly in the range above 1000 cm−1, contain contributions from C–F stretching, suggesting that fluorination considerably affects the vibrational levels. Out of the twelve, four modes are observed at a higher frequency for the anti conformer than for its syn counterpart. Apart from the aforementioned OH torsion fundamental, these include the 857/844 cm−1 bands corresponding to an out-of-plane C–H bending mode analogous to ν17b of phenol. While for the anti conformer the calculated displacement vectors show an out-of-plane motion of the hydrogen atoms at positions 2, 4, and 6, for the syn conformer the hydrogen atom at position 2 – between the OH and F substituents – is stationary. The orientation of the hydroxyl group therefore appears to have an influence on both frequency and normal coordinate of the vibration. The final mode of the group is the 1211/1195 cm−1 band corresponding to an in-plane C–H and O–H bending, with some C–F stretching character. Importantly, while we do observe a large disparity between the frequencies of other modes involving C–F stretching, it appears that this mode is not strongly affected.
Yet again, we can make a direct comparison between a number of the 3-fluorophenol modes and their phenol counterparts. The ν16a mode (454/452 cm−1) is blue-shifted by about 50 cm−1 upon halogenation, a shift identical with that observed for 3-chlorophenol. ν4, observed at 675/686 cm−1, shows a minor red shift for the both conformers of 3CP and for anti-3FP and no shift whatsoever for syn-3FP. This is to be expected as in phenol there is no involvement of C3 or H3 and, consequently, the frequency of ν4 ought not to be significantly affected by meta-substitution. The previously discussed ν17b analogue is significantly red-shifted with respect to the phenol mode (by 24/37 cm−1). Unlike for 3CP, where there is virtually no shift, the ν12 mode is slightly blue shifted with respect to phenol. Finally, the analogue of the ν13 mode is significantly blue shifted for 3FP by over 30 cm−1 for both conformers.
Not all features in the spectrum can be straightforwardly assigned. Due to the increase in spectral bandwidth with increasing frequency, similarly to 3-chlorophenol the C–C stretching modes cannot be resolved. Apart from these vibrations, in the spectrum of the anti conformer we observe several modes which are not accounted for by harmonic calculations. Based on the experimental frequencies, we tentatively assign the 1715 cm−1 mode as the first overtone of ν17b. An alternative assignment, brought forward by anharmonic calculations, is that to the overtone of a weak band predicted at 848 cm−1 (scaled harmonic frequency) which is not resolved in our experimental spectrum. The feature observed at 785 cm−1 in the anti conformer spectrum is most likely a combination mode. Based on the closest frequency match, we tentatively assign it as a combination of OH torsion and the 473 cm−1 bending mode. The 1662 cm−1 band was assigned following analogous reasoning.
3.3 Discussion
What becomes immediately apparent by directly comparing the spectra of the two molecules is that their infrared activities are very similar, with a large number of bands populating the spectral range of interest (see Fig. 2). As mentioned in Section 3.2, 3FP shows a larger number of conformer-specific frequencies than its chlorinated counterpart.Both 3CP and 3FP exhibit a number of modes which can be compared with the vibrations of phenol. In the case of 3CP, there appears to be a clear correlation between heavy atom substitution and a considerable shift in the frequency of vibrations directly affected by substitution. For 3FP, this relationship is less clear, however overall we see significant deviation between the 3FP and phenol modes. One indirect effect of meta-halogenation on the infrared spectrum is the shift in frequencies of the ν13 mode analogues, which is the (primarily) C–O stretching mode in phenol. While for 3CP we observe a minor red shift, the ν13 vibration of 3FP is blue-shifted with respect to phenol by over 30 cm−1 for both conformers. This discrepancy can be explained by the strong inductive electron-withdrawing effect of fluorine. Fluorine is a strong σ electron withdrawing substituent and thus, with a minor decrease in the C–O bond length caused by fluorination,15 the stretching frequency increases.
For any experiment aimed at studying interconversion dynamics, accurate knowledge of the potential energy surface describing the torsional modes is of high interest. The separation of the torsional vibrational modes of 3FP observed by Manocha et al.12 is confirmed in the current experiments, like the lack thereof for 3CP, but the assignment we make is the reverse. Manocha et al. suggested that the separation in the OH torsional modes of 3FP is due to a difference in the potential energy minima of the two conformers. In their computations, they found that syn-3FP is more stable, but more recent calculations at various levels of theory consistently find that the anti conformer is the more stable one.15,18 In line with these results, the current calculations place the anti-3FP conformer energy below its syn counterpart, with an energy difference of 55 cm−1, lower than the 70 cm−1 found by Moreira et al.18 Simultaneously, our calculated energy difference of 2 cm−1, (well below the expected accuracy of the current level of theory) between the two conformers of 3CP is consistent with the lack of separation between the two torsional modes.
Given the accurate predictions of the current computations for the experimental IR spectra, we calculated the potential energy surfaces of the torsional modes of 3FP and 3CP (Fig. 5). The results are presented referenced to the interconversion barrier, which is found to lie at ∼1400 cm−1. This value implies that a direct, ladder-like IR excitation of τOH is an improbable route for successful interconversion, given the need to (a) absorb five quanta and (b) the significant anharmonicity of the potential, illustrated by the bands assigned to overtones of τOH. However, the observation of interconversion in matrices suggest that an alternative pathway is available, likely including excitation of a higher-frequency mode, followed by intramolecular vibrational distribution. This pathway could be studied by several approaches. First, isomer population changes and barrier heights can be experimentally studied via hole-filling spectroscopy.40,41 These studies rely on laser-induced isomerization, followed by collisional cooling of the formed isomers, yielding sharp transition lines. However, in a dynamics experiment, such collisions, which typically take place at much larger timescales, are likely irrelevant. Therefore, it will be of interest to also probe the UV spectra directly after IR excitation, monitoring the (transiently) populated vibrational states. Probing dynamics of such processes on their natural timescale requires short laser pulses, which are characterised by a much larger bandwidth than the nanosecond pulses employed in this experiment. The increased bandwidth reduces spectral resolution, thus rendering conformer separation based on resonant ionisation impossible. Therefore, we are currently working on the introduction of electrostatic selection techniques for these experiments, that yield conformer-selected molecular beams.42 Secondly, the use of alternative detection techniques, such as velocity-map imaging would enable obtaining spectral information (in the form of a photoelectron spectrum) with just one excitation wavelength. Finally, a crucial requirement for time-resolved experiments is the ability to isolate single IR picosecond pulses rather than a 10 μs FEL pulse train. This was recently demonstrated, resulting in micropulse energies exceeding 100 μJ,43 which should be sufficient to saturate the majority of vibrational transitions. Experiments aimed at exploiting the combination of these technical improvements are currently in preparation in our Laboratory.
4 Conclusions
In this work we presented IR ion-dip spectra of gas-phase, jet-cooled 3CP and 3FP encompassing the majority of the fingerprint region. With the aid of DFT calculations and thanks to conformer-selectivity of the method we were able to assign the large majority of bands. Our assignment revises a previous one of the OH torsional modes of 3FP, attributing the higher frequency vibration to the anti conformer.Our simulated spectra, calculated at the B3LYP/def2-tzvp level of theory, provide a good match for the experimental results within the harmonic approximation, with the exception of the OH torsional mode. Alternative approaches, like Born–Oppenheimer Molecular Dynamics (BOMD) calculations were suggested for phenol derivatives and could be implemented should a higher degree of accuracy be required to identify hydroxyl group torsional modes.10,24 Furthermore, simple anharmonic correction seems to be of limited use in assigning modes falling beyond the scope of the harmonic approximation, apart from the relatively well reproduced first overtones of the OH torsional mode. A simple, one-dimensional harmonic oscillator model of the OH torsional mode gives strength to the identification of several higher overtones of the torsional mode.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is part of the project “HFML-FELIX: a Dutch Centre of Excellence for Science under Extreme Conditions” (with project number 184.035.011) of the research programme “Nationale Roadmap Grootschalige Wetenschappelijke Infastructuur” which is (partly) financed by the Dutch Research Council (NWO). We further gratefully acknowledge NWO for the support of the FELIX Laboratory and NWO Rekentijd for the computational resources (grant 2021.055). DAH acknowledges support by NWO through grant number VI-VIDI-193.037. We thank the SURFsara Supercomputer Centre staff for their continuous support. Finally, we would like to thank Prof. Ad van der Avoird for fruitful discussions on the theoretical treatment of the OH torsional overtone bands.Notes and references
- J. I. Seeman, Chem. Rev., 1983, 83, 83–134 CrossRef CAS.
- R. W. Hoffmann, Angew. Chem., Int. Ed., 2000, 39, 2054–2070 CrossRef PubMed.
- R. Chen, Y. Shen, S. Yang and Y. Zhang, Angew. Chem., Int. Ed., 2020, 59, 14198–14210 CrossRef CAS PubMed.
- P. S. Tseng, C. Ande, K. W. Moremen and D. Crich, Angew. Chem., Int. Ed., 2023, 62, e202217809 CrossRef CAS PubMed.
- M. Rabiller, M. Getlik, S. Klüter, A. Richters, S. Tückmantel, J. R. Simard and D. Rauh, Arch. Pharm., 2010, 343, 193–206 CrossRef CAS PubMed.
- G. Gil-Ramirez, D. A. Leigh and A. J. Stephens, Angew. Chem., Int. Ed., 2015, 54, 6110–6150 CrossRef CAS PubMed.
- B. S. Murray, L. Menin, R. Scopelliti and P. J. Dyson, Chem. Sci., 2014, 5, 2536–2545 RSC.
- S. Kassem, T. V. Leeuwen, A. S. Lubbe, M. R. Wilson, B. L. Feringa and D. A. Leigh, Chem. Soc. Rev., 2017, 46, 2592–2621 RSC.
- T. Watanabe, T. Ebata, S. Tanabe and N. Mikami, J. Chem. Phys., 1996, 105, 408–419 CrossRef.
- V. Yatsyna, D. J. Bakker, R. Feifel, A. M. Rijs and V. Zhaunerchyk, Phys. Chem. Chem. Phys., 2016, 18, 6275–6283 RSC.
- N. E. Henriksen, Chem. Soc. Rev., 2002, 31, 37–42 RSC.
- A. Manocha, G. Carlson and W. Fateley, J. Phys. Chem., 1973, 77, 2094–2098 CrossRef CAS.
- M. Ito and A. Oikawa, J. Mol. Struct., 1985, 126, 133–140 CrossRef CAS.
- E. Fujimaki, A. Fujii, T. Ebata and N. Mikami, J. Chem. Phys., 1999, 110, 6045–6056 CrossRef.
- A. Bell, J. Singer, D. Desmond, O. Mahassneh and J. van Wijngaarden, J. Mol. Spectrosc., 2017, 331, 53–59 CrossRef CAS.
- K. Yosida, K. Suzuki, S.-I. Ishiuchi, M. Sakai, M. Fujii, C. E. H. Dessent and K. Müller-Dethlefs, Phys. Chem. Chem. Phys., 2002, 4, 2534–2538 RSC.
- A. J. Lopes Jesus, J. R. de Lucena Junior, R. Fausto and I. Reva, Molecules, 2022, 27, 8248 CrossRef CAS PubMed.
- M. A. Moreira, R. A. Cormanich, F. M. P. de Rezende, J. M. Silla, C. F. Tormena, R. Rittner, T. C. Ramalho and M. P. Freitas, J. Mol. Struct., 2012, 1009, 11–15 CrossRef CAS.
- M. C. Cockett, M. Takahashi, K. Okuyama and K. Kimura, Chem. Phys. Lett., 1991, 187, 250–256 CrossRef.
- M. Czaplicka and B. Kaczmarczyk, Talanta, 2006, 70, 940–949 CrossRef CAS PubMed.
- S. J. Harris, T. N. Karsili, D. Murdock, T. A. Oliver, A. M. Wenge, D. K. Zaouris, M. N. Ashfold, J. N. Harvey, J. D. Few, S. Gowrie, G. Hancock, D. J. Hadden, G. M. Roberts, V. G. Stavros, G. Spighi, L. Poisson and B. Soep, J. Phys. Chem. A, 2015, 119, 6045–6056 CrossRef CAS PubMed.
- P. Buschmann, K. G. Lengsfeld, S. Herbers, S. Genuit, C. M. Höhne and J. U. Grabow, J. Mol. Struct., 2020, 1217, 128224 CrossRef CAS.
- S. Nakagawa, Y. Matsushita, T. Suzuki and T. Ichimura, J. Mol. Struct., 2005, 779, 68–71 CrossRef CAS.
- D. J. Bakker, Q. Ong, A. Dey, J. Mahé, M.-P. Gaigeot and A. M. Rijs, J. Mol. Spectrosc., 2017, 342, 4–16 CrossRef CAS.
- D. Oepts, A. F. G. van der Meer and P. W. Van Amersfoort, Infrared Phys. Technol., 1995, 36, 297–308 CrossRef CAS.
- R. H. Page, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 4621–4636 CrossRef CAS.
- J. M. Bakker, L. MacAleese, G. Meijer and G. von Helden, Phys. Rev. Lett., 2003, 91, 203003 CrossRef PubMed.
- K. Schwing and M. Gerhards, Int. Rev. Phys. Chem., 2016, 35, 569–677 Search PubMed.
- S. Bakels, M. P. Gaigeot and A. M. Rijs, Chem. Rev., 2020, 120, 3233–3260 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108 CrossRef PubMed.
- G. Varsanyi and S. Szoke, Vibrational spectra of benzene derivatives, Academic Press, New York, London, 1969 Search PubMed.
- H. D. Bist, J. C. Brand and D. R. Williams, J. Mol. Spectrosc., 1967, 24, 402–412 CrossRef CAS.
- W. Roth, P. Imhof, M. Gerhards, S. Schumm and K. Kleinermanns, Chem. Phys., 2000, 252, 247–256 CrossRef CAS.
- A. B. Dempster, J. Mol. Spectrosc., 1970, 35, 18–26 CrossRef CAS.
- H. N. Al-Jallo and M. G. Jalhoom, Spectrochim. Acta, Part A, 1972, 28, 1663–1692 CrossRef.
- B. C. Dian, A. Longarte and T. S. Zwier, Science, 2002, 296, 2369–2373 CrossRef CAS PubMed.
- B. C. Dian, J. R. Clarkson and T. S. Zwier, Science, 2004, 303, 1169–1173 CrossRef CAS PubMed.
- Y.-P. Chang, D. A. Horke, S. Trippel and J. Küpper, Int. Rev. Phys. Chem., 2015, 34, 557–590 Search PubMed.
- T. Janssen, C. S. Davies, M. Gidding, V. Chernyy, J. M. Bakker and A. Kirilyuk, Rev. Sci. Instrum., 2022, 93, 043007 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04352a |
| This journal is © the Owner Societies 2025 |