Decomposition pathways of isoprene-derived hydrotrioxides and their clustering abilities in the atmosphere

Abstract

In atmospheric gas-phase chemistry, hydrotrioxides (ROOOH) are formed as intermediates in the reactions of peroxyl radicals (RO₂) with OH radicals, and their stabilization has been confirmed experimentally by direct observation. In this study, we systematically investigated the probable decomposition pathways of isoprene-derived ROOOHs in the atmosphere. The kinetic analysis confirmed that the fast fragmentation of hydrotrioxides into their respective alkoxy radicals and hydroperoxyl radicals dominates over the other decomposition mechanisms. We also explored the decomposition of ROOOH proceeding via³(RO⋯HO₂) product complexes, through which an intermolecular hydrogen transfer results in the formation of alcohol and molecular oxygen with a relatively low energy barrier. Furthermore, we studied the clustering abilities of hydrotrioxides with various types of atmospheric vapors, particularly acids and amines. The results indicate that the binding strength of these hydrotrioxides with other vapors is too low to drive clustering processes at ambient atmospheric concentrations, however, hydrotrioxides interact more strongly with bases and acid–base clusters than alcohols or hydroperoxides. These findings provide insight into the atmospheric stability and reactivity of hydrotrioxides, with implications for understanding their role in processes such as secondary organic aerosol formation.

---

1 Introduction

Isoprene, recognized as one of the most abundant biogenic volatile organic compounds (BVOCs), is emitted by plants into the atmosphere. With global emissions of approximately 500 Tg, it is comparable in magnitude to the emissions of all other non-methane BVOCs combined and equal to the global emissions of methane.^1,2 Isoprene undergoes rapid oxidation within a few hours of emission via reaction with OH radicals and subsequent addition of molecular oxygen, resulting in the formation of peroxy radicals (RO₂).³ These organic peroxy radicals originating from isoprene (ISOPOO) follow different unimolecular and bimolecular pathways depending on the concentrations of atmospheric radicals such as OH, HO₂, NO and RO₂, as well as temperature.^4–8 It had been previously speculated that the gas-phase addition of the hydroxyl radical to the organic peroxy radical could lead to the formation of hydrotrioxides.⁹

Hydrotrioxides are compounds that are characterized by the linear linkage of three oxygen atoms to each other. Previously regarded as chemically unstable, they are generated during the ozonolysis of organic compounds in the aqueous phase at low temperatures. The decomposition of hydrotrioxides may result in the release of singlet state molecular oxygen, which is a strong oxidant.^10,11 Recently, direct observation of hydrotrioxide formation via the RO₂ + OH mechanism has been experimentally demonstrated under atmospherically relevant conditions.¹² The kinetic analysis of the RO₂ + OH mechanism suggests that the bimolecular rate coefficient of HO–C₅H₈OOOH formation is 5.1 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹, and that of higher oxidized HO–C₅H₇(O₂H)OOOH formation is 1.1 × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹.¹²

Because of their thermal lifetime in the gas phase and the presence of an oxygen-containing functional group, isoprene-derived hydrotrioxides could participate in new particle formation or growth. In the atmosphere, these sticky oxygenated organic compounds can contribute to the formation of secondary organic aerosols (SOAs) through clustering mechanisms.^7,13–15 The clustering mechanism by vapor molecules colliding and sticking to each other plays a crucial role in the formation of new particles. Sulfuric acid is a main driver of the initial particle formation in many environments.^16–21 Additionally, it is clear that oxygenated organic compounds play an important role in the formation and growth of aerosol particles.^22,23 Moreover, it is known that oxidation products containing only peroxy acid, hydroperoxides, and carbonyl groups do not have the capabilities to drive the process of new particle formation.^24,25 This suggests that the oxygen-to-carbon ratio does not solely determine the volatility and ability to form clusters.^26,27 However, certain factors involving the precise molecular arrangement and the number of hydrogen bonding sites affect the strength of intermolecular interactions. Thus, to expand our understanding of the behavior of hydrotrioxides in the real atmosphere, we investigated the cluster stabilities of this type of oxygenated organic compound with H₂O, acids, bases, and the dimer, taking into account that R¹-OOOH has a long enough lifetime in the atmosphere to cluster with itself.

Therefore, this work focuses on the fate of these isoprene-derived hydrotrioxides in the atmosphere involving their unimolecular decomposition pathways and clustering capabilities with atmospheric vapors. Additionally, this study highlights the cost-effective quantum chemistry methodology that corroborates with the experimental decomposition rates, particularly for the simplest organic trioxide system, CH₃OOOH.²⁸ The two different decomposition pathways are presented below. The reaction pathway (1) involves fragmentation into two radical systems, forming the respective alkoxy radical and a hydroperoxy radical. Reaction pathway (2) indicates the dissociation reaction in which molecular oxygen and the corresponding alcohol are formed. It should be noted that this kind of reaction may occur either on a singlet or triplet potential energy surface (PES), wherein the favorable pathway is via a triplet potential energy surface, assuming that the triplet complex [RO⋯HO₂] undergoes a very fast inter-system crossing (ISC),²⁹ especially in the gas phase. An alternative decomposition pathway has also been explored in this study. The detailed mechanism and its energetics are available in the ESI† of this manuscript.

ROOOH → RO + HO₂ (1)

ROOOH → ROH + O₂ (2)

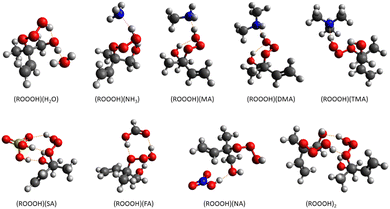
For the kinetic and thermodynamic analysis of these probable decomposition pathways, a total of ten hydrotrioxides are considered. To reduce computational costs, HOOOH and CH₃OOOH are initially used as model systems for the study, and the other eight isoprene-derived hydrotrioxides that are formed from the first and second generation RO₂ systems are subsequently studied. Their probable formation mechanisms are described in Fig. 1 and 2. Mass peaks corresponding to the first and second-generation ROOOH have already been experimentally observed from isoprene + OH under atmospheric conditions (see Fig. 3).¹² It is to be noted that all hydrotrioxide conformers studied here are based on theoretical models (as we cannot distinguish the isomers corresponding to the mass signals). However, the stability of these hydrotrioxides depends on the distribution of ISOPOO radicals. This distribution, in turn, is affected by the arrangement of cis/trans allylic radicals and the rates at which oxygen is added at the β and δ positions. Previous assessments of the initial distribution of peroxy radicals have relied on either computational estimates³⁰ or analysis of bulk products.³¹ Teng et al.³² presented a summary of the initial (kinetic) ISOPOO radical distribution resulting from the OH-isoprene + O₂ system at 296 K. Their results indicate that (1-OH,2-OO)-denoted by R¹-OO in this study has the highest kinetic ISOPOO distribution with a yield of 0.479 among six ISOPOO isomers. This agrees with the hypothesis of the formation of the first generation of R¹-OOOH, as described and validated by experimental detection under atmospheric conditions.¹²

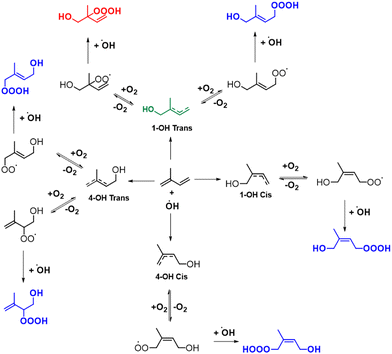Fig. 1 Proposed formation mechanisms of the isoprene-derived hydrotrioxides (HO–C₅H₈OOOH) from isoprene via auto-oxidation. Note: green and red represent the dominant product yield as described in Berndt et al.,¹² while blue represents other conformers of isoprene-derived hydrotrioxides.

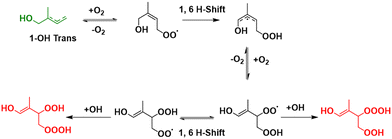Fig. 2 Formation mechanisms of the second generation of isoprene-derived hydrotrioxides (HO–C₅H₈(O₂)OOOH) from 1-OH trans, as described in Berndt et al.¹² Note: green and red represent the most dominant product yield in their respective channel.

Fig. 3 All the isomers of isoprene-derived hydrotrioxides with labels of 1–8 investigated in this study.

Gas phase hydrotrioxide decomposition has previously been studied directly by Berndt et al.¹²via experiments and indirectly by achieving a thorough product decomposition yield by Assaf et al.²⁸ and Caravan et al.³³ Computational studies of the simplest organic trioxides have been performed by Müller et al.,²⁹ Liu et al.³⁴ and Assaf et al.,²⁸ though most notable is perhaps the multi-reference calculations performed by Berndt et al.¹² Multi-reference methods have further been used to study the bimolecular reaction of CH₃OOOH with OH by Anglada and Solé.³⁵ We will now briefly summarize their findings. The RO₂ + OH reactions that form ROOOH are known to be exothermic by more than 30 kcal mol⁻¹,¹² which means that the excess energy may have an impact on the ratios of atmospheric products. At atmospheric pressures, only 2–10% of CH₃OOOH formed from CH₃O₂ + OH is thermalized, 75–78% of C₂H₅OOOH formed from C₂H₅O₂ + OH, and nearly all the ROOOH formed from larger RO₂^28,33 are stabilized. Thus we assume that all the isoprene-derived ROOOH studied in this work are fully stabilized under atmospheric pressure. All results known to us agree that the main products of trioxide decomposition are those of pathway (1), but there is some disagreement on the importance of pathway (2) as a minor channel. In the computational study of CH₃O₂ + OH by Müller et al.,²⁹ a total CH₃OH yield of 30% was suggested, but direct measurements of the formed CH₃OH by Caravan et al.³³ showed a yield of 7%. This agrees reasonably well with low-pressure (0.066 atm) experiments by Assaf et al.²⁸ producing 90% of HO₂ and ≪1% of stabilized CH₃OOOH. Pathway (2) has previously been studied computationally by Müller et al.²⁹ and Berndt et al.¹² The former assumes that the branching between pathways (1) and (2) starts from the (CH₃O + HO₂) complex after the trioxide moiety has already decomposed. In their calculations, the activation barrier of pathway (2) is 19.5 kcal mol⁻¹ in the triplet state and 20.9 kcal mol⁻¹ in the singlet state relative to the ground state energy of CH₃OOOH. The calculations of Berndt et al.¹² instead suggest an activation barrier of over 40 kcal mol⁻¹, but their discussion implies that this transition state was for the H-shift reaction occurring before trioxide decomposition (leading to an ‘unfavorable 4-membered ring’ structure). Pathway (1), in contrast, requires only 25–30 kcal mol⁻¹ depending on the level of electronic structure theory employed.¹² The implication is that this mechanism of direct alcohol formation from ROOOH is not responsible for the formation CH₃OH observed by Caravan et al.³³ The post-ROOOH decomposition H-shift mechanism suggested by Müller et al.²⁹ is in better agreement with the existing experiments, despite their likely overestimation of the CH₃OH yield from this channel.

2 Methods

2.1 Computational details

Different quantum chemical methods were applied to study the decomposition pathways of the hydrotrioxides studied. To calculate the lowest energy conformer of each reactant and product system, a systematic conformational search was performed using the conformer–rotamer ensemble sampling tool (CREST) software at the semi-empirical extended tight-binding method (GNF2-xTB).^36,37 Geometry optimization was performed for the conformers generated in the previous step, out of which, conformers with less than 2 kcal mol⁻¹ in relative electronic energy were selected, followed by a frequency calculation computed using density functional theory (DFT) at the ωB97X-D³⁸/6-31+G*^39,40 level of theory.

The lowest-energy conformer in each reactant system was identified, and its DFT structure was selected for a relaxed PES scan to locate the transition state (TS) structure over the desired bond length, depending on which decomposition pathway to investigate. The next step was to optimize the TS structure produced in each pathway and compute frequencies. In optimization and frequency calculations of all structures, we employed default criteria (such as SCF = tight, the default grid ultrafine) as implemented in Gaussian 16 RevC.02 software.⁴¹ Intrinsic reaction coordinate (IRC) calculations were performed to confirm that the transition state corresponds to the correct reaction channel.

Furthermore, on top of the lowest energy DFT reactant, TS, and product structures, single-point energy corrections were calculated using the DLPNO-CCSD(T)/aug-cc-pVTZ level.^42–44 We used tight pair natural orbital criteria (TightPNO),⁴⁵ tight self-consistent field criteria (TightSCF), and a default integration grid as implemented in Orca version 5.0.3.⁴⁶ In DLPNO calculations, the auxiliary basis aug-cc-pVQZ/C was used. Unless otherwise specified, all DFT calculations were performed using Gaussian 16 RevC.02 software,⁴¹ and single point energies were calculated in ORCA version 5.0.3.⁴⁶ The difference in the energies between the TS and the reactant equals the barrier heights of a reaction.

In particular, for the H-shift reactions initiated from the product complex ³(RO⋯HO₂), we specifically employed the ωB97X-D3⁴⁷/6-31+G* level of theory and performed all the calculations associated with in ORCA version 6.0.0.^46,48–54 Apart from this exception, a similar conformer sampling workflow was followed. The choice of constrained parameters in the CREST conformer generation turned out to be especially crucial for converging all of the TS conformers, so we will provide some additional details. The coordinates constrained in the CREST runs for these H-shift reactions were the C–O distance in the alkoxy radical, O–H and O–O distances and the H–O–O angle in the HO₂ radical, as well as the intermolecular O⋯H distance and O⋯H–O angle. For β-unsaturated alkoxy radicals, the O–C–C angle was also constrained during the conformer search to prevent unwanted epoxidation reactions. The equilibrium values of the constraint potential for the O⋯H and OH distances were specifically chosen to be slightly shifted to the product side of the TS values (this meant 1.3–1.4 Å for distance O⋯H and 1.05–1.10 Å for distance OH) to prevent the TS conformers from falling in the (RO⋯HO₂) well during optimization. Here, frequency calculations were performed for all conformers to ensure that the saddle point corresponded to the correct reaction. All calculations for this reaction channel were performed on the triplet surface, as the calculations on CH₃OOOH by Müller et al.²⁹ produced both a lower barrier compared to the singlet surface and a very rapid singlet-to-triplet ISC. We thus assumed the triplet surface energetics of the (ISOPO⋯HO₂) → ISOPOH + O₂ reaction to be sufficient for estimating their atmospheric importance. The geometries of the complexes (RO⋯HO₂) and (ROH⋯O₂) were determined by IRC from the lowest free energy TS conformer.

The rate coefficients for the decomposition pathway (2) were calculated with the Eyring equation of transition state theory (TST).

where Q_TS and Q_R are the partition functions of lowest-free energy TS and reactant, respectively, and κ_t is the quantum-chemical tunneling coefficient calculated from the TS connecting reactants and products, using the Eckart tunneling correction. E_TS and E_R correspond to the zero-point corrected energies of the transition state and reactant, k_B is the Boltzmann constant, T is the temperature (=298 K), and h is the Planck's constant. The partition functions and the zero-point energy were calculated using DFT at ωB97X-D/6-31+G* and the reaction barrier energy (E_TS − E_R) was corrected using DLPNO-CCSD(T)/aug-cc-pVTZ single point energy calculations.

The reaction dynamics corresponding to the pathway (1) involving fragmentation into alkoxy radicals and hydroperoxyl radicals was simulated using the master equation solver for multi energy-well reactions (MESMER) software.⁵⁵ The simulation conditions and parameters used were analogous to those parameters utilized in the α-pinene ring-break reaction by Kurtén et al.,⁵⁶ also presented in Table S7 in the ESI.† The inverse Laplace transform (ILT) method was employed to calculate both the forward (RO + OOH) and backward dissociation rates (ROO + OH) of hydrotrioxides, assuming a barrierless channel. The association rate coefficients required for simulating both the forward and backward dissociation rates were calculated using long-range transition state theory.⁵⁷ The zero-point corrected energies were calculated using DLPNO//DFT and the rotational constants and vibrational frequencies were calculated at the DFT level.⁴⁷ N₂ was used as a bath gas and the collisional energy transfer parameter of ΔE_down = 200 cm⁻¹ described from the exponential down model was used consistently in all simulations. The OH concentration of 10⁶ molecules cm⁻³ was used as an excess reactant concentration. In addition, the values of the Lennard-Jones parameter of intermediates (ROOOH) were calculated following the approach used in Gao et al.⁵⁸ and Tee et al.,⁵⁹ derived using a group additive technique by Joback and Reid,⁶⁰ to estimate the critical properties of pure compounds. We also employed a canonical detailed balance approach to understand the rates of pathway (1). The detailed methodology of this approach can be found in the ESI† of this manuscript.

2.2 Cluster thermodynamics calculations

The clustering abilities of nine atmospherically relevant molecules with two types of ROOOH as well as ROH and ROOH have been investigated using quantum chemical calculations involving different levels of theory. A systematic configuration sampling was followed to obtain the global minimum cluster structures and their potential energy surfaces.⁶¹

(1) At first, 3000 random guesses and 100 exploration loops were conducted to create the initial conformation of clusters in the ABCluster program.^62,63

(2) Out of which around 200 of the lowest energy structures have been explored by maintaining boundary wall conditions and subsequently optimized by the tight-binding method GFN2-xTB.

(3) Based on the electronic energies, radius of gyration, and dipole moments, duplicate structures were filtered out.⁶¹

(4) All unique conformers were further optimized at the ωB97X-D/6-31+G* level of theory.

(5) Possible duplicates were removed and unique structures within an energy threshold of N kcal mol⁻¹ were selected. Here N in the number of molecules in the cluster. For instance, in the case of dimers, structures within energies of 2 kcal mol⁻¹ were selected for the next step. Depending on the system, we found 5–20 unique conformers within that energy threshold.

(6) Final optimization and calculation of the vibrational frequencies were performed at the ωB97X-D/6-31++G** level.⁶⁴

(7) The Gibbs free energy at 298 K was calculated and the minimum free energy structure was located. For that cluster, the single-point energy correction was performed using the highly accurate level of theory DLPNO-CCSD(T)/aug-cc-pVTZ.⁴⁴

The global minimum Gibbs free energy structure of each cluster calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G** level was taken for calculating the Gibbs binding free energy.

3 Results and discussion

Our study focuses on the unimolecular decomposition of hydrotrioxides in the atmosphere. The idea is to understand the fate of ROOOH chemistry and explore which reaction channel outperforms other pathways kinetically and is sufficiently fast to be feasible in the atmosphere. Additionally, we study the binding capabilities of model CH₃OOOH and R¹-OOOH with various combinations of monomeric units consisting of small neutral, acidic, and basic molecules of the atmosphere. These results will enhance the understanding of ROOOH's relative stability and adequate lifetime to form clusters and ultimately its role in new particle formation.

3.1 Unimolecular decomposition mechanisms

Building upon the fundamentals of isoprene-derived hydrotrioxides, we systemically present the detailed mechanism of each decomposition pathway in this section. The energetics and rate coefficients are calculated to determine the feasibility in atmospheric conditions as well as parameters to drive the competition between these reaction channels. We also explore an alternate reaction channel that connects both pathways and could shift the reaction dynamics. Additionally, a small benchmarking study is performed, specifically focusing on the decomposition rates of the pathway (1) of CH₃OOOH.

3.1.1 Formation of alkoxy and hydroperoxyl radicals. In this section, we discuss the fragmentation channel where hydrotrioxide molecules break into RO and HO₂ radicals indicated as pathway (1). It is found that this dissociation mechanism into radicals proceeds through a barrierless channel, leading to products that are higher in energy than ROOOH. Thus, to calculate the unimolecular reaction rate, we employ two approaches: (a) canonical detailed balance and (b) solution of a chemical master equation (ME). It is worth noting that the latter approach takes into account the excess vibrational energy while calculating the energy-resolved rate coefficients using a micro-canonical model. At the same time, the overall kinetics modeled by the ME also include the treatment of collisional energy transfer.

We present the decomposition energies of the pathway (1) in terms of zero-point corrected electronic energies along with their respective rate coefficients at 298 K (see Table 1). The rate coefficients obtained for all trioxide systems using both approaches are of a comparable order of magnitude. However, there is a one to three factor of magnitude overestimation in the canonical detailed balance approach. The fact that the master equation phenomenological rate coefficients are smaller than the ones given by the canonical detailed balance, signifies that excess energy does not play any role here. This observation is also supported by the finding that larger trioxide systems decompose faster than the smaller systems such as CH₃OOOH and HOOOH. This is because larger systems would have reacted slower if excess vibrational energy came into play, as they have more vibrational modes to accommodate the excess energy, suggesting that the rate of activating collisions is controlling the reaction rate. This means that the reaction is at the “fall-off” region, and the ROOOH dissociation via pathway (1) is not at the high-pressure limit at 1 atm, as evidenced by the pressure-dependence profile (see Fig. 4). Canonical detailed balance assumes that the reaction is at the high-pressure limit (which for CH₃OOOH occurs only at pressures > 20 atm), where the rate of collisional energy transfer is much faster than the rate of dissociation. This is an interesting result from an atmospheric point of view and contradicts the prediction suggested by Müller et al.²⁹ citing that the dissociation to RO + HO₂, especially those formed from the biogenic terpenoids, would be substantially slower than those from CH₃OOOH due to the larger number of modes, which can “dilute” the excess energy. However, it is noteworthy that on comparing the experimental lifetimes of hydrotrioxide systems studied by both Assaf et al.,²⁸ which is CH₃OOOH and Berndt et al.,¹² that of HO–C₅H₈OOOH, the unimolecular decomposition rates are 1.1 × 10⁻⁴ s⁻¹ and approximately 8 × 10⁻⁴ s⁻¹ (considering that 20 minutes is the lower bound thermal atmospheric lifetime for this system), respectively. This is consistent with the trend observed in the MESMER simulations under this study, which predict a slower decomposition for CH₃OOOH due to fall-off effects.

Table 1 Single-point energy corrected decomposition energies (ΔE_d in kcal mol⁻¹) and excess energy (ΔE_ex in kcal mol⁻¹) of the decomposition pathway (1) with their respective rate coefficients k^a_uni and k^b_uni at 298 K (in s⁻¹) where k^a_uni is the dissociation rates of pathway (1) calculated using canonical detailed balance and k^b_uni is the dissociation rates of pathway (1) calculated using MESMER

System	ΔEd	ΔEex	k assoc	k ^auni	k ^buni
Note: kassoc (cm^3 molecule^−1 s^−1) is the association rate of the reaction ROO + OH calculated using long-range transition state theory.^57
HOOOH	29.4	29.4	5.9 × 10^−10	1.6 × 10^−5	3.5 × 10^−8
CH3OOOH	25.1	28.8	6.4 × 10^−10	8.8 × 10^−1	3.0 × 10^−3
R^1-OOOH	26.7	29.7	5.2 × 10^−10	1.1	3.1 × 10^−1
R^2-OOOH	26.6	29.6	5.6 × 10^−10	1.9 × 10^−1	1.1 × 10^−1
R^3-OOOH	27.0	29.0	6.1 × 10^−10	5.1 × 10^−1	1.8 × 10^−1
R^4-OOOH	26.1	29.6	5.8 × 10^−10	2.0	6.4 × 10^−1
R^5-OOOH	26.3	29.4	5.7 × 10^−10	1.1 × 10^−1	8.1 × 10^−2
R^6-OOOH	26.7	30.9	6.0 × 10^−10	4.8 × 10^−1	1.9 × 10^−1
R^7-OOOH	30.7	29.9	7.1 × 10^−10	9.7 × 10^−3	4.5 × 10^−3
R^8-OOOH	26.8	28.7	5.8 × 10^−10	5.4 × 10^−1	3.2 × 10^−1

---

Fig. 4 Pressure dependent decomposition rates of CH₃OOOH computed with MESMER calculated using our DLPNO//DFT energies.

At the same time, the unimolecular decomposition rate coefficient obtained in this study, in particular of [CH₃OOOH → CH₃O + HO₂] = 3 × 10⁻³ s⁻¹ agrees well with the analogous systems previously studied.^28,65,66 Iyer et al.⁶⁵ presented that for an adduct system containing a carbonyl group such as CH(O)CH₂OOOH, the dominant channel is CH(O)CH₂O + HO₂ with a first-order decomposition rate of 2.7 × 10⁻³ s⁻¹. Similarly, Liu et al.⁶⁶ investigated the reaction mechanism of the CH₃CH₂OOOH complex and concluded that CH₃CH₂O + HO₂ are the main products on the singlet surface. Assuming that pathway (1) is the major channel of decomposition, the unimolecular lifetime of all the isoprene-derived hydrotrioxides under this study range from seconds to a few minutes, in contrast with HOOOH and CH₃OOOH with lifetimes spanning over days to minutes, respectively.

Benchmarking of computational methods. Hydrotrioxides are known to be highly multi-configurational, requiring computationally resource-heavy multi-reference methods for their energies to be determined accurately.^12,35 The largest ROOOH system for which these multi-reference calculations have been performed is CH₃OOOH, which is less than half the size of our isoprene-derived ROOOH both in terms of nuclei and electrons. Due to the power-law scaling of computational cost with system size, cost-efficient DLPNO-CCSD(T) single points on DFT-optimized geometries were preferred. For this reason, a comparison of the various computational methods used on the CH₃OOOH system was made for reference. In Table 2, a comparison of the computational results of Müller et al.²⁹ and Berndt et al.¹² are compared to our DLPNO-CCSD(T)//DFT computations, all calculated using the ORCA version 5.0.4 program.⁴⁶ The decomposition energy is defined as:

E_d = E_RO + E_HO2 − E_ROOOH (5)

Table 2 Comparison of E_d along with its electronic energy component E_d (e) (in kcal mol⁻¹) for CH₃OOOH calculated using various methods

Single-point	Optimization	E d	E d (e)	E d (ZPE)	Source
Abbreviations: aVTZ: aug-cc-pVTZ^43 jVTZ: jun-cc-pV(T+d)Z.^67 VnZ-F12: cc-VnZ-F12. Sources:a This work.b Müller et al.^29c Berndt et al.^12
	ωB97X-D3^47/6-31+G*	20.92	25.61	−5.26
	ωB97X-D3/jVTZ	20.35	26.09	−5.17
	M06-2X^68/jVTZ	24.88	29.86	−4.97
DLPNO-CCSD(T)^42/aVTZ	ωB97X-D3/6-31+G*	24.96	30.11	−5.26
DLPNO-CCSD(T)/aVTZ	ωB97X-D3/jVTZ	24.84	30.13	−5.17
DLPNO-CCSD(T)/aVTZ	M06-2X/jVTZ	25.04	30.01	−4.97
UCCSD(T)-F12/VDZ-F12^69	M06-2X/jVTZ	24.82	29.79	−4.97
UCCSD(T)-F12/VTZ-F12	M06-2X-D3/6-311++G(3df,3pd)	24.7	—	—
UCCSD(T)-F12a/VDZ-F12	M06-2X/aVTZ	25.8	—	—
CASPT2(14,12)/aVTZ	CASSCF(14,12)/aVTZ	28.3	—	—
UCCSD(T)/aVTZ	UCCSD(T)/aVTZ	30.6	—	—

---

For the calculations performed in this work, electronic energy (e) and zero-point energy (ZPE) contributions to E_d are also presented. The results are comparable to the similar benchmarking performed by Berndt et al.¹² CCSD(T)//DFT methods systematically underestimate E_d by 3–5 kcal mol⁻¹ (ref. 12) relative to the CASPT2//CASSCF and UCCSD(T)//UCCSD(T) results. As reported in that study, M06-2X seems to perform much better than ωB97X-D3 when it comes to determining energetics without coupled cluster single-point energy corrections. On the other hand, all the chosen CCSD(T)//DFT method combinations seem to agree remarkably well, implying that the choice of density functional and optimization basis set does not have a huge impact on the relative accuracy of the results. Furthermore, splitting E_d into electronic and ZPE contributions shows that all DFT-calculated ZPEs fit within a span of 0.3 kcal mol⁻¹. Our conclusion from this comparison was that the ROOOH reaction energetics may be determined using the reasonably cheap combination of DLPNO-CCSD(T)/aug-cc-pVTZ and ωB97X-D3/6-31+G*, as all CCSD(T)//DFT methods seem to produce similar results regardless of the choice of DFT method and basis set combination.

Another way to benchmark the accuracy of our computations is to use the experimental decomposition rate of 1.1 × 10⁻⁴ s⁻¹ at 300 K with a temperature-dependence of 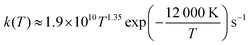provided by Assaf et al.²⁸ Identifying the decomposition energies in Table 2 that are most capable of reproducing this value, would provide additional hints as to where the observed systematic error in the decomposition energies comes from. Computational decomposition rates were determined using master equation solver for multi energy-well reactions (MESMER) software with parameters described in the methods section. The results are shown in Fig. 5.

Fig. 5 Comparison of the Assaf et al.²⁸ experimental k_d(T) with MESMER calculated using the UCCSD(T) and CASPT2(14,12) energies from Berndt et al.,¹² the UCCSD(T)//M06-2X-D3 energies from Müller et al.²⁹ and our DLPNO//DFT energies calculated at the DLPNO-CCSD(T)/aug-cc-pVTZ and ωB97X-D/6-31+G* level of theory.

As seen in the figure, the CASPT2//CASSCF results (in red line) come the closest to replicating the experimental results (purple line), suggesting that this is the level of theory required to calculate accurate energetics for hydrotrioxide compounds. The usage of DLPNO//DFT energies (orange line) results in an overestimation of the decomposition rate by a factor of approximately 10², which is a quite significant result for the atmospheric implication of our results, as multiplying the ISOPOOOH decomposition rates from the given value in Table 1 with 10⁻² results in atmospheric lifetimes of minutes to a few hours. This means that ISOPOOOH trioxides might indeed live long enough to cluster in the atmosphere. This suggests that the systematic error observed in Table 2 comes from the DFT-optimized geometries rather than the coupled-cluster single point. This is valuable information for future computational studies attempting to capture the accurate gas phase kinetics of hydrotrioxide compounds.

3.1.2 Dissociation into alcohol and molecular oxygen from a trioxide moiety. This study evaluates the energetic and rate coefficients of the decomposition reaction pathway (2) associated with isoprene-derived hydrotrioxide conformers. Pathway (2) is a dissociation channel wherein molecular oxygen (in either its triplet or singlet state) and alcohol are generated directly from the corresponding trioxide moiety. Overall decomposition energies (energy difference between products and reactant) of this reaction channel vary depending on whether it occurs in the singlet or triplet surface, out of which the latter is lower in energy and thus more favorable. In Table 3 we present the barrier energies of this channel for the studied hydrotrioxides. The energy barriers of this decomposition pathway are above 40 kcal mol⁻¹ and the rate coefficients for all the studied trioxides calculated based on the single conformer TST span around 10⁻¹⁵ s⁻¹, meaning that the reaction is too slow to occur under atmospheric conditions. Likewise, the conclusion would remain the same even if a more precise approach, such as multiconformer TST, was used, as the variation would still be within the same order of magnitude for comparable systems.⁷⁰

Table 3 Single-point energy corrected energy barriers (ΔE^TS in kcal mol⁻¹) and Gibbs free energy barriers (ΔG^# in kcal mol⁻¹) of decomposition pathway (2) with their respective tunneling coefficients (κ_t) and unimolecular rate coefficients at 298 K (k_uni in s⁻¹)

System	ΔE^TS	ΔG^#	κ t	k uni
HOOOH	44.9	44.9	8.7 × 10^5	7.4 × 10^−15
CH3OOOH	43.1	43.1	1.2 × 10^4	2.0 × 10^−15
R^1-OOOH	43.7	42.9	1.6 × 10^3	3.8 × 10^−16
R^2-OOOH	43.0	43.3	2.4 × 10^3	2.9 × 10^−16
R^3-OOOH	40.6	40.8	4.0 × 10^1	3.1 × 10^−16
R^4-OOOH	40.9	42.8	4.0 × 10^3	2.9 × 10^−13
R^5-OOOH	43.6	43.8	2.3 × 10^4	1.2 × 10^−15
R^6-OOOH	42.9	43.1	6.1 × 10^1	9.6 × 10^−18
R^7-OOOH	40.9	40.8	6.8 × 10^3	5.7 × 10^−14
R^8-OOOH	41.2	41.5	7.1 × 10^3	1.7 × 10^−14

---

However, in the aqueous phase, the presence of excess water has been observed to lower the activation energies and accelerate the decomposition rate significantly.¹² This effect is due to the transition state (TS) structure shifting from an unfavorable 4-membered ring to a 6-membered ring involving a water molecule, which facilitates the non-radical decomposition of the hydrotrioxides. Berndt et al.¹² estimated the pseudo-first-order rate coefficient at 100% RH at 298 K to be about 10⁻¹⁵ s⁻¹, inferring that the gas-phase decomposition into alcohol and singlet oxygen, both with or without water catalysis, is highly unlikely to be significant under atmospheric conditions. This conclusion is consistent with both our study and the experimental findings of Assaf et al.²⁸ and Caravan et al.³³ In contrast, Müller et al.²⁹ suggested that pathway (2) might still play a major role, particularly for CH₃OOOH, which could act as a key precursor for the formation of atmospheric methanol. Building upon the hypothesis by Müller et al.²⁹ and contrasting high energy barriers of this reaction pathway (2) (see Table 3), we study an alternate reaction channel for the formation of alcohol proceeded via product complex (PC) of [RO⋯HO₂], from the trioxide moiety, succeeded by the intermolecular transfer of hydrogen. The detailed mechanism of this channel and its energetics are described below.

Formation of alcohol and triplet oxygen from the product complex. As seen in Table 4, a significant isomer dependence was observed in the energetics of the complex H-shift channel. Compared to CH₃OOOH with its experimentally observed alcohol yield of 7%, all ISOPOOOH systems had higher barriers of ROH formation relative to the trioxide ground state, and almost all had higher barriers relative to the RO⋯HO₂ complex. However, the most interesting energy comparison in terms of alcohol yields is perhaps that between the TS and the free RO and HO₂ radicals, as this energy difference drives the competition between reaction channels (1) and (2). Based on these results we would expect R⁷-OOOH, R⁸-OOOH, R²-OOOH, and possibly R³-OOOH to have larger alcohol yields compared to CH₃OOOH.

Table 4 Energetics of reaction channel 2 (ROH + O₂) for all the systems except R⁵-OOOH for which we were unable to locate a transition state. Tri: trioxide, PC: product complex (RO⋯HO₂), RP: the free radical pair, RO + HO₂. TS: H-shift transition state. Presented energies are in kcal mol⁻¹

System	E ^(RP–PC)	E ^(TS–Tri)	E ^(TS–PC)	E ^(RP–TS)
CH3OOOH	6.60	21.47	2.98	3.62
R^1-OOOH	9.32	23.31	5.84	3.48
R^2-OOOH	8.91	21.87	4.14	4.77
R^3-OOOH	9.52	22.89	5.48	4.04
R^4-OOOH	6.71	23.55	4.15	2.56
R^6-OOOH	6.39	23.45	2.99	3.40
R^7-OOOH	11.76	22.84	3.85	7.91
R^8-OOOH	7.94	23.48	3.08	4.86

---

We do not determine accurate ROH + O₂ yields from ISOPOOOH decomposition using the ab initio methods in this study, as there are a multitude of physical factors complicating these calculations. Firstly, we were unable to locate the TS of trioxide decomposition into (RO⋯HO₂) with DFT, likely due to the significant multiconfigurational character of O–O bond dissociations. Berndt et al.¹² successfully located this TS using CASPT2(14,12) for CH₃OOOH, and reported it to be 2.2 kcal mol⁻¹ below the free CH₃O and HO₂ radicals, and approximately 6 kcal mol⁻¹ higher than the (CH₃O⋯HO₂) complex. The exact height of this TS determines the amount of excess energy the (RO⋯HO₂) complex has upon formation, contributing to the competition between the dissociation and H-shift channels. Secondly, the very low energetic barrier of the H-shift relative to the (RO⋯HO₂) complex suggests that the barriers connecting various conformers of the (RO⋯HO₂) complex could affect which TS conformers are accessible. The existence of competing roaming radical reactions,⁷¹ such as HO₂ addition to the C=C moiety, cannot be neglected a priori. Thirdly, any reaction channels that exist within the (RO⋯HO₂) complex may be complicated by unimolecular decomposition or isomerization of the ISOPO alkoxy radicals,⁷² as seen in the (RO⋯OR) intermediate in RO₂ + RO₂ reactions.⁷³ While our reported energies and LC-TST rates provide a good first-order estimation of the relative ROH + O₂ yields from ISOPOOOH decomposition reactions, any of the three factors mentioned above could decisively shift the product yields one way or the other. Therefore, we suggest that experimental methods capable of isomer separation are essential to fully understand product distributions.

The potential energy surface illustrated in Fig. 7 depicts the distinguishable energetics depending on which mechanistic route it undertakes (see green and blue lines). For instance, the channel where CH₃OOOH undergoes decomposition pathway (1) and pathway (2), respectively via product complex (CH₃O⋯HO₂) on the triplet surface is shown to have remarkable stabilized products. The energetics of this particular channel (green and red lines) are shown in Table 4. Interestingly, in the case of pathway (2), there lies a stark difference in barrier height (>20 kcal mol⁻¹) between ^ATS(II) and ^BTS(II), where A and B represent decomposition from the trioxide system and product complex, respectively. A similar trend can also be observed consistently in the case of larger organic isoprene-derived hydrotrioxides, see Tables 3 and 4. The DFT optimized transition state structures, ^BTS(II) for all the studied systems, except R⁵-OOOH, are presented in Fig. 6.

Fig. 6 DFT optimized transition state structures of the decomposition reaction channel from the product complex (PC) of hydrotrioxides forming respective alcohol and triplet state O₂. Color coding: grey is carbon, red is oxygen, and white is hydrogen.

Fig. 7 Potential energy surface for CH₃OOOH decomposition reactions. DLPNO-corrected electronic energies (in kcal mol⁻¹) relative to hydrotrioxide based on the DFT geometries calculated at ωB97X-D3/6-31+G*. Note: ^ATS(II) and ^BTS(II) represent the transition states of decomposition pathway (2) from A, reactant hydrotrioxide (blue line) and B, product complex (green line). Color coding: grey is carbon, red is oxygen, and white is hydrogen.

3.2 Cluster formations

The Gibbs binding free energies of clusters are calculated as the difference between the Gibbs free energies of the cluster and its monomers. We investigated the cluster formation capabilities of ROOOH with several atmospherically relevant molecules. They are categorized as (a) acidic; sulfuric acid (SA), formic acid (FA), nitric acid (NA), (b) basic; ammonia (NH₃), methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA) and (c) neutral; water (H₂O).

3.2.1 Formation of ROOOH-cluster. In Fig. 8, the global minimum molecular structure of studied clusters formed between ROOOH and other molecules are shown, and their Gibbs free energies are listed in Table 5. The DFT-calculated formation free energies for each cluster are provided in the ESI.† The observed trend in the binding affinities among these monomeric units suggests that ROOOH has a strong preference for forming clusters, following the order: acid > base > neutral molecules. For clustering with acidic molecules, the cluster formation between formic acid and ROOOH is found to be the most favorable with a reaction-free energy of −10.1 kcal mol⁻¹, followed closely by sulfuric acid with a value of −9.8 kcal mol⁻¹, both involving three hydrogen bonds. In contrast, although nitric acid has higher acidity than formic acid, its cluster formation free energy with ROOOH is lower at −5.4 kcal mol⁻¹ due to the presence of solely one hydrogen bond. The range of Gibbs binding free energies for these clusters with acidic molecules indicates that the binding affinity is influenced by the number of intermolecular hydrogen bonds formed. The clusters formed between basic molecules and trioxide moieties exhibit a single hydrogen bond, specifically between the nitrogen atom of the base and the hydrogen atom of the trioxide molecule. However, the Gibbs binding free energies are proportional to the basicity of the participating molecule. For instance, TMA which has the highest basicity among amines in the gas phase has the strongest bonding with the trioxide molecule with a free energy value of −7.1 kcal mol⁻¹, followed by DMA (−6.9 kcal mol⁻¹), MA (−6.2 kcal mol⁻¹) and ultimately ammonia with the lowest value of −5.2 kcal mol⁻¹. The presence of two inter-molecular hydrogen bonds concerning the self-clustering of ROOOH molecules results in free binding energies of −5.2 kcal mol⁻¹. Similar clustering trends are also observed in the case where a dimeric unit of small atmospheric-relevant molecules, as categorized above, forms a cluster with either ROOOH or CH₃OOOH molecules. The energetics and molecular structures of these larger clusters are provided in the ESI† of this manuscript.

Fig. 8 Global minimum molecular structure of studied clusters formed between ROOOH and H₂O, NH₃, MA, DMA, TMA, SA, FA, NA, or self-clustering calculated at the ωB97X-D/6-31++G** level of theory. Color coding: grey is carbon, red is oxygen, blue is nitrogen, yellow is sulfur and white is hydrogen.

Table 5 DLPNO-corrected Gibbs free binding energy (ΔG^Cluster in kcal mol⁻¹) at 298 K at 1 atm of ROOOH with atmospheric relevant molecules. Note: MA: methylamine (CH₃NH₂), DMA: dimethylamine ((CH₃)₂NH), TMA: trimethylamine ((CH₃)₃N), SA: sulfuric acid (H₂SO₄), NA: nitric acid (HNO₃), and FA: formic acid (HCOOH)

Cluster type	ΔG^Cluster
Water	−0.99
NH3	−5.23
MA	−6.22
DMA	−6.98
TMA	−7.14
SA	−9.87
FA	−10.18
NA	−5.37
Dimer	−5.23

---

Overall, the observed Gibbs binding energies between various atmospheric vapors and hydrotrioxides infer that it is very unlikely to drive clustering formation in the gas-phase. In addition to Gibbs free binding energies, the atmospheric concentrations of participating vapors are important in determining their clustering potential. Consequently, it is challenging to define a specific free energy threshold that would result in evaporation rates lower than collision rates. However, for atmospheric vapors of concentrations in the ppt range, a Gibbs free binding energy below −12 kcal mol⁻¹ at 298 K is generally required to lead to clusters with a possibility to grow,^25,74–76 which is not the case in our clustering results of organic hydrotrioxides with small atmospheric vapors. Nonetheless, at a lower temperature, the Gibbs binding energy also gets lower. For particle growth, continuous collisions with available vapors are essential to form larger clusters. However, at lower temperatures such as the upper troposphere, collision frequency reduces, and even a highly negative ΔG does not necessarily lead to significant particle formation rates. Moreover, Gibbs free energies at T = 298 K are reasonably representative of the conditions most relevant for SOA formation.⁷⁷ Previous experimental findings shed light on the participation of oxygenated organic compounds in the initial steps of new particle formation.^78,79 The reason for this event, could be there are additional mechanisms, especially via ion-induced⁸⁰ or covalent interactions that are overlooked when studying cluster formation. Therefore, to gain a deeper understanding of cluster formation, it is recommended to investigate cluster-phase chemical reactions involving oxygenated organic compounds, such as hydrotrioxides, in addition to their non-covalent interactions.

3.2.2 Comparison of clustering abilities with hydrotrioxide, hydroperoxyl and hydroxyl moieties. While it is clear that CH₃OH, CH₃OOH, and CH₃OOOH cannot form stable clusters under atmospheric conditions, we can still compare their cluster formation energies with small nucleation precursors. This comparison aims to assess whether trioxides form stronger or weaker interactions with acids, bases, and neutral compounds than the corresponding hydroperoxides or alcohols. The molecular structures of various studied clusters with other atmospherically relevant molecules are shown in Fig. 9 and their Gibbs free binding energies are listed in Table 6.

Fig. 9 Global minimum molecular structure of studied clusters formed between CH₃-OH/OOH/OOOH and trimethylamine (TMA), ammonia (NH₃), water, formic acid (FA), or sulfuric acid (SA), respectively calculated at the ωB97X-D/6-31++G** level of theory. Color coding: grey is carbon, red is oxygen, blue is nitrogen, yellow is sulfur and white is hydrogen.

Table 6 DLPNO-corrected Gibbs free binding energy (ΔG^Cluster in kcal mol⁻¹) at 298 K at 1 atm of CH₃OH, CH₃OOH and CH₃OOOH with atmospheric relevant molecules. Note: MA: methylamine (CH₃NH₂), DMA: dimethylamine ((CH₃)₂NH), TMA: trimethylamine ((CH₃)₃N), SA: sulfuric acid (H₂SO₄), NA: nitric acid (HNO₃), and FA: formic acid (HCOOH)

Cluster type	CH3OH	CH3OOH	CH3OOOH
Water	3.34	3.40	2.51
NH3	2.32	1.05	0.45
MA	0.71	1.03	−0.52
DMA	1.63	0.98	−1.19
TMA	0.39	0.32	−1.43
SA	−3.19	−2.39	−2.65
NA	−0.68	0.38	0.58
FA	−3.82	−4.49	−4.76
Dimer	2.27	2.09	1.67

---

The Gibbs free binding energies of CH₃-OH/OOH/OOOH clusters with water or for self-clustering are positive in all cases, with the smallest positive values observed for CH₃OOOH. In interactions with basic molecules, cluster formation capabilities show proportionality with an increase in the number of oxygen atoms, progressing from CH₃OH to CH₃OOOH. This trend indicates that hydrotrioxides may form stronger clusters with bases than hydroperoxides or alcohols. On vice versa, with the acidic molecules, the range of Gibbs free formation energies suggests that the binding capabilities decrease with an increase in the number of oxygen atoms from CH₃OH to CH₃OOOH (except in the case of clustering with formic acid). Consistent with the trends observed in clustering with isoprene-derived hydrotrioxides, the binding capabilities improve with stronger bases (NH₃ < MA < DMA < TMA, in both CH₃OOH/OOOH). Moreover, these outcomes demonstrate that, besides the number of hydrogen bonding sites, factors such as molecular rearrangement and the size of substituent groups bonded to oxygen atoms significantly impact the interaction strength required for new particle formation.

4 Conclusion

In this work, we investigated the decomposition pathways of isoprene-derived hydrotrioxides, as well as those of HOOOH and CH₃OOOH as model systems. Based on the quantum chemical calculations conducted, the barrierless dissociation reaction into the corresponding alkoxy and hydroperoxyl radicals outcompetes the other pathways. The rate coefficient of pathway (1) is on the order of 10⁻¹ s⁻¹, indicating that this isoprene-derived hydrotrioxide decomposition channel is reasonably fast under atmospherically relevant conditions. Due to the 7% yield of CH₃OH in the experiment by Caravan et al.,³³ we studied the detailed mechanism of pathway (2), which involves dissociation into an alcohol and molecular oxygen. Our study demonstrates that even for larger isoprene-derived hydrotrioxides, the transition state arising from the product complex (RO⋯HO₂) has half the barrier energy compared to that arising directly from the trioxide (ROOOH) moiety. This finding is in agreement with the prediction of Müller et al.²⁹ of the methanol formation mechanism, despite their overestimation of the yield. Moreover, we also briefly compared the alcohol yield among different isomers of isoprene-derived hydrotrioxide, and also with that of CH₃OOOH based on the energy difference that drives the competition between pathway (1) and pathway (2). We expect that R²-OOOH, R⁷-OOOH, R⁸-OOOH and possibly R³-OOOH will have a higher alcohol yield relative to the CH₃OOOH. It should be noted that, in this work, we produce accurate transition states of this H-shift via the product complex formation for larger hydrotrioxides, using a cost-effective quantum chemical method.

We conducted a small benchmarking study to elucidate the accurate rates for pathway (1), especially for CH₃OOOH employing two approaches, using decomposition energies calculated at various quantum chemical methods. This benchmark analysis reveals that the discrepancies in the theoretical rates of pathway (1) when compared to the experimental rates were mainly due to the systemic error in DFT optimization. This is useful information for future computational studies regarding the gas phase kinetics of hydrotrioxides.

Furthermore, due to the reasonable stability of this isoprene-derivative of hydrotrioxides and their comparable lifetime in the atmosphere as estimated in a previous study,¹² we performed cluster formation studies with other relevant atmospheric molecules consisting of acids, bases, water, and the ROOOH dimer. It is evident that small oxygenated organic compounds cannot form hydrogen-bonded clusters with other small vapor molecules that are stable against evaporation under atmospheric conditions. However, we can capture the trends by comparing the interactions between different functional groups. We found that hydrotrioxides form stronger bound complexes with bases as well as sulfuric acid–ammonia clusters compared to corresponding alcohols and hydroperoxides. However, hydrotrioxides are unlikely to drive atmospheric new-particle formation due to their relatively weak binding with other atmospheric vapors. Overall, this infers that the decomposition process acts as a dominant factor over clustering reactions in the atmosphere. Accurately identifying the reaction mechanisms of ROOOH chemistry is crucial for advancing our understanding of atmospheric oxidation chemistry and aerosol formation.

Author contributions

EA performed the calculations and wrote the manuscript. LF carried out the comparison for “Benchmarking of computational methods” in Section 3.1.1, as well as performed calculations for the “formation of alcohol and triplet oxygen from product complex” in Section 3.1.2, for which he contributed to writing these sections. TGA assisted with the MESMER calculations and data interpretation. GH helped with the kinetics calculations. BNF contributed to the analysis and review. NM conceptualized this research work, was involved in data interpretation, and assisted with writing. All authors proofread this manuscript.

Data availability

All the calculated output files (at various levels of theories) corresponding to the three decomposition pathways and clustering studies that support the findings of our study will be available in the Zenodo repository.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Academy of Finland (grant no. 347775) for financial support and the CSC-IT Center for Science in Espoo, Finland, for computational resources. Benjamin acknowledges and thanks Carlsberg for their Internationalisation Fellowship CF22-0754. We also thank Siddharth Iyer and Theo Kurtén for their thoughtful discussion on the decomposition pathways related to organic hydrotrioxides.

Notes and references

1. R. Atkinson and J. Arey, Atmos. Environ., 2003, 37, 197–219.
2. A. Guenther, X. Jiang, C. L. Heald, T. Sakulyanontvittaya, T. A. Duhl, L. Emmons and X. Wang, Geosci. Model Dev., 2012, 5, 1471–1492.
3. D. Medeiros, M. Blitz, L. James, T. Speak and P. Seakins, J. Phys. Chem. A, 2018, 122, 7239–7255.
4. T. Berndt, N. Hyttinen, H. Herrmann and A. Hansel, Commun. Chem., 2019, 2, 21.
5. K. H. Møller, K. H. Bates and H. G. Kjaergaard, J. Phys. Chem. A, 2019, 123, 920–932.
6. J. Peeters, T. L. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939.
7. P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes and M. D. Smarte, et al. , Chem. Rev., 2018, 118, 3337–3390.
8. S. Wang, M. Riva, C. Yan, M. Ehn and L. Wang, Environ. Sci. Technol., 2018, 52, 12255–12264.
9. K. Sindelarova, C. Granier, I. Bouarar, A. Guenther, S. Tilmes, T. Stavrakou, J.-F. Müller, U. Kuhn, P. Stefani and W. Knorr, Atmos. Chem. Phys., 2014, 14, 9317–9341.
10. F. E. Stary, D. E. Emge and R. W. Murray, J. Am. Chem. Soc., 1976, 98, 1880–1884.
11. M. Zarth and A. De Meijere, Chem. Ber., 1985, 118, 2429–2449.
12. T. Berndt, J. Chen, E. R. Kjærgaard, K. H. Møller, A. Tilgner, E. H. Hoffmann, H. Herrmann, J. D. Crounse, P. O. Wennberg and H. G. Kjaergaard, Science, 2022, 376, 979–982.
13. K. H. Bates and D. J. Jacob, Atmos. Chem. Phys., 2019, 19, 9613–9640.
14. B. H. Lee, S. Iyer, T. Kurtén, J. G. Varelas, J. Luo, R. J. Thomson and J. A. Thornton, Environ. Sci.: Atmos., 2023, 3, 399–407.
15. V. Loukonen, T. Kurtén, I. Ortega, H. Vehkamäki, A. A. Padua, K. Sellegri and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 4961–4974.
16. M. Kulmala, L. Pirjola and J. M. Mäkelä, Nature, 2000, 404, 66–69.
17. M. Liu, N. Myllys, Y. Han, Z. Wang, L. Chen, W. Liu and J. Xu, Front. Ecol. Evol., 2022, 10, 875585.
18. S. Chee, K. Barsanti, J. N. Smith and N. Myllys, Atmos. Chem. Phys., 2021, 21, 11637–11654.
19. T. Olenius, O. Kupiainen-Määttä, I. Ortega, T. Kurtén and H. Vehkamäki, J. Chem. Phys., 2013, 139, 8.
20. Y. Xu, A. B. Nadykto, F. Yu, J. Herb and W. Wang, J. Phys. Chem. A, 2010, 114, 387–396.
21. A. B. Nadykto, F. Yu, M. V. Jakovleva, J. Herb and Y. Xu, Entropy, 2011, 13, 554–569.
22. M. Ehn, J. A. Thornton, E. Kleist, M. Sipilae, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I.-H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurtén, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard, M. Canagaratna, M. Dal Maso, T. Berndt, T. Petäjä, A. Wahner, V.-M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479.
23. N. Myllys, T. Olenius, T. Kurtén, H. Vehkamäki, I. Riipinen and J. Elm, J. Phys. Chem. A, 2017, 121, 4812–4824.
24. J. Elm, N. Myllys, N. Hyttinen and T. Kurten, J. Phys. Chem. A, 2015, 119, 8414–8421.
25. J. Elm, N. Myllys and T. Kurtén, J. Phys. Chem. A, 2017, 121, 4578–4587.
26. J. Elm, N. Myllys, J.-N. Luy, T. Kurten and H. Vehkamaki, J. Phys. Chem. A, 2016, 120, 2240–2249.
27. T. Kurten, K. Tiusanen, P. Roldin, M. Rissanen, J.-N. Luy, M. Boy, M. Ehn and N. Donahue, J. Phys. Chem. A, 2016, 120, 2569–2582.
28. E. Assaf, C. Schoemaecker, L. Vereecken and C. Fittschen, Int. J. Chem. Kinet., 2018, 50, 670–680.
29. J.-F. Müller, Z. Liu, V. S. Nguyen, T. Stavrakou, J. N. Harvey and J. Peeters, Nat. Commun., 2016, 7, 13213.
30. W. Lei, R. Zhang, W. S. McGivern, A. Derecskei-Kovacs and S. W. North, J. Phys. Chem. A, 2000, 105, 471–477.
31. F. Paulot, J. D. Crounse, H. G. Kjaergaard, J. H. Kroll, J. H. Seinfeld and P. O. Wennberg, Atmos. Chem. Phys., 2009, 9, 1479–1501.
32. A. P. Teng, J. D. Crounse and P. O. Wennberg, J. Am. Chem. Soc., 2017, 139, 5367–5377.
33. R. L. Caravan, M. A. H. Khan, J. Zádor, L. Sheps, I. O. Antonov, B. Rotavera, K. Ramasesha, K. Au, M.-W. Chen and D. Rösch, et al. , Nat. Commun., 2018, 9, 4343.
34. Y. Liu, L. Chen, D. Chen, W. Wang, F. Liu and W. Wang, Chem. Res. Chin. Univ., 2017, 33, 623–630.
35. J. M. Anglada and A. Solé, Phys. Chem. Chem. Phys., 2018, 20, 27406–27417.
36. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
37. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
38. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
39. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
40. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
42. Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101.
43. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
44. N. Myllys, J. Elm, R. Halonen, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 621–630.
45. D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539.
46. F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606.
47. Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272.
48. F. Neese, J. Comput. Chem., 2003, 24, 1740–1747.
49. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
50. D. Bykov, T. Petrenko, R. Izsak, S. Kossmann, U. Becker, E. Valeev and F. Neese, Mol. Phys., 2015, 113, 1961–1977.
51. B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109.
52. F. Neese, J. Comput. Chem., 2022, 1–16.
53. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
54. F. Neese, Chem. Phys. Lett., 2000, 325, 93–98.
55. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
56. T. Kurtén, K. H. Møller, T. B. Nguyen, R. H. Schwantes, P. K. Misztal, L. Su, P. O. Wennberg, J. L. Fry and H. G. Kjaergaard, J. Phys. Chem. Lett., 2017, 8, 2826–2834.
57. Y. Georgievskii and S. J. Klippenstein, J. Chem. Phys., 2005, 122, 194103.
58. C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225.
59. L. S. Tee, S. Gotoh and W. E. Stewart, Ind. Eng. Chem. Fundam., 1966, 5, 356–363.
60. K. Joback and R. Reid, Chem. Eng. Commun., 1987, 57, 233–243.
61. J. Kubečka, V. Besel, T. Kurtén, N. Myllys and H. Vehkamäki, J. Phys. Chem. A, 2019, 123, 6022–6033.
62. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181.
63. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
64. N. Myllys, J. Elm and T. Kurtén, Comput. Theor. Chem., 2016, 1098, 1–12.
65. S. Iyer, M. P. Rissanen and T. Kurtén, J. Phys. Chem. Lett., 2019, 10, 2051–2057.
66. Y. Liu, L. Chen, D. Chen, W. Wang, F. Liu and W. Wang, Chem. Res. Chin. Univ., 2017, 33, 623–630.
67. E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 10–18.
68. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
69. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054105.
70. D. Pasik, S. Iyer and N. Myllys, Phys. Chem. Chem. Phys., 2024, 26, 2560–2567.
71. S. J. Klippenstein, Y. Georgievskii and L. B. Harding, J. Phys. Chem. A, 2011, 115, 14370–14381.
72. P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes, M. D. Smarte, J. M. St Clair, A. P. Teng, X. Zhang and J. H. Seinfeld, Chem. Rev., 2018, 118, 3337–3390.
73. O. Perakyla, T. Berndt, L. Franzon, G. Hasan, M. Meder, R. R. Valiev, C. D. Daub, J. G. Varelas, F. M. Geiger and R. J. Thomson, et al. , J. Am. Chem. Soc., 2023, 145, 7780–7790.
74. J. Elm, J. Phys. Chem. A, 2019, 123, 3170–3175.
75. N. Myllys, J. Kubečka, V. Besel, D. Alfaouri, T. Olenius, J. N. Smith and M. Passananti, Atmos. Chem. Phys., 2019, 19, 9753–9768.
76. A. N. Pedersen, Y. Knattrup and J. Elm, Aerosol Res., 2024, 2, 123–134.
77. W. C. Porter, J. L. Jimenez and K. C. Barsanti, ACS Earth Space Chem., 2021, 5, 2380–2397.
78. M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I.-H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurtén, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard, M. Canagaratna, M. D. Maso, T. Berndt, T. Petäjä, A. Wahner, V.-M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479.
79. F. Riccobono, S. Schobesberger, C. E. Scott, J. Dommen, I. K. Ortega, L. Rondo, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, A. Downard, E. M. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, A. Hansel, H. Junninen, M. Kajos, H. Keskinen, A. Kupc, A. Kürten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, T. Nieminen, A. Onnela, T. Petäjä, A. P. Praplan, F. D. Santos, S. Schallhart, J. H. Seinfeld, M. Sipilä, D. V. Spracklen, Y. Stozhkov, F. Stratmann, A. Tomé, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, D. Wimmer, K. S. Carslaw, J. Curtius, N. M. Donahue, J. Kirkby, M. Kulmala, D. R. Worsnop and U. Baltensperger, Science, 2014, 344, 717–721.
80. J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Tröstl, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A.-K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kürten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Peräkylä, F. Piel, T. Petäjä, A. P. Praplan, K. Pringle, A. Rap, N. A. D. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipilä, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tomé, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Nature, 2016, 533, 521–526.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04329d

---