Grain size modulation to optimize the wave-absorbing properties of FeSiCr alloy micropowder
Received
19th June 2024
, Accepted 26th November 2024
First published on 27th November 2024
Abstract
In this paper, the ball-milled flake FeSiCr alloy is subjected to a vacuum annealing temperature between 300 and 500 °C. The results show that the appropriate heat treatment temperature increases the average grain size of the material, eliminates defects and internal stresses, and improves the complex permeability of the material. The optimum wave-absorbing performance of the material is achieved when the heat treatment temperature is 400 °C with the minimum reflectivity RLmin reaching −56.33 dB at a frequency f of 3.97 GHz, corresponding to the thickness of the wave-absorbing coating, d = 4.0 mm. This work provides an important reference value for application of FeSi-based alloy micropowder soft magnetic materials in the field of microwave absorption.
1. Introduction
In recent years, electronic information technology has flourished with the rapid progress of wireless communication technology.1 At present, more and more electronic devices are being used in a wide range of areas, and the ensuing increasingly serious problem of electromagnetic radiation pollution has become a focus of attention.2–5 The wave absorbing materials used for electromagnetic protection are the key to solving the problem of electromagnetic radiation pollution. Currently, wave-absorbing materials are widely used in civil, commercial and military fields, and have become a hotspot for researchers.6–9
FeSi-based soft magnetic alloys have high Curie temperatures, good thermal stability and high permeability, and have great potential in high-temperature magnetic wave-absorbing materials.10,11 The flattening of spherical FeSi-based alloys by a ball milling process is an effective means to further improve the electromagnetic properties of the materials, but the defects and internal stresses in the materials after ball milling unfavorably influence the microwave permeability of the materials.12 Reportedly, the annealing process can improve the soft magnetic properties of mechanically alloyed nanocrystalline materials by increasing the average grain size of the materials and eliminating defects and internal stresses.12–18 For example, Gong et al.11 carried out vacuum annealing of flaky Fe–Co–Zr alloys prepared by aerosolization and mechanical ball milling at different temperatures, and the results showed that the average grain size increased and the internal strain decreased with the increase in annealing temperature. The saturation flux density of the annealed samples decreased slightly and the coercivity decreased significantly. The annealed samples depicted larger values of μ′ compared to the ball-milled samples, while the maximum value of μ′′ increased with increasing temperature. This study showed that the appropriate annealing temperature helped to improve the microwave absorbing properties of the metal flakes. Ding et al.17 subjected the flaky nanocrystalline structured Fe–Si powders obtained by mechanical alloying (ball milling) to vacuum heat treatment at 200–700 °C, and the results showed that the annealing process at the appropriate temperature (450 °C) could improve the magnetic properties of mechanically alloyed nanocrystalline materials by eliminating the internal stresses and increasing the average grain size. Li et al.19 made flake nanocrystalline structured FeSiAl alloys using a high-energy ball milling method and vacuum annealing at 400–800 °C under a N2 atmosphere, and the results showed that the annealing heat treatment eliminated the internal defects and residual stresses of the flake nanocrystalline structured FeSiAl alloys, and increased the magnetic permeability. However, when annealed at a temperature of 600 °C or higher, N2 reacts with FeSiAl and nitrides are generated on the surface of the samples, the reaction process becomes more prominent with the increase in temperature, and the nitrides impede the movement of free electrons and lower the dielectric constant. Zhou et al.20 vacuum heat-treated lamellar FeSiAl nano-micropowder obtained from ball milling at 573 K to improve the grain size and magnetic permeability of the material.
This research work comparatively investigates the effects of heat treatment temperature on the surface morphology, grain size, electromagnetic properties and wave-absorbing properties of flaky FeSiCr nanopowders by vacuum annealing of ball-milled flaky FeSiCr soft magnetic alloy micropowder at 300–500 °C. The study of grain growth and the changing law of electromagnetic properties of FeSi-based nanocrystalline wave-absorbing materials at high temperature has an important reference value for the development of wave-absorbing materials.
2. Experimental
The ball-milled FeSiCr micropowder (marked as S0) (Fe-84.8 wt% Si-5.3 wt% Cr-9.9 wt%) (Hunan HuaLiu New Material Co., Ltd) was placed in a tube furnace and sealed, the vacuum of the tube furnace was then evacuated to 10−1 Pa with a mechanical pump, and then argon was introduced at the same pressure inside and outside the chamber. The argon gas was kept in circulation at a constant flow rate, the heating rate was 5 °C min−1, the heat treatment holding time was 3 h, and the heat treatment temperatures were 300 °C, 400 °C, and 500 °C, marked as S1, S2 and S3, respectively. The phase structure of the samples was analyzed using an X-ray diffractometer Pana lytic Empyrean with Cu Kα radiation (Cu Kα radiation, scanning angle 5–90°, room temperature). The morphological structure of the samples was characterized by scanning electron microscopy (SEM-FEI MLA650F, USA). The electromagnetic parameters were measured by a vector network analyzer (3672B-S, CETC, China) after 50 wt% of the sample was homogeneously mixed with 50 wt% of paraffin wax and formed into a coaxial ring (Φouter = 7.0 mm, Φinner = 3 mm, thickness = 3 mm).
3. Results and discussion
Fig. 1(a) shows the XRD patterns of samples S0–S3. As shown, the characteristic peaks of samples S0–S3 at 2θ = 44.7°, 65.2° and 82.5° correspond to the (110), (200), and (211) crystal planes of the Fe8SiCr phase, respectively (JCPDS card no. 65-5584). Compared with the non-vacuum annealing sample S0, the diffraction peak intensities of samples S1–S3 gradually increase, and the half-peak widths narrow as the vacuum annealing temperature is increased from 300 °C to 500 °C. This is attributed to the annealing effect of the vacuum annealing, which repaired the internal crystal structure of the lamellar FeSiCr while eliminating the internal stresses and defects of the lamellar FeSiCr alloy micropowder.21,22Fig. 1(b) shows the average grain size plots of the S0–S3 samples. In this case, the average grain size of the FeSiCr alloy micropowder was calculated according to Scherrer's formula and Hall–Williamson's formula:23,24| | D = kλ/(β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (1) |
| | β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = (kλ/D) + 4ε θ = (kλ/D) + 4ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
where β is the half-peak width, k is the Scherrer's constant of 0.89, λ is the X-ray wavelength taken as 0.154 nm, θ is the diffraction angle, and D is the average grain size. From Fig. 1(b), it can be seen that the grain sizes of samples S1–S3 increased after vacuum heat treatment compared to sample S0. Along with the increase in grain size, the lattice distortion degree of the samples decreases, the orderliness increases, and the internal stress decreases.23
 |
| | Fig. 1 (a) XRD pattern and (b) grain size map of the S0–S3 samples. | |
Fig. 2 (a)–(d) show the SEM images of samples S0–S3, respectively. Fig. 2(a)–(d) show that the surface morphology of the FeSiCr micropowder has no obvious change with the increase in the vacuum annealing temperature, and it still presents a flaky morphology. This indicates that the vacuum annealing did not have much effect on the micro-morphology of the samples. In order to distinguish whether the phases of other oxides were generated during the vacuum annealing, TEM was used to characterize sample S2. Fig. 2(e) and (f) show the TEM morphology of sample S2, which can be seen to be flaky. Fig. 2(g) shows the HRTEM image of the area shown in the orange box in (f). As shown, the measured lattice stripe spacings of 0.144 nm and 0.116 nm correspond to the (200) and (211) crystal planes of the Fe8SiCr phase, respectively. Fig. 2(i)–(k) show the EDS mapping of sample S2 in the field of view of Fig. 2(h), which corresponds to the three elements of Fe, Si and Cr, respectively, and the three elements can be seen uniformly distributed on the FeSiCr surface. In general, the original morphology of the samples was maintained during the vacuum annealing and no other oxide phases were produced.
 |
| | Fig. 2 (a)–(d) SEM images of the S0–S3 samples; (e)–(f) TEM, (g) HRTEM, and (h)–(k) EDS element mapping images of the S3 samples, respectively. | |
Fig. 3(a)–(d) show the electromagnetic parameters of samples S0–S3 in the frequency range of 2–18 GHz, and Fig. 3(e) and (f) show the M–H plot and eddy current loss (C0) plot of samples S0–S3, respectively. From Fig. 3(a) and (b), it can be seen that the real (ε′) and imaginary (ε′′) parts of the dielectric constants of samples S0–S3 decrease with the increase in the vacuum annealing temperature. Based on the Debye relaxation theory, the complex dielectric constant εr can be expressed by eqn (3)–(5):25
| |  | (3) |
| | 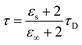 | (4) |
| |  | (5) |
where
ω is the angular frequency,
τ is the polarization relaxation time,
εs and
ε∞ denote the static permittivity and the relative permittivity in the high-frequency limit, respectively,
τD is the temperature-dependent relaxation time,
k is the Boltzmann constant, and
T is the temperature. The vacuum annealing eliminates the defects and internal stresses inside the FeSiCr soft magnetic alloy micropowder during ball milling, and the inhomogeneity is weakened, which makes the free energy Δ
E value increase, and according to
eqn (3)–(5), the value of
τD increases, and thus the intrinsic electric dipole orientation polarization relaxation time
τ increases, thus causing the complex permittivity
εr to decrease.
26
 |
| | Fig. 3 Complex permittivity (a) and (b), complex permeability (c) and (d), M–H curves (e) and C0 plots (f) for the S0–S3 samples. | |
From Fig. 3(c) and (d), the μ′ and μ′′ of the heat-treated S1–S3 samples are improved compared to the sample S0. This is because the crystallization effect and stress relief brought about by the vacuum heat treatment improves the soft magnetic properties of the FeSiCr micropowder, reduces the magnetic anisotropy of the material, and enhances the overall complex permeability of the magnetic powder.27 It is noteworthy that the composite permeability of the S3 sample is reduced relative to the composite permeability of the S2 sample due to the fact that at the higher temperature, the crystallinity of the S3 sample is the highest, as can be observed from Fig. 1(b). However, excessively high crystallinity leads to an increase in grain size and a decrease in the interaction of magnetic moments, resulting in a decrease in magnetic permeability.28
Fig. 3(e) shows the hysteresis line profiles of the S0–S3 samples. The vacuum annealing enhances the saturation magnetization, Js values, of the S1–S3 samples relative to the S0 sample. Based on the magnetic domain theory, the magnetic permeability can be expressed as:29,30
where
Js is the saturation magnetization,
p is a dimensionless perfector with a value close to 1, and
k represents the effective anisotropy constant. Therefore, an enhancement in
Js leads to a concomitant enhancement in the complex permeability
μr.
Eddy current loss (C0 = μ′′(μ′)−2f−1) is a common type of magnetic loss in magnetic materials. The magnetic flux and magnetic induction strength of ferromagnetic metal in an alternating electric field will issue a corresponding change according to the law of electromagnetic induction, and this change will cause the generation of annular induced eddy currents inside the ferromagnetic metal in the direction perpendicular to the magnetic flux. The generation of eddy currents excites a magnetic field to stop the change in magnetic flux caused by the external magnetic field, and therefore, the increase in eddy current losses reduces the permeability of the ferromagnetic metal.29 In general, for the magnetic loss mechanism of wave-absorbing materials in this frequency band, eddy current loss and natural resonance dominate.31,32 Among them, when the value of C0 is constant, the magnetic loss mechanism is caused by eddy current loss; when C0 varies with frequency, natural resonance dominates.29 From Fig. 3(f), it can be seen that the C0 values of samples S1–S3 fluctuate with the frequency change in the frequency range of 2–18 GHz, which indicates that the natural resonance losses dominate the magnetic losses. The reduction of eddy current losses leads to an increase in the permeability of ferromagnetic metals, thus compared to sample S0, the heat treatment leads to a reduction in internal defects in samples S1–S3, which have an inhibitory effect on the formation of eddy currents, leading to an increase in permeability.33
According to the transmission theory, the reflectivity RL of the incident electromagnetic wave can be calculated by eqn (7) and (8):27,34
| |  | (7) |
| | RL (dB) = −20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg|(Zin − Z0)/(Zin + Z0)| lg|(Zin − Z0)/(Zin + Z0)| | (8) |
where,
f,
d and
c represent frequency, coating thickness and speed of light respectively. The smaller the RL value is, the stronger the wave-absorbing performance of wave-absorbing materials. In general, the frequency range of RL ≤ −10 dB is called the effective absorption bandwidth, and in this range, the absorption efficiency is 90%; when RL ≤ −20 dB, 99.9% of the electromagnetic wave is absorbed.
34,35Fig. 4(a)–(d) show the 3D plots of the reflection losses of samples S
0–S
3 as a function of
f and
d. From
Fig. 4(c) and (d), it is obviously observed that samples S
2 and S
3 have excellent wave-absorbing properties. Sample S
2 has RL
min = −56.33 dB at
f = 3.97 GHz,
d = 4.0 mm; sample S
3 has RL
min = −44.41 dB at
f = 3.75 GHz,
d = 4.23 mm. In order to compare the wave absorption performance of samples S
2 and S
3 more obviously, the histograms of effective absorption bandwidth (EAB) (RL ≤ −10 dB and ≤ −20 dB) at different thicknesses are calculated in this paper, as shown in
Fig. 4(e) and (f). Samples S
2 and S
3 have wide effective bandwidths in the thickness range of 1.5–2.5 mm with RL ≤ −10 dB and in the thickness range of 2.5–3.5 mm with RL ≤ −20 dB. In summary, samples S
2 and S
3 have superior microwave absorption properties in the majority of the thickness range (1.5–3.5 mm).
 |
| | Fig. 4 (a)–(d) 3D plots of reflectance relative to f and d. (e) and (f) Histograms of EAB ≤ −10 dB and EAB ≤ −20 dB for different matching thicknesses for the S0–S3 samples. | |
The electromagnetic wave loss mechanism of the material needs to be resolved next. Fig. 5(a)–(d) show the plots of dielectric loss coefficient (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δE), Cole–Cole curve, magnetic loss coefficient (tan
δE), Cole–Cole curve, magnetic loss coefficient (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δM), and attenuation constant of samples S0–S3, respectively. From Fig. 5(a), the tan
δM), and attenuation constant of samples S0–S3, respectively. From Fig. 5(a), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δE (tan
δE (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δE = ε′′/ε′) values of the S1–S3 samples after vacuum annealing decrease relative to the S0 samples, which is attributed to the fact that the reduction of the complex dielectric constant of the material makes the dielectric loss weakened as well. According to the Debye relaxation theory, a Cole–Cole semicircle represents a Debye relaxation loss process with the following expression:36–38
δE = ε′′/ε′) values of the S1–S3 samples after vacuum annealing decrease relative to the S0 samples, which is attributed to the fact that the reduction of the complex dielectric constant of the material makes the dielectric loss weakened as well. According to the Debye relaxation theory, a Cole–Cole semicircle represents a Debye relaxation loss process with the following expression:36–38
| |  | (9) |
| |  | (10) |
| |  | (11) |
where
ω (
ω = 2π
f) is the angular frequency,
τ is the polarization relaxation time, and
εs and
ε∞ denote the static permittivity and the relative permittivity in the high frequency limit, respectively. From
Fig. 5(b), it can be observed that the Cole–Cole curves of each sample appear as multiple segments in the shape of semicircles, indicating that multiple polarization relaxation processes occur under the alternating electric field. Compared to the S
0 sample, the number of Debye relaxation semicircles of the S
1–S
3 samples after vacuum annealing is reduced, which indicates the weakening of the dielectric loss of the S
1–S
3 samples.
 |
| | Fig. 5 Plots of dielectric loss (a), Cole–Cole curve (b), magnetic loss (c) and decay constant (d) for the S0–S3 samples. | |
In Fig. 5(c), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δM (tan
δM (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δM = μ′′/μ′) values of the S1–S3 samples are significantly enhanced relative to those of the S0 samples. This is because the vacuum annealing has eliminated the internal stresses and defects generated by the mechanical ball milling, improved the soft magnetic properties, reduced the magnetic anisotropy, and increased the complex permeability of the materials, which has led to an enhancement of the material's magnetic loss.
δM = μ′′/μ′) values of the S1–S3 samples are significantly enhanced relative to those of the S0 samples. This is because the vacuum annealing has eliminated the internal stresses and defects generated by the mechanical ball milling, improved the soft magnetic properties, reduced the magnetic anisotropy, and increased the complex permeability of the materials, which has led to an enhancement of the material's magnetic loss.
The magnitude of the attenuation constant (α) value is usually used to indicate the strength of the material's loss capability for electromagnetic waves, with the following expression:39
| | 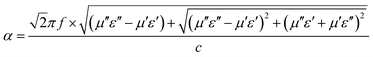 | (12) |
From Fig. 5(d), the α value of the S1–S3 samples decreases with the increase in vacuum annealing temperature, which indicates that the higher the vacuum annealing temperature, the weaker the electromagnetic wave loss ability of the FeSiCr micropowder. Sample S1 has the largest α value but relatively low wave-absorbing performance; sample S2 has the best wave-absorbing performance, but the α value is not the largest, so it is necessary to consider the effect of impedance matching on the wave-absorbing performance of the material.
To further analyze sample S2, which has the best electromagnetic wave absorption performance, the COMSOL finite element method is applied to establish the FeSiCr model,40 and simulate and analyze the surface current density (SCD) and volume loss density (VLD). From Fig. 4, the S2 sample has the best electromagnetic wave absorption performance at f = 3.97 GHz; moreover, as known from Fig. 5(d), the S2 sample has the best attenuation constant at f = 18 GHz. Therefore, we simulate the SCD and VLD of sample S2 at f = 3.97 GHz and f = 18 GHz. As shown in Fig. 6, by comparing the left and right SCD distributions and VLD values at f equal to 3.97 GHz and 18 GHz, respectively, we found that the surface current density of sample S2 is the smallest at f = 3.97 GHz, indicating the optimal impedance matching performance.41 In addition, we also analyzed the VLD maps at f = 3.97 GHz and 18 GHz. As shown in Fig. 6(c) and (d), the bulk loss density of sample S2 at f = 18 GHz is much higher than that at f = 3.97 GHz, which is the same as the variation in the attenuation constant in Fig. 5(d). Impedance matching is the key to determining the wave-absorbing performance of materials. However, the excellent wave-absorbing performance is not only related to the impedance matching but also to the attenuation constant, and both are indispensable.
 |
| | Fig. 6 (a) SCD of S2 at f = 3.97 GHz, (b) SCD of S2 at f = 18 GHz, (c) VLD of S2 at f = 3.97 GHz, and (d) VLD of S2 at f = 18 GHz. | |
Eqn (13)–(15) are the |Δ| function equations, and the impedance matching can be evaluated by the |Δ| value; a smaller |Δ| value indicates the better impedance matching, and the region of |Δ| ≤ 0.4 is usually regarded as the effective impedance matching.42,43 The variation in the |Δ| function for the S0–S3 samples is obtained by calculation as shown in Fig. 7(a)–(d).
| |  | (13) |
| |  | (14) |
| |  | (15) |
where
f is the frequency,
d is the thickness of the wave-absorbing coating,
c is the speed of light,

is the real part of the permittivity,

is the real part of the magnetic permeability,
δe is the tangent of the dielectric loss, and
δm is the tangent of the magnetic loss.
Fig. 7(e) shows pie charts of the percentage area of the region with |
Δ| ≤ 0.4 obtained from the calculation. Sample S
1 has the highest
α value and the strongest attenuation ability, but its |
Δ| ≤ 0.4 area is the smallest, and its impedance matching is poor, while sample S
3 has the largest area of |
Δ| ≤ 0.4 but has the smallest
α value, and sample S
2 has the optimal reflective loss among all the samples and relatively high
α, which is also a good attenuation of the electromagnetic wave. Meanwhile, the impedance matching of sample S
2 is not the best among all the samples, however, the moderate impedance matching makes the three of them reach a balance within the material, which leads to the optimized wave-absorbing performance of sample S
2. This suggests that a balance between the electromagnetic wave attenuation ability and impedance matching is needed when the electromagnetic parameters of the material are regulated to improve the wave-absorbing performance.
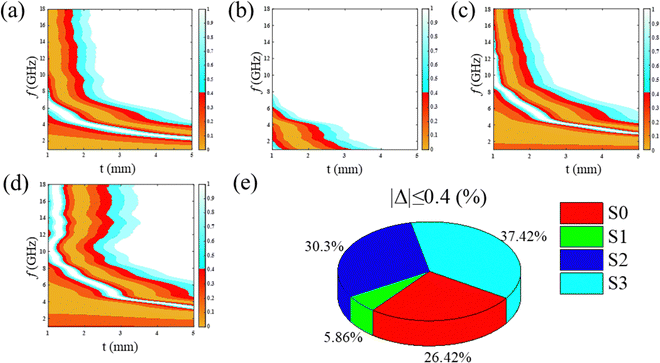 |
| | Fig. 7 Impedance matching plots for samples S0–S3 (a)–(d) and pie charts of the percentage area of the region with |Δ| ≤ 0.4 (e). | |
Fig. 8 shows the flow chart of heat treatment of FeSiCr and the microwave absorption mechanism. After vacuum annealing, the internal stresses of the material are eliminated, defects are reduced, and magnetic losses are increased. At a simultaneous time, a suitable impedance matching of FeSiCr was ensured, enabling the effective absorption and loss of the incident electromagnetic waves. In addition, due to the enhanced soft magnetic properties of the materials, the magnetic loss mechanism is increased, and it can be seen in Fig. 3(f) that natural resonance dominates in the magnetic loss mechanism. In summary, the synergistic effect of interfacial polarization, magnetic loss and natural resonance increases the microwave absorption performance of the FeSiCr soft magnetic alloy.
 |
| | Fig. 8 The thermal treatment flow chart of FeSiCr and the EMW absorption mechanism. | |
4. Conclusions
Vacuum annealing at 300 °C, 400 °C and 500 °C was carried out on the flaky FeSiCr micropowder, respectively. The results show that the FeSiCr magnetic powders eliminated the residual internal stresses and defects of the materials after vacuum annealing (300–500 °C), so that the crystallinity of the S1–S3 samples gradually became better. With the increase in heat treatment temperature, the average grain size of the FeSiCr magnetic powder wave-absorbing materials increases, the macroscopic morphology remains stable, and the magnetic permeability is enhanced. The material exhibits the optimized wave-absorbing performance when the heat treatment temperature is 400 °C; RLmin = −56.33 dB at f = 3.97 GHz, which corresponds to the thickness of wave-absorbing coating, d = 4.0 mm. Vacuum annealing at the appropriate temperature can increase the permeability, balance the electromagnetic wave attenuation ability and impedance matching of the material, and thus achieve the enhancement of wave-absorbing performance. This research work provides a certain reference value for the application of FeSi-based soft magnetic alloy micropowder in the field of wave-absorbing materials.
Author contributions
Weiwei Dong and Wenmiao Zhang: conceptualization, methodology, investigation, writing – original draft preparation, funding acquisition. Lei Wang: writing – review & editing, funding acquisition, supervision. Sajjad Ur Rehman: experiments. Yifeng Hu, Tongxiang Liang, Changcai Chen, Jianping Zou: experiments, data acquisition. Haiping Zou: supervision, writing – review & editing, Funding acquisition.
Data availability
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of interest
All the authors listed declare that the paper (“Grain size modulation to optimize the wave-absorbing properties of FeSiCr alloy micropowder”) is original research that has not been submitted for publication to other journals, and all the authors listed have read the paper and agree with its submission to Physical Chemistry Chemical Physics.
Acknowledgements
Weiwei Dong and Wenmiao Zhang contributed equally to this article. This work was supported by the Program for Qingjiang Excellent Young Talents, JXUST (No. JXUSTQJYX2020001), the National Natural Science Foundation of China (No. 52001147), the Jiangxi Provincial Natural Science Foundation (No. 20212BAB204021), and the Jiangxi Province Key Laboratory of Magnetic Metallic Materials and Devices (2024SSY05061).
References
- H. Yang, X. Jiang and J. Sun,
et al., Ferrite doped sucrose-derived porous carbon composites inspired by Pharaoh's Serpent for broadband electromagnetic wave absorption, J. Alloys Compd., 2024, 989, 174402 CrossRef CAS.
- T. X. Liu and Y. Pang,
et al., Co/C nanoparticles with low graphitization degree: a high-performance microwave-absorbing material, J. Mater. Chem. C, 2016, 4(8), 1727–1735 RSC.
- X. Zhang, J. Qiao and Y. Jiang,
et al., Carbon-based MOF derivatives: emerging efficient electromagnetic wave absorption agents, Nano-Micro Lett., 2021, 13, 1–31 CrossRef CAS PubMed.
- Y. Zhang, H. B. Zhang and X. Wu,
et al., Nanolayered cobalt@carbon hybrids derived from metal–organic frameworks for microwave absorption, ACS Appl. Nano Mater., 2019, 2(4), 2325–2335 CrossRef CAS.
- F. Meng, H. Wang and F. Huang,
et al., Graphene-based microwave absorbing composites: A review and prospective, Composites, Part B, 2018, 137, 260–277 CrossRef CAS.
- F. Wu, P. Liu and J. Wang,
et al., Fabrication of magnetic tubular fiber with multi-layer heterostructure and its microwave absorbing properties, J. Colloid Interface Sci., 2020, 577, 242–255 CrossRef CAS PubMed.
- X. Tian, F. Meng and F. Meng,
et al., Synergistic enhancement of microwave absorption using hybridized polyaniline@ helical CNTs with dual chirality, ACS Appl. Mater. Interfaces, 2017, 9(18), 15711–15718 CrossRef CAS PubMed.
- H. Lv, G. Ji and W. Liu,
et al., Achieving hierarchical hollow carbon@Fe@Fe3O4 nanospheres with superior microwave absorption properties and lightweight features, J. Mater. Chem. C, 2015, 3(39), 10232–10241 RSC.
- Z. Jia, K. Lin and G. Wu,
et al., Recent progresses of high-temperature microwave-absorbing materials, NANO, 2018, 13(06), 1830005 CrossRef CAS.
- G. Sun, B. Dong and M. Cao,
et al., Hierarchical dendrite-like magnetic materials of Fe3O4, γ-Fe2O3, and Fe with high performance of microwave absorption, Chem. Mater., 2011, 23(6), 1587–1593 CrossRef CAS.
- L. Wang and S. U. Rehman,
et al., Microwave absorbing property enhancement of FeSiCr nanomaterials by regulating nanoparticle size, J. Alloys Compd., 2019, 803, 631–636 CrossRef CAS.
- R. Z. Gong, X. Wang and W. M. Cheng,
et al., Annealing effect on the magnetic properties of Fe–Co–Zr alloy flakes, Mater. Lett., 2008, 62, 266–268 CrossRef CAS.
- T. R. Malow and C. C. Koch, Grain growth in nanocrystalline iron prepared by mechanical attrition, Acta Mater., 1997, 45(5), 2177–2186 CrossRef CAS.
- C. E. Krill III, L. Helfen and D. Michels,
et al., Size-dependent grain-growth kinetics observed in nanocrystalline Fe, Phys. Rev. Lett., 2001, 86(5), 842 CrossRef PubMed.
- T. D. Shen, R. B. Schwarz and J. D. Thompson,
et al., Soft magnetism in mechanically alloyed nanocrystalline materials, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 72(1), 8014431 CrossRef.
- G. Herzer, Grain size dependence of coercivity and permeability in nanocrystalline ferromagnets, IEEE Trans. Magn., 1990, 26, 1397–1402 CrossRef CAS.
- J. Ding, Y. Li and L. F. Chen,
et al., Microstructure and soft magnetic properties of nanocrystalline Fe–Si powders, J. Alloys Compd., 2001, 314, 262–267 CrossRef CAS.
- K. Lu, Nanocrystalline metals crystallized from amorphous solids: Nano crystallization, structure, and properties, Mater. Sci. Eng., R, 1996, 16(4), 161–221 CrossRef.
- Z. Li, J. J. Wang and F. Zhao, Study on the electromagnetic properties and microwave absorbing mechanism of flaky FeSiAl alloy based on annealing and phosphate coating, Mater. Res. Express, 2021, 8, 066526 CrossRef CAS.
- T. D. Zhou, P. H. Zhou and D. F. Liang,
et al., Structure and electromagnetic characteristics of flaky FeSiAl powders made by melt-quenching, J. Alloys Compd., 2009, 484(1–2), 545–549 CrossRef CAS.
- G. Sun, B. Dong and M. Cao,
et al., Hierarchical dendrite-like magnetic materials of Fe3O4, γ-Fe2O3, and Fe
with high performance of microwave absorption, Chem. Mater., 2011, 23(6), 1587–1593 CrossRef CAS.
- Y. Qing, W. Zhou and F. Luo,
et al., Optimization of electromagnetic matching of carbonyl iron/BaTiO3 composites for microwave absorption, J. Magn. Magn. Mater., 2011, 323(5), 600–606 CrossRef CAS.
- A. L. Patterson, The Scherrer formula for X-ray particle size determination, Phys. Rev., 1939, 56(10), 978 CrossRef CAS.
- S. Takaki, T. Matsumura and T. Tsuchiyama, Proposal of simplified modified Williamson-Hall equation, ISIJ Int., 2018, 58(12), 2354–2356 CrossRef CAS.
- L. L. Zhang, W. M. Zhang and S. U. Rehman,
et al., Optimization of microwave absorption properties of flaky FeSiAl magnetic alloy by surface modification, J. Alloys Compd., 2023, 949, 169756 CrossRef CAS.
- H. Fröhlich, Theory of Dielectrics breakdown, Nature, 1943, 3829 Search PubMed.
- Y. Feng, C. Tang and T. Qiu, Effect of ball milling and moderate surface oxidization on the microwave absorption properties of FeSiAl composites, Mater. Sci. Eng. B, 2013, 178(16), 1005–1011 CrossRef CAS.
-
S.-B. Liao, Ferromagnetism (lower volume) [M], Science Press, Beijing, 2000.1–88 Search PubMed.
-
K. H. J. Buschow and F. R. Deboer, Physics of Magnetism and Magnetic Materials, 2003, pp. 147–163 Search PubMed.
- L. Wang, Q. L. Tan and S. U. Rehman,
et al., Optimizing the microwave absorption properties of core–shell NiO@FeNiMo nanocomposites by regulating the oxide shell thickness, J. Magn. Magn. Mater., 2022, 544, 168669 CrossRef CAS.
- W. Zhang, H. Du and L. Wang,
et al., Preparation of MIL-88 (Fe)@ Fe2O3@ FeSiCr double core–shell-structural composites and their wave-absorbing properties, Phys. Chem. Chem. Phys., 2024, 26(3), 1671–1683 RSC.
- H. Du, W. Zhang and L. Wang,
et al., Heterostructured C@ Fe3O4@ FeSiCr composite absorbing material derived from MIL-88 (Fe)@ FeSiCr, J. Alloys Compd., 2023, 968, 172129 CrossRef CAS.
- B. Zhang, J. Wang and T. Wang,
et al., High-performance microwave absorption epoxy composites filled with hollow nickel nanoparticles modified graphene via chemical etching method, Compos. Sci. Technol., 2019, 176, 54–63 CrossRef CAS.
- S. Wei, T. Chen and Q. Wang,
et al., Metal-organic framework derived hollow CoFe@C composites by the tunable chemical composition for efficient microwave absorption, J. Colloid Interface Sci., 2021, 593, 370–379 CrossRef CAS PubMed.
- Y. Duan, W. Liu and L. Song,
et al., A discrete structure: FeSiAl/carbon black composite absorption coatings, Mater. Res. Bull., 2017, 88, 41–48 CrossRef CAS.
- L. Rao, Z. Liu and L. Wang,
et al., Dimensional engineering of hierarchical nanopagodas for customizing cross-scale magnetic coupling networks to enhance electromagnetic wave absorption, Adv. Funct. Mater., 2023, 33(47), 2306984 CrossRef CAS.
- H. Yang, Z. Shen and H. Peng,
et al., 1D-3D mixed-dimensional MnO2@nanoporous carbon composites derived from Mn-metal organic framework with full-band ultra-strong microwave absorption response, Chem. Eng. J., 2021, 417, 128087 CrossRef CAS.
- H. Yang, B. Zhang and J. Sun,
et al., Efficient Fe3O4@ porous carbon microwave absorber constructed from cotton cellulose nanofibers hydrogel, J. Alloys Compd., 2024, 997, 174956 CrossRef CAS.
- T. Wu, Y. Liu and X. Zeng,
et al., Facile hydrothermal synthesis of Fe3O4/C core–shell nanorings for efficient low-frequency microwave absorption, ACS Appl. Mater. Interfaces, 2016, 8(11), 7370–7380 CrossRef CAS PubMed.
- S. Q. Shen, F. L. Long and L. Ur Wang,
et al., Application of MOF derived porous carbon to regulate electromagnetic wave absorption performance and mechanism of ZnFe2O4@ZnO, J. Alloys Compd., 2024, 990, 174422 CrossRef CAS.
- D. T. Zhi, T. Li and Z. H. Qi,
et al., Core-shell heterogeneous graphene-based aerogel microspheres for high-performance broadband microwave absorption via resonance loss and sequential attenuation, Chem. Eng. J., 2022, 433, 134496 CrossRef CAS.
- X. Zhang, G. Ji and W. Liu,
et al., A novel Co/TiO2 nanocomposite derived from a metal–organic framework: synthesis and efficient microwave absorption, J. Mater. Chem. C, 2016, 4(9), 1860–1870 RSC.
- F. L. Long, L. Wang and S. Ur Rehman,
et al., Honeycomb-like structured ZnFe2O4@C derived from ZnFe2O4@ZIF-8 for electromagnetic wave absorption, J. Magn. Magn. Mater., 2023, 568, 170253 CrossRef CAS.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  *abd,
Sajjad Ur
Rehman
a,
Yifeng
Hu
a,
Haiping
Zou
*cd,
Tongxiang
Liang
*abd,
Sajjad Ur
Rehman
a,
Yifeng
Hu
a,
Haiping
Zou
*cd,
Tongxiang
Liang
 a,
Changcai
Chen
ab and
Jianping
Zou
a,
Changcai
Chen
ab and
Jianping
Zou
 a
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)
θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = (kλ/D) + 4ε
θ = (kλ/D) + 4ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ

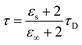



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg|(Zin − Z0)/(Zin + Z0)|
lg|(Zin − Z0)/(Zin + Z0)|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δE), Cole–Cole curve, magnetic loss coefficient (tan
δE), Cole–Cole curve, magnetic loss coefficient (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δM), and attenuation constant of samples S0–S3, respectively. From Fig. 5(a), the tan
δM), and attenuation constant of samples S0–S3, respectively. From Fig. 5(a), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δE (tan
δE (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δE = ε′′/ε′) values of the S1–S3 samples after vacuum annealing decrease relative to the S0 samples, which is attributed to the fact that the reduction of the complex dielectric constant of the material makes the dielectric loss weakened as well. According to the Debye relaxation theory, a Cole–Cole semicircle represents a Debye relaxation loss process with the following expression:36–38
δE = ε′′/ε′) values of the S1–S3 samples after vacuum annealing decrease relative to the S0 samples, which is attributed to the fact that the reduction of the complex dielectric constant of the material makes the dielectric loss weakened as well. According to the Debye relaxation theory, a Cole–Cole semicircle represents a Debye relaxation loss process with the following expression:36–38



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δM (tan
δM (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δM = μ′′/μ′) values of the S1–S3 samples are significantly enhanced relative to those of the S0 samples. This is because the vacuum annealing has eliminated the internal stresses and defects generated by the mechanical ball milling, improved the soft magnetic properties, reduced the magnetic anisotropy, and increased the complex permeability of the materials, which has led to an enhancement of the material's magnetic loss.
δM = μ′′/μ′) values of the S1–S3 samples are significantly enhanced relative to those of the S0 samples. This is because the vacuum annealing has eliminated the internal stresses and defects generated by the mechanical ball milling, improved the soft magnetic properties, reduced the magnetic anisotropy, and increased the complex permeability of the materials, which has led to an enhancement of the material's magnetic loss.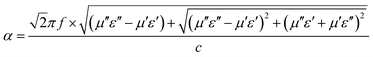




 is the real part of the permittivity,
is the real part of the permittivity,  is the real part of the magnetic permeability, δe is the tangent of the dielectric loss, and δm is the tangent of the magnetic loss. Fig. 7(e) shows pie charts of the percentage area of the region with |Δ| ≤ 0.4 obtained from the calculation. Sample S1 has the highest α value and the strongest attenuation ability, but its |Δ| ≤ 0.4 area is the smallest, and its impedance matching is poor, while sample S3 has the largest area of |Δ| ≤ 0.4 but has the smallest α value, and sample S2 has the optimal reflective loss among all the samples and relatively high α, which is also a good attenuation of the electromagnetic wave. Meanwhile, the impedance matching of sample S2 is not the best among all the samples, however, the moderate impedance matching makes the three of them reach a balance within the material, which leads to the optimized wave-absorbing performance of sample S2. This suggests that a balance between the electromagnetic wave attenuation ability and impedance matching is needed when the electromagnetic parameters of the material are regulated to improve the wave-absorbing performance.
is the real part of the magnetic permeability, δe is the tangent of the dielectric loss, and δm is the tangent of the magnetic loss. Fig. 7(e) shows pie charts of the percentage area of the region with |Δ| ≤ 0.4 obtained from the calculation. Sample S1 has the highest α value and the strongest attenuation ability, but its |Δ| ≤ 0.4 area is the smallest, and its impedance matching is poor, while sample S3 has the largest area of |Δ| ≤ 0.4 but has the smallest α value, and sample S2 has the optimal reflective loss among all the samples and relatively high α, which is also a good attenuation of the electromagnetic wave. Meanwhile, the impedance matching of sample S2 is not the best among all the samples, however, the moderate impedance matching makes the three of them reach a balance within the material, which leads to the optimized wave-absorbing performance of sample S2. This suggests that a balance between the electromagnetic wave attenuation ability and impedance matching is needed when the electromagnetic parameters of the material are regulated to improve the wave-absorbing performance.



