Assessment of the Piris natural orbital functionals on transition metal dihydrides

Abstract

Transition metal dihydrides can be seen as a starting point for the study of the interaction between H₂ and d-metal ligands that are widely recognized as challenging molecules for electronic structure methods due to their possible multireference character and electronic correlation effects. The performance of different proposed Piris natural orbital functionals (PNOFs), such as PNOF5, PNOF7, and the global functional (GNOF), in predicting the formation of 3d-transition metal dihydrides was evaluated. A comparison between the results of the PNOFs and several state-of-the-art techniques has been carried out. It was found that all PNOF methods are consistent when static correlation effects are negligible. In particular, PNOF7 demonstrated the most accurate ratio for predicting the formation of the dihydrides and energy profiles, according to multireference methods. On the other hand, although the GNOF method successfully predicts the equilibrium geometries, it overstabilizes systems with high static correlation, such as low multiplicity dihydrides of intermediate 3d-series transition metals. As a whole, they indicate activation of the H₂ bond for all metals and also the formation of dihydrides, except for Co, Cu and Zn.

---

1. Introduction

Although gas phase transition metal dihydrides (TM-dihydrides) have been investigated during the last few decades,^1–5 those studies are frequently carried out within different approaches making it challenging to have a systematic picture of their properties. It is worth mentioning that these kinds of compounds are of interest in astrochemistry and catalysis. This presents a great opportunity to carry out a full investigation of the stability and properties of 3d series TM-dihydrides, also including the H₂ bond activation by a transition metal.⁶ In particular, transition metal atom interactions with molecular hydrogen lead to three possible scenarios: the formation of a linear or bent dihydride, where the H–H bond largely exceeds the equilibrium distance (∼0.74 Å); the activation of the H–H bond, moderately enlarging the interatomic distance; and finally, the dissociation limit, where no interaction between the metal and the H₂ molecule is observed. These possible results depend on the spin multiplicity of each system.

Experimental data obtained through electron-spin resonance spectroscopy and infrared spectroscopy indicate that the formed TM-dihydrides exhibit a bent geometry.^7–10 However, it is notable that not all theoretical methods agree.¹¹

In this investigation, we have computed the electronic structure of the 3d series TM-dihydride with a large variety of state-of-the-art computational methods. Since the main interaction between the TM and H₂ is purely of σ-nature,^1,6 the analysis of the stability based on the electronic structure computations is expected to be greatly simplified.

In theoretical and computational chemistry, methods such as density functional theory (DFT) address a wide range of problems, leading to its ubiquity in various chemistry scenarios. Nonetheless, it is important to acknowledge the limitations of density functionals in certain areas, such as inorganic and transition-metal chemistry.^12,13 Notably, this approach is known to encounter challenges, including self-interaction and delocalization errors, which can result in unphysical or spurious outcomes.^14–16 While DFT can yield favorable results, particularly in the analysis of relative energies, this is often attributable to the error cancellation rather than to the enhancement of the method itself. Consequently, it is imperative to adopt a more systematic approach in the study of challenging systems, such as transition metal hydrides.

In recent years, an alternative family of methods based on the reduced density matrix (RDM)^17–20 has gained prominence in the study of strongly correlated systems. In particular, Piris natural orbital functionals (PNOFs)^21–24 excel in the progressive inclusion of dynamic and static correlation. While in DFT it is necessary to find a functional for the kinetic energy, in the theory of PNOFs this energy is defined by the one-particle RDM. Additionally, the two-particle RDM is reconstructed in terms of the one-particle RDM through a cumulant expansion.^25,26 This has led to the development of a series of JKL-type functionals known as PNOF_i (i = 1–7) and a global functional (GNOF), where J, K, and L represent Coulomb, exchange, and time-reversal integrals, respectively. Of particular note are PNOF5, PNOF7, and GNOF, which are based on an extended electron pairing scheme that allows the treatment of static electronic correlation. PNOF5 accounts intrapair correlation and a Hartree–Fock interpair contribution, while PNOF7 also includes static interpair correlation and GNOF integrates dynamic interpair correlation.^21–24,27

One of the primary purposes of this investigation is to evaluate the performance of PNOFs in the calculation of the electronic structure of TM-dihydrides. In previous works, these functionals have shown good performance in the determination of the fundamental states of multireferential molecules, such as carbenes,²⁸ and transition metal-containing systems.^29,30 It is therefore anticipated that they will provide the appropriate treatment in this study.

The following section outlines the methodologies employed to perform the calculations. Thereafter, a comprehensive account of the results obtained using diverse approaches is presented, and finally, a synthesis of the findings of this study is provided.

2. Methodological details

The electronic structure of metal dihydrides has been computed at different spin multiplicities at their equilibrium geometries. Relative energies were analyzed, so errors related to the basis set size, with respect to absolute energies, can be ruled out. Reduced density matrix functional theory has been employed by using the PNOF approach within the PyNOF package.³¹ The extended pairing scheme^21,22,26,32 has been employed in which the largest number of weakly occupied orbitals is assigned to each strongly occupied orbital, determined by the def2-TZVPD basis set,^33,34 as detailed in Section S3 of the ESI.† In order to speed up the geometry optimization procedure, the identity resolution scheme in the context of PNOFs³⁵ has been employed, along with the parameterization of occupation numbers using the softmax function.³⁶

Energy and optimization calculations were performed using PNOF5, PNOF7, and the global functional (GNOF), expecting the electron correlation to be progressively recovered. Besides, the multireference character for every system has been evaluated using PNOF7 with the M-diagnostic³⁷ adapted to PyNOF.

To verify the profiles for selected systems, the PNOF7 method based on the many-body perturbation theory (NOF-MBPT) was used to compute the energies at the same spin and geometrical configurations. They include dynamic electron correlation by means of coupled cluster (NOF-c-CCSD) and second order Møller–Plesset (NOF-c-MP2) approximations.²³

The electronic structure and geometry optimization for every spin multiplicity was also obtained by the coupled cluster method with perturbative triple excitations (CCSD(T)), as coded in the Psi4 suite of programs,³⁸ with the same basis set, so that they can be compared with the PNOF tendencies. Also, the T₁ diagnostic³⁹ was employed to measure multireference character and, the observed deviations δ_s from the expected square of the total spin, 〈S²〉, was used as a metric to measure spin contamination arising from the UHF-CCSD(T) method.

Finally, CASSCF and MRCI calculations were performed using ORCA software.^40,41 The path to achieve this results consists of single point calculations of MP2, followed for CASSCF⁴² and MRCI+Q^43,44 employing the orbitals resulting of the previous step. The active space consists of 7, 8 and 11 electrons in 10 orbitals for VH₂, CrH₂ and CoH₂ respectively.

3. Results and discussion

3.1. 3d TM series calculations and general trends

The geometries for the four initial multiplicities of the first-row transition metal dihydrides, TMH₂ (TM = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, and Zn), were optimized to evaluate the performance of the different PNOFs for systems that present static and dynamic correlation. Furthermore, these results were utilized to predict the formation of the metal dihydride, the activation of the H₂ bond, or the dissociation limit, as Fig. 1 illustrates. The PNOF and CCSD(T) methods describe angular geometries for all hydrides, except for ZnH₂ with septet multiplicity where a linear geometry is predicted. In most cases, the TM–H and H–H bond distances are consistent for both theories. All distance and angle calculations are provided in the ESI.†

Fig. 1 Examples that illustrate the outcomes obtained through CCSD(T) and the PNOFs in the calculation of geometry of systems including TM and H₂. The three common stages, formation of the dihydride (a), activation of the H–H bond (b), and no formation of the molecule (c) are shown.

The T₁ diagnostic³⁹ with CCSD(T)^45,46 and the M-diagnostic with PNOF7 were computed to gain insight into the multireference nature of all systems. Moreover, the observed deviation δ_s from the expected square of the total spin, designated as 〈S²〉, was evaluated as a metric associated with the spin contamination affecting the CCSD(T) method, which is recognized to increase in value for strongly correlated systems. These values are presented in Table 1, with those indicating a multireference character highlighted in blue to facilitate identification. It is possible to split the systems into three different groups according to their multireference character, which can be related to dⁿ, the number of electrons in the d orbital, increasing as follows: the group composed of the outer elements, located in the first row of transition metals, with n = 1, 9 and 10, recognized for a small implication of the static correlation; the group of intermediate elements, with n = 2, 3, 7 and 8, moderately affected by the static correlation; and the group of elements situated in the center of this series, with n = 4, 5 and 6, strongly influenced by this type of correlation.

Table 1 Diagnostics that indicate a multireference character for TMH₂ systems with the “m” different multiplicities: observed deviations δ_s associated with CCSD(T) from the expected square of the total spin, 〈S²〉, followed by T₁ for CCSD(T) and M for PNOF methods. Systems where T₁ ≥ 0.045 and M ≥ 0.10 show the predominance of static correlation and are highlighted in bold, which in general correspond to d⁴, d⁵ and d⁶ configurations

TM	m	Diagnostics
		δ s	T1	M
Sc	2	0.009	0.021	0.04
	4	0.005	0.050	0.04
	6	0.002	0.019	0.03
	8	0.002	0.026	0.04
Ti	1	0.000	0.048	0.85
	3	0.020	0.034	0.05
	5	0.004	0.029	0.03
	7	0.002	0.019	0.03
V	2	0.007	0.129	0.94
	4	0.018	0.039	0.05
	6	0.002	0.035	0.03
	8	0.001	0.018	0.03
Cr	1	0.000	0.050	0.99
	3	0.029	0.061	0.81
	5	0.060	0.047	0.10
	7	0.000	0.018	0.03
Mn	2	0.728	0.084	0.98
	4	0.098	0.060	0.98
	6	0.011	0.021	0.021
	8	0.001	0.015	0.04
Fe	1	0.000	0.077	0.97
	3	0.082	0.068	0.97
	5	0.006	0.022	0.19
	7	0.004	0.018	0.04
Co	2	0.108	0.104	1.00
	4	0.015	0.035	0.17
	6	0.004	0.018	0.04
	8	0.002	0.014	0.01
Ni	1	0.000	0.088	0.56
	3	0.001	0.023	0.03
	6	0.004	0.019	0.03
	7	0.001	0.015	0.01
Cu	2	0.002	0.023	0.03
	4	0.018	0.050	0.06
	6	0.001	0.014	0.01
	8	0.002	0.010	0.01
Zn	1	0.000	0.017	0.11
	3	0.004	0.017	0.04
	5	0.002	0.013	0.01
	7	0.001	0.009	0.00

---

To facilitate a comparative analysis of the predicted tendencies by each method, the relative energies with respect to the lowest multiplicity state per metal are presented in Fig. 2–4. The data points with the highest multiplicity for the groups of intermediate and outer elements were excluded from the analysis for two reasons: their convergence is observed to tend towards a single direction, and their exclusion facilitates the visualization of the differences between the remaining data points.

Fig. 2 Relative energy profiles for the PNOFs and CCSD(T) with the def2-TZVPD basis set for the outer 3d-series metals. ΔE = E_m − E_l, where E_m is the energy for any multiplicity and E_l for the lowest. All methods exhibit a similar tendency.

Fig. 3 Relative energy profiles for the PNOFs and CCSD(T) with the def2-TZVPD basis set for the middle 3d-series metals. ΔE = E_m − E_l, where E_m is the energy for any multiplicity and E_l for the lowest.

Fig. 4 Relative energy profiles for the PNOFs and CCSD(T) with the def2-TZVPD basis set for the outer 3d-series metals. ΔE = E_m − E_l, where E_m is the energy for any multiplicity and E_l for the lowest. Most methods predict less negative energy for lower multiplicity states, while GNOF predicts that this is the ground state.

The resemblance between CCSD(T) and PNOF tendencies is more pronounced for the group of outer elements than for the others. It is noticeable that they are barely affected by the inclusion of static correlation. In contrast, this resemblance decreases for the intermediates and is no longer apparent for the central elements. The latter case coincides with the systems in which the treatment of static correlation is crucial. Moreover, in general, all methods demonstrate a convergence towards the same values of energy, distance, and angle, which becomes increasingly pronounced with the rise in multiplicity. This behavior indicates that the characterization of the systems becomes increasingly intricate with the augmentation of the multireference nature. In order to conduct a more comprehensive examination of the comparative energy analysis, we will consider a division of the TM-dihydrides based on the relevance of the treatment of static correlation in their analysis and the number of electrons in the d orbital, as previously mentioned. This analysis will consider the geometries at equilibrium identical unless otherwise stated.

3.2. Outer d-series metals, dⁿ (n = 1, 9, 10)

For the Sc, Cu, and Zn systems presented in Fig. 2, the PNOFs and CCSD(T) yield identical energetic trends. In general, the energy of the states increases as the multiplicity rises. Further examination of the plots reveals that, although the results of all functionals are close between them and with CCSD(T), PNOF7 tends to yield the lowest results, while GNOF provides the highest and PNOF5 is situated between the two, in a manner similar to CCSD(T). This similarity is to be expected, given that in the case of these metals the effect of the static correlation is not significant, as can be seen from the results presented in Table 1. Thus, for these metals, the description provided by a functional with an incomplete inclusion of electronic correlation, such as PNOF5, is sufficient to reproduce the trend obtained by more sophisticated methods. However, as will be seen later, this functional reproduces a different equilibrium geometry from the rest, and in that case, it must resort to PNOF7 or GNOF.

3.3. Middle d-series metals, dⁿ (n = 2, 3, 7, 8)

This group is presented in Fig. 3. For the titanium system, the methods indicate that the ground state corresponds to a triplet multiplicity. In particular, the GNOF predicts a degeneracy between singlet and triplet multiplicity, where the singlet exhibits multireferential character, as corroborated by diagnostics in Table 1. These results contrast with those of the other methods since they predict a difference of at least 20 kcal mol⁻¹ between both multiplicities, suggesting that GNOF may be overstabilizing the lower multiplicity. The behavior of the vanadium system is analogous to that of titanium, where GNOF is distinguished by stabilizing the lowest multiplicity with multireference character, describing a degeneracy between doublet and quadruplet states. The energy trend between the remaining PNOFs and CCSD(T) is consistent and a notable discrepancy of approximately 30 kcal mol⁻¹ is observed between the two states. Additionally, it is noteworthy that PNOF7 is the sole method that predicts degeneracy between the quadruplet and the sextuplet.

On the other hand, GNOF and CCSD(T) yield identical results for the systems with cobalt and nickel, both methods indicate that the ground state corresponds respectively to the multireference states, quartet and singlet. PNOF5 and PNOF7 exhibit a deviation from the aforementioned trend. Regarding cobalt, they demonstrate a substantial discrepancy in energy between the doublet and quadruplet, which modifies the trend concerning its analog GNOF. For nickel, both functionals propose that the ground state corresponds to the triplet, which differs from GNOF and CCSD(T). In addition, in the case of cobalt, there is great consistency between the geometries predicted by CCSD(T) and GNOF for all multiplicities, in contrast to PNOF5 and PNOF7. To illustrate, in the quadruplet, the geometry obtained for PNOF7 exhibits an angle about 18° smaller than that in the other methods and a TM–H distance three times larger than that predicted by CCSD(T) and GNOF. Meanwhile, the H–H distance shows a less pronounced difference, amounting to a decimal fraction of an angstrom. Regarding PNOF5, while the discrepancy is less pronounced, the geometry also differs from that of the other methodologies. In the case of the sextuplet the roles are reversed: PNOF5 exhibits anomalous values in its geometry, displaying a twice smaller angle and a twice larger TM–H distance, while the H–H distance changes by a tenth fraction of an angstrom. Concerning PNOF7, the differences are small but significant enough to differentiate from the values obtained with GNOF and CCSD(T).

Finally, the tendencies predicted by CCSD(T) and GNOF for the nickel system are in good agreement, presenting a large gap between the triplet and quintet states. In contrast, PNOF7 predicts the degeneracy between the two considered multiplicities. Additionally, neither PNOF5 nor PNOF7 reproduce an increase in energy between the singlet and triplet states.

3.4. Center d-series metals with a ground state of high spin multiplicity, dⁿ (n = 4, 5, 6)

In the case of the systems with Cr, Mn, and Fe depicted in Fig. 4, the behavior described by GNOF shifts toward positive values and can be attributed to the overstabilization of the lowest multiplicity states. This tendency is opposite to that of other methods, which predict the highest energies for singlets and triplets. In particular, PNOF7 and GNOF prognosticate greater degeneration for the triplet and quintet states in the chromium systems compared to the CCSD(T) and PNOF5 methods. These latter methods generally show an equivalent tendency for all multiplicities.

In manganese, there are significant differences between the predicted trends by each method. Nevertheless, all PNOFs consistently suggest that the lowest multiplicity state is the sextuplet. In contrast, CCSD(T) predicts a smaller energy difference between the quadruplet, sextuplet, and octuplet than is predicted by the PNOF methods. Moreover, it predicts that the lowest energy state is the highest multiplicity state. In contrast to GNOF, the PNOF5 and PNOF7 methods predict that the lowest energy state for iron is the quintet. The CCSD(T) method yields equal energies for the triplet and quintet states, which are identified as the lowest energy states. In this series all methods converged to the same equilibrium geometry, thus ensuring comparability of the results.

3.5. Static and dynamic correlation: progressive inclusion

The good performance of the PNOF5 method in the outer 3d-series seems to indicate that the dynamic intrapair correlation is sufficient to describe the relative stability of these systems. Conversely, for the middle 3d-series, it is more noticeable that at least the static interpair correlation is required. In some cases, the dynamic correlation incorporated into the GNOF functional can reproduce the trends observed in other methods, especially for the high multiplicity states with lower static correlation effects. Notably, in the center 3d-series the dynamic correlation added by GNOF seems to overstabilize the lower multiplicity states. To further explore this argument, calculations were performed using some NOF-MBPT methods that include dynamic correlation with perturbative methods. In Fig. 5 the results of the relative energies for the center 3d-series are illustrated. In addition, the systems with nickel showing a similar trend between CCSD(T) and GNOF are included. In general, the NOF-c-MP2 and NOF-c-CCSD methods show trends that are more similar to those of PNOF5 and PNOF7. This reinforces that GNOF overstabilizes these systems that exhibit a higher multireference character.

Fig. 5 Relative energy profiles for the PNOFs and CCSD(T) with the def2-TZVPD basis set for Cr, Mn, Fe and Ni. ΔE = E_m − E_l, where E_m is the energy for any multiplicity and E_l for the lowest. The methods that include dynamic correlation with perturbative methods show a tendency to align with the trends observed in the PNOF5 and PNOF7 methods.

3.6. TM–H₂ and H–H interactions

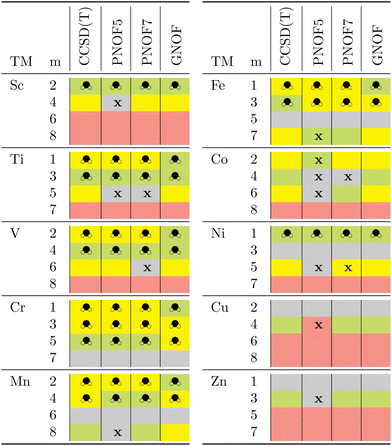
To assert whether the interaction of transition metals with the hydrogen molecule results in the formation of the dihydride, the geometries of each system were subjected to quantitative analysis. Table 2 provides a color-coded analysis of the main stages identified through the calculations. The ground state of each dihydride is highlighted in green. When more than one cell in the same column is highlighted in green, this indicates a degeneracy between the states in question. In this work, this is defined as an energy difference of less than 5 kcal mol⁻¹. In contrast, systems that may potentially give rise to the formation of the dihydride or represent the activation of the H–H bond are indicated in yellow. The gray color shows the states where the H–H bond is formed, whereas the red color denotes those systems where the atoms are dissociated. The boxes with an x indicate that the geometry optimized by the method is not consistent with that indicated by the other methods and is therefore not comparable. As can be seen in the table, in general, the most stable TM-dihydrides tend to exhibit the lowest multiplicities and there is a discernible increase in the probability of high multiplicity hydrides forming as one progresses from the outer to the middle 3d-series metals, particularly for Cr.

Table 2 Classification of TM–H₂ systems, for activation of the H₂ bond and dihydride formation cases, the ground state is highlighted in green and the rest in yellow. Non-interacting systems are shown in gray and unstable conformations in red. More than one configuration can be highlighted in green if their energy difference is lower than 5 kcal mol⁻¹. Furthermore, the icon means at that multiplicity the hydride is formed, while x indicates that the method does not reproduce a similar equilibrium geometry concerning the rest

---

3.7. Comparison with multireference methods

Given the multireference character and high values of the spin contamination metric associated with CCSD(T) for the center and middle series, some examples of CASSCF and MRCI methods are shown for selected systems.

The examination of Fig. 6 demonstrates that the PNOF methods agree with the MRCI tendency, with the exception of the GNOF, which seems to resemble the CASSCF profile in some multiplicities for vanadium and cobalt systems. This suggests that the treatment of dynamical correlation in the GNOF may be the origin of the discrepancy to other NOFs, due to overstabilization of low multiplicities with a relevant multireference character. In particular, PNOF7 provides a closer description with respect to multireference computations, followed by PNOF5 that also shows high accuracy in predicting the formation of TM-dihydrides. Furthermore, CCSD(T) performs similarly to MRCI for VH₂ and CrH₂, where few or no multiplicity states exhibit a multireference character, as evidenced by low values for T₁ and M correlation diagnostics as shown in Table 1. These observations propose that CCSD(T) remains a reliable reference for those systems, since its tendency aligns with the majority of methods. On the other hand, the discrepancy between CCSD(T) and MRCI in the CoH₂ system indicates that multireference methods are necessary to obtain accurate descriptions when significant values of δ_s, T₁ or M are observed. Nevertheless, it is important to note that the complexity of identifying cases where multireferential methods are necessary, based on diverse diagnoses, can be avoided by using NOF methods. This assertion is substantiated by the analysis of different cases, in which the methods systematically replicate the results of the valid reference for each metal without additional aid.

Fig. 6 Relative energy profiles for PNOFs, CCSD(T), CASSCF and MRCI with the def2-TZVPD basis set for VH₂, CrH₂ and CoH₂. In the notation ΔE = E_m − E_l, where E_m is the energy for any multiplicity and E_l for the lowest.

4. Conclusions

In this work, we carried out electronic structure computations of transition metal dihydrides at different spin multiplicities in order to evaluate the performance of PNOFs. In general, we found that the PNOF and CCSD(T) methods behave consistently and show the need for static correlation in the study of these systems. When differences were found with the reference results, multireference calculations were performed and the outcomes agreed with the NOF methods.

A notable consistency has been observed among perturbative, multireference, and NOF methods, thereby affirming their efficacy in describing multireference systems. In particular, PNOF7 demonstrated the most accurate ratio for predicting the formation of TM-dihydrides and energy profiles, according to multireference methods. On the other hand, GNOF overstabilizes low multiplicity states for titanium, vanadium and cobalt systems that show multireference character. However, the equilibrium geometries predicted by the GNOF and CCSD(T) are quite in accordance for all cases. Therefore, general structure optimizations might be performed using this functional and subsequent energy characterization with PNOF7.

Furthermore, it was established that the formation of TM-dihydrides exhibits enhanced stability at the lowest multiplicities. Additionally, PNOFs indicate that the formation of high multiplicity dihydrides is frequent for mid-series elements such as Cr, Mn, and Fe metals. This behavior is consistent with that expected for these metals.

In this line, we expect these results motivate the utilization of these NOF approaches to the study of the hydrogen–hydrogen bond activation and the formation of molecules with larger d-metal ligands where static correlation plays a dominant role.

Author contributions

Lizeth Franco: data curation (equal); dormal analysis (equal); investigation (equal); methodology (equal); validation (equal); visualization (equal); writing – original draft (equal). Roberto Rojas-Hernández: data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); validation (equal); visualization (equal); writing – original draft (equal). Ivan A. Bonfil-Rivera: data curation (equal); formal analysis (equal); investigation (equal); methodology (equal); validation (equal); visualization (equal); writing – original draft (equal). Emilio Orgaz: conceptualization (equal); investigation (equal); methodology (equal); project administration (equal); resources (equal); supervision (equal); validation (equal); visualization (equal); writing – original draft (equal); writing – review & editing (equal). Jorge M. del Campo: conceptualization (equal); funding acquisition (equal); investigation (equal); methodology (equal); project administration (equal); resources (equal); supervision (equal); validation (equal); visualization (equal); writing – original draft (equal); writing – review & editing (equal).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L. Franco with CVU Grant No. 1312732 acknowledges “Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCyT)” for a master's scholarship. R. Rojas-Hernández acknowledge the funding through project Grant No. IN201822 from “Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica (PAPIIT)”. I. A. Bonfil-Rivera with CVU Grant No. 2038028 acknowledges “Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCyT)” for master's scholarship and the funding through project Grant No. IN201822 “Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica (PAPIIT)”. J. M. del Campo, L. Franco, I. A. Bonfil-Rivera and R. Rojas-Hernández acknowledge funding with project Grant No. IN201822 from PAPIIT, and computing resources from “Laboratorio Nacional de Cómputo de Alto Desempeño (LANCAD)” with project Grant No. LANCAD-UNAMDGTIC-270.

Notes and references

1. J. Demuynck and H. F. Schaefer III, J. Chem. Phys., 1980, 72, 311–315.
2. A. E. Stevens, C. S. Feigerle and W. C. Lineberger, J. Chem. Phys., 1983, 78, 5420–5431.
3. Z. L. Xiao, R. H. Hauge and J. L. Margrave, J. Phys. Chem., 1991, 95, 2696–2700.
4. J. L. Elkind and P. B. Armentrout, J. Phys. Chem., 1987, 91, 2037–2045.
5. H. Körsgen, P. Mürtz, K. Lipus, W. Urban, J. P. Towle and J. M. Brown, J. Chem. Phys., 1996, 104, 4859–4861.
6. G. J. Kubas, J. Organomet. Chem., 2001, 635, 37–68.
7. R. J. V. Zee, S. Li, Y. M. Hamrick and W. Weltner, J. Chem. Phys., 1992, 97, 8123–8129.
8. G. A. Ozin and J. G. McCaffrey, J. Phys. Chem., 1984, 88, 645–648.
9. R. J. V. Zee, T. C. DeVore, J. L. Wilkerson and W. Weltner, J. Chem. Phys., 1978, 69, 1869–1875.
10. R. V. Zee, C. Brown and W. Weltner, Chem. Phys. Lett., 1979, 64, 325–328.
11. X. Wang and L. Andrews, J. Phys. Chem. A, 2005, 109, 9021–9027.
12. A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320.
13. F. Furche and J. P. Perdew, J. Chem. Phys., 2006, 124, 044103.
14. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
15. P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 20.
16. P. Mori-Sánchez, A. J. Cohen and W. Yang, Phys. Rev. Lett., 2008, 100, 146401.
17. S. M. Valone, J. Chem. Phys., 1980, 73, 4653–4655.
18. S. M. Valone, J. Chem. Phys., 1980, 73, 1344–1349.
19. D. A. Mazziotti, Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules, Wiley, 2007, vol. 134.
20. D. A. Mazziotti, Phys. Chem. Chem. Phys., 2012, 112, 244–262.
21. M. Piris, X. Lopez, F. Ruipérez, J. M. Matxain and J. M. Ugalde, J. Chem. Phys., 2011, 134, 164102.
22. M. Piris, Phys. Rev. Lett., 2017, 119, 063002.
23. M. Rodríguez-Mayorga, I. Mitxelena, F. Bruneval and M. Piris, J. Chem. Theory Comput., 2021, 17, 7562–7574.
24. M. Piris, Phys. Rev. Lett., 2017, 119, 063002.
25. W. Kutzelnigg and D. Mukherjee, J. Chem. Phys., 1999, 110, 2800–2809.
26. M. Piris, J. M. Matxain and X. Lopez, J. Chem. Phys., 2013, 139, 234109.
27. M. Piris, Novel Treatments of Strong Correlations, Academic Press, 2024, vol. 90, pp. 15–66.
28. L. Franco, J. F. H. Lew-Yee and J. M. del Campo, AIP Adv., 2023, 13, 65213.
29. J. F. H. Lew-Yee, J. M. del Campo and M. Piris, J. Chem. Theory Comput., 2023, 19, 211–220.
30. F. Ruipérez, M. Piris, J. M. Ugalde and J. M. Matxain, Phys. Chem. Chem. Phys., 2013, 15, 2055–2062.
31. J. F. H. Lew-Yee, M. Piris and J. M. del Campo, PyNOF, https://github.com/felipelewyee/PyNOF, 2024.
32. M. Piris, J. Chem. Phys., 2014, 141, 044107.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
35. J. F. H. Lew-Yee, M. Piris and J. M. del Campo, J. Chem. Phys., 2021, 154, 064102.
36. L. Franco, I. A. Bonfil-Rivera, J. F. Huan Lew-Yee, M. Piris, J. M. del Campo and R. A. Vargas-Hernández, J. Chem. Phys., 2024, 160, 244107.
37. J. F. H. Lew-Yee and J. M. del Campo, J. Chem. Phys., 2022, 157, 104113.
38. D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. OBrien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, I. Schaefer, F. Henry, A. Y. Sokolov, K. Patkowski, I. DePrince, A. Eugene, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108.
39. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207.
40. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, L224108.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
42. M. Ugandi and M. Roemelt, Int. J. Quantum Chem., 2023, 123, e27045.
43. C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463–1470.
44. F. Neese, Chem. Phys. Lett., 2000, 325, 93–98.
45. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
46. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.

---

Footnote

† Electronic supplementary information (ESI) available: (1) Geometries and relative energies for all methods, (2) pertubative method computations, and (3) an extended pairing scheme explanation. See DOI: https://doi.org/10.1039/d4cp04010d

---