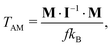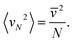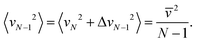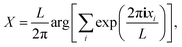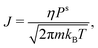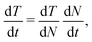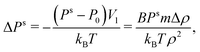Molecular dynamics of evaporative cooling of water clusters

Abstract

The cooling of water clusters through evaporation into a vacuum is studied using classical molecular dynamics with the SPC water model, and the results are compared with macroscopic theory. A simple model based on the Hertz–Knudsen equation significantly underestimates cooling rates. A modified approach that accounts for the Kelvin equation provides better results. Further insight is gained by comparing temperatures derived from different degrees of freedom. While the rotational temperature of the clusters is only slightly lower than their internal temperature and decreases over time, the translational temperature of the clusters, considered as individual particles, remains nearly unchanged.

---

1 Introduction

Nucleation is an important process in the formation of a new, more stable phase, which is separated from a less stable phase by a first-order phase transition. Nucleation from vapor to liquid occurs in many industrial processes, primitive solar nebulae, planetary atmospheres, and other environments. The pristine particle undergoes further changes in a dilute gas or vacuum. In the laboratory, one can observe such nucleation in the supersonic expansion. Here, a pressurized gas expands through a nozzle into a vacuum.^1–4 The jet adiabatically cools down, reaching supersonic speeds, which leads to nucleation into clusters of various sizes that eventually freeze.^5–8 Water clusters obtained via supersonic expansion⁴ can serve as proxies for atmospheric aerosol particles⁹ and contribute to our understanding of various aspects of surface chemistry.¹⁰ Frozen clusters^11,12 can mimic ice particles^13–18 which play a crucial role in atmospheric chemistry.

The process of supersonic expansion has been extensively studied both experimentally^19–23 and theoretically.^24–26 Experimental measurements of nucleation rates, cluster size distributions, and other properties are used to test nucleation theories.^27–34 Spectroscopic techniques provide insight into the thermodynamic properties and cluster pickup characteristics.^35–40 Numerous experiments, particularly in Laval nozzles, have determined nucleation rates during expansion,^20,21,41 while conical nozzles have been explored in other studies.⁴² These experimental efforts are complemented by a variety of modeling and computational approaches.^5,43–47

In our laboratory, we have developed an original method for simulating supersonic expansion.⁴⁸ A parcel of gas flowing through a nozzle is enclosed in an expanding periodic box and simulated using classical molecular dynamics. During the expansion, the pressure–volume work is determined. Using this and the Bernoulli equation, the flux is calculated. If the flux is not constant (i.e., the system does not reach a steady-state condition), the expansion protocol is modified, and the simulation is repeated until the results align with the equations of fluid dynamics. The obtained cluster distribution^49,50 is in agreement with experimental results. We also found that the clusters are warmer than the global system temperature, which includes the surrounding dilute gas. Since the results for different cluster temperatures (internal, rotational, and translational) were inconclusive, we initiated the current project to simulate the cooling process through evaporation into a vacuum.

One significant study⁵¹ explores the thermochemical and kinetic aspects of cooling isolated liquid droplets, particularly amorphous water, via evaporation. It reveals that centrally placed electric charges in molecular clusters make evaporation more endothermic, especially in smaller clusters, leading to larger cluster size distributions and higher temperatures. The role of inert gases in the evaporative cooling of water clusters has been also studied.⁵² It shows that hydrogen-bonded water clusters with adsorbed inert gases can control fragmentation in mass spectrometry by rapidly lowering internal energy, thus reducing fragmentation rates. This approach facilitates the production of “unprotonated” water clusters, whose structures match theoretical predictions, and could expand mass spectrometry applications to complex polymers, including biopolymers. Studies on alkali metal ion-doped water–argon clusters reveal that these ions lower the O–H stretch frequencies and increase IR intensity of the symmetric mode, enhancing our understanding of ion solvation in water. Simulations closely match experimental temperatures, further illuminating the cooling process.^53,54

Traditional models like the Hertz–Knudsen relation have been used to describe evaporation but have limitations. Newer models, such as those based on liquid film evaporation into a vacuum, better match simulation results and offer more accurate descriptions of water droplet evaporation.^55–57 Research on evaporative cooling during supersonic expansion has introduced the energy balance model that predicts water cluster temperatures accurately. Reduced cooling in larger clusters indicates the onset of crystallinity, offering a new structural marker.³⁵ Lastly, research on Na(NH₃)_n clusters shows that their dissociation dynamics are driven by ionic evaporation, with this effect being more pronounced in smaller clusters. In larger clusters, ionic state evaporation plays a dominant role, highlighting the influence of ionization cross-section variations in femtosecond experiments.⁵⁸

This work tackles the topic from a purely simulation side. A range of clusters have been simulated and the results have been compared with thermodynamic models.

2 Theory

2.1 Temperature of evaporating clusters

2.1.1 Temperatures. In classical statistical mechanics, the kinetic temperature is calculated from the total kinetic energy as T = 2E_kin/fk_B, where k_B is the Boltzmann constant and f is the number of mechanical degrees of freedom. For rigid water it holds f = 6N, where N is the number of model water molecules in a cluster.

For technical reasons, it is useful to calculate the translational kinetic energy, E_tr, and the corresponding temperature, T_tr = 2E_tr/fk_B (f = 3N), from the velocities of the molecular centers of mass (CoMs) or, alternatively, from the linear momenta of the molecules. Then, the internal temperature of molecules can be calculated from the difference E_kin–E_tr. Since the SPC water is rigid, f = 3N and this temperature includes only rotations; we will denote it as T_rot. For systems in equilibrium, T_rot = T_tr should hold. To quantify this condition, we define the equipartition error as

ΔT_eqp = T_tr − T_rot. (1)

In contrast, we can treat individual clusters as large particles. The translational kinetic temperature of the clusters, considered as particles, can be calculated from their linear momenta (LM) or, equivalently, from the velocities of their centers of mass. We will denote this temperature as T_LM. Since we always have only one cluster in a simulation box, the number of degrees of freedom is f = 3. Similarly, we define the rotational temperature of a “cluster as particle” from its angular momentum (AM). To do this, the cluster is centered to its CoM, its linear momentum is removed, and the inertia tensor I and the vector of angular momentum M are calculated. The corresponding rotational temperature is

where again f = 3.

2.1.2 Translational temperature of clusters as particles. The following analysis is based on the concept of equilibrium between an N-cluster and its vapor, as assumed for a critical cluster in classical nucleation theory (CNT). The vapor is treated as ideal gas, which implies that individual evaporation and condensation events are independent. Due to this separation, the velocity v₁ of an evaporating molecule, projected towards the CoM of the remaining (N − 1)-cluster, follows the 1D Maxwell–Boltzmann distribution at the system temperature. 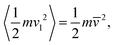For the kinetic energy in this direction it holdswhere v̄² = k_BT/m and m denotes the mass of a molecule. In the following discussion, condensation events will be ignored, resulting in the cooling of the cluster during evaporation into a vacuum.

Let us first assume that the N-cluster has zero velocity of its CoM, v_N = 0. The velocities of the evaporated molecule and the remaining (N − 1)-cluster must then satisfy the momentum conservation law,

v₁ + (N − 1)v_N−1 = 0.

The kinetic energy should be equal to . For the energy divided by , it holds

v₁² + (N − 1)v_N−1² = v̄².

By solving this set of equations we get the recoil velocity
Let us rename this quantity to Δv_N−1 and let us assume now that the original N-cluster has a velocity v_N (in the above-defined direction) corresponding to the Maxwell–Boltzmann law at temperature T. Then
Since the recoil velocity is not correlated with v_N, 〈v_N·Δv_N−1〉 = 0, the averaged velocities squared (variances) are additive,
Since the mass of this cluster is (N − 1)m, we get from eqn (2) that the translational temperature of the (N − 1)-cluster equals T.

In other words, the translational temperature of clusters “as particles”, T_LM, remains unchanged on evaporation of one molecule. However, the cluster (internal) temperature decreases by Q/N on one evaporation event, where Q is the ratio of the vaporization enthalpy and the isobaric heat capacity, Q = Δ_vapH/C_p ≈ 540–600 K (for real bulk water in dependence on temperature). The translational temperature in the second evaporation event (assuming that N is large enough) decreases by 2Q/N², in the third event by 3Q/N², and after n_ev evaporations the decrease is which is a second-order effect. We thus conclude that T_LM remains nearly constant during evaporative cooling.

2.2 Simulation methodology

Water was modeled using an SPC potential⁵⁹ truncated and smoothed at 12.7 Å, see ref. 50 for the formulas. No cutoff corrections are applied. While it is technically possible to use the full potential in Cartesian space, removing a molecule would lead to a sudden energy change, which would disrupt adiabacity.

In ref. 50, we evaluated the impact of truncation on the similar SPC/E model. We found that the surface tension, 62 mN m⁻¹ for the full SPC/E, is reduced by 0.7 mN m⁻¹ and 2.65 mN m⁻¹ due to the truncation of electrostatic and dispersion forces, respectively. The dielectric constant remains unaffected within the standard error of 0.8, and the density change is less than 0.3%.

Due to technical constraints, the simulations were performed in the cubic periodic boundary conditions with box edge length L = 48 Å. To handle nonbonded interactions efficiently, the linked-cell list method was used. The Verlet/leap-frog method was employed for integrating the equations of motion, and the SHAKE algorithm was implemented to preserve molecular rigidity. For a good time reversibility, SHAKE employs superrelaxation with a bond length tolerance of 10⁻¹⁰ Å

The kinetic energy was calculated by the leap-frog formula, which for one atom i at time t reads as

where v_i represents the particle's velocity vector and h = 1.67 fs. Other temperatures are calculated similarly.

Each simulation began with a pre-formed cluster. Velocities were reassigned according to the Maxwell–Boltzmann distribution, followed by a 20 ps equilibration phase using the Andersen thermostat applied to the molecular centers of mass, with a correlation time τ_T = 1 ps. Afterward, the thermostat was turned off, and a microcanonical simulation ensued. During each cycle, lasting 60h = 0.1 ps, the cluster center along the x-coordinate was calculated using the formula

where i is the imaginary unit. In the above equation, arg refers to the phase (or angle) of the complex number and the sum is taken over the centers of mass of the molecules. The same calculations are performed in the y and z directions. If any atom of a molecule is located more than L/2 − 2 Å from the cluster center, it is removed, and the microcanonical simulation is restarted with N − 1. The shell width of 2 Å (effectively 4 Å due to the periodic boundary conditions) is sufficient to capture all evaporating molecules, even in the rare cases where two molecules have vaporized simultaneously.

2.3 Evaporative cooling model

In this section, we develop a continuous macroscopic model of evaporative cooling of a spherical cluster to a vacuum. We assume that the evaporation can be expressed by the Hertz–Knudsen effusion formula
where J is the flux (in molecules per unit area and time), P^s is the saturated vapor pressure, and η is the sticking coefficient. This formula with η = 1 (aka Knudsen effusion) is exact for a virtual planar plaquette in the gas phase. If we place this plaquette next to the liquid surface in equilibrium, the flux is the sum of the effusing molecules (η) and the molecules reflected from the surface (1 − η). Since almost all incoming thermal molecules are attached at water surface, η = 1 is sufficiently accurate. Note that it was proposed⁵⁶ to use an “outer temperature” in the Hertz–Knudsen formula; however, we do not know this temperature in the evaporation to a vacuum.

The saturated vapor pressure P^s_r above a spherical droplet of radius r is higher than vapor pressure P^s over a flat surface, and can be (for r large enough) approximated by the Kelvin (Ostwald–Freundlich) equation,⁶⁰

where σ is the water surface tension, and the molecular volume V₁ is calculated from the density.

The evaporation rate is given by the Hertz–Knudsen flux and the surface area A = 4πr² of the cluster,

As the cluster evaporates, the temperature decreases. The cooling rate is

where C_p,1 is the isobaric heat capacity per molecule and Δ_vapH₁ is the enthalpy of vaporization per molecule. For consistency, the enthaply is calculated from P^s_r using the Clausius–Clapeyron equation,

Δ_vapH₁ = RT²d ln P^s_r/dT,

assuming that the vapor is ideal gas and the liquid volume is negligible. The cluster heat capacity for rigid molecular models is

C_p,1 = ∂H₁/∂T = 4k_B − ∂Δ_vapH₁/∂T,

because the enthalphy per molecule is H₁ = 〈E_pot + E_kin〉 + pV₁ and we again neglect pV₁ for liquid. Further, 〈E_kin〉 = 3k_BT and Δ_vapH₁ = k_BT − 〈E_pot〉 (assuming pV₁ = k_BT for vapor).

In addition to this model taking into account the Kelvin equation, we test also a simple model using P^s instead of P^s_r in the above equations.

Mathematically, the problem reduces to a set of two ordinary differential equations. The first one is eqn (4) and the second is

with eqn (4) and (5) combined. The initial values are the cluster size, N₀, and its temperature, T₀, at time t = 0. These equations have been solved numerically using Maple⁶¹ by the Implicit Rosenbrock third-fourth order Runge–Kutta method. Parameter “stiff” allows for a change of time scale by many orders (another possibility would be a change of the independent variable from t to ln t).

2.4 Input data for the evaporation model

The evaporative cooling model in Section 2.3 is based on the thermodynamic properties of the same molecular model as used in the simulation of evaporation – the truncated SPC force field. It is not our aim to compare the force field-based results to real experiments.

In classical mechanics, atomic masses can be adjusted without affecting the thermodynamic averages of static quantities. Therefore, we equalized the masses of atoms (in g mol⁻¹: O = 8, H = 5) in these calculations, allowing the use of a longer time step of h = 2 fs. The rigid geometry of a molecule was maintained using SHAKE (accuracy 10⁻⁹, with superrelaxation), and a constant temperature was ensured by the Nosé–Hoover thermostat (characteristic time τ_T = 0.25 ps, TRVP (k = 2)⁶²).

2.4.1 Slab geometry simulations. The first series of simulations to provide the data for the evaporative cooling model was performed in the slab geometry for temperatures T = 250, 300, 350 and 400 K, the box aspect ratio L_z/L_x = L_z/L_y = 3, and N = 1000 particles. Three variables have been obtained, see Table 1.

Table 1 Simulation results of the short-range SPC water model in the slab geometry, N = 1000, L_z/L_x = 3

T (K)	σ (N m^−1)	P ^s ^a (bar)	P ^s ^b (bar)	ρ ^(l) (kg m^−3)
a From Pzz. b From gas density and the virial equation of state.
250	0.059177(37)	∼0	∼0	1000.9(2)
300	0.051525(33)	∼0	∼0	972.4(2)
350	0.043133(46)	0.490(51)	0.508	929.4(2)
400	0.033942(50)	2.923(61)	2.927	874.2(1)

---

1. The surface tension is calculated by formula⁶³

where P_kk are the diagonal components of the pressure tensor. The surface tension is well described by the Guggenheim–Katayama equation

σ = a(c − T)^b, (7)

where a = 0.0014683095, b = 0.6629252, c = 514.0737 with σ in N m⁻¹ and T in K. It may be of interest that this equation has been motivated by critical phenomena; however, our data are far from the critical point and consequently parameters b and c cannot be interpreted either as the critical exponent (experimentally b ∼ 1.26 = 2ν, where ν is the correlation length critical exponent) or the critical temperature in K (c = 647.096).

2. The saturated vapor pressure equals the zz-component of the pressure tensor. For T ≤ 300 K, the accuracy is not sufficient because the vapor pressure is too low. Note that the “kinetic pressure correction”,⁶⁴ which takes care about zero linear momentum in the periodic boundary conditions, is not (and should not be) included here.

3. The liquid density at the vapor pressure was obtained from the z-density profile. These densities differ slightly from those calculated in a box, see Table 2.

Table 2 Simulation results of the short-range SPC water model in a box, N = 1000, interpolated from a series of NVT simulations. Error estimates at low T are increased because od slow convergence

T (K)	ΔvapHm (J mol^−1)	ρ (kg m^−3)
250	46 615.5(50)	1001.23(30)
300	44 018.9(20)	973.14(12)
350	41 576.7(15)	929.64(8)
400	39 160.0(12)	874.58(7)

---

4. Similarly, the vapor density is obtained. The pressure obtained from the gas density by the virial equation of state with the second virial coefficient shows a good agreement with the P_zz-based pressure.

2.4.2 Simulations in a box. The enthalpies of vaporization and densities have been calculated from a series of NVT (N = 1000) simulations at several densities, fitting the pressures to a polynomial, determining the density corresponding to the vapor pressure, and interpolating the averaged potential energy per molecule, 〈E_pot〉. Other simulation parameters are the same as for the slab. The results are collected in Table 2. We have not used a single NPT simulation because in general the bulk modulus is needed for a correction (see below), and the bulk modulus is obtained more accurately using a pressure–volume dependence from a series of NVT simulations rather than from the volume fluctuation in one NPT simulation. The vaporization enthalpy per molecule is then

Δ_vapH₁ = −〈E_pot〉 + k_BT.

The simplifications are the same as for the Clausius–Clapeyron equation: the liquid volume is neglected and the vapor is ideal gas.

The mass densities have been fitted to

ρ = 960.86537 + 0.80351917T− 0.002548497T²

where ρ is in kg m⁻³ and T in K. The T = 250 K point is an outlier due to a long relaxation time, but the error is only 1 kg m⁻³.

2.4.3 Widom particle insertion. At 350 K and lower temperatures, the Widom method with a gradually growing particle is used⁶³ to determine the vapor pressure, see Table 3.

Table 3 Saturated vapor pressure of the short-range SPC model, calculated by the Widom method, where k denotes the number of steps and w the product of Widom insertion factors, see eqn (9)

T (K)	k	w	P ^s∞ [bar]
a Not used because affected by vapor nonideality.
250	32	1 090 005(9747)	0.001060(10)
300	26	33 657(300)	0.04003(36)
350	10	3167.4(91)	0.4741(14)
400	12	599.5(18)	2.693(9)^a

---

The Widom method is based on a numerical derivative of the residual (not containing the kinetic term) Helmholtz energy. Using the discrete step of ΔN = 1, the residual chemical potential (relative to the chemical potential of ideal gas at the same temperature T and number density n = (N + 1/2)/V, where V is the system volume) becomes

where β = k_BT, Ψ represents the potential energy increment from inserting a virtual (N + 1)-th molecule into the box, and 〈·〉₊₁ denotes averaging over random positions of the inserted molecule.

Since inserting a molecule into a dense liquid is difficult, a small molecule is inserted first. A series of (N + 1)VT simulations is then performed with an incomplete molecule, which is periodically virtually expanded to the next bigger one until the full molecule is reached. Then

where w₀ is given by eqn (8) with the small molecule. For steps i > 0 it holds

w_i = 〈e^{−βΨ(i−1→i)}〉_(N+1)VT, (10)

where, Ψ(i − 1 → i) is the energy change of swelling the additional molecule.

In the simulation, the equilibrium number density n₀ at a pressure P₀ close to the (yet unknown) vapor pressure is determined as in Section 2.4.2. The volume is set to V = (N + 1/2)/n₀ and w is calculated. The vapor pressure is

where φ^s is the vapor fugacity coefficient which is 1 for ideal gas; this is a good approximation except for T = 400 K. If the pressure estimate P₀ is not accurate enough, one may add a correction
where V_l is the molecular volume in liquid, B the isothermal bulk modulus (reciprocal value of compressibility), and Δρ = ρ(P^s) − ρ(P₀). The derivation of this formula follows the path of the derivation of the Kelvin equation. This correction was not applied in this study because P^s was close enough to P₀.

In step i = 0, the virtual particle was inserted N-times every 0.1 ps, in steps i > 0, the average was accumaled also every 0.1 ps. The parameters of the small molecules (Lennard-Jones cross-terms and partial charges) are collected in Tables 14 and 15 (ref. 65) along with the partial averaged Boltzmann factors, w_i, and their error estimates.

2.4.4 Thermodynamic description of truncated SPC water. Since the vaporization enthalpy of our model (based on classical mechanics) is very accurately (0.1%) a linear function of temperature, we use the following version of the integrated Clausius–Clapeyron equation

ln P^s = a − b/T + c ln(T), (12)

where P^s and T are in Pa and K, respectively. Parameters a = 65.2516, b = 7053.87, c = −5.860739 have been obtained by simultaneous fitting of the enthalpies and the available saturated vapor pressures. To do this, the estimated standard errors in enthalpies were multiplied by 10 because the enthalpy values are much more accurate that the saturated pressures (in spite of convergence problems at T = 250 K).

3 Results and discussion

3.1 Cluster sizes

The time-dependence of the averaged cluster size, N, is shown in Fig. 1. The calculations are based on m = 5001 independent evaporative runs for N₀ = 60, 100 and 160 molecules. The N₀ = 40 calculations (shorter) are based on m = 17 576 independent runs. The simulation methodology is described in Section 2.2.

Fig. 1 The number of particles in clusters as a function of time (logarithmic scale).

It is seen that there is a small artefact at short times corresponding to occasional evaporation events during the cluster preparation. This phenomenon decreases the average number of particles by several tenths on average.

Both models (see Section 2.3) predict slower evaporation than the simulations. The more accurate model taking into account the cluster thermodynamics as described by the Kelvin equation works better than the simple model with clusters just replaced by bulk water. Roughly we may conclude that including the Kelvin equation takes into account about one half of the finite-size phenomena. The agreement is better for larger clusters, but the convergence (if it exists) for N → ∞ is slow.

3.2 Cluster temperatures

The cooling profiles are shown in Fig. 2. Again, the macroscopic evaporation models predict slower evaporation and consequently smaller cooling rates. Since the models do not account for recoil, we also provide T_kin/LM (shown as a dashed yellow line over the black solid of T_kin) where the linear momentum is removed. However, the difference from T_kin is negligible. Rotations are not removed because T_kin ≈ T_AM with a higher precision than T_kin compares to T_AM.

Fig. 2 Cooling profiles of clusters. T_kin is the total kinetic temperature and T_kin/LM is the total kinetic temperature with the linear momentum removed. Symbols T_LM and T_AM denote the respective translational (calculated from the linear momentum) and rotational (from the angular momentum) temperatures, the error bar (1σ) shown in the left top corner applies to both.

The translational and rotational temperatures of whole clusters “as particles” are based on three degrees of fredom and m independent measurements. Since the variance of a single kinetic degree of freedom is Var T_kin = 2T², the standard error of both T_LM and T_AM is given by 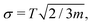which is depicted as an error bar in Fig. 2.

The translational temperature of whole clusters, T_LM, remains constant within statistical noise, which is in agreement with the theory explained in Section 2.1.2.

The rotational temperature of whole clusters, T_AM, is lower than the cluster internal temperature for N = 40 and N = 60, although for the latter, the difference is close to the common confidence limit of 2σ. For large clusters (N = 100 and N = 160), this observation is inconclusive because the differences are comparable to the error bars, and T_AM is already lower than T_kin/LM at the start of evaporation (by 1σ and 1.7σ, respectively).

At the same time, the decrease in T_AM is approximately −T/N or − 2T/N; therefore, we suggest that it is a finite-size effect on the order of . In other words, the cluster rotations are almost thermalized with the internal cluster temperature, except for small clusters where the rotations are slightly colder. Thermalization of the angular momentum is possible because the clusters are in a liquid state. For solid clusters undergoing sublimation, one would expect a constant T_AM, similarly to what is observed for T_LM.

3.3 Equipartition

The last observation is rather technical. The equipartition error ΔT_eqp according to eqn (1) should equal zero for systems in equilibrium. It converges to zero as for Verlet-like integrators, which is a purely numerical effect. In addition, ΔT_eqp depends on the formula used to calculate the velocities. If the more common velocity Verlet formula v_i(t) = [r(t + h) − r(t − h)]/2h = [v_i(t − h/2) + v_i(t + h/2)]/2 is used to calculate E_kin instead of the leap-frog-based eqn (3), the value of ΔT_eqp has oposite sign and is twice as large^62,64 – this is the reason why we prefer eqn (3). Note that the kinetic energy formulas are independent of the specific details of the Verlet or leap-frog algorithm. However, for the leap-frog method, the formula in eqn (3) is more natural, while the previously defined v_i(t) appears in the velocity Verlet method. (We note in passing that Beeman's method uses yet another velocity, specifically v_i(t) = [2v_i(t + h/2) + 5v_i(t − h/2) − v_i(t − 3h/2)]/6).

Simulations in a box with the same setup as for the cluster simulations (i.e., without equalizing masses and with h = 1.67 fs) give ΔT_eqp = −0.53 K for T = 250 K, which decreases to −0.88 K for T = 400 K. The equipartition errors for cluster simulations are drawn in Fig. 3. It is seen that the values are negative at simulation start in agreement with the numerical error. However, they grow to +1 or +2 K as the evaporation proceeds. The sign is in accord with the observation that the total angular momentum of evaporating cluster is on average smaller that would correspond to its internal temperature.

Fig. 3 Equipartition error as a function of time for evaporating clusters. The data are smoothed (rectangular window 10 ps wide) and reduced.

Our equilibrium calculations (see Section 2.4) were performed with a longer timestep, h = 2 fs, and equalized masses. The equipartition error ΔT_eqp is smaller in absolute value, ranging from −0.2 K at T = 250 K to −0.28 K at T = 400 K.

4 Conclusions

First, the evaporative cooling of water clusters has been simulated. The results are in a qualitative agreement with a model of evaporative cooling assuming the Hertz–Knudsen flux. The model taking into account the change of the chemical potential due to the Kelvin equation is more accurate, yet it does not take into account all finite-size effects.

Next, the kinetic energy of the system of clusters “as particles” does not decrease with temperature but remains constant, in agreement with the theoretical considerations in Section 2.1.2. This does not apply to the rotational temperature, which is slightly colder than the internal cluster temperature; however, for larger clusters, this observation is inconclusive.

Author contributions

MK performed the MD calculations of cluster evaporation. JJ coded the evaporation model. JK proposed the idea and performed simulations of the truncated SPC water model (to be used in the model of evaporation), and also finalized the paper using parts of the PhD thesis by MK.

Data availability

Averaged convergence profiles of the evaporation, data used to draw the figures, and selected raw simulation data are available.⁶⁵

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Czech Science Foundation, project 22-28869S, and by the project “The Energy Conversion and Storage”, funded as project no. CZ.02.01.01/00/22_008/0004617 by Programme Johannes Amos Comenius, call Excellent Research.

References

1. J. Lengyel, A. Pysanenko, V. Poterya, P. Slavíček, M. Fárník, J. Kočišek and J. Fedor, Phys. Rev. Lett., 2014, 112, 113401.
2. A. Bende, G. Perretta, P. Sementa and T. M. Di Palma, ChemPhysChem, 2015, 16, 3021–3029.
3. R. Baumfalk, U. Buck, C. Frischkorn, S. Gandhi and C. Lauenstein, Ber. Bunsen-Ges., 1997, 101, 606–613.
4. A. Borner, Z. Li and D. A. Levin, J. Chem. Phys., 2013, 138, 064302.
5. W. Christen, K. Rademann and U. Even, J. Chem. Phys. A, 2010, 114, 11189–11201.
6. R. L. Johnston, Atomic and Molecular Clusters, CRC Press, 2002.
7. U. Buck and R. Krohne, J. Chem. Phys., 1996, 105, 5408–5415.
8. C. Bobbert, S. Schütte, C. Steinbach and U. Buck, Eur. Phys. J. D, 2002, 19, 183–192.
9. C. E. Kolb and D. R. Worsnop, Annu. Rev. Phys. Chem., 2012, 63, 471–491.
10. T. Bartels-Rausch, Nature, 2013, 494, 27–29.
11. A. J. Amaya, H. Pathak, V. P. Modak, H. Laksmono, N. D. Loh, J. A. Sellberg, R. G. Sierra, T. A. McQueen, M. J. Hayes, G. J. Williams, M. Messerschmidt, S. Boutet, M. J. Bogan, A. Nilsson, C. A. Stan and B. E. Wyslouzil, J. Phys. Chem. Lett., 2017, 8, 3216–3222.
12. A. J. Amaya and B. E. Wyslouzil, J. Chem. Phys., 2018, 148, 084501.
13. A. Bogdan, M. J. Molina, H. Tenhu, E. Mayer and T. Loerting, Nat. Chem., 2010, 2, 197–201.
14. D. R. Moberg, D. Becker, C. W. Dierking, F. Zurheide, B. Bandow, U. Buck, A. Hudait, V. Molinero, F. Paesani and T. Zeuch, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24413–24419.
15. T. E. Gartmann, L. Ban, B. L. Yoder, S. Hartweg, E. Chasovskikh and R. Signorell, J. Phys. Chem. Lett., 2019, 10, 4777–4782.
16. B. Bandow and B. Hartke, J. Chem. Phys. A, 2006, 110, 5809–5822.
17. R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2011, 112, 1957–2011.
18. J. M. Anglada, G. J. Hoffman, L. V. Slipchenko, M. M. Costa, M. F. Ruiz-López and J. S. Francisco, J. Chem. Phys. A, 2013, 117, 10381–10396.
19. A. Bhabhe, H. Pathak and B. E. Wyslouzil, J. Chem. Phys. A, 2013, 117, 5472–5482.
20. D. Ghosh, A. Manka, R. Strey, S. Seifert, R. E. Winans and B. E. Wyslouzil, J. Chem. Phys., 2008, 129, 124302.
21. A. Khan, C. H. Heath, U. M. Dieregsweiler, B. E. Wyslouzil and R. Strey, J. Chem. Phys., 2003, 119, 3138–3147.
22. A. Manka, H. Pathak, S. Tanimura, J. Wölk, R. Strey and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2012, 14, 4505.
23. K. A. Streletzky, Y. Zvinevich, B. E. Wyslouzil and R. Strey, J. Chem. Phys., 2002, 116, 4058–4070.
24. E. Rathakrishnan, Gas Dynamics, PHI Learning, 2017.
25. S. Toxvaerd, J. Chem. Phys., 2015, 143, 154705.
26. W. Sun, S. Chen, Y. Hou, S. Bu, Z. Ma and L. Zhang, Int. J. Multiphase Flow, 2019, 121, 103118.
27. S. Sinha, A. Bhabhe, H. Laksmono, J. Wölk, R. Strey and B. Wyslouzil, J. Chem. Phys., 2010, 132, 064304.
28. Y. J. Kim, B. E. Wyslouzil, G. Wilemski, J. Wölk and R. Strey, J. Chem. Phys. A, 2004, 108, 4365–4377.
29. J. Farges, M. de Feraudy, B. Raoult and G. Torchet, Surf. Sci., 1981, 106, 95–100.
30. X.-Z. Wu, J.-J. Yan, W.-J. Li, D.-D. Pan and G.-Y. Liu, Exp. Therm. Fluid Sci., 2010, 34, 10–19.
31. H. Bae, I. Kim, E. Kim and J.-W. Lee, J. Aerosol Sci., 2010, 41, 243–256.
32. P. Parneix and F. Calvo, EPJ Web Conf., 2011, 18, 03003.
33. K. K. Dingilian, R. Halonen, V. Tikkanen, B. Reischl, H. Vehkamäki and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2020, 22, 19282–19298.
34. R. Halonen, V. Tikkanen, B. Reischl, K. K. Dingilian, B. E. Wyslouzil and H. Vehkamäki, Phys. Chem. Chem. Phys., 2021, 23, 4517–4529.
35. D. Becker, C. W. Dierking, J. Suchan, F. Zurheide, J. Lengyel, M. Fárník, P. Slavíček, U. Buck and T. Zeuch, Phys. Chem. Chem. Phys., 2021, 23, 7682–7695.
36. U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863–3890.
37. U. Buck and F. Huisken, Chem. Rev., 2000, 101, 205–206.
38. U. Buck, R. Krohne and P. Lohbrandt, J. Chem. Phys., 1997, 106, 3205–3215.
39. N. I. Hammer, J. R. Roscioli, J. C. Bopp, J. M. Headrick and M. A. Johnson, J. Chem. Phys., 2005, 123, 244311.
40. Y.-F. Lee, A.-M. Kelterer, G. Matisz, S. Kunsági-Máté, C.-Y. Chung and Y.-P. Lee, J. Chem. Phys., 2017, 146, 144308.
41. S. Tanimura, H. Pathak and B. E. Wyslouzil, J. Chem. Phys., 2013, 139, 174311.
42. P. Hirunsit, Z. Huang, T. Srinophakun, M. Charoenchaitrakool and S. Kawi, Powder Technol., 2005, 154, 83–94.
43. A. Borner, Z. Li and D. A. Levin, AIP Conf. Proc., 2012, 1501, 565–572.
44. R. Jansen, N. Gimelshein, S. Gimelshein and I. Wysong, J. Chem. Phys., 2011, 134, 104105.
45. G. Colonna and M. Capitelli, J. Thermophys. Heat Transfer, 2001, 15, 308–316.
46. G. Cao, L. Pan and K. Xu, J. Comput. Phys., 2021, 439, 110402.
47. A. Bastida, J. Zúñiga, A. Requena, B. Miguel, J. A. Beswick, J. Vigué and N. Halberstadt, J. Chem. Phys., 2002, 116, 1944–1953.
48. M. Klíma and J. Kolafa, J. Chem. Theory Comput., 2018, 14, 2332–2340.
49. D. Celný, M. Klíma and J. Kolafa, J. Chem. Theory Comput., 2021, 17, 7397–7405.
50. M. Klíma, D. Celný, J. Janek and J. Kolafa, J. Chem. Phys., 2023, 159, 124302.
51. C. E. Klots, J. Chem. Phys., 1985, 83, 5854–5860.
52. R. T. Jongma, Y. Huang, S. Shi and A. M. Wodtke, J. Chem. Phys. A, 1998, 102, 8847–8854.
53. T. D. Vaden, C. J. Weinheimer and J. M. Lisy, J. Chem. Phys., 2004, 121, 3102–3107.
54. O. M. Cabarcos and J. M. Lisy, Int. J. Mass Spectrom., 1999, 185–187, 883–903.
55. A. H. Persad and C. A. Ward, Chem. Rev., 2016, 116, 7727–7767.
56. R. Hołyst and M. Litniewski, J. Chem. Phys., 2009, 130, 074707.
57. L. Dombrovsky, A. Fedorets, V. Levashov, A. Kryukov, E. Bormashenko and M. Nosonovsky, Atmosphere, 2020, 11, 965.
58. G. Grégoire, M. Mons, I. Dimicoli, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, J. Chem. Phys., 1999, 110, 1521–1525.
59. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Interaction Models for Water in Relation to Protein Hydration, ed. B. Pullman, Springer Netherlands, Dordrecht, 1981, pp. 331–342.
60. P. Atkins and J. de Paula, Atkins’ Physical Chemistry, Oxford University Press, 9th edn, 2010.
61. MapleSoft, Maple, 2024, https://www.maplesoft.com/products/maple/.
62. J. Kolafa and M. Lísal, J. Chem. Theory Comput., 2011, 7, 3596–3607.
63. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 2017.
64. J. Janek and J. Kolafa, J. Chem. Phys., 2024, 160, 184111.
65. J. Kolafa, K. Bouzek and Š. Paušová, Dataset of ‘Molecular dynamics of evaporative cooling of water clusters’ DOI:10.5281/zenodo.13932327.

---