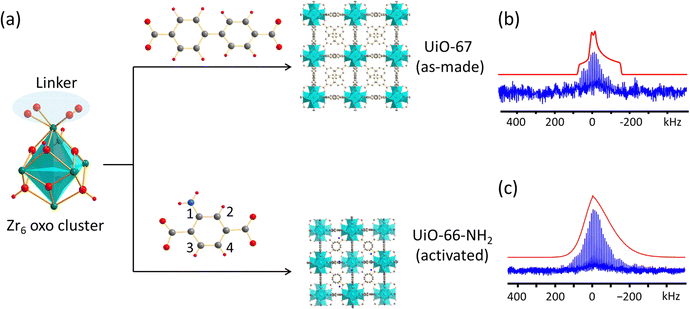
Open Access Article
Open Access ArticleLocal order, disorder, and everything in between: using 91Zr solid-state NMR spectroscopy to probe zirconium-based metal–organic frameworks†
Wanli
Zhang
a,
Bryan E. G.
Lucier
 a,
Vinicius
Martins
a,
Tahereh
Azizivahed
a,
Ivan
Hung
a,
Vinicius
Martins
a,
Tahereh
Azizivahed
a,
Ivan
Hung
 b,
Yijue
Xu
b,
Yijue
Xu
 b,
Zhehong
Gan
b,
Zhehong
Gan
 b,
Amrit
Venkatesh
b,
Amrit
Venkatesh
 bcd,
Tian Wei
Goh
bcd,
Tian Wei
Goh
 cd,
Wenyu
Huang
cd,
Wenyu
Huang
 cd,
Aaron J.
Rossini
cd,
Aaron J.
Rossini
 cd and
Yining
Huang
cd and
Yining
Huang
 *a
*a
aDepartment of Chemistry, University of Western Ontario, London, Ontario N6A 5B7, Canada. E-mail: yhuang@uwo.ca
bNational High Magnetic Field Laboratory, 1800 East Paul Dirac Drive, Tallahassee, Florida 32310, USA
cU.S. Department of Energy Ames National Laboratory, Ames, Iowa 50011, USA
dDepartment of Chemistry, Iowa State University, Ames, Iowa 50011, USA
First published on 6th February 2025
Abstract
Characterization of metal centers in metal–organic frameworks (MOFs) is critical for rational design and further understanding of structure–property relationships. The short-range structure about Zr atoms is challenging to properly elucidate in many Zr MOFs, particularly when local disorder is present. Static 91Zr solid-state NMR spectra of the seven zirconium MOFs UiO-66, UiO-66-NH2, UiO-67, MOF-801, MOF-808, DUT-68 and DUT-69 have been acquired at high magnetic fields of 35.2 T and 19.6 T, yielding valuable information on the local structure, site symmetry and order about Zr. 91Zr NMR is very sensitive to differences in MOF short-range structure caused by guest molecules, linker substitution and post-synthetic treatment. Complementary density functional theory (DFT) calculations assist in the interpretation and assignment of 91Zr solid-state NMR spectra, lend insight into structural origins of 91Zr NMR parameters and enable determination of local Zr coordination environments. This approach can be extended to many other materials containing zirconium.
Introduction
Metal–organic frameworks (MOFs) are hybrid materials composed of metal centers or metal-based clusters connected by organic linkers. This class of compounds has many applications, including in the fields of catalysis, gas storage, gas separation and energy storage.1 MOFs are composed of crystalline one-, two-, or three-dimensional structures, and the accompanying high degree of long-range order typically allows for straightforward structural determination via X-ray or neutron diffraction-based experiments. MOFs often harbor various types of short-range disorder that is difficult to investigate using diffraction-based crystallographic methods, including local compositional variations, positional disorder, atomic displacements, defect sites, and dynamic guests;2 many of these modes of disorder are present in Zr MOFs.3–5 When a crystal used in X-ray diffraction is not perfectly ordered, the amount of chemical disorder can be quantified by the fractional occupancy and/or anisotropic atomic displacement, but these values only reflect average disorder across the entire long-range ordered structure and cannot offer short-range insight.6 Solid-state NMR spectroscopy is an excellent complementary tool to diffraction, as it is very sensitive to the local environment around the nucleus and is applicable to disordered systems.6–8Zirconium-based MOFs are particularly attractive due to their high chemical stability, structural tunability, and diverse potential applications.9 For example, the UiO-66 MOF has demonstrated excellent catalytic performance for many reactions,10,11 and its structure can also be tailored through defect engineering.12 A common strategy to obtain highly crystalline Zr-MOFs involves the use of a modulation agent during synthesis;9 however, modulators typically produce structures with short-range disorder about the metal centers and organic linkers.3–5 The metal centers in MOFs play crucial roles in many applications; thus, fully understanding the short-range structure and local order around the metal is crucial for rational design of MOFs tailored for specific applications.13
Solid-state NMR spectroscopy has proven useful for investigating the local structures around metal ions in MOFs.14–18 Most NMR-active metal isotopes are quadrupolar nuclei and are intrinsically insensitive, including 91Zr. The only NMR-active Zr isotope, 91Zr (spin 5/2), has a very low magnetogyric ratio (γ) of −2.49750 × 107 rad T−1 s−1,19 a low natural isotope abundance of 11.23%,20 and a moderate quadrupole moment Q(91Zr) = −0.176 (barn);21 these properties often give rise to broad 91Zr solid-state NMR spectra with low signal-to-noise ratios that are challenging to acquire.22 MOF unit cells are typically large, resulting in significant weight dilution of Zr metal centers. The reduced density of 91Zr spins poses an additional challenge for acquisition of 91Zr solid-state NMR spectra at natural isotopic abundance. Due to these unfavorable conditions, there have been only three successful reported 91Zr solid-state NMR experiments on MOFs.4,16,23
Despite the multiple challenges associated with 91Zr NMR spectroscopy, this route has the potential to provide a wealth of information on the short-range metal environments in Zr-MOFs. The Q interacts with the electric field gradient (EFG) surrounding Zr in a process known as the quadrupolar interaction (QI). The QI is very sensitive to the local structure because, while Q is a constant, the EFG arises from the surrounding electronic environment. The quadrupolar coupling constant (CQ) and the asymmetry parameter (ηQ) are used to describe the QI. A higher CQ value corresponds to a larger EFG and a less symmetric local environment; larger CQ values give rise to broader 91Zr solid-state NMR spectra that are more challenging to collect. The ηQ value ranges from zero to one and reflects the axial symmetry of the EFG tensor; by extension, ηQ quantifies the local axial symmetry of the EFG about Zr. A lower ηQ corresponds to a more axially symmetric environment. 91Zr solid-state NMR spectra are also influenced to a lesser degree by the chemical shift (CS) interaction, particularly the isotropic chemical shift (δiso),24 although the 91Zr solid-state NMR spectrum of UiO-66_Ac30 at 35.2 T in this work illustrates how chemical shift anisotropy (CSA) can have some impact.
The development of NMR instruments with high magnetic fields (>18.8 T) in recent decades have rendered solid-state NMR of unreceptive nuclei feasible, including 91Zr. Higher magnetic fields enhance the inherent sensitivity of the NMR experiment and also significantly reduce spectral line broadening associated with quadrupolar nuclei, as the second-order QI is inversely proportional to the magnetic field strength. Leveraging these advantages, high-field 91Zr solid-state NMR spectroscopy has been used to investigate ordered materials such as zirconium halides, zirconium phosphates, and zirconocenes.23–29 The quadrupolar Carr−Purcell Meiboom−Gill (QCPMG)30 pulse sequence has also proven useful for acquiring NMR spectra of insensitive quadrupolar nuclei such as 91Zr.31 Despite the vast potential of 91Zr solid-state NMR spectroscopy, molecular-level characterization of Zr-based MOFs is rare and often challenging.4,16,23
91Zr solid-state NMR spectroscopy at high magnetic fields of 35.2 and 19.6 T has been used to characterize several representative Zr-MOFs, with the results also providing insights into the local disorder known to exist in such systems.2 The well-known UiO-66 and UiO-67 MOFs are first examined, revealing a lower rotational site symmetry around Zr than was indicated from the single crystal structure. The impact of missing-linker defects in UiO-66 MOFs is characterized. The origins and effects of linker-related disorder are probed in the UiO-66-NH2 MOF. Using MOF-801, we then show how 91Zr NMR spectroscopy can be used to monitor the Zr local environment during thermal activation of a MOF. Chemical-induced changes in the Zr local structure are explored in the post-acidification treatment of MOF-808. Finally, the influence of a synthesis modulator on local order and structure is illustrated using the DUT-68 and DUT-69 MOFs. DFT calculations can provide detailed insight into the origin of QI parameters; we have performed calculations using plane-wave DFT and cluster DFT approaches that shed light on the structural origins of these 91Zr NMR spectra (Fig. S9 and Table S2, ESI†).
Results and discussion
UiO-66 was first reported in 2008 and is one of the most well-known and widely studied Zr-MOFs.32 This material has exhibited exceptional tunability and can incorporate various chemical functionalities,10 which is promising for applications in fields such as gas adsorption, gas separation, catalysis, and chemical sensing.10,12 The structure of UiO-66 was initially solved using powder X-ray diffraction (PXRD),32 and later by single crystal XRD.33 UiO-66 resides in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, with the zirconium-oxo secondary building units (SBUs) occupying the vertices and face-centered locations in the cubic unit cell (Fig. 1(a)); the SBUs are connected by benzene-1,4-dicarboxylate (BDC) linkers. Each Zr is coordinated to eight oxygen atoms, where the four oxygens termed O1 originate from four separate BDC linkers and the other four O2 oxygens are μ3-O atoms from O2− and OH− groups. SCXRD experiments33 revealed that the μ3-O site is disordered with a 0.5 fractional occupancy in both possible positions (O2i and O2ii), while Zr possesses local C4 rotational symmetry.
m space group, with the zirconium-oxo secondary building units (SBUs) occupying the vertices and face-centered locations in the cubic unit cell (Fig. 1(a)); the SBUs are connected by benzene-1,4-dicarboxylate (BDC) linkers. Each Zr is coordinated to eight oxygen atoms, where the four oxygens termed O1 originate from four separate BDC linkers and the other four O2 oxygens are μ3-O atoms from O2− and OH− groups. SCXRD experiments33 revealed that the μ3-O site is disordered with a 0.5 fractional occupancy in both possible positions (O2i and O2ii), while Zr possesses local C4 rotational symmetry.
 | ||
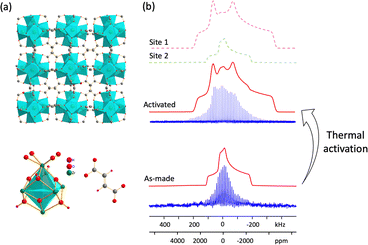
| Fig. 1 (a) The long-range structure of UiO-66, along with the local structure about Zr from single crystal XRD.33 (b) Experimental (blue) and simulated (red) static 91Zr QCPMG solid-state NMR spectra of as-made and activated UiO-66 obtained at a magnetic field of 35.2 T. (c) CQ and ηQ values calculated using plane-wave DFT plotted versus the number of water molecules incorporated in each primitive cell. The activated structure has zero water molecules per primitive cell, while the as-made structure features eight water molecules per cell. | ||
The static 91Zr solid-state NMR spectra of as-made and activated UiO-66 acquired at 35.2 T are shown in Fig. 1(b). Thermal activation of UiO-66 was carried out to remove water from the pores of the MOF, which was confirmed by 1H–13C CP/MAS and 1H MAS NMR experiments (Fig. S2, ESI†). The spectrum of activated UiO-66 features a relatively well-defined QI-dominated powder pattern corresponding to a CQ(91Zr) of 35.5(3) MHz, ηQ of 0.78(3), and δiso of −150(50) ppm (Table 1). The intensity of the experimental NMR spectrum at lower frequencies (i.e., lower ppm values) is slightly less in comparison to analytical simulations. This difference can be attributed to imperfections in the rf pulses (see numerical simulations, Fig. S10, ESI†), anisotropy of the spin echo transverse relaxation times  across the frequency range, and local disorder. The non-zero ηQ indicates that there cannot be ≥C3 rotational symmetry at Zr, which conflicts with the reported C4 rotational symmetry.33 The possible positions for the two O2− and two OH− groups (O2i and O2ii, Fig. 1(a), occupancies of 0.5 each) lead to four possible oxygen structural configurations about Zr in line with the Fm
across the frequency range, and local disorder. The non-zero ηQ indicates that there cannot be ≥C3 rotational symmetry at Zr, which conflicts with the reported C4 rotational symmetry.33 The possible positions for the two O2− and two OH− groups (O2i and O2ii, Fig. 1(a), occupancies of 0.5 each) lead to four possible oxygen structural configurations about Zr in line with the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Fig. S11, ESI†): (1) two O2− and two OH− groups occupy O2i; (2) two O2− and two OH− groups occupy O2ii; (3) two OH− groups are located at O2i and two O2− groups are located at O2ii; (4) two OH− groups are located at O2ii and two O2− groups are located at O2i. If all instances are equally probable, the experimental 91Zr NMR spectrum should be composed of contributions from all four possible configurations.
m space group (Fig. S11, ESI†): (1) two O2− and two OH− groups occupy O2i; (2) two O2− and two OH− groups occupy O2ii; (3) two OH− groups are located at O2i and two O2− groups are located at O2ii; (4) two OH− groups are located at O2ii and two O2− groups are located at O2i. If all instances are equally probable, the experimental 91Zr NMR spectrum should be composed of contributions from all four possible configurations.
| δ iso (ppm) | C Q (MHz) | η Q | Source of local disorder at Zr | ||
|---|---|---|---|---|---|
a Simulations for UiO-66_Ac30 included CSA parameters as indicated in Fig. 2.
b In these simulations, a value of 0 was used for  , and the uncertainty in this parameter was determined to be no larger than 0.05.
c The DFT calculations were performed on the structure with minimal energy, and the averaged values from plane-wave and cluster DFT calculations are listed here (details in Table S3, ESI).
d The Czjzek model was used for this simulation, and the resulting , and the uncertainty in this parameter was determined to be no larger than 0.05.
c The DFT calculations were performed on the structure with minimal energy, and the averaged values from plane-wave and cluster DFT calculations are listed here (details in Table S3, ESI).
d The Czjzek model was used for this simulation, and the resulting  value is listed here. Please refer to the SI for a more detailed description of the Czjzek and extended Czjzek models. value is listed here. Please refer to the SI for a more detailed description of the Czjzek and extended Czjzek models.
|
|||||
| UiO-66 (as made) | |||||
| Experimental | −100(50) | 31.5(3) | 0.85(3) | 0.00(5)b | — |
| Plane-wave DFT | −309 | 29.5 | 0.82 | — | — |
| Cluster DFT | −46 | 28.5 | 0.92 | — | — |
| UiO-66 (activated) | |||||
| Experimental | −150(50) | 35.5(3) | 0.78(3) | 0.00(5)b | — |
| Plane-wave DFT | −286 | 30.7 | 0.73 | — | — |
| Cluster DFT | −34 | 29.1 | 0.58 | — | — |
| UiO-66_Ac30 (activated)a | |||||
| Experimental | −100(30) | 32.5(3) | 0.79(3) | 0.00(5)b | — |
| UiO-67 (as made) | |||||
| Experimental | −20(30) | 23.2(7) | 0.91(3) | 0.00(5)b | — |
| Plane-wave DFT | −286 | 28.9 | 0.73 | — | — |
| Cluster DFT | −39 | 25.3 | 0.92 | — | — |
| UiO-66-NH2 (activated) | |||||
| Experimental | 150(20) | 26.5(8) | 0.72(5) | 0.60(6) | BDC-NH2 linker |
| Plane-wave DFTc | −236 | 29.6 | 0.75 | — | — |
| Cluster DFTc | −39 | 30.6 | 0.63 | — | — |
| MOF-808 (activated) | |||||
| Experimental | 80(10) | 18.4(5) | 0.90(3) | 0.07(2) | HCOO− ions |
| Plane-wave DFT | 176 | 16.6 | 0.86 | — | — |
| Cluster model | −53 | 17.6 | 0.89 | — | — |
| MOF-808-1.3SO4 (as made) | |||||
| Experimental | 50(10) | 17.0(5) | 0.72(4) | 0.35(4) | SO42− ions |
| MOF-801 (as-made) | |||||
| Experimental | 0(50) | 20.0(6) | 0.90(3) | 0.10(3) | H2O molecules |
| Cluster model | −9 | 26.6 | 0.84 | — | — |
| MOF-801 (activated) | |||||
| Experimental/site 1 | 0(40) | 29.0(10) | 0.65(3) | 0.00(5)b | — |
| Experimental/site 2 | 0(50) | 20.0(6) | 0.90(4) | 0.10(3) | H2O molecules |
| Plane-wave DFT | −221 | 30.8 | 0.64 | — | — |
| Cluster model | −8 | 31.2 | 0.50 | — | — |
| DUT-68 (as made) | |||||
| Experimental | −38.0(10) | 14.9(6)d | N/A | — | Zr-oxo clusters in pore |
| DUT-69 (as made) | |||||
| Experimental/site 1 | 150(20) | 18.5(3) | 0.38(2) | — | — |
| Experimental/site 2 | 0(20) | 19.1(4) | 0.85(3) | — | — |
Using the four possible oxygen configurations in UiO-66 as starting points, plane-wave DFT geometry optimizations were performed on all atoms in the four structures. Geometry optimization using all four possible configurations as a starting point yielded the same outcome: the O2− groups move to the O2i sites, while the OH− groups move to the O2ii sites, in an outcome resembling the aforementioned situation (4). Plane-wave DFT calculations produced a CQ(91Zr) of 30.7 MHz and ηQ of 0.73 in all cases, which were in good agreement with experimental findings. The optimized structure featured a Zr–OH− (Zr–O2ii) bond length of 2.265 Å, which is considerably longer than the Zr–O2− (Zr–O2i) length of 2.066 Å. The single-crystal XRD structure of UiO-6633 indicates there are two distinct Zr–O bond lengths of 2.063 and 2.271 Å in the Zr cluster, though no specific assignment to O2− or OH− moieties was provided. Our DFT optimized Zr–O and Zr–OH bond lengths are consistent with the experimental observations and provide possible assignments for the two different bond lengths. These calculated bond lengths, paired with the non-zero experimental ηQ value, indicate that the actual Zr rotational site symmetry is ≤C2 rather than C4. Despite the fractional occupancy of the O2 sites, our 91Zr NMR spectra and DFT calculations indicate there is a relatively ordered local short-range environment around Zr. It appears that one configuration is prevalent: two OH− groups are located at O2i and two O2− groups are at O2ii.
The static 91Zr NMR spectrum of as-made UiO-66 containing water molecules in the pores (Fig. 1(b)) yielded a CQ(91Zr) of 31.5(3) MHz, a ηQ of 0.85(3) and a δiso of −100(50) ppm. The significant increase in ηQ over activated UiO-66 corresponds to a lower degree of 91Zr EFG axial symmetry, which is due to guest water molecules in the pores. The water oxygen atom is situated 1.97 Å from the framework OH− group in the crystal structure (Fig. 1(c)).33 Seeing as the primitive cell contains eight equivalent water positions, calculations of 91Zr NMR parameters following the plane-wave DFT geometry optimizations were performed on structures incorporating one to eight water molecules, with CQ and ηQ results plotted in Fig. 1(c). It was found that ηQ increased and CQ decreased with the number of water molecules, indicating a decrease of axial symmetry but an increase in overall spherical symmetry about Zr with increasing water population; this observation is in good agreement with the activated and as-made experimental findings. Cluster DFT calculations on the {Zr8O4(OH)4(COO)12(C6H4COOH)12·H2O} and {Zr8O4(OH)4(COO)12(C6H4COOH)12} models (Fig. S12(a), ESI†) yielded trends similar to those from plane-wave DFT calculations (Table 1). The case of UiO-66 demonstrates how 91Zr NMR is very sensitive to changes in the local environment owing to guest molecules, and how 91Zr NMR can be used to characterize the short-range order about Zr in MOFs; both approaches are significantly more effective when paired with DFT calculations.
Engineering linker or cluster defects in crystalline MOFs to better address applications in gas adsorption,34 separation,35 and catalysis is of significant interest.36 While the impact of missing linker defects in UiO-66 has been studied in terms of structural and thermal stability, the local atomic-scale structure of these defects has been notoriously difficult to characterize.37 A well-known study used single crystal XRD to determine that missing linker structural defects originated from water molecules coordinated directly to the zirconium centers, with charge compensation provided by a hydroxide ion that was hydrogen-bonded to a nodal μ3-OH species.33 Despite several efforts, a definitive determination of the local structure of these UiO-66 defects has remained elusive.
To further investigate the impact of missing linker defects, UiO-66 synthesized with an acetic acid modulator to increase the concentration of defects (termed UiO-66_Ac30) and a sample of UiO-66_Ac30 treated at 300 °C to remove acetate groups (denoted UiO-66_Ac30 (heat-treated)) were examined using solid-state NMR spectroscopy. The amount of acetic groups in UiO-66_Ac30 was estimated to be 12% from 1H solution NMR spectra (Fig. S13, ESI†). The one-dimensional 1H and 13C NMR spectra of UiO-66_Ac30 (Fig. 2(a)) contain signals originating from the acetate, DMF and phenyl groups.38 The resonance assignments were confirmed from the through-space correlations evident in 1H–13C CP HETCOR NMR spectra (Fig. 2(a), right). The two-dimensional 1H–1H DQ-SQ NMR spectrum (Fig. 2(a), left) reveals that the DMF methyl groups and acetate moieties are spatially proximate to aromatic hydrogen atoms. These observations are indicative of interactions between solvent DMF and the UiO-66 carboxylate framework linkers. Note that the secondary 1H NMR signal from DMF, typically found between 7 and 8 ppm, is not prominently visible in our 1H MAS NMR spectra of the as-made UiO-66 samples due to the strong intensity of the nearby aromatic signal. This observation aligns with previous studies on UiO-66 MOFs that reported the secondary DMF signal was present as only a weak resonance or a minor shoulder feature in the spectra.23,38,39
Heat treatment of UiO-66_Ac30 to produce UiO-66_Ac30 (heat-treated) resulted in several spectral changes (Fig. 2(b)). The 1H signal intensity of the methyl groups in UiO-66_Ac30 (heat-treated) was significantly diminished. The 1H NMR signals at 2.1 ppm and 2.5 ppm from UiO-66_Ac30 likely originate from terminal μ1-OH and/or μ1-OH2 groups at defect sites,39 but may also have contributions from μ3-OH species in regions without defects.38,40–42 After heat treatment of UiO-66_Ac30, the aromatic and Cα13C NMR signals were shifted from 130 ppm to 129 ppm and 138 ppm to 136 ppm, respectively, which was presumably due to the removal of DMF. As the samples were exposed to air after synthesis, the removal of UiO-66_Ac30 (heat-treated) acetate groups likely resulted in the formation of μ1-OH or μ1-OH2 species at the vacant Zr sites in the cluster.
To probe the Zr local environment further, 91Zr solid-state NMR experiments were performed at 35.2 T. The 91Zr NMR spectrum of UiO-66_Ac30 contains a well-defined second-order quadrupolar powder pattern that has features which can only be modeled using 91Zr CSA (Fig. 2(c)). The similarity in the measured quadrupolar parameters between UiO-66_Ac30 and UiO-66 (as-made), along with the well-defined features of the 91Zr NMR spectrum of UiO-66_Ac30, indicates the first coordination sphere of Zr is largely preserved in UiO-66_Ac30 and contains both BDC and acetate ligands. 91Zr QCPMG experiments on UiO-66_Ac30 (heat-treated) revealed that a longer  was present, resulting in a slower decay of the signal during the QCPMG echo train, which in turn yielded a higher signal-to-noise ratio. This observation was somewhat unexpected in these non-decoupled spectra, since the presence of μ1-OH hydrogen proximate to 91Zr should result in stronger 91Zr–1H dipolar couplings and a reduced
was present, resulting in a slower decay of the signal during the QCPMG echo train, which in turn yielded a higher signal-to-noise ratio. This observation was somewhat unexpected in these non-decoupled spectra, since the presence of μ1-OH hydrogen proximate to 91Zr should result in stronger 91Zr–1H dipolar couplings and a reduced  . The observed 91Zr NMR spectrum of UiO-66_Ac30 (heat-treated) appears otherwise identical to that of UiO-66_Ac30. This could be because the relatively small amount of defective Zr sites are associated with much higher CQ(91Zr) values, making the corresponding very broad resonances nearly impossible to observe using 91Zr solid-state NMR experiments.
. The observed 91Zr NMR spectrum of UiO-66_Ac30 (heat-treated) appears otherwise identical to that of UiO-66_Ac30. This could be because the relatively small amount of defective Zr sites are associated with much higher CQ(91Zr) values, making the corresponding very broad resonances nearly impossible to observe using 91Zr solid-state NMR experiments.
We performed DFT calculations on cluster models to generate potential models for defective Zr sites in UiO-66 (Fig. S12, ESI†). The defective unsaturated Zr4+ center yielded a calculated CQ value of 69.6 MHz, which would give rise to resonances four times broader than those of the main 91Zr NMR signals, making them challenging or impossible to observe using existing NMR instrumentation and methods. When OH− or H2O is bound to a defective Zr4+ center at distances larger than ca. 3 Å, the calculated CQ also becomes very large (i.e., >50 MHz, Fig. S12(b), ESI†). When the bond length between Zr and μ1-OH at defect sites in UiO-66 is relatively short (e.g., 2.26 Å, similar to that of Zr-μ3-OH), DFT calculations predict a comparable CQ(91Zr) value to that of defect-free Zr in UiO-66; distinguishing between the two different signals does not appear to be possible from these 91Zr NMR experiments. This explanation aligns with the structural similarity proposed in the Cluster 4 model (Fig. S12, ESI†), where the local Zr environment containing defects could be nearly identical to that of defect-free Zr. This is consistent with the hypothesis of μ1-OH or μ1-OH2 species formation at the vacant Zr sites in the cluster. While these results indicate that 91Zr solid-state NMR could potentially be used to probe the local environment in defective Zr MOFs, measures to significantly increase experimental sensitivity and resolution would be required. Further evaluation will be necessary to unequivocally establish the local structure of these defects in UiO-66, which is beyond the scope of this work.
The concept of reticular synthesis, in which MOFs of similar topology can be created using related organic linkers (e.g., linkers of different lengths), is instrumental to the design and synthesis of new MOFs.43,44 A striking example of reticular synthesis is modification of the UiO-66 synthesis to generate UiO-67; the linker was changed from BDC to 4,4′-biphenyl-dicarboxylate (BPDC), resulting in a pore size increase from 8 Å to 12 Å, while the Zr6O8(OH)8 SBU and overall MOF topology were preserved.32 The static 91Zr NMR spectrum of UiO-67 at 35.2 T (Fig. 3(b)) features a single Zr site corresponding to a CQ(91Zr) of 23.2(7) MHz, a ηQ of 0.91(3) and a δiso of −20(30) ppm, which has lower CQ and higher ηQ values than those observed from UiO-66. Potential root causes for the different NMR parameters between UiO-66 and -67 were then investigated.
The local geometry and symmetry at Zr is intimately linked to 91Zr EFG parameters, particularly CQ(91Zr). In an Archimedean antiprism with eight local nodes (i.e., the coordination environment about Zr in this system), the s/l ratio can be used to quantify the degree of local distortion from ideal geometry, where s refers to the edge length of the square planes and l is the edge length of triangular faces in the distorted antiprism (Fig. S14(b), ESI†). The distortion parameter ξ, also known as the Poraï-Koshits and Aslanov criteria,26,45 can then be used to measure distortion. In this case,  a perfect antiprism yields ξ = 0, where larger ξ values correspond to higher degrees of distortion and thus increased CQ(91Zr). An examination of geometry-optimized structures reveals the Zr local distortion parameter in UiO-67 (ξ = 1.11) is smaller than that of UiO-66 (ξ = 1.33), which explains the lower CQ(91Zr) value observed in UiO-67. The relatively larger ηQ and lower axial symmetry at Zr in UiO-67 may originate from the flexibility of BPDC linker phenyl rings.46 To further investigate, DFT calculations were performed on two cluster models of {Zr8O4(OH)4(COO)12(C12H8COOH)12} (Fig. S14, ESI†), where the first model (model 1) employed two coplanar phenyl rings, while the second model (model 2) introduced a dihedral angle of 32.7° between the two phenyl groups, which was taken from the SCXRD structure.46 DFT calculations predicted a relatively smaller CQ value and a larger ηQ when the non-zero dihedral angle was present, with calculations producing values similar to experimental findings. In this instance, the combination of 91Zr NMR experiments and DFT calculations illustrates how 91Zr NMR parameters are sensitive not only to the local bonding geometry, but also to linkers and their orientations beyond the immediate coordination environment.
a perfect antiprism yields ξ = 0, where larger ξ values correspond to higher degrees of distortion and thus increased CQ(91Zr). An examination of geometry-optimized structures reveals the Zr local distortion parameter in UiO-67 (ξ = 1.11) is smaller than that of UiO-66 (ξ = 1.33), which explains the lower CQ(91Zr) value observed in UiO-67. The relatively larger ηQ and lower axial symmetry at Zr in UiO-67 may originate from the flexibility of BPDC linker phenyl rings.46 To further investigate, DFT calculations were performed on two cluster models of {Zr8O4(OH)4(COO)12(C12H8COOH)12} (Fig. S14, ESI†), where the first model (model 1) employed two coplanar phenyl rings, while the second model (model 2) introduced a dihedral angle of 32.7° between the two phenyl groups, which was taken from the SCXRD structure.46 DFT calculations predicted a relatively smaller CQ value and a larger ηQ when the non-zero dihedral angle was present, with calculations producing values similar to experimental findings. In this instance, the combination of 91Zr NMR experiments and DFT calculations illustrates how 91Zr NMR parameters are sensitive not only to the local bonding geometry, but also to linkers and their orientations beyond the immediate coordination environment.
Derivatives of UiO-66 can be prepared by introducing functional groups, such as –NH2, to address specific applications. For instance, the CO2/N2 selectivity of UiO-66-NH2 is enhanced over that of UiO-66, owing to strong interactions between CO2 and the –NH2 linker group.47 The various possible crystallographic positions of the –NH2 group introduces significant uncertainty to the UiO-66-NH2 unit cell. The PXRD patterns of UiO-66-NH2 and UiO-66 are almost identical, indicating commonalities between long-range structures (Fig. S1, ESI†). The 1H–13C CP/MAS NMR and 1H MAS NMR (Fig. S4, ESI†) of activated UiO-66-NH2 indicates that there are very few guest solvent molecules remaining after activation. The 1H–13C CP/MAS NMR spectra of UiO-66-NH2 feature relatively broader signals compared to the corresponding spectra of UiO-66, which is due to the presence of increased local disorder (Fig. S4, caption, ESI†).40 The 91Zr NMR experiments at 35.2 T were performed on an activated sample to prevent any influence on the local environment from guest solvents. The static 91Zr NMR spectrum of UiO-66-NH2(activated) at 35.2 T (Fig. 3(c)) features a broad, asymmetric powder pattern that lacks clear features and tails off in intensity toward the low frequency range; these signs are indicative of a distribution of EFG parameters arising from local disorder.
The 91Zr NMR lineshape of UiO-66-NH2 is featureless, arising from a Gaussian-like distribution of 91Zr NMR parameters. This stands in marked contrast to the 91Zr NMR spectra of both as-made and activated UiO-66 (Fig. 1), which exhibit well-defined lineshapes typical of a quadrupolar nucleus in an ordered local environment. As the Zr6-oxo cluster in the UiO-66 and UiO-66-NH2 materials is the same, the differences between the 91Zr NMR spectra of UiO-66-NH2 and UiO-66 must originate from the –NH2 group of the organic linker in UiO-66-NH2. The linker appears to be associated with local disorder about Zr beyond the first coordination sphere.
The EFG at Zr in a given system is determined by both (i) the immediate local environment and (ii) the surroundings beyond the first coordination sphere. In situations of high local order about Zr, the 91Zr EFG tensor and NMR spectrum correspond to well-defined CQ and ηQ values. In contrast, when local disorder is present about Zr, there is an intrinsic distribution of 91Zr EFG tensor parameters arising from the range of potential local chemical environments. An extended Czjzek model (ECM) can be used to quantify the effects of local disorder on the 91Zr EFG distribution.48 The ECM is appropriate for modeling the EFG distribution in a local Zr environment that contains contributions from both the ordered immediate coordination environment and the disordered, more distant surroundings. An ECM utilizes a combination of fixed CQ and ηQ values along with a separate distribution of values drawn from a range of CQ and ηQ; a more detailed description on ECM is contained in the ESI.† An ECM allows for a quantitative measure of the local disorder in MOFs based on NMR spectra.15,49
In the case of UiO-66-NH2, an ECM using a fixed CQ(91Zr) of 26.5(8) MHz and fixed ηQ of 0.72(5) was used to fit the experimental 91Zr NMR spectrum, along with a 0.6 measure of disorder  simulations using other
simulations using other  values are shown in Fig. S15(a) (ESI†) and the best-fit CQ and ηQ distributions are illustrated in Fig. S15(b) (ESI†). The fixed 91Zr EFG contribution to the NMR spectrum of UiO-66-NH2 arises from the ordered ZrO8 immediate local environment, which is similar to that of UiO-66. The need for an ECM and large distribution in 91Zr NMR parameters (i.e.,
values are shown in Fig. S15(a) (ESI†) and the best-fit CQ and ηQ distributions are illustrated in Fig. S15(b) (ESI†). The fixed 91Zr EFG contribution to the NMR spectrum of UiO-66-NH2 arises from the ordered ZrO8 immediate local environment, which is similar to that of UiO-66. The need for an ECM and large distribution in 91Zr NMR parameters (i.e.,  ) is rooted in the disordered nature of the amino linker groups, since a given linker amino group may assume one of four positions with respect to Zr. One Zr6 cluster (Zr6O8(OH)8(BDC-NH2)12) in the primitive cell is attached to twelve linkers, which leads to 412 ≈ 1.6 × 107 different spatial atomic configurations beyond the first coordination sphere of Zr, and a correspondingly sizable distribution of 91Zr EFG parameters. DFT calculations of 91Zr NMR parameters using the reported most stable configuration of UiO-66-NH2 based on relative energies50 yielded CQ and ηQ values close to the fixed experimental CQ and ηQ used in the ECM simulations (Table 1), confirming that the immediate local environment about Zr is relatively ordered; however, 91Zr NMR simulations based on DFT calculations were unsatisfactory matches for the entire experimental spectrum (Fig. S16, ESI†), owing to local disorder beyond the first coordination sphere of Zr. These UiO-66-NH2 results clearly show how 91Zr NMR can be used to investigate local disorder in MOFs and to confirm the presence of a distribution of Zr local environments.
) is rooted in the disordered nature of the amino linker groups, since a given linker amino group may assume one of four positions with respect to Zr. One Zr6 cluster (Zr6O8(OH)8(BDC-NH2)12) in the primitive cell is attached to twelve linkers, which leads to 412 ≈ 1.6 × 107 different spatial atomic configurations beyond the first coordination sphere of Zr, and a correspondingly sizable distribution of 91Zr EFG parameters. DFT calculations of 91Zr NMR parameters using the reported most stable configuration of UiO-66-NH2 based on relative energies50 yielded CQ and ηQ values close to the fixed experimental CQ and ηQ used in the ECM simulations (Table 1), confirming that the immediate local environment about Zr is relatively ordered; however, 91Zr NMR simulations based on DFT calculations were unsatisfactory matches for the entire experimental spectrum (Fig. S16, ESI†), owing to local disorder beyond the first coordination sphere of Zr. These UiO-66-NH2 results clearly show how 91Zr NMR can be used to investigate local disorder in MOFs and to confirm the presence of a distribution of Zr local environments.
MOF-808 is a mesoporous MOF with high thermal and mechanical stability that has potential applications in gas separation, gas adsorption, and catalysis.51 The MOF-808 framework is composed of Zr6O4(OH)4 nodes connected by benzene-1,3,5-tricarboxylate (BTC) linkers to form a structure with one unique Zr site that crystallizes in the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic space group (Fig. 4(a)). Each Zr6 node has twelve-fold connectivity and is bound to six BTC linkers and six formate ligands. The 91Zr NMR spectra of MOF-808 at 19.6 T (Fig. 4(b)) can be simulated by a single Zr resonance corresponding to a CQ value of 18.4(5) MHz and a ηQ of 0.90(3). The relatively lower CQ and higher ηQ values versus the UiO-66/67 MOFs are due to the different Zr local coordination modes. In MOF-808, each Zr is bound to four μ3-O atoms, two carboxyl O atoms, and two O atoms from terminal formate ions, while Zr is bound to four μ3-O atoms and four carboxyl O atoms in UiO-66/67. To investigate the impact of these different local configurations, both plane-wave and cluster DFT calculations were performed on the optimized structure, yielding results in good agreement with experimental findings (Table 1).
m cubic space group (Fig. 4(a)). Each Zr6 node has twelve-fold connectivity and is bound to six BTC linkers and six formate ligands. The 91Zr NMR spectra of MOF-808 at 19.6 T (Fig. 4(b)) can be simulated by a single Zr resonance corresponding to a CQ value of 18.4(5) MHz and a ηQ of 0.90(3). The relatively lower CQ and higher ηQ values versus the UiO-66/67 MOFs are due to the different Zr local coordination modes. In MOF-808, each Zr is bound to four μ3-O atoms, two carboxyl O atoms, and two O atoms from terminal formate ions, while Zr is bound to four μ3-O atoms and four carboxyl O atoms in UiO-66/67. To investigate the impact of these different local configurations, both plane-wave and cluster DFT calculations were performed on the optimized structure, yielding results in good agreement with experimental findings (Table 1).
A sulfated version of MOF-808 was synthesized using post-synthetic modification52 of activated MOF-808 with 0.01 M sulfuric acid for 24 hours, yielding MOF-808-1.3SO4. The product was analogous to MOF-808-xSO4, where x is the average number of sulfate groups per secondary building unit (SBU) from elemental analysis;53 an illustration of a Zr6 oxo cluster substituted with two SO42− groups is shown in Fig. 4(c). The 1H–13C CP/MAS NMR spectrum of MOF-808-1.3SO4 contains a much less intense carboxylic carbon signal compared to that of MOF-808 (Fig. S6, ESI†), which indicates that HCOO− groups have been partially replaced by SO42−. In this system, the SO42− ions replace formate ions and directly form Zr–O bonds.52 The 91Zr NMR spectra of MOF-808-1.3SO4 is shown in Fig. 4(b), along with our attempts to use simulations involving both a discrete set of NMR parameters and an ECM to extract 91Zr NMR parameters. The 91Zr NMR spectrum of acidified MOF-808-1.3SO4 is relatively featureless, in contrast to the more well-defined spectrum of activated MOF-808. These results indicate there is some degree of local disorder about Zr centers in the acidified MOF, which is due to the random replacement of formate ions with SO42− groups. The 91Zr NMR powder pattern of MOF-808-1.3SO4 was successfully simulated using an ECM employing a fixed CQ(91Zr) value of 17.0(5) MHz, a fixed ηQ of 0.72(4), and a 0.35 measure of disorder  (Fig. S17, ESI†). The fixed 91Zr EFG tensor components originate from the coordinated μ3-O atoms and O atoms from BTC linkers, while the disordered component (i.e.,
(Fig. S17, ESI†). The fixed 91Zr EFG tensor components originate from the coordinated μ3-O atoms and O atoms from BTC linkers, while the disordered component (i.e.,  ) arise from the various possible partial substitution configurations of the six proximate formate ligands by SO42− ions. The
) arise from the various possible partial substitution configurations of the six proximate formate ligands by SO42− ions. The  value in the 91Zr ECM NMR simulation of MOF-808-1.3SO4 is substantially smaller than that of UiO-66-NH2, since there are far fewer possible local environments. A more intense acidification treatment using 0.1 M H2SO4 was applied to obtain MOF-808-2.3SO4, which yielded a 91Zr NMR spectrum very similar to that of MOF-808-1.3SO4, and no significant differences were apparent with regards to local order (Fig. S18(a), ESI†). In contrast, the 91Zr NMR signals in the time domain (i.e., prior to Fourier transform) were clearly distinct, with the MOF-808-2.3SO4 signal associated with a
value in the 91Zr ECM NMR simulation of MOF-808-1.3SO4 is substantially smaller than that of UiO-66-NH2, since there are far fewer possible local environments. A more intense acidification treatment using 0.1 M H2SO4 was applied to obtain MOF-808-2.3SO4, which yielded a 91Zr NMR spectrum very similar to that of MOF-808-1.3SO4, and no significant differences were apparent with regards to local order (Fig. S18(a), ESI†). In contrast, the 91Zr NMR signals in the time domain (i.e., prior to Fourier transform) were clearly distinct, with the MOF-808-2.3SO4 signal associated with a  relaxation time ca. 25% less than that of the MOF-808-1.3SO4 version (Fig. S18(b), ESI†). This finding suggests that while there may be a limit to the level of acid substitution level in this system quantifiable by 91Zr NMR frequency domain spectra, the time domain signals can still yield valuable information on the local Zr environment. These examples illustrate how 91Zr NMR can be used to understand the degree of local order about metal centers in MOFs.
relaxation time ca. 25% less than that of the MOF-808-1.3SO4 version (Fig. S18(b), ESI†). This finding suggests that while there may be a limit to the level of acid substitution level in this system quantifiable by 91Zr NMR frequency domain spectra, the time domain signals can still yield valuable information on the local Zr environment. These examples illustrate how 91Zr NMR can be used to understand the degree of local order about metal centers in MOFs.
The intrinsically high stability of Zr-based MOFs makes these materials excellent candidates for water capture. MOF-801, or Zr-fumarate (Zr6O4(OH)4(fumarate)6), has one of the highest documented MOF water uptake values, does not lose water capacity after five adsorption and desorption cycles, can be readily regenerated at room temperature,51 and also has a high adsorption capacity for hydrocarbons.54 The structure of MOF-801 was solved using PXRD55 and SCXRD.51 MOF-801 has one unique Zr site and resides in the cubic Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group, which is of lower symmetry than UiO-66; no face-centered symmetry is present, owing to the fumarate linker that is not strictly linear (Fig. 5(a)). The static 91Zr NMR spectrum of as-made MOF-801 at 19.6 T is shown in Fig. 5(b), featuring spectral intensity that gradually tails off to low frequency, indicating that some degree of disorder is present; the spectrum was accordingly simulated using an ECM (Table 1). The 91Zr NMR parameters of as-made MOF-801 indicate that a significantly higher degree of overall symmetry about Zr (lower CQ) but a slightly lower amount of axial symmetry (higher ηQ) are present in comparison to Zr within UiO-66. The presence of a hydrogen-bonded network of water molecules in the as-made MOF-801 pores explains both 91Zr NMR trends,51 and is one source of the local disorder at Zr.
space group, which is of lower symmetry than UiO-66; no face-centered symmetry is present, owing to the fumarate linker that is not strictly linear (Fig. 5(a)). The static 91Zr NMR spectrum of as-made MOF-801 at 19.6 T is shown in Fig. 5(b), featuring spectral intensity that gradually tails off to low frequency, indicating that some degree of disorder is present; the spectrum was accordingly simulated using an ECM (Table 1). The 91Zr NMR parameters of as-made MOF-801 indicate that a significantly higher degree of overall symmetry about Zr (lower CQ) but a slightly lower amount of axial symmetry (higher ηQ) are present in comparison to Zr within UiO-66. The presence of a hydrogen-bonded network of water molecules in the as-made MOF-801 pores explains both 91Zr NMR trends,51 and is one source of the local disorder at Zr.
Thermal activation was performed to remove water from the pores of MOF-801. The 91Zr NMR spectrum of activated MOF-801 again consisted of a distribution of similar Zr sites. This spectrum was simulated using a dominant signal of 85% relative intensity with a CQ of 29.0(10) MHz and ηQ of 0.65(5), along with a minor resonance of 15% intensity using the same 91Zr NMR parameters of as-made MOF-801; the minor site arises from insufficient activation or water adsorption from air during NMR sample preparation. Plane-wave DFT calculations on the fully optimized empty (i.e., activated) structure of MOF-801 yielded a CQ of 30.2 MHz and ηQ of 0.62, which were very good matches to the major Zr signal in the activated NMR spectrum. To probe the effect of adsorbed water molecules on the 91Zr NMR parameters, cluster DFT calculations were performed (Fig. S19, ESI†). The {Zr8O4(OH)4(COO)12(C2H2COOH)12·4H2O} model using the water position closest to Zr based on the crystal structure51 produced a relatively smaller CQ of 26.6 MHz but a larger ηQ of 0.84, and both values were closer to the as-made MOF-801 experimental values. In contrast, cluster DFT calculations on {Zr8O4(OH)4(COO)12(C2H2COOH)12} without water yielded a larger CQ of 31.2 MHz and smaller ηQ of 0.50, which were better matches to the activated MOF-801 experimental data. These 91Zr NMR and DFT calculation results illustrate how 91Zr NMR parameters are highly sensitive to changes in the local environment.
The selection of a specific modulator during MOF synthesis is very important, as this can affect MOF nucleation, topology, and properties. The reaction of ZrCl4 and 2,5-thiophenedicarboxylic acid (H2TDC) in DMF (DMF = dimethylformamide), using 180 equivalents of acetic acid as the modulator, yields the Zr6O6(OH)2(TDC)4.5(CH3COO) MOF, also known as DUT-68(Zr), which resides in the Im3![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) space group.56 The 91Zr NMR spectrum at 19.6 T (Fig. 6(c)) indicates that a distribution of Zr local environments are present; simulations using a Czjzek model yielded
space group.56 The 91Zr NMR spectrum at 19.6 T (Fig. 6(c)) indicates that a distribution of Zr local environments are present; simulations using a Czjzek model yielded  (Fig. S20, ESI†). Further examination of the SCXRD structure56 revealed two potential sources for the 91Zr NMR parameter distribution (Fig. S21, ESI†): (i) the framework features two crystallographically independent eight-connected Zr6O6(OH)2(TDC)4.5(CH3COO) clusters, along with six inequivalent Zr sites in each Zr-oxo SBU; (ii) DUT-68 has four relatively large pores measuring 27.7 Å, 13.9 Å, 12.5 Å and 8 Å in diameter, which contain occluded and disordered Zr-oxo clusters.56 The multitude of Zr local environments resulting from these two structural factors give rise to significant local disorder, explaining the relatively featureless 91Zr NMR spectral appearance.
(Fig. S20, ESI†). Further examination of the SCXRD structure56 revealed two potential sources for the 91Zr NMR parameter distribution (Fig. S21, ESI†): (i) the framework features two crystallographically independent eight-connected Zr6O6(OH)2(TDC)4.5(CH3COO) clusters, along with six inequivalent Zr sites in each Zr-oxo SBU; (ii) DUT-68 has four relatively large pores measuring 27.7 Å, 13.9 Å, 12.5 Å and 8 Å in diameter, which contain occluded and disordered Zr-oxo clusters.56 The multitude of Zr local environments resulting from these two structural factors give rise to significant local disorder, explaining the relatively featureless 91Zr NMR spectral appearance.
DUT-69(Zr) can be obtained from the same route as DUT-68(Zr), but using only 50 equivalents of the acetic acid modulator during synthesis. DUT-69(Zr) has a composition of Zr6O4(OH)4(TDC)5(CH3COO)2(H2O)2 and consists of a uninodal 10-connected framework with the bct topology, along with octahedral cages measuring ca. 5 Å in diameter (Fig. 6(b)). There is a single type of Zr6 cluster in DUT-69 that features six inequivalent Zr sites, with the local SBU connectivity shown in Fig. S22(a) (ESI†). In the SBU, Zr1 and Zr4 are each bound to three TDC linkers and one water, Zr2 and Zr5 are connected to three TDC linkers and one molecule of CH3COO−, while Zr3 and Zr6 are coordinated to four TDC linkers. The static 91Zr NMR spectrum of DUT-69 at 19.6 T is shown in Fig. 6(c). Accurate simulation required the use of two distinct Zr signals arising from two unique Zr sites (Table 1); site 1 corresponded to a CQ of 18.5(3) MHz and ηQ of 0.38(2), and site 2 was simulated using a CQ of 19.1(4) MHz and ηQ of 0.85(3). Both plane-wave and cluster DFT calculations were performed on the optimized structure (Table S4, ESI†) to assign the two 91Zr NMR resonances. Simulated NMR spectra based on the DFT-calculated 91Zr NMR parameters were constructed (Fig. S22, ESI†), which contained lineshapes similar to the experimental spectrum. These simulated spectra were used as guides to assign the experimental 91Zr NMR spectrum; site 1 in the experimental spectrum was assigned to Zr2 and Zr3, while site 2 was assigned to Zr1, Zr4, Zr5, and Zr6. We note that both plane-wave and cluster DFT approaches overestimated experimental CQ values, which is likely due to inaccuracies regarding the CH3COO− local environment in the crystal structure.56
During the review of our manuscript, a study by Nadol et al.23 was published, employing low-temperature (140 K) 91Zr NMR with the WURST-CPMG sequence to investigate the stability of Zr MOFs, including UiO-66 and MOF-801. Their work focused on analyzing Zr MOF stability, while our study explores local disorder across 11 Zr MOFs. Significant differences in 91Zr NMR parameters were observed, likely due to temperature effects. For UiO-66, Nadol et al. reported δiso = −28 ± 50 ppm, CQ = 22.1 MHz, and ηQ = 0.61 at 140 K, while our room-temperature results yielded δiso = −100 ± 50 ppm, CQ = 31.5 ± 0.3 MHz, and ηQ = 0.85 ± 0.03. Similarly, for MOF-801, their parameters at 140 K were δiso = −30 ppm, CQ = 31.8 MHz, and ηQ = 0.75, compared to our values of δiso = 0 ± 40 ppm, CQ = 29.0 ± 1.0 MHz, and ηQ = 0.65 ± 0.03 at 298 K.
While Nadol et al. enhanced the signal-to-noise ratio by performing experiments at 140 K, our use of a 35.2 T ultra-high magnetic field with a standard CPMG sequence establishes that high signal-to-noise ratio 91Zr spectra can be achieved at room temperature. Performing experiments at ultrahigh field allows researchers to probe the temperature-dependent chemical environments of Zr sites under conditions closer to those envisoned for practical applications.
Conclusions
In summary, wideline and ultra-wideline 91Zr solid-state NMR spectra of Zr MOFs have been successfully obtained, yielding rich information on the Zr local environments and local order in each system. The 91Zr solid-state NMR spectra are sensitive to the nature of coordinated ligands along with the degree of local disorder, and indicate the presence of guest solvents, specific linker orientations, and the number of possible linker configurations; these experiments can also shed light on the results of ion exchange reactions. Plane-wave and cluster DFT calculations are valuable complementary methods that can assist in the analysis of 91Zr NMR parameters and their specific structural origins. The detailed data available from 91Zr SSMR spectroscopy and DFT calculations in this work illustrates how this approach should be a powerful avenue to investigate Zr-containing MOFs going forward.Experimental details
Sample synthesis
All chemicals were purchased from Sigma-Aldrich and used without further purification.Different activation procedures were used to ensure complete removal of guest molecules while preserving framework structure. For most MOFs examined aside from UiO-66_Ac30, activation at 150 °C under dynamic vacuum (<1 mbar) for 24 hours was used to remove non-coordinated solvent molecules. For UiO-66_Ac30, a higher activation temperature of 300 °C under vacuum was required to effectively eliminate CH3COOH, H2O, and DMF molecules directly coordinated to the Zr centers based on the procedure described by Kandiah et al.53
Solid-state NMR experiments
All 91Zr solid-state NMR experiments at 35.2 T (ν0(91Zr) = 139.46 MHz) were performed on the series-connected hybrid (SCH) magnet58 at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, FL, USA, using a Bruker NEO console. A single channel home-built static probe with a 4 mm coil was used for static quadrupolar Carr–Purcell–Meiboom–Gill (QCPMG)30 NMR experiments with a 90° pulse length of 1.45 μs. The post-pulse ring-down time in the Meiboom–Gill (MG) loops was set to 20.3 μs, and the number of MG loops was adjusted such that the complete free induction decay (FID) of transverse magnetization was acquired (i.e., T2 decay mechanisms prevented any further detectable refocusing of the signal). The experimental settings corresponded to a spikelet separation of ca. 9.5 kHz in the frequency domain.91Zr solid-state NMR spectra of UiO-66_Ac30 and UiO-66_Ac30 (heat treated) samples were also recorded at 35.2 T using static QCPMG experiments. Central transition (CT) selective π/2 and π pulse lengths of 1.4 and 2.8 μs, respectively, were used. Spectra were obtained at three and five offsets (separated by ca. 75.5 kHz) for UiO-66_Ac30 and UiO-66_Ac30 (heat treated), respectively, using the VOCS (variable offset cumulative spectra) acquisition method59 to ensure uniform excitation of the 91Zr NMR spectra. The QCPMG spikelet separation was set to be ca. 6.3 kHz.
Solid-state 91Zr NMR spectra at 19.6 T (ν0(91Zr) = 77.3 MHz) were also recorded at the NHMFL. A Bruker Avance console and a home-built wide-line probe were used, with all MOF samples packed into a 4 mm MAS rotor. Static 91Zr NMR spectra were obtained using the QCPMG sequence with a 90° pulse length of 2.0 μs. More detailed acquisition parameters for each MOF are shown in Table S1 (ESI†).
Additional details on 13C and 1H NMR experiments can be found in SI, and the corresponding spectra are shown in Fig. S2–S7 (ESI†).
Theoretical calculations
All calculations were performed on SHARCNET computational clusters (https://www.sharcnet.ca/). The CASTEP software package60 was used to perform ab initio plane-wave density functional theory (DFT) calculations of 91Zr EFG tensor parameters. Perdew, Burke, and Ernzerhof (PBE) functionals61 and the generalized gradient approximation (GGA) for the exchange correlation energy were used in all instances, along with a plane-wave basis set cutoff energy of 800 eV. Calculations employed “on-the-fly” ultrasoft pseudopotentials62 and the gauge-including projector-augmented wave (GIPAW)63 formalism. The crystal structures were taken from the Cambridge Crystallographic Data Centre (CCDC) dataset and subjected to geometry optimization using CASTEP; settings included a total energy convergence tolerance of 1 × 10−5 eV per atom, a maximum ionic force tolerance of 0.03 eV Å−1, a maximum ionic displacement tolerance of 0.001 Å, and a maximum stress component tolerance of 0.05 GPa. To assess the accuracy of the plane-wave DFT approach for 91Zr NMR parameters, calculations were performed for a series of simple compounds in which the 91Zr NMR parameters had previously been experimentally determined (Fig. S8 and Table S2, ESI†). Visualization of the EFG tensors produced from CASTEP calculations was performed using the MagresView code.64To address fractional occupancy sites in a crystal structure, one can generate a series of potential structural models based on the different possible atomic arrangements at defined positions within the unit cell or supercell.65 When fractional occupation issues lead to a large number of possible configurations (e.g., solvent positions in a MOF), calculations and the accompanying analyses become extremely challenging. To investigate the impact of solvent molecules in MOFs, DFT calculations on isolated molecular clusters (“cluster model” DFT calculations) were employed. Cluster model DFT calculations were performed using the Gaussian 16 software package66 and the B3LYP method. The Zr basis set consisted of a (17s13p9d) configuration contracted to [12s9p5d], with two sets of diffuse p functions (αp = 0.11323 and 0.04108) and one diffuse d function (αd = 0.0382).24 The 6-311G** basis set was used for all other atoms. The EFG tensors calculated using the cluster model DFT calculations were visualized using the EFGShield software package.67
Data availability
The data supporting this article have been included as part of the ESI,† including sample preparation, solid-state NMR experimental details, powder XRD patterns, DFT calculations, additional 91Zr experimental and simulated NMR spectra. Additional data that support the findings of this study are available from the corresponding author upon request.Author contributions
W. Z.: conceptualization, investigation, formal analysis, computation, writing, review, editing; B. E. G. L.: writing, review, editing; V. M.: investigation, review, editing; T. A.: investigation, I. H., Y. X., T. W. G.: investigation; A. V.: investigation, review, editing; Z. G., W. H., A. J. R.: resources, funding, review, editing; Y. H.: conceptualization, resources, funding, formal analysis, writing, review, editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. H. thanks the Natural Science and Engineering Research Council (NSERC) of Canada for a Discovery Grant. Synthesis of UiO-66 samples and solid-state NMR experiments (A. V., T. W. G, W. H., A. J. R.) were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The Ames Laboratory is operated for the U.S. DOE by Iowa State University under Contract DE-AC02-07CH11358. This work was made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: https://www.sharcnet.ca), Compute/Calcul Canada, and the Digital Research Alliance of Canada. The National High Magnetic Field Laboratory is supported by the National Science Foundation through NSF/DMR-1644779 and NSF/DMR-2128556, and the State of Florida.References
- H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed
.
- A. K. Cheetham, T. D. Bennett, F.-X. Coudert and A. L. Goodwin, Dalton Trans., 2016, 45, 4113–4126 RSC
.
- C. Koschnick, M. W. Terban, R. Frison, M. Etter, F. A. Böhm, D. M. Proserpio, S. Krause, R. E. Dinnebier, S. Canossa and B. V. Lotsch, J. Am. Chem. Soc., 2023, 145, 10051–10060 CrossRef CAS PubMed
.
- C. Koschnick, R. Stäglich, T. Scholz, M. W. Terban, A. von Mankowski, G. Savasci, F. Binder, A. Schökel, M. Etter and J. Nuss, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed
.
- S. Tatay, S. Martínez-Giménez, A. Rubio-Gaspar, E. Gómez-Oliveira, J. Castells-Gil, Z. Dong, Á. Mayoral, N. Almora-Barrios, N. M. Padial and C. Martí-Gastaldo, Nat. Commun., 2023, 14, 6962 CrossRef CAS PubMed
.
- D. Massiot, R. J. Messinger, S. Cadars, M. Deschamps, V. Montouillout, N. Pellerin, E. Veron, M. Allix, P. Florian and F. Fayon, Acc. Chem. Res., 2013, 46, 1975–1984 CrossRef CAS PubMed
.
- J. Kümmerlen and A. Sebald, Organometallics, 1997, 16, 2971–2980 CrossRef
.
- P. Florian and D. Massiot, CrystEngComm, 2013, 15, 8623–8626 RSC
.
- S. Yuan, J.-S. Qin, C. T. Lollar and H.-C. Zhou, ACS Cent. Sci., 2018, 4, 440–450 CrossRef CAS PubMed
.
- J. Winarta, B. Shan, S. M. Mcintyre, L. Ye, C. Wang, J. Liu and B. Mu, Cryst. Growth Des., 2019, 20, 1347–1362 CrossRef
.
- J. N. Hall and P. Bollini, React. Chem. Eng., 2019, 4, 207–222 RSC
.
- Y. Feng, Q. Chen, M. Jiang and J. Yao, Ind. Eng. Chem. Res., 2019, 58, 17646–17659 CrossRef CAS
.
- T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F. X. Coudert, Nat. Chem., 2016, 9, 11–16 CrossRef PubMed
.
- C. He, S. Li, Y. Xiao, J. Xu and F. Deng, Solid State Nucl. Magn. Reson., 2022, 117, 101772 CrossRef CAS PubMed
.
- O. V. Petrov, V. Chlan, J. Rohlíček, J. Demel, J. Veselý and J. Lang, J. Phys. Chem. C, 2020, 124, 12569–12579 CrossRef CAS
.
- P. He, B. E. G. Lucier, V. V. Terskikh, Q. Shi, J. Dong, Y. Chu, A. Zheng, A. Sutrisno and Y. Huang, J. Phys. Chem. C, 2014, 118, 23728–23744 CrossRef CAS
.
- Y. T. A. Wong, V. Martins, B. E. G. Lucier and Y. Huang, Chem. – Eur. J., 2019, 25, 1848–1853 CrossRef CAS PubMed
.
- R. S. K. Madsen, A. Qiao, J. Sen, I. Hung, K. Chen, Z. Gan, S. Sen and Y. Yue, Science, 2020, 367, 1473–1476 CrossRef CAS PubMed
.
- R. K. Harris, E. D. Becker, S. M. C. de Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795–1818 CrossRef CAS
.
- J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. De Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss and T. Walczyk, Pure Appl. Chem., 2016, 88, 293–306 CrossRef CAS
.
- N. J. Stone, At. Data Nucl. Data Tables, 2016, 111, 1–28 CrossRef
.
- B. E. G. Lucier and Y. Huang, Annu. Rep. NMR Spectrosc., 2015, 84, 233–289 CrossRef CAS
.
- A. Nadol, F. Venel, R. Giovine, M. Leloire, C. Volkringer, T. Loiseau, C. Gervais, C. Mellot-Draznieks, B. Doumert and J. Trébosc, Chem. Sci., 2025, 16, 69–82 RSC
.
- A. J. Rossini, I. Hung, S. A. Johnson, C. Slebodnick, M. Mensch, P. A. Deck and R. W. Schurko, J. Am. Chem. Soc., 2010, 132, 18301–18317 CrossRef CAS PubMed
.
- Z. Yan, C. W. Kirby and Y. Huang, J. Phys. Chem. C, 2008, 112, 8575–8586 CrossRef CAS
.
- O. Pauvert, F. Fayon, A. Rakhmatullin, S. Kramer, M. Horvatic, D. Avignant, C. Berthier, M. Deschamps, D. Massiot and C. Bessada, Inorg. Chem., 2009, 48, 8709–8717 CrossRef CAS PubMed
.
- J. Zhu, Z. Lin, Z. Yan and Y. Huang, Chem. Phys. Lett., 2008, 461, 260–265 CrossRef CAS
.
- J. Czernek, L. Kobera, L. Havlak, V. Czerneková, J. Rohlíček, J. Bárta and J. Brus, Chem. Phys. Lett., 2020, 738, 136855 CrossRef CAS
.
- A. F. R. Kilpatrick, N. H. Rees, Z. R. Turner, J.-C. Buffet and D. O’Hare, Mater. Chem. Front., 2020, 4, 3226–3233 RSC
.
- F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, J. Phys. Chem. A, 1997, 101, 8597–8606 CrossRef CAS
.
- F. H. Larsen, J. Skibsted, H. J. Jakobsen and N. C. Nielsen, J. Am. Chem. Soc., 2000, 122, 7080–7086 CrossRef CAS
.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef PubMed
.
- C. A. Trickett, K. J. Gagnon, S. Lee, F. Gándara, H. Bürgi and O. M. Yaghi, Angew. Chem., Int. Ed., 2015, 54, 11162–11167 CrossRef CAS PubMed
.
- H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525–10532 CrossRef CAS PubMed
.
- Q. Qian, P. A. Asinger, M. J. Lee, G. Han, K. Mizrahi Rodriguez, S. Lin, F. M. Benedetti, A. X. Wu, W. S. Chi and Z. P. Smith, Chem. Rev., 2020, 120, 8161–8266 CrossRef CAS PubMed
.
- D. Yang and B. C. Gates, ACS Catal., 2019, 9, 1779–1798 CrossRef CAS
.
- L. Valenzano, B. Civalleri, S. Chavan, S. Bordiga, M. H. Nilsen, S. Jakobsen, K. P. Lillerud and C. Lamberti, Chem. Mater., 2011, 23, 1700–1718 CrossRef CAS
.
- F. Venel, C. Volkringer, O. Lafon and F. Pourpoint, Solid State Nucl. Magn. Reson., 2022, 120, 101797 CrossRef CAS PubMed
.
- Y. Ma, X. Han, S. Xu, Z. Wang, W. Li, I. Da Silva, S. Chansai, D. Lee, Y. Zou and M. Nikiel, J. Am. Chem. Soc., 2021, 143, 10977–10985 CrossRef CAS PubMed
.
- S. Devautour-Vinot, G. Maurin, C. Serre, P. Horcajada, D. P. da Cunha and V. Guillerm, Chem. Mater., 2012, 24, 2168–2177 CrossRef CAS
.
- J. Tang, S. Li, Y. Su, Y. Chu, J. Xu and F. Deng, J. Phys. Chem. C, 2020, 124, 17640–17647 CrossRef CAS
.
- W.-L. Peng, F. Liu, X. Yi, S. Sun, H. Shi, Y. Hui, W. Chen, X. Yu, Z. Liu and Y. Qin, J. Phys. Chem. Lett., 2022, 13, 9295–9302 CrossRef CAS PubMed
.
- O. M. Yaghi, M. O’Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS PubMed
.
- Z. Chen, S. L. Hanna, L. R. Redfern, D. Alezi, T. Islamoglu and O. K. Farha, Coord. Chem. Rev., 2019, 386, 32–49 CrossRef CAS
.
- M. A. Porai-Koshits and L. A. Aslanov, J. Struct. Chem., 1972, 13, 244–253 CrossRef
.
- S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370–5372 CrossRef
.
- X. Jiang, S. Li, S. He, Y. Bai and L. Shao, J. Mater. Chem. A, 2018, 6, 15064–15073 RSC
.
- F. Vasconcelos, S. Cristol, J.-F. Paul, L. Delevoye, F. Mauri, T. Charpentier and G. Le Caër, J. Phys.: Condens. Matter, 2013, 25, 255402 CrossRef PubMed
.
- J. Xu, E. S. M. Blaakmeer, A. S. Lipton, T. M. McDonald, Y. M. Liu, B. Smit, J. R. Long, A. P. M. Kentgens and J. A. Reimer, J. Phys. Chem. C, 2017, 121, 19938–19945 CrossRef CAS
.
- B. Ni, W. Sun, J. Kang and Y. Zhang, J. Phys. Chem. C, 2020, 124, 11595–11608 CrossRef CAS
.
- H. Furukawa, F. Gándara, Y. B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381 CrossRef CAS PubMed
.
- J. Jiang, F. Gándara, Y.-B. Zhang, K. Na, O. M. Yaghi and W. G. Klemperer, J. Am. Chem. Soc., 2014, 136, 12844–12847 CrossRef CAS PubMed
.
- C. A. Trickett, T. M. Osborn Popp, J. Su, C. Yan, J. Weisberg, A. Huq, P. Urban, J. Jiang, M. J. Kalmutzki and Q. Liu, Nat. Chem., 2019, 11, 170–176 CrossRef CAS PubMed
.
- P. Iacomi, F. Formalik, J. Marreiros, J. Shang, J. Rogacka, A. Mohmeyer, P. Behrens, R. Ameloot, B. Kuchta and P. L. Llewellyn, Chem. Mater., 2019, 31, 8413–8423 CrossRef CAS
.
- G. Wißmann, A. Schaate, S. Lilienthal, I. Bremer, A. M. Schneider and P. Behrens, Microporous Mesoporous Mater., 2012, 152, 64–70 CrossRef
.
- V. Bon, I. Senkovska, I. A. Baburin and S. Kaskel, Cryst. Growth Des., 2013, 13, 1231–1237 CrossRef CAS
.
- F. Vermoortele, B. Bueken, G. Le Bars, B. Van de Voorde, M. Vandichel, K. Houthoofd, A. Vimont, M. Daturi, M. Waroquier and V. Van Speybroeck, J. Am. Chem. Soc., 2013, 135, 11465–11468 CrossRef CAS PubMed
.
- Z. Gan, I. Hung, X. Wang, J. Paulino, G. Wu, I. M. Litvak, P. L. Gor’kov, W. W. Brey, P. Lendi, J. L. Schiano, M. D. Bird, I. R. Dixon, J. Toth, G. S. Boebinger and T. A. Cross, J. Magn. Reson., 2017, 284, 125–136 CrossRef CAS PubMed
.
- D. Massiot, I. Farnan, N. Gautier, D. Trumeau, A. Trokiner and J. P. Coutures, Solid State Nucl. Magn. Reson., 1995, 4, 241–248 CrossRef CAS PubMed
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B, 2007, 76, 024401 CrossRef
.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef
.
- S. Sturniolo, T. F. G. Green, R. M. Hanson, M. Zilka, K. Refson, P. Hodgkinson, S. P. Brown and J. R. Yates, Solid State Nucl. Magn. Reson., 2016, 78, 64–70 CrossRef CAS PubMed
.
- S. Cadars, A. Lesage, C. J. Pickard, P. Sautet and L. Emsley, J. Phys. Chem. A, 2009, 113, 902–911 CrossRef CAS PubMed
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson and H. H. Nakatsuji, et al., Gaussian 16, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. Adiga, D. Aebi and D. L. Bryce, Can. J. Chem., 2007, 85, 496–505 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03704a |
| This journal is © the Owner Societies 2025 |