Overlooked hydroperoxyl radical reactions in ammonia oxidation under combustion conditions

Abstract

The present work focuses on highlighting bimolecular reactions in the NH₃ system involving HO₂, an important radical at intermediate combustion temperatures. The reaction mechanism generator (RMG) tool was used to identify potentially significant reactions, and the automated rate calculator (ARC) tool was used to automatically compute rate coefficients at the ΛCCSD(T)/aug-cc-pVTZ-F12//B2PLYP-D3/aug-cc-pVTZ level of theory. Several reactions explored in this work, such as N + HO₂ ⇌ NH + O₂, NH + HO₂ ⇌ NH₂ + O₂, NNH + HO₂ ⇌ N₂H₂ + O₂, and HNO₂ + HO₂ ⇌ NO₂ + H₂O₂, have not been thoroughly investigated in the existing literature. In particular, the reaction HNO + HO₂ ⇌ HNOH + O₂, though known, lacks a precise rate coefficient in recent chemical kinetic models for ammonia. This study provides computed rate coefficients for 10 hydrogen abstraction and disproportionation reactions involving HO₂ in the NH₃ system. The reaction rate coefficients computed here may improve future low- and intermediate-temperature oxidation models of NH₃.

---

1. Introduction

Ammonia has great potential to become a future zero-carbon energy carrier.^1–5 The advantages of ammonia as a fuel include a relatively high power-to-fuel-to-power (PFP) efficiency,⁶ a large-scale distribution infrastructure that is already in place, a high-octane rating, and a narrow flammability range, making it relatively safe in terms of explosion risks. On the other hand, ammonia is toxic, emits significant levels of pollutants upon combustion (NO_x and NH₃ residuals) and has a relatively low reactivity as a fuel.³ A commonly proposed solution to this problem involves mixing ammonia with small amounts of additional fuels, such as hydrogen. To make ammonia a viable energy carrier, it is crucial to have a reliable and versatile predictive⁷ chemical kinetic model for its ignition and oxidation. Although an ammonia oxidation system involves relatively small molecules and substantial research efforts have been made to model it, there is still an ongoing debate regarding its ignition and oxidation chemistry.^8–10

The main oxygen-containing radicals in the ammonia oxidation system are O, OH, O₂, HO₂, NO, NO₂, H₂NO, and HNOH.¹¹ At intermediate temperatures typical of ignition engines, HO₂ is the main radical chain carrier. This study aims to identify and examine previously unexplored hydrogen abstraction and disproportionation reactions in the ammonia system involving HO₂, and to compute the rate coefficients for these reactions.

Dean and Bozzelli¹² estimated the rate coefficient of HNO + O₂ ⇌ NO + HO₂ by analogy to other RH + O₂ reactions. Klippenstein et al.¹³ computed the rate coefficient for NNH + O₂ ⇌ N₂ + HO₂ at the CASPT2/aug-cc-pVDZ level¹⁴ when exploring the role of NNH in NO formation. Stagni and Cavallotti¹⁵ computed a rate coefficient for H₂NO + HO₂ ⇌ HNO + H₂O₂ and H₂NO + O₂ ⇌ HNO + HO₂ at the CASPT2/aug-cc-pVTZ level, while Chavarrio Cañas et al.¹⁶ computed rate coefficients for the latter reaction on both the doublet and the quartet surfaces at the W3X-L//CCSD/cc-pVTZ level (where the triplet HNO is the product on the quartet surface). Klippenstein and Glarborg¹⁷ computed the rate coefficient of NH₂ + HO₂ ⇌ NH₃ + O₂ at the CCSD(T)-F12/CBS level. Chavarrio Cañas et al.¹⁶ again computed rate coefficients for the same reactants on both the singlet and triplet surfaces at the W3X-L//CCSD/cc-pVTZ level (with singlet O₂ as the product on the singlet surface).

The research described above represents a significant body of work. However, no systematic study on HO₂ reactivity has been conducted specifically for ammonia oxidation systems. This study thoroughly examines additional significant hydrogen abstraction and disproportionation reactions involving HO₂ in the NH₃ oxidation system that remain unexplored.

2. Methods

Quantum chemical computations and statistical mechanics

Ab initio calculations were automatically performed using the open-source automated rate calculator (ARC) software tool,¹⁸ an extensible codebase to automatically calculate thermochemical properties and reaction rate coefficients. Statistical mechanics processing of the electronic structure calculations was performed using Arkane.¹⁹ The transition state theory equation for rate coefficient computation is given in the ESI† (eqn S1). Detailed explanations of the equations used in Arkane are available in the literature.¹⁹ 3D conformer geometry searches were conducted using ARC with a dihedral angle combination approach based on a random set of force field (MMFF94s²⁰) conformers generated using RDKit.²¹ Up to ten lowest energy force field conformers identified per species were optimized at the ωB97X-D/Def2-SVP^22,23 level of theory (termed “L1”). The lowest energy density functional theory (DFT) conformer was optimized at the double hybrid B2PLYP functional²⁴ with Grimme's dispersion correction and Becke–Johnson damping, D3(BJ),^25,26 coupled with Dunning's correlation-consistent basis set augmented with diffuse functions, aug-cc-pVTZ,²⁷ level of theory. Harmonic frequencies were subsequently computed at the same level of theory. ARC calculated a frequency scaling factor of 0.995 for B2PLYP-D3/aug-cc-pVTZ (termed “L2”) following the method recommended by Truhlar et al.²⁸

Torsional modes were automatically identified as rotatable single bonds in each species, considering relevant resonance structures²⁹ and treated with continuous constrained potential energy surface (PES) optimizations with all other internal coordinates relaxed using the “L2” level of theory at a resolution of 10°. If a scan resulted in a lower-energy structure than the original conformer geometry optimized at the same level, ARC identified the former as the new lowest-energy conformer, deleted all other running jobs for the species, and spawned the computations again starting from the updated geometry. The 1D torsional PESs were fitted to truncated Fourier series and used as input to compute energy levels and hence the partition function of the anharmonic mode using Arkane.¹⁹ Quantum tunneling effects were considered using the Eckart correction function.³⁰

Single-point energies were calculated using three methods for comparison, one of which is multireference (MR), and the other two are single reference (SR). The MR method is multiconfiguration reference configuration-interaction method with the Davidson correction (MRCI + Q).^31–33 The SR approaches comprised the explicitly correlated CCSD(T)-F12a³⁴ and the left-eigenvector-based ΛCCSD(T).^35,36 Although formally a single-reference coupled-cluster method, ΛCCSD(T) exploits its left-eigenvector-based triples correction to achieve enhanced error cancellation in systems exhibiting moderate static correlation, allowing it to approach MR benchmark accuracy in many near-degenerate situations.^37–39 All ΛCCSD(T) single-point energies reported here employ an RHF reference determinant; we note that CCSD(T) built on a broken-symmetry UHF reference may yield even lower errors in certain MR-like cases.³⁷ Nonetheless, ΛCCSD(T) often exhibits enhanced numerical stability and more consistent error cancellation than RHF-based CCSD(T) under moderate static correlation, making it a robust choice for near-degenerate reaction pathways.³⁹ All single-point energy calculations employed the aug-cc-pVTZ basis set.²⁷

All DFT calculations mentioned above were performed in Gaussian 16.⁴⁰ CCSD(T)-F12a computations were performed in Molpro 2022.3.0,⁴¹ with the unrestricted Hartree–Fock (UHF)⁴² reference wavefunction. MRCI calculations were performed with Orca 5.0.4,⁴³ using the complete-active-space self-consistent-field (CASSCF)⁴⁴ reference wavefunction (see Table S2 in the ESI† for the number of active electrons and orbitals), and ΛCCSD(T) calculations were performed with the MRCC software⁴⁵ via Psi4's interface⁴⁶ using UHF as a reference wavefunction.

All electronic structure calculations were processed by Arkane¹⁹ for computation of the thermochemical partition functions and reaction rate coefficients. Empirical systematic errors in atomization energies were corrected using atom energy corrections implemented in Arkane^19,47 when available, or computed in the present work for the respective level of theory.

Reaction TS searches were automated using a bimolecular reaction orientation module implemented in ARC.¹⁸ The generated TS guesses are then optimized at the “L1” level. They are clustered by nearly identical internal coordinates after the “L1” geometry optimization, and representative structures from each cluster were ranked by their relative DFT electronic energy. The algorithm then analyzed TS candidate structures in ascending energy order and performed another saddle-point optimization and ro-vibrational analyses at the “L2” level. The algorithm was terminated once an “L2” optimized TS guess passed all relevant checks, i.e., reaction path energy, normal mode displacement analysis, and intrinsic reaction coordinate calculations.⁴⁸

Reaction identification

The reaction mechanism generator (RMG)^49,50 was used to identify reactions in the subset of interest, i.e., hydrogen abstraction and disproportionation reactions with estimated rate coefficients involving HO₂ either as an attacking radical or as a result of a radical attack by O₂. The model was generated for temperature, pressure and equivalence ratio ranges of 700–1500 K, 1–50 bar, and 0.5–1.5, respectively. A termination rate ratio criterion was set, stopping model generation when the characteristic rate reached 1% of the maximum characteristic rate in the system. The characteristic rate is a function of time and is defined as the root mean square of net rates of production of all the species in the model.

Chemical kinetic modeling

Two recent models, one by Zhang et al.⁵¹ and another by Zhu et al.,⁵² were used as the basis for simulations in this work. An updated version of each model was created by incorporating all the reactions and rate coefficients computed in this study into the existing literature models. Four of the reactions reported here already existed in the Sarathy et al. model, and three already existed in the Zhu model; their rate coefficients were updated. The models were simulated in a continuously stirred reactor using Cantera v. 3.1.0.⁵³ Rates of production (ROP) were computed using Cantera, and flux diagrams were generated using features of The Tandem Tool (T3) for automated chemical kinetic model development.⁵⁴

3. Results and discussion

Eleven reactions were identified by RMG as belonging to either the hydrogen abstraction or the disproportionation family involving HO₂ and having an estimated rate. Of the eleven reactions, ten belong to the hydrogen abstraction reaction family. In five hydrogen abstraction reactions (R1–R5, Table 1) the hydrogen atom in HO₂ is abstracted and O₂ is formed, and in the other five reactions (R6–R10, Table 1), HO₂ is the abstracting radical, forming H₂O₂. One reaction (R11, Table 1) belongs to the disproportionation reaction family.⁵⁵ It involves an O₂ molecule abstracting a hydrogen atom from a position adjacent to a radical atom, forming HO₂.

Table 1 Zero-point energy comparisons of the differences between product and reactant wells, ΔE₀(P − R), for the studied reactions at several levels of theory: CCSD(T)-F12a, ΛCCSD(T) and MRCI + Q

No.	Reaction	m^a	TS T1 diagnostic coefficient^b	P − R^c CCSD(T)^d	P − R^c ΛCCSD(T)^e	P − R^c MRCI^f
a The reaction multiplicity.b The T1 diagnostic coefficient^56–58 of the corresponding TS is based on the CCSD(T)-F12a computation.c Energy differences in kJ mol^−1 between the corresponding products well and reactants well in the direction the reaction is written here.d As computed at the CCSD(T)-F12a/aug-cc-pVTZ-F12//B2PLYPD3/aug-cc-pVTZ level of theory.e As computed at the ΛCCSD(T)/aug-cc-pVTZ//B2PLYPD3/aug-cc-pVTZ level of theory.f As computed at the MRCI + Q/aug-cc-pVTZ//B2PLYPD3/aug-cc-pVTZ level of theory.g See text for a detailed discussion of the multiplicity of reaction R2.
R1	N + HO2 ⇌ NH + O2	5	0.046	−125.5	−119.3	−139.0
R2	NH + HO2 ⇌ NH2 + O2	2, 4^g	0.043	−183.4	−182.7	−190.3
R3	NO + HO2 ⇌ HNO + O2	3	0.045	4.1	1.7	−7.2
R4	H2NO + HO2 ⇌ NH3O + O2	3	0.053	13.5	−14.3	−32.6
R5	NNH + HO2 ⇌ N2H2 + O2	3	0.043	−60.3	−64	−77.5
R6	NH2 + HO2 ⇌ NH + H2O2	3	0.047	24.2	23.5	18.3
R7	NH3 + HO2 ⇌ NH2 + H2O2	2	0.041	81.8	81.8	77.1
R8	N2H3 + HO2 ⇌ H2NN(T) + H2O2	3	0.047	−6.8	−6.5	−12.1
R9	HNO2 + HO2 ⇌ NO2 + H2O2	2	0.040	−70.4	−67.5	−72.0
R10	N2H2 + HO2 ⇌ NNH + H2O2	2	0.049	−98.6	−95.2	−97.0
R11	HNO + HO2 ⇌ HNOH + O2	2	0.040	−18.5	−26.0	−52.8

---

The T1 diagnostic coefficients^56–58 of the species participating in these reactions, along with their SMILES representations,⁵⁹ are given in Table S1 (ESI†). The T1 diagnostic coefficients of the TSs are given in Table 1. The inspected energy wells had no imaginary frequencies, and all TSs had only one imaginary frequency as listed in Table S2 (ESI†). The TS geometries of all reactions are shown in Fig. 1 and are listed in Table S2 (ESI†) together with all the respective vibrational frequencies. The multiplicity of each reaction surface is provided in Table 1, the multiplicity of reaction R2 is discussed in details below. The computed rate coefficients at the ΛCCSD(T)/aug-cc-pVTZ//B2PLYP-D3/aug-cc-pVTZ level of theory are given in Table 3 and in Chemkin and Cantera formats in Tables S3 and S4 (ESI†), respectively.

Fig. 1 TS geometries of the explored reactions. For reaction R2 (Table 1), two TS geometries are given at the two relevant multiplicities of 2 and 4. Distances are reported in Angstrom, angles and dihedrals are reported in degrees. Dihedral labels refer to consecutive atoms. Element legend: red: oxygen, blue: nitrogen, white: hydrogen. The Cartesian geometry is reported in Table S2 (ESI†).

Some of the species (NO, H₂NO, NNH, H₂NN(T), N₂H₃, HNOH, NO₂, and notably HO₂) and all TSs have a relatively high T1 diagnostic coefficient (Table 1 and Table S1, ESI†), which may indicate a strong MR character. Table 1 shows the differences in energy at 0 K including zero-point energy corrections⁶² between the wells of the products and reactants of each reaction, while Table 2 shows the deviation of these computed reaction energies from the corresponding enthalpy differences reported by ATcT.^60,61 In both cases, values are reported as differences between the product and reactant wells. The high T1 diagnostic coefficients observed for many species and all TSs suggest that MR methods may be necessary.

Table 2 Deviation between reaction enthalpies from the ATcT and computed zero-point corrected reaction energies for various levels of theory. Both ATcT and computed values correspond to the energy difference between product and reactant wells in the direction written. Reported values are defined as

No.	Reaction	ATcT^a – CCSD(T)^b	ATcT^a – ΛCCSD(T)^c	ATcT^a –MRCI^d
a values are taken from the active thermochemical tables (ATcT, version 1.130),^60,61 all energy differences are reported in kJ mol^−1.b As computed at the CCSD(T)-F12a/aug-cc-pVTZ-F12//B2PLYPD3/aug-cc-pVTZ level of theory.c As computed at the ΛCCSD(T)/aug-cc-pVTZ//B2PLYPD3/aug-cc-pVTZ level of theory.d As computed at the MRCI + Q/aug-cc-pVTZ//B2PLYPD3/aug-cc-pVTZ level of theory.e TS2 exhibits a strong MR characteristic (Table S5, ESI), therefore the calculated rate coefficient for R2 carries a correspondingly higher uncertainty.f The active thermochemical tables version 1.130 did not have values for H2NN(T), hence no comparison to ATcT is given for this reaction.
R1	N + HO2 ⇌ NH + O2	−1.4	−7.6	12.1
R2	NH + HO2 ⇌ NH2 + O2^e	−1.5	−2.2	5.4
R3	NO + HO2 ⇌ HNO + O2	−0.1	2.5	11.4
R4	H2NO + HO2 ⇌ NH3O + O2	−1.0	−0.2	18.1
R5	NNH + HO2 ⇌ N2H2 + O2	0.2	3.9	17.4
R6	NH2 + HO2 ⇌ NH + H2O2	1.1	1.8	7.0
R7	NH3 + HO2 ⇌ NH2 + H2O2	1.2	1.2	5.9
R8	N2H3 + HO2 ⇌ H2NN(T) + H2O2^f	—	—	—
R9	HNO2 + HO2 ⇌ NO2 + H2O2	−0.5	−3.4	1.1
R10	N2H2 + HO2 ⇌ NNH + H2O2	−5.3	2.3	29.0
R11	HNO + HO2 ⇌ HNOH + O2	−0.9	−4.3	−2.5

---

Table 3 Rate coefficients computed at the ΛCCSD(T)/aug-cc-pVTZ//B2PLYPD3/aug-cc-PVTZ level of theory reported in the modified Arrhenius expression format, k = A·Tⁿ·e^−E_a/RT, fitted between 300–3000 K

No.	Reaction	A (cm^3 mol^−1 s^−1)	n	Ea (kJ mol^−1)
a A rate coefficient for reaction R2 is not provided because the transition states pronounced multireference character (Table S5, ESI) precludes accurate barrier estimation by the methods used in this study.
R1	N + HO2 ⇌ NH + O2	1.82 × 10^−27	9.81	60.5
R2	NH + HO2 ⇌ NH2 + O2^a	—	—	—
R3	NO + HO2 ⇌ HNO + O2	1.19 × 10^−5	5.06	29.9
R4	H2NO + HO2 ⇌ NH3O + O2	1.40 × 10^−5	4.53	8.1
R5	NNH + HO2 ⇌ N2H2 + O2	6.25 × 10^−5	4.57	2.2
R6	NH2 + HO2 ⇌ NH + H2O2	1.97 × 10^−5	5.23	34.2
R7	NH3 + HO2 ⇌ NH2 + H2O2	4.44 × 10^−1	4.00	75.5
R8	N2H3 + HO2 ⇌ H2NN(T) + H2O2	2.79 × 10^−3	4.00	7.9
R9	HNO2 + HO2 ⇌ NO2 + H2O2	2.49 × 10^−3	4.52	0.2
R10	N2H2 + HO2 ⇌ NNH + H2O2	7.79 × 10^−1	3.96	−0.6
R11	HNO + HO2 ⇌ HNOH + O2	3.08 × 10^0	2.98	2.4

---

The MRCI calculations performed in this work exhibit significant deviations compared to the experimentally-based ATcT values (Table 2). Specifically, the MRCI method shows a significant average deviation of 10.5 kJ mol⁻¹ with a standard deviation of 9.2 kJ mol⁻¹ from the ATcT values (Table 2). In contrast, the SR methods performed remarkably well in reproducing the ATcT data. Both CCSD(T)-F12 and ΛCCSD(T) methods exhibit excellent agreement with the ATcT values, with average deviations of just 0.2 and −0.6 kJ mol⁻¹ and standard deviations of 2.0 and 3.7 kJ mol⁻¹, respectively (Table 1). For example, the ΛCCSD(T)/aug-cc-pVTZ and MRCI + Q/aug-cc-pVTZ methods disagree with one another in the computed ΔE₀(P − R) by 10.6 kJ mol⁻¹ on average with a standard deviation of 9.8 kJ mol⁻¹ (Table 1) after excluding the large deviation observed for reaction R4. When R4 is included, the average difference increases to 21.3 kJ mol⁻¹.

Although MRCI captures MR effects, it falls short in accurately describing the energetics of key stationary points and is thus likely to produce inaccurate predictions for these reaction systems. This discrepancy can be attributed to limitations in capturing dynamic electron correlation, an area where CCSD(T) and ΛCCSD(T) are known to excel, but where MR methods often struggle. Furthermore, the lack of size extensivity in MRCI + Q further undermines its suitability for modeling bimolecular reaction energetics.

Coupled-cluster theory is widely recognized for its high accuracy and broad applicability, and it is considered the “gold standard” in quantum chemistry. Indeed, CCSD(T) performed exceptionally well for all species, even those with MR characteristics, compared to the experimentally-based data (Table 2). However, it may introduce deviations relative to the ground truth when applied to TSs because of their strong MR characteristics. Although ΛCCSD(T) remains formally a single-reference method, it has been shown to handle systems with multireference character, such as predictive singlet–triplet gaps, very effectively when supplied with a suitable reference wavefunction.^37,63 Consequently, ΛCCSD(T) offers greater numerical stability in non-equilibrium geometries than standard CCSD(T). High-spin TSs, such as TS1, are therefore expected to benefit substantially from the left-eigenvector-based triples correction built into ΛCCSD(T). Accordingly, we adopt the ΛCCSD(T) values for computing the rate coefficients in the present work. As shown in Table S5 (ESI†), all TS wavefunctions except TS2 at m = 2 are dominated by a single CASSCF configuration (leading weight ≥0.889), confirming that single-reference methods are appropriate for those barriers. By contrast, TS2's largest configuration weight for m = 2 is only 0.417, placing it firmly in the strong MR regime. Accordingly, the reaction R2 results presented here should be regarded as preliminary, and a more rigorous MR treatment is required for quantitative accuracy.

Reactive collisions between NH(T) and O₂(T) can lead to the formation of NO(D) + OH(D), HNO(S) + O(S), HNO(T) + O(T), and NO₂(D) + H(D) when reacting unimolecularly and to N(D) + HO₂(D) or N(Q) + HO₂(D) either unimolecularly or bimolecularly (where S, D, T, and Q refer to singlet, doublet, triplet, and quartet spin states, respectively). Talipov et al.⁶⁴ computed rate coefficient values for the production of NO + OH and HNO + O, while Baulch et al.⁶⁵ commented that experimental and theoretical studies suggest that the formation of NO₂ + H in this system is negligible. Talipov et al.⁶⁴ studied the unimolecular NH + O₂ PES. However, to our knowledge, there is no relation in the literature for reaction R1, NH(T) + O₂(T) ⇌ N(Q) + HO₂(D) (listed in Table 1 in reverse for context). No rate, measured or computed, is available for this reaction, and none of the recent NH₃ oxidation models^{11,51,52,66–81} considered it. The rate coefficient of reaction R1 is plotted in Fig. S1 (ESI†).

Here, we calculated a bimolecular rate coefficient for the reaction NH(T) + O₂(T) ⇌ N(Q) + HO₂(D) in both directions, and neglected the N(D) + HO₂(D) products since N(D) is ∼300 kJ mol⁻¹ higher than N(Q) (the ground state), making the electronically-excited well negligible under typical combustion conditions. The rate coefficient comparison in Fig. 2 shows that the pathway leading to the N + HO₂ products only becomes significant above 2000 K, and that the main products of NH + O₂ are expected to be HNO + O. The rate coefficient in the reverse direction, N + HO₂ ⇌ NH + O₂ as written in Table 1, is still relatively low: ∼3.3 × 10⁵ cm³ (mol s)⁻¹ at 1000 K (Fig. S1, ESI†). In this direction (as in Table 1) reaction R1 is exothermic by ∼120 kJ mol⁻¹ with an energy barrier of ∼140 kJ mol⁻¹ (Table S2, ESI†). Due to the relative importance of the N and HO₂ radicals in this system, it is recommended to consider reaction R1 in future models.

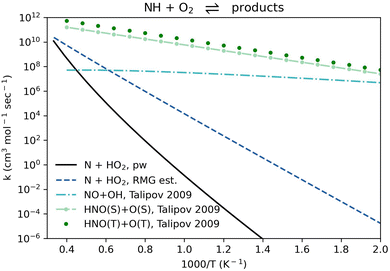Fig. 2 Comparison of rate coefficients for NH + O₂ giving N + HO₂ (reaction R1, given in reverse in Table 1) computed here (pw) and compared to RMG's estimate, and giving NO + OH and HNO + O as recommended by Talipov et al.⁶⁴

Reaction R2, NH + HO₂ ⇌ NH₂ + O₂, was previously considered to proceed via the doublet or quartet surfaces (‘m = 2’ and ‘m = 4’, respectively).⁸² Both transition states (Fig. 1) are similar in terms of bond lengths (including the lengths of the reactive bonds) and angles, but differ in the torsional angle formed by the internal NH rotor, i.e., the dihedral angle of the hydrogen atom bonded to N relative to the N–H–O plane (Fig. 1).

Reaction R2 on the doublet PES (m = 2) proceeds through a complex electronic reconfiguration, as depicted in the spin-conserving paths (A) and (B) in Fig. 3. A key aspect of this reaction is the redistribution of electrons during the transformation of reactants into products, which is directly connected to the spin state of O₂ and NH. In path (A), triplet NH (arbitrarily assigned spins “up, up”) captures a hydrogen atom with a spin “down” electron, leaving a singlet O₂ in the products. In path (B), when considered in reverse, ground state triplet O₂ abstracts a hydrogen atom from NH₂ with a spin “up” electron if triplet O₂ is arbitrarily assigned spins “down, down”. In this path, a singlet NH is formed with a b¹Σ⁺ electronic configuration (Fig. 3), which can quickly convert into the more stable NH a¹Δ configuration (that is, with two pairs of lone electrons). The R2 reaction via paths (A) or (B) on the doublet PES (m = 2) has a different reactant well (singlet NH) or a different product well (singlet O₂) relative to the quartet PES (m = 4) pathway of R2. Therefore, R2m2 and R2m4 are not only different paths (on different spin surfaces) of the same reaction, but rather different reactions altogether with distinct reactant and product electronic configuration. Reacting NH(T) + HO₂ on the quartet surface yield NH₂ + O₂(T), while on the doublet surface the products will be NH₂ + O₂(S). The R2m2-A and R2m2-B paths (Fig. 3) are not the same reaction themselves, due to the different electronic configurations of their reactants and products. We identified a single TS on the m = 2 PES (Fig. 1), and the question of whether R2m = 2 path A and R2m = 2 path B (Fig. 3) share the same TS remains open.

Fig. 3 The electronic configuration of the reactants and products of reaction R2 on the doublet potential energy surface (R2m2). (A) forming singlet O₂ 1Δg, (B) reacting singlet NH b¹Σ⁺. Lowercase letters, arrows, and colors represent specific electron spins in each reaction path separately. The image does not show all bonding electrons and does not show the oxygen lone electron pairs.

Recent NH₃ oxidation models^{11,51,52,66–81} consider NH₂ + O₂ ⇌ H₂NO + O and NH₂ + O₂ ⇌ HNO + OH as the only reactions on the NH₂O₂ PES, e.g., as computed by Klippenstein et al.¹³ These models do not consider reaction R2, NH₂ + O₂ ⇌ NH + HO₂ (listed in Table 1 in reverse for context), which might become relatively significant at high temperatures (Fig. 4). Furthermore, reaction R2 could be significant in NH₃ systems in the exothermic (forward) direction, affecting the interconversion of two main radicals in this system, NH₂ and NH.

Fig. 4 Comparison of rate coefficients for NH₂ + O₂ giving NH + HO₂ (reaction R2, given in reverse in Table 1) with a comparison of RMG's estimate, and giving H₂NO + O and HNO + OH as computed by Klippenstein et al.¹³

Reaction R3, NO + HO₂ ⇌ HNO + O₂, is a radical chain-terminating reaction that competes with the pressure-dependent reaction NO + HO₂ ⇌ NO₂ + OH. The rate coefficients computed here are in agreement with a previous work by Wang et al.⁸⁴ performed at the CCSD(T)/CBS//B2PLYPD3/aug-cc-pVTZ level of theory. Using the updated rate coefficient could be crucial for NH₃ oxidation models to properly represent the radical pool, replacing the relatively high values previously used by recent NH₃ models^{11,51,52,66–81} (Fig. 5).

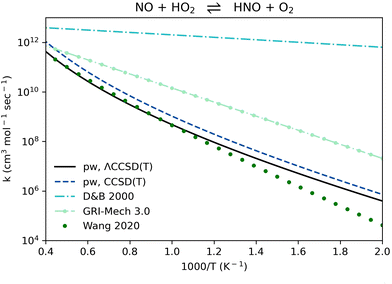Fig. 5 Comparison of rate coefficients for NO + HO₂ ⇌ HNO + O₂ (reaction R3, Table 1) computed here (pw) using ΛCCSD(T)/aug-cc-pVTZ//B2PLYPD3/aug-cc-pVTZ and using CCSD(T)-F12a/aug-cc-pVTZ-F12//B2PLYPD3/aug-cc-pVTZ, compared to an estimation by Dean and Bozzelli 2000,¹² to the GRI-Mech 3.0 value,⁸³ and to a CCSD(T)/CBS//aug-cc-pVTZ//B2PLYPD3/aug-cc-pVTZ computation by Wang et al. 2020.⁸⁴

The rate coefficient for reaction R4, H₂NO + HO₂ ⇌ NH₃O + O₂, was not reported previously, and it is plotted in Fig. S2 (ESI†). This reaction is exothermic by ∼14 kJ mol⁻¹ (Table S2, ESI†). Its rate coefficient is considerably lower than the RMG estimated value (Fig. S2, ESI†). This divergence could likely stem from the zwitterion generated in this reaction (i.e., NH₃O, SMILES:⁵⁹ “[NH³⁺][O⁻]”) and the absence of relevant training reactions within the RMG database. This reaction seems to be relatively slow, and after a rate coefficient refinement by ARC, the generated RMG model did not consider this reaction again for a temperature range of 700–1500 K. The current exercise shows that reaction R4 is probably insignificant for NH₃ oxidation models.

The dominant radicals that abstract a hydrogen atom from N₂H₂ to form NNH are H, NH, NH₂, O, OH, and HO₂, as summarized in Fig. 6. The rate coefficient for HO₂ as the attacking radical computed here (reaction R10) is lower than the rate coefficients of most other attacking radicals. The rate coefficient of reaction R5, N₂H₂ + O₂ ⇌ NNH + HO₂ (listed in Table 1 in reverse for context), is smaller than the rate coefficients of its sister reactions (Fig. 6). Nonetheless, reaction R5 could be important for modeling the ammonia oxidation system: although its rate coefficient at low temperatures is orders of magnitude lower than the parallel pathways in the comparison (Fig. 6), the high concentration of O₂ is orders of magnitude higher than the concentration of all other attacking radicals in typical NH₃ oxidation systems. Therefore, the rate of reaction R5 could become significant at temperatures higher than 1000 K, especially in lean fuel or stoichiometric combustion mixtures.

Fig. 6 Comparison of reaction rate coefficients of various radicals abstracting a hydrogen atom from N₂H₂ forming NNH. Sources: Li and Sarathy 2020,⁸⁵ Raghuanth et al. 2014,⁸⁶ Dean and Bozzelli 2000,¹² Diévart and Catoire 2020,⁸⁷ and two reactions from the present work (pw). The reactions N₂H₂ + HO₂ ⇌ NNH + H₂O₂ and N₂H₂ + O₂ ⇌ NNH + HO₂ are shown in Table 1 (reactions R10 and R5 in reverse, respectively).

Reaction R6, NH₂ + HO₂ ⇌ NH + H₂O₂, also only becomes significant in the high temperature range relative to the other consumption channels of NH₂ + HO₂ (Fig. 7). Since the HO₂ radical is mostly important at the low and intermediate temperature ranges, it is reasonable to omit reaction R6 from NH₃ oxidation models.

Fig. 7 Comparison of rate coefficients for NH₂ + HO₂ giving NH + H₂O₂ (reaction R6) computed here (pw) and giving NH₃ + O₂, HNO + H₂O, and H₂NO + OH as recommended by Glarborg et al. 2021.⁸⁸

Reaction R7, NH₃ + HO₂ ⇌ NH₂ + H₂O₂, is critical to predict the low- and intermediate-temperature oxidation of ammonia, since it describes the direct interaction between NH₃ and the main radical carrier in this temperature range, HO₂. The endothermicity of reaction R7 is about 80 kJ mol⁻¹ (Table S2, ESI†). Its rate coefficient was recently computed at the CASPT2/aug-cc-pVTZ//M06-2X/aug-cc-pVTZ level of theory,⁷⁰ and the rate coefficient computed in the present work is in satisfying agreement with this reported calculation (Fig. S3, ESI†).

Reaction R8, N₂H₃ + HO₂ ⇌ H₂NN(T) + H₂O₂, has a relatively insignificant rate coefficient throughout the temperature range of interest compared to competing pathways that produce N₂H₂ + H₂O₂ or N₂H₄ + O₂ (Fig. S4, ESI†). Similar to reaction R6, it is also reasonable to omit reaction R8 from NH₃ combustion models.

To our knowledge, the rate coefficient of reaction R9, HNO₂ + HO₂ ⇌ NO₂ + H₂O₂, was not previously reported. The RMG estimation is in good agreement with the computed value (Fig. 8). This new pathway could become important for NO₂ formation in locations in the flame where the concentration of HO₂ is significant.

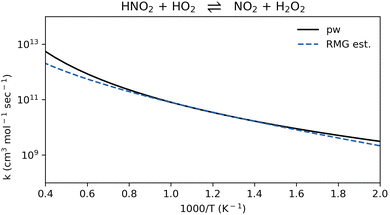Fig. 8 Comparison of rate coefficients for the reaction HNO₂ + HO₂ ⇌ N₂O + H₂O₂ (reaction R9) computed here (pw) and compared to RMG's estimate.

Reaction R11, HNOH + O₂ ⇌ HNO + HO₂ (listed in Table 1 in reverse for context), appears in all recent NH₃ oxidation models examined here.^{11,51,66–81} Its rate coefficient in all of these models was taken from a single source, an estimation made by Miller and Glarborg in 1999.⁸⁹ The rate coefficient of reaction R11, HNO + HO₂ ⇌ HNOH + O₂, computed in the present work falls between the 1999 estimation and the updated RMG estimation (Fig. 9). It generally follows the same temperature dependence suggested by RMG, yet it is about 3 orders of magnitude lower. The 1999 estimation is adequate only at the very high temperature range (> 2000 K), yet it significantly under-predicts the rate coefficient at the intermediate and low temperature ranges. It is recommended to use the updated rate coefficient provided here for reaction R11 in future ammonia modeling efforts.

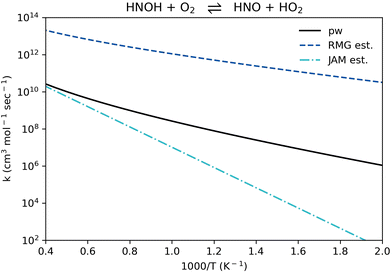Fig. 9 Comparison of rate coefficients for the reaction HNOH + O₂ ⇌ HNO + HO₂ (reaction R11, given in reverse in Table 1) computed here (pw) and compared to RMG's estimate and to J. A. Miller and P. Glarborg's estimate.⁸⁹

Fig. 10 and 11 illustrate the impact of incorporating reactions R1–R11 with the rate coefficients recommended in the present work into two recent ammonia combustion models: “Model 1” by Zhang et al.⁵¹ and “Model 2” by Zhu et al.⁵² The modified models show significant changes in reaction pathways and species flux distributions compared to their original counterparts. In Model 1, the added reactions alter the dominant formation routes to HO₂ (Fig. 10(A) and (B)). After updating Model 1, the flux through the main pathway NH₃ + O₂ ⇌ NH₂ + HO₂ decreases, while new minor pathways for HO₂ formation emerge involving N₂H₂, NNH, and HNOH reactions with O₂. This change was not observed for Model 2.

Fig. 10 Partial flux diagrams showing only the dioxigen species (O₂, HO₂, and H₂O₂) for Model 1” by Zhang et al.⁵¹ and “Model 2” by Zhu et al.⁵² (A), and (C) show the fluxes obtained from the original models without modifications, (B), (D) show the fluxes obtained after adopting the rate coefficients recommended by the present work into the corresponding models (see text). Percentages correspond to the relative flux through each pathway for a stoichiometric feed of NH₃ and air simulated in a continuous stirred reactor with volume of 20 cm³ at 1200 K, 10 bar, and a residence time of 1 second.

Fig. 11 Partial flux diagrams showing only major N₂H₂ → NNH pathways for “Model 1” by Zhang et al.⁵¹ and “Model 2” by Zhu et al.⁵² (A), and (C) show the fluxes obtained from the original models without modifications, (B), (D) show the fluxes obtained after adopting the rate coefficients recommended by the present work into the corresponding models (see text). Percentages correspond to the relative flux through each pathway for a stoichiometric feed of NH₃ and air simulated in a continuous stirred reactor with volume of 20 cm³ at 1200 K, 10 bar, and a residence time of 1 second. ROP – net rate of production.

The most significant changes, however, are observed in the formation of NNH radicals from N₂H₂ (Fig. 11). In the original Model 1 and Model 2 simulations (Fig. 11(A) and (C)), the N₂H₂ ⇌ NNH conversion is dominated by NH₂-mediated hydrogen abstraction (56% and 86%, respectively). Upon adding R1–R11 (Fig. 11(B) and (D)), the dominant channel shifts to O₂-mediated hydrogen abstraction, resulting in HO₂ formation and accounting for more than 90% of the flux in both cases. The NH₂-mediate pathway contributes less than 10% of the flux at the examined conditions. The total net rate of production of NNH from N₂H₂ increases by ~5× and ~10× after updating the two examined models (Fig. 11). This large shift in flux is attributed to reaction R5.

These results demonstrate that the incorporation of reactions R1–R11 enables both models to capture new mechanistic pathways that were previously underrepresented. Since ammonia modeling is an ongoing effort in the community and recent models still require significant updates,⁹⁰ we did not perform a thorough kinetic analysis here. The representative conditions chosen here (1200 K, 10 bar, 1 second in Fig. 10 and 11) show the potential impact of incorporating updated HO₂ kinetics in NH₃ modeling in future models.

4. Conclusions

This work reports the identification of a subset of reactions automatically suggested during chemical kinetic model generation with respective rate coefficients automatically computed using ab initio methods. While not all reactions were determined as significant after quantum chemical computations, the potential importance of some of the identified reactions was shown. This automated approach of using software such as RMG to automatically suggest reactions that could be significant has some shortcomings since RMG's rate coefficient estimations could be inaccurate for reactions for which training data is scarce. Nonetheless, this approach was successful in highlighting previously overlooked reactions that might be important for modeling the NH₃ oxidation system.

Bimolecular reactions involving HO₂ in the NH₃ oxidation system, most previously unexplored (reactions R1, R2, R4, R5, R6, R8, R9), were studied and their rate coefficients were computed at the ΛCCSD(T)/cc-pVTZ-F12//B2PLYP-D3/aug-cc-pVTZ level of theory. This level of theory appears to evaluate the reaction wells to within reasonable accuracy, averaging at about −0.6 kJ mol⁻¹. This method also claims the static correlation to some extent while being an SR method, which could reduce the effects the relatively large T1 diagnostic coefficient indicates. In addition, high spin systems are often misrepresented by CCSD(T), and are better described by post-CCSD(T) methods, such as the one shown in this paper.

Previous literature studies examined the NHO₂ system primarily from the NH + O₂ direction and determined that NO + OH and HNO + O are the major products. In this direction, the formation of N + HO₂ is indeed insignificant below 2000 K. However, in the reverse direction, N + HO₂ ⇌ NH + O₂, the rate coefficient of reaction R1 is significant, and the reaction is highly exothermic.

Reaction R2, NH + HO₂ ⇌ NH₂ + O₂, which might be an important channel of NH₂ + O₂ reactivity, was not assigned a rate coefficient in this study due to the severe multireference character of the transition state and the resulting inability of our chosen methods to estimate its activation barrier. While O₂ was found to react relatively slowly with N₂H₂ to form NNH, an ROP analysis showed that reaction R5, NNH + HO₂ ⇌ N₂H₂ + O₂, is pivotal for the N₂H₂ → NNH transformation. An updated rate coefficient for reaction R11, HNOH + O₂ ⇌ HNO + HO₂, is given in replacement of an estimated value used throughout the recent NH₃ oxidation models. Incorporating the updated rate coefficient for reaction R11 is expected to result in a shift of the dominant pathway for the conversion of HNOH into HNO, increasing the overall flux of converting HNOH into HNO.

The incorporation of the computed rate coefficients into two recent literature models demonstrated the mechanistic relevance of several of these reactions. The dominant N₂H₂ → NNH channel shifted from NH₂-mediated to O₂-mediated pathways, increasing the rate of NNH formation by up to an order of magnitude, while fluxes across species involved in HO₂ formation were redistributed in one of the tested models. The flux analysis demonstrates the potential of incorporating these updated HO₂-involving reactions in future modeling efforts.

It is recommended to consider at least reactions R1, R3, R5, R7, R9, R10, and R11 in future relevant NH₃ chemical kinetic oxidation models, and a rate coefficient for reaction R2 should further be computed at an appropriate MR level. Additional reactions from the present work could be relevant if relatively high temperature ranges are of interest.

Author contributions

K. K.: formal analysis and methodology, M. K.: formal analysis and methodology, A. G. D.: Formal analysis, methodology, conceptualization, funding acquisition, and supervision.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

This publication was made possible by the generous support of the Government of Portugal through the Portuguese Foundation for International Cooperation in Science, Technology and Higher Education and was undertaken in the MIT Portugal Program as part of a broader collaboration with Prof. William H. Green and his research group at MIT. Financial support from the Stephen and Nancy Grand Technion Energy Program (GTEP) is gratefully acknowledged.

References

1. A. Valera-Medina, H. Xiao, M. Owen-Jones, W. David and P. Bowen, Ammonia for power, Prog. Energy Combust. Sci., 2018, 69, 63–102.
2. H. Kobayashi, A. Hayakawa, K. Somarathne and E. Okafor, Science and technology of ammonia combustion, Proc. Combust. Inst., 2019, 37, 109–133.
3. O. Herbinet, P. Bartocci and A. Grinberg Dana, On the use of ammonia as a fuel – A perspective, Fuel Commun., 2022, 11, 100064.
4. O. Elishav, B. Mosevitzky Lis, E. M. Miller, D. J. Arent, A. Valera-Medina, A. Grinberg Dana, G. E. Shter and G. S. Grader, Progress and Prospective of Nitrogen-Based Alternative Fuels, Chem. Rev., 2020, 120, 5352–5436.
5. A. M. Elbaz, S. Wang, T. F. Guiberti and W. L. Roberts, Review on the recent advances on ammonia combustion from the fundamentals to the applications, Fuel Commun., 2022, 10, 100053.
6. A. Grinberg Dana, O. Elishav, A. Bardow, G. E. Shter and G. S. Grader, Nitrogen-Based Fuels: A Power-to-Fuel-to-Power Analysis, Angew. Chem., Int. Ed., 2016, 55, 8798–8805.
7. W. H. Green, Moving from postdictive to predictive kinetics in reaction engineering, AIChE J., 2020, 66, e17059.
8. A. Valera-Medina, F. Amer-Hatem, A. K. Azad, I. C. Dedoussi, M. de Joannon, R. X. Fernandes, P. Glarborg, H. Hashemi, X. He and S. Mashruk, et al., Review on Ammonia as a Potential Fuel: From Synthesis to Economics, Energy Fuels, 2021, 35, 6964–7029.
9. T. F. Guiberti, G. Pezzella, A. Hayakawa and S. M. Sarathy, Mini Review of Ammonia for Power and Propulsion: Advances and Perspectives, Energy Fuels, 2023, 37, 14538–14555.
10. S. Girhe, A. Snackers, T. Lehmann, R. Langer, F. Loffredo, R. Glaznev, J. Beeckmann and H. Pitsch, Ammonia and ammonia/hydrogen combustion: Comprehensive quantitative assessment of kinetic models and examination of critical parameters, Combust. Flame, 2024, 267, 113560.
11. P. Glarborg, J. A. Miller, B. Ruscic and S. J. Klippenstein, Modeling nitrogen chemistry in combustion, Prog. Energy Combust. Sci., 2018, 67, 31–68.
12. A. M. Dean and J. W. Bozzelli, in Gas-Phase Combustion Chemistry: Combustion Chemistry of Nitrogen, ed. W. C. Gardiner, Springer, New York, 2000, pp. 125–341.
13. S. J. Klippenstein, L. B. Harding, P. Glarborg and J. A. Miller, The role of NNH in NO formation and control, Combust. Flame, 2011, 158, 774–789.
14. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299–306.
15. A. Stagni and C. Cavallotti, H-abstractions by O₂, NO₂, NH₂, and HO₂ from H₂NO: Theoretical study and implications for ammonia low-temperature kinetics, Proc. Combust. Inst., 2023, 39, 633–641.
16. J. E. Chavarrio Cañas, M. Monge-Palacios, X. Zhang and S. M. Sarathy, Probing the gas-phase oxidation of ammonia: Addressing uncertainties with theoretical calculations, Combust. Flame, 2022, 235, 111708.
17. S. J. Klippenstein and P. Glarborg, Theoretical kinetics predictions for NH₂ + HO₂, Combust. Flame, 2022, 236, 111787.
18. A. Grinberg Dana; D. Ranasinghe; H. Wu; C. Grambow; X. Dong; M. Johnson; M. Goldman; M. Liu and W. Green, ARC – Automated Rate Calculator, version 1.1.0, github.com/ReactionMechanismGenerator/ARC, 2019.
19. A. Grinberg Dana, M. S. Johnson, J. W. Allen, S. Sharma, S. Raman, M. Liu, C. W. Gao, C. A. Grambow, M. J. Goldman and D. S. Ranasinghe, et al., Automated reaction kinetics and network exploration (Arkane): A statistical mechanics, thermo dynamics, transition state theory, and master equation software, Int. J. Chem. Kinet., 2023, 55, 300–323.
20. T. A. Halgren, MMFF VI. MMFF94s option for energy minimization studies, J. Comput. Chem., 1999, 20, 720–729.
21. G. Landrum, RDKit: Open-Source Cheminformatics Software, https://www.rdkit.org.
22. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
23. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
24. S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 034108.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
26. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
27. J. Dunning and H. Thom, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
28. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887.
29. A. Grinberg Dana, M. Liu and W. H. Green, Automated chemical resonance generation and structure filtration for kinetic modeling, Int. J. Chem. Kinet., 2019, 51, 760–776.
30. C. Eckart, The Penetration of a Potential Barrier by Electrons, Phys. Rev., 1930, 35, 1303–1309.
31. G. Knizia and H.-J. Werner, Explicitly correlated RMP2 for high-spin open-shell reference states, J. Chem. Phys., 2008, 128, 154103.
32. T. Shiozaki and H.-J. Werner, Multireference explicitly correlated F12 theories, Mol. Phys., 2013, 111, 607–630.
33. E. R. Davidson and D. W. Silver, Size consistency in the dilute helium gas electronic structure, Chem. Phys. Lett., 1977, 52, 403–406.
34. T. B. Adler, G. Knizia and H.-J. Werner, A simple and efficient CCSD (T)-F12 approximation. The, J. Chem. Phys., 2007, 127, 221106.
35. S. A. Kucharski and R. J. Bartlett, An efficient way to include connected quadruple contributions into the coupled cluster method, J. Chem. Phys., 1998, 108, 9221–9226.
36. A. G. Taube and R. J. Bartlett, Improving upon CCSD (T): ΛCCSD (T). I. Potential energy surfaces, J. Chem. Phys., 2008, 128, 044110.
37. J. T. Margraf, A. Perera, J. J. Lutz and R. J. Bartlett, Single-reference coupled cluster theory for multi-reference problems, J. Chem. Phys., 2017, 147, 184101.
38. M. Spiegel, E. Semidalas, J. M. L. Martin, M. R. Bentley and J. F. Stanton, Post-CCSD(T) corrections to bond distances and vibrational frequencies: the power of Λ, Mol. Phys., 2023, 122, e2252114.
39. A. G. Taube and R. J. Bartlett, Improving upon CCSD(T): ΛCCSD(T). II. Stationary formulation and derivatives, J. Chem. Phys., 2008, 128, 044111.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01., Gaussian, Inc., Wallingford CT, 2019.
41. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
42. G. W. Pratt Jr, Unrestricted Hartree-Fock method, Phys. Rev., 1956, 102, 1303.
43. F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
44. J. Olsen, The CASSCF method: A perspective and commentary, Int. J. Quantum Chem., 2011, 111, 3267–3272.
45. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy and B. Hégely, et al., The MRCC program system: Accurate quantum chemistry from water to proteins, J. Chem. Phys., 2020, 152.
46. J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke and M. L. Abrams, et al., Psi4: an open-source ab initio electronic structure program, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565.
47. H. Wu, A. M. Payne, H.-W. Pang, A. Menon, C. A. Grambow, D. S. Ranasinghe, X. Dong, A. Grinberg Dana and W. H. Green, Toward Accurate Quantum Mechanical Thermochemistry: (1) Extensible Implementation and Comparison of Bond Additivity Corrections and Isodesmic Reactions, J. Phys. Chem. A, 2024, 128, 4335–4352.
48. K. Fukui, The path of chemical reactions-the IRC approach, Acc. Chem. Res., 1981, 14, 363–368.
49. M. Liu, A. Grinberg Dana, M. Johnson, M. Goldman, A. Jocher, A. Payne, C. Grambow, K. Han, N. Yee and E. Mazeau, et al., Reaction Mechanism Generator v3.0: Advances in Automatic Mechanism Generation, J. Chem. Inf. Model., 2021, 61(6), 2686–2696.
50. M. S. Johnson, X. Dong, A. Grinberg Dana, Y. Chung, D. J. Farina, R. J. Gillis, M. Liu, N. W. Yee, K. Blondal and E. Mazeau, et al., RMG Database for Chemical Property Prediction, J. Chem. Inf. Model., 2022, 62, 4906–4915.
51. X. Zhang, K. K. Yalamanchi and S. Mani Sarathy, Combustion chemistry of ammonia/C1 fuels: A comprehensive kinetic modeling study, Fuel, 2023, 341, 127676.
52. Y. Zhu, H. J. Curran, S. Girhe, Y. Murakami, H. Pitsch, K. Senecal, L. Yang and C.-W. Zhou, The combustion chemistry of ammonia and ammonia/hydrogen mixtures: A comprehensive chemical kinetic modeling study, Combust. Flame, 2024, 260, 113239.
53. Cantera: an open-source suite of tools for problems involving chemical kinetics, thermodynamics, and transport processes, cantera.org.
54. C. Pieters; K. Kaplan; K. Spiekermann; W. Green and A. Grinberg Dana, The Tandem Tool (T3) for automated chemical kinetic model development, github.com/ReactionMechanismGenerator/T3, Version 0.1.0, 2023.
55. C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225.
56. T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36, 199–207.
57. D. Jayatilaka and T. J. Lee, Open-shell coupled-cluster theory, J. Chem. Phys., 1993, 98, 9734–9747.
58. T. J. Lee and G. E. Scuseria, Achieving Chemical Accuracy with Coupled-Cluster Theory. In Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, ed. S. R. Langhoff, Springer, Netherlands: Dordrecht, 1995, pp. 47–108.
59. D. Weininger, SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36.
60. A. Burcat and B. Ruscic, Third millenium ideal gas and condensed phase thermochemical database for combustion (with update from active thermochemical tables), 2005.
61. B. Ruscic Active Thermochemical Tables (ATcT) values based on ver. 1.130 of the Thermochemical Network, 2024. https://atct.anl.gov/ (Accessed August 2024).
62. M. Girod and B. Grammaticos, The zero-point energy correction and its effect on nuclear dynamics, Nucl. Phys. A, 1979, 330, 40–52.
63. A. G. Taube, Alternative perturbation theories for triple excitations in coupled-cluster theory, Mol. Phys., 2010, 108, 2951–2960.
64. M. R. Talipov, S. L. Khursan and R. L. Safiullin, RRKM and Ab Initio Investigation of the NH (X) Oxidation by Dioxygen, J. Phys. Chem. A, 2009, 113, 6468–6476.
65. D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe and W. Tsang, et al., Evaluated Kinetic Data for Combustion Modeling: Supplement II, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397.
66. J. Otomo, M. Koshi, T. Mitsumori, H. Iwasaki and K. Yamada, Chemical kinetic modeling of ammonia oxidation with improved reaction mechanism for ammonia/air and ammonia/hydrogen/air combustion, Int. J. Hydrogen Energy, 2018, 43, 3004–3014.
67. K. P. Shrestha, L. Seidel, T. Zeuch and F. Mauss, Detailed Kinetic Mechanism for the Oxidation of Ammonia Including the Formation and Reduction of Nitrogen Oxides, Energy Fuels, 2018, 32, 10202–10217.
68. B. Mei, X. Zhang, S. Ma, M. Cui, H. Guo, Z. Cao and Y. Li, Experimental and kinetic modeling investigation on the laminar flame propagation of ammonia under oxygen enrichment and elevated pressure conditions, Combust. Flame, 2019, 210, 236–246.
69. R. Li, A. A. Konnov, G. He, F. Qin and D. Zhang, Chemical mechanism development and reduction for combustion of NH₃/H₂/CH₄ mixtures, Fuel, 2019, 257, 116059.
70. A. Stagni, C. Cavallotti, S. Arunthanayothin, Y. Song, O. Herbinet, F. Battin-Leclerc and T. Faravelli, An experimental, theoretical and kinetic-modeling study of the gas-phase oxidation of ammonia, React. Chem. Eng., 2020, 5, 696–711.
71. G. Issayev, B. R. Giri, A. M. Elbaz, K. P. Shrestha, F. Mauss, W. L. Roberts and A. Farooq, Combustion behavior of ammonia blended with diethyl ether, Proc. Combust. Inst., 2021, 38, 499–506.
72. S. Arunthanayothin, A. Stagni, Y. Song, O. Herbinet, T. Faravelli and F. Battin-Leclerc, Ammonia–methane interaction in jet-stirred and flow reactors: An experimental and kinetic modeling study, Proc. Combust. Inst., 2021, 38, 345–353.
73. A. Bertolino, M. Fürst, A. Stagni, A. Frassoldati, M. Pelucchi, C. Cavallotti, T. Faravelli and A. Parente, An evolutionary, data-driven approach for mechanism optimization: theory and application to ammonia combustion, Combust. Flame, 2021, 229, 111366.
74. X. Zhang, S. P. Moosakutty, R. P. Rajan, M. Younes and S. M. Sarathy, Combustion chemistry of ammonia/hydrogen mixtures: Jet-stirred reactor measurements and comprehensive kinetic modeling, Combust. Flame, 2021, 234, 111653.
75. K. P. Shrestha, C. Lhuillier, A. A. Barbosa, P. Brequigny, F. Contino, C. Mounaïm-Rousselle, L. Seidel and F. Mauss, An experimental and modeling study of ammonia with enriched oxygen content and ammonia/hydrogen laminar flame speed at elevated pressure and temperature, Proc. Combust. Inst., 2021, 38, 2163–2174.
76. K. P. Shrestha, B. R. Giri, A. M. Elbaz, G. Issayev, W. L. Roberts, L. Seidel, F. Mauss and A. Farooq, A detailed chemical insights into the kinetics of diethyl ether enhancing ammonia combustion and the importance of NO_x recycling mechanism, Fuel Commun., 2022, 10, 100051.
77. G. J. Gotama, A. Hayakawa, E. C. Okafor, R. Kanoshima, M. Hayashi, T. Kudo and H. Kobayashi, Measurement of the laminar burning velocity and kinetics study of the importance of the hydrogen recovery mechanism of ammonia/hydrogen/air premixed flames, Combust. Flame, 2022, 236, 111753.
78. J. Zhang, B. Mei, W. Li, J. Fang, Y. Zhang, C. Cao and Y. Li, Unraveling Pressure Effects in Laminar Flame Propagation of Ammonia: A Comparative Study with Hydrogen, Methane, and Ammonia/Hydrogen, Energy Fuels, 2022, 36, 8528–8537.
79. J. Liu, C. Zou and J. Luo, Experimental and modeling study on the ignition delay times of ammonia/methane mixtures at high dilution and high temperatures, Proc. Combust. Inst., 2022, 39(4), 4399–4407.
80. R. Tang, Q. Xu, J. Pan, J. Gao, Z. Wang, H. Wei and G. Shu, An experimental and modeling study of ammonia oxidation in a jet stirred reactor, Combust. Flame, 2022, 240, 112007.
81. P. García-Ruiz, M. Uruén, M. Abián and M. Alzueta, High pressure ammonia oxidation in a flow reactor, Fuel, 2023, 348, 128302.
82. R. Sumathi and S. Peyerimhoff, Theoretical investigations on the reactions NH + HO₂ and NH₂ + O₂: Electronic structure calculations and kinetic analysis. The, J. Chem. Phys., 1998, 108, 5510–5521.
83. GRI-Mech 3.0, https://combustion.berkeley.edu/gri-mech/.
84. Q.-D. Wang, Y. Sun and H. J. Curran, Comparative Chemical Kinetic Analysis and Skeletal Mechanism Generation for Syngas Combustion with NO_x Chemistry, Energy Fuels, 2020, 34, 949–964.
85. Y. Li and S. M. Sarathy, Probing hydrogen–nitrogen chemistry: A theoretical study of important reactions in N_xH_y, HCN and HNCO oxidation, Int. J. Hydrogen Energy, 2020, 45, 23624–23637.
86. P. Raghunath, N. Nghia and M.-C. Lin, Ab Initio Chemical Kinetics of Key Processes in the Hypergolic Ignition of Hydrazine and Nitrogen Tetroxide. In Energetic Materials, ed. J. R. Sabin, Advances in Quantum Chemistry; Academic Press, 2014, ch. 7, vol. 69, pp. 253–301.
87. P. Diévart and L. Catoire, Contributions of Experimental Data Obtained in Concentrated Mixtures to Kinetic Studies: Application to Monomethylhydrazine Pyrolysis, J. Phys. Chem. A, 2020, 124, 6214–6236.
88. P. Glarborg, H. Hashemi, S. Cheskis and A. W. Jasper, On the Rate Constant for NH₂ + HO₂ and Third-Body Collision Efficiencies for NH₂ + H(+M) and NH₂ + NH₂(+M). The, J. Phys. Chem. A, 2021, 125, 1505–1516.
89. J. A. Miller and P. Glarborg, Modeling the thermal De-NOx process: Closing in on a final solution, Int. J. Chem. Kinet., 1999, 31, 757–765.
90. A. Grinberg Dana, K. Kaplan, M. Keslin, C. Cao and W. H. Green, Thermodynamic and Chemical Kinetic Parameters in Ammonia Oxidation: A Comparison of Recent Studies and Parameter Recommendations, Energy Fuels, 2024, 38, 22482–22500.

---

Footnote

† Electronic supplementary information (ESI) available: A PDF file with: Table S1: species SMILES representation and T1 diagnostic coefficient; Table S2: transition state geometries, frequencies, and reaction path zero-point energies; details on rate coefficient kinetic computations and statistical mechanics; Fig. S1: the rate coefficients for N + HO₂ ⇌ NH + O₂ (reaction R1) computed here and estimated by RMG; Fig. S2: the rate coefficients for NH₂O + HO₂ ⇌ NH₃O + O₂ (reaction R4) computed here and estimated by RMG; Fig. S3: comparison of rate coefficients for NH₃ + HO₂ ⇌ NH₂ + H₂O₂ (reaction R7); Fig. S4: comparison of rate coefficients for N₂H₃ + HO₂ giving H₂NN(T) + H₂O₂ (Reaction R8); Table S3: Chemkin format thermodynamic NASA polynomials for NH₃O and H₂NN(T) and kinetic rate coefficients for the reactions reported in the manuscript; Table S4: Cantera format thermodynamic NASA polynomials for NH₃O and H₂NN(T) and kinetic rate coefficients for the reactions reported in the manuscript; A ZIP file with all species and TS geometries as individual XYZ files; Table S5: the main reference determinants of the CASSCF calculation for each TS. See DOI: https://doi.org/10.1039/d4cp01761g

---