Suboxides and subselenides: intermediate reaction products to form Ga2O3, Ga2Se3, In2O3, In2Se3, SnO2, and SnSe2 during molecular-beam epitaxy
Received
25th April 2024
, Accepted 18th November 2024
First published on 20th November 2024
Abstract
The molecular-beam epitaxial (MBE) growth of III-O and IV-O materials (e.g., Ga2O3, In2O3, and SnO2) is known to be reaction-limited by complex 2-step kinetics and the desorption of volatile suboxides (e.g., Ga2O, In2O, SnO). We find that the different surface reactivities of suboxides and respective elements (e.g., Ga, In, Sn) with active oxygen define the film-growth-windows (FGWs) and suboxide-formation-windows (SFWs) of III-O and IV-O materials, respectively. To generalize, we provide elementary reaction pathways and respective Gibbs energies to form binary III-O, III-Se, IV-O, and IV-Se ground-states as well as their subcompounds during their MBE growth. We apply the 2-step kinetics model established for oxides to identify the subselenide-limited growth of Ga2Se3 as the specific example for III-Se materials. Our kinetic and thermodynamic conclusions suggest subcompound-limited growth may be an inherent property for the growth of III–VI and IV–VI thin films by MBE and related epitaxial growth techniques.
I. Introduction
In ‘classical’ molecular-beam epitaxy (MBE) elemental cations react directly with reactive anions to form the intended compound on a heated single-crystalline substrate.1–4 This is because the MBE growth of III–V and II–VI materials is governed by simple 1-step reaction kinetics.3,5–10 This basic surface physics and reaction kinetics has been one of the prerequisites to controllably synthesize functional thin films at the highest crystalline level,11,12 for example, enabling the discovery of novel physics at thin film interfaces.13
On the other hand, the MBE growth of III-O and IV-O materials is more complex and determined by complex 2-step reaction kinetics and limited by the formation of volatile suboxides (e.g., Ga2O, In2O, and SnO).14–19 These complex surface reactions kinetically prohibit the growth of functional III-O and IV-O thin films in their adsorption-controlled growth regimes.20,21
Based on the common valences between III–VI or IV–VI materials, it is conceivable that the growth kinetics of III-Se and IV-Se is similar to that of III-O and IV-O compounds. Previous MBE studies on Ga2Se3 and In2Se3 indicate their growth to be limited by the formation of their subselenides Ga2Se and In2Se, respectively22–24—similar to Ga2O3 and In2O3 being limited by the formation of their suboxides Ga2O and In2O. However, the underlying reaction kinetics that form III-Se and IV-Se thin films remains elusive and the lack of microscopically understanding their reaction pathways hinders the full exploration of growth conditions and their impact on the phase formation and material properties of functional selenide-based thin films.25–29
In this paper, we start with identifying the surface reactivities (ηM) of elemental metal (with M = Ga, In, and Sn) as well as the surface reactivities (ηS) of molecular suboxides (with S = Ga2O, In2O, and SnO) reacting with oxygen, and find that ηM ≥ ηS. As a consequence of ηM ≥ ηS, the film-growth-windows (FGWs) of III-O and IV-O materials fundamentally change upon growth conditions; as we explicitly demonstrate by the example of Ga2O3. We next model the growth of Ga2Se3 by complex 2-step kinetics and obtain a similar result as established for Ga2O3 growth.30 To strengthen our model results, we provide elemental reaction pathways and thermodynamic calculations for the Ga2O3, Ga2Se3, In2O3, In2Se3, SnO2, and SnSe2 growth systems. In all cases, we obtain that suboxides and subselenides are the cationic-like volatile species in each material system and we propose that subcompounds (e.g., suboxides and subselenides) are the intermediate and rate-limiting reaction products for III–VI and IV–VI MBE growth, in general.
II. Suboxide-formation-window (SFW) versus film-growth-window (FGW)
To understand the origin of different surface reactivities between adsorbed metals (e.g., Ga) and formed suboxides (e.g., Ga2O) reacting with oxygen, Fig. 1(a)–(g) collect published growth rate (Γ) data of Ga2O3,15,31–33 In2O3,31 and SnO2,14 normalized by their respective nominal oxygen flux, ϕO. It depicts the fundamental Γ evolutions depending on the metal-to-oxygen flux ratio, R = ϕM/ϕO, at given growth temperature, TG, and metal flux, ϕM.
 |
| | Fig. 1 (a)–(d) Γ normalized by ϕO (Γ/ϕO) of β-Ga2O3 (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) as a function of the Ga-to-O ratio (R = ϕGa/ϕO), measured at different TG. Data is taken from ref. 31. (e) Γ/ϕO as a function of R of β-Ga2O3(010) [squares], β-Ga2O3( 01) as a function of the Ga-to-O ratio (R = ϕGa/ϕO), measured at different TG. Data is taken from ref. 31. (e) Γ/ϕO as a function of R of β-Ga2O3(010) [squares], β-Ga2O3(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) [discs, same data as shown in panel (c)], β-Ga2O3(001) [diamonds], and β-Ga2O3(100) [hexagons]. Data is taken from ref. 15 and 31–33. (f) Γ/ϕO of bixbiyte In2O3(111) as a function of the In-to-O ratio (R = ϕIn/ϕO), measured at different TG. Data is taken from ref. 17. (g) Γ/ϕO of SnO2(101) as a function of the Sn-to-O flux ratio (R = ϕSn/ϕO), obtained at different ϕO. Data is taken from ref. 14. (h) Growth-system-dependent maximum M-to-S formation (solid triangles) [eqn (4)–(6)] and maximum S-to-O formation (i.e., the maximum Γ, open triangles) [eqn (1)–(3)] as a function of TG. Symbols represent experimental data, solid and dotted lines are numeric models18,31 serving as guides to the eye. 01) [discs, same data as shown in panel (c)], β-Ga2O3(001) [diamonds], and β-Ga2O3(100) [hexagons]. Data is taken from ref. 15 and 31–33. (f) Γ/ϕO of bixbiyte In2O3(111) as a function of the In-to-O ratio (R = ϕIn/ϕO), measured at different TG. Data is taken from ref. 17. (g) Γ/ϕO of SnO2(101) as a function of the Sn-to-O flux ratio (R = ϕSn/ϕO), obtained at different ϕO. Data is taken from ref. 14. (h) Growth-system-dependent maximum M-to-S formation (solid triangles) [eqn (4)–(6)] and maximum S-to-O formation (i.e., the maximum Γ, open triangles) [eqn (1)–(3)] as a function of TG. Symbols represent experimental data, solid and dotted lines are numeric models18,31 serving as guides to the eye. | |
We start with the observed Γ plateaus: the solid lines in Fig. 1(a)–(g) reflect the film-growth-windows (FGWs) of Ga2O3, In2O3, and SnO2, obtained by experimental data (shown by the open symbols). At elevated TG, a Γ plateau emerges and widens with increasing TG. We define the value of Γ at the plateau as the value of maximum cation incorporation into the thin film at given TG. Based on the 2-step kinetics of these materials,20,31 this Γ value thus gives the maximum available oxygen reservoir for suboxide-to-oxide formation (S-to-O). This also defines the 2nd reaction step to form the oxides Ga2O3, In2O3, and SnO2, via the reactions:31
| |  | (1) |
| |  | (2) |
| |  | (3) |
with reaction rate constant,
K. Adsorbate and solid phases are denoted as a and s, respectively.
To explain the origin of the Γ plateau as well as the onset of the Γ decrease, we now define the suboxide-reaction-window (SRW) for metal-to-suboxide formation (M-to-S). This defines the 1st reaction step to form Ga2O3, In2O3, and SnO2 through forming the suboxides Ga2O, In2O, and SnO, respectively, via the reactions:31
| |  | (4) |
| | 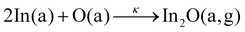 | (5) |
| |  | (6) |
with reaction rate constant,
κ. The gaseous phase is denoted as g and refers to the volatility of suboxides during growth. The SRW is indicated by the dotted lines in
Fig. 1(b)–(e) and (g) and obtained by extending the
Γ evolutions from extending the M-rich growth regime (the
decreasing Γ with
ϕM) as well as the O-rich regime (the
increasing Γ with
ϕM) until both lines intersect—always forming a triangular shape. The suboxides formed during the 1
st reaction step,
eqn (4)–(6), can be further oxidized to the solid compound through a 2
nd reaction step,
eqn (1)–(3), or desorb from the growth surface and limit
Γ. As a result, the SRW for M-to-S formation is equal to or wider than the FGW for S-to-O formation,
i.e.,
κ ≥
K, depending on
TG. To illustrate their quantitative differences, the maximum (normalized) formation rates of Ga
2O and Ga
2O
3 as well as of In
2O and In
2O
3 are plotted as a function of
TG in
Fig. 1(h). A detailed explanation of this effect is given in
Fig. 2. The maximum suboxide formation is defined as the peak value of the SRWs, seen by dotted lines in
Fig. 1(b)–(d) and (g). In the case of SnO
2, we obtain the suboxide formation is about 1.4
Γ for all
ϕO at
TG = 650 °C. Overall, the reactivity of Sn > In > Ga with O is higher than the one of SnO > In
2O > Ga
2O with O, respectively. This feature can also be referred to the different vapor pressures and surface reactivities of the respective elements and suboxides.
16,18,34–38
 |
| | Fig. 2
Γ evolutions for III-O compounds, explicitly drawn for Ga2O3. Four distinct growth regimes (i)–(iv) are identified (details provided in the text). (a) The gray and purple areas reflect the modelled film-growth-windows (FGWs) for Ga2O3 based on the data obtained at TG = 500 °C [Fig. 1(a)] and TG = 600 °C [Fig. 1(c)], respectively. The difference (Δ) between SFW and FGW for Ga-to-Ga2O formation [eqn (4)] and Ga2O-to-Ga2O3 formation [eqn (1)] is drawn as the pale purple area at TG = 600 °C. At TG = 500 °C this difference is zero, i.e., Δ = 0. The length of the Γ plateau is given by λ [regime (ii)] and the width of regime (iii) is defined as ω. All parameters shown here are collected in Table 1. (b) FGWs of Ga2O3 as a function of R modelled for 400 °C ≤ TG ≤ 1200 °C (the pale blue lines), using a numerical approach based on the models given in ref. 18 and 39. At low TG = 400 °C, the triangular shape defines the maximum accessible ηM = ηS ⇒ SRF = FGW (the dark blue line) divided in regimes (i), (iii), and (iv). With increasing TG, regime (ii) emerges and the ‘shape’ of the FGW fundamentally changes to a trapezoidal shape due to ηM > ηS ⇒ SRF > FGW (the dark blue line in the center). The fact that SRF ≥ FGW, changes λ, Δ, and ω, depending on TG. As a consequence, regime (iii) becomes narrower until it vanishes at high TG. The black dashed lines correspond to the solid black model lines in Fig. 1(a)–(d) and serve as a guide to the eye. | |
Fig. 1(f) and (g) depict the Γ evolutions of In2O3 and SnO2, respectively, as a function of R, showing qualitatively the same kinetic behaviour as observed for Ga2O3. The quantitative differences in Γ between III-O and IV-O materials arise from the different group III-O and IV-O suboxide stoichiometries as well as their different surface reactivities.16,37
Note, for the sake of simplicity, reactions (1)–(6) are selected as specific examples but may be generalized for other III-O and IV-O materials. For example, the knowledge of the 2-step reaction kinetics was used to form Al2O3,40 rutile GeO2,41 or amorphous GeO242via the formation of their suboxides Al2O and GeO, respectively. We further note that a ‘direct reaction’ to form the solid-state compound, e.g., via 2Ga + 3O → Ga2O3, can be kinetically excluded. This assumption is reasonable as the formation of complex compounds can be (usually) described by a set of elementary reactions rather than by non-elementary reactions.43 In other words, forming the oxide thin film via a set of multiple elementary surface reactions via a suboxide formation step is kinetically preferred over a single non-elemental surface reaction step. As the suboxide itself may also undergo a multi-step reaction pathway, we propose a general reaction scheme to form binary III–VI and IV–VI materials and sketch their possible reaction pathways in Fig. 5 (see below).
A. Surface-orientation Γ dependence of Ga2O3
Fig. 1(e) shows the comparison of β-Ga2O3 FGWs for different surface orientations of β-Ga2O3(010), β-Ga2O3(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01), β-Ga2O3(001), and β-Ga2O3(100) as a function of R, at otherwise similar growth conditions.15,17,32,33 At given TG ≈ 600 °C,15,31–33 the orientation dependence of Γ on the (hkl) plane, Γ(hkl), for β-Ga2O3 is quantified as
01), β-Ga2O3(001), and β-Ga2O3(100) as a function of R, at otherwise similar growth conditions.15,17,32,33 At given TG ≈ 600 °C,15,31–33 the orientation dependence of Γ on the (hkl) plane, Γ(hkl), for β-Ga2O3 is quantified as| | Γ(010) ≈ 1.5Γ(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) ≈ 3.7Γ(001) ≈ 7.7Γ(100). 01) ≈ 3.7Γ(001) ≈ 7.7Γ(100). | (7) |
Note this quantification depends on the adsorption and desorption kinetics of Ga2O on the respective β-Ga2O3 (hkl) growth plane and strongly depends on TG.15,30,44 For example, at TG = 500 °C the relation Γ(010) ≈ 2.1Γ(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) was observed,20 suggesting a different functional dependence of sticking coefficients on the respective Ga2O3 growth surface. We thus qualitatively propose, the orientation-dependent Γ evolution of Ga2O3 can be explained by an interplay of the corresponding orientation-dependent O sticking coefficients (σ) and suboxide surface reactivities ηS, leading to:
01) was observed,20 suggesting a different functional dependence of sticking coefficients on the respective Ga2O3 growth surface. We thus qualitatively propose, the orientation-dependent Γ evolution of Ga2O3 can be explained by an interplay of the corresponding orientation-dependent O sticking coefficients (σ) and suboxide surface reactivities ηS, leading to:| | Γ(010) > Γ(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) > Γ(001) > Γ(100). 01) > Γ(001) > Γ(100). | (8) |
A similar orientation-dependent Γ of β-Ga2O3 in binary Ga–O and Ga2O–O systems is reported in ref. 18, 33 and 44.
B. Suboxides limiting the growth domain of III-O compounds
For all compounds, we find that SRW ≥ FGW, thus, the physical origin of changing FGWs and emerging Γ plateaus can now explained.
Fig. 2(a) sketches the Γ evolutions of Ga2O3 (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) at TG = 500 °C (the gray shaded area) and TG = 600 °C (the purple shaded area), see also Fig. 1(a) and (c). Four regimes are indicated: (i) the O-rich growth regime, i.e., the increasing Γ with increasing Ga flux, ϕGa. In this regime, enough O adsorbates are available to fully oxidize all adsorbed Ga via the consecutive reaction Ga → Ga2O → Ga2O3 [reactions (4) and (1)]. (ii) The ‘pseudo’ O-rich growth regime identified by the width of the Γ plateau, λ. Here, enough O adsorbates are available to oxidize all adsorbed Ga to its suboxide via Ga → Ga2O [reaction (4)] but not enough O is available to oxidize all formed suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]—due to thermally-induced suboxide desorption. In other words, the Γ plateau emerges once the formed Ga2O adsorbate density exceeds the O adsorbate density available for reaction Ga2O → Ga2O3 [reaction (1)].21 (iii) The Ga-rich growth regime identified by the decreasing Γ with ϕGa and its width, ω. Here, not enough O is available to oxidize all remaining suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]. Now, this is due to an O-deficient-induced suboxide desorption mechanism—in addition to the thermally-induced suboxide desorption identified for regime (ii). (iv) The no-growth regime where Ga2O3 growth ceases for R ≥ Rm. Here, not enough O is available to oxidize Ga → Ga2O [reaction (4)] and reaction (1) becomes kinetically forbidden as all available O is consumed in reaction (4).
01) at TG = 500 °C (the gray shaded area) and TG = 600 °C (the purple shaded area), see also Fig. 1(a) and (c). Four regimes are indicated: (i) the O-rich growth regime, i.e., the increasing Γ with increasing Ga flux, ϕGa. In this regime, enough O adsorbates are available to fully oxidize all adsorbed Ga via the consecutive reaction Ga → Ga2O → Ga2O3 [reactions (4) and (1)]. (ii) The ‘pseudo’ O-rich growth regime identified by the width of the Γ plateau, λ. Here, enough O adsorbates are available to oxidize all adsorbed Ga to its suboxide via Ga → Ga2O [reaction (4)] but not enough O is available to oxidize all formed suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]—due to thermally-induced suboxide desorption. In other words, the Γ plateau emerges once the formed Ga2O adsorbate density exceeds the O adsorbate density available for reaction Ga2O → Ga2O3 [reaction (1)].21 (iii) The Ga-rich growth regime identified by the decreasing Γ with ϕGa and its width, ω. Here, not enough O is available to oxidize all remaining suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]. Now, this is due to an O-deficient-induced suboxide desorption mechanism—in addition to the thermally-induced suboxide desorption identified for regime (ii). (iv) The no-growth regime where Ga2O3 growth ceases for R ≥ Rm. Here, not enough O is available to oxidize Ga → Ga2O [reaction (4)] and reaction (1) becomes kinetically forbidden as all available O is consumed in reaction (4).
We next answer the question: Why does Γ start to decrease at Ro [see Fig. 2(a)] and regime (iii) is entered? Each leaving Ga2O that cannot be oxidized removes 2 × Ga but only 1 × O from the growth front, producing a more O-rich Ga-to-O surface ratio than expected from the nominally supplied ϕGa and ϕO. Nevertheless, for R > Ro, ϕGa and resulting Ga adsorbate density exceed a critical value, resulting in a Ga-rich growth surface and thus regime (iii) is entered. In this regime, not enough O is available to oxidize all formed Ga2O that have remained on the growth surface (i.e., Ga2O molecules that have not desorbed), and Γ decreases due to the O-surface-deficiency-induced suboxide desorption. As specific example, all parameters and values for Ga2O3 are indicated in Fig. 2(a) and collected in Table 1, which, in turn, are extracted from the data plotted in Fig. 1(a)–(d). After considering all desorbing species, it is found that the Ga2O3 growth surface becomes stoichiometric once
| |  | (9) |
see
Fig. 2 and
Table 1.
Table 1 Stoichiometric M-to-O flux ratio, R*. Maximum suboxide formation rate, Γ*, for Ga-to-Ga2O oxidation. The growth rate value at the plateau, Γp. Maximum flux ratio where Ga2O3 growth is possible, Rm. The flux ratio at the beginning of the plateau, Ri (with ‘i’ for in). The flux ratio at the end of the plateau, Ro (with ‘o’ for out). The maximum Ga adsorbates, nGa, and the maximum O adsorbates, nO. The difference Δ between the Ga2O SRW and the Ga2O3 FGW. The length λ of the plateau and the width ω of the Ga-rich regime (ii). Finally, the Ga-to-O adsorbate ratio at the end of the plateau, nGa/nO = x/y = constant ≤ ϕGa/ϕO [see eqn (9)]. Parameters are indicated in Fig. 2(a) and values are extracted from the data shown in Fig. 1(a)–(d). This example may serve as a blueprint for all discussed III–VI and IV–VI materials
|
T
G (°C) |
R* = 2Γ* = 1/3Rm |
R
i = nGa = 2Γp |
R
o
|
λ = Ro − Ri |
n
O = 1/2(3R* − λ) |
Δ = Γ* − Γp |
ω = 3R* − Ro |
n
Ga/nO |
| 500 |
2/3 |
2/3 |
2/3 |
0 |
1 |
0 |
4/3 |
=2/3 |
| 550 |
0.58 |
0.48 |
0.79 |
0.31 |
0.72 |
0.05 |
0.97 |
≈2/3 |
| 600 |
0.52 |
0.36 |
0.85 |
0.49 |
0.54 |
0.08 |
0.71 |
≈2/3 |
| 675 |
0.48 |
0.24 |
0.97 |
0.73 |
0.36 |
0.12 |
0.42 |
≈2/3 |
The above findings have fundamental consequences for the Γ evolution of III–VI and IV–VI compounds. For example, λ increases and ω decreases with increasing TG because of the enhanced thermally-induced suboxide desorption. As a result, the ‘shape’ of the accessible FGW changes upon growth conditions. Based on the data plotted in Fig. 1(a)–(d), Fig. 2(b) now depicts such an Γ evolution as a function of R and different TG (here of Ga2O3).
At low TG, the triangular shape of the modeled Γ defines the maximum possible FGW for these materials. With increasing TG, the Γ plateau emerges and the growth domain becomes trapezoidal and narrows until growth eventually ceases. This finding reveals that the growth of Ga2O3 in the Ga-rich regime and elevated TG is hardly possible, associated with extremely slow Γ. Nevertheless, these growth conditions are desired to improve the crystallographic and transport properties of Ga2O3 grown by conventional MBE.28 The same argument holds for In2O3, for example.
A solution to overcome these intrinsic and detrimental growth limits for group III and group IV oxides is the use of recent advances in their thin film synthesis, such as suboxide MBE (S-MBE),20,21,45 metal-exchange catalysis (MEXCAT)18,37 with metal-oxide-catalyzed epitaxy (MOCATAXY),17,46 thermal laser epitaxy (TLE),40 or hybrid MBE (hMBE).47,48
These findings can also be transferred to IV-O materials, e.g., SnO2. In contrast to the ‘asymmetric’ Γ plateau observed for III-O materials (Fig. 2), the Γ plateau observed for IV-O materials is ‘symmetric’ as plotted for SnO2 in Fig. 1(g). The occurrence of an asymmetric Γ plateau (III–VI) or symmetric Γ plateau (IV–VI) can be explained by the different stoichiometries of III-O and IV-O suboxides. For example, during the growth of SnO2 the desorption of SnO removes 1 × Sn and 1 × O, resulting in the observed symmetric Γ plateau. In contrast to SnO2, during the growth of Ga2O3 the desorption of Ga2O removes 2 × Ga and 1 × O, resulting in the observed asymmetric Γ plateau. Another quantitative consequence of the different suboxide stoichiometries is the differently observed slopes in their M-rich regimes for III-O and IV-O materials with
| |  | (10) |
respectively. For example, see
Fig. 1(a) for III-O and
Fig. 1(g) for IV-O materials.
III. Subselenide-limited growth of Ga2Se3
The formation of suboxides has been experimentally reported14–16 and identified as the growth-limiting step for III-O and IV-O materials and reaction-rate models describing the complex 2-step kinetics for these materials have been developed.18,31 We anticipate the same kinetics and models can be applied to other III–VI and IV–VI compounds. Therefore, we now apply the 2-step model to the growth of III-Se materials, explicitly, to the growth of Ga2Se3.
Fig. 3 shows the Γ evolution of Ga2Se3 as a function of the Se-to-Ga ratio, r. The 2-step model described above for oxides is applied to the data and describes the growth kinetics for Ga2Se3 very accurately—indicating its MBE growth is limited by Ga2Se desorption. A similar Γ-behavior is also reported for the growth of In2Se3 by MBE.23 In ref. 22 and 23, it was speculated that the growth of Ga2Se3 and In2Se3 ceases in the excess of Ga and In fluxes, respectively, due to the re-evaporation of the Ga and Se compounds. However, the physical origin for the observed Γ evolutions for Ga2Se3 and In2Se3 remained elusive.22,23 The black lines in Fig. 3 show numeric model calculations by a subselenide-mediated 2-step model. Three distinct regimes are identified: (I) no growth regime for 0 < r = ϕSe/ϕGa ≤ 1/2, because all reactive Se is consumed for Ga2Se formation, i.e., r = 1/2 defines the stoichiometric flux ratio for 2Ga + Se → Ga2Se formation, e.g., viareaction (14). (II) The Ga-rich regime is entered for 1/2 < r ≤ 3/2, because not enough reactive Se is available to convert Ga2Se → Ga2Se3, e.g., viareaction (15). The stoichiometric flux ratio for Ga2Se3 formation is thus r = 3/2. (III) For r > 3/2 the Se-rich flux regime is entered and enough reactive Se is available to selenize Ga → Ga2Se → Ga2Se3. Γ is now limited by the supplied ϕGa.
 |
| | Fig. 3 Normalized Γ/ϕGa of α-Ga2Se3 as a function of the Se-to-Ga flux ratio, ϕSe/ϕGa = r. Data is taken from ref. 22, Ga and Se densities in α-Ga2Se349 are used to convert ϕGa, ϕSe, and Γ into nm−2 s−1. The solid black line is the application of the 2-step model to the experimental data. The data and model shown in the main graph and the inset are complementary but displayed for the sake of readability. In the Se-rich rich regime, Γ is maximized and limited by the supplied ϕGa. Note, the horizontal axis in this graph is swapped when compared to the horizontal axes in Fig. 1. | |
Based on the data shown in Fig. 1–3, we can now generalize eqn (10) for III–VI and VI-VI materials for the anion-rich regime (A), plateau regime (P), and cation-rich regime (C) as
| |  | (11) |
IV. Thermodynamic analysis and surface reactions
To support and strengthen our prediction that suboxides and subselenides limit the growth of oxides and selenides, respectively, we now perform thermodynamical calculations. Equilibrium calculations are performed using the SGTE substance database (SSUB5)50 within the Thermo-Calc software51 to assess the evaporation behavior of cation-like and anion-like species as a function of temperature of the binary oxides Ga2O3, In2O3, and SnO2 and the complementary, binary selenides Ga2Se3, In2Se3, and SnSe2. The results are plotted in Fig. 4.
 |
| | Fig. 4 (a) Calculated partial pressures of the gas species C = Ga, In, Sn, A = O, Se, Cy−xAy−x = GaO, InO, InSe, SnO, SnSe [reaction (12)], and CxAy−x = Ga2O, In2O, In2Se [reactions (13) and (14)]. | |
For the investigated compounds Ga2O3, In2O3, SnO2, In2Se3, and SnSe2, we find that the most volatile, cationic-like species at relevant TG are the suboxides and subselenides Ga2O, In2O, SnO, In2Se, and SnSe, respectively, and are in accordance with our kinetics findings that their growth is reaction-limited by subcompound formation and their subsequent desorption. Note, for the Ga2Se3 system, the subselenides GaSe and Ga2Se are missing in the SSUB5 and other thermodynamic databases, thus, we use the kinetic data shown in Fig. 3 to identify that the growth of Ga2Se3 is reaction-limited by the subselenide Ga2Se. This is in agreement with all other investigated growth systems. For example, if Ga was the volatile, cationic species limiting the growth of Ga2Se3, Γ would reach a plateau in the Ga-rich regime instead, being similar to the growth kinetics observed for binary III-N compounds.8 The fact that Γ of Ga2Se3 and In2Se3 decrease in the Ga-rich and In-rich regimes, respectively, can thus be explained by the desorption of Ga2Se and In2Se. We note that the desorption of GaSe and InSe would also explain a decreasing Γ in the cation-rich regimes but with different slopes as given in eqn (11).
In addition, calculated Gibbs energies (ΔG) to form Ga2Se3 further strengthen our hypothesis of a 2-step reaction kinetics underlying the formation of III-Se compounds. To unambiguously identify the growth-rate-limiting steps of Ga2Se3 and In2Se3, in situ line-of-sight mass spectroscopy will reveal which subcompound is formed on the respective growth surface.
To microscopically understand the observed and modeled Γ evolutions (Fig. 1–3) and evaporation of suboxides and subselenides, a general reaction scheme for III–VI and IV–VI compounds is proposed in Fig. 5. It depicts a CxAy layer (e.g., Ga2Se3), impinging cation flux ϕc and anion flux ϕa, producing the cation (C), anion (A), and subcompound surface populations Cy−xAy−x (e.g., GaSe), CxAy−x (e.g., Ga2Se), CxA2(y−x) (e.g., Ga2Se2). Stoichiometric coefficients for III–VI and IV–VI materials are x = 2 and y = 3 as well as x = 1 and y = 2, respectively. The reaction scheme depicted in Fig. 5 is an extension and refinement of the reaction scheme introduced in ref. 31.
 |
| | Fig. 5 MBE reaction scheme for binary III–VI and IV–VI materials, showing impinging ϕc and ϕa, resulting cation nc, anion na, respective subcompound reservoirs, and the final compound CxAy. Chemical reactions (12)–(17) are indicated by reaction rate constants ki. | |
Consecutive reaction pathways to form III-O, III-Se, IV-O, and IV-Se are:
| |  | (12) |
| | 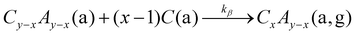 | (13) |
| |  | (14) |
| |  | (15) |
| |  | (16) |
| | 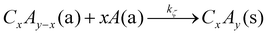 | (17) |
with reaction rate constant
ki with
i =
α,
β,
γ,
δ,
ε,
ζ. In
eqn (13), the relation
y − 1 =
x is used. Note, for the growth of IV–VI compounds,
reactions (13) and (16) are forbidden and
reactions (15) and (17) are identical due to their stoichiometric coefficients
x = 1 and
y = 2. Consequently, the surface reaction pathways for IV–VI are not as complex as for III–VI compounds.
It has been shown for III-O materials (e.g., Ga2O3) and IV-O materials (e.g., SnO2) that these compounds can be chemically decomposed (etched) by their respective elemental metal (e.g., Ga or Sn) to form its respective suboxide (e.g., GaO, Ga2O, or SnO)16via the reactions
| |  | (18) |
| |  | (19) |
with etching rate constants
eα and
eβ to form the subcompounds
Cy−xAy−x (
e.g., GaO or GaSe) and
CxAy−x (
e.g., Ga
2O or Ga
2Se), respectively. Note, for III-O materials only
reaction (19) has been experimentally observed under MBE conditions.
16
Finally, Fig. 6 plots our calculated ΔG using eqn (20)–(24) as a function of TG of Ga2O3, Ga2Se3, In2O3, In2Se3, SnO2, and SnSe2 (calculations are given in the Appendix I). We calculated ΔG for growth and etch reactions (12)–(19) once data were available.52 For all investigated materials and relevant TG, the formation of the suboxide and subselenide is thermodynamically feasible. This is in agreement with the observed III-O and IV-O kinetics and we further calculate that III-Se and IV-Se compounds can be chemically decomposed by their elemental metal to form their respective subselenide through reactions (18) and (19). We thus conjecture that the formation of suboxides and subselenides is kinetically and thermodynamically favorable and the rate-limiting step for a wide-range of III-O, III-Se, IV-O, and IV-Se compound materials.
 |
| | Fig. 6 The Gibbs energy (ΔG) as a function of temperature T. Values of ΔG are in eV per formula unit (f.u.). (a)–(f) ΔG for subcompound formations viaeqn (12) [black solid lines] and eqn (13) [dark-blue dotted lines]. (g)–(l) ΔG for solid thin film formations viaeqn (17) [blue solid lines]. (m)–(r) ΔG for thin film etching to form subcompounds viaeqn (18) [gray dotted lines] and eqn (19) [gray solid lines]. | |
V. Conclusions
We identify by published growth rate (Γ) data of the Ga2O3, In2O3, and SnO2 growth systems that the elements Ga, In, and Sn possess a higher reaction efficiency (ηM) with adsorbed O than their corresponding volatile suboxides (ηS) Ga2O, In2O, and SnO. We find that ηM ≥ ηS and quantified the fundamental growth domain of III–VI materials whose regimes strongly depend on MBE growth conditions and find that SFW ≥ FGW. In particular, we observe a vanishing M-rich growth regime with increasing TG, leading to off-stoichiometric growth surfaces concerning their initially adsorbed densities of group III and group VI elements.
By combining a 2-step kinetic model to experimental Γ data of Ga2Se3 with our thermodynamic analysis and calculations we find the volatile species for the Ga2Se3, In2Se3, and SnSe2 systems are the subselenides Ga2Se, In2Se, and SnSe, respectively. We provide a detailed reaction diagram for the growth of III-O, III-Se, IV-O, and IV-Se materials systems, supported by thermodynamic calculations.
The identified thermodynamic and kinetic feasibility of the proposed 2-step reaction mechanisms for III-Se and IV-Se materials let us conclude that III-Se and IV-Se compounds grow via (qualitatively) the same 2-step reaction mechanism—similar to what is established for III-O and IV-O materials.21,31,38 To unambiguously identify the growth-rate-limiting steps and volatile species of the proposed binary III-O, III-Se, IV-O, and IV-Se growth systems [e.g., eqn (12)–(19)], in situ line-of-sight mass spectroscopy will reveal which subcompound is formed on the respective growth surface.
Author contributions
Patrick Vogt: conceptualization (lead), data curation (lead), formal analysis (lead), investigation (lead), methodology (lead), writing original draft (lead). Shun-Li Shang: methodology (equal), data curation (equal), formal analysis (supporting), investigation (supporting), writing original draft (supporting). Zi-Kui Liu: data curation (supporting), investigation (supporting), methodology (supporting), writing original draft (supporting).
Data availability
Data is available upon reasonable request from the corresponding authors.
Conflicts of interest
The authors have no conflicts of interest to declare.
Appendices
Appendix I
Thin film growth via MBE takes place under isobaric-isothermal conditions. The change in the Gibbs energy ΔG(T) at given temperature T is| | | ΔG(T) = ΔH(T) − TΔS(T), | (20) |
with the change in enthalpy ΔH(T) and the change in entropy ΔS(T) determined as| |  | (21) |
| |  | (22) |
respectively. ΔH0 and ΔS0 denote the change in ΔH and ΔS at room temperature, T0 = 295 K. The heat capacity C(T) is calculated as| | | C(T) = a + b 10−3T + c 106T−2 + d 10−6T2. | (23) |
For all discussed species, ΔH0, ΔS0, a, b, c, and d are taken from ref. 52. A chemical reaction may occur spontaneously once ΔG < 0. For a given reaction, with reactants Ri and products Pj, it can be determined by the sum of the Gibbs energies of Pj,  minus the sum of the Gibbs energies of Ri,
minus the sum of the Gibbs energies of Ri, 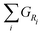 , i.e.
, i.e.| |  | (24) |
The stoichiometric coefficients of Ri and Pj are denoted as ri and pj, respectively.
Acknowledgements
PV acknowledges the Max Planck Institute for Solid State Research for financial support and Martin Eickhoff and Alexander Karg for fruitful discussions regarding the reaction chemistries of III-O compounds. SLS and ZKL acknowledge the support from Endowed Dorothy Pate Enright Professorship at the Pennsylvania State University.
References
- J. R. Arthur, J. Appl. Phys., 1968, 39, 4032, DOI:10.1063/1.1656901.
- M. Copel, M. C. Reuter, E. Kaxiras and R. M. Tromp, Phys. Rev. Lett., 1989, 63, 632, DOI:10.1103/PhysRevLett.63.632.
- K. Ploog, Annu. Rev. Mater. Sci., 1982, 12, 123, DOI:10.1146/annurev.ms.12.080182.001011.
- J. Neugebauer, T. K. Zywietz, M. Scheffler, J. E. Northrup, H. Chen and R. M. Feenstra, Phys. Rev. Lett., 2003, 90, 056101, DOI:10.1103/PhysRevLett.90.056101.
- K. Ploog, Annu. Rev. Mater. Sci., 1981, 11, 171, DOI:10.1146/annurev.ms.11.080181.001131.
- H. Riechert, R. Averbeck, A. Graber, M. Schienle, U. Straub and H. Tews, MRS Online Proc. Libr., 1996, 449, 149–159, DOI:10.1557/PROC-449-149.
- E. Calleja, M. A. Sánchez-García, F. J. Sánchez, F. Calle, F. B. Naranjo and E. Muñoz,
et al.
, J. Cryst. Growth, 1999, 201, 296, DOI:10.1016/S0022-0248(98)01346-3.
- S. Fernández-Garrido, G. Koblmüller, E. Calleja and J. S. Speck, J. Appl. Phys., 2008, 104, 1, DOI:10.1063/1.2968442.
- Z. Zhu, M. Hagino, K. Uesugi, S. Kamiyama, M. Fujimoto and T. Yao, Jpn. J. Appl. Phys., 1989, 28, 1659, DOI:10.1143/JJAP.28.1659.
- K. Kato, M. Sano, K. Miyamoto and T. Yao, Jpn. J. Appl. Phys., 2003, 42, 2241, DOI:10.1143/JJAP.42.2241.
- L. Pfeiffer, K. W. West, H. L. Stormer and K. W. Baldwin, Appl. Phys. Lett., 1989, 55, 1888, DOI:10.1063/1.102162.
- D. G. Schlom and L. N. Pfeiffer, Nat. Mater., 2010, 9, 881, DOI:10.1038/nmat2888.
- D. C. Tsui, H. L. Stormer and A. C. Gossard, Phys. Rev. Lett., 1982, 48, 1559, DOI:10.1103/PhysRevLett.48.1559.
- M. E. White, M. Y. Tsai, F. Wu and J. S. Speck, J. Vac. Sci. Technol., A, 2008, 26, 1300, DOI:10.1116/1.2966423.
- M. Y. Tsai, O. Bierwagen, M. E. White and J. S. Speck, J. Vac. Sci. Technol., A, 2010, 28, 354, DOI:10.1116/1.3294715.
- P. Vogt and O. Bierwagen, Appl. Phys. Lett., 2015, 106, 081910, DOI:10.1063/1.4913447.
- P. Vogt, A. Mauze, F. Wu, B. Bonef and J. S. Speck, Appl. Phys. Express, 2018, 11, 115503, DOI:10.7567/APEX.11.115503.
- P. Vogt, F. V. E. Hensling, K. Azizie, J. P. McCandless, J. Park and K. DeLello,
et al.
, Phys. Rev. Appl., 2022, 17, 034021, DOI:10.1103/PhysRevApplied.17.034021.
- S. Raghuvansy, J. P. McCandless, M. Schowalter, A. Karg, M. Alonso-Orts and M. S. Williams,
et al.
, APL Mater., 2023, 11, 111113, DOI:10.1063/5.0174373.
- P. Vogt, F. V. E. Hensling, K. Azizie, C. S. Chang, D. Turner and J. Park,
et al.
, APL Mater., 2021, 9, 031101, DOI:10.1063/5.0035469.
-
P. Vogt, D. G. Schlom, F. V. E. Hensling, K. Azizie, Z. K. Liu and B. J. Bocklund, et al., United States Patent., 2022,
11462402, https://patents.google.com/patent/US11462402B2/en Search PubMed.
- N. Teraguchi, F. Kato, M. Konagai, K. Takahashi, Y. Nakamura and N. Otsuka, Appl. Phys. Lett., 1991, 59, 567, DOI:10.1063/1.105388.
- T. Okamoto, A. Yamada and M. Konagai, J. Cryst. Growth, 1997, 175, 1045, DOI:10.1016/S0022-0248(96)00984-0.
- T. Shimada, F. S. Ohuchi, A. Koma and J. Jpn, Appl. Phys., 1993, 32, 1182, DOI:10.1143/JJAP.32.1182.
- G. Han, Z. G. Chen, J. Drennan and J. Zou, Small, 2014, 10, 2747, DOI:10.1002/smll.201400104.
- N. Balakrishnan, E. D. Steer, E. F. Smith, Z. R. Kudrynskyi, Z. D. Kovalyuk and L. Eaves,
et al.
, 2D Mater., 2018, 5, 035026, DOI:10.1088/2053-1583/aac479.
- J. B. Varley, J. R. Weber, A. Janotti and C. G. Van de Walle, Appl. Phys. Lett., 2010, 97, 142106, DOI:10.1063/1.3499306.
- J. B. Varley, H. Peelaers, A. Janotti and C. G. Van de Walle, J. Phys.: Condens. Matter, 2011, 23, 334212, DOI:10.1088/0953-8984/23/33/334212.
- D. S. Liu, M. Hilse, A. R. Lupini, J. M. Redwing and R. Engel-Herbert, ACS Appl. Nano Mater., 2023, 6, 15029, DOI:10.1021/acsanm.3c02602.
- P. Vogt and O. Bierwagen, Appl. Phys. Lett., 2016, 108, 072101, DOI:10.1063/1.4942002.
- E. Ahmadi, O. S. Koksaldi, S. W. Kaun, O. Yuichi, D. B. Short and U. K. Mishra,
et al.
, Appl. Phys. Express, 2017, 10, 041102, DOI:10.7567/APEX.10.041102.
- Y. Oshima, E. Ahmadi, S. Kaun, F. Wu and J. S. Speck, Semicond. Sci. Technol., 2018, 33, 015013 CrossRef.
- P. Vogt and O. Bierwagen, Phys. Rev. Mater., 2018, 2, 120401(R), DOI:10.1103/PhysRevMaterials.2.120401.
- C. J. Frosch and C. D. Thurmond, J. Phys. Chem., 1962, 66, 877, DOI:10.1021/j100811a027.
- J. Valderrama-N and K. T. Jacob, Thermochim. Acta, 1977, 21, 215, DOI:10.1016/0040-6031(77)85019-3.
- R. Colin, J. Drowart and G. Verhaegen, Trans. Faraday Soc., 1965, 61, 1364, 10.1039/TF9656101364.
- P. Vogt, O. Brandt, H. Riechert, J. Lähnemann and O. Bierwagen, Phys. Rev. Lett., 2017, 119, 196001, DOI:10.1103/PhysRevLett.119.196001.
- K. M. Adkison, S. L. Shang, B. J. Bocklund, D. Klimm, D. G. Schlom and Z. K. Liu, APL Mater., 2020, 8, 081110 CrossRef CAS.
-
P. Vogt, Growth Kinetics, Thermodynamics, and Phase Formation of group-III and IV oxides during Molecular Beam Epitaxy, Humboldt University of Berlin, 2017 DOI:10.18452/18036.
- L. N. Majer, T. Acartürk, P. A. Aken, W. Braun, L. Camuti and J. Eckl-Haese,
et al.
, APL Mater., 2024, 12, 091112, DOI:10.1063/5.0224092.
- S. Chae, H. Paik, N. M. Vu, E. Kioupakis and J. T. Heron, Appl. Phys. Lett., 2020, 117, 072105, DOI:10.1063/5.0018031.
- W. Chen, K. Egbo, H. Tornatzky, M. Ramsteiner, M. R. Wagner and O. Bierwagen, APL Mater., 2023, 11, 071110, DOI:10.1063/5.0155869.
-
M. E. Davis and R. J. Davis, Fundamentals of Chemical Reaction Engineering, McGraw-Hili, 1221 Avenue of the Americas, New York, NY, 2003, 10020 Search PubMed.
- K. Sasak, A. Kuramata, T. Masui, E. G. Víllora, K. Shimamura and S. Yamakoshi, Appl. Phys. Express, 2012, 5, 035502 CrossRef.
- K. Azizie, F. V. E. Hensling, C. A. Gorsak, Y. Kim, N. A. Pieczulewski and D. M. Dryden,
et al.
, APL Mater., 2023, 11, 041102, DOI:10.1063/5.0139622.
- A. Mauze, Y. Zhang, T. Itoh, F. Wu and J. S. Speck, APL Mater., 2020, 8, 021104, DOI:10.1063/1.5135930.
- F. Liu, T. K. Truttmann, D. Lee, B. E. Matthews, I. Laraib and A. Janotti,
et al.
, Commun. Mater., 2022, 3, 69, DOI:10.1038/s43246-022-00290-y.
- Z. Wen, K. Khan, X. Zhai and E. Ahmadi, Appl. Phys. Lett., 2023, 122, 082101, DOI:10.1063/5.0142107.
- C. H. Ho, ACS Omega, 2020, 5, 18527, DOI:10.1021/acsomega.0c02623.
- Scientific Group Thermodata Europe (SGTE) Thermodynamic Properties of Inorganic Materials, in Lehrstuhl fuer Theoretische Huettenkunde (Ed), Landolt-Boernstein New Ser Gr IV, Springer, Verlag Berlin Heidelberg, 1999, vol. 19A.
- J. O. Andersson, T. Helander, L. Hoglund, P. Shi and B. Sundman, Thermo-Calc DICTRA: computational tools for materials science, Calphad, 2002, 26, 273 CrossRef CAS.
-
M. Binnewies and E. Mielke, Thermochemical Data of Elements and Compounds, Wiley VCH, 2nd edn, 2002 DOI:10.1002/9783527619818.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Shun-Li
Shang
*a,
Shun-Li
Shang
 b and
Zi-Kui
Liu
b and
Zi-Kui
Liu
 b
b

![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) as a function of the Ga-to-O ratio (R = ϕGa/ϕO), measured at different TG. Data is taken from ref. 31. (e) Γ/ϕO as a function of R of β-Ga2O3(010) [squares], β-Ga2O3(
01) as a function of the Ga-to-O ratio (R = ϕGa/ϕO), measured at different TG. Data is taken from ref. 31. (e) Γ/ϕO as a function of R of β-Ga2O3(010) [squares], β-Ga2O3(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) [discs, same data as shown in panel (c)], β-Ga2O3(001) [diamonds], and β-Ga2O3(100) [hexagons]. Data is taken from ref. 15 and 31–33. (f) Γ/ϕO of bixbiyte In2O3(111) as a function of the In-to-O ratio (R = ϕIn/ϕO), measured at different TG. Data is taken from ref. 17. (g) Γ/ϕO of SnO2(101) as a function of the Sn-to-O flux ratio (R = ϕSn/ϕO), obtained at different ϕO. Data is taken from ref. 14. (h) Growth-system-dependent maximum M-to-S formation (solid triangles) [eqn (4)–(6)] and maximum S-to-O formation (i.e., the maximum Γ, open triangles) [eqn (1)–(3)] as a function of TG. Symbols represent experimental data, solid and dotted lines are numeric models18,31 serving as guides to the eye.
01) [discs, same data as shown in panel (c)], β-Ga2O3(001) [diamonds], and β-Ga2O3(100) [hexagons]. Data is taken from ref. 15 and 31–33. (f) Γ/ϕO of bixbiyte In2O3(111) as a function of the In-to-O ratio (R = ϕIn/ϕO), measured at different TG. Data is taken from ref. 17. (g) Γ/ϕO of SnO2(101) as a function of the Sn-to-O flux ratio (R = ϕSn/ϕO), obtained at different ϕO. Data is taken from ref. 14. (h) Growth-system-dependent maximum M-to-S formation (solid triangles) [eqn (4)–(6)] and maximum S-to-O formation (i.e., the maximum Γ, open triangles) [eqn (1)–(3)] as a function of TG. Symbols represent experimental data, solid and dotted lines are numeric models18,31 serving as guides to the eye.



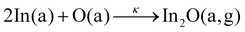


![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01), β-Ga2O3(001), and β-Ga2O3(100) as a function of R, at otherwise similar growth conditions.15,17,32,33 At given TG ≈ 600 °C,15,31–33 the orientation dependence of Γ on the (hkl) plane, Γ(hkl), for β-Ga2O3 is quantified as
01), β-Ga2O3(001), and β-Ga2O3(100) as a function of R, at otherwise similar growth conditions.15,17,32,33 At given TG ≈ 600 °C,15,31–33 the orientation dependence of Γ on the (hkl) plane, Γ(hkl), for β-Ga2O3 is quantified as![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) ≈ 3.7Γ(001) ≈ 7.7Γ(100).
01) ≈ 3.7Γ(001) ≈ 7.7Γ(100).![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) was observed,20 suggesting a different functional dependence of sticking coefficients on the respective Ga2O3 growth surface. We thus qualitatively propose, the orientation-dependent Γ evolution of Ga2O3 can be explained by an interplay of the corresponding orientation-dependent O sticking coefficients (σ) and suboxide surface reactivities ηS, leading to:
01) was observed,20 suggesting a different functional dependence of sticking coefficients on the respective Ga2O3 growth surface. We thus qualitatively propose, the orientation-dependent Γ evolution of Ga2O3 can be explained by an interplay of the corresponding orientation-dependent O sticking coefficients (σ) and suboxide surface reactivities ηS, leading to:![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) > Γ(001) > Γ(100).
01) > Γ(001) > Γ(100).![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) at TG = 500 °C (the gray shaded area) and TG = 600 °C (the purple shaded area), see also Fig. 1(a) and (c). Four regimes are indicated: (i) the O-rich growth regime, i.e., the increasing Γ with increasing Ga flux, ϕGa. In this regime, enough O adsorbates are available to fully oxidize all adsorbed Ga via the consecutive reaction Ga → Ga2O → Ga2O3 [reactions (4) and (1)]. (ii) The ‘pseudo’ O-rich growth regime identified by the width of the Γ plateau, λ. Here, enough O adsorbates are available to oxidize all adsorbed Ga to its suboxide via Ga → Ga2O [reaction (4)] but not enough O is available to oxidize all formed suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]—due to thermally-induced suboxide desorption. In other words, the Γ plateau emerges once the formed Ga2O adsorbate density exceeds the O adsorbate density available for reaction Ga2O → Ga2O3 [reaction (1)].21 (iii) The Ga-rich growth regime identified by the decreasing Γ with ϕGa and its width, ω. Here, not enough O is available to oxidize all remaining suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]. Now, this is due to an O-deficient-induced suboxide desorption mechanism—in addition to the thermally-induced suboxide desorption identified for regime (ii). (iv) The no-growth regime where Ga2O3 growth ceases for R ≥ Rm. Here, not enough O is available to oxidize Ga → Ga2O [reaction (4)] and reaction (1) becomes kinetically forbidden as all available O is consumed in reaction (4).
01) at TG = 500 °C (the gray shaded area) and TG = 600 °C (the purple shaded area), see also Fig. 1(a) and (c). Four regimes are indicated: (i) the O-rich growth regime, i.e., the increasing Γ with increasing Ga flux, ϕGa. In this regime, enough O adsorbates are available to fully oxidize all adsorbed Ga via the consecutive reaction Ga → Ga2O → Ga2O3 [reactions (4) and (1)]. (ii) The ‘pseudo’ O-rich growth regime identified by the width of the Γ plateau, λ. Here, enough O adsorbates are available to oxidize all adsorbed Ga to its suboxide via Ga → Ga2O [reaction (4)] but not enough O is available to oxidize all formed suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]—due to thermally-induced suboxide desorption. In other words, the Γ plateau emerges once the formed Ga2O adsorbate density exceeds the O adsorbate density available for reaction Ga2O → Ga2O3 [reaction (1)].21 (iii) The Ga-rich growth regime identified by the decreasing Γ with ϕGa and its width, ω. Here, not enough O is available to oxidize all remaining suboxides to its solid-state compound via Ga2O → Ga2O3 [reaction (1)]. Now, this is due to an O-deficient-induced suboxide desorption mechanism—in addition to the thermally-induced suboxide desorption identified for regime (ii). (iv) The no-growth regime where Ga2O3 growth ceases for R ≥ Rm. Here, not enough O is available to oxidize Ga → Ga2O [reaction (4)] and reaction (1) becomes kinetically forbidden as all available O is consumed in reaction (4).






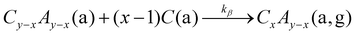



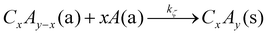





 minus the sum of the Gibbs energies of Ri,
minus the sum of the Gibbs energies of Ri, 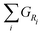 , i.e.
, i.e.
