Open Access Article
Open Access ArticleCross-correlated experimental and theoretical characterisation of orpiment As2S3, a potential material for new advanced technological applications†
Gianfranco
Ulian
 ,
Francesca
Ranellucci
and
Giovanni
Valdrè
,
Francesca
Ranellucci
and
Giovanni
Valdrè
 *
*
Dipartimento di Scienze Biologiche, Geologiche e Ambientali, Università di Bologna, P. Porta San Donato 1, I-40126, Bologna, Italy. E-mail: giovanni.valdre@unibo.it
First published on 17th July 2025
Abstract
In the ever-growing search for new materials in optical, electronic and photovoltaic applications, chalcogenides, such as amorphous diarsenic trisulfide (As2S3), are being deeply investigated. However, very few and incomplete data are available on crystalline As2S3 (space group P21/n), known as mineral orpiment. In the present work, several experimental techniques were employed to analyse the crystal structure, morphology, chemical composition and vibrational properties of the bulk and mechanically cleaved (010) orpiment surface. Also, cross-correlated atomic-scale ab initio simulations corroborated and explained the new experimental data. Orpiment showed a semiconducting behaviour, with an indirect band gap of 2.44 eV and an optical Γ–Γ gap of 2.63 eV, which agrees with previous optical-absorption edge measurements. Furthermore, the complete stiffness tensor and the phonon band structure were reported for the first time. All these quantities are of utmost importance for devising new possible applications of crystalline orpiment in the technological and materials science fields.
Introduction
In the last decades, the world population has exponentially increased its energy requirements for daily, industrial, and third-sector activities. On the one hand, this need is translated into an increase in the consumption of fossil fuels (carbon, oil) and other non-renewable resources, a trend that rose by about 51% from 1995 to 2015 and it is expected to increase by another 18% from 2015 to 2035.1 On the other hand, new materials are required for advanced applications in different and manifold fields, e.g., optoelectronics and sensors, efficient conversion of heat electricity (thermoelectric materials), photovoltaic and other renewable energy production systems, catalysis, wearable electronic devices, etc.2–6In this context, metal chalcogenide minerals and materials made of sulphur, selenium, and tellurium have gathered significant attention due to their unique properties and versatility in these technological applications and research fields.7 Among them, diarsenic trisulfide (As2S3) is an interesting material because of its reversible and/or irreversible changes of physico-chemical properties induced by irradiation with light of suitable energy and intensity or by thermal-annealing, which are peculiar features that can be exploited in optics and optoelectronics.8 However, most of the research on this material was principally focused on the electronic properties of amorphous glass and thin films,9 where the physics governing them is related to short-range atomic order. Presently, little information is available on As2S3 crystalline compounds, which instead present periodic structures with long-range order.
The natural equivalent of crystalline As2S3 is known as the mineral orpiment (space group P21/n, monoclinic crystal system), formed as a hot-spring deposit, an alteration product (especially from realgar), or as a low-temperature product in hydrothermal veins, whose crystallographic features were described in detail in the review of Bonazzi and Bindi.10 Very briefly, the structure is made of AsS3 pyramids connected via S atoms to form diarsenic trisulphide layers (see Fig. 1) stacked along the [010] direction and held by weak (van der Waals) interactions. Differently from those found in other minerals and materials such as graphite, molybdenite MoS2 and phyllosilicates, these layers are not atomic-flat and present a puckered morphology at the sub-nanometric level. However, orpiment shares with the cited compounds the perfect and easy cleavage characteristics of the As2S3 layers [on the (010) plane], thus making this mineral suitable for 2D applications.11
In addition to its technological applications, orpiment was widely used in ancient times as a natural pigment due to its yellow colour, hence its Latin name auripigmentum (golden pigment). Archaeometric analyses revealed its presence in several works of art, e.g., in The Jewish Bride of Rembrandt12 and a Viking Age structure in the Surtshellir cave (Iceland).13
For the identification of orpiment in cultural heritage, destructive and non-invasive techniques such as X-ray fluorescence and Raman spectroscopy are employed. However, concerning the latter technique, very few studies in the scientific literature reported a detailed analysis of crystalline As2S3,14 where not every vibrational band was assigned to specific normal modes. Moreover, confocal Raman spectroscopy is currently used in 2D materials research, e.g., to measure the number of layers in 2D materials by analysing the position, width, and intensity of Raman peaks,15 to probe the electronic properties and perform qualitative structural characterisation,16 and to detect strain and thermal conductivity changes.17 Hence, a detailed knowledge of the vibrational properties of orpiment is required not only for better identification of the mineral for cultural heritage but also for high-quality characterisation of bulk and 2D As2S3, to understand its stability and, eventually, to develop new applications and two-dimensional materials such as heterojunctions.
In addition, in the literature there are incomplete data concerning the elastic behaviour of orpiment, where only ten of the thirteen independent elastic stiffness tensor components were obtained by Brillouin scattering experiments.18 This is an important information regarding the stability of the mineral in both geological/geophysical and materials science/technological fields, which may help the development of new applications of crystalline As2S3 in optical and electronic devices.
The present work was conceived to fill the knowledge gaps previously introduced and, at the same time, to provide new insights into the properties of this peculiar mineral, which is a potential material also for 2D applications. To this aim, a cross-correlated experimental and theoretical characterisation of crystalline As2S3 extracted from a natural sample was devised. From the experiments, the crystallographic features, chemical composition and Raman spectrum of the bulk, and the morphology and Raman spectra of exfoliated (few-layers) specimens on the (010) crystalline plane were investigated. These new data were corroborated by atomic-scale simulations within the density functional theory (DFT) framework, employing a state-of-the-art computational approach based on the use of hybrid functionals. The cross-correlation of the experimental and theoretical results was used to assess the quality of the simulations, providing consistent and predictive data on the electronic, vibrational and elastic properties of orpiment.
Materials and methods
Orpiment sample and experimental methods
The As2S3 orpiment sample used for the present study was a polycrystalline specimen kindly provided by the “G. Bombicci” Mineralogy Museum of the University of Bologna, Italy. This sample can be considered a model system for orpiment because of its purity, and it was then suitable to assess the quality of theoretical simulations. A portion of the mineral was ground to a fine powder before the subsequent analyses. At the same time, orpiment flakes from several nanometres up to a few micrometres thick were carefully separated by mechanical means19 and deposited on aluminium stubs.X-ray powder diffraction
X-ray powder diffraction (XRPD) patterns were collected using a Philips PW 1710 diffractometer equipped with a graphite monochromator on the diffracted beam. Cu Kα X-rays were generated with 40 kV and 30 mA power supply. The patterns were collected between 3° and 70° 2θ, with an angular step of 0.02° and an integration time of 2 seconds. The specimen was ground for 20 minutes in an agate mortar and the powder was collected in a lateral-loading holder to avoid or minimize any possible preferential orientation of the crystallites. The diffractograms were analysed with the computer program Profex,20 which interfaces the BGMN program21 and was used for the Rietveld refinement within the fundamental parameters approach. The unit-cell parameters and experimental details of the refinement protocol and results are reported in Table 1.| Parameter | Value |
|---|---|
| Empirical formula | As2S3 |
| Formula weight | 246.02 |
| Temperature | 298 K |
| Wavelength | 1.540598 Å |
| Crystal system | Monoclinic |
| Space group | P21/n |
| Unit cell dimensions | a = 11.42632(8) Å |
| b = 9.58649(5) Å | |
| c = 4.25947(4) Å | |
| α = γ = 90°, β = 90.377(6)° | |
| Unit cell volume | 466.570(41) Å3 |
| Z | 4 |
| Density (calculated) | 3.502 g cm−3 |
| θ range for data collection | 3.0–70.0° |
| Index ranges | −8 ≤ h ≤ 8; −7 ≤ k ≤ 7; −3 ≤ l ≤ 3 |
| No. of points | 3351 |
| No. of peaks | 402 |
| No. of parameters | 63 |
| Refinement method | BGMN |
| R wp | 11.22 |
| R exp | 10.39 |
| Goodness-of-fit on F2 | 1.08 |
| χ 2 | 1.17 |
Environmental scanning electron microscopy
A Thermo Scientific Quattro S environmental scanning electron microscope (ESEM) with a field-emission gun, equipped with backscattered electron (BS) and cathodoluminescence (CL) detectors and X-ray microanalysis with a silicon-drift detector (SDD-EDS), was employed to study the morphology and local chemistry of the orpiment sample. After careful calibration, the ESEM analyses were carried out under low vacuum conditions, with a water vapour pressure of 100 Pa inside the instrument chamber, an acceleration voltage of 15 kV and a beam current of 0.43 nA. Within these instrumental settings, no conductive coating was needed, obtaining an adequate compromise between imaging resolution and EDS chemical sensitivity.Confocal Raman microspectrometry
The Raman spectroscopy analysis was performed with a WITec alpha300R confocal Raman microscopy system, made of an optical microscope and an ultra-high throughput UHTS 300 VIS spectrometer with a CCD camera and gratings of 600 g mm−1. Green (532 nm) and red (785 nm) laser beam sources were used for the Raman excitation, setting the power between 1 mW (green laser) and 30 mW (red laser) to prevent heating the sample and photobleaching. The laser beam was focused on the sample with 20×, 50× and 100× Zeiss microscope objectives with a low numerical aperture objective (NA = 0.40) to avoid optical artefacts. The backscattered Raman spectra were collected in confocal mode between 100 and 1700 cm−1, with a resolution of about 2.7 cm−1 and an acquisition time of 10 minutes. The Rayleigh scattering line was removed using an edge filter.Computational methods
The simulations reported in the present work were performed using the CRYSTAL17 ab initio code, which implements the Kohn–Sham self-consistent field (SCF) method.22 In the following, details on the computational approach are explained.Hamiltonian, basis set and computational parameters
Among the several available density functional theory functionals, two hybrid ones were employed, i.e., B3LYP23,24 and HSE06.25 The first one is a global hybrid (GH) functional that calculates the total exchange–correlation energy according to the following formula:| EGHxc = (1 − A)EDFx + AEHFx + EDFc | (1) |
HSE06 is instead a range-separated hybrid (RSH) functional, where the amount of the exact Hartree–Fock exchange depends on the distance between electrons. Currently, three ranges are considered (short, medium, and long) in the separation of the Coulomb operator, according to the following error function:
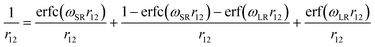 | (2) |
| ERSHxc = EDFxc +cSR(EHFx.SR − EDFx,SR) + cMR(EHFx.MR − EDFx,MR) + cLR(EHFx.LR − EDFx,LR) | (3) |
Both functionals are well-known in the scientific community for their accuracy in the calculation of the structural,28,29 vibrational,30,31 electronic,32 elastic,33,34 surface,35–37 and thermodynamic38–40 properties. In the present work, both hybrid functionals were employed, with B3LYP being used mainly to calculate the phonon properties (e.g., IR and Raman spectra) of orpiment, whereas HSE06 was chosen to calculate the electronic band structure of the mineral and monolayers. Geometry optimization of the different models was always carried out with the two functionals before calculating any of the cited properties to ensure the consistency of the data.
However, hybrid DFT functionals do not generally treat long-range interactions accurately, which are fundamental for minerals like orpiment because they hold the As2S3 layers together along the b-axis direction. In the present work, the DFT-D3 correction was adopted to add a posteriori the following contribution to the total energy of the system:41
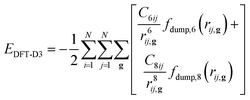 | (4) |
| fdump,6(rij,g) = s6[1 + e−d(rij,g/RvdW−1)]−1 | (5) |
 | (6) |
 and f(R0ij) = α1R0ij + α2, s6 = 1, s8 = 1.9889, whereas α1 and α2 are adjustable parameters. This approach was proved suitable for different kinds of crystalline materials with heterodesmic structures, such as phyllosilicates,46 layered hydroxides,47 and composite 2D materials.32,48 Also, compared to previous formulations, such as the DFT-D2 scheme, the DFT-D3 approach is less empirical.
and f(R0ij) = α1R0ij + α2, s6 = 1, s8 = 1.9889, whereas α1 and α2 are adjustable parameters. This approach was proved suitable for different kinds of crystalline materials with heterodesmic structures, such as phyllosilicates,46 layered hydroxides,47 and composite 2D materials.32,48 Also, compared to previous formulations, such as the DFT-D2 scheme, the DFT-D3 approach is less empirical.
In CRYSTAL17, the multi-electronic wave function was built from a linear combination of Gaussian-type functions (GTF), within the so-called linear combination of atomic orbitals (LCAO) approach. The arsenic atom was described using a double-zeta molecular basis set that (i) included small-core relativistic effective core potential to treat the relativistic effect of core electrons and (ii) was modified to reduce too diffuse functions that would lead to numerical instabilities, as described and developed by Heyd et al.49 The sulphur atom was modelled from a modified 6-311G(d) molecular basis set of double-zeta quality used by the same cited authors. Each basis set includes s, p, and d orbitals. Detailed and specific information can be found in the work of Heyd and colleagues.49
The total energy was calculated on a pruned grid with 75 radial points and a maximum number of 974 angular points in regions relevant for chemical bonding, subdivided in five shells with different angular grids.22 The self-consistent field (SCF) iteration was stopped when the energy difference between two consecutive steps was lower than 10−8 Ha, whereas a tighter criterion (10−10 Ha) was employed for the calculation of the vibrational properties. The numerical accuracy for the calculation of the Coulomb integrals was set to 10−7 (ITOL1 to ITOL3 keywords in CRYSTAL), whereas ITOL4 and ITOL5 were set to 10−9 and 10−30, respectively. The Hamiltonian matrix was diagonalized on a 6 × 6 × 6 grid50 with 80k points in the reciprocal space.
Structural relaxation and vibrational properties
The unit cell parameters and atomic coordinates were relaxed at 0 K and 0 GPa using the analytical gradient method for the atomic positions and a numerical gradient for the cell parameters. The Hessian matrix is upgraded with the Broyden–Fletcher–Goldfarb–Shanno algorithm.51–55 The tolerances for the maximum allowed gradient and the maximum atomic displacement have been set to 10−5 Ha bohr−1 and 4 × 10−5 bohr, respectively.Zone-central (i.e., Γ-point) normal modes were calculated by diagonalizing the mass-weighted Hessian matrix W (dynamical matrix), whose elements are the second derivatives of the lattice potential for mass-weighted atomic displacements:30
 | (7) |
The infrared spectrum was calculated analytically as a raw superposition of p Lorentzian functions, according to the formula:
 | (8) |
 | (9) |
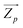 the mass-weighted effective mode Born charge vector. The latter was obtained analytically through a coupled-perturbed Kohn–Sham (CPKS) approach.56
the mass-weighted effective mode Born charge vector. The latter was obtained analytically through a coupled-perturbed Kohn–Sham (CPKS) approach.56
The Raman intensities were calculated using the approximation proposed by Placzek57 which considers the material as a polycrystalline powder. The intensity was then modelled with a pseudo-Voigt functional form:58
| A(ν) = ηL(ν) + (1 − η)G(ν) | (10) |
 | (11) |
 | (12) |
 | (13) |
In addition, phonon dispersion relations were calculated using a supercell approach, considering a 2 × 2 × 2 expansion of the cell (160 atoms), sampling the reciprocal space 8k points.62
Calculation of the elastic moduli
The elastic moduli (also known as the stiffness tensor) were calculated using a procedure implemented in the CRYSTAL code,63 whose formulation and algorithms are briefly explained in this section. Considering an elastic regime of deformation, solids can be described by Hooke's law: | (14) |
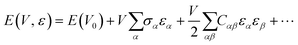 | (15) |
 | (16) |
Results
Crystallography and crystal-chemistry of bulk orpiment
Combined X-ray diffraction and electron microscopy with energy-dispersive spectroscopy were employed to both characterise and provide evidence of the purity of the orpiment specimen. The XRD diffractogram of the powdered mineral sample in Fig. 2 presented only the reflections of As2S3, with no other minerals within the instrumental sensitivity. The peaks are generally sharp, particularly the one at 18.47° 2θ, highlighting the high crystallinity of the sample.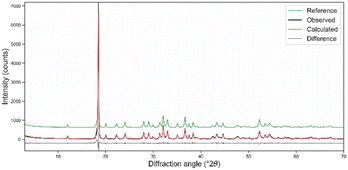 | ||
| Fig. 2 Powder diffraction data of orpiment As2S3 and Rietveld refinement analysis. The difference between the calculated and measured intensities is reported below the profile. The reference XRPD pattern was taken from the American Mineralogist Crystal Structure Database #0010733, related to the sc-XRD data of Mullen and Nowacki.26 | ||
At the same time, several flakes of the mineral were imaged using environmental scanning electron microscopy and chemically analysed using EDS spectroscopy. An example of one of the orpiment crystalline flakes studied in the present work is shown in Fig. 3a. The flake is large (3.3 mm × 1.4 mm) and presents micrometre-wide atomic-flat areas locally interrupted by folding of the layers (see Fig. 3b–d). In addition, smaller platelets with different thicknesses and pseudo-hexagonal morphologies due to the {100} and {101} forms were observed (Fig. 3b). The flat terraces in the different investigated samples were employed for microchemical analyses with EDS spectroscopy, providing a homogeneous mean atomic composition (As2.05S2.95) that is consistent with the ideal orpiment. Examples of the characteristic EDS spectra are reported in Fig. S1 in the ESI.†
From the crystallographic perspective, the Rietveld structural refinement (Table 1) resulted in unit cell parameters a = 11.42632(8) Å, b = 9.58649(5) Å, c = 4.25947(4) Å and β = 90.377(6)°, and the As–S bond lengths were within 2.211 Å and 2.328 Å. The lattice data and internal geometry (bond lengths and angles) are reported in Table 2, whereas the coordinates of the symmetrically inequivalent As and S atoms are presented in Table 3.
| Bond lengths (Å) | ||||
|---|---|---|---|---|
| As1–S1 | 2.293 | 2.276 | 2.228 | 2.292 |
| As1–S2 | 2.310 | 2.288 | 2.315 | 2.270 |
| As1–S3 | 2.330 | 2.308 | 2.328 | 2.289 |
| 〈As1–S〉 | 2.311 | 2.291 | 2.290 | 2.284 |
| As2–S1 | 2.328 | 2.307 | 2.211 | 2.308 |
| As2–S2 | 2.319 | 2.305 | 2.211 | 2.293 |
| As2–S3 | 2.276 | 2.254 | 2.306 | 2.243 |
| 〈As2–S〉 | 2.307 | 2.288 | 2.243 | 2.281 |
| Bond angles (°) | ||||
|---|---|---|---|---|
| XRPD = X-ray powder diffraction, sc-XRD = single-crystal X-ray diffraction. Ω is the unit cell volume, I is the interlayer distance between two As2S3 units.a Present work.b Mullen and Nowacki.26 | ||||
| S1–As1–S2 | 97.90 | 97.48 | 97.49 | 98.61 |
| S1–As1–S3 | 104.04 | 103.80 | 104.58 | 104.08 |
| S2–As1–S3 | 93.57 | 92.99 | 96.54 | 94.58 |
| S1–As2–S2 | 96.94 | 96.51 | 99.78 | 98.61 |
| S1–As2–S3 | 92.77 | 91.91 | 93.52 | 92.76 |
| S2–As2–S3 | 105.07 | 104.62 | 103.93 | 104.99 |
| 〈S–As–S〉 | 98.38 | 97.89 | 99.31 | 98.94 |
| As1–S1–As2 | 102.76 | 102.41 | 105.63 | 103.73 |
| As1–S2–As2 | 100.02 | 99.53 | 102.47 | 100.99 |
| As1–S3–As2 | 87.18 | 86.34 | 86.50 | 87.94 |
| 〈As–S–As〉 | 96.65 | 96.09 | 98.20 | 97.55 |
| Atom | B3LYP-D3a | HSE06-D3a | XRPDa | sc-XRDb | |
|---|---|---|---|---|---|
| XRPD = X-ray powder diffraction, sc-XRD = single-crystal X-ray diffraction.a Present work.b Mullen and Nowacki.26 | |||||
| As1 | x | 0.2645 | 0.2640 | 0.2652(8) | 0.2647 |
| y | 0.1868 | 0.1874 | 0.1907(4) | 0.1917 | |
| z | 0.8734 | 0.8725 | 0.8534(23) | 0.8627 | |
| As2 | x | 0.4884 | 0.4892 | 0.4875(6) | 0.4868 |
| y | 0.3218 | 0.3225 | 0.3200(4) | 0.3212 | |
| z | 0.3735 | 0.3733 | 0.3660(21) | 0.3607 | |
| S1 | x | 0.3998 | 0.3995 | 0.4035(14) | 0.4015 |
| y | 0.1129 | 0.1132 | 0.1206(11) | 0.1213 | |
| z | 0.5101 | 0.5041 | 0.5112(36) | 0.5081 | |
| S2 | x | 0.3486 | 0.3490 | 0.3501(13) | 0.3474 |
| y | 0.4025 | 0.4039 | 0.3952(12) | 0.3972 | |
| z | 0.0152 | 0.0089 | 0.0149(41) | 0.0101 | |
| S3 | x | 0.1231 | 0.1226 | 0.1185(17) | 0.1223 |
| y | 0.2952 | 0.2968 | 0.2995(7) | 0.2935 | |
| z | 0.5552 | 0.5512 | 0.5524(38) | 0.5590 | |
The refined orpiment structure was used as the starting model for atomic-scale DFT simulations using the B3LYP-D3 and HSE06-D3 approaches. After relaxing the orpiment lattice and atomic positions within the P21/n space group under static conditions (0 K without any vibrational contribution), the calculated crystal volume was smaller than the experimental one by about 4% (B3LYP-D3) and 8% (HSE06-D3). This effect is due to a combination of the shrinking of the b- and c-axes (ca. 2.5–4.3%), and a slight expansion of the a-axis. The theoretical volume shrinking is then due to (i) the absence of thermal contributions to the lattice geometry, (ii) the use of hybrid functionals that generally provide a better description of the atomic bonds (vide infra) and (iii) the DFT-D3 correction. The variation observed in the c lattice parameter was reflected in the internal geometry, with As–S bonds slightly larger than the experimental ones up to about 1.5% and smaller S–As–S angles, especially the S2–As1–S3 and the S1–As2–S2 that are oriented along the c-axis. Conversely, the main reason for the smaller b lattice parameter is the calculated interlayer distance I, which was underestimated by about 8% with both DFT functionals. Indeed, the separation between the As2S3 layers was affected by the long-range interactions, with the DFT-D3 scheme probably providing an overestimation of the attraction between the layers. Despite these small differences, both theoretical approaches were able to provide a good description of the orpiment unit cell, considering also the different temperatures of the refinement, 0 K within DFT, and 298 K during the experiments.
In addition, to better highlight the importance of including the effects of long-range interactions in the physical treatment of van der Waals materials like orpiment, the lattice and internal geometry of the mineral were optimised without the DFT-D3 correction. The unit cell volume was severely overestimated by about 40% and 25% with the B3LYP and HSE06 functionals, respectively. This is mostly due to the increased length of the b-axis (+23% with B3LYP and +15% with HSE06) and c-axis (+20% and +11%), although the a lattice parameter was underestimated by about −3% with B3LYP and −1% with HSE06. While a rather large increase of the unit cell parameter b was expected, it is hypothesised that the overestimation of the c-axis length is probably due to a reduced intra-layer interaction between the lone pairs of the As and S atoms.
Vibrational features of bulk orpiment
As explained in the Introduction section, Raman spectroscopy is one of the main diagnostic tools used in mineralogy and archaeometry to characterise mineralogical species in a rock or artistic work. In the following, a detailed vibrational analysis of orpiment is reported.The unit cell of the mineral contains four asymmetric units As2S3, for a total of N = 20 atoms. Thus, according to the character table of the P21/n space group (C2h point group), the total representation of the degrees of freedom of orpiment is given by:
| Γtotal = 15Ag + 15Au + 15Bg + 15Bu, | (17) |
| Γoptic = 15Ag + 14Au + 15Bg + 13Bu | (18) |
Examples of the experimental analyses performed with confocal Raman microspectrometry on flat terraces of orpiment are shown in Fig. 4, which reports the area under investigation as seen with optical microscopy and the associated Raman spectra collected in different points marked with crosses in the image. All the spectra were collected using an excitation wavelength of 532 nm (green laser) with low-power settings to prevent any damage to the sample.
A similar analysis was performed on smaller flakes (thin layers) extracted from the orpiment specimen and deposited on aluminium stubs, with Fig. 5 showing some of these thin samples as an example. In this case, the green laser source was too energetic even for low output powers, hence a red laser (785 nm) was used (see Fig. 5d). No operations were performed on the reported Raman spectra but the removal of cosmic ray radiation and intensity normalization, the latter to ease the comparison between different acquisitions.
In general, the spectra presented sharp bands (mean full width at half maximum, FWHM, of about 10 cm−1) that can be subdivided into two main regions: the first one was located between 250 cm−1 and 400 cm−1 and presented the most intense Raman bands, where four signals at about 292 cm−1, 311 cm−1, 356 cm−1 and 380 cm−1 can be observed. Conversely, the second spectral region was in the 100–250 cm−1 range, with four bands of weak intensity centred at 67 cm−1, 137 cm−1, 156 cm−1 and 203 cm−1. In addition, it was observed with the 785 nm laser source a low-intensity, broad Raman band at about 180 cm−1. This band could be due to an overlap of two vibrational modes at 179 cm−1 and 184 cm−1, according to the deconvolution performed by using two Lorentzian peak functions.
The calculated Raman spectrum of orpiment (see Fig. S2 in the ESI†), the graphical inspection of the vibrational motions and the analysis of the potential energy distribution obtained from CRYSTAL simulations were employed to assign each mode to specific bands in the experimental spectra. A detailed comparison between the theoretical and experimental results is reported in Table 4.
| IRREP | B3LYP-D3 | ΔHSE06-D3 | Experimental | ||
|---|---|---|---|---|---|
| ν (cm−1) | I (‰) | ν (cm−1) | 532 nm | 785 nm | |
| HSE06-D3 was reported as differences with the B3LYP-D3 results (ΔHSE06-D3). Experimental Raman bands were reported according to the employed excitation laser source. | |||||
| A g | 33.7 | 103.6 | 0.7 | ||
| 42.8 | 33.8 | 0.1 | |||
| 69.7 | 5.2 | 0.9 | |||
| 80.5 | 79.8 | 0.4 | 67 | 68 | |
| 145.7 | 254.0 | 3.2 | 137 | 135 | |
| 157.1 | 65.4 | 1.8 | 154 | 154 | |
| 172.3 | 172.0 | 1.1 | 179 | ||
| 192.6 | 50.9 | 2.0 | |||
| 210.1 | 320.4 | 0.0 | 202 | 201 | |
| 284.3 | 482.3 | 13.6 | 292 | 291 | |
| 314.0 | 597.6 | 9.9 | 311 | 310 | |
| 356.9 | 1000.0 | 10.5 | 356 | 355 | |
| 359.4 | 780.4 | 10.6 | |||
| 363.9 | 460.5 | 9.7 | |||
| 388.1 | 506.0 | 12.8 | 378 | 381 | |
| B g | 66.3 | 25.7 | 0.7 | 63 | 62 |
| 84.3 | 6.6 | −3.4 | |||
| 104.7 | 11.6 | 1.5 | |||
| 109.6 | 46.2 | 2.2 | |||
| 145.2 | 2.7 | 1.4 | |||
| 152.5 | 25.0 | 3.4 | |||
| 166.0 | 73.4 | 1.2 | |||
| 187.0 | 117.8 | 1.7 | 184 | 184 | |
| 199.5 | 31.1 | 4.9 | |||
| 310.5 | 211.4 | 9.3 | 307 | 308 | |
| 321.1 | 26.2 | 10.9 | |||
| 343.0 | 8.5 | 10.7 | |||
| 365.0 | 1.9 | 11.7 | |||
| 374.1 | 53.7 | 13.0 | |||
| 403.8 | 1.3 | 12.0 | |||
The quantum mechanical approach was able to describe the overall features of the Raman spectrum of the mineral, with generally small shifts of the band positions and comparable intensities of the signals. However, the HSE06-D3 method proved to be slightly overbinding, with blue-shifted modes compared to the B3LYP-D3 approach. For this reason, the following presentation and comparison with the experiments were performed considering this latter functional.
According to the simulations, the most intense Raman signals were due to As–S out-of-plane stretching modes at 357 cm−1 (As1–S3 + As2–S3), 359 cm−1 (As1–S1 + As2–S1), 364 cm−1 (As2–S2) and 388 cm−1 (As1 – S2), and to As–S in-plane stretching modes at 314 cm−1 (As1–S1 + As2–S2), 311 cm−1 (As1–S1 + As2–S3) and 284 cm−1 (As1–S3). Thus, the theoretical results suggested that the experimental band at 355 cm−1 was given by two overlapping modes. Also, the shoulder calculated at 364 cm−1 was probably not detected at the experimental level because the spectral resolution of the instrument (2.7 cm−1) was not able to discern this mode from the band centred at 356 cm−1, resulting in a further convolution of the signals. For the sake of completeness, a graphical representation of the eigenvectors of atomic displacements is reported in Fig. S3 in the ESI.†
In the low-frequency region, i.e., below 100 cm−1, the calculated modes were mostly rotations of the As2S3 units because of variations in the torsional angles. Here, the most intense signal was at ca. 80 cm−1. The spectral region between 100 cm−1 and 250 cm−1 presented four low-intensity modes at 146 cm−1, 172 cm−1, 187 cm−1, and 210 cm−1, which were associated with in-plane, out-of-plane, symmetric and asymmetric As1–S–As2 bending modes, respectively. The modes at 146 cm−1, 172 cm−1, and 210 cm−1 correlated well with those experimentally found at about 137 cm−1, 154 cm−1 and 202 cm−1, respectively.
DFT simulations were also used to calculate the infrared spectrum of the mineral, which is reported in Fig. S4 in the ESI.† Although IR spectroscopy was generally not employed in previous studies for the characterisation of chalcogenides, e.g., in pigments, because of the lower limit of about 400 cm−1, newer technologies such as nano-IR extended the detection capabilities to the low-wavenumber region. Thus, for the sake of completeness, the analysis of the vibrational modes active in infrared is here presented. As per the simulations, the most prominent IR bands of orpiment were in the range of 250–400 cm−1, with the highest intensity signal at 282 cm−1 associated with the in-plane As1–S3 stretching mode, followed by the other As–S stretching modes at 314 cm−1 (in-plane), 356 cm−1 (out-of-plane), and 390 cm−1 (out-of-plane). In the As–S–As bending region, i.e., 150–230 cm−1, the highest bands were located at 185 cm−1 and about 150 cm−1.
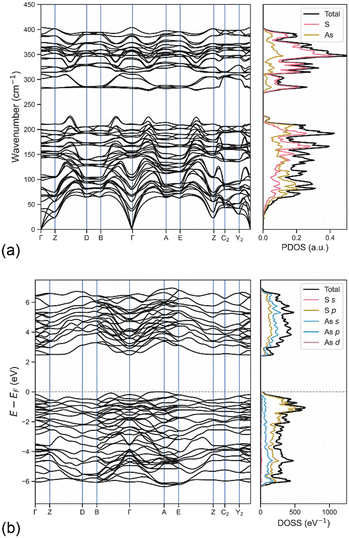
In addition, the phonon dispersion relations calculated on the 2 × 2 × 2 supercell containing 160 atoms with the DFT/B3LYP-D3 approach in the Γ–Z–D–B–Γ–A–E–Z–C2–Y2–Γ path in reciprocal space and the associated phonon density of states (PDOS) are reported in Fig. 6a. The separation between the phonon bands related to the stretching modes and those of the acoustic, rotational and bending modes is clearly visible and in agreement with the zone-centre Raman spectrum. The PDOS highlighted the higher contribution of sulphur atoms in the stretching of the As–S atoms, whereas the other modes showed a more uniform distribution between the two types of atoms. In addition, no negative phonon band, i.e., the so-called soft phonons, was observed in the band structure, which means that the mineral is stable, further confirming the quality of the simulation approach employed to investigate orpiment.
Electronic properties
The band structure and the orbital-projected density of states (DOSS) of the mineral were calculated at the DFT/HSE06-D3 level to evaluate the electronic properties of orpiment As2S3. This hybrid functional generally provides better description of these properties because of more balanced short- and long-range electronic correlation effects than B3LYP. The same path in the first Brillouin zone previously described for the phonon band structure was used to sample the energy of the crystalline orbitals in reciprocal space. The use of the range-separated hybrid functional was justified by the accuracy for this kind of property, which is generally higher than that of other functionals.According to the results reported in Fig. 6b, orpiment is a semi-conducting mineral with an indirect band gap Eg = 2.44 eV in the Γ–A direction. It is worth highlighting that the bands close to the Fermi level, both in the valence and in the conduction regions, showed small corrugation, meaning that direct electronic transitions, i.e., optical transitions, may occur as well. For instance, the Γ–Γ transition was observed at 2.63 eV and it could be useful for optoelectronic applications of the mineral. According to the projected DOSS, the highest valence bands were mainly given by S-3p states and by a small contribution arising from the As-4p and As-4s orbitals. In the conduction region, the bands are formed by hybridisation of the S-3p and As-4p states, with a slightly higher contribution from arsenic. Conversely, the As-3d orbitals lowly participated in the topmost valence and bottommost conduction bands. For the sake of completeness, similar electronic results were obtained at the DFT/B3LYP-D3 level of theory, albeit the calculated band gap was slightly larger (Eg = 2.87 eV) than that observed with the HSE06-D3 approach (Eg = 2.44 eV).
In addition, using the coupled-perturbed Kohn–Sham approach56 described in the Computational methods section, it was possible to calculate the high-frequency dielectric tensor ε∞, whose components were ε∞,xx = 8.265, ε∞,yy = 5.300 and ε∞,zz = 6.505. By using the oscillator strength fn,ij of each calculated vibrational mode,70 the static dielectric tensor components were calculated as ε0,ij = ε∞,ij + Fij, with  , resulting in ε0,xx = 13.239, ε0,yy = 5.888 and ε0,zz = 9.956.
, resulting in ε0,xx = 13.239, ε0,yy = 5.888 and ε0,zz = 9.956.
Elastic properties
Voigt's representation (6 × 6 matrix) of the stiffness tensor C of orpiment As2S3 (monoclinic system) is as follows: | (19) |
The mineral is highly anisotropic, with C11 ≫ C22 > C33, meaning that the uniaxial compression of the a-axis is more difficult than that of the other two crystallographic directions. In addition, it can be noted that the C15, C25, C35 and C46 moduli presented very small values, suggesting that the elastic properties of orpiment were closer to those of an orthorhombic crystal than those of a monoclinic one. This behaviour is consistent with the crystal structure of the mineral, whose β lattice parameter (90.46°) is close to the ideal 90°.
From the stiffness tensor, it is possible to calculate the elastic properties of polycrystalline aggregates, e.g., the bulk (K) and shear (μ) moduli according to Reuss (R, lower bound) and Voigt (V, upper bound) given by the following equations:64
| KV = (a + 2b)/9 | (20) |
| KR = (d + 2e)−1 | (21) |
| μV = (a + 3c − b)/15 | (22) |
| μR = 15/[4(d − e) + 3f] | (23) |
| a = C11 + C22 + C33, b = C12 + C13 + C23c = C44 + C55 + C66, d = S11 + S22 + S33e = S12 + S13 + S23, f = S44 + S55 + S66 | (24) |
The mean bulk and shear moduli are given by the Voigt–Reuss–Hill averaging method:71
 | (25) |
 | (26) |
 | (27) |
 | (28) |
Also, the same elastic properties were calculated for single crystals, which depend on the specific crystallographic direction.72 Graphical representations of Young's modulus E, linear compressibility β = 1/K, shear modulus μ and Poisson's ratio υ are reported in Fig. S5 in the ESI.† From the plots on the (xy), (xz), and (yz) Cartesian planes, the anisotropy of the elastic properties of orpiment was further highlighted.
Finally, the solution of the Christoffel equation73 allowed the analysis of the propagation of acoustic (seismic) waves in orpiment. This eigenvalue equation led to three solutions, i.e., the slow secondary (vS2), fast secondary (vS1) and primary (vP) wave velocities that were plotted as a Lambert projection of the upper hemisphere in Fig. S6a–c (ESI†). The results showed that the maximum acoustic velocity was along the [100] direction for vP and vS1. The percentages of anisotropy for vP, vS1 and vS2 were 63.7%, 33.8 and 55.1, respectively, calculated as A = 200(vmax − vmin)/(vmax + vmin). The S-wave anisotropy, which is also called shear wave splitting, is about 68%.
Discussion and conclusions
As previously explained in the Introduction section, the present work aimed to provide new, solid information on the crystallographic, lattice dynamics (i.e., vibrational), electronic and elastic properties of crystalline orpiment As2S3, an important chalcogenide material that could be used in several technological applications.The powdered specimen analysed by X-ray powder diffraction presented lattice parameters and atomic coordinates obtained from Rietveld structural refinement that were in good agreement with the single-crystal XRD diffraction results of Mullen and Nowacki,74 with absolute variations in the range of 0.08–0.43% (see Table 1). The exfoliation of the orpiment sample for the subsequent ESEM-EDS and confocal Raman microspectrometry was carried out easily, suggesting and confirming the weak adhesion between the layers. The morphology from ESEM revealed that the cleaved sub-samples were multilayered As2S3 units; however, by employing suitable materials (e.g., thermal release tapes) and substrates (SiO2/Si wafers), this procedure could be enhanced to reach the desired two-dimensional single layer of orpiment.75 Other cleaving techniques, such as liquid exfoliation,76 are currently under investigation.
The collected Raman spectra of the mineral with both excitation sources of 532 nm and 785 nm were in good agreement with previous measurements reported in the scientific literature,14,77,78 and the present new data could be used as references for future studies in archaeometry, archaeology and cultural heritage. The cross-correlation between experiments and DFT simulations helped in identifying which mode(s) belong to each visible band in the spectra and provided further information on the overlap of the peaks. In particular, in the work of Scheuermann and Ritter14 three bands at 350.9 cm−1, 353.5 cm−1 and 363.1 cm−1 were detected by using a high-resolution spectrometer (1 cm−1). In the present work, these three bands were calculated from the DFT simulations at 357 cm−1 (shift of +7 cm−1), 359 cm−1 (+6 cm−1) and 364 cm−1 (+1 cm−1), with intensities comparable to the experimental ones of Scheuermann and Ritter.14 It is worth noting that the present Raman microspectrometry analysis detected only a single band centred at 356 cm−1 due to a combination of the lower resolution of the instrumentation (2.7 cm−1) and the different intensities of the vibrational modes. Furthermore, Scheuermann and Ritter14 observed a very weak band at 324 cm−1, which was assigned to an overtone of the mode falling at 161 cm−1, nevertheless, a fundamental vibrational mode (As–S stretching) was calculated in the present study at 321 cm−1. Given the very small shift (ca. −3 cm−1) and similar relative intensity of the bands, and since overtones fall below nν (n = 2 and ν is the vibrational frequency), it is here suggested that the previous assignment was not properly defined.
The good comparison between the theoretical data and the experimental ones gave more confidence in evaluating other properties of bulk orpiment from DFT simulations. The indirect band gaps of As2S3 calculated at the HSE06-D3 and B3LYP-D3 levels of theory were 2.44 eV and 2.87 eV, respectively, which were in line with Eg = 2.6–2.7 eV determined experimentally from the optical-absorption edge on crystalline samples.79,80 These band gaps are larger than those of As2S3 glass9,81–84 and biologically synthesised nanofibers,85 both presenting an amorphous structure, whose Eg figures are about 2.1–2.5 eV. However, it must be remembered that the optical-absorption edge method provides direct valence–conduction band transitions, which for indirect-gap minerals and materials are larger. From this perspective, the Γ–Γ transition obtained from the HSE06-D3 approach (2.63 eV) was inside the Eg range measured during experiments.
Furthermore, the present study showed a slightly larger band gap compared to previous ab initio theoretical simulations, mainly because of the use of hybrid functionals. Generally, local density approximation (LDA) and generalized gradient approximation approaches led to underestimated Eg values, which is a well-documented issue in the scientific literature. For instance, Kaur and colleagues86 obtained from DFT/GGA simulations with norm-conserving pseudopotentials Eg = 1.925 eV, whereas Patel and collaborators87 calculated with the PBE (GGA) functional and projector-augmented wave basis sets a band gap of 2.08 eV. Notwithstanding the different Eg values, our investigation confirmed the indirect band gap and the semiconducting nature of crystalline As2S3 and provided more accurate results on the electronic band structure of the mineral.38,39
Regarding the elasticity of orpiment, as reported in the Introduction section, few data are available in the scientific literature from both experimental and theoretical perspectives. Brillouin scattering analysis was performed by McNeil and Grimsditch18 on two natural samples which allowed obtaining ten of the thirteen independent elastic moduli, whose values were C11 = 99.6(1.0) GPa, C22 = 27.1(3) GPa, C33 = 21.9(1.4) GPa, C44 = 1.1(2) GPa, C55 = 24.0(8) GPa, C66 = 0.7(2) GPa, C13 = 20.6(1.9) GPa, C15 = −0.3(8) GPa, C35 = −1.2(9) GPa, and |C11| = 0.2(2) GPa (see Table 5). In general, the present simulation results were in good agreement with the experimental ones, with a small overestimation (maximum deviation of +20 GPa for the C11 component) that was due to the use of Gaussian-type orbital basis sets. As previously explained,88,89 the stiffer behaviour originated from the Pulay stress, i.e., an effect associated with the incompleteness of atom-centred basis sets. More into detail, the Pulay stress occurs during the derivation of the basis sets for the atomic positions and results in a small increase of the elastic moduli.
We found in the literature only the theoretical study on the elastic properties of As2S3 that was reported by Jiang and coworkers,90 who performed molecular mechanics simulations using the Dreiding force field. However, the cited authors employed a non-canonical space group setting for orpiment, i.e., the orthorhombic space group Pnma, imposing all lattice angles to 90°. The relaxed crystal structure (a = 10.779 Å, b = 3.304 Å, c = 13.565 Å) exhibited relatively large variations and a different crystal orientation compared to the experimental XRD refinements. The modelling and computational approach proposed by Jiang and coworkers90 could explain the deviations observed in the calculated elastic moduli, e.g., C11 = 31.3 GPa, C22 = 130.4 GPa, C33 = 32.9 GPa, and C44 = 7.9 GPa. Also, only seven of the nine independent elastic moduli for an orthorhombic system91 were reported, and no information on the crystal orientation to the Cartesian axes during the calculation of the elastic tensor was provided. According to the space group employed by the authors, it was supposed that the crystallographic axes were oriented parallel to the ones of the Cartesian reference system, i.e., a||x, b||y and c||z. Instead, the present simulations at the DFT/B3LYP-D3 level of theory considered the correct crystallographic setting of the mineral, confirming the experimental results from Brillouin scattering and providing the complete set of thirteen independent elastic tensor components.
All the present data suggest that orpiment As2S3 (space group P21/n) is a potentially interesting mineral and material with peculiar structural, electronic and elastic properties that could be exploited in two-dimensional materials research and development of devices. The proposed combined experimental–theoretical approach with cross-correlation of the results provided new insights into this material and assessed the quality and predictive power of the simulations. This study suggested that crystalline As2S3 (i) is phononically and mechanically stable under ambient conditions, (ii) presents an indirect band gap of about 2.44 eV and an optical transition of ca. 2.63 eV, and (iii) can be easily exfoliated in thin, few-layer structures. Hence, the cleavage can be pushed down to the monolayer without extreme difficulties using the scotch tape technique.
The present research aimed at obtaining a fundamental understanding of the features of orpiment, which presents layers with a puckered morphology at the atomic scale. This peculiar feature distinguishes this mineral from other well-known 2D materials, for instance, graphene and monolayer molybdenite MoS2, which instead exhibit atomic-flat surfaces. The atomic structure, i.e., the crystallography, is one of the key properties that control both the interaction between two layered materials and the modulation of the physical (electronic, optical, elastic) properties of the interface. Work is in progress in this sense to exfoliate single monolayers of As2S3, whose mineralogical, physical and chemical properties will be investigated with the same cross-correlation approach here employed to understand how extreme exfoliation (i.e., down to a single- and few-layers of As2S3) changes the behaviour of the material. Then, new applications of this two-dimensional material could be devised in different applications, for example, optoelectronics, 2D materials development, sensors and catalysis.
Data availability
The results obtained in the present work are also available in a data repository at https://doi.org/10.17632/wnfzg8rgsz.1.Author contributions
Conceptualization, G. U. and G. V.; methodology, G. U. and F. R.; validation, G. U. and G. V.; formal analysis, G. U. and F. R.; investigation, G. U. and G. V.; data curation, G. U.; writing – review and editing, G. U. and G. V.; visualization, G. U. and F. R.; supervision, G. V. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the University of Bologna for supporting the present research. All the simulations were performed with the computational resources (HPC cluster) and software license of the Interdisciplinary Research Centre of Biomineralogy, Crystallography and Biomaterials, Department of Biological, Geological and Environmental Sciences, University of Bologna. G. U. wishes to thank the Italian Society of Mineralogy and Petrology (Società Italiana di Mineralogia e Petrologia, SIMP) for supporting the present research through the research grant in memory of Prof. Fiorenzo Mazzi, awarded in 2023.References
- L. Yildiz, in Comprehensive Energy Systems, 2018, vol. 1–5, pp. 521–567 Search PubMed.
- L. E. Bell, J. Electron. Mater., 2009, 38, 1344–1349 CrossRef CAS.
- A. G. El-Shamy, Mater. Today Phys., 2023, 35, 101101 CrossRef CAS.
- M. L. Kolhe, K. J. Karande and S. G. Deshmukh, Artificial Intelligence, Internet of Things (IoT) and Smart Materials for Energy Applications, 2022 Search PubMed.
- L. Wang, L. Huang, W. C. Tan, X. Feng, L. Chen, X. Huang and K. W. Ang, Small Methods, 2018, 2, 1700294 CrossRef.
- P. You, G. Tang and F. Yan, Mater. Today Energy, 2019, 11, 128–158 CrossRef CAS.
- B. J. Eggleton, B. Luther-Davies and K. Richardson, Nat. Photonics, 2011, 5, 141–148 CrossRef CAS.
- P. Němec, J. Jedelský, M. Frumar, Z. Černošek and M. Vlček, J. Non-Cryst. Solids, 2005, 351, 3497–3502 CrossRef.
- I. Banik, J. Optoelectron. Adv. Mater., 2016, 18, 226–234 CAS.
- P. Bonazzi and L. Bindi, Z. Kristallogr., 2008, 223, 132–147 CAS.
- A. Patel, D. Singh, Y. Sonvane, P. B. Thakor and R. Ahuja, Mater. Res. Proc., 2022, 22, 57–64 CAS.
- A. van Loon, P. Noble, A. Krekeler, G. Snickt, K. Janssens, Y. Abe, I. Nakai and J. Dik, Heritage Sci., 2017, 5, 22 CrossRef.
- K. P. Smith and G. Ólafsson, J. Archaeol. Sci. Rep., 2023, 47, 103724 Search PubMed.
- W. Scheuermann and G. J. Ritter, Z. Naturforsch., A: Phys. Sci., 1969, 24, 408–411 Search PubMed.
- D. B. Jones, J. R. Gascooke and C. T. Gibson, Carbon, 2024, 229, 119546 CrossRef CAS.
- D. Mrđenović, Z. F. Cai, Y. Pandey, G. L. Bartolomeo, R. Zenobi and N. Kumar, Nanoscale, 2022, 15, 963–974 RSC.
- S. Zhang, N. Zhang, Y. Zhao, T. Cheng, X. Li, R. Feng, H. Xu, Z. Liu, J. Zhang and L. Tong, Chem. Soc. Rev., 2018, 47, 3217–3240 RSC.
- L. E. McNeil and M. Grimsditch, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 4174–4177 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- N. Doebelin and R. Kleeberg, J. Appl. Crystallogr., 2015, 48, 1573–1580 CrossRef CAS PubMed.
- J. Bergmann and R. Kleeberg, Mater. Sci. Forum, 1998, 278-281, 300–305 CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rerat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, E1360 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- D. J. E. Mullen and W. Nowacki, Z. Kristallogr., 1972, 136, 48–65 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Ulian and G. Valdrè, J. Appl. Crystallogr., 2024, 57, 220–231 CrossRef CAS.
- G. Ulian and G. Valdrè, Minerals, 2022, 12, 1323 CrossRef CAS.
- F. Pascale, C. M. Zicovich-Wilson, F. L. Gejo, B. Civalleri, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 888–897 CrossRef CAS PubMed.
- F. Pascale, S. Tosoni, C. Zicovich-Wilson, P. Ugliengo, R. Orlando and R. Dovesi, Chem. Phys. Lett., 2004, 396, 308–315 CrossRef CAS.
- G. Ulian, D. Moro and G. Valdrè, Compos. Struct., 2021, 255, 112978 CrossRef CAS.
- G. Ulian, D. Moro and G. Valdrè, Am. Mineral., 2021, 106, 1928–1939 CrossRef.
- W. F. Perger, Int. J. Quantum Chem., 2010, 110, 1916–1922 CrossRef CAS.
- D. Moro, G. Ulian and G. Valdrè, Appl. Clay Sci., 2019, 172, 28–39 CrossRef CAS.
- D. Moro, G. Ulian and G. Valdrè, J. Microsc., 2020, 280, 204–221 CrossRef CAS PubMed.
- D. Moro, G. Ulian and G. Valdrè, Appl. Clay Sci., 2020, 197, 105777 CrossRef CAS.
- G. Ottonello, B. Civalleri, J. Ganguly, M. V. Zuccolini and Y. Noel, Phys. Chem. Miner., 2009, 36, 87–106 CrossRef CAS.
- G. Ulian, D. Moro and G. Valdrè, Am. Mineral., 2020, 105, 1212–1222 CrossRef.
- G. Ulian and G. Valdrè, Int. J. Quantum Chem., 2020, 120, e26069 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- G. Ulian and G. Valdrè, Appl. Clay Sci., 2023, 246, 107166 CrossRef CAS.
- G. Ulian and G. Valdrè, Phys. Chem. Miner., 2019, 46, 101–117 CrossRef CAS.
- G. Ulian and G. Valdrè, Sci. Rep., 2023, 13, 23090 CrossRef CAS PubMed.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 8, 5188–5192 CrossRef.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 222–231 CrossRef.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647–656 CrossRef.
- A. M. Ferrari, L. Valenzano, A. Meyer, R. Orlando and R. Dovesi, J. Phys. Chem. A, 2009, 113, 11289–11294 CrossRef CAS PubMed.
- G. Placzek, Handbuch der Radiologie, Akademische Verlagsgeselschft, Leipzig, 1934 Search PubMed.
- L. Maschio, B. Kirtman, M. Rerat, R. Orlando and R. Dovesi, J. Chem. Phys., 2013, 139, 164101 CrossRef PubMed.
- M. Ferrero, M. Rerat, B. Kirtman and R. Dovesi, J. Chem. Phys., 2008, 129, 244110 CrossRef PubMed.
- M. Ferrero, M. Rerat, R. Orlando and R. Dovesi, J. Comput. Chem., 2008, 29, 1450–1459 CrossRef CAS PubMed.
- M. Ferrero, M. Rerat, R. Orlando and R. Dovesi, J. Chem. Phys., 2008, 128, 014110 CrossRef PubMed.
- M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, 1993 Search PubMed.
- W. F. Perger, J. Criswell, B. Civalleri and R. Dovesi, Comput. Phys. Commun., 2009, 180, 1753–1759 CrossRef CAS.
- J. F. Nye, Physical properties of crystals, Oxford University Press, Oxford, 1957 Search PubMed.
- A. Erba, Phys. Chem. Chem. Phys., 2016, 18, 13984–13992 RSC.
- G. Ulian and G. Valdrè, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 1042–1059 CrossRef CAS PubMed.
- J. W. Jaeken and S. Cottenier, Comput. Phys. Commun., 2016, 207, 445–451 CrossRef CAS.
- G. Ulian and G. Valdrè, J. Appl. Crystallogr., 2022, 55, 386–396 CrossRef CAS PubMed.
- G. Ulian and G. Valdrè, Comput. Geosci., 2024, 188, 105615 CrossRef.
- G. Ulian and G. Valdrè, Sci. Rep., 2023, 13, 2725 CrossRef CAS PubMed.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- R. Gaillac, P. Pullumbi and F. X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201 CrossRef PubMed.
- M. J. P. Musgrave, Crystal Acoustics: introduction to the study of elastic waves and vibrations in crystals, Holden-Day, San Francisco, CA, USA, 1970 Search PubMed.
- D. J. E. Mullen and W. Nowacki, Z. Kristallogr., Kristallgeom., Kristallphys., Kristallchem., 1972, 136, 48–65 CrossRef CAS.
- F. Bonaccorso, A. Lombardo, T. Hasan, Z. P. Sun, L. Colombo and A. C. Ferrari, Mater. Today, 2012, 15, 564–589 CrossRef CAS.
- U. Khan, A. O'Neill, M. Lotya, S. De and J. N. Coleman, Small, 2010, 6, 864–871 CrossRef CAS PubMed.
- F. S. Gard, D. M. Santos, M. B. Daizo, J. L. Mijares, P. B. Bozzano, C. A. Danón, M. Reinoso and E. B. Halac, Surf. Interface Anal., 2020, 52, 755–769 CrossRef CAS.
- R. Mazzeo, P. Baraldi, R. Lujàn and C. Fagnano, J. Raman Spectrosc., 2004, 35, 678–685 CrossRef CAS.
- J. M. Besson, J. Cernogora and R. Zallen, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 3866–3876 CrossRef CAS.
- R. Zallen and D. F. Blossey, in Optical and Electrical Properties, ed. P. A. Lee, Springer Netherlands, Dordrecht, 1976, pp. 231–272, DOI:10.1007/978-94-010-1478-6_3.
- P. E. Lippens, M. A. El Idrissi Raghni, J. Olivier-Fourcade and J. C. Jumas, J. Alloys Compd., 2000, 298, 47–50 CrossRef CAS.
- V. Matějec, J. Pedliková and I. Barton, J. Sol-Gel Sci. Technol., 2018, 87, 696–703 CrossRef.
- V. Matějec, J. Pedliková, I. Barton, J. Zavadil and P. Kostka, J. Non-Cryst. Solids, 2016, 431, 47–51 CrossRef.
- M. Popescu and D. Mezzane, Optoelectron. Adv. Mater., Rapid Commun., 2008, 2, 26–28 CAS.
- I. R. McFarlane, J. R. Lazzari-Dean and M. Y. El-Naggar, Acta Biomater., 2015, 13, 364–373 CrossRef CAS PubMed.
- V. Kaur, S. K. Tripathi and S. Prakash, AIP Conf. Proc., 2016, 1728, 020433 CrossRef.
- A. Patel, D. Singh, Y. Sonvane, P. B. Thakor and R. Ahuja, Comput. Mater. Sci., 2020, 183, 109913 CrossRef CAS.
- G. Ulian, D. Moro and G. Valdrè, Compos., Part C: Open Access, 2021, 6, 100184 CAS.
- G. Ulian and G. Valdrè, Sci. Rep., 2022, 12, 299 CrossRef CAS PubMed.
- L. Jiang, M. Wu, P. Shi and C. Zhang, Int. J. Photoenergy, 2020, 2020, 8852665 Search PubMed.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Document S1, Fig. S1–S6, and Table S1. See DOI: https://doi.org/10.1039/d5ce00525f |
| This journal is © The Royal Society of Chemistry 2025 |