Open Access Article
Open Access ArticleChiral resolution of copper aspartate under reaction–diffusion: synergy of experiment and simulation†
Poh Ying
Fong
 a,
Sehrish
Khan
a,
Hatem M.
Titi
a,
Sehrish
Khan
a,
Hatem M.
Titi
 b,
Manal
Ammar
c,
Fiorenzo
Vetrone
d,
Mazen
Al-Ghoul
*c and
Louis A.
Cuccia
b,
Manal
Ammar
c,
Fiorenzo
Vetrone
d,
Mazen
Al-Ghoul
*c and
Louis A.
Cuccia
 *a
*a
aDepartment of Chemistry and Biochemistry, Concordia University, 7141 Sherbrooke Street West, H4B 1R6 Montreal, Canada. E-mail: sekha8@ulaval.ca; louis.cuccia@concordia.ca
bDepartment of Chemistry, McGill University, 801 Sherbrooke Street West, H3A 0B8 Montreal, Canada
cDepartment of Chemistry, American University of Beirut, P.O. Box 11-0236, Riad El-Solh, 1107 2020 Beirut, Lebanon. E-mail: mazen.ghoul@aub.edu.lb
dCentre Énergie, Matériaux et Télécommunications, Institut National de la Recherche Scientifique, Université du Québec, 1650 Boul. Lionel-Boulet, J3X 1P7 Varennes, Canada
First published on 11th June 2025
Abstract
Chiral resolution is essential in the pharmaceutical and food industries and in materials science, due to the unique properties of enantiomers. Here, we investigate the coordination polymerization of homochiral (L- and D-) and racemic (DL-) copper aspartate (CuAsp), as well as the spatiotemporal resolution of racemic aspartic acid (DL-Asp) using L- and D-proline (Pro) as tailor-made additives (TMAs), all within the reaction–diffusion framework (RDF) in a quasi-one-dimensional (1D) agar gel system. We combine experimental approaches—leading to spherulitic CuAsp coordination polymers characterized by solid-state circular dichroism (CD), powder X-ray diffraction (PXRD), and thermal analyses—with a newly developed simulation model grounded in classical reaction–diffusion and Cahn–Hilliard equations. These numerical simulations reproduce the experimentally observed Liesegang banding and the chiral inversion phenomenon, where the earliest precipitates adopt the opposite handedness to the proline dopant, consistent with Harada's application of the ‘rule of reversal’. Parameter choices in the model draw on Harada's original insights, capturing both racemic and chiral scenarios. The simulations confirm how slight adjustments to nucleation barriers and stability can account for increased solubility in enantiopure conditions and partial chiral switching in doped systems. Experimentally, CuAsp near the liquid–gel interface crystallizes in the opposite configuration of the TMA, while more distant regions show varied chirality due to concentration gradients. Overall, both experiment and simulation highlight how the RDF, combined with a modest chiral bias, offers a versatile method for effecting chiral resolution in conglomerate crystalline systems, with broad potential for enantioselective separation strategies.
Introduction
Coordination polymers (CPs) are versatile metal–ligand compounds that can form one-, two- or three-dimensional structures.1,2 Their ability to incorporate various metals and ligands has led to a wide range of applications, including magnetism,3 gas adsorption,4 catalysis,5 luminescence,6 and drug delivery.7 Recent advancements have focused on chiral CPs due to their complex architectures and potential in enantioselective separation and asymmetric catalysis.2,8 The ideal enantiopure ligand should be accessible, cost-effective, environmentally friendly, and exhibit flexible coordination behavior.2 Strategic selection and design of chiral ligands are crucial for developing multifunctional chiral CPs. Amino acids, in particular, have garnered significant attention for their efficient coordination with metal ions.9–11 Their distinct amino, carboxylate, and side chain functional groups render them ideal for complexation.12,13 Several research groups have demonstrated the fabrication of 1D nanostructures, such as nanofibers,9,10,14 nanowires,15 nanobelts,16 and nanorods11 from metal–amino acid assemblies. For example, Imaz et al. successfully prepared CuAsp nanofibers at the interface of a Cu2+ solution with a water/ethanol mixture containing deprotonated L- or D-Asp.9 Similarly, Pu et al. and Wu et al. demonstrated the self-assembly of CuGlu,10,17 CuAsp,10 and CuAmi10 at room temperature. Their studies revealed that crystallization is driven by coordination between deprotonated amino acids and Cu2+ metal ions in a proposed square planar coordination geometry. Furthermore, amino acid chirality influences supramolecular self-assembly.10,17Chiral resolution is crucial in the pharmaceutical and food industries, where enantiopure products are essential.18 Various techniques have been developed to resolve conglomerate crystalline systems,19–23 with preferential crystallization (PC) being particularly effective in resolving conglomerate crystals by seeding a supersaturated solution with the preferred enantiomer.20 Pioneering work by Kaoru Harada more than 50 years ago demonstrated the successful separation of DL-Asp, DL-Glu, and DL-Asn using homochiral amino acid-copper complexes.24–27 Addadi et al. later introduced the ‘rule of reversal’ to rationalize how the enantiomer with the opposite configuration crystallizes preferentially in the presence of homochiral tailor-made additives (TMAs).28 This inversion is not adequately explained by stereoselective ligand exchange alone. Harada's original experiments showed that, despite differences in ligand exchange rates between L- and D-aspartate, the configuration of the earliest precipitates reflected not kinetic preference, but rather differences in solubility, local supersaturation, and nucleation kinetics. At low additive-to-racemate ratios, the system favors the opposite enantiomer due to these subtle physicochemical effects. At higher additive concentrations, or later stages of crystallization, the preferred enantiomer can switch—leading to band-by-band enantiomeric alternation as observed in reaction–diffusion systems. Homochiral TMAs share a similar structure with the solute molecules, allowing for enantioselective adsorption, which in turn hinders nucleation and crystal growth of one enantiomer.19,28–30 More recently, Kongsamai et al. explored the resolution of DL-Asn·H2O using D-Asp and D-Glu,31 while Gou et al. and Sun et al. reported higher product yields and purity of (S)-mandelic acid and L-norvaline, respectively, using PC with TMAs.32,33 The reaction–diffusion framework (RDF) offers a robust platform for investigating chiral resolution and pattern formation in coordination polymers, functioning under far-from-equilibrium conditions.34 In this framework, a metal ion such as Cu2+ diffuses through a gel medium containing a chiral ligand (homochiral or racemic), creating a dynamic concentration gradient. This gradient drives the nucleation and growth of coordination polymers, resulting in highly organized structures.35,36 What distinguishes RDF is its ability to facilitate self-organization at multiple scales. While distinct patterns, such as Liesegang rings or spherulites, emerge at the macroscopic level, there is also concurrent self-organization at the microscopic scale, where molecular interactions dictate the arrangement of atoms within the coordination polymer.35,37 This hierarchical self-organization is a hallmark of far-from-equilibrium systems, where the continuous influx of energy or matter drives complexity and order.34
One of the remarkable features of RDF-based self-organization is its capacity for selective spatial segregation. As the system evolves, distinct bands of precipitated material form in the gel.37 This spatial organization not only allows for the segregation of particles based on size but also provides a strategy for attempting to segregate various chiral compounds into these bands. Through the careful control of reaction conditions, such as ion concentration and ligand chirality, this method may enable the separation of enantiomers in situ, as different chiral species preferentially nucleate and crystallize in specific bands. This capability opens new possibilities for chiral resolution and enantioselective separations in structured environments.
In the present study, the diffusion of Cu2+ into a gel matrix containing deprotonated aspartate ligand results in the formation of blue spherulites made of a coordination polymer of CuAsp. This process exemplifies self-organization across length scales, as the spherulites exhibit macroscopic symmetry, while the chiral nature of the ligands dictates their microscopic arrangement. The far-from-equilibrium nature of the RDF ensures that the system does not settle into a static, low-energy arrangement but instead continues to evolve,38 allowing for the emergence of intricate spatial patterns and chiral resolution.
Inspired by the work of Imaz et al.9 and Harada et al.,27 this study aims to explore the chiral crystallization of L- and D-aspartate and the spatiotemporal resolution of DL-aspartate using homochiral additives in an agar gel medium. Harada's work focused on the chiral resolution of racemic aspartic acid using various copper-amino acid complexes under controlled conditions, revealing a phenomenon of “chiral inversion” in the earliest precipitates. Specifically, when L-proline was introduced, D-aspartate tended to crystallize first, while D-proline favored initial L-aspartate precipitation. This behavior could not be attributed solely to a simple ligand-exchange mechanism; instead, solubility differences and kinetic factors (including local complexation equilibria and diffusion-limited growth) emerged as critical contributors. As the reaction front advanced and dopant concentrations shifted, later-formed precipitates sometimes reverted to the same chirality as the proline additive, underscoring the dynamic nature of the enantiomeric composition over time. Through the application of the RDF, this work seeks to uncover new insights into the mechanisms driving chiral resolution and the role of amino acid chirality in the formation of coordination polymers. The findings contribute to the broader understanding of chiral materials design and the development of novel techniques for enantioselective separation in structured environments.
Results and discussion
Coordination polymerization and characterization of L-, D-, and DL-CuAsp in agar gel
Research on the coordination polymerization of CuAsp has traditionally focused on solution-based self-assembly processes.9,10 However, to our knowledge, the coordination polymerization of CuAsp in hydrogels has yet to be reported. Taking advantage of the RDF, we successfully achieved the periodic precipitation (Liesegang banding) of L-, D-, and DL-CuAsp coordination polymers in a 1D agar gel system (Fig. 1). The diffusion of Cu(NO3)2·3H2O solution, serving as the outer electrolyte, into the gel containing deprotonated Asp led to the formation of distinct blue spherulites. The temporal evolution of this periodic precipitation is depicted in Fig. S1.† | ||
| Fig. 1 Periodic precipitation of L-, D-, and DL-CuAsp coordination polymers in a 1% agar gel system. (a) L-CuAsp, (b) D-CuAsp, and (c) DL-CuAsp, showing distinct Liesegang banding patterns. The diffusion of Cu(NO3)2·3H2O (outer electrolyte) into the gel containing deprotonated Asp (inner electrolyte) leads to the formation of blue CuAsp spherulites. The initial concentrations used were [Cu2+] = 300 mM in the outer electrolyte and [Asp] = 50 mM, [NaOH] = 100 mM in the inner electrolyte, with 1% agar as the gel matrix. The reaction was conducted at ∼22 °C. The spatiotemporal evolution of the precipitation process is shown in Fig. S1.† | ||
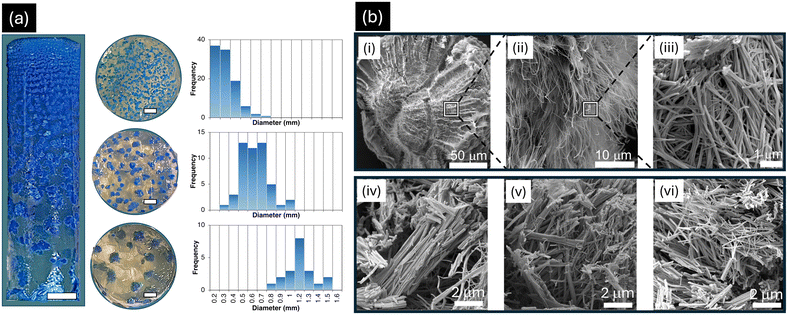
A notable 6-fold higher concentration of Cu2+ outer electrolyte was used to create a high level of supersaturation at the liquid–gel interface, facilitating rapid diffusion.35 This setup established a concentration gradient, where supersaturation decreased progressively with distance from the interface.35 At the interface, the highest concentration of Cu2+ ions leads to rapid nucleation due to high supersaturation. Since nucleation dominates crystal growth at high supersaturation, many small spherulites form simultaneously, competing for available ions (Fig. 2a). This results in a high number of nuclei, limiting the growth of each crystal. Furthermore, in the middle zone, the supersaturation decreases as Cu2+ ions diffuse further from the liquid–gel interface. Here, nucleation slows down, allowing the spherulites that form to grow larger as crystal growth begins to dominate over nucleation. This creates a balance between nucleation and crystal growth, leading to intermediate particle sizes (Fig. 2a). When Cu2+ ions reach the bottom zone, supersaturation is significantly lower. Fewer nuclei form in this region, allowing the already formed spherulites to grow larger due to reduced ion competition. Crystal growth is the dominant process, leading to the formation of large spherulites (Fig. 2a).
Spherulite formation is a common phenomenon in RDFs.39 It begins with the nucleation at a single point. Once nucleation occurs, anisotropic forces drive the directional growth of nanofibers of CuAsp coordination polymers away from the nucleus, resulting from the established concentration gradient. As the CuAsp nanofibers grow, they align radially from the nucleation site, with the diffusion flux continuing to supply material that contributes to the growth of the fibers. This results in the formation of bundles of nanofibers, where each bundle maintains a preferred orientation driven by the anisotropy in the reaction environment.39 These nanofiber bundles progressively organize into a hierarchical structure, with the inner layers of the spherulite formed first, followed by the addition of outer layers as the reaction continues. The hierarchical organization is a crucial feature of spherulitic growth, where small-scale units such as nanofibers are integrated into progressively larger structures, ultimately forming a spherulite with a radial, starburst-like morphology. This self-organization across multiple scales, from nanofibers to macroscopic crystals, is a hallmark of the far-from-equilibrium conditions maintained in the reaction–diffusion system.39 The continuous supply of Cu2+, combined with anisotropic forces, ensures that the spherulite grows symmetrically and retains its distinctive hierarchical architecture. Thus, RDF not only promotes radial growth but also fosters the creation of well-ordered, complex structures that are characteristic of spherulites. This described mechanism is clearly illustrated in the SEM micrographs where the CuAsp nanofibers are densely aggregated around the spherulite's nucleus (Fig. 2b(i–iii)). Interestingly, although the overall size of the spherulites increased (from 0.3 to 1.2 mm; Fig. 2a), the diameters of the nanofibers progressively decreased along the reaction tube (Fig. 2b(iv–vi)), ranging from 100 nm near the interface to 50 nm near the diffusion front, aligning closely with homochiral CuAsp nanofibers reported by Imaz et al.9 This decrease in fiber thickness can also be attributed to the reduction of supersaturation along the tube. For example, as nucleation near the gel interface is abundant, the supply of ions is divided among many forming nuclei. This allows the nanofibers to grow thicker due to the abundance of material at the initial stages of fiber formation. This fact is reversed further away from the interface.
Noteworthy differences in precipitation Liesegang patterns were observed when comparing homochiral L-CuAsp or D-CuAsp to DL-CuAsp. Homochiral CuAsp spherulites formed densely packed arrays, while DL-CuAsp spherulites were more sparsely distributed. Liesegang bands result from periodic precipitation in reaction–diffusion systems as the reactant concentration fluctuates due to diffusion and supersaturation cycles.38 The spacing of these bands is directly influenced by the nucleation rate, which in turn is affected by the solubility of the precipitating compound. For homochiral CuAsp, the lower solubility of L- or D-Asp (between 4 mg mL−1 and 5 mg mL−1 at 25 °C)40,41 means that precipitation occurs more readily, leading to closely spaced Liesegang bands because the system reaches the necessary concentration for nucleation frequently along the diffusion front. This rapid nucleation results in shorter intervals between precipitation bands as new crystals form in quick succession. For DL-CuAsp, its higher solubility (7.8 mg mL−1 at 25 °C),40,41 means that the system requires a greater concentration of Cu2+ ions to reach supersaturation, leading to wider spacing between precipitation events. This results in more sparsely distributed Liesegang bands, as nucleation happens less frequently due to the slower approach to supersaturation in the higher-solubility DL-Asp solution. Additionally, the slower formation of coordination complexes in DL-CuAsp, compared to homochiral CuAsp, can be attributed to the incompatibility between L- and D-Asp in nanofiber formation. This suggests that CuAsp crystallizes as a conglomerate (vide infra). Wu et al. demonstrated that mixing equal concentrations of Cu2+ solution with deprotonated L- or D-Asp leads to rapid gelation, while DL-Asp forms a blue gel more slowly at the same concentration, indicating faster assembly rates for homochiral CuAsp than for DL-CuAsp.9,10
Powder X-ray diffraction (PXRD) analysis confirmed the crystalline nature of CuAsp (Fig. 3a). Both L- and D-CuAsp exhibit the same diffraction patterns, in agreement with Wu et al.,10 indicating that both forms share the same crystal packing. Remarkably, DL-CuAsp gave the same diffraction pattern. The identical PXRD patterns observed for all three forms (L-, D-, and DL-CuAsp) imply that the coordination environment around Cu2+ and the packing arrangement remain consistent regardless of whether the system is homochiral or racemic. This uniformity suggests that the presence of both L-and D- in DL-CuAsp does not disrupt the crystal structure but rather crystallizes in a conglomerate. Unfortunately, a detailed analysis of the structural connectivity was not feasible due to their sub-200 nm diameter nanofibers, the inability to obtain large single crystals, and the unsuccessful attempts at electron diffraction. Pawley refinement of the PXRD pattern for L-CuAsp was performed to confirm the structural integrity and phase purity of the coordination polymer. The refinement (Fig. S4†) showed excellent agreement between experimental and fitted profiles, yielding low residuals (Rwp = 3.87%, Rp = 2.87%). The extracted unit cell parameters (a = 22.07 Å, b = 9.17 Å, c = 5.10 Å, β = 133.95°) match the expected monoclinic symmetry (space group P121), and the refined crystallite size (C = 13.56 ± 0.28 nm) confirms the nanocrystalline nature of the material. These results strongly support the high crystallinity and single-phase character of the synthesized L-CuAsp. Imaz and coworkers suggested that the CuAsp nanofibers were aligned in 1D [Cu(Asp)(H2O)x]n polymeric chains,9 while Wu et al. later proposed that the CuAsp coordination complex adopts a square-planar geometry, where the Cu2+ ion is bonded to the α-carboxylate oxygen and amino nitrogen atoms of Asp, forming a typical five-membered glycinate chelate ring.10
Attenuated total reflectance Fourier-transform infrared (ATR-FTIR) characterization was performed to probe the assembly process of the nanofibers. The coordination of aspartate with Cu2+ is evident when comparing the IR spectra of the starting material (L-aspartic acid) with the coordination polymers L-, D-, and DL-CuAsp (Fig. S2†). A detailed analysis of the IR spectrum of L-aspartic acid reveals characteristic peaks at 3132 cm−1 (νN–H), 3000 cm−1 (νC–H), 1680 cm−1 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1612 cm−1 (νCOOH), and 1070 cm−1 (νC–N). Additional peaks at 1344 cm−1 and 1210 cm−1 correspond to C–H stretching and CH2 twisting, respectively. Peaks at 890 cm−1, 640 cm−1, and 475 cm−1 are attributed to C–C stretching, COOH bending, and NH3 torsion vibrations, respectively. Deprotonation of the COOH groups, prior to coordination with Cu2+, is confirmed by the shift of the C
O), 1612 cm−1 (νCOOH), and 1070 cm−1 (νC–N). Additional peaks at 1344 cm−1 and 1210 cm−1 correspond to C–H stretching and CH2 twisting, respectively. Peaks at 890 cm−1, 640 cm−1, and 475 cm−1 are attributed to C–C stretching, COOH bending, and NH3 torsion vibrations, respectively. Deprotonation of the COOH groups, prior to coordination with Cu2+, is confirmed by the shift of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration to 1580 cm−1.10 The band observed at 675 cm−1 is attributed to Cu–O stretching, while the band at 420 cm−1 in all three coordination polymers corresponds to the asymmetric stretching mode of the Cu–N bonds (395–455 cm−1).42,43 All three CPs, L-, D-, and DL-CuAsp CPs, exhibit virtually identical IR spectra.
O stretching vibration to 1580 cm−1.10 The band observed at 675 cm−1 is attributed to Cu–O stretching, while the band at 420 cm−1 in all three coordination polymers corresponds to the asymmetric stretching mode of the Cu–N bonds (395–455 cm−1).42,43 All three CPs, L-, D-, and DL-CuAsp CPs, exhibit virtually identical IR spectra.
We conducted further experiments to shed light on the underlying CuAsp structure. The IR shows a broad peak in the range of 2800–3600 cm−1, corresponding to the presence of water molecules. To confirm the presence of water as part of the structure, the thermal stability of the compound L-CuAsp was investigated using variable temperature PXRD (VTPXRD) and thermogravimetric analysis (TGA). The VTPXRD reveals changes in 2θ, especially at 18.1°, 19.2°, 19.5°, 25.4°, and 26.2°, starting when the sample was heated from 90 °C until 125 °C. These changes may correspond to the loss of solvents from the structure. The temperature and experimental preparation suggest the loss of free water molecules at around 90 °C, while the coordinated water molecules can be released above 110 °C (Fig. 3b). The structure remains intact up to 170 °C, followed by the material's complete amorphization. TGA was used to investigate the number of water molecules in the structure (Fig. 3c). The weight loss due to water ends at 130 °C, with a weight loss drop of approximately 27%. The material then shows thermal stability between 170–200 °C, which aligns very well with the amorphization of the compound, as observed in the VTPXRD. The decomposition led to the formation of CuO at 370 °C. Interestingly, the calculated number of water molecules from the weight loss is approximately four. It is worth mentioning that the pure enantiomers and the racemate have the same profile and weight loss, indicating they have a similar structure, which agrees with conglomerate crystallization and supports the results from the PXRD analysis. The water uptake of a dry sample of L-CuAsp was also investigated using dynamic vapour sorption (DVS, Fig. 3d). First, the CP was activated by heating the sample at 100 °C for 4 hours; then, the dried sample was placed on the DVS, and the relative humidity was gradually increased starting from 0 RH% up to 95 RH%, with increments of 5 RH%. The compound shows a water uptake and desorption of 28.5%, which agrees with the TGA results. Based on the DVS results, the surface area (SA) calculation using the Brunauer–Emmett–Teller (BET) method shows an SA of 170.5 m2 g−1.
To assess porosity, N2 adsorption–desorption isotherms of L-, D-, and DL-CuAsp were measured at 77 K (Fig. S3†), all exhibiting type IV isotherms with H3-type hysteresis loops. These features indicate mesoporosity and are typically associated with slit-like pores formed by fibrous aggregates. While PXRD confirms that the L-, D-, and DL-CuAsp coordination polymers share the same crystalline phase, nitrogen sorption measurements reveal differences in their textural properties. DL-CuAsp exhibits the largest total pore volume (0.684 cm3 g−1), the highest average BET pore diameter (293.6 Å), and a BET surface area of 93.2 m2 g−1—indicative of substantial mesoporosity, likely due to looser crystallite packing or interparticle voids formed by mixing of L- and D-domains. In contrast, the enantiopure forms show comparable BET surface areas—88.1 m2 g−1 for L-CuAsp and 93.7 m2 g−1 for D-CuAsp—but smaller average pore diameters (76.6 Å for L-CuAsp and 39.7 Å for D-CuAsp) and lower total pore volumes (0.169 cm3 g−1 and 0.093 cm3 g−1, respectively). The initial rapid uptake at low relative pressures corresponds to monolayer formation in mesopores, while the steep uptake at higher pressures is attributed to capillary condensation. The observed hysteresis further supports the presence of non-rigid, fibrous pore architectures.44 Micropore surface areas and volumes also differ (L-CuAsp: 26.6 m2 g−1, 0.0111 cm3 g−1; D-CuAsp: 84.8 m2 g−1, 0.0327 cm3 g−1), but these variations are likely due to sample preparation or measurement variability, as the materials are mirror-image isostructures. Thus, deviations in BET parameters are interpreted as experimental scatter rather than inherent differences in porosity.
Solid-state circular dichroism (CD) was employed to investigate the chirality of CuAsp polymers (Fig. 4). L-CuAsp exhibited a positive Cotton effect, while D-CuAsp showed a negative Cotton effect at 745 nm, with both crossing at 655 nm, indicating the presence of a chiral coordination sphere of the Cu2+ with chiral Asp.9 In contrast, DL-CuAsp showed no Cotton effect, nor did the individual DL-CuAsp spherulites (Fig. S5†). This observation apparently contradicts crystallization as a conglomerate, as indicated by the identical PXRD pattern shared by DL- and homochiral CuAsp. Herein, it is believed that the nanofibers within each DL-CuAsp spherulite are individually homochiral. Still, their aggregation presents racemic-like behavior in CD analysis, reconciling the PXRD data with the lack of chiral signals in the CD results. These findings demonstrate that RDF enables the periodic precipitation of L-, D-, and DL-CuAsp coordination polymers in agar gel.
Chiral resolution of DL-Asp in the presence of homochiral proline (Pro)-copper complexes in agar gel
Homochiral L- and D-Pro-copper complexes as tailor-made additives (TMAs) were used to achieve spatiotemporal chiral resolution of DL-Asp in the gel. The diffusion of homochiral Pro-copper complexes (L-Pro or D-Pro) into the agar gel containing DL-Asp results in spatially distinct bands of CuAsp coordination polymers. The spatial organization is guided by the concentration gradients established by RDF, which controls where and how the chiral molecules crystallize. Drawing from Harada's research, when the mole ratio of the chiral amino acid to DL-Asp is less than 1, the second crop of crystals maintains the same configuration as the first crop. Yet, when the mole ratio is equal to or greater than 1, the configuration of the second crop reverses relative to the first crop.27 To confirm proper complexation, UV-vis absorption analysis was performed, revealing an adsorption shift from 800 nm to approximately 725 nm regardless of the concentration of Pro, indicating the formation of a Pro-Cu(II) complex in solution (Fig. S6†).After diffusing chiral Pro-copper complexes into DL-Asp gel, distinct spatiotemporal regions of CuAsp polymers were observed (Fig. 5). The evolution of this periodic precipitation is shown in Fig. S7.† Samples obtained near the interface consistently showed chirality opposite to the introduced TMAs. Solid-state CD analysis reveals a negative Cotton effect in the presence of L-Pro-copper complexes, suggesting the predominance of D-CuAsp (Fig. 5a and c). In contrast, the presence of D-Pro-copper complexes led to positive Cotton effects, indicating L-CuAsp formation near the liquid–gel interface (Fig. 5b and d). These findings align with the ‘rule of reversal’, where the presence of a homochiral additive influences the chiral environment, promoting the crystallization of the opposite enantiomer. However, the overall chiral intensity decreased when L- and D-Pro-copper complexes were introduced, compared to the coordination polymers formed in the absence of TMAs. This suggests that although these TMAs selectively attached to the nanofibers of the conglomerates with the same configuration, they only partially resolved the DL-Asp conglomerates. This differential impact could be attributed to the inherent differences in how L- and D-Pro complexes interact with DL-Asp and the agar gel environment. Notably, fewer precipitates formed at higher concentrations of Pro-copper complexes than those formed at lower concentrations, likely due to the slower coordination rate: at higher concentrations, the Pro-copper complexes may create a denser environment around the aspartate ligands, leading to increased steric hindrance and reduced mobility. This congestion can slow the rate at which the Pro-copper complexes effectively coordinate with the aspartate, impeding efficient nucleation and subsequent crystal growth. The slower coordination rate thus limits the number of nucleation sites available, resulting in a reduced number of precipitates despite the higher concentration of reactants. Additionally, higher concentrations of TMAs may promote the formation of transient or less stable intermediates, further delaying or hindering the crystallization process.
During crystallizations involving L-Pro-copper additive, mainly coordination polymers with negative Cotton effects were observed across all zones (Fig. 5a and c), indicating the predominant formation of D-CuAsp. A lower chiral intensity was observed with 100 mM L-Pro-copper than 200 mM L-Pro-copper. In the case of 100 mM D-Pro-copper additive, a gradual chiral switching of the coordination polymers from positive to negative Cotton effect was observed (Fig. 5b). In contrast, two chiral switching events occurred in the presence of 200 mM D-Pro (Fig. 5d). This switching develops on Harada's work in solution and is attributed to the slower coordination rates and higher steric hindrance introduced by the excessive presence of Pro-copper complexes, which could inhibit effective nucleation and crystallization. The reduced efficiency suggests an optimal concentration range for the TMAs where they exert maximum influence on the chiral resolution process. Beyond this range, the coordination kinetics may not favor the formation of organized chiral domains.
A factor that can rationalize the effect of L- and D-Pro-copper additive on the chiral distribution of CuAsp could be related to the composition of the agar gel itself, which primarily consists of D-galactose. In the context of the ‘rule of reversal’, the gel may also influence the chiral crystallization of CuAsp.29 In other words, the agar could act as a chiral competitor, diminishing the chiral influence of the D-Pro-copper additive. This would be particularly noticeable as the distance from the interface increases and the concentration of the TMA decreases, allowing the agar's intrinsic chirality to become more influential. This result may indicate that while the RDF can create favorable conditions for chiral resolution, the specific chiral interactions and competition with the gel matrix must be considered to optimize the outcome.
Theoretical model
To provide a quantitative understanding of the observed spatiotemporal chiral resolution in RDF, we developed a theoretical model coupling classical reaction–diffusion equations with Cahn–Hilliard equations to describe Liesegang precipitate formation and evolution for the L- and D-enantiomers of CuAsp in the presence of homochiral copper-proline complexes as tailor-made additives (TMAs). Notably, the Cahn–Hilliard equations inherently account for phase separation driven by the competition between diffusion and phase segregation, effectively mimicking the periodic banding observed in Liesegang patterns. This characteristic arises from the interplay between local supersaturation, nucleation kinetics, and diffusive transport, generating alternating regions of precipitate-rich and precipitate-poor phases.45–47The general formulation of the model includes concentration fields for the Cu2+ ions (C), L- and D-aspartate ions (AL, AD), and L-Pro-copper complexes (PL). The precipitates formed by the coordination polymers of L- and D-CuAsp are represented by volume fractions ϕL and ϕD, respectively. The dynamics of the system are governed by reaction–diffusion equations coupled to the phase separation described by the Cahn–Hilliard equations.
The reaction–diffusion equations of all components are given by:
 | (1) |
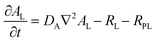 | (2) |
 | (3) |
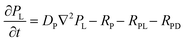 | (4) |
| RL = kL × C × AL; RD = kD × C × AD | (5) |
| RPL = kPL × PL × AL; RPD = kPD × PL × AD | (6) |
The reaction rates RL and RD represent the polymerization rates of L- and D-CuAsp formed via the direct reaction between free copper ions and aspartate. Since this process does not involve any chiral influence, the rate constants kL and kD are expected to be equal, reflecting the intrinsic symmetry of the racemic system in the absence of a chiral selector. In contrast, RPL and RPD describe the polymerization rates arising from the interaction between the L-proline-copper complex, for example, and aspartate. Here, the chiral environment introduced by the L-proline ligand is expected to differentiate between L- and D-aspartate, leading to distinct rate constants kPL and kPD. These rate constants, representing stereoselective ligand exchange, are hypothesized to differ in magnitude, and this asymmetry is proposed to be a factor governing the enantiomeric bias observed in the resulting Liesegang bands. Furthermore, when L-proline is replaced with its mirror image, D-proline, the stereochemical preference is reversed, causing the relative magnitudes of kPL and kPD to switch accordingly. This reversal underscores the chiral origin of the selectivity in the reaction pathway.
The Cahn–Hillard equations that describe the time evolution of the order parameters (precipitate volume fractions) representing the coordination polymers, ϕL and ϕD, are given by:
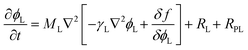 | (7) |
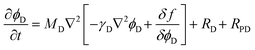 | (8) |
To account for the asymmetric behavior observed between the L- and D-coordination polymers, we consider a generalized free energy density fϕL, ϕD that includes distinct thermodynamic parameters for each enantiomer and assumes a double-well potential function:
 | (9) |
Numerical solutions and results
The Cahn–Hilliard eqn (7) and (8)—used to capture phase separation and band formation—are solved in tandem with the RD eqn (1)–(4) to account for simultaneous diffusion, nucleation, and precipitate growth. By adjusting the nucleation barrier (a), stability (b), and enantiomeric coupling (χ) parameters, the simulations reproduce both the classical Liesegang spacing/width laws and the chiral inversion phenomena observed experimentally.The spatial domain is discretized using a second-order finite difference scheme for all Laplacian terms, applying Dirichlet or Neumann boundary conditions as appropriate (e.g., Dirichlet for concentration at the gel inlet, no-flux for the precipitates). We employ the method of lines, converting the PDE system into a large set of ordinary differential equations (ODEs) for each grid point. A stiff ODE solver (such as MATLAB's ODE15s) then integrates these ODEs in time, ensuring stability under the often-steep gradients characteristic of Liesegang precipitation.
Fig. 6(a) presents numerical simulation results obtained in the absence of any chiral proline additive. Initially, the gel contains equal concentrations of L- and D-aspartate enantiomers, representing a racemic mixture, with copper ions introduced as an inner electrolyte diffusing into the gel. The parameters used in this simulation were set symmetrically for both enantiomers (aL = aD = 0.5, bL = bD = 0.5) to ensure equivalent nucleation barriers and equilibrium stability. Additionally, a small negative coupling constant (χ) = −0.01 was chosen, explicitly promoting the coexistence of both enantiomeric precipitates. Under these conditions, clear and well-defined Liesegang bands formed for both normalized ϕL and ϕD, demonstrating periodic precipitation along the spatial domain. Notably, the resulting band pattern follows classical Liesegang laws: the spacing between consecutive bands increases with distance from the gel–electrolyte interface (spacing law), and the band widths also increase progressively along the same direction (width law). The solutions for ϕL and ϕD overlap strongly in both position and amplitude, confirming the formation of a racemic (achiral) coordination polymer. This result aligns closely with experimental observations, reinforcing that racemic starting conditions yield exclusively achiral Liesegang band structures. Fig. 6(b) shows the results of a simulation in which only L-aspartate is initially present in the gel, at the same concentration as the total aspartate content in the racemic case of Fig. 6a. This setup mimics enantiopure conditions without any chiral additive. To reflect the known increase in solubility and reduced stability of enantiopure coordination polymers compared to racemic ones, we selected a higher nucleation barrier (aL > 0.5) and a lower stability parameter (bL < 0.5) than those used in Fig. 1a. These parameter choices explicitly encode the experimentally observed solubility differences and account for the altered precipitation behavior of the pure enantiomer system. The resulting Liesegang pattern is markedly different from the racemic case: while banding still emerges, the number of discrete bands is reduced, and they appear further from the source of copper diffusion. Moreover, the early region near the gel–electrolyte interface is dominated by a continuous precipitation zone rather than distinct bands. This qualitative change in pattern morphology is consistent with experimental reports of altered Liesegang structures under enantiopure conditions, and it highlights the model's capacity to capture the subtle interplay between solubility, nucleation kinetics, and pattern formation in chiral systems.
Fig. 7(a) presents the simulated Liesegang bands in the presence of L-proline as a chiral additive. To reflect the experimental observation that early bands precipitate with the opposite chirality to the additive (Harada et al.), we selected parameters such that the D-coordination polymer has a lower nucleation barrier and higher stability (aL > aD, bL < bD), making D-aspartate more likely to nucleate and grow initially. Consistent with Harada's results, the plot shows that the D-precipitate (red) dominates in both early and subsequent bands, while the L-precipitate (blue) remains suppressed until late in the gel. The inset bar chart quantifies the enantiomeric excess (EE) for each indexed band, demonstrating a strongly positive (D-favored) EE in the earliest bands, which gradually evolves but remains predominantly D-enriched. This matches the “chirality inversion” phenomenon in which the enantiomeric configuration of the precipitate is opposite to that of the additive in initial Liesegang bands.
In contrast, Fig. 7(b) illustrates the scenario when D-proline is used. Here, we reverse the parameter assignments such that L-aspartate (blue) is initially favored (lower aL, higher bL), reflecting the reported inversion in which the precipitate's handedness initially opposes that of the dopant. Indeed, the early bands now predominantly show an L-configuration (blue). Over time, however, the enantiomeric excess switches from L-negative to D-positive and back again, as shown in the inset bar plot where some bands exhibit strong L-enrichment while others flip to D-dominance. Such a switching phenomenon has also been observed experimentally in chiral resolution systems, pointing to subtle kinetic–thermodynamic interactions in the presence of a strong chiral dopant. This highlights that as the reaction–diffusion front moves, and local conditions (e.g., concentration of free proline) change, the favored enantiomer can shift accordingly. It is also noteworthy that it was ultimately found that the asymmetry in the kinetic parameters a and b plays a more dominant role than the ligand exchange rate constants themselves in determining the extent of enantiomeric excess in the banding pattern.
Overall, these simulations align well with the key findings in this work, which showed that adding L- or D-proline to racemic aspartic acid solutions can yield initial precipitates of the opposite chirality, and that later bands can partially switch or evolve in handedness. The adjustments to the nucleation barrier (a) and stability (b) for each enantiomeric species (Lvs.D) successfully capture these effects: the aspartate with the lower effective aa and higher bb spontaneously nucleates earlier, forming the earliest Liesegang bands, while the other enantiomer may eventually precipitate in later bands or intersperse periodically, leading to the observed “flip” or switching behavior in enantiomeric excess.
Conclusions
In this study, we demonstrated a reaction–diffusion framework (RDF) that drives both the formation and chiral resolution of CuAsp coordination polymers. Experimentally, homochiral L- or D-aspartate formed dense Liesegang bands, while racemic DL-aspartate produced more widely spaced bands, reflecting their solubility differences. Solid-state CD confirmed that DL-CuAsp behaved as a conglomerate, showing no net chiral signal despite its homochiral nanofibers. When L- or D-proline copper complexes (TMAs) were introduced to a DL-Asp gel, chiral inversion was observed at the gel interface, consistent with Harada's earlier findings. Further from the interface, local conditions (additive depletion, agar gel chirality, and changing supersaturation) promoted partial switching in enantiomeric excess, highlighting a dynamic interplay of diffusion and kinetic/thermodynamic factors.By incorporating a newly added theoretical and numerical simulation section, we showed how modified reaction–diffusion and Cahn–Hilliard equations comprehensively reproduce these experimental behaviors. We set distinct nucleation (a) and stability (b) parameters in line with Harada's solubility-based rationale, accurately capturing racemic versus enantiopure scenarios as well as TMA-induced chiral inversion and band-by-band switching. The simulations not only confirm the experimentally observed Liesegang band spacing and width laws but also illuminate how fine-tuning such parameters can yield different chiral outcomes. Overall, our results highlight the RDF's capability – complemented by predictive simulations – to enable chiral resolution in situ while forming well-defined coordination polymer structures. In the context of this study, both experimental and simulated results support this behavior: early Liesegang bands form with the opposite handedness to the proline dopant, while later bands show chiral switching as local conditions evolve. This dynamic phenomenon, captured through the interplay of RDF, Cahn–Hilliard modeling, and chiral TMAs, underscores the rule of reversal as a hallmark of nonequilibrium chiral crystallization. Future research will extend these approaches to other amino acids or ligands, exploring advanced gel matrices and dopants, thereby refining this combined experimental modeling platform for chiral material design and chiral resolution.
Data availability
The data supporting this work is included within the main article and/or the ESI.†Author contributions
Poh Ying Fong: investigation, visualization, formal analysis, writing – original draft; Sehrish Khan: investigation, visualization, formal analysis; Hatem M. Titi: investigation, formal analysis, visualization, writing; Manal Ammar: investigation, formal analysis; Fiorenzo Vetrone: supervision, resources, conceptualization, editing; Mazen Al-Ghoul: supervision, conceptualization, investigation, methodology, theory and simulation, writing; Louis A. Cuccia: supervision, resources, funding acquisition, conceptualization, investigation, methodology, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from NSERC Canada, the FQRNT-supported multi-university Québec Centre for Advanced Materials (QCAM), and Concordia University are greatly acknowledged. MAG acknowledges the support from the American University of Beirut Research Board. Clauda Medlej is acknowledged for BET measurements. We thank Dr. Ashlee Howarth for allowing access to PXRD instrumentation and Dr. Mihails Arhangelskis for his support with the crystal structure studies.References
- G. Chakraborty, I.-H. Park, R. Medishetty and J. J. Vittal, Chem. Rev., 2021, 121, 3751–3891 CrossRef CAS PubMed
.
- E. R. Engel and J. L. Scott, Green Chem., 2020, 22, 3693–3715 RSC
.
- J. Zhang, W. Kosaka, Y. Kitagawa and H. Miyasaka, Nat. Chem., 2021, 13, 191–199 CrossRef CAS PubMed
.
- H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Mater. Today, 2018, 21, 108–121 CrossRef CAS
.
- L. Jiao, Adv. Mater., 2018, 30, e1703663 CrossRef PubMed
.
- S. Wang, Y. Hou, E. Wang, Y. Li, L. Xu, J. Peng, S. Liu and C. Hu, New J. Chem., 2003, 27, 1144–1147 RSC
.
- I. Imaz, M. Rubio-Martínez, L. García-Fernández, F. García, D. Ruiz-Molina, J. Hernando, V. Puntes and D. Maspoch, Chem. Commun., 2010, 46, 4737–4739 RSC
.
- C. Cruz, C. Gonzalez, F. Rubio, J. Erices, K. Wrighton-Araneda, D. Cortés-Arriagada, D. Venegas-Yazigi, N. Audebrand and V. Paredes-García, Cryst. Growth Des., 2022, 22, 237–250 CrossRef CAS
.
- I. Imaz, M. Rubio-Martínez, W. J. Saletra, D. B. Amabilino and D. Maspoch, J. Am. Chem. Soc., 2009, 131, 18222–18223 CrossRef CAS PubMed
.
- H. Wu, C. Tian, Y. Zhang, C. Yang, S. Zhang and Z. Jiang, Chem. Commun., 2015, 51, 6329–6332 RSC
.
- M. Mizutani, N. Maejima, K. Jitsukawa, H. Masuda and H. Einaga, Inorg. Chim. Acta, 1998, 283, 105–110 CrossRef CAS
.
- C. Wang, N. Zhang, C.-Y. Hou, X.-X. Han, C.-H. Liu, Y.-H. Xing, F.-Y. Bai and L.-X. Sun, Transition Met. Chem., 2020, 45, 423–433 CrossRef CAS
.
- I. Imaz, M. Rubio-Martinez, J. An, I. Sole-Font, N. L. Rosi and D. Maspoch, Chem. Commun., 2011, 47, 7287–7302 RSC
.
- J. Puigmartí-Luis, M. Rubio-Martínez, U. Hartfelder, I. Imaz, D. Maspoch and P. S. Dittrich, J. Am. Chem. Soc., 2011, 133, 4216–4219 CrossRef PubMed
.
- Q. Zhou, R. Sun, Y. Ren, R. Tian, J. Yang, H. Pang, K. Huang, X. Tian, L. Xu and Y. Tang, Carbon Energy, 2023, 5(1), e273 CrossRef CAS
.
- C. Li, K. Deng, Z. Tang and L. Jiang, J. Am. Chem. Soc., 2010, 132, 8202 CrossRef CAS PubMed
.
- F. Pu, X. Liu, B. Xu, J. Ren and X. Qu, Chem. – Eur. J., 2012, 18, 4322–4328 CrossRef CAS PubMed
.
- O. Shemchuk, F. Grepioni, T. Leyssens and D. Braga, Isr. J. Chem., 2021, 61, 563–572 CrossRef CAS
.
- L. Addadi, Z. Berkovitch-Yellin, N. Domb, E. Gati, M. Lahav and L. Leiserowitz, Nature, 1982, 296, 21–26 CrossRef CAS
.
-
G. Coquerel, Novel Optical Resolution Technologies, 2007, pp. 1–51 Search PubMed
.
- G. Springuel and T. Leyssens, Cryst. Growth Des., 2012, 12, 3374–3378 CrossRef CAS
.
- B. Tang, W. Wang, H. Hou, Y. Liu, Z. Liu, L. Geng, L. Sun and A. Luo, Chin. Chem. Lett., 2022, 33, 898–902 CrossRef CAS
.
- H. L. Lee, Y. L. Hung, A. Amin, D. E. Pratama and T. Lee, Ind. Eng. Chem. Res., 2023, 62, 1946–1957 CrossRef CAS
.
- K. Harada, Nature, 1965, 205, 590–591 CrossRef CAS
.
- K. Harada, Bull. Chem. Soc. Jpn., 1965, 38, 1552–1555 CrossRef CAS PubMed
.
- K. Harada and T. Iwasaki, Chem. Lett., 1972, 1, 1057–1059 CrossRef
.
- K. Harada and W. Tso, Bull. Chem. Soc. Jpn., 1972, 45, 2859–2862 CrossRef CAS
.
- L. Addadi, J. van Mil, E. Gati and M. Lahav, Amplification of optical activity by crystallization in the presence of tailor-made additives. The “inversion rule”, Springer, 1981, pp. 355–364 Search PubMed.
- J. Van Mil, L. Addadi, E. Gati and M. Lahav, J. Am. Chem. Soc., 1982, 104, 3429–3434 CrossRef CAS
.
- I. Weissbuch, L. Addadi, L. Leiserowitz and M. Lahav, J. Am. Chem. Soc., 1988, 110, 561–567 CrossRef CAS
.
- P. Kongsamai, C. Flood, J. H. Horst and A. E. Flood, Chem. Eng. Technol., 2018, 41, 1173–1179 CrossRef CAS
.
- L. Gou, H. Lorenz and A. Seidel-Morgenstern, Cryst. Growth Des., 2012, 12, 5197–5202 CrossRef CAS
.
- J. Sun, Y. Wang, Z. Gao, J. Gong and W. Tang, Additive-assisted preferential crystallization of racemic component: A case of norvaline, J. Ind. Eng. Chem., 2022, 110, 206–216 CrossRef CAS
.
- E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144 CrossRef PubMed
.
- R. Issa, M. Hmadeh and M. Al-Ghoul, Trans. Tech. Publ., 2017, 380, 39–47 Search PubMed
.
- R. Issa, F. A. Ibrahim, M. Al-Ghoul and M. Hmadeh, Nano Res., 2021, 14, 423–431 CrossRef CAS
.
- R. Zakhia Douaihy, M. Al-Ghoul and M. Hmadeh, Small, 2019, 15, 1901605 CrossRef PubMed
.
- H. Nabika, M. Itatani and I. Lagzi, Langmuir, 2019, 36, 481–497 CrossRef PubMed
.
- A. G. Shtukenberg, Y. O. Punin, E. Gunn and B. Kahr, Chem. Rev., 2012, 112, 1805–1838 CrossRef CAS PubMed
.
- J. B. Dalton and C. L. Schmidt, J. Biol. Chem., 1933, 103, 549–578 CrossRef CAS
.
- T. Lee and Y. K. Lin, Cryst. Growth Des., 2010, 10, 1652–1660 CrossRef CAS
.
- K. Nakamoto and A. E. Martell, J. Chem. Phys., 1960, 32, 588–597 CrossRef CAS
.
- J. Zhou, X. Li, L. Yang, S. Yan, M. Wang, D. Cheng, Q. Chen, Y. Dong, P. Liu and W. Cai, Anal. Chim. Acta, 2015, 899, 57–65 CrossRef CAS PubMed
.
- C. Ziejewska, A. Grela and M. Hebda, Materials, 2023, 16, 2044 CrossRef CAS PubMed
.
-
B. C. Eu and M. Al-Ghoul, Chemical Thermodynamics:
Reversible and Irreversible Thermodynamics, World Scientific, 2017 Search PubMed
.
- M. Dayeh, M. Ammar and M. Al-Ghoul, RSC Adv., 2014, 4, 60034–60038 RSC
.
- M. Al-Ghoul and R. Sultan, Phys. Rev. E, 2019, 100, 052214 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ce00376h |
| This journal is © The Royal Society of Chemistry 2025 |