Dynamic deformation modeling for the interfaces of growth, etching, and deposition under switching flow in TSSG-SiC growth

Abstract

The top-seeded solution growth (TSSG) method is promising for growing high-quality, large-size bulk silicon carbide (SiC) crystals and is being applied in mass production. Quasi-steady global modeling is almost the standard method for optimizing hot-zone and process parameters. For the first time, a transient global model was developed to simulate solution flow, mass transport, and dynamic geometry changes during the TSSG-SiC process. The switching flow condition, achieved through dynamic control of crucible and crystal rotations, was incorporated into the growth simulation. Carbon dissolution, transport, and incorporation were coupled within this transient global modeling. Generalized boundary conditions for growth, etching, and deposition interfaces were implemented to model dynamic interface deformation. Fast crucible rotation induced an inward flow, leading to a large carbon concentration gradient and rapid but non-uniform SiC crystal growth. Conversely, strong crystal rotation generated an outward flow, resulting in homogeneous carbon distribution and slow but uniform SiC crystal growth. Consequently, the carbon transport under switching flow caused periodic fluctuations in growth, etching, and deposition rates. Furthermore, we utilized our transient model to optimize the final crystal shape by adjusting the duration ratio between inward and outward flow periods. This dynamic process modeling enables the optimization and adaptive control of growth conditions for cost-effective TSSG-SiC crystal growth.

---

1. Introduction

Silicon carbide (SiC), a prominent third-generation semiconductor, exhibits exceptional properties including high thermal conductivity, high breakdown voltage, and a wide bandgap.^1,2 These outstanding characteristics enable SiC-based power devices to operate at elevated temperatures, high voltages, and high frequencies, resulting in improved conversion efficiency, reduced size, and simplified cooling systems.³ Notably, the burgeoning electric vehicle market has become a significant driver for the adoption of wide bandgap power devices and electronics based on SiC.⁴

The top-seeded solution growth (TSSG) method for SiC crystals, derived from the Czochralski (CZ) technique, presents a promising alternative to the conventional physical vapor transport (PVT) method. TSSG offers a scalable route to obtaining large-size SiC crystals with superior structural quality.⁵ In TSSG-SiC growth, a graphite crucible serves as both the solution container and the carbon source, facilitating SiC crystal growth by transporting dissolved carbon within a silicon-based solvent to a SiC seed crystal.^6,7 A key advantage of the TSSG method lies in its ability to achieve defect reduction through macrostep propagation, effectively eliminating threading screw dislocations (TSDs) and threading edge dislocations (TEDs) initially present in the seed crystal.^8,9 However, achieving the growth of larger and longer SiC ingots remains a significant challenge due to inherent long-term instabilities in the TSSG-SiC process.^10–12

Over the past decade of conducting SiC crystal growth experiments for various sizes, we have encountered several issues stemming from long-term instability. These include temporal variations in growth rate, a gradual increase in inclusion density, progressive deterioration of macroscopic morphology, and heterocrystalline attachment during later stages. In the TSSG-SiC process, long-term instability primarily arises from two mechanisms: the evolving geometry of the solution domain¹⁰ and the switching flow induced by the rotation of the crucible and seed.¹³ Firstly, the graphite crucible, acting as the carbon source, undergoes continuous etching by the silicon-based solution. Simultaneously, single crystal growth occurs epitaxially on the cooler SiC seed, while polycrystalline SiC may spontaneously nucleate and deposit on the crucible walls. These concurrent phenomena lead to dynamic alterations in the solution domain over time. Secondly, switching flow, characterized by periodic transitions between inward and outward flow beneath the seed crystal, is commonly employed to stabilize step growth and improve crystal morphology. This switching flow pattern is intrinsically coupled with crucible etching, crystal growth, and polycrystal deposition.

However, the majority of existing modeling efforts have focused on hot-zone design, parameter optimization, and the initial effects of seed and crucible rotation.^11,14–21 Few studies have addressed the dynamic geometrical changes through long-term transient modeling. Mukaiyama et al.²² investigated the impact of crucible shape evolution on flow, thermal fields, and carbon transport by analyzing several quasi-steady-state simulations. Employing a similar approach but with shorter time steps, Dang et al.¹⁰ developed an adaptive optimization strategy for the crystal growth rate, crucible etching rate, and polycrystal deposition rate, aided by machine learning. Notably, both of these studies manually imposed deformations of the solution domain for discrete states and then performed steady-state simulations with constant rotation rates.

The present study addresses this gap by focusing on the transient modeling of solution flow, mass transport, and dynamic geometry changes in TSSG-SiC crystal growth under switching flow conditions. Utilizing our 6-inch TSSG-SiC furnace as a basis, we conducted transient global simulations for various flow regimes, including inward flow, outward flow, switching flow, and imbalance switching flow. Carbon dissolution, transport, and incorporation were also fully coupled within this transient global simulation framework.

2. Models and methodology

Fig. 1 schematically illustrates the 6-inch TSSG-SiC furnace employed for both the crystal growth experiments and the corresponding transient global simulations. The system primarily comprises an induction coil assembly, thermal insulation, a graphite crucible, a SiC seed crystal, and the Si–Cr–Al solvent. The graphite crucible serves as the source of carbon and the container for the Si–Cr–Al solvent. It has an inner diameter of 210 mm, and the initial solution depth is 55 mm. For 6-inch crystal growth, the SiC seed crystal has a diameter of 150 mm. A 3 kHz radio-frequency induction heating system is utilized to heat the crucible. During the growth process, the temperature of the SiC seed crystal was maintained at 2153 K by a PID controller under a 1 atm helium atmosphere.

Fig. 1 The schematic of the TSSG-SiC furnace for the growth experiment.

2.1 Transient global modeling of TSSG-SiC

A two-dimensional (2D) transient global model was developed to simulate heat transfer and mass transport throughout the crystal growth process. For simplification, the following assumptions were made: (1) the furnace was axisymmetric; (2) all radiative surfaces were diffuse gray; (3) the solution was incompressible and the Boussinesq approximation was valid; (4) the helium gas within the furnace was ideal and transparent, adhering to the low Mach number approximation; and (5) the carbon concentration within the solution was sufficiently low to neglect solute convection.

The electromagnetic field generated by the induction coils was calculated using the COMSOL Multiphysics package to determine the heat generation density and Lorentz force density, thereby establishing the temperature distribution throughout the system. Subsequently, the flow and concentration fields were computed, incorporating dynamic geometry changes. The electromagnetic field solution was integrated into the transient global model as the Lorentz force term in the momentum equation and the heating source in the heat transfer equation. The governing equations, including the continuity, momentum, and heat transfer equations, were solved using the finite element method (FEM).²¹ Considering that the turbulence feature of the solution flow in 6-inch TSSG-Si growth, the low-Reynolds number k-ε model is used in this study.

2.2 Mass transport and chemical model

The carbon transport is dominated by the turbulent solution flow. Thus, the carbon conservation equation in solution is as follows:

The equilibrium molar concentration of carbon was applied for the boundary condition at the crystal–solution and crucible–solution interfaces as

where ρ is the density of solution, M_C is the molar weight of carbon, ω_eq is the equilibrium mass fraction of carbon.

For the carbon solubility in a Si-40 mol% Cr system, the temperature dependence of the carbon solubility was calculated by using the following expression:¹⁰

ω_eq = exp (3.924 − 19 255/T). (3)

Zero-flux condition was applied for the boundary condition at the gas–solution interface as

∇C·n = 0.

2.3 The generalized boundary condition for dynamic deformations

To accurately predict dynamic deformation, generalized boundary conditions were implemented based on the carbon fluxes at the seed–solution and crucible–solution interfaces. Fig. 2 illustrates the schematic representation of these generalized boundary conditions and the resulting deformations of the solution domain.

Fig. 2 The generalized boundary conditions and deformations of the solution domain.

The carbon flux was calculated as

J = D∇C·n, (4)

where is the unit normal vector of the local interfaces.

Since the equilibrium carbon concentration is a function of temperature, the reaction direction depends on the normal temperature gradient at the solution domain interface. When the normal temperature gradient is positive, indicating that the solid is hotter than the solution, carbon dissolves from the interface. Conversely, when the normal temperature gradient is negative, indicating that the solid is colder than the solution, SiC grows at the seed–solution interface or deposits at the solution–crucible interface. If carbon dissolves from the interface, the solution domain expands towards the solid. Conversely, if carbon is absorbed by the interface, the solid domain encroaches upon the solution domain.

We could assume the normal deformation:

Δl = V_dΔt. (5)

Case 1: if ∂T/∂n ≥ 0, then the etching reaction proceeds [C(s) ⇒ C(l)], which means C^s_eq ≥ C, so the deformation rate is

V_d = J/ρ_c. (6)

Case 2: if ∂T/∂n < 0, then the growth or deposition reaction proceeds [Si + C ⇒ SiC], which means C^s_eq < C, so the deformation rate is

where α is the growth rate parameter. Polycrystalline precipitates form more readily than single SiC crystals. Consequently, we assigned a growth rate coefficient (α) of 0.22 to the SiC seed and 1.9 to the crucible wall, values determined through fitting to our growth experiments.

3. Results and discussion

Given that heat and carbon transport are predominantly governed by turbulent solution flow, the flow pattern exerts a decisive influence on TSSG-SiC crystal growth. The flow pattern is controlled by varying the crystal and crucible rotation rates. Utilizing a PID controller to regulate the coil current, a temperature of 2153 K was maintained at the center of the seed holder.

3.1 The growth mode comparison between inward and outward flow

Inward flow was generated by rapid crucible rotation, whereas outward flow was induced by strong crystal rotation. For the inward flow condition, the crystal rotation was set to 0.1 rpm and the crucible rotation to −25 rpm. Conversely, for the outward flow condition, the crystal rotation was set to 40 rpm and the crucible rotation to −5 rpm. In the inward flow case, illustrated in the left section of Fig. 3(a), the vortex above the bottom wall became significantly stronger and extended towards the growth interface due to the higher crucible rotation rate of −25 rpm and the lower crystal rotation rate of 0.1 rpm. As observed in the left section of Fig. 3(a), the velocity magnitude exhibited a clear radial gradient, indicating that crucible rotation dominated the flow throughout the solution zone. In essence, the circumferential flow generated by crucible rotation was the dominant flow pattern relative to the inward flow in the r–z plane. Fundamentally, rapid crucible rotation was utilized to suppress turbulent solution flow. This weak inward flow pattern influenced the heat transport and temperature distribution, as depicted in the right section of Fig. 3(a). The temperature distribution was primarily governed by thermal diffusion rather than solution convection, resulting in a steep radial temperature gradient. The temperature difference within the solution domain was approximately 2.7 K.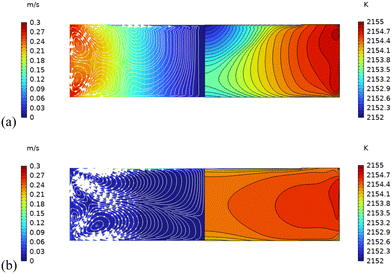

Fig. 3 Flow and thermal fields controlled by the crucible and seed rotations. (a) Inward flow and (b) outward flow.

In the outward flow case, illustrated in the left section of Fig. 3(b), crystal rotation dominated the flow beneath the growth interface due to the high rotation rate of 40 rpm. An outward flow, directed from the center to the periphery, was generated under the SiC seed. This outward vortex occupied nearly half of the solution domain, while smaller vortices, induced by the Lorentz force and crucible rotation, were confined to the lower left corner of the solution domain. The velocity magnitude contour revealed that the circumferential flow generated by crystal rotation affected only a limited region, contrasting with the inward flow case. The outward flow in the r–z plane governed the solution flow and resulted in convection-dominated heat transport within the solution. Consequently, a homogeneous temperature distribution with a small temperature difference of 1.0 K was observed in the right section of Fig. 3(b).

The temperature distribution surrounding the solution domain influences carbon dissolution and incorporation, while the flow patterns primarily govern carbon transport within the solution. Fig. 4(a) and (b) illustrate the carbon concentration and supersaturation distributions in the solution domain for the inward and outward flow conditions, respectively. The carbon supersaturation S in the solution, which indicates the carbon precipitation (S > 0) or carbon dissolution (S < 0), is defined as follows:

S = (C − C_eq)/C_eq. (8)

Fig. 4 Carbon concentrations and supersaturation distributions. (a) Inward flow and (b) outward flow.

Consistent with the thermal transport characteristics depicted in Fig. 3, dissolved carbon was transported from the crucible wall towards the crystallization zone beneath the seed during inward flow, as shown in the left section of Fig. 4(a). The supersaturation distribution, illustrated in the right section, revealed high levels beneath the seed and above the bottom wall, indicating regions favorable for SiC formation. Notably, the steep radial carbon gradient beneath the seed could negatively impact the radial uniformity of the growth rate.

Under the outward flow conditions, carbon dissolved from the crucible was efficiently transported and thoroughly mixed within the solution. The carbon concentration contour in Fig. 4(b) illustrates this homogeneous distribution. In particular, the shallow carbon gradient beneath the seed could result in a weak growth driving force. The supersaturation distribution, depicted in the right section, revealed lower levels beneath the seed compared to the inward flow case.

A comparison of the growth modes under inward and outward flow conditions is presented by plotting the respective growth rates in Fig. 5. The outward flow, generated by strong crystal rotation, yielded homogeneous thermal and carbon distributions, leading to slow but uniform SiC crystal growth. Conversely, the inward flow, driven by rapid crucible rotation, resulted in steeper thermal and carbon gradients and consequently, fast but non-uniform SiC crystal growth. The average growth rate under inward flow was approximately twice that observed under outward flow. However, due to the limited penetration of the inward flow towards the central region of the growth interface, the significantly lower growth rate in this area poses a challenge for long-term, uniform SiC crystal growth.

Fig. 5 The growth rate distributions of inward flow and outward flow.

3.2 Dynamic deformation predictions for different flow conditions

Utilizing the transient global model with generalized boundary conditions for dynamic deformation, we were able to predict the temporal evolution of the solution domain geometry resulting from crystal growth, crucible etching, and polycrystal deposition. Concurrently, the thermal and flow fields dynamically interacted with these geometric changes throughout the entire growth process. Initially, dynamic deformation modeling was performed for both outward and inward flow conditions over a duration of 60 hours. Based on their distinct growth modes, inward and outward flow patterns led to different deformation characteristics at the growth, etching, and deposition interfaces.

The initial and final thermal fields for the inward and outward flow conditions are presented in Fig. 6(a) and (b), respectively. Dynamic deformations were predicted at the seed–solution, sidewall–solution, and bottom wall–solution interfaces, corresponding to growth, etching, and deposition processes. Owing to the larger initial temperature difference under the inward flow condition, the total deformations over 60 hours, encompassing growth height, etching depth, and deposition thickness, were more pronounced than in the outward flow scenario. As a consequence of the solution domain shrinkage, the temperature difference decreased by 0.2 K for both inward and outward flow from 0 to 60 hours. Conversely, the maximum temperature within the solution domain increased by 0.2 K for both flow conditions due to the geometric changes occurring during the 60-hour period. Furthermore, the growth temperature beneath the seed increased by 0.4 K due to the increase in crystal thickness.

Fig. 6 Thermal fields in solution and crystal domains for 0 h (left) and 60 h (right). (a) Inward flow condition and (b) outward flow condition.

The initial and final supersaturation distributions for the inward and outward flow conditions are presented in Fig. 7(a) and (b), respectively. Despite the changes in the solution domain after 60 hours of growth, the characteristic supersaturation distributions for both flow conditions were largely retained. As the driving force for growth, etching, and deposition, these distinct supersaturation distributions along the deforming interfaces resulted in the different interface morphologies observed for the inward and outward flow conditions. Negative supersaturation values led to etching along the sidewall, while positive supersaturation values promoted growth at the seed–solution interface or deposition at the bottom wall–solution interface. The crucible sidewalls underwent etching by the solution flow, resulting in a concave shape. Concurrently, polycrystalline SiC was deposited on the bottom wall, forming convex deposition layers. These final geometric changes are illustrated in the right sections of Fig. 7(a) and (b). In contrast, the degree of deformation was greater under inward flow compared to outward flow, which exhibited a significantly more homogeneous supersaturation distribution.

Fig. 7 Supersaturation distribution in the solution domain for 0 h (left) and 60 h (right). (a) Inward flow condition and (b) outward flow condition.

The mean growth rate along the growth interface over 60 hours is plotted in Fig. 8 for both inward and outward flow conditions. The time-averaged growth rate was 45.8 μm h⁻¹ for inward flow growth and 21.7 μm h⁻¹ for outward flow growth. Although the growth rates fluctuated over time, no clear increasing or decreasing trend was observed within the 60-hour duration for either flow condition. This may be attributed to the limited fraction of carbon atoms that can effectively incorporate into the SiC crystal at the seed interface.

Fig. 8 Mean radial growth rate for 60 hours of growth.

Following similar calculation procedures to determine the time-averaged growth rate, we derived the time-averaged etching rate and deposition rate. The time-averaged etching rate was 123.1 μm h⁻¹ for inward flow etching and 84.3 μm h⁻¹ for outward flow etching, values influenced by the flow pattern and temperature difference within the solution. The time-averaged deposition rate was 41.0 μm h⁻¹ for inward flow deposition and 2.9 μm h⁻¹ for outward flow deposition. The significantly lower deposition rate under outward flow indicates a smaller supersaturation along the bottom wall.

3.3 Effect of switching flow conditions on long-time growth

The implementation of switching flow has been demonstrated to improve step morphology.¹³ To enhance the stability of step growth, inward and outward flow conditions are periodically alternated. As discussed in sections 3.1 and 3.2, inward and outward flow patterns exhibit distinct growth modes. This suggests that the effectiveness of switching flow is also contingent upon its parameter settings, such as the switching period, phase duration, and transition time. We investigated two switching flow rotation schemes, as depicted in Fig. 9(a) and (b): a normal scheme with equal phase durations for inward and outward flow, and an imbalanced scheme featuring a shorter inward flow duration and a longer outward flow duration. The switching period was set to 360 seconds, with a transition time of 30 seconds.

Fig. 9 Rotation scheme of the crystal and crucible to create switching flow: (a) the normal switching flow and (b) the imbalance switching flow.

To facilitate comparison across different conditions, we also conducted transient global simulations for the 60-hour growth process. The mean growth rates for four cases, including switching flow, imbalanced flow, inward flow, and outward flow, are plotted in Fig. 10 for two periods of switching flow. The mean growth rates under switching flow and imbalanced flow fluctuated between the values observed for pure outward and inward flow conditions, occasionally falling outside this range. In the imbalanced flow case, one-third of the growth period involved inward flow, while two-thirds involved outward flow. Consequently, the imbalanced flow exhibited a low growth rate for approximately 240 seconds, in contrast to the 180-second duration observed in the switching flow. This resulted in a higher time-averaged growth rate for switching flow (32.6 μm h⁻¹) compared to imbalanced flow (24.7 μm h⁻¹). Given the growth rate disparity between inward and outward flow, the imbalanced flow could ensure that approximately half of the grown SiC ingot experienced inward flow, while the other half experienced outward flow. This revised switching flow scheme (the imbalanced flow) may be advantageous for achieving improved uniformity of step morphology during long-term growth runs.

Fig. 10 Comparison of mean growth rates in two periods.

Fig. 11(a)–(c) compare the final growth, etching, and deposition interface shapes for all four cases, respectively. Inward flow resulted in the thickest ingot with a maximum thickness of 3.7 mm, while outward flow ensured a uniform radial growth rate but yielded the thinnest ingot with a maximum length of 1.8 mm (Fig. 11(a)). Consequently, switching flow conditions represent a potential compromise between rapid and uniform growth. Notably, in addition to promoting more stable growth, the imbalanced switching flow produced a significantly flatter growth interface compared to conventional switching flow. Therefore, different flow patterns can influence the growth process by modulating the growth rate and interface morphology.

Fig. 11 Comparison of final growth, etching and, deposition interface shapes: (a) the growth interfaces after 60 h; (b) the crucible sidewall shapes after 60 h; (c) the bottom deposition shapes after 60 h.

The mean etching and deposition rates also fluctuated between the outward flow phase and the inward flow phase, mirroring the behavior of the mean growth rate. The corresponding final etching and deposition interface shapes in Fig. 11(b) and (c) exhibited similar trends. The highest growth rate under inward flow led to the greatest etching depth and the thickest deposition layer, and conversely. Thus, a shorter inward flow phase, as implemented in the imbalanced flow scheme, could potentially prolong the crucible lifetime while maintaining moderate growth, etching, and deposition rates.

4. Conclusions

A transient global model was developed for the first time to simulate induction heating, heat transport, and turbulent solution flow. Carbon dissolution, transport, and incorporation were also coupled within this transient simulation framework. We implemented generalized boundary conditions for the growth, etching, and deposition interfaces to enable dynamic deformation modeling, where the normal direction of interface deformation was determined by the carbon flux. This approach allowed us to predict the time-varying growth rates under inward flow, outward flow, switching flow, and imbalanced switching flow conditions. Our findings indicate that switching flow can combine the advantages of both inward and outward flow conditions. Furthermore, imbalanced switching flow can yield a flatter growth interface compared to conventional switching flow. The visualization of the entire growth process provided by this model suggests that the optimization and adaptive control of growth conditions will become more accessible and cost-effective for the production of large-diameter TSSG-SiC crystals.

Data availability

The data that support the findings of this study are available from the corresponding author, Xin Liu, upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by New Energy and Industrial Technology Development Organization (NEDO), Grant No. 20240000000429 (2020-2024).

References

1. G. Iannaccone, C. Sbrana, I. Morelli and S. Strangio, Power Electronics Based on Wide-Bandgap Semiconductors: Opportunities and Challenges, IEEE Access, 2021, 9, 139446–139456.
2. A. Kumar, M. Moradpour, M. Losito, W.-T. Franke, S. Ramasamy, R. Baccoli and G. Gatto, Wide Band Gap Devices and Their Application in Power Electronics, Energies, 2022, 15, 9172.
3. K. Tsunenobu and C. James, Physical Properties of Silicon Carbide, in Fundamentals of Silicon Carbide Technology, 2014, pp. 11–38.
4. F. Di Giovanni, Silicon Carbide: Physics, Manufacturing, and Its Role in Large-Scale Vehicle Electrification, Chips, 2023, 2, 209–222.
5. G.-Q. Liang, H. Qian, Y.-L. Su, L. Shi, Q. Li and Y. Liu, Review of solution growth techniques for 4H-SiC single crystal, China Foundry, 2023, 20, 159–178.
6. D. H. Hofmann and M. H. Müller, Prospects of the use of liquid phase techniques for the growth of bulk silicon carbide crystals, Mater. Sci. Eng., B, 1999, 61–62, 29–39.
7. M. Syväjärvi, R. Yakimova and E. Janzén, Interfacial Properties in Liquid Phase Growth of SiC, J. Electrochem. Soc., 1999, 146, 1565.
8. K. Murayama, T. Hori, S. Harada, S. Xiao, M. Tagawa and T. Ujihara, Two-step SiC solution growth for dislocation reduction, J. Cryst. Growth, 2017, 468, 874–878.
9. S. Harada, Y. Yamamoto, K. Seki, A. Horio, T. Mitsuhashi, M. Tagawa and T. Ujihara, Evolution of threading screw dislocation conversion during solution growth of 4H-SiC, APL Mater., 2013, 1, 022109.
10. Y. Dang, C. Zhu, M. Ikumi, M. Takaishi, W. Yu, W. Huang, X. Liu, K. Kutsukake, S. Harada, M. Tagawa and T. Ujihara, Adaptive process control for crystal growth using machine learning for high-speed prediction: application to SiC solution growth, CrystEngComm, 2021, 23, 1982–1990.
11. Y. Dang, C. Zhu, X. Liu, W. Yu, X. Liu, K. Suzuki, T. Furusho, S. Harada, M. Tagawa and T. Ujihara, Numerical investigation of solute evaporation in crystal growth from solution: A case study of SiC growth by TSSG method, J. Cryst. Growth, 2022, 579, 126448.
12. K. Kutsukake, Review of machine learning applications for crystal growth research, J. Cryst. Growth, 2024, 630, 127598.
13. C. Zhu, S. Harada, K. Seki, H. Zhang, H. Niinomi, M. Tagawa and T. Ujihara, Influence of Solution Flow on Step Bunching in Solution Growth of SiC Crystals, Cryst. Growth Des., 2013, 13, 3691–3696.
14. Y. Liu, M. Li, Z. Yan, X. Qi, W. Ma, J. Chen, Y. Xu and Z. Hu, Effects of coil frequency on the carbon transport in the top-seeded solution growth of SiC single crystal, J. Cryst. Growth, 2024, 643, 127801.
15. M.-T. Ha and S.-M. Jeong, A review of the simulation studies on the bulk growth of silicon carbide single crystals, J. Korean Ceram. Soc., 2022, 59, 153–179.
16. W. Yu, C. Zhu, Y. Tsunooka, W. Huang, Y. Dang, K. Kutsukake, S. Harada, M. Tagawa and T. Ujihara, Geometrical design of a crystal growth system guided by a machine learning algorithm, CrystEngComm, 2021, 23, 2695–2702.
17. L. Wang, A. Sekimoto, Y. Takehara, Y. Okano, T. Ujihara and S. Dost, Optimal Control of SiC Crystal Growth in the RF-TSSG System Using Reinforcement Learning, Crystals, 2020, 10, 791.
18. M.-T. Ha, L. V. Lich, Y.-J. Shin, S.-Y. Bae, M.-H. Lee and S.-M. Jeong, Improvement of SiC Crystal Growth Rate and Uniformity via Top-Seeded Solution Growth under External Static Magnetic Field: A Numerical Investigation, Materials, 2020, 13(3), 651.
19. L. Wang, T. Horiuchi, A. Sekimoto, Y. Okano, T. Ujihara and S. Dost, Numerical investigation of the effect of static magnetic field on the TSSG growth of SiC, J. Cryst. Growth, 2018, 498, 140–147.
20. B. Liu, Y. Yu, X. Tang and B. Gao, Optimization of crucible and heating model for large-sized silicon carbide ingot growth in top-seeded solution growth, J. Cryst. Growth, 2020, 533, 125406.
21. Z. Sui, L. Xu, C. Cui, R. Wang, X. Pi, D. Yang and X. Han, Effects of solution height and crystal rotation on the solution flow behavior in the top-seeded solution growth of SiC single crystals, CrystEngComm, 2024, 26, 1022–1031.
22. Y. Mukaiyama, M. Iizuka, A. Vorob'ev and V. Kalaev, Numerical investigation of the effect of shape change in graphite crucible during top-seeded solution growth of SiC, J. Cryst. Growth, 2017, 475, 178–185.

---