Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Control of crystal size distribution in continuous cooling crystallization using non-isothermal Taylor vortex†
Zun-Hua
Li‡
a,
Zhao-Hui
Wu‡
 b,
Gerard
Coquerel
*c,
Bum Jun
Park
b,
Gerard
Coquerel
*c,
Bum Jun
Park
 *d and
Woo-Sik
Kim
*d and
Woo-Sik
Kim
 *d
*d
aHunan Engineering Technology Research Center for Comprehensive Development and Utilization of Biomass Resources, College of Chemistry and Bioengineering, Hunan University of Science and Engineering, 425199 Yongzhou, Hunan, China
bHunan Key Laboratory of Applied Environmental Photocatalysis, Changsha University, Changsha 410022, Hunan, China
cSMS Laboratory UR3233, University of Rouen Normandy, F-76000 Rouen, France. E-mail: gerard.coquerel@univ-rouen.fr
dFunctional Crystallization Center, Department of Chemical Engineering (BK21 FOUR, Integrated Engineering Program), College of Engineering, Kyung Hee University, Yongin-si 17104, Republic of Korea. E-mail: bjpark@khu.ac.kr; wskim@khu.ac.kr
First published on 21st April 2025
Abstract
The establishment of a non-isothermal Taylor vortex flow within a Couette–Taylor (CT) crystallizer, achieved by applying varying temperatures to the inner and outer cylinders, facilitates precise regulation of the crystal size distribution (CSD) during continuous cooling crystallization. This methodology transforms initially generated crystals into a suspension characterized by a narrow CSD through the implementation of internal heating and cooling cycles. The efficacy of this process, particularly concerning L-lysine crystals, is influenced by the temperature gradient, the flow direction between the cylinders, and specific non-isothermal parameters. Under optimal conditions, which include a temperature difference of 18.1 ± 0.2 °C, a rotational speed of 200 rpm, and an average residence time of 2.5 minutes, the non-isothermal Taylor vortex has been shown to effectively reduce the CSD by promoting dissolution-recrystallization cycles.
1. Introduction
Crystal size distribution (CSD) serves as a pivotal factor influencing the quality of crystals in both industrial and pharmaceutical contexts. The CSD affects a range of subsequent processes, including filtration, drying, and the washing of crystals, in addition to impacting the efficacy and performance of solid products.1–3 Consequently, meticulous regulation of CSD is crucial for achieving the intended quality of crystalline products.The regulation of CSD during crystallization can be accomplished through the manipulation of supersaturation or concentration profiles.4–6 Various strategies, including seeded crystallization, programmed concentration profiles, and non-isothermal methods are effective in controlling CSD within batch crystallization processes.7–10 A prevalent approach involves the integration of non-isothermal techniques with seeded strategies to manage both CSD and crystal size during cooling crystallization.11–14 For instance, the implementation of successive dissolution–recrystallization cycles facilitates the attainment of a uniform CSD in the suspension, as demonstrated in the cooling crystallization of potash alum in aqueous solutions.15 Furthermore, in the crystallization of paracetamol utilizing automated direct nucleation control (ADNC), the application of heating and cooling cycles serves to eliminate undesirable fine crystals and mitigate secondary nucleation, thereby ensuring a consistent and targeted CSD throughout the ADNC process.12
The efficacy of the non-isothermal method in batch cooling crystallization is contingent upon various operational parameters, including the quantity and size of seeds, heating and cooling rates, and the number of cycles employed.16–18 Accurate adjustment of these parameters is essential for attaining the desired CSD. Typically, this technique necessitates a minimum duration of 30 hours in batch crystallization to reach the targeted CSD. Conversely, continuous crystallization utilizing the non-isothermal approach presents several productivity advantages, such as reduced crystallization times, the absence of scale-up difficulties, and lower manufacturing costs, as initially proposed by Saeman.19–21 This continuous crystallization technique fundamentally relies on dissolution–recrystallization cycles, which incorporate size-classification devices for the withdrawal of crystals and an additional dissolver. Excess fine crystals from the withdrawn suspension are completely dissolved back into the solution and recirculated into the crystallizer for further recrystallization. This simultaneous dissolution–recrystallization process for the removal of fines in a continuous mixed suspension allows the nucleus segregation time during size control procedures to be adjusted between 10 and 20 minutes. By employing a combination of drowning-out with fines dissolution and cooling crystallization (DFC), larger 1,3,5-trinitro-1,3,5-triazinane crystals with enhanced yields were produced in a double-jacketed glass crystallizer within a timeframe of 55 minutes. The DFC method has been recognized as effective in improving both crystal size and CSD when compared to crystals produced solely through the drowning-out method.22
Additionally, Majumder and Nagy investigated the control of CSD for potash alum in water by utilizing an optimal temperature profile within a continuous plug flow crystallizer (PFC) comprising multiple segments. Their findings indicated that it is feasible to replicate a programmed cooling process characteristic of batch crystallization within the continuous PFC framework. By optimizing the temperatures of the segments, they successfully achieved a targeted CSD while minimizing the presence of fine crystals through dissolution steps. The simulated CSD corresponded closely with the experimental CSD, thereby validating the fines removal strategy.23 Nonetheless, the precise control of process parameters imposes limitations on the flexibility and scalability of this PFC continuous crystallizer for industrial applications.
The non-isothermal method employing simultaneous heating and cooling cycles has demonstrated efficacy in regulating CSD during continuous crystallization processes. However, its implementation in various continuous crystallizers remains infrequent, primarily due to challenges associated with execution and process management. Key parameters such as supersaturation, residence time, and mixing intensity are essential for achieving the desired CSD in continuous cooling or antisolvent crystallization.24–28 Nevertheless, the impact of these parameters on the nucleation process in continuous crystallization utilizing non-isothermal techniques has not been thoroughly investigated. Consequently, we propose a versatile non-isothermal approach that incorporates simultaneous heating and cooling within a continuous Couette–Taylor (CT) crystallizer to enhance the control of L-lysine CSD in a reduced timeframe. By generating a non-isothermal Taylor vortex fluid motion between inner and outer cylinders maintained at different temperatures, we aim to improve the regulation of CSD. This methodology capitalizes on the advantages of Taylor vortex flow in facilitating heat and mass transfer,29–31 and the non-isothermal Taylor vortex represents a promising strategy for managing CSD in seeded batch crystallization.32,33 This study aims to explore the potential of this technique for effective CSD and crystal size regulation of L-lysine, while also examining the operational mechanisms and influential parameters associated with this non-isothermal continuous Taylor vortex system featuring a simultaneous heating–cooling cycle for dissolution and recrystallization processes.
2. Experiments
The configuration of a CT crystallizer, characterized by two coaxially arranged stainless steel cylinders with an interstitial gap for continuous cooling crystallization, is depicted in Fig. 1(a). The crystallizer exhibited a length of 30 cm, with the inner and outer cylinder radii measuring 2.4 and 2.8 cm, respectively. Additionally, the interstitial space between the inner and outer cylinders was recorded at 0.4 cm. In this CT crystallizer, the rotation of the inner cylinder above a certain threshold, combined with the axial flow of the feed solution, facilitates a continuous Taylor vortex fluid motion within the gap. Each cylinder is equipped with thermal jackets, allowing for independent temperature regulation. When the temperatures of both cylinders are equal, an isothermal continuous Taylor vortex flow is established. Conversely, when the cylinders are maintained at different temperatures, a non-isothermal continuous Taylor vortex flow is generated within the gap of the CT crystallizer. In this scenario, one cylinder is heated to a high temperature (Th) to elevate the temperature of the bulk solution, while the other is maintained at a lower temperature (Tc) to induce cooling. This arrangement permits two distinct non-isothermal operational modes: one in which the inner cylinder serves as the heating source (Tih) and the outer cylinder functions as the cooling source (Toc), and another mode with the temperature roles reversed. Furthermore, by meticulously adjusting the heating and cooling temperatures of the cylinders in these non-isothermal modes, a temperature difference (ΔT = Th − Tc) is established between the two cylinders and the bulk solution temperature (Tb) within the CT crystallizer. | ||
| Fig. 1 (a) Schematic diagram of the CT crystallizer configuration. (b) Experimental setup for implementing the non-isothermal approach in the CT crystallizer. | ||
A feed solution of L-lysine with a concentration of 900 g L−1 was formulated by dissolving L-lysine in deionized water at a saturation temperature of 43 °C. The temperature of the solution was subsequently elevated to 50 °C to ensure complete dissolution before its utilization as the feeding solution. In the CT crystallizer (Fig. 1(b)), which was initially filled with pure deionized water, the temperatures of both cylinders were maintained at 28 °C, thereby establishing a uniform bulk solution temperature (Tb). During this phase, with the cylinder temperatures equal to Tb, the CT crystallizer underwent a pre-operational period lasting 20 minutes. Following this, the L-lysine feed solution was continuously introduced into the CT crystallizer at a designated flow rate (corresponding to a mean residence time) and a specified rotation speed until a steady state was achieved. To systematically assess the performance of the isothermal CT crystallizer, the Tb, mean residence time, and rotation speed were varied within the ranges of 20 to 32 °C, 2.5 to 15 minutes, and 200 to 900 rpm, respectively. In non-isothermal modes, a temperature difference (ΔT) between the two cylinders was established by incrementally increasing the temperature of one cylinder while concurrently decreasing that of the other, all while maintaining a Tb of 28 °C. Furthermore, the ΔT value varied from 0 to 18.1 °C, with adjustments made to the mean residence time and rotation speed from 2.5 to 15 minutes and from 200 to 900 rpm, respectively. The temperatures within the non-isothermal CT crystallizer were estimated based on the heat transfer dynamics between the heating and cooling surfaces of the cylinders and the bulk solution, as detailed in the Appendix.
The temperatures of both the inner and outer cylinders, as well as the temperature at the axial position of the CT crystallizer, were continuously monitored using temperature sensors (TMP119, Texas Instruments, Dallas, Texas, USA) and recorded in situ via the LabVIEW software (National Instruments, USA). During the steady-state phase of each experiment, a predetermined volume of crystal suspension was extracted from four distinct ports along the axial direction of the CT crystallizer for crystal size analysis. The CSD of the suspension was examined utilizing a video microscope (IT system, Sometech, USA). Subsequently, the lengths of over 500 crystals captured in the images were quantified using size measurement software (Xojo Binary Project, Xojo Inc., USA). The coefficient of variation (CV) for the crystal was determined utilizing the methodology established by Mullin.34 The focused beam reflectance measurement (FBRM) instrument (FBRM G400, Mettler Toledo, Columbus, OH, USA) was utilized to conduct continuous monitoring of both the crystal size and numbers. The FBRM probe was directly incorporated into the CT crystallizer. Throughout the experiment, the crystal size and numbers within the CT crystallizer were recorded at intervals of 10 seconds.
3. Results and discussion
3.1 Schematic illustration of non-isothermal CT crystallizer
As depicted in Fig. 2, the continuous crystallization process in the CT crystallizer employs the initial driving force for nucleation alongside an internal heating–cooling cycle to promote concurrent dissolution and recrystallization. The process begins with the feed solution (point B), which is at a saturated concentration (C0) and temperature (Ts), being heated to a higher temperature (T0, point A) to ensure complete dissolution. This solution is then continuously introduced into the CT crystallizer, where it attains a bulk solution temperature (Tb, point O) that lies between the heating (Td) and cooling (Tr) temperatures. The substantial supersaturation generated between the initial concentration and the bulk solution (ΔC = C0 − Cb) rapidly induces nucleation, and by application of the lever rule the maximum yield could be computed. The newly formed crystals are subjected to periodic circulation between the heating and cooling cylinders, gradually progressing towards the discharge point of the CT crystallizer. During this transit, crystals dissolve at the boundary layer of the heating cylinder (Td), which increases the solution's concentration from Cb to Cd (point C), thereby facilitating the dissolution of particularly fine crystals (route ‘b’). This concentrated solution is subsequently directed to the boundary layer of the cooling cylinder (Tr, point D) for recrystallization (route ‘a’), effectively utilizing the elevated concentration to achieve a new equilibrium at the lower temperature (Tr). The cyclic heating and cooling dynamics, driven by the temperature difference (ΔT = Td − Tr) within the CT crystallizer, proficiently modulate the CSD by systematically disintegrating fine crystals while promoting the growth of the remaining ones. Consequently, the regulation of CSD through the non-isothermal Taylor vortex is influenced by various factors, including ΔT, the non-isothermal operational modes, Tb, mean residence time, and rotation speed. | ||
| Fig. 2 Schematic representation of the internal heating–cooling cycle in the non-isothermal Taylor vortex during continuous cooling crystallization. | ||
3.2 Comparison between non-isothermal and isothermal modes
This study examines the effects of two non-isothermal modes in conjunction with an isothermal mode on the CSD at various axial positions within the CT crystallizer, as depicted in Fig. 3. Non-isothermal mode-I utilized the inner cylinder (Ti) for heating and the outer cylinder (To) for cooling (Ti > To), whereas non-isothermal mode-II employed the opposite configuration (Ti < To). Fig. 3(a) presents the experimental results obtained under non-isothermal mode-I, revealing a distinct trend. At port 1, the number of crystals reaches its maximum, accompanied by a wide CSD; however, the mean crystal size remains relatively small. As one moves axially through the CT crystallizer towards port 2, there is a significant reduction in the number of crystals, while the CSD gradually narrows. Simultaneously, the mean crystal size shows a corresponding increase. This trend continues through the subsequent ports, culminating at port 4, where the crystal number is at its lowest across the entire CT crystallizer, the CSD is most concentrated, and the crystal size is at its maximum.Further analysis of the data depicted in Fig. 3(b) and (c) indicate that in both non-isothermal mode-II and isothermal mode, the changes in crystal number, mean crystal size, and CSD closely resemble those observed in non-isothermal mode-I. Specifically, across various ports along the axial direction of the CT crystallizer, the crystal number generally exhibits a decreasing trend, while the mean crystal size progressively increases and the CSD narrows. Nonetheless, a thorough examination of the three crystallization modes reveals a consistent pattern: regardless of the port, non-isothermal mode-II consistently produces the highest crystal number. In contrast, although the isothermal mode does not yield the highest crystal number, it is characterized by the largest mean crystal size and an exceptionally broad CSD. This observation underscores significant variations in crystal growth behavior associated with different crystallization patterns, providing valuable experimental insights for the optimization of future crystallization processes. A comprehensive understanding of these variations facilitates the targeted selection and modification of crystallization patterns to meet specific requirements regarding crystal number, mean crystal size, and CSD across various application contexts, ultimately enhancing the quality and performance of crystallization products.
Moreover, the mean crystal size (Fig. 4(a)) and the CV (Fig. 4(b)) were employed to assess the dimensions and dispersity of the CSD within the crystal suspension. In both non-isothermal modes, an increase in mean crystal size and a reduction in CV were observed along the axial length of the CT crystallizer. Specifically, in non-isothermal mode-I, the mean crystal size increased from 33.0 μm at port-I to 64.1 μm at port-IV, with the CV decreasing from 0.4977 to 0.3283. In non-isothermal mode-II, the mean crystal size progressed from 30.9 μm with a CV of 0.5465 to a mean crystal size of 59.0 μm and a CV of 0.4634. A similar pattern was observed in the isothermal mode, where the mean crystal size increased from 44.9 μm to 67.0 μm, and the CV exhibited a slight decrease from 0.5845 to 0.5046 along the axial position of the CT crystallizer.
The results of this study reveal that the crystal size in isothermal crystallization modes is larger than that observed in non-isothermal modes. Additionally, the isothermal mode demonstrates a higher CV, suggesting the presence of a substantial quantity of fine crystals. This finding appears to present a paradox. The underlying reasons for this phenomenon can be explained as follows. The differences between isothermal and non-isothermal crystallization processes can be understood through the dynamic interactions of nucleation and growth, as well as the mechanisms that regulate supersaturation levels. In the isothermal mode, the maintenance of a constant temperature leads to elevated initial supersaturation, which triggers a significant amount of instantaneous nucleation, resulting in the formation of fine crystals. However, as the solute becomes depleted, the growth rate is limited due to the decreasing supersaturation, leading to a polydisperse system characterized by the coexistence of both large and fine crystals. This situation results in an increased mean crystal size alongside a heightened CV. Furthermore, the elevated concentration of the solution indicates that a portion of the solute remains unconverted into crystalline form, reflecting low yield and inadequate growth.
In contrast, the non-isothermal mode maintains dynamic supersaturation through temperature fluctuations, which promotes the continuous growth of pre-existing crystals while inhibiting the formation of new nuclei, thereby suppressing secondary nucleation. As a result, this mode yields larger crystal sizes and a more uniform distribution, as evidenced by a lower CV, while the decrease in solution concentration indicates improved solute conversion efficiency. The essence of this seemingly contradictory phenomenon lies in the fact that the static supersaturation distribution characteristic of isothermal modes fosters a nucleation-dominated “burst-arrest” mechanism, whereas the dynamic regulation inherent to non-isothermal modes enables a growth-dominated “gradual optimization” process, guided by thermodynamic principles.
Furthermore, the crystal numbers were measured using FBRM, as shown in Fig. 4(c). The findings demonstrate a consistent pattern across these three modes: at port-I within the CT crystallizer, a significant quantity of fine crystals undergo nucleation. As the suspension moves in a retrograde direction within the CT crystallizer, the fine crystals progressively dissolve on the heating boundary layer, whereas the larger crystals situated on the cooling boundary layer continue to undergo growth, increasing their dimensions. Consequently, along the axial length of the CT crystallizer, there is a gradual reduction in the number of crystals, accompanied by a corresponding increase in mean crystal size and a decrease in CV, a phenomenon that is effectively depicted in Fig. 4(a) and (b). This suggests that the persistence of supersaturation and the rapid growth of smaller crystals in the supersaturated solution are characteristics common to continuous cooling crystallization processes.
In addition, the simulated Tb in all operational modes exhibited a rapid decline from the initial feeding temperature to the designated Tb, with temperature measurements at each port (red points) corroborating the precision of the temperature simulation (Fig. 5). This observation suggests a heightened level of supersaturation at the initial feeding port, which is favorable for nucleation. In addition, in the non-isothermal mode-I, the radial temperature exhibited a gradual increase from the outer cooling cylinder to the inner heating cylinder. Conversely, in non-isothermal mode-II, the radial temperature demonstrated a gradual decrease from the outer heating cylinder to the inner cooling cylinder. Additionally, in the isothermal mode, the radial temperature remained constant throughout the transition from the outer cylinder to the inner cylinder. Furthermore, our prior research on non-isothermal batch cooling crystallization indicates that a cooling surface temperature that is lower than the saturation temperature of the bulk solution facilitates rapid nucleation due to the increased supersaturation within the non-isothermal CT crystallizer.32,33 Consequently, it is reasonable to conclude that the non-isothermal continuous CT crystallizer yields initial nuclei that are smaller in size, exhibit a lower CV, and possess a higher population density in comparison to the isothermal continuous CT crystallizer.
The driving mechanisms for dissolution and recrystallization during the heating–cooling cycle were analyzed within the context of a non-isothermal continuous CT crystallizer. Specifically, the temperature difference between the heating cylinder (Td) and the bulk solution (Tb) functions as the driving force for dissolution (ΔTd = Td − Tb) within the heating boundary layer. Conversely, the temperature difference between the bulk solution (Tb) and the cooling surface of the cylinder (Tr) serves as the driving force for recrystallization (ΔTr = Tb − Tr) within the cooling boundary layer. These driving forces, which are critical to the efficacy of CSD control, exhibit variability in the continuous CT crystallizer operating under two distinct non-isothermal modes, as illustrated in Fig. 5 and 6(a). Notably, the driving force for dissolution, ΔTd = 8.6 °C in non-isothermal mode-I, surpasses that of ΔTd = 6.2 °C in non-isothermal mode-II, indicating an increased propensity for the disintegration of fine crystals in non-isothermal mode-I. Comparable findings regarding the influence of varying non-isothermal modes on CSD and mean crystal size, as influenced by dissolution and recrystallization forces, were documented in our prior research.32,33 Furthermore, the concentration of the bulk solution along the axial direction of the continuous CT crystallizer exhibited a gradual decline in both non-isothermal and isothermal modes, although it consistently remained marginally above the equilibrium concentration at Tb = 28 °C, as shown in Fig. 6(b).
As a result, the size of the crystals in the supersaturated solution increased, as evidenced by the optical microscope images presented in Fig. 7. In conclusion, the CV obtained through non-isothermal methods was found to be superior to that achieved through isothermal methods, with a more pronounced reduction in CV observed in the non-isothermal mode. Furthermore, within the non-isothermal approaches, mode-I produced larger average crystal sizes and lower CVs in comparison to mode-II, which can be attributed to the more effective dissolution of fine crystals. This indicates that mode-I is more efficient than Mode-II.
3.3 Effect of heating and cooling medium flow directions on CSD
In the context of non-isothermal mode-I, the flow directions of the heating and cooling mediums within the inner and outer cylinders may either align with or oppose the direction of the feed flow in the non-isothermal crystallizer. The feed flow direction is maintained as a constant reference. When the flow of the medium in either the inner or outer cylinder is co-current with the feed flow direction, it is designated as “co”; conversely, when the medium flow in these cylinders is counter current to the feed flow, it is referred to as “counter”. This results in the identification of four distinct flow configurations: direction-I (counter–counter), direction-II (counter-co), direction-III (co–co), and direction-IV (co-ounter), as depicted in Fig. 8. The corresponding heat transfer equations for each configuration are presented in the Appendix.The influence of medium flow directions on CSD was investigated under controlled conditions, specifically at a ΔT of 16.4 ± 0.2 °C, a rotational speed of 500 rpm, a Tb of 28 °C, a mean residence time of 5 minutes, and utilizing non-isothermal mode-I, as depicted in Fig. 9 and 10. The CV of 0.3283 recorded at port-IV in direction-I (counter–counter) is lower than those observed in the other three flow directions at port-IV, despite the mean crystal sizes being similar across all directions. This discrepancy can be explained by the varying driving forces for dissolution (ΔTd) and recrystallization (ΔTr), which are affected by the heating and cooling cycles within the non-isothermal continuous CT crystallizer.
Temperature simulations examining various medium flow directions (Fig. S1 in the ESI†) and the associated concentration profiles (Fig. 11(a)) indicate that the initial nucleation driving forces across all directions are comparable. This similarity arises from the uniform heating and cooling surface temperatures of both the inner and outer cylinders. As a result, the nuclei formed initially display analogous sizes and CVs across the different flow directions. However, the driving forces for dissolution (ΔTd) and recrystallization (ΔTr) exhibit variation among the directions, as elaborated in Fig. 11(b). In direction-I, the driving forces for dissolution (ΔTd) and recrystallization (ΔTr) are recorded at 8.6 °C and 7.8 °C, respectively, which are closely aligned with those observed in direction-II (ΔTd = 7.3 °C and ΔTr = 8.8 °C). Conversely, direction-III and direction-IV present driving forces for dissolution and recrystallization of approximately ΔTd = 6.0 °C and ΔTr = 10.2 °C, respectively. Previous research indicates that a well-balanced dissolution-growth driving force is more effective in facilitating fine destruction.32,33 Consequently, it is reasonable to conclude that the CVs in direction-I and direction-II are lower than those in direction-III and direction-IV. However, owing to the reduced effectiveness of fine destruction in direction-II, the improvement of CSD, which indicates a reduction in the CV, is less significant in comparison to direction-I. Therefore, sufficient fine destruction achieved through internal heating–cooling cycles within the non-isothermal continuous CT crystallizer can significantly improve CSD.
3.4 Effect of temperature difference on CSD
Fig. 12 illustrates the influence of the temperature difference (ΔT = Td − Tr) between the inner and outer cylinders on CSD under non-isothermal mode-I and direction-I conditions. The rotational speed was held constant at 500 rpm, and the mean residence time was maintained at 5 minutes. Furthermore, the Tb was constantly set at 28 °C, while the ΔT was varied from 0 to 18.1 °C. It was observed that both the mean crystal size and the CV at port-IV exhibited a gradual decrease with an increase in ΔT. Specifically, at a constant ΔT of 18.1 ± 0.2 °C, the crystal suspension attained its minimum size of 58.2 μm, accompanied by a reduced CV of 0.2791. Under these conditions within the CT crystallizer, the heating temperature of the inner cylinder was elevated from 28 to 37.6 °C, while the corresponding cooling temperature of the outer cylinder was decreased from 28 to 19.5 °C.Furthermore, the temperature profiles and concentration at each specified ΔT were analyzed (Fig. S2† and 13(a)). The analysis revealed a progressive increase in the heating temperature and a corresponding decrease in the cooling temperature. Our prior research on non-isothermal batch cooling crystallization indicated that establishing a lower temperature at the cooling surface resulted in heightened supersaturation, which facilitated the formation of initial nuclei due to the rapid cooling to lower temperatures associated with an increased temperature difference.32,33 This phenomenon resulted in the generation of nuclei characterized by smaller sizes, reduced CVs, and greater populations upon the introduction of the feed solution into the non-isothermal continuous CT crystallizer (Fig. S3†). Simultaneously, the driving forces for dissolution (ΔTd) and recrystallization (ΔTr) were observed to increase with the temperature difference (Fig. 13(b)). Notably, the driving force for dissolution (ΔTd) constantly exceeded that for recrystallization (ΔTr), thereby enhancing the efficiency of fine crystal destruction at the heating boundary layer and promoting crystal growth at the cooling boundary layer. This mechanism contributed to an improved CV of the crystal suspension along the axial direction of the non-isothermal continuous CT crystallizer at elevated temperature differences (Fig. S3†).
3.5 Effect of Taylor vortex motion on CSD
As indicated in our prior research, the influence of Taylor fluid motion, which is affected by rotational speed, on CSD during non-isothermal crystallization diverges from its effect in isothermal crystallization.32,33 Notably, increased rotational speed facilitates earlier nucleation at lower levels of supersaturation, attributable to the enhanced alignment of molecules at the cooling surface during non-isothermal batch cooling crystallization. As a result, crystals formed under higher rotational speeds tend to be larger and display a wider CV. This phenomenon was similarly observed in the non-isothermal continuous CT crystallizer, where rotational speeds ranged from 200 to 900 rpm. The ΔT, Tb, and mean residence time were consistently maintained at 16.4 ± 0.2 °C, 28.0 °C, and 5 minutes, respectively. Consequently, both the mean crystal size and CV exhibited an increase in correlation with the intensity of the Taylor vortex motion, as illustrated in Fig. 14 and S4.†This finding was corroborated through simulations of temperature and measurements of the corresponding bulk solution concentration at varying rotation speeds within the non-isothermal continuous CT crystallizer. The results indicated a more rapid decrease in the temperature of the bulk solution (Tb) with increasing rotation speed (Fig. 15(a)), suggesting that nucleation occurs earlier at elevated rotation speeds, as predicted by the Tb simulation. Furthermore, the measured bulk concentration at port-I exhibited a slight decline with increasing rotation speed, attributed to effective mass transfer associated with the formation of nuclei (Fig. 15(b)). Additionally, the initial crystals collected from port-I at higher rotation speeds were observed to be larger and exhibited a broader CSD, which further substantiates this finding (Fig. 15(c) and S4†). Consequently, it is reasonable to infer that the final crystal size and CV of the crystal suspension are larger and broader at higher rotation speeds, despite the influences of dissolution and recrystallization occurring within the non-isothermal Taylor vortex.
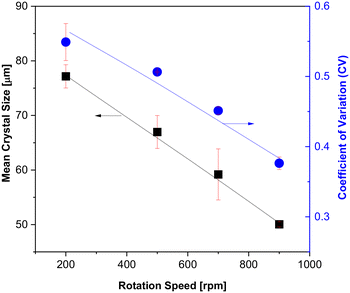
The influence of rotation speed on CSD in the isothermal continuous CT crystallizer differs from the behavior observed in the non-isothermal continuous CT crystallizer, particularly when the Tb is maintained at 28 °C (Fig. 16 and S5†). Specifically, in the isothermal continuous CT crystallizer, an increase in rotation speed from 200 to 900 rpm results in a reduction of both the mean crystal size and the CV, with values decreasing from 77.2 to 50.1 μm and from 0.5490 to 0.3763, respectively. In the absence of a temperature gradient between the inner and outer cylinders, the initially elevated temperature of the feeding solution is rapidly reduced to the designated Tb at higher rotation speeds.
In contrast, the temperature of the feeding solution exhibits a more gradual decrease along the axial position of the CT crystallizer, as evidenced by the temperature simulation of the bulk solution (Fig. 17(a) and S6(a)†) and the effective heat transfer (Fig. S6(b)†). Consequently, the cooling rate of the feeding solution is influenced by the rotation speed within the isothermal continuous CT crystallizer. Building upon our prior investigations into isothermal batch cooling crystallization with differing cooling rates, it is evident that a rapid cooling rate facilitates the formation of small crystals characterized by a narrow CSD and a high population density, due to the establishment of high and narrowly distributed supersaturation levels.32,33 Conversely, a slower cooling rate results in the formation of larger crystals with a broader CSD, which can be attributed to lower and more widely distributed supersaturation levels. The concentration and supersaturation at port-I, which is critical for initial nucleation, as well as the concentration at port-IV for the final state (Fig. 17(b)), indicate that concentration diminishes with an increase in rotation speed, while the corresponding supersaturation for initial nucleation exhibits an inverse relationship. This observation is consistent with findings from isothermal batch cooling crystallization conducted under varying cooling rates. It is important to highlight that throughout the experiment, even when rapid cooling is considered, no incrustation was observed at any of the tested rotation speeds.
Furthermore, the influence of supersaturation on CSD within the isothermal continuous CT crystallizer was substantiated through a series of experiments that involved varying the set Tb from 20 to 32 °C. The results indicated that both the mean crystal size and the CV of the crystal suspension exhibited an increase with the elevation of Tb, as illustrated in Fig. 18(a) and S7(a)–(d).† An analysis of the simulation of the bulk solution, presented in Fig. 18(b), revealed that the rate of decline in Tb towards the set temperature accelerated as the set temperature was decreased. Simultaneously, the measured Tb at port-I exhibited a gradual increase, aligning more closely with each respective set Tb, which resulted in varying supersaturation ratios for the initial nucleation process (Fig. S7(e)†). Notably, a higher supersaturation ratio of 1.35 was attained for initial nucleation at the lower set Tb of 20.0 °C, whereas a lower supersaturation ratio of 1.18 acted as the driving force for initial nucleation at the elevated set Tb of 32.0 °C. Consequently, the higher supersaturation ratio facilitated the formation of smaller crystals with a narrower CSD and a greater population, while the lower supersaturation ratio resulted in the production of larger crystals with a broader CSD and a reduced population within the isothermal continuous CT crystallizer. Thus, it can be concluded that the supersaturation ratio, which is influenced by the cooling rate of the bulk solution, plays a critical role in regulating initial nucleation and CSD in the isothermal continuous CT crystallizer. In contrast, in the non-isothermal continuous CT crystallizer, the cooling temperature necessary for the induction of early nuclei primarily governs the initial nucleation and CSD.
3.6 Effect of mean residence time on CSD
The dynamics of Taylor vortex flow and heat transfer are influenced by the axial feeding flow rate, as illustrated in Fig. S8,† corroborating the results of prior research.32,33 Adjustments to the axial feeding flow rate affect both the duration for the feed solution to enter the CT crystallizer and the retention time of the crystal suspension within the CT crystallizer. Specifically, a rapid axial feeding flow rate corresponds to a reduced mean residence time, whereas a slower flow rate results in an extended mean residence time. These variations in mean residence time subsequently impact the efficiency of initial nucleation in both non-isothermal and isothermal continuous CT crystallizers, with the Tb maintained at 28 °C and the rotational speed held constant at 500 rpm, as demonstrated in Fig. 19, S9 and S10.† Notably, in non-isothermal continuous CT crystallizers, an increase in mean residence time from 2.5 to 15 minutes leads to an increase in both the mean crystal size and the CV at port-IV, from 61.1 to 107.9 μm and from 0.3285 to 0.6446, respectively (Fig. 19(a) and S9†). Similarly, in isothermal continuous CT crystallizers, an increase in mean residence time from 2.5 to 15 minutes results in an increase in mean crystal size and CV at port-IV from 45.4 to 84.8 μm and from 0.4122 to 0.6982, respectively (Fig. 19(b) and S10†).The variations in the influence of mean residence time on crystal size and the CV between non-isothermal and isothermal CT continuous crystallizers can be attributed to the dynamic modulation of crystallization kinetics by the temperature gradient. In non-isothermal conditions, temperature variations periodically modify the local supersaturation, prompting crystals to alternately experience growth in cooler regions and partial dissolution in warmer regions. This phenomenon enhances the Ostwald ripening effect, favoring the growth of larger crystals while smaller ones are diminished, thereby resulting in a notable increase in average crystal size. Concurrently, the interplay between selective growth and crystal fragmentation induced by the temperature gradient mitigates the disparity in size distribution, leading to a relatively modest rise in CV. Conversely, in isothermal conditions, the continuous decline in supersaturation with extended residence time progressively restricts the growth rate. Consequently, smaller crystals generated during the initial nucleation phase coexist with larger crystals that exhibit slower growth in subsequent stages, culminating in a more dispersed size distribution characterized by a higher CV. Furthermore, the absence of dynamic regulation associated with temperature results in a lesser increase in average size compared to non-isothermal systems. This distinction fundamentally underscores the differing predominant influences of thermodynamic (non-isothermal) and purely kinetic (isothermal) factors in the competitive processes of nucleation, growth, and ripening throughout the crystallization process.
Simulations of Tb in both isothermal and non-isothermal continuous CT crystallizers reveal that Tb decreases rapidly to the designated set point with an extended mean residence time, while the decrease is more gradual with a reduced mean residence time (Fig. 20(a)). It is important to highlight that throughout the mean residence time experiments, temperature measurements were conducted, confirming that even with a short mean residence time of 2.5 minutes, the mother liquor achieved the temperature corresponding to Tb. Moreover, the duration of time plays a crucial role in regulating supersaturation, which is essential for both nucleation and crystal growth in these crystallizers (Fig. 20(b)). The findings indicated that an increase in mean residence time corresponds to a decrease in the supersaturation of the bulk solution at port-I. When a shorter mean residence time is employed, rapid nucleation and crystal growth occur due to elevated supersaturation levels, irrespective of the type of crystallizer, leading to a crystal suspension characterized by smaller size and narrower CSD. In contrast, when a longer mean residence time is implemented, nucleation and crystal growth transpire over an extended duration in both crystallizer types. Consequently, it is reasonable to conclude that the mean crystal size and CV increase with the mean residence time in both isothermal and non-isothermal continuous CT crystallizers.
Conclusions
The effective application of non-isothermal Taylor vortex flow within a continuous CT crystallizer has markedly enhanced control over CSD. This approach involves the establishment of distinct thermal conditions for the inner and outer cylinders, coupled with the rotation of the inner cylinder, thereby creating a dynamic environment conducive to crystal dissolution and recrystallization. Specifically, one cylinder is maintained at a temperature above Tb to facilitate the dissolution of crystals, while the other is cooled below this temperature to promote crystal growth. This cyclic process leads to the periodic disintegration of fine crystals followed by their growth, thereby improving the uniformity of the crystal suspension. Furthermore, the efficacy of non-isothermal continuous Taylor vortex flow in refining CSD is intricately linked to various operational modes, flow directions, and specific parameters within the CT crystallizer. The temperature of the cooling surface is particularly significant in influencing nucleation, which in turn affects the final size and distribution of the crystals. Non-isothermal Taylor vortex flow, particularly in mode-I (where the inner cylinder is heated and the outer cylinder is cooled) and mode-II (the reverse configuration), yields narrower crystal size distributions compared to isothermal conditions. Mode-I, in particular, exhibits superior performance in generating uniform crystals with a lower CV, a result attributed to its more effective heating and cooling cycles. In addition, the flow directions of the heating and cooling mediums were found to influence the CSD. It was observed that the CV values in direction-I and direction-II were lower than those in direction-III and direction-IV.Furthermore, an increase in the temperature difference between the heating and cooling cylinders in both isothermal and non-isothermal continuous CT crystallizers correlates with a reduction in mean crystal size and CV, as it promotes the formation of smaller initial crystals and enhances the efficiency of the heating–cooling cycle. Conversely, elevated rotation speeds contribute to larger crystal sizes and a broader CSD in non-isothermal continuous CT crystallizers, as intensified Taylor vortex motion facilitates nucleation at lower levels of supersaturation. However, elevated rotation speeds contribute to smaller crystal sizes and a narrower CSD in isothermal continuous CT crystallizers. Additionally, slower feed flow rates (extended residence times) prolong the supersaturation profile, resulting in larger crystals and a wider CSD, regardless of the crystallization mode employed. Moreover, the optimization of cooling crystallization for L-lysine under non-isothermal conditions exemplifies the versatility and applicability of this technique in practical processes. This method enables precise control over crystal characteristics, thereby enhancing the efficiency and quality of crystalline products across various industrial applications.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Zun-Hua Li: data curation, visualization, writing – original draft, writing – review & editing. Zhao-Hui Wu: conceptualization, visualization, writing – original draft, data curation. Gerard Coquerel: conceptualization, writing – review & editing, supervision. Bum Jun Park: writing – review & editing, resources, supervision, project administration. Woo-Sik Kim: conceptualization, supervision, project administration, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Appendix
Mathematical model of heat transfer
Fig. 8 presented four typical directions of medium flow in the inner and outer cylinders. The following assumptions are made for heat transfer in the system:1. The heat transfer mode is built up at a steady state;
2. One-dimensional convection in r-direction;
3. Constant heat transfer coefficient, and constant flux in the heating and cooling cylinders annulus and crystallized annulus,
4. Fully developed CT flow in the crystallized annulus condition;
5. The contact resistance between walls, and natural convection and gravity effects are negligible.
Under the above assumptions, as well as the first law of thermodynamics, the heat transfer balance equation is:
| The accumulated heat rate = The input heat rate − The output heat rate + The generated heat rate |
For the CT crystallizer system, the generation of heat rate and the accumulated heat rate are zero at a steady state. Take direction I for example, the derivation of each division of heat transfer in CT crystallizer and the final evaluation is presented as follows:For heating the inner cylinder:
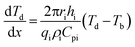 | (1) |
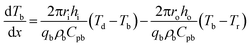 | (2) |
 | (3) |
The equations are solved and simulated by software of Mathematica and the results are shown as follows:
 | (4) |

 M1 = −a + b + c − d, N1 = −ab + ad − cd, Δ1 = M12 − 4N1. Ma1 = −a − b + c + d, Md1 = −a + b + c + d.
M1 = −a + b + c − d, N1 = −ab + ad − cd, Δ1 = M12 − 4N1. Ma1 = −a − b + c + d, Md1 = −a + b + c + d.
Similarly, the heat transfer at other different flow directions is built up.
For direction II:
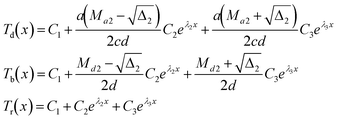
| (5) |
 λ1 = 0,
λ1 = 0, 
 M2 = −a + b + c + d, N2 = −ab − ad + cd, Δ2 = M22 − 4N2. Ma2 = a + b − c + d, Md2 = a − b − c + d.
M2 = −a + b + c + d, N2 = −ab − ad + cd, Δ2 = M22 − 4N2. Ma2 = a + b − c + d, Md2 = a − b − c + d.
For direction III:

| (6) |
 λ1 = 0,
λ1 = 0, 
 M3 = a + b + c + d, N3 = ab + ad + cd, Δ3 = M32 − 4N3. Ma3 = a − b + c − d, Md3 = a − b − c + d.
M3 = a + b + c + d, N3 = ab + ad + cd, Δ3 = M32 − 4N3. Ma3 = a − b + c − d, Md3 = a − b − c + d.
For direction IV:

| (7) |
 λ1 = 0,
λ1 = 0, 
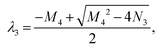 M4 = a + b + c − d, N4 = ab − ad − cd, Δ4 = M42 − 4N4. Ma4 = a − b + c + d, Md4 = a + b + c + d.
M4 = a + b + c − d, N4 = ab − ad − cd, Δ4 = M42 − 4N4. Ma4 = a − b + c + d, Md4 = a + b + c + d.
Eventually, the software of Mathematica can carry out the simulations once the initial temperature and appropriate heat transfer coefficient are assigned.
Acknowledgements
This work was supported by the Engineering Research Center of Excellence Program (NRF-2021R1A5A6002853) and Basic Science Research Program [NRF-2020R1A6A1A03048004] of the National Research Foundation of Korea (NRF).References
- H. F. Kraus, D. Acevedo, T. F. O'Connor, D. Liu and A. Mohammad, Cryst. Growth Des., 2024, 24, 5569–5581 CrossRef CAS.
- V. Tiwari, G. Walker and V. V. Ranade, Cryst. Growth Des., 2023, 23, 8620–8636 CrossRef CAS.
- A. Zaykovskaya and M. Louhi-Kultanen, Cryst. Growth Des., 2023, 23, 1813–1820 CrossRef CAS PubMed.
- S. Chergaoui, J. Lauzer, D. P. Debecker, T. Leyssens and P. J. Luis, J. Membr. Sci., 2024, 694, 122415 CrossRef CAS.
- C. D. P. V. Zambrano and M. Jiang, CrystEngComm, 2023, 25, 2227–2236 RSC.
- N. Nandan and J. V. Parambil, Crystals, 2023, 13, 1094 CrossRef CAS.
- R. Leeming, T. Mahmud, K. J. Roberts, N. George, J. Webb, E. Simone and C. J. Brown, Ind. Eng. Chem. Res., 2023, 62, 11067–11081 CrossRef CAS PubMed.
- W. Li, L. E. Hatcher, C. C. Wilson, C. D. Rielly and B. Benyahia, Chem. Eng. Res. Des., 2024, 202, 126–146 CrossRef CAS.
- Y. Kim, Y. Kawajiri, R. W. Rousseau and M. A. Grover, Ind. Eng. Chem. Res., 2023, 62, 2866–2881 CrossRef CAS.
- Z. Wu, S. Yang and W. Wu, CrystEngComm, 2016, 18, 2222–2238 RSC.
- M. Shoji and H. Takiyama, Cryst. Growth Des., 2012, 12, 5241–5246 CrossRef CAS.
- A. Saleemi, C. Rielly and Z. K. Nagy, CrystEngComm, 2012, 14, 2196–2203 RSC.
- H.-J. Pan and J. D. Ward, Ind. Eng. Chem. Res., 2021, 60, 12614–12628 CrossRef CAS.
- E. Simone, A. R. Klapwijk, C. C. Wilson and Z. K. Nagy, Cryst. Growth Des., 2017, 17, 1695–1706 CrossRef CAS PubMed.
- M. Shoji, T. Eto and H. Takiyama, J. Chem. Eng. Jpn., 2011, 44, 191–196 CrossRef CAS.
- P. Binel and M. Mazzotti, Ind. Eng. Chem. Res., 2022, 61, 16220–16232 CAS.
- F. Civati, V. Svoboda, S. J. Urwin, P. McArdle, A. Erxleben, D. Croker and J. ter Horst, Cryst. Growth Des., 2021, 21, 1496–1506 CrossRef CAS.
- F. Salvatori and M. Mazzotti, Ind. Eng. Chem. Res., 2018, 57, 15522–15533 CAS.
- W. Saeman, AIChE J., 1956, 2, 107–112 CrossRef CAS.
- M. Jiang, Z. L. Zhu, E. Jimenez, C. D. Papageorgiou, J. Waetzig, A. Hardy, M. Langston and R. D. Braatz, Cryst. Growth Des., 2014, 14, 851–860 CrossRef CAS.
- Z. Sun, J. L. Quon, C. D. Papageorgiou, B. Benyahia and C. D. Rielly, Cryst. Growth Des., 2022, 22, 4730–4744 CrossRef CAS PubMed.
- J.-W. Kim, D. B. Park, H.-M. Shim, H.-S. Kim and K.-K. Koo, Ind. Eng. Chem. Res., 2012, 51, 3758–3765 CrossRef CAS.
- A. Majumder and Z. K. Nagy, AIChE J., 2013, 59, 4582–4594 CrossRef CAS.
- Y. Zhao, V. K. Kamaraju, G. Hou, G. Power, P. Donnellan and B. Glennon, Chem. Eng. Sci., 2015, 138, 106–115 CrossRef.
- A. D. Randolph and T. Rivera, Ind. Eng. Chem. Process Des. Dev., 1978, 17, 182–188 CrossRef.
- A. J. Alvarez and A. S. Myerson, Cryst. Growth Des., 2010, 10, 2219–2228 CrossRef CAS.
- B. S. Choi and T. A. Ring, Fluid Phase Equilib., 2005, 228, 99–107 CrossRef.
- L. D. Shiau and T. S. Lu, Comput. Chem. Eng., 2006, 30, 970–977 CrossRef CAS.
- S. Poncet, S. Haddadi and S. Viazzo, Int. J. Heat Fluid Flow, 2011, 32, 128–144 CrossRef.
- M. N. Noui-Mehidi, N. Ohmura, K. Nishiyama and J. Wu, J. Chem. Eng. Jpn., 2007, 40, 951–956 CrossRef CAS.
- H. S. Dou, B. C. Khoo and K. S. Yeo, Int. J. Therm. Sci., 2007, 46, 262–275 CrossRef CAS.
- Z. Wu, S. Seok, D. H. Kim and W.-S. Kim, Cryst. Growth Des., 2015, 15, 5675–5684 CrossRef CAS.
- Z. Wu, D. H. Kim and W.-S. Kim, Cryst. Growth Des., 2017, 17, 28–36 CrossRef CAS.
- J. W. Mullin, Crystallization, Butterworth Heinemann, Oxford, UK, 4th edn, 2001 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ce00171d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |