Crystal growth and magnetic properties of hexagonal Ba₄CuNb₃O₁₂ single crystals

Abstract

We report a systematic investigation of the growth of high-quality hexagonal perovskite Ba₄CuNb₃O₁₂ single crystals using the flux method. The optimal growth involved using the tetragonal phase BaCu_0.33Nb_0.67O₃ as the precursor, with 20 g CuO as the flux, a cooling rate of 1 °C h⁻¹ between 1350 °C and 1100 °C, and a cooling rate of 2 °C h⁻¹ from 1100 °C to 930 °C. The magnetic properties along the ab-plane and the perpendicular direction are thoroughly studied. Fitting the inverse magnetic susceptibility data from 2 K to 300 K with the modified Curie–Weiss (CW) law yields a Weiss temperature (θ_CW) of −1.14 K, indicating the presence of antiferromagnetic correlations in the ground state between Cu²⁺ ions via superexchange interactions. Furthermore, the specific heat data of Ba₄CuNb₃O₁₂ align well with the Debye–Einstein phonon model, allowing us to estimate the Debye temperature of 199 K and the average phonon velocity of 2014.98 m s⁻¹.

---

1. Introduction

Hexagonal perovskite oxides have garnered increasing attention due to their rich physicochemical properties and potential applications.^1–3 Their crystal structures are of the hexagonal perovskite type, characterized by the stacking of BO₆ octahedra along the c-axis in different arrangements, with the B-site typically occupied by a transition metal. For instance, Xu et al. first reported the synthesis of two-dimensional triangular frustrated Ba₃CoNb₂O₉ single crystals⁴ and quasi-one-dimensional Sr₆Co₅O₁₅ single crystals doped with different amounts of Fe elements.⁵ Li et al. synthesized a hexagonal perovskite oxide (2H, 6H, and 10H)-BaCo_0.9Ru_0.1O_3−δ with different [BaO₃] layers in a unit cell and systematically explored its electrocatalytic oxygen evolution performance.⁶ Although 8H-hexagonal perovskite oxides are relatively common, as seen in systems like Ba₈Ti₃Ta₄O₂₄,⁷ Ba₄LiM₃O₁₂ (M = Nb and Ta),^8,9 Ba₈Ti₃Nb₄O₂₄,^10,11 Ba₄Na₃RuO₁₂,¹² and Ba₈MnNb₆O₂₄,¹³ 8H-hexagonal perovskites containing copper atoms are very rare. It is also worth noting that, in addition to the detailed study of the magnetism of Ba₈MnNb₆O₂₄, which confirmed a 120° ordering ground state below the antiferromagnetic transition temperature T_N = 1.45 K,¹⁴ research on the other 8H-hexagonal perovskite materials often focuses primarily on their crystal structure, with limited studies on their magnetic properties.¹²

The 8H-hexagonal perovskite structure requires a high coordination number between ions, with the size and charge of the A-site and B-site ions needing to meet specific conditions. Copper ions are prone to redox reactions, especially the conversion between Cu²⁺ (S = 1/2) and Cu⁺ (non-magnetic S = 0). This redox behavior can lead to structural instability or phase transition, further limiting the stability of copper-containing compounds in the 8H-hexagonal perovskite oxides. As a typical example of 8H-hexagonal perovskite oxides, Ba₄CuNb₃O₁₂ crystallizes in the P6₃/mmc space group, and the Nb1O₆ octahedron along the c-axis shares corners with the face-sharing (Nb2/Cu)O₆ octahedron, as illustrated in Fig. 1(a). Furthermore, the structural projection onto the ab-plane reveals that Nb1 atoms form a honeycomb structure, while Nb2/Cu atoms arrange in a triangular lattice, as shown in Fig. 1(b). Since Kumada et al. first synthesized Ba₄CuNb₃O₁₂ polycrystalline powders,¹⁵ there have been no reports on their physical properties, nor have any single crystal studies been published to date. If Cu forms a perfect triangular lattice system in this system, the presence of geometric frustration could lead to the system exhibiting a spin liquid or quantum spin liquid ground state.¹⁶ However, the random occupation of Nb2 and Cu atoms in Ba₄CuNb₃O₁₂ disrupts the perfect triangular lattice structure, similar to the site mixing of Mg²⁺ and Ga³⁺ in YbMgGaO₄,^17,18 yet the magnetic ground state of Ba₄CuNb₃O₁₂ remains an interesting subject for further exploration.

Fig. 1 (a) Crystal structure of Ba₄CuNb₃O₁₂. (b) Projection of the crystal structure onto the ab-plane.

In this study, we conducted a comprehensive investigation of the growth of Ba₄CuNb₃O₁₂ single crystals using the flux method, thereby identifying the optimal synthesis route. We also examined the magnetism of the Ba₄CuNb₃O₁₂ single crystal both along and perpendicular to the ab-plane. Our results confirm that its ground state is antiferromagnetic. The specific heat behavior of Ba₄CuNb₃O₁₂ is in good agreement with that of the Debye–Einstein phonon model, and furthermore, it can be concluded that the average phonon velocity is 2014.98 m s⁻¹.

2. Characterization section

The single crystal structure and elemental composition were characterized at 298 K using X-ray diffraction (XRD, Rigaku SmartLab SE diffractometer), energy-dispersive spectroscopy (EDS, JEOL JSM-6700F), X-ray fluorescence (XRF, XRF-1800), and X-ray photoelectron spectroscopy (XPS, ESCALAB250Xi). Magnetization measurements were performed with a magnetic property measurement system (MPMS3, Quantum Design), while the specific heat was measured using the relaxation method on a physical property measurement system (PPMS, Quantum Design). In particular, in the measurement process of the direct current magnetic susceptibility (χ) of field-cooling (FC) the temperature rise test is adopted, namely the field cooled warming (FCW) process. In the single crystal XRD characterization, the tested single crystal is millimeter-sized, and the sample used for magnetic and specific heat measurements is taken from the single crystal shown in the upper right corner of Fig. 5(a), with a mass of 6.52 mg.

3. Synthesis steps of Ba₄CuNb₃O₁₂ single crystals

3.1 Synthesis of polycrystalline precursors

We first fully ground BaCO₃ (SCR, 99%), CuO (SCR, 99%), and Nb₂O₅ (SCR, 99%) in a molar ratio of 3 : 1 : 1, and then transferred the mixture to an Al₂O₃ crucible and calcined it at 1200 °C for 48 hours. From the XRD patterns in Fig. 2, we can observe that the main phase of the product is BaCu_0.33Nb_0.67O₃ with the P4/mmm space group, along with some impurity phase Ba₅Nb₄O_15.33, unreacted Nb₂O₅ and BaO formed after the high-temperature decomposition of BaCO₃. Our next step is to use these polycrystalline powders to prepare single crystals via the flux method. In addition, from the perspective of single crystal growth, a small amount of the impure phase in the polycrystalline powder does not significantly affect the final crystal quality, as the type and proportion of the flux, along with the reaction temperature, are the key factors.⁵

Fig. 2 XRD patterns of the obtained polycrystalline samples.

3.2 Exploration of the best method for single crystal synthesis

3.2.1 Method I. The BaCu_0.33Nb_0.67O₃ polycrystalline powder was weighted to 5 g and mixed with 10 g of CuO as a flux. The mixture was thoroughly ground for about half an hour and then transferred into a 50 ml Al₂O₃ crucible. The Al₂O₃ crucible, sealed with a high-temperature ceramic sealant, was placed into a muffle furnace. It was heated to 1350 °C and held for 1 hour, then cooled down to 1100 °C at a rate of 1 °C h⁻¹, further cooled to 930 °C at 2 °C h⁻¹, and finally, the muffle furnace power was turned off. At room temperature, the sealed Al₂O₃ crucible was broken open, revealing that the entire crucible had turned brown, with no single crystals formed, as shown in Fig. 3(a). To further determine the crystal structure of the final product, the material was scraped from the crucible wall using a blade and then XRD testing was performed.

Fig. 3 (a) The crucible and the product obtained using method I. (b) XRD results of the product after thorough grinding.

The XRD results show that the synthesized product contains our target compound, the hexagonal perovskite Ba₄CuNb₃O₁₂, along with an additional phase of BaNb₂O₆ with the Pmma space group. Moreover, the product also contains a small amount of BaNb₃O₆ with the R3m space group. This suggests that during the process of single crystal growth, the crystal system of the obtained product may differ from that of the raw material. At 1350 °C, which is above the melting point of CuO, the mixture must be in a molten state, and as the temperature gradually decreases, the different elements can recombine to form new phases. Although no single crystal was obtained via method I, the target hexagonal crystal system Ba₄CuNb₃O₁₂ is synthesized, and additionally, the remaining product adhered to the crucible is very small, so in the improved method, the amount of the CuO flux should be increased.

3.2.2 Method II. To obtain high-quality single crystals of Ba₄CuNb₃O₁₂, we made slight adjustments to synthesis method I, increasing the CuO flux to 15 g while keeping the other reaction conditions unchanged. It is noteworthy that we successfully synthesized sheet-like single crystals of Ba₄CuNb₃O₁₂ using method II, with approximate dimensions of (1.5–2.0) mm × (0.6–1.0) mm × (0.3–0.4) mm (inset of Fig. 4(b)), which has never been reported before. The single crystal X-ray diffraction results show that its surface corresponds to the (00l) crystal system (Fig. 4(b)), meaning that the surface of the sheet-like single crystal is the ab-plane.

Fig. 4 (a) Powder XRD pattern of the Ba₄CuNb₃O₁₂ sample synthesized by method II. (b) The (00l) diffraction pattern of the Ba₄CuNb₃O₁₂ single crystal. Inset: Photograph of single crystals, with each small grid representing 1 mm. The blue star represents the sample holder silicon wafer signal.

Furthermore, to assess the quality of the crystals, we ground the obtained single crystals into powder and performed XRD characterization, as shown in Fig. 4(a). The results show that a small amount of BaNb₃O₆ is still in the Ba₄CuNb₃O₁₂ single crystals, due to the gradual growth of the crystal nucleus during the crystallization process of Ba₄CuNb₃O₁₂, which partially encapsulated and generated the formed BaNb₃O₆. Additionally, compared to method I, the product synthesized using method II does not contain the BaNb₂O₆ phase. Interestingly, by simply adjusting the content of the CuO flux, we can not only obtain single crystals but also further reduce the amount of the impurity phase.

3.2.3 Method III. We chose to continue to increase the mass of the CuO flux to 20 g, and the rest of the growth conditions were the same as in method I, which is referred to here as method III. Interestingly, the ab-plane of the single crystal Ba₄CuNb₃O₁₂ we obtained is hexagonal, which is consistent with the sixfold symmetry of the crystal structure, and the size of the largest single crystal is about 3.0 mm × 3.0 mm × 0.5 mm (Fig. 5(a)). Furthermore, the XRD results of the Ba₄CuNb₃O₁₂ single crystal show only sharp (00l) peaks in the range of 10–80°, confirming its very high crystallinity (Fig. 5(b)). The high-quality single crystals of Ba₄CuNb₃O₁₂ were fully ground and tested by XRD, and the results confirmed that the obtained phase is pure. As shown in Fig. 5(c), the XRD refinement results show that the unit cell parameters of Ba₄CuNb₃O₁₂, belonging to the P6₃/mmc space group, are a = b = 5.7830(4) Å and c = 18.9289(6) Å, and the detailed refinement parameters are presented in Table 1.

Fig. 5 (a) Photograph of the Ba₄CuNb₃O₁₂ single crystal, with each small grid representing 1 mm. (b) The (00l) diffraction pattern of the Ba₄CuNb₃O₁₂ single crystal. (c) Powder XRD pattern of Ba₄CuNb₃O₁₂. (d) EDS spectrum and elemental mapping (inset).

Table 1 Crystal data and structure refinement for Ba₄CuNb₃O₁₂

Parameter			Value
Compound			Ba4CuNb3O12
Space group			P63/mmc
a/b/Å			5.7830(4)
c/Å			18.9289(6)
Cell volume/Å^3			548.23(5)
R wp/%			9.22
R p/%			7.04
χ ^2			5.01
Atom	Wyck.	Site	x/a	y/b	z/c
Ba1	2a	-3m.	0	0	0
Ba2	2d	-6m2	1/3	2/3	3/4
Ba3	4f	3m.	1/3	2/3	0.13488
Nb4	4f	3m.	1/3	2/3	9/16
Nb5	4e	3m.	0	0	0.1829
Cu6	4e	3m.	0	0	0.1829
O7	6g	.2/m	1/2	0	0
O8	6h	mm2	0.161	0.322	1/4
O9	12k	.m.	0.82642	0.65284	0.1187

---

The EDS analysis clearly shows the presence of the elements Ba, Cu, Nb, and O, while the C element originates from the conductive carbon glue (Fig. 5(d)). Additionally, the EDS mapping reveals that Ba, Cu, Nb, and O are uniformly distributed across the tested area (inset of Fig. 5(d)). The EDS results indicate that the ratio of Cu and Nb elements is close to 1 : 3, but the Ba content is significantly higher, likely due to the presence of residual BaCO₃ or BaO attached on the surface (Fig. S1†). Furthermore, we ground the Ba₄CuNb₃O₁₂ single crystals into polycrystalline powder with a mass of about 25 mg and performed XRF testing (Fig. S1†). The results showed that the ratio of Ba, Cu and Nb is 4 : 1.85 : 2.38, which is similar to the results given by Kumada et al.¹⁵ However, in order to maintain consistency with the previous work,¹⁵ we still used the expression form Ba₄CuNb₃O₁₂ throughout the full text. In the chemical formula Ba₄CuNb₃O₁₂, Ba ions have a +2 valence state, and Nb ions are +5. To ensure charge balance in the formula, Cu ions must be +1. However, under the high-temperature conditions of single crystal growth, some Cu⁺ will be converted into Cu²⁺. As shown in Fig. S2,† the XPS results show that the ratio of Cu⁺ to Cu²⁺ is approximately 1.12 : 1, and it should be noted that Cu⁺ is non-magnetic (S = 0), while Cu²⁺ is magnetic (S = 1/2).

3.2.4 Method IV and method V. Among the three synthesis methods mentioned above, we successfully achieved the first synthesis of high-quality Ba₄CuNb₃O₁₂ single crystals by simply adjusting the CuO flux content. However, to further optimize the synthesis method, we made additional improvements based on method III. In method IV, we kept the CuO flux amount constant at 20 g and adjusted the cooling rate to 1.5 °C h⁻¹ within the temperature range of 1350 °C to 1100 °C. In method V, we further adjusted the cooling rate in this temperature zone to 3 °C h⁻¹. The Ba₄CuNb₃O₁₂ single crystals synthesized by method IV and method V are shown in Fig. 6(a) and (b), respectively. Compared to method III, a slight increase in the cooling rate to 1.5 °C h⁻¹ has little effect on the size and crystal quality of the Ba₄CuNb₃O₁₂ single crystal, as shown in Fig. 6(a). However, when the cooling rate is significantly increased to 3.0 °C h⁻¹, the size of the synthesized single crystal is significantly reduced, and its crystallinity deteriorates. For Pb₂CoWO₆ single crystal growth, reducing the cooling rate does not significantly change the crystal morphology, but it does cause a noticeable shift in the dominant crystal plane from (111) to (100).¹⁹ However, for Pb(Zn_1/3Nb_2/3)O₃, altering the cooling rate can significantly influence the hardness of the generated single crystal and also change its color.²⁰

Fig. 6 The (00l) diffraction patterns of the Ba₄CuNb₃O₁₂ single crystal synthesized by (a) method IV and (b) method V. Inset: Photograph of the Ba₄CuNb₃O₁₂ single crystal, with each small grid representing 1 mm.

4. Magnetic properties

We systematically studied the magnetic properties of high-quality single crystals of Ba₄CuNb₃O₁₂ synthesized using method III, as shown in Fig. 7. When the magnetic field is along the ab-plane, the zero-field-cooling (ZFC) and field-cooling (FC) magnetic susceptibility (χ) gradually increase with decreasing temperature, and there is no magnetic phase transition. In addition, the magnetic susceptibility curves for FC and ZFC almost overlap. When the magnetic field is perpendicular to the ab-plane, the magnetic susceptibility behavior is identical to that when the field is applied along the ab-plane (Fig. 7(b)), which is quite unusual in single crystal systems, as strong anisotropy is typically observed in such materials. In a single crystal system, the crystal structure exhibits anisotropy, and the magnetic ions located at the lattice points often also exhibit magnetic anisotropy. For example, in the triangular lattice systems such as Ba₃CoSb₂O₉ (ref. 21 and 22) and Cs₂CuCl₄,²³ magnetic susceptibility anisotropy is observed even within the paramagnetic temperature range. Furthermore, for the spin liquid candidate material YMgGaO₄,²⁴ the θ_CW values are approximately −1.47 K and −2.7 K when the magnetic field is applied parallel and perpendicular to the c-axis, respectively. The magnetism in Ba₄CuNb₃O₁₂ originates from Cu²⁺, and the isotropic magnetism should be attributed to the randomness in atomic occupancy between Cu and Nb in the face-sharing CuO₆ and NbO₆ octahedra.

Fig. 7 ZFC and FC magnetic susceptibility of the Ba₄CuNb₃O₁₂ single crystal for a field (a) along the ab-plane and (b) perpendicular to the ab-plane. Inset of (b): the four magnetic susceptibility curves in the main figures (a) and (b), reflecting a high degree of overlap. (c) Temperature dependence of the inverse magnetic susceptibility for a field along the ab-plane. The red line represents the modified Curie–Weiss fitting. (d) Magnetization curves for a field applied along the ab-plane and perpendicular to the ab-plane. Inset: Magnification of the magnetic moment under a high magnetic field. (e) Schematic diagram of the measurement geometry for the (f) angular (θ)-dependent magnetization curve.

The temperature-dependent 1/χ results indicate that the modified CW law, χ = χ₀ + C/(T − θ_CW), is valid in the temperature range of 2 K to 300 K. Here, C is the Curie constant, and χ₀ represents the temperature-independent contributions from the core-diamagnetic (originating from both the sample and the sample holder) and Van Vleck susceptibility (Fig. 7(c)).^25,26 The effective magnetic moment (μ_eff) of Cu²⁺ is fitted to be 1.14 μ_B, with a θ_CW of −1.14 K and a χ₀ value of −0.00012 emu mol⁻¹ Oe⁻¹. The negative θ_CW indicates the existence of antiferromagnetic correlation in the system. Importantly, in the ground state of Ba₄CuNb₃O₁₂, magnetic Cu²⁺ ions can undergo superexchange interactions with the nearest Cu²⁺ ions via the Cu²⁺–O–O–(Nb⁵⁺/Cu⁺)–O–O–Cu²⁺ pathway, leading to the formation of antiferromagnetic correlations (Fig. S3†).²⁷ Certainly, this represents only the most probable superexchange pathway, and due to the randomness of the Cu²⁺ position, other possible superexchange pathways are not discussed in detail.

Notably, the obtained μ_eff = 1.14 μ_B is lower than the theoretical value of g[S(S + 1)]^1/2 = 1.73 μ_B, (assuming g = 2.0 and S = 1/2), where the spin–orbit coupling effect is ignored. In some spin-frustrated systems, the observed magnetic moment is lower than the theoretical value.^28,29 In an antiferromagnetic system, the frustration parameter is given by f = |θ_CW|/T_N. For the Ba₄CuNb₃O₁₂ single crystal, since the T_N value cannot be determined from magnetic susceptibility data, estimating the frustration parameter is challenging. This also requires testing of the magnetic properties at lower temperatures, such as ³He refrigeration or dilution refrigeration (³He–⁴He) equipment. Furthermore, it is important to note that if Cu atoms form a perfect triangular lattice, as seen in systems like Ba₃CuSb₂O₉,²⁹ spin frustration is highly likely to occur. In Ba₄CuNb₃O₁₂, Cu and Nb atoms jointly form a triangular lattice, the random occupancy of Cu ions makes geometric frustration unlikely (Fig. 1(b)). However, the spin frustration may still arise due to competition between the nearest-neighbor and next-nearest-neighbor magnetic exchange interactions.^30–32

To investigate the possible existence of a spin glass or cluster glass state in the Ba₄CuNb₃O₁₂ single crystal, we conducted AC magnetic susceptibility tests (Fig. S4†). The results show that when the AC magnetic field is applied along the ab-plane with no DC magnetic field, the Ba₄CuNb₃O₁₂ single crystal exhibits a peak at approximately 25 K with noticeable frequency dependence. However, since the peak position remains unchanged with frequency, the presence of a spin glass or cluster glass state can be ruled out. In fact, a similar frequency-dependent variation in the peak intensity has also been observed in La_1.5Ca_0.5(Co_0.5Fe_0.5)IrO₆ (ref. 33) and Sr₆(Co_0.8Fe_0.2)₅O₁₅,²⁶ though the peak position remains unchanged, and the underlying physical origin of this behavior requires further investigation. Additionally, as for whether there is a short-range magnetic correlation, it is still difficult to give a clear conclusion based on the AC magnetic susceptibility.

The magnetization curves M(H) measured at 2 K in the field range of −7 to 7 T show similar behavior for both field orientations (Fig. 7(d)). At 7 T, the magnetic moments along the c-axis and the ab-plane are 0.38 μ_B and 0.35 μ_B, respectively, as shown in the inset of Fig. 7(d). However, the slight difference in magnetic moments between the two, within [(0.38 − 0.35)/0.38] × 100% = 7.89%, may be attributed to the fact that the spins of Cu ions tend to align in the ab-plane, indicating easy-plane anisotropy rather than easy-axis anisotropy.³⁴ Furthermore, we obtained the angle-dependence of the magnetization curve for a magnetic field 0.1 T along the ab-plane at 10 K, as shown in Fig. 7(e) and (f). When the magnetic field rotates within the ab-plane, the magnetic moment remains constant, indicating the isotropic nature of the in-plane magnetism.

5. Specific heat

The specific heat results of the Ba₄CuNb₃O₁₂ single crystal show no magnetic phase transition within the temperature range of 2 K to 200 K (Fig. 8), which is consistent with the magnetic behavior observed in the magnetic susceptibility curve. Importantly, our experimental data are well fitted by the Debye–Einstein model (red solid line in Fig. 8)
which describes the phonon behavior (x = ℏω/k_BT). Here, ω, R, Θ_D, Θ_Ei, N_D and N_Ei represent the phonon frequency, universal gas constant, Debye temperature, Einstein temperature, the number of acoustic phonon branches, and the number of optical branches with the same Θ_Ei, respectively.^35,36 The best fitting parameters can be obtained as Θ_D = 199 K, Θ_E1 = 307 K, Θ_E2 = 510 K, Θ_E3 = 2100 K, N_D = 3, N_E1 = 2, N_E2 = 3, and N_E3 = 52. Furthermore, according to the formula 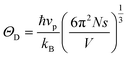, where N is the number of molecules per mole, s is the number of atoms in each molecule, and V is the volume of the crystal, and the average velocity v_p of phonons is calculated to be 2014.98 m s⁻¹.

Fig. 8 Specific heat of the Ba₄CuNb₃O₁₂ single crystal. The red solid line represents the phonon specific heat contribution fitted using the Debye–Einstein model.

In addition, since the ratio of Nb2 to Cu atoms in the triangular lattice formed by Nb2/Cu is about 1 : 2, this configuration effectively places two non-magnetic Nb2 atoms and one magnetic Cu atom at the triangular lattice sites. The spin exchange interaction is between Cu atoms via O atoms. The insufficient number of Cu atoms occupying the lattice sites increases the exchange path, which weakens the correlation between the Cu atoms (Fig. S3†). In geometrically frustrated systems, such as those with triangular, kagome, and honeycomb lattices, the introduction of non-magnetic atoms can often have a significant impact on the spin exchange interactions between magnetic atoms, thereby altering the ground state of the system.^37,38

Summary

In summary, we thoroughly explored the flux method for growing Ba₄CuNb₃O₁₂ single crystals and identified the most effective synthesis approach. Additionally, we investigated the magnetic properties of the Ba₄CuNb₃O₁₂ single crystal, both parallel and perpendicular to the ab-plane, with the findings confirming that the material exhibits an antiferromagnetic ground state. The reduced occupancy of Cu atoms at the triangular lattice sites extends the exchange path, weakening the interactions between the Cu atoms in Ba₄CuNb₃O₁₂. Furthermore, the specific heat data of Ba₄CuNb₃O₁₂ exhibit a strong correspondence with the Debye–Einstein phonon model, yielding estimates for the Debye temperature and the average phonon velocity as 199 K and 2014.98 m s⁻¹, respectively.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

Yuhu Huang and Wen Xie: data curation, investigation, software, and validation. Fei Zheng: investigation, formal analysis, software, and reviewing. Chao Zhang: data curation, formal analysis, and supervision. Han-Shu Xu: methodology, writing – original draft, supervision, and review and editing, funding acquisition, formal analysis, and visualization.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We deeply appreciate Prof. Kaibin Tang (USTC) for his constructive comments on this work, and we are also grateful to Ivan Kostylev (OIST) for his technical support. This work is supported by the National Natural Science Foundation of China (Grant No. 12204452) and the Grants for Scientific Research of BSKY from Anhui Medical University.

References

1. L. T. Nguyen and R. J. Cava, Hexagonal perovskites as quantum materials, Chem. Rev., 2020, 121(5), 2935–2965.
2. K. Matsuzaki, K. Saito, Y. Ikeda, Y. Nambu and M. Yashima, High proton conduction in the octahedral layers of fully hydrated hexagonal perovskite-related oxides, J. Am. Chem. Soc., 2024, 146(27), 18544–18555.
3. H.-C. zur Loye, Q. Zhao, D. E. Bugaris and W. M. Chance, 2 H-perovskite related oxides: Synthesis, structures, and predictions, CrystEngComm, 2012, 14(1), 23–39.
4. H.-S. Xu, Y. Huang, J. Li and F. Zheng, Magnetic Properties and Specific Heat of Quasi-Two-Dimensional Triangular Lattice Antiferromagnet Ba₃CoNb₂O₉ Single Crystals, J. Phys. Chem. C, 2025, 129(2), 1562–1567.
5. Y. Huang and H.-S. Xu, Growth of Fe-Substituted Sr₆Co₅O₁₅ Hexagonal Perovskite Single Crystals by a Flux Method, Cryst. Growth Des., 2023, 23(5), 3747–3753.
6. J. Li, H.-S. Xu, J. Hu, Y. Huang, W. Xie, D. Yu and K. Tang, Comparative Study on the Electrocatalytic Performance of ABO₃-Based Hexagonal Perovskite Oxides with Different [AO₃] Layers, Inorg. Chem., 2024, 63(50), 23601–23613.
7. W. Cao, X. Yang, F. Lu, W. Zhu, L. Liu, X. Kuang and M. Allix, 8H–10H stacking periodicity control in twinned hexagonal perovskite dielectrics, Inorg. Chem., 2018, 57(7), 4117–4124.
8. E. F. Jendrek Jr., A. D. Potoff and L. Katz, A single-crystal study of eight-layer barium niobium lithium oxide, Ba₄Nb₃LiO₁₂, J. Solid State Chem., 1974, 9(4), 375–379.
9. T. Negas, R. Roth, H. Parker and W. Brower, Crystal chemistry of lithium in octahedrally coordinated structures. I. Synthesis of Ba8 (Me₆Li₂) O₂₄ (Me = Nb or Ta) and Ba₁₀ (W₆Li₄) O₃₀. II. The tetragonal bronze phase in the system BaO Nb₂O₅ Li₂O, J. Solid State Chem., 1973, 8(1), 1–13.
10. N. Teneze, P. Boullay, V. Petricek, G. Trolliard and D. Mercurio, Structural study of the cation ordering in the ternary oxide Ba₈Ti₃Nb₄O₂₄, Solid State Sci., 2002, 4(9), 1129–1136.
11. R. Rawal, A. Feteira, A. A. Flores, N. C. Hyatt, A. R. West, D. C. Sinclair, K. Sarma and N. M. Alford, Dielectric properties of the “twinned” 8H-hexagonal perovskite Ba₈Nb₄Ti₃O₂₄, J. Am. Ceram. Soc., 2006, 89(1), 336–339.
12. P. Battle, S. Kim and A. Powell, The crystal structure and electronic properties of Ba₄Ru₃MO₁₂ (M = Li, Na, Mg, Zn), J. Solid State Chem., 1992, 101(1), 161–172.
13. F. Tao, C. Liang, X. Wang, X. Li, F. Porcher, M. Allix, F. Lu, H. Gong, L. Liu and X. Kuang, 8-layer shifted hexagonal perovskite Ba₈MnNb₆O₂₄: long-range ordering of high-spin d5 Mn²⁺ layers and electronic structure, Inorg. Chem., 2018, 57(10), 5732–5742.
14. R. Rawl, L. Ge, Z. Lu, Z. Evenson, C. Dela Cruz, Q. Huang, M. Lee, E. Choi, M. Mourigal and H. Zhou, Ba₈MnNb₆O₂₄: A model two-dimensional spin-5 2 triangular lattice antiferromagnet, Phys. Rev. Mater., 2019, 3(5), 054412.
15. N. Kumada, W. Zhang, Q. Dong, T. Mochizuki, Y. Yonesaki, T. Takei and N. Kinomura, Crystal structure and X-ray diffraction data of a new hexagonal perovskite compound, Ba₄CuNb₃O₁₂, Powder Diffr., 2011, 26(3), 244–247.
16. L. Balents, Spin liquids in frustrated magnets, Nature, 2010, 464(7286), 199–208.
17. Z. Zhu, P. A. Maksimov, S. R. White and A. L. Chernyshev, Disorder-Induced Mimicry of a Spin Liquid in YbMgGaO₄, Phys. Rev. Lett., 2017, 119(15), 157201.
18. Y. Li, D. Adroja, R. I. Bewley, D. Voneshen, A. A. Tsirlin, P. Gegenwart and Q. Zhang, Crystalline Electric-Field Randomness in the Triangular Lattice Spin-Liquid YbMgGaO₄, Phys. Rev. Lett., 2017, 118(10), 107202.
19. B. Sun, R. Boutellier, P. Sciau, E. Burkhardt, V. Rodriguez and H. Schmid, High temperature solution growth of perovskite Pb₂CoWO₆ single crystals, J. Cryst. Growth, 1991, 112(1), 71–83.
20. M. L. Mulvihill, S. E. Park, G. Risch, Z. Li, K. U. K. Uchino and T. R. S. T. R. Shrout, The role of processing variables in the flux growth of lead zinc niobate-lead titanate relaxor ferroelectric single crystals, Jpn. J. Appl. Phys., 1996, 35(7R), 3984.
21. A. Sera, Y. Kousaka, J. Akimitsu, M. Sera, T. Kawamata, Y. Koike and K. Inoue, S = 1 2 triangular-lattice antiferromagnets Ba₃CoSb₂O₉ and CsCuCl₃: Role of spin-orbit coupling, crystalline electric field effect, and Dzyaloshinskii-Moriya interaction, Phys. Rev. B, 2016, 94(21), 214408.
22. H. D. Zhou, C. Xu, A. M. Hallas, H. J. Silverstein, C. R. Wiebe, I. Umegaki, J. Q. Yan, T. P. Murphy, J.-H. Park and Y. Qiu, Successive Phase Transitions and Extended Spin-Excitation Continuum in the S = ½ Triangular-Lattice Antiferromagnet Ba₃CoSb₂O₉, Phys. Rev. Lett., 2012, 109(26), 267206.
23. Y. Tokiwa, T. Radu, R. Coldea, H. Wilhelm, Z. Tylczynski and F. Steglich, Magnetic phase transitions in the two-dimensional frustrated quantum antiferromagnet Cs₂CuCl₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(13), 134414.
24. Y. Li, G. Chen, W. Tong, L. Pi, J. Liu, Z. Yang, X. Wang and Q. Zhang, Rare-earth triangular lattice spin liquid: a single-crystal study of YbMgGaO₄, Phys. Rev. Lett., 2015, 115(16), 167203.
25. S. Mugiraneza and A. M. Hallas, Tutorial: a beginner's guide to interpreting magnetic susceptibility data with the Curie-Weiss law, Commun. Phys., 2022, 5(1), 95.
26. H.-S. Xu, S. Zeng, S. Fang, Y. Huang, W. Xie, H. Huang, Y. Lu and K.-B. Tang, Tunability of magnetization in hexagonal perovskite Sr₆Co₅O₁₅ ceramics through 20% Fe-substitution, J. Magn. Magn. Mater., 2023, 573, 170648.
27. J. Cheng, W. Tian, J. Zhou, V. M. Lynch, H. Steinfink, A. Manthiram, A. F. May, V. O. Garlea, J. C. Neuefeind and J. Yan, Crystal and magnetic structures and physical properties of a new pyroxene NaMnGe₂O₆ synthesized under high pressure, J. Am. Chem. Soc., 2013, 135(7), 2776–2786.
28. H. D. Zhou, B. W. Vogt, J. A. Janik, Y. J. Jo, L. Balicas, Y. Qiu, J. R. D. Copley, J. S. Gardner and C. R. Wiebe, Partial Field-Induced Magnetic Order in the Spin-Liquid Kagome Nd₃Ga₅SiO₁₄, Phys. Rev. Lett., 2007, 99(23), 236401.
29. J. E. Greedan, Geometrically frustrated magnetic materials, J. Mater. Chem., 2001, 11(1), 37–53.
30. Y. Ishiguro, K. Kimura, S. Nakatsuji, S. Tsutsui, A. Q. Baron, T. Kimura and Y. Wakabayashi, Dynamical spin–orbital correlation in the frustrated magnet Ba₃CuSb₂O₉, Nat. Commun., 2013, 4(1), 2022.
31. Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato and G. Saito, Spin liquid state in an organic Mott insulator with a triangular lattice, Phys. Rev. Lett., 2003, 91(10), 107001.
32. R. Coldea, D. Tennant, A. Tsvelik and Z. Tylczynski, Experimental realization of a 2D fractional quantum spin liquid, Phys. Rev. Lett., 2001, 86(7), 1335.
33. L. Bufaiçal, M. Heringer, J. Jesus, A. Caytuero, C. Macchiutti, E. Bittar and E. Baggio-Saitovitch, Structural, electronic and magnetic properties of La_1.5Ca_0.5(Co_0.5Fe_0.5) IrO₆ double perovskite, J. Magn. Magn. Mater., 2022, 556, 169408.
34. K. Y. Povarov, L. Facheris, S. Velja, D. Blosser, Z. Yan, S. Gvasaliya and A. Zheludev, et al. , Phys. Rev. Res., 2020, 2(4), 043384.
35. P. Svoboda, P. Javorský, M. Diviš, V. Sechovský, F. Honda, G. Oomi and A. A. Menovsky, Importance of anharmonic terms in the analysis of the specific heat of UNi₂Si₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(21), 212408.
36. F. W. de Wette and A. D. Kulkarni, Phonon dispersion, phonon specific heat, and Debye temperature of high-temperature superconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(22), 14922–14925.
37. Z. Zhang, D. Louca, A. Visinoiu, S. H. Lee, J. D. Thompson, T. Proffen, A. Llobet, Y. Qiu, S. Park and Y. Ueda, Local order and frustration in the geometrically frustrated spinels Cd_1-xZn_xV₂O₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(1), 014108.
38. J. P. Sheckelton, J. R. Neilson and T. M. McQueen, Electronic tunability of the frustrated triangular-lattice cluster magnet LiZn_2−xMo₃O₈, Mater. Horiz., 2015, 2(1), 76–80.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ce00085h

---