Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystal growth of calcium oxalate mono- and dihydrate under laminar flow in microfluidic devices†
Fatma
İbiş-Özdemir
a,
René
Smeets
a,
Jiali
Wang
a,
Priya
Dhand
a,
Majid
Mohamedhoesein
a,
Frederico Marques
Penha
 b,
Johan
Grievink
a,
Antoine E. D. M.
van der Heijden
a,
Herman J. M.
Kramer
a and
Huseyin Burak
Eral
b,
Johan
Grievink
a,
Antoine E. D. M.
van der Heijden
a,
Herman J. M.
Kramer
a and
Huseyin Burak
Eral
 *ac
*ac
aComplex Fluid Processing, Process & Energy Department, Delft University of Technology, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands. E-mail: H.B.Eral@tudelft.nl
bDepartment of Chemical Engineering, KTH Royal Institute of Technology, Teknikringen 42, SE100-44 Stockholm, Sweden
cVan't Hoff Laboratory for Physical and Colloid Chemistry, Debye Institute for Nanomaterials Science Utrecht University, 3584 CH Utrecht, The Netherlands
First published on 2nd January 2025
Abstract
Calcium oxalate (CaOx) crystallization under laminar flow conditions, relevant for kidney stone formation, was studied in a microfluidic device simulating the geometry of kidney collecting ducts. In a typical microfluidic experiment, two reactive solutions with designated concentrations of calcium (Ca) and oxalate (Ox) ions were brought into contact in a microfluidic channel to create a laminar co-current flow of the two streams. As the streams flow co-currently in the channel, diffusion takes place between the two streams across the channel width, resulting in reactive crystallization leading to CaOx nucleation and growth of CaOx crystals along the mixing front. We studied the growth of these crystals in artificial urine as a function of the fluid flow rate in the channel, the molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox in the medium and the presence of an organic protein, osteopontin (OPN), known to inhibit the growth of CaOx crystals. Three different flow velocities at a fixed molar ratio of Ca
Ox in the medium and the presence of an organic protein, osteopontin (OPN), known to inhibit the growth of CaOx crystals. Three different flow velocities at a fixed molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox = 7.5 and four molar ratios of Ca
Ox = 7.5 and four molar ratios of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox at a fixed mean flow velocity of 0.035 m s−1 were tested. Lastly, three additive OPN concentrations were evaluated: 2.4 × 10−8 mol m−3, 6 × 10−8 mol m−3 and 8.4 × 10−8 mol m−3. The mean flow velocity did not alter the crystal growth of CaOx in the studied range, whereas altering the molar ratio of Ca
Ox at a fixed mean flow velocity of 0.035 m s−1 were tested. Lastly, three additive OPN concentrations were evaluated: 2.4 × 10−8 mol m−3, 6 × 10−8 mol m−3 and 8.4 × 10−8 mol m−3. The mean flow velocity did not alter the crystal growth of CaOx in the studied range, whereas altering the molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox had a high impact on the growth rate. In addition, the type of pseudopolymorph which nucleated appears to depend strongly on the molar ratio. At a low Ca
Ox had a high impact on the growth rate. In addition, the type of pseudopolymorph which nucleated appears to depend strongly on the molar ratio. At a low Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox ratio, both calcium oxalate monohydrate (COM) and calcium oxalate dihydrate (COD) nucleated simultaneously and the growth of the two pseudopolymorphic forms of CaOx crystals was observed. The lowest applied OPN concentration decreased the growth rate of COD, while higher concentrations of OPN slowed down the nucleation kinetics to a point that it completely inhibited the formation of any CaOx crystal in artificial urine within the investigated timeframe. COD was seen under all the conditions investigated, whilst COM was seen in experiments for Ca
Ox ratio, both calcium oxalate monohydrate (COM) and calcium oxalate dihydrate (COD) nucleated simultaneously and the growth of the two pseudopolymorphic forms of CaOx crystals was observed. The lowest applied OPN concentration decreased the growth rate of COD, while higher concentrations of OPN slowed down the nucleation kinetics to a point that it completely inhibited the formation of any CaOx crystal in artificial urine within the investigated timeframe. COD was seen under all the conditions investigated, whilst COM was seen in experiments for Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox molar ratio values between 5 and 6. Our results were rationalized using finite element simulations supported by solution chemistry modelling.
Ox molar ratio values between 5 and 6. Our results were rationalized using finite element simulations supported by solution chemistry modelling.
1. Introduction
Kidney stones are a serious health problem affecting around 12% of the world's population.1–4 Each human kidney has approximately 1.2 million nephrons comprised of hollow tubes assembled into a single cell layer. It is the smallest structural and functional unit of this organ. The nephrons comprise a renal corpuscle, proximal tubule, loop of Henle, distal tubule, and collecting duct system.5–7 Around ten nephrons give birth to one single collecting duct whose diameter is about 100 μm.8,9 The urine flow rate is roughly 10.0 nl min−1, showing laminar flow inside such a collecting duct.8,10 Overall, the urinary system filters around 150–180 L per day fluid from renal blood flow to keep essential compounds in the blood while removing toxins, ions, and metabolic waste products. Per day, 1.5 liters of urine are extracted after absorbing water through diffusion and active transport.11,12 If during this extraction process in the kidney, the solution reaches supersaturated conditions for certain minerals, crystallization of so-called kidney stones can occur. A plethora of physicochemical phenomena such as nucleation, crystal growth, aggregation and adhesion play a role in forming such kidney stones, making their formation a challenging multiscale process to understand.2–4,11,12Approximately 80% of kidney stones are comprised of calcium oxalate (CaOx).13–15 CaOx occurs in nature as monohydrate (whewellite, CaC2O4·H2O, COM), dihydrate (weddellite, CaC2O4·2H2O, COD) and trihydrate (caoxite, CaC2O4·3H2O, COT), differing by the amount of H2O in their crystalline structure.16–18 Different hydrated forms are also known as pseudopolymorphs which is a type of polymorphism and characterized by solvate compounds. Calcium oxalate monohydrate (COM) is the most common and stable form with very low water solubility; 1.24 × 10−4 M in ultrapure water at 37 °C.16,19–21 Kidney stones occur when the urine volume is low, and calcium, salt, oxalate, and urate concentrations are high.22
Research has been done on the formation of CaOx in a large variety of solutions ranging from pure calcium and oxalate to complex solutions that mimic the kidney's solutions. These studies showed that numerous compounds may either promote or inhibit the production of stones. Various inorganic and organic compounds such as citrate, magnesium, nephrocalcin, urine prothrombin fragment-1, and osteopontin (OPN) are thought to inhibit stone formation.23 OPN is a single-chain protein with a molecular weight of roughly 33 kDa, present in urine in amounts greater than 100 nM.24 Studies show that OPN hinders crystal formation and alters the shape of CaOx crystals.1,24–26
In vitro studies focusing on CaOx stone formation in water or artificial urine with different additives have been extensively reported.27–35 Researchers have examined the effect of the molar ratio,28 potential inhibitors,27,31,36 and quality of water on kidney stone formation.30 To control momentum, heat and mass transfer on the micro-scale, microfluidic approaches have been proposed and successfully implemented for kidney stone formation.21,37–39 We report on the growth of calcium oxalate (CaOx) crystals in a microchannel, mimicking the geometry of kidney collecting ducts under flow conditions relevant for kidney stone formation. In this device, two solutions carrying Ca2+ and Ox2− ions, respectively, are brought into contact with each other in the microchannel and time-lapse images of the emerging crystals are analyzed to determine the type of pseudopolymorph that nucleated and to quantify the average growth rates of the formed crystals. The growth rate of the nucleated COM or COD crystals in artificial urine was studied as a function of the fluid flow rate in the channel, the molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox, and the inhibitor concentration. To qualitatively rationalize the crystals growing in microfluidic devices, the velocity and the concentration of a diffusing species under laminar flow in the microchannel were calculated via COMSOL Multiphysics. The values from COMSOL were used in solution chemistry modelling using Joint Expert Speciation System (JESS) software to find supersaturation values (see details in the ESI†).
Ox, and the inhibitor concentration. To qualitatively rationalize the crystals growing in microfluidic devices, the velocity and the concentration of a diffusing species under laminar flow in the microchannel were calculated via COMSOL Multiphysics. The values from COMSOL were used in solution chemistry modelling using Joint Expert Speciation System (JESS) software to find supersaturation values (see details in the ESI†).
2. Materials and methods
2.1. Microfluidic device
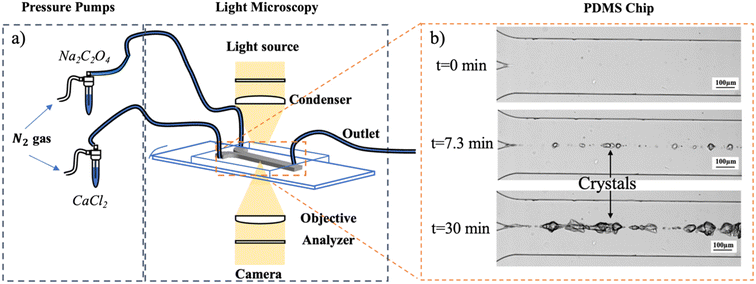
A microfluidic device, fabricated with polydimethylsiloxane (PDMS, (C2H6OSi)n, The Dow Chemical Company), is used to mimic the collecting duct in a nephron. The microchannel has a length of 1500 μm, a depth of 45 μm and a width of 295 μm.A mixture of PDMS and curing agents at a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (w/w) ratio is arranged to prepare the chips. The mixture is stirred manually until it is filled with air bubbles and becomes cloudy. Upon mixing, the mixture is centrifuged (Universal 320 R, Hettich Zentrifugen) at 7400 rpm and 20 °C for 15 minutes to remove air bubbles. Then, the transparent PDMS mixture is put onto a silicon wafer (Fig. S1 in the ESI†) produced by lithography in a cleanroom, previously hydrophobized with a thin layer of trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma-Aldrich, CAS 78560-45-9) to make the peeling process easier. The silicon wafer is put upside down in a desiccator with 10 μl of trichlorosilane and connected to a vacuum pump. The pressure is lowered to 100 mbar and kept for two hours. After this process, the trichlorosilane-coated silicon wafer can be used four times; then, the hydrophobization protocol needs to be repeated to use the wafer again. The wafer filled with the PDMS mixture is later placed in a desiccator connected to a vacuum pump for 1 hour to eliminate the air bubbles created during the pouring step. The wafer is placed in a 65 °C oven overnight to ensure that the PDMS is completely cured.
1 (w/w) ratio is arranged to prepare the chips. The mixture is stirred manually until it is filled with air bubbles and becomes cloudy. Upon mixing, the mixture is centrifuged (Universal 320 R, Hettich Zentrifugen) at 7400 rpm and 20 °C for 15 minutes to remove air bubbles. Then, the transparent PDMS mixture is put onto a silicon wafer (Fig. S1 in the ESI†) produced by lithography in a cleanroom, previously hydrophobized with a thin layer of trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma-Aldrich, CAS 78560-45-9) to make the peeling process easier. The silicon wafer is put upside down in a desiccator with 10 μl of trichlorosilane and connected to a vacuum pump. The pressure is lowered to 100 mbar and kept for two hours. After this process, the trichlorosilane-coated silicon wafer can be used four times; then, the hydrophobization protocol needs to be repeated to use the wafer again. The wafer filled with the PDMS mixture is later placed in a desiccator connected to a vacuum pump for 1 hour to eliminate the air bubbles created during the pouring step. The wafer is placed in a 65 °C oven overnight to ensure that the PDMS is completely cured.
Spin coating (Polos 300, The Netherlands) is used to make a closed microfluidic system. A 0.5 ml aliquot of a mixture of PDMS and curing agent at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio is poured onto a glass slide (VWR International), and the glass slide is fully covered with a thin layer of PDMS at 4500 rpm for one minute. The spin-coated glass slide is placed in a 90 °C oven for 20 minutes. The solid PDMS is bonded to a glass slide to make a closed microfluidic device. This device is left in the oven at 65 °C overnight to cure thoroughly. Three holes are punched in the PDMS chip after the curing step is completed: two for inlets and one for an outlet. The resulting microfluidic device is displayed in Fig. S1 in the ESI.†
1 ratio is poured onto a glass slide (VWR International), and the glass slide is fully covered with a thin layer of PDMS at 4500 rpm for one minute. The spin-coated glass slide is placed in a 90 °C oven for 20 minutes. The solid PDMS is bonded to a glass slide to make a closed microfluidic device. This device is left in the oven at 65 °C overnight to cure thoroughly. Three holes are punched in the PDMS chip after the curing step is completed: two for inlets and one for an outlet. The resulting microfluidic device is displayed in Fig. S1 in the ESI.†
2.2. Experimental set-up
In the microfluidic device, the growth of CaOx crystals was induced by sending in two inlets calcium chloride (CaCl2) and sodium oxalate (Na2C2O4) aqueous solutions in artificial urine, respectively, (see subsection 1.2.5.). The reservoirs with filtered (0.45 μm filter) CaCl2 and Na2C2O4 aqueous solutions were connected to a pressure pump (Fluigent, MFCS- EZ) and the microfluidic device with capillary tubing (Warner Instruments, 0.28 mm inner diameter) (Fig. 1a). The volumetric flow rate resulting from a fixed applied pressure used in this study was measured by weighing the amount of water pumped through the system as a function of time. With known channel dimensions, the calculated volumetric flow rate was converted to mean flow velocities reported. The applied pressure difference of 25–85 dPa resulted in flow velocities of 0.015–0.075 m s−1, respectively. Crystal growth was monitored using an automated optical microscope (Nikon Ti Series Inverted Microscope). One image was saved every 4 seconds for 30 minutes. The crystal growth at t = 0, t = 7.3, and t = 30 minutes for experiment AU4 is shown in Fig. 1b.2.3. COMSOL model and JESS software
To rationalize the crystal growth of calcium oxalate qualitatively, the concentration gradients established due to the diffusion and convection in the laminar flow in the microchannel were calculated using COMSOL Multiphysics (see the ESI†). The calculated concentration profiles (considering 1.2, 1.6, 2.0 and 2.4 mol m−3 Na2C2O4 at fixed 12 mol m−3 CaCl2) in the channel were then used to calculate the relative supersaturation (σ) (Table 2) profiles in artificial urine values using Joint Expert Speciation System (JESS) software (see the ESI†). Since OPN and creatinine were not included in the JESS database, these compounds were not considered in the supersaturation profile estimation.2.4. Calculation method for the crystal growth rate
The image analysis tool Cellprofiler was used to analyze crystal areas using crystal images from the experiments. This detection was repeated for consecutive images with a time step of 40 seconds for 7.3 minutes starting at the emergence of the first crystal. This period for the growth rate calculation was chosen to avoid interferences in growth rate calculations by agglomeration in the channels observed at later stages in the experiments. An equivalent spherical shape was considered to calculate the radial growth of CaOx crystals. The measured 2D surface area (A) of about five crystals was converted to average radial size (ravg) using eqn (1).

| (1) |
2.5. Solution preparation with artificial urine
Artificial urine solution was prepared following the procedure reported by Streit et al.40 (see Table 1). The ingredients (Table 1) were dissolved in ultrapure water using an ultrasonic probe to prepare artificial urine. CaCl2 and Na2C2O4 were added and dissolved in artificial urine in separate beakers just before the experiments and sent to the microchannel via two different inlets. The CaCl2 and Na2C2O4 concentrations added to fresh artificial urine are seen in Table 2.| Compounds | Molarity [mM] | Source |
|---|---|---|
| Sodium chloride (NaCl) | 90 | Fluka |
| Potassium chloride (KCl) | 42 | Emsure |
| Ammonium chloride (NH4Cl) | 20 | Sigma-Aldrich |
| Creatinine (C4H7N3O) | 7 | Sigma-Aldrich |
| Urea (CH4N2O) | 300 | Emprove |
| Trisodium citrate (Na3C6H5O7) | 2 | Emprove |
| Magnesium sulphate heptahydrate (MgSO4·7H2O) | 2 | Sigma-Aldrich |
| Sodium sulphate (NaSO4) | 13 | Sigma-Aldrich |
| Monobasic sodium phosphate (NaH2PO4) | 16 | Sigma-Aldrich |
| Experiment name | Molar ratio Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox Ox |
Added CaCl2 [mol m−3] | Added NaC2O4 [mol m−3] | U [m s−1] | σ values for COM from JESS | σ values for COD from JESS |
|---|---|---|---|---|---|---|
| AU1 | 7.5 | 12 | 1.6 | 0.015 | 46.8 | 17.8 |
| AU2 | 0.035 | |||||
| AU3 | 0.075 | |||||
| AU4 | 5 | 2.4 | 0.035 | 67.6 | 26.3 | |
| AU5 | 6 | 2.0 | 57.5 | 21.9 | ||
| AU6 | 10 | 1.2 | 34.7 | 13.5 |
Three main conditions, varying velocity, the molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox, in other words, supersaturation (σ) (in Table 2), and addition of OPN (Table 3), were tested in nine different experiments in artificial urine (AU) at room temperature.
Ox, in other words, supersaturation (σ) (in Table 2), and addition of OPN (Table 3), were tested in nine different experiments in artificial urine (AU) at room temperature.
| Experiment name | Molar ratio Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox Ox |
Added CaCl2 [mol m−3] | Added NaC2O4 [mol m−3] | Added OPN [10−8 mol m−3] | U [m s−1] |
|---|---|---|---|---|---|
| AU7 | 7.5 | 12 | 1.6 | 2.4 | 0.015 |
| AU8 | 6.0 | ||||
| AU9 | 8.4 |
It is noteworthy that the concentration of calcium was kept constant and higher than the other ions throughout all the experiments, in an effort to resemble the hypercalciuria condition in kidney stone patients – high Ca levels in the urine – while different flow velocities simulate urine flows – low urine flows reportedly increase kidney stone occurrence.14,16,41–43
3. Results and discussion
The growth rates (ṙavg) of both COM & COD crystals in artificial urine were determined under nine different conditions (Fig. 2–4). The concentrations of calcium and oxalate ions were estimated as a function of the position in the channel using COMSOL. The supersaturation profiles (σ) of COM and COD were calculated using these concentration profiles in JESS. As the crystals settled in the channel, the growth rates of individual crystals could be determined.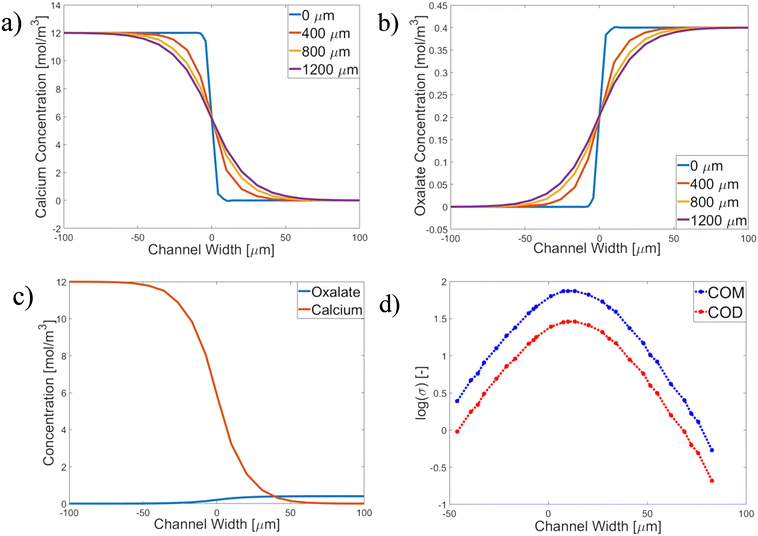 | ||
| Fig. 2 Calcium and oxalate concentration profiles and σ-profile of experiment AU3 ([Ca2+] = 12 mol m−3 and [Ox2−] = 1.6 mol m−3 at U = 0.075 m s−1, see Table 3) at the bottom of the channel with (a) concentration profiles of Ca2+ at different length positions (along the microchannel); (b) concentration profiles of Ox2− at different length positions; (c) concentration profiles of Ca2+ (red) and Ox2− (blue) at x = 800 μm (see Fig. S3 in the ESI†) considering that Ca2+ was fed at the right inlet (negative width region) and Ox2− at the upper inlet (positive width region) (experiment AU3). (d) Logarithmic σ-profiles along the channel width for both COM and COD at x = 8000 μm. | ||
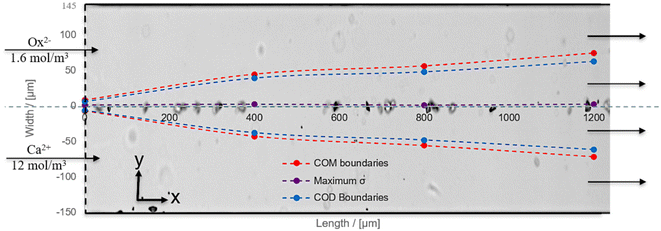 | ||
| Fig. 3 COMSOL model combined with the image from artificial urine experiments at t = 7.3 min after the first observed crystal. Display of the situation for artificial urine experiment AU2 (see Fig. 4) with its experimental image. | ||
Summarized in Table 4 are the values for the flow velocity, the concentration of OPN, and the estimated relative supersaturation (σ) using JESS in the different experiments, along with the determined values of the average growth rates at t = 7.3 min.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox ratio, flow velocity (U), added amount of OPN, supersaturation ratio values (σ) from JESS and growth rate (ṙavg) are shown. The presence of OPN was not taken into account in the calculation of supersaturation
Ox ratio, flow velocity (U), added amount of OPN, supersaturation ratio values (σ) from JESS and growth rate (ṙavg) are shown. The presence of OPN was not taken into account in the calculation of supersaturation
| Experimental conditions | COM | COD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment name | Molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox Ox |
U [m s−1] | OPN [10−8 mol m−3] | σ [−] | ṙ avg [10−8 m s−1] | Std dev. [10−8 m s−1] | σ [−] | ṙ avg [10−8 m s−1] | Std dev. [10−8 m s−1] |
| AU1 | 7.5 | 0.015 | — | 46.8 | — | — | 17.8 | 0.95 | 0.27 |
| AU2 | 7.5 | 0.035 | — | 46.8 | — | — | 17.8 | 0.93 | 0.45 |
| AU3 | 7.5 | 0.075 | — | 46.8 | — | — | 17.8 | 0.92 | 0.22 |
| AU4 | 5 | 0.035 | — | 67.6 | 0.48 | 0.27 | 26.3 | 3.05 | 0.43 |
| AU5 | 6 | 0.035 | — | 57.5 | 0.50 | 0.28 | 21.9 | 2.33 | 0.12 |
| AU6 | 10 | 0.035 | — | 34.7 | — | — | 13.5 | 0.78 | 0.31 |
| AU7 | 7.5 | 0.015 | 2.4 | 46.8 | — | — | 17.8 | 0.34 | 0.15 |
| AU8 | 7.5 | 0.015 | 6.0 | 46.8 | — | — | 17.8 | — | — |
| AU9 | 7.5 | 0.015 | 8.4 | 46.8 | — | — | 17.8 | — | — |
3.1. Calculation of the supersaturation profile in the microscopy experiments using COMSOL and JESS
Calcium and oxalate concentration and supersaturation profiles through the channel were simulated using COMSOL. Fig. 2 shows the results for experiment AU3 (see Table 3 for the conditions). Fig. 2a and b show the concentration profiles in the channel. Because fixed crystals were observed on the bottom of the channel wall, c- and σ-profiles are shown at the channel bottom (z = 0 μm) at various length positions. The profiles at different positions change and become smoother further down the length of the channel due to diffusion of the Ca and Ox ions (see the ESI†). Fig. 2c shows the concentration profile at x = 800 μm for the ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox = 7.5 (experiment AU3) and Fig. 2d displays the logarithmic supersaturation σ-profiles with respect to COM and COD vs. the channel width at x = 800 μm (length) and z = 0 μm (depth) (the detailed COMSOL method is described in the ESI,† sections S2 and S3). The maximum supersaturation values for COM and COD are seen at y ∼ 2 μm (width) as log(σCOM) = 1.67 (σ = 46.8) and log(σCOD) = 1.25 (σ = 17.8).
Ox = 7.5 (experiment AU3) and Fig. 2d displays the logarithmic supersaturation σ-profiles with respect to COM and COD vs. the channel width at x = 800 μm (length) and z = 0 μm (depth) (the detailed COMSOL method is described in the ESI,† sections S2 and S3). The maximum supersaturation values for COM and COD are seen at y ∼ 2 μm (width) as log(σCOM) = 1.67 (σ = 46.8) and log(σCOD) = 1.25 (σ = 17.8).
The analysis of σ-profiles is done for all length positions and plotted in Fig. 3 after σ calculation with JESS using COMSOL concentration profiles (for details, see the ESI†). The supersaturation for COM is between the red lines, and for COD between the blue lines, while the maximum values of the supersaturation are close to the central dashed line in Fig. 3 (purple dots). Fig. 3 shows the results of experiment AU2 at 7.3 min after the first crystal was observed. The σ-profile is superimposed on the microscopy image of AU2. The trend of the σ-profile from COMSOL overlaps with the measured result. AU2 has 12 mol m−3 calcium and 1.6 mol m−3 oxalate with a molar ratio of 7.5 at a velocity value of 0.035 m s−1. The difference in the concentration of the ions plays a role in the ion diffusion rate.
Fig. 3 shows that the small difference in ion concentrations allows effective diffusion of the oxalate ions into the calcium-rich side and σmax is reached at ≈ 2 μm in the oxalate-rich side. The crystals (experiment AU2) emerged and grew at the interface, near the center of the channel, which overlaps with the COMSOL result.
3.2. Effect of average flow velocity on CaOx crystallization
To investigate the effect of flow velocity on the growth of the CaOx crystals, artificial urine experiments (AU1, AU2 and AU3) were performed with different velocities of 0.015, 0.035, 0.075 m s−1 at a fixed supersaturation value of COD of 17.8. The choice of flow speed range studied was based on reported flow rate values in the human collecting duct in the literature and experimental feasibility. First, we attempted to match the reported flow velocity in the collecting duct of the human kidneys (10 nl min−1 ∼ 0.0016 m s−1),32 which was not possible due to its very low value. Secondly, the maximum flow rate (0.075 m s−1) was experimentally chosen considering the retention of the crystals in the microchannel – higher flow rates would drag the newly formed crystals out. Then, the lowest flow rate studied was selected so that the experiments could be conducted within reasonably accessible timescales in our laboratory. The maximum flow rate (0.075 m s−1) was experimentally chosen considering the retention of the crystals in the microchannel – higher flow rates would drag the newly formed crystals out. Then, the lower flow rates were arbitrarily selected to investigate the effect of the flow rates on CaOx crystal growth, in an effort to understand the effect of low urine fluxes on kidney stone growth. Fig. 4 shows micrographs of the microfluidic channels at different times during the experiment. On the left side, the two inlet channels and their junction, where the CaCl2 and Na2C2O4 solutions meet, can be visualized, as detailed previously (Fig. 1). Crystals exhibiting tetragonal shapes were observed in the middle of the channel, which coincides with the interface between the two flows. In this work, crystals formed in the channels typically showed either tetragonal or oval shapes. In further analysis to identify the polymorphs, the spectrum for a tetragonal crystal revealed Raman shifts at 910 and 1474–1478 cm−1 (ref. 44–47) compatible with COD, while oval crystals were identified as COM33 (section 7, ESI†). Hence, only COD crystals were seen at the interface under this supersaturation value. The composition of artificial urine containing magnesium and other trace metals may be responsible for the stabilization of the COD form at these supersaturation values, favoring the formation of COD over COM.48–50COD crystals were monitored in the channels for 7.3 min after the first crystal emerged for each channel. The average growth rates (ṙavg) of COD were estimated to be 0.95 ± 0.27 × 10−8 m s−1, 0.93 ± 0.45 × 10−8 m s−1, and 0.92 ± 0.22 × 10−8 m s−1 with flow velocities of 0.015, 0.035, and 0.075 m s−1, respectively (Table 4). The results showed that varying the flow velocity did not significantly affect the average growth rate (ṙavg), possibly due to the low Reynolds number (Re = 6.7 at the maximum velocity of 0.075 m s−1). Since the flow from both inlets is laminar and co-current (x-axis), there is no influence in the diffusion of the ions from one stream to the other (y-axis); hence, the growth rates remain unaffected regardless of the flow velocities. Additionally, according to the COMSOL simulations (Fig. S4†), σ-profiles along the channel surface are not influenced significantly by varying U in the applied order of magnitude. The transport-reaction kinetics for crystal growth are limited by the reaction, such that an increase in mass transport towards the surface would not lead to faster crystal growth. Hence, even if crystals grow large enough to reach parts of the channel where the fluid flow is highly convective, the growth rate is not expected to vary, since the system is reaction limited. Moreover, crystal growth occurs at the solid–liquid interface, where v = 0 m s−1, so diffusion governs mass transfer.
3.3. The effect of the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Ox molar ratio on CaOx crystallization
Ox molar ratio on CaOx crystallization
Fig. 5 shows the experiments performed with different oxalate concentrations at a fixed calcium (12 mol m−3) concentration. The molar ratios of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox in the experiments were 5, 6, 7.5, and 10 for AU4, AU5, AU2 and AU6, respectively. AU2 and AU6 resulted in the lowest values of supersaturation for COD: 17.8 and 13.5 and for COM: 46.8 and 34.7, respectively. In the experiments AU4 and AU5 with values of supersaturation COD: 26.3 and 21.9 and COM: 67.6 and 57.5, respectively, both crystal shapes, identified as COD and COM crystals were observed together. Our results using artificial urine are in line with Daudon et al.51 results on patients' urine samples. These authors worked on 6869 urine samples with COM and COD crystals together. They reported that patients with higher Ca
Ox in the experiments were 5, 6, 7.5, and 10 for AU4, AU5, AU2 and AU6, respectively. AU2 and AU6 resulted in the lowest values of supersaturation for COD: 17.8 and 13.5 and for COM: 46.8 and 34.7, respectively. In the experiments AU4 and AU5 with values of supersaturation COD: 26.3 and 21.9 and COM: 67.6 and 57.5, respectively, both crystal shapes, identified as COD and COM crystals were observed together. Our results using artificial urine are in line with Daudon et al.51 results on patients' urine samples. These authors worked on 6869 urine samples with COM and COD crystals together. They reported that patients with higher Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox ratios (>14) excreted predominantly COD crystals, while patients with low Ca
Ox ratios (>14) excreted predominantly COD crystals, while patients with low Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox ratios (<5) excreted mostly COM. For the Ca
Ox ratios (<5) excreted mostly COM. For the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox ratios between these values, COM and COD were more equally distributed.
Ox ratios between these values, COM and COD were more equally distributed.
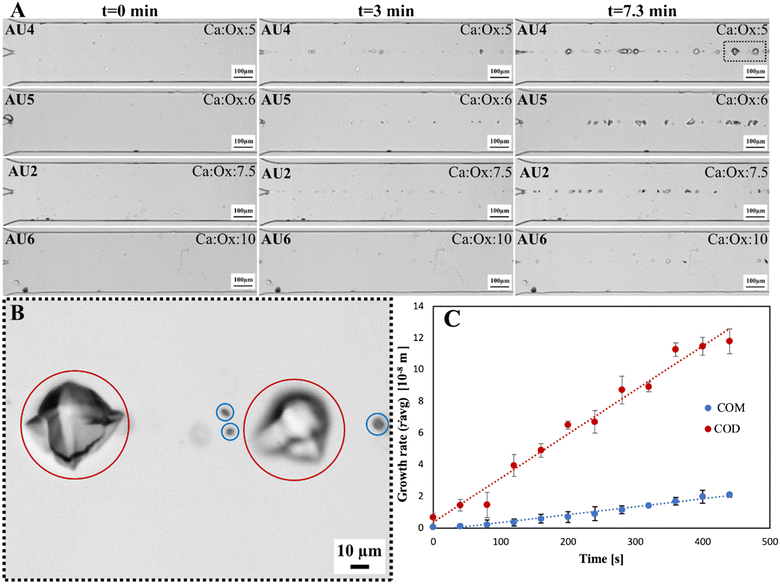 | ||
Fig. 5 A) Microscopy images of the microfluidic channel for four experiments AU4, AU5, AU2 and AU6 (different rows) for molar ratios of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox of 5, 6, 7.5 and 10 at a fixed flow velocity of 0.035 m s−1. Three time-lapses are shown after the first appearance of crystals (in columns) monitored with a 10× objective. B) The zoomed-in image of sample AU4 at t = 7.3 min visible in figure A in the black rectangle emphasizes the difference in growth rates between COM and COD crystals, circled blue and red, respectively (it is noteworthy that the crystals are blurred, which can be attributed to the difficulty in focusing due to different crystal heights – more images can be seen in the ESI,† Fig. S8). C) The average radius of three COM and two COD crystals (example sample) as a function of time from experiment AU4. The equation for COM is ṙavg = 0.0048 t + 1.124 with its standard deviation, 0.0027 μm s−1. The equation for COD is ṙavg = 0.0305 t + 2.109 with its standard deviation, 0.0043 μm s−1. Ox of 5, 6, 7.5 and 10 at a fixed flow velocity of 0.035 m s−1. Three time-lapses are shown after the first appearance of crystals (in columns) monitored with a 10× objective. B) The zoomed-in image of sample AU4 at t = 7.3 min visible in figure A in the black rectangle emphasizes the difference in growth rates between COM and COD crystals, circled blue and red, respectively (it is noteworthy that the crystals are blurred, which can be attributed to the difficulty in focusing due to different crystal heights – more images can be seen in the ESI,† Fig. S8). C) The average radius of three COM and two COD crystals (example sample) as a function of time from experiment AU4. The equation for COM is ṙavg = 0.0048 t + 1.124 with its standard deviation, 0.0027 μm s−1. The equation for COD is ṙavg = 0.0305 t + 2.109 with its standard deviation, 0.0043 μm s−1. | ||
An example of how the average crystal growth rate of COM and COD is calculated is shown in Fig. 5C. The average size of five crystals (two COD and three COM crystals) was plotted as a function of time in Fig. 5C – as an example of the measurements conducted under various conditions studied. The slope of the linear fit to the data provides the average growth rate under given conditions. The estimation of the growth rate in each experiment was later generalized in a larger sample set for each experiment. The growth rate of the COD crystals showed strong dependence on the supersaturation, as can be seen in Table 4, and is the lowest at the highest Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox molar ratio of 10 in sample AU6. Surprisingly, the growth rates of the COM crystals did not vary significantly for the Ca
Ox molar ratio of 10 in sample AU6. Surprisingly, the growth rates of the COM crystals did not vary significantly for the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox ratio of 5 and 6, the highest supersaturation within these experiments.
Ox ratio of 5 and 6, the highest supersaturation within these experiments.
3.4. Effect of osteopontin on CaOx crystallization
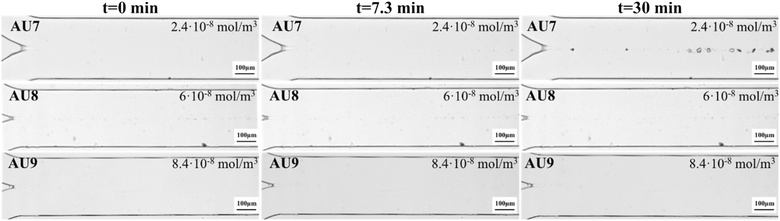
Fig. 6 shows the formation and growth of CaOx crystals as a function of OPN concentrations of 2.4 × 10−8 mol m−3, 6.0 × 10−8 mol m−3 and 8.4 × 10−8 mol m−3 at a fixed Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox molar ratio of 7.5 and flow velocity of 0.015 m s−1. It is noteworthy that AU1, shown in Fig. 4, can be used as a control experiment for the effect of OPN on the growth of CaOx crystals, since it was conducted under the same flow and Ca
Ox molar ratio of 7.5 and flow velocity of 0.015 m s−1. It is noteworthy that AU1, shown in Fig. 4, can be used as a control experiment for the effect of OPN on the growth of CaOx crystals, since it was conducted under the same flow and Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox molar ratio conditions. The growth rate calculation was done using the images taken up until t = 7.3 min after the first crystal emerged, as for all the other conditions. To clarify the inhibition effect of OPN and show small COD crystals clearly, the images at t = 30 min are added in Fig. 6.
Ox molar ratio conditions. The growth rate calculation was done using the images taken up until t = 7.3 min after the first crystal emerged, as for all the other conditions. To clarify the inhibition effect of OPN and show small COD crystals clearly, the images at t = 30 min are added in Fig. 6.
Contrary to what was observed in AU1 (Fig. 4), where COM crystals were observed up to 7.3 min, when OPN was added, the formation of a few COD crystals was only observed with the lowest OPN concentration of 2.4 × 10−8 mol m−3 for sample AU7 (Fig. 6). The higher OPN concentrations of 6.0 × 10−8 mol m−3 and 8.4 × 10−8 mol m−3 in AU8 and AU9 showed no CaOx crystal formation in artificial urine up until 30 min of observation. Thus, within this time, the nucleation was inhibited. To see the effect of the lowest OPN concentration, experiment AU7 should be compared with the control experiment, AU1, which has the same values of molar ratio and velocity (see Fig. 4 and Table 4). The growth rate of COD decreased from 0.95 ± 0.27 × 10−8 m s−1 (AU1) to 0.34 ± 0.15 × 10−8 m s−1 (AU7).
Studies in the literature claim that OPN can inhibit crystal growth and change the morphology of CaOx crystals.52–54 Moreover, the chemical structure of OPN, rich in dicarboxylic acid groups, might encourage binding to a mineral surface,52 thus a stronger interaction of OPN with CaOx crystal faces is likely to hinder crystal growth.55
The dual modulatory role of OPN has been discussed in the literature,26 thus it is noteworthy to discuss it here. As shown in this study, in vitro experiments indicate that OPN inhibits the growth of CaOx crystals within the observation window. Yet, in the kidneys, the presence of OPN may trigger cell differentiation, mast cell degranulation and release of inflammatory mediators promoting stone formation. Moreover, the presence of competing ions such as phosphate32 has been overlooked. Our results clearly do not include the OPN–kidney cell interactions, therefore this should be considered as a physiochemical model study.
As our experiments focus only on growth of crystals nucleated on PDMS chip walls, we rationalize that these crystals nucleated via heterogeneous nucleation. Homogeneous nucleation can still occur in the solution yet our experimental setup does not allow us to observe homogeneous nucleation occurring in solution. Regarding the role of aggregation particularly in the presence of OPN26 and homogeneous nucleation in measured growth rates, the design of our experiments does not allow us to observe the growth of crystals nucleating in bulk via homogeneous nucleation and their aggregation. In other words, the observed growth rates are only extracted from crystals nucleated on the wall that are multiple crystal diameters away from each other.
4. Conclusion
We report the growth rates of CaOx crystals in artificial urine, in a geometry mimicking the collecting duct of the kidneys, under flow conditions relevant to kidney stone formation. The effect of varying flow velocities, the molar ratio of Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox, i.e., distinct supersaturation, and OPN concentrations on the growth of CaOx crystals was investigated. Mainly COD crystals were observed in the channels. Altering the flow velocity in the channel did not affect crystal growth at a fixed supersaturation ratio. However, an increase in the oxalate concentration at a fixed value of the Ca concentration (decreasing the Ca
Ox, i.e., distinct supersaturation, and OPN concentrations on the growth of CaOx crystals was investigated. Mainly COD crystals were observed in the channels. Altering the flow velocity in the channel did not affect crystal growth at a fixed supersaturation ratio. However, an increase in the oxalate concentration at a fixed value of the Ca concentration (decreasing the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ox molar ratio, hence increasing the supersaturation at a fixed flow velocity) resulted in a clear increase in the average growth rate of COD crystals. In addition, for the lower molar ratios of calcium and oxalate (5 and 6), COM nucleation was also observed competing with the COD nucleation. The growth rate of the COM crystals did not show a clear dependence on the estimated supersaturation and was much lower than the COD growth rates. The presence of the lowest amount (i.e. 2.4 × 10−8 mol m−3) of OPN in artificial urine decreased the growth rate of the COD crystals. With increasing OPN concentration, it was found that OPN inhibits crystal formation for both pseudopolymorphs of CaOx in artificial urine within the studied timeframe. This study focuses only on the physiochemical aspects of CaOx crystallization under flow conditions ignoring the dynamic effects arising from cellular interactions ever present in the kidneys. Therefore, we hope our study inspires future studies where the complexity of cell interactions in the kidneys is incorporated in microfluidic environments mimicking the kidneys.
Ox molar ratio, hence increasing the supersaturation at a fixed flow velocity) resulted in a clear increase in the average growth rate of COD crystals. In addition, for the lower molar ratios of calcium and oxalate (5 and 6), COM nucleation was also observed competing with the COD nucleation. The growth rate of the COM crystals did not show a clear dependence on the estimated supersaturation and was much lower than the COD growth rates. The presence of the lowest amount (i.e. 2.4 × 10−8 mol m−3) of OPN in artificial urine decreased the growth rate of the COD crystals. With increasing OPN concentration, it was found that OPN inhibits crystal formation for both pseudopolymorphs of CaOx in artificial urine within the studied timeframe. This study focuses only on the physiochemical aspects of CaOx crystallization under flow conditions ignoring the dynamic effects arising from cellular interactions ever present in the kidneys. Therefore, we hope our study inspires future studies where the complexity of cell interactions in the kidneys is incorporated in microfluidic environments mimicking the kidneys.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.† Any extra data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.References
- J. A. Wesson, R. J. Johnson, M. Mazzali, A. M. Beshensky, S. Stietz, C. Giachelli, L. Liaw, C. E. Alpers, W. G. Couser, J. G. Kleinman and J. Hughes, Osteopontin is a critical inhibitor of calcium oxalate crystal formation and retention in renal tubules, J. Am. Soc. Nephrol., 2003, 14(1), 139–147 CrossRef.
- V. Romero, H. Akpinar and D. G. Assimos, Kidney stones: a global picture of prevalence, incidence, and associated risk factors, Rev. Urol., 2010, 12(2–3), e86–e96 Search PubMed.
- T. Alelign and B. Petros, Kidney Stone Disease: An Update on Current Concepts, Adv. Urol., 2018, 3068365 Search PubMed.
- W. Wang, J. Fan, G. Huang, J. Li, X. Zhu, Y. Tian and L. Su, Prevalence of kidney stones in mainland China: A systematic review, Sci. Rep., 2017, 7(1), 41630 CrossRef.
- I. Ogobuiro and F. Tuma, Physiology renal, StatPearls - NCBI Bookshelf, 2020 Search PubMed.
- H. W. Smith, The kidney: structure and function in health and disease, Oxford University Press, USA, 1951, vol. 1 Search PubMed.
- M. K. Bruce and A. S. Bruce, Renal physiology, Elsevier Mosby, Philadelphia, PA, 2013, p. 79 Search PubMed.
- G. Laffite, C. Leroy, C. Bonhomme, L. Bonhomme-Coury, E. Letavernier, M. Daudon, V. Frochot, J. P. Haymann, S. L. Rouzière, T. Ivan, D. Bazin, F. Babonneaub and A. Abou-Hassan, Calcium oxalate precipitation by diffusion using laminar microfluidics: toward a biomimetic model of pathological microcalcifications, Lab Chip, 2016, 16(7), 1157–1160 RSC.
- P. D. Vize, A. S. Woolf and J. B. L. Bard, The kidney: from normal development to congenital disease, 2003, vol. 42 Search PubMed.
- P. Tabeling, Introduction to microfluidics, OUP Oxford, 2005 Search PubMed.
- J. E. Hall and M. E. Hall, Guyton and Hall textbook of medical physiology e-Book, Elsevier Health Sciences, 2020 Search PubMed.
- A. Asmar, P. K. Cramon, L. Simonsen, M. Asmar, C. M. Sorensen, S. Madsbad, C. Moro, B. Hartmann, B. L. Jensen, J. J. Holst and J. Bulow, Extracellular Fluid Volume Expansion Uncovers a Natriuretic Action of GLP-1: A Functional GLP-1-Renal Axis in Man, J. Clin. Endocrinol. Metab., 2019, 104(7), 2509–2519 CrossRef.
- G. Bihl and A. Meyers, Recurrent renal stone disease—advances in pathogenesis and clinical management, Lancet, 2001, 358(9282), 651–656 CrossRef.
- F. L. Coe, M. J. Favus, C. Y. C. Pak, J. H. Parks, G. M. Preminger and D. A. Tolley, Kidney stones: Medical and surgical management, Br. J. Urol., 1996, 78(3), 482 Search PubMed.
- T. M. Reynolds, Best Practice No 181: Chemical pathology clinical investigation and management of nephrolithiasis, J. Clin. Pathol., 2005, 58(2), 134–140 CrossRef CAS.
- E. M. Worcester and F. L. Coe, Nephrolithiasis, Prim. Care, 2008, 35(2), 369–391 CrossRef , vii.
- K. Skorecki, G. M. Chertow, P. A. Marsden, M. W. Taal, S. L. Alan and V. Luyckx, Brenner and Rector's The Kidney E-Book, Elsevier Health Sciences, 2015 Search PubMed.
- C. Conti, M. Casati, C. Colombo, E. Possenti, M. Realini, G. D. Gatta, M. Merlini, L. Brambilla and G. Zerbi, Synthesis of calcium oxalate trihydrate: New data by vibrational spectroscopy and synchrotron X-ray diffraction, Spectrochim. Acta, Part A, 2015, 150, 721–730 CrossRef CAS PubMed.
- V. Y. Bird and S. R. Khan, How do stones form? Is unification of theories on stone formation possible?, Arch. Esp. Urol., 2017, 70(1), 12 Search PubMed.
- X. Y. Sun, C. Y. Zhang, P. Bhadja and J. M. Ouyang, Preparation, properties, formation mechanisms, and cytotoxicity of calcium oxalate monohydrate with various morphologies, CrystEngComm, 2018, 20(1), 75–87 RSC.
- E. A. Boadi, S. Shin, F. Gombedza and B. C. Bandyopadhyay, Differential biomolecular recognition by synthetic vs. biologically-derived components in the stone-forming process using 3D microfluidics, J. Mater. Chem. B, 2022, 10(1), 34–46 RSC.
- V. N. Ratkalkar and J. G. Kleinman, Mechanisms of stone formation, Clin. Rev. Bone Miner. Metab., 2011, 9(3–4), 187–197 CrossRef CAS PubMed.
- K. P. Aggarwal, S. Narula, M. Kakkar and C. Tandon, Nephrolithiasis: Molecular Mechanism of Renal Stone Formation and the Critical Role Played by Modulators, BioMed Res. Int., 2013, 2013, 292953 Search PubMed.
- S. R. Qiu, A. Wierzbicki, C. A. Orme, A. M. Cody, J. R. Hoyer, G. H. Nancollas, S. Zepeda and J. J. De Yoreo, Molecular modulation of calcium oxalate crystallization by osteopontin and citrate, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(7), 1811–1815 CrossRef CAS PubMed.
- D. T. Denhardt, Osteopontin: Role in Cell Signalling and Adhesion, New York Academy of Sciences, 1995 Search PubMed.
- P. Peerapen and V. Thongboonkerd, Kidney stone prevention, Adv. Nutr., 2023, 14(3), 555–569 CrossRef CAS.
- H. Fleisch, Inhibitors and promoters of stone formation, Kidney Int., 1978, 13(5), 361–371 CrossRef CAS.
- P. Brown, D. Ackerman and B. Finlayson, Calcium oxalate dihydrate (weddellite) precipitation, J. Cryst. Growth, 1989, 98(3), 285–292 CrossRef CAS.
- D. S. Ipe, E. Horton and G. C. Ulett, The Basics of Bacteriuria: Strategies of Microbes for Persistence in Urine, Front. Cell. Infect. Microbiol., 2016, 6, 14 Search PubMed.
- P. Mitra, D. K. Pal and M. Das, Does quality of drinking water matter in kidney stone disease: A study in West Bengal, India, Investig. Clin. Urol., 2018, 59(3), 158–165 CrossRef PubMed.
- X. Geng, R. D. Sosa, M. A. Reynolds, J. C. Conrad and J. D. Rimer, Alginate as a green inhibitor of barite nucleation and crystal growth, Mol. Syst. Des. Eng., 2021,(7), 508–519 RSC.
- F. Gombedza, S. Evans, S. Shin, E. Awuah Boadi, Q. Zhang, Z. Nie and B. C. Bandyopadhyay, Melamine promotes calcium crystal formation in three-dimensional microfluidic device, Sci. Rep., 2019, 9(1), 875 CrossRef.
- F. Ibis, M. A. Nuhu, F. M. Penha, T. W. Yu, A. E. D. M. van der Heijden, H. J. M. Kramer and H. B. Eral, Role of Hyaluronic Acid on the Nucleation Kinetics of Calcium Oxalate Hydrates in Artificial Urine Quantified with Droplet Microfluidics, Cryst. Growth Des., 2022, 22(6), 3834–3844 CrossRef CAS.
- F. Ibis, Kidney stone in a chip: Understanding calcium oxalate kidney stone formation, TU Delft, 2022.
- F. Ibis, T. W. Yu, F. M. Penha, D. Ganguly, M. A. Nuhu, A. E. D. M. van der Heijden, H. J. M. Kramer and H. B. Eral, Nucleation kinetics of calcium oxalate monohydrate as a function of pH, magnesium, and osteopontin concentration quantified with droplet microfluidics, Biomicrofluidics, 2021, 15(2021), 1–17 Search PubMed.
- W. G. Robertson, Do “inhibitors of crystallisation” play any role in the prevention of kidney stones? A critique, Urolithiasis, 2017, 45(1), 43–56 CrossRef CAS.
- P. Laval, J.-B. Salmon and M. Joanicot, A microfluidic device for investigating crystal nucleation kinetics, J. Cryst. Growth, 2007, 303(2), 622–628 CrossRef CAS.
- R. M. Tona, T. A. O. McDonald, N. Akhavein, J. D. Larkin and D. Lai, Microfluidic droplet liquid reactors for active pharmaceutical ingredient crystallization by diffusion controlled solvent extraction, Lab Chip, 2019, 19(12), 2127–2137 RSC.
- S. Li, J. Ihli, W. J. Marchant, M. Zeng, L. Chen, K. Wehbe, G. Cinque, O. Cespedes, N. Kapur and F. C. Meldrum, Synchrotron FTIR mapping of mineralization in a microfluidic device, Lab Chip, 2017, 17(9), 1616–1624 RSC.
- J. Streit, L. Tran-Ho and E. Königsberger, Solubility of the three calcium oxalate hydrates in sodium chloride solutionsand urine-like liquors, Monatsh. Chem., 1998, 129(12), 1225–1236 CAS.
- D. J. Kok and S. E. Papapoulos, Physicochemical considerations in the development and prevention of calcium oxalate urolithiasis, Bone Miner., 1993, 20(1), 1–15 CrossRef CAS.
- D. A. Bushinsky, J. R. Asplin, M. D. Grynpas, A. P. Evan, W. R. Parker, K. M. Alexander and F. L. Coe, Calcium oxalate stone formation in genetic hypercalciuric stone-forming rats, Kidney Int., 2002, 61(3), 975–987 CrossRef CAS PubMed.
- V. N. Ratkalkar and J. G. Kleinman, Mechanisms of Stone Formation, Clin. Rev. Bone Miner. Metab., 2011, 9(3–4), 187–197 CrossRef CAS.
- K. Rakotozandriny, S. Bourg, P. Papp, Á. Tóth, D. Horváth, I. T. Lucas, F. Babonneau, C. Bonhomme and A. Abou-Hassan, Investigating CaOx Crystal Formation in the Absence and Presence of Polyphenols under Microfluidic Conditions in Relation with Nephrolithiasis, Cryst. Growth Des., 2020, 20(12), 7683–7693 CrossRef CAS.
- C. A. Kuliasha, D. Rodriguez, A. Lovett and L. B. Gower, In situ flow cell platform for examining calcium oxalate and calcium phosphate crystallization on films of basement membrane extract in the presence of urinary ‘inhibitors’, CrystEngComm, 2020, 22(8), 1448–1458 RSC.
- V. Castiglione, P. Y. Sacre, E. Cavalier, P. Hubert, R. Gadisseur and E. Ziemons, Raman chemical imaging, a new tool in kidney stone structure analysis: Case-study and comparison to Fourier Transform Infrared spectroscopy, PLoS One, 2018, 13(8), 1–18 CrossRef.
- H. G. Edwards, M. R. Seaward, S. J. Attwood, S. J. Little, L. F. de Oliveira and M. Tretiach, FT-Raman spectroscopy of lichens on dolomitic rocks: an assessment of metal oxalate formation, Analyst, 2003, 128(10), 1218–1221 RSC.
- X. Martin, L. H. Smith and P. G. Werness, Calcium oxalate dihydrate formation in urine, Kidney Int., 1984, 25(6), 948–952 CrossRef CAS.
- R. Walton, J. Kavanagh, B. Heywood and P. Rao, The association of different urinary proteins with calcium oxalate hydromorphs. Evidence for non-specific interactions, Biochim. Biophys. Acta, Gen. Subj., 2005, 1723(1–3), 175–183 CrossRef CAS PubMed.
- B. Tomazic and G. Nancollas, The kinetics of dissolution of calcium oxalate hydrates, J. Cryst. Growth, 1979, 46(3), 355–361 CrossRef CAS.
- M. Daudon, E. Letavernier, V. Frochot, J.-P. Haymann, D. Bazin and P. Jungers, Respective influence of calcium and oxalate urine concentration on the formation of calcium oxalate monohydrate or dihydrate crystals, C. R. Chim., 2016, 19(11–12), 1504–1513 CrossRef CAS.
- S. Qiu, A. Wierzbicki, C. Orme, A. Cody, J. Hoyer, G. Nancollas, S. Zepeda and J. De Yoreo, Molecular modulation of calcium oxalate crystallization by osteopontin and citrate, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(7), 1811–1815 CrossRef CAS.
- D. T. Denhardt, Osteopontin: role in cell signalling and adhesion, New York Academy of Sciences, 1995 Search PubMed.
- J. A. Wesson, R. J. Johnson, M. Mazzali, A. M. Beshensky, S. Stietz, C. Giachelli, L. Liaw, C. E. Alpers, W. G. Couser, J. G. Kleinman and J. Hughes, Osteopontin is a critical inhibitor of calcium oxalate crystal formation and retention in renal tubules, J. Am. Soc. Nephrol., 2003, 14(1), 139–147 CrossRef CAS.
- L. Addadi and S. Weiner, Interactions between acidic proteins and crystals: stereochemical requirements in biomineralization, Proc. Natl. Acad. Sci. U. S. A., 1985, 82(12), 4110–4114 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ce01038h |
| This journal is © The Royal Society of Chemistry 2025 |