Unveiling the physical mechanisms underpinning bandgap variations in chalcopyrite crystals (ABX₂) using interpretable artificial intelligence

Abstract

We propose an interpretable AI approach integrating hybrid DFT, symbolic regression, and data mining to predict chalcopyrite (ABX₂) bandgaps. Key factors, including atomic size, molar volume, and electron affinity, are identified, offering insights into bandgap-composition relationship and guiding high-performance materials design.

---

Ternary chalcopyrite crystals (ABX₂) are essential in various technological applications due to their tunable bandgaps, determined by the selection of A, B, and X elements. Large-bandgap materials, such as ZnSnP₂,¹ are used in nonlinear optics because of the strong nonlinearity and high optical damage thresholds, making them ideal for applications like laser technology and frequency doubling. Moderate-bandgap crystals, like CdGeAs₂,² are widely employed in photovoltaic cells due to their high absorption coefficients, which make them excellent candidates for thin-film solar cells, enhancing solar energy conversion efficiency. Small-bandgap materials, such as CuMnS₂,³ show promise in thermoelectric devices due to their high electrical conductivity and thermoelectric efficiency,^4,5 enabling effective waste heat recovery and power generation in thermoelectric modules. The broad range of ABX₂ chalcopyrite crystals’ applications highlights the importance of precisely targeting specific bandgap values to meet the demands for different technological advancements.⁶ By selecting appropriate combinations of A, B, and X elements, researchers can tailor the properties of these materials to optimize their performance in various fields, from renewable energy to advanced optical systems. The ability to fine-tune the bandgaps of chalcopyrite crystals underscores their versatility and significance in modern technology. Therefore, models that can rapidly and reliably predict the bandgaps of these materials are highly desirable.

Bandgaps of compounds are typically obtained through experimental measurements,^7,8 which often require significant time and material resources, especially for large-scale compounds. As a more efficient alternative, density functional theory (DFT) calculations have become effective means for determining the bandgaps of semiconductor materials.^9–12 However, DFT calculations with standard approximations to the exchange–correlation functional (local density, generalized gradient, and meta-generalized-gradient approximations) often significantly underestimate bandgap values.¹³ On the other hand, the much more accurate many-body perturbation theory method GW is too computationally expensive for intermediate-throughput screening. To achieve good accuracy in bandgap calculations while keeping computational cost not too high, hybrid functionals, such as Heyd–Scuseria–Ernzerhof (HSE06) functional, have been proposed.^14,15 Despite having moderate computational cost, these methods are still too expensive for high-throughput exploration of materials space containing thousands of candidates.^16,17 The thriving development of AI has driven the integration of machine learning with theoretical calculations to accelerate the discovery of materials with desirable properties by extracting informative insights from large datasets.^18,19 For instance, Gladkikh et al. trained an alternating conditional expectation (ACE) model to predict the bandgaps of ABX₃ perovskites, and used a support vector machine (SVM) model to determine the gap type.²⁰ Tawfi et al. employed feedforward neural network (FNN), SVM, relevance vector machines (RVM), and random forest (RF) models to predict the electronic properties of mixed 2D materials.²¹ However, these models lack interpretability and cannot explain the physical relationship between the predicted bandgap and the chemical composition.^22–24 The accuracy and interpretability of machine learning models are both crucial for the rational design of materials.^25,26 In this letter, we introduce an interpretable AI approach that combines data mining and compressed-sensing-based symbolic regression, incorporating feature importance assessment in relation to the target properties of materials. This approach not only facilitates the high-throughput screening of materials with targeted bandgap values, but also elucidates the underlying physical mechanisms driving bandgap variations. Using this strategy, we have pinpointed the key factors influencing the bandgap values of ternary chalcopyrite crystals.

To investigate the composition-bandgap relationship for ABX₂ crystals, we calculated the bandgap values of 122 crystals (Table S1, ESI†) using the hybrid functional HSE06 including spin–orbit interaction. The data for ab initio calculations were selected via an active-learning cycle (see ESI† for computational details). This cycle continued until bandgap values predicted by the model aligned with those calculated by HSE06. The ABX₂ ternary chalcopyrite crystals (Fig. S1, ESI†) are defined by their composition, where the A site is occupied by transition metals or alkaline-earth metals Be, Mg, Ca, Cu, Zn, Pd, Ag, Cd, and Au, the B site is filled by post-transition metals or metalloids including Al, Si, Ga, Ge, In, Sn, Sb, Tl, Pb, and Bi, and the X site consists of pnictogens or chalcogens N, P, S, As, Se, Sb, and Te. We allocated 80% of these 122 datasets for model training, reserving the remaining 20% exclusively for testing the predictive accuracy of the models. A complete list of materials features used for training AI models is provided in Table S2 (ESI†).

Among the features listed above, number of valence electrons (NVE) is determined by the number of electrons in an element's outermost shell. Thermal conductivity (TC) values are measured at 25 °C, and electronegativity (EN) is reported on the Pauling scale. Additionally, molar volume (MV) is measured under standard atmospheric pressure at 298 K.

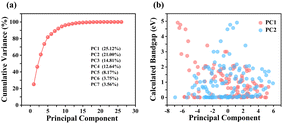
We initially conducted principal component analysis (PCA) to evaluate the potential linear relationship between primary features and HSE06-calculated bandgap values (G_HSE). Each principal component (PC) represents a linear combination of 36 primary features. Within the training dataset, the leading two PCs accounted for only 25.12% and 21.00% of the variance, respectively, as shown in Fig. 1(a). To capture the essence of the original dataset adequately, where cumulative explained variance exceeds 90%, including more than seven PCs becomes necessary. However, this contradicts the goal of efficient dimensionality reduction. Fig. 1(b) further highlights this challenge, showing a weak correlation between PC1, PC2, and G_HSE. These results indicate that neither individual features nor their simple linear combinations correlate well with G_HSE, emphasizing the need for models capable of unveiling nonlinear relationships. The complexity of the bandgap-composition relationship is reflected in the diversity of band structure types within the considered class, including deep- and shallow-impurity-like semiconducting structures, wide-gap semiconductors, and metals (Fig. S2 and S3, ESI†). Consequently, we employed the sure independence screening plus sparsifying operator (SISSO) approach to find a nonlinear relationship between primary features and G_HSE.^27–29 In SISSO, target property is expressed as a linear combination of derived features, which are obtained as (possibly) non-linear mathematical expressions involving primary features. In this study, we focus on prediction of the bandgap value. Considering the diversity of the band structure type, it would be interesting to develop models for predicting other features of the band structure describing its topology. However, this is beyond the scope of this paper.

Fig. 1 Results of principal component analysis. (a) The cumulative explained variance as a function of the number of principal components included. (b) The correlation between the calculated bandgap of the chalcopyrite crystals and the first two principal components.

A training dataset of 60 systems was initially selected from over 600 candidates for HSE06 calculations to determine their G_HSE. The developed SISSO model was then employed to predict G_HSE for the remaining candidates, with those exhibiting the smallest or largest predicted G_HSE systematically added to the training dataset. This iterative refinement process continued until the distribution ranges of calculated and predicted G_HSE closely matched, resulting in an optimized dataset of 122 systems. Fig. 2(a) and (b) show heatmap of the Pearson's correlation coefficient matrix among the 36 primary atomic features and the bandgap distribution within the training dataset. In SISSO, to prevent overfitting as model complexity increases, we employ twenty-fold cross-validation to determine the optimal model dimensionality (i.e., the number of derived features in the linear combination) (Table S3, ESI†). The average RMSE of the twenty-fold cross-validation as a function of model dimensionality is shown in Fig. 2(c). This reveals that the five-dimensional model possesses a balance between high accuracy and simplicity, thus identifying it as the optimal SISSO model. The distribution of deviations between the predicted and calculated G_HSE values for this model is shown in Fig. 2(d), with most errors concentrated below 0.2 eV. The components of the optimal SISSO model, including its coefficients and importance scores, are collected in Table S4 (ESI†). These complex formulas of the model highlight the intricate relationships between the primary features and bandgap.

Fig. 2 Identification of optimal SISSO models. (a) Heatmap of the Pearson's correlation coefficient matrix, which shows the relationships among the 36 primary features, (b) the bandgap distribution within the training dataset calculated using HSE06, (c) the RMSE values obtained from 20-fold cross-validation for the 122 data, and (d) the prediction error versus the calculated G_HSE of the chalcopyrite crystals.

The most significant descriptor component, d1, has the highest importance score, calculated as the relative increase of fitting RMSE after this component is removed (see ESI,† for details). It indicates that B elements with larger molar volumes (MVb), and larger atomic radii of atoms at the X site (ARCc) typically correspond to smaller bandgaps in ABX₂ ternary chalcopyrite crystals. A larger MVb results in the expansion of the crystal lattice, which reduces overlap of atomic orbitals, thereby decreasing the bandgap. Larger atomic radii at the X site have a similar effect. Conversely, thermal conductivity of A-site elemental crystal (TCa) results in the increase of band gap in ABX₂. Since A elements are metals at normal conditions, their thermal conductivity is determined by the presence of nearly free electrons. With right ligands these electrons can make strong covalent or ionic bonds, which increases the bandgap. These insights demonstrate that the SISSO model can effectively unravel the underlying physical mechanisms governing the properties of chalcopyrite crystals.

SISSO aids in identifying critical descriptor components by selecting important primary features and feature combinations relevant to G_HSE values. However, it does not directly elucidate which combinations of features are likely to result in too low or too high bandgap. To deepen our understanding of the underlying mechanisms and the significance of primary features, we employ a modified version of SGD approach.³⁰ Here, only the primary features from the SISSO model and SISSO-predicted G_HSE values are used for SGD analysis.

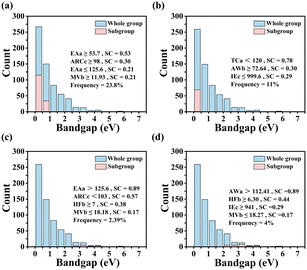
The best subgroups found are shown in Table S5 (ESI†), along with the degenerate propositions. The degeneracy is determined by the condition that the number of common data points in the original subgroup and the subgroup obtained by replacing a proposition with another one is greater than 99% of the larger of the two subgroups. The selector of the best subgroup that minimizes G_HSE with cutoff 1 eV (i.e., under condition G_HSE < 1 eV) is defined as follows: (ARCc ≥ 98 pm), (EAa ≤ 125.6 kJ mol⁻¹), (EAa ≥ 53.7 kJ mol⁻¹), and (MVb ≥ 11.93 cm³ mol⁻¹). The subgroup contains ∼24% of the whole dataset samples (Fig. 3a). The selector is well consistent with the SISSO model, indicating that larger ARCc and MVb lead to smaller G_HSE. This is explained by reduction of atomic orbital overlap when the lattice is expanded due to larger volume of the unit cell. On top of this, SGD reveals that the electron affinity of atom A is an important feature that controls whether bandgaps are lower than 1 eV. In particular, the electron affinity should not be too low (EAa ≥ 53.7 kJ mol⁻¹) or too high (EAa ≤ 125.6 kJ mol⁻¹). The latter condition is degenerate with AWa ≤ 112.41 a.m.u. and ENa ≤ 2.20. Lowering the cutoff to 0.5 eV results in the best subgroup (AWb ≥ 72.64 a.m.u.) AND (TCa < 120 W m⁻¹ K⁻¹) AND (IEc ≤ 999.6 kJ mol⁻¹). The first proposition is degenerate with MVb ≥ 13.65 cm³ mol⁻¹, which is similar to the proposition MVb ≥ 11.93 cm³ mol⁻¹ in case of a 1 eV cutoff, indicating that a larger size of atom B consistently leads to a smaller bandgap in ABX₂. The proposition TCa < 120 W m⁻¹ K⁻¹ is also consistent with a straightforward interpretation of the SISSO model. Lower thermal conductivity of elemental A metals implies more tightly bound and localized electrons that do not form strong bonds. The proposition IEc ≤ 999.6 kJ mol⁻¹ rules out X = N and P, which could make strong covalent bonds with A, resulting in increased bandgap.

Fig. 3 Exploration of physical insights into the SISSO model. The bandgap distribution for the whole dataset, and the subgroups selected by SGD: (a) and (b) The results of minimizing the bandgap with the cutoff smaller than 1 and 0.5 eV, respectively. (c) and (d) The results of maximizing the bandgap of crystals greater than 2.5 and 2 eV, respectively.

The selector for the best subgroup that maximizes bandgaps above 2 eV is defined as follows: (AWa > 112.41 a.m.u.), (HFb ≥ 6.30 kJ mol⁻¹), (MVb ≤ 18.27 cm³ mol⁻¹), and (IEc ≥ 941 kJ mol⁻¹). Increasing the cutoff to 2.5 eV yields best subgroup (ARCc < 103 pm), (EAa > 125.6 kJ mol⁻¹), (HFb ≥ 7 kJ mol⁻¹), and (MVb ≤ 18.18 cm³ mol⁻¹). Consistently, these subgroups contain conditions opposite to those for the subgroups with smaller gaps. A smaller atomic radius of X and a smaller molar volume of B result in shorter interatomic distances, improving orbital overlap and therefore increasing bandgap. The degenerate propositions AWa > 112.41 a.m.u. and EAa > 125.6 kJ mol⁻¹ select only one element (Au), whose high electron affinity makes possible formation of strong covalent bonds with neighboring atoms. Similarly, degenerate propositions HFb ≥ 7 kJ mol⁻¹ and EAb ≥ 42.5 kJ mol⁻¹ select atoms that can form strong localized bonds, resulting in larger gap (Table S5, ESI†).

Relying solely on elemental and atomic features, the SISSO model enables us to predict the bandgap for a wide array of chalcopyrite crystals. We predicted the G_HSE values for 506 new chalcopyrite crystals, and the results are shown in Fig. 4. Based on the high-throughput screening results, we have identified chalcopyrite materials with bandgaps in a range suitable for tandem solar cell and other applications.^31,32 In Table S6 (ESI†) we list 43 materials with direct HSE06 bandgaps in the range 0.6–2 eV.

Fig. 4 High-throughput screening results for chalcopyrite crystal bandgaps using SISSO. The horizontal axis displays the type of B-site elements, while the vertical axis displays the combined types of A-site and X-site elements, denoted as “A_X”.

In summary, we have developed a unified model that quantitatively describes bandgap variations in chalcopyrite crystals by integrating HSE06 calculations with AI. This model not only accurately describes composition-bandgap relationship, but also elucidates the underlying physical mechanisms responsible for these variations. Using data mining approach SGD, we identified combinations of features that result in a reduction or an increase of bandgap. SGD finds that size of atom X, molar volume of elemental B crystal, and electron affinity of atoms A and B are important for maximizing or minimizing the gap. The geometric features describe orbital overlap, which directly affects the bandgap. The electron affinity describes the ability of atoms form stronger covalent bonds with neighboring atoms, which leads to higher bandgaps. These findings underscore the transformative potential of interpretable AI algorithms in paving new paths for the rational design of high-performance materials.

This work was financially supported by the National Key R&D Program of China (2023YFA1506902, 2022YFA1505500), National Natural Science Foundation of China (22302173), and the Fundamental Research Funds for the Central Universities. The development of the subgroup discovery method was supported by Russian Science Foundation, grant number 24-13-00317.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. R. A. Makin, K. York, S. M. Durbin, N. Senabulya, J. Mathis, R. Clarke, N. Feldberg, P. Miska, C. M. Jones and Z. Deng, Phys. Rev. Lett., 2019, 122, 256403.
2. W. Feng, D. Xiao, J. Ding and Y. Yao, Phys. Rev. Lett., 2011, 106, 016402.
3. S. Picozzi, Y.-J. Zhao, A. J. Freeman and B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205206.
4. L. Wu, S.-Y. Chen, F.-J. Fan, T.-T. Zhuang, C.-M. Dai and S.-H. Yu, J. Am. Chem. Soc., 2016, 138, 5576–5584.
5. M. Sandroni, K. D. Wegner, D. Aldakov and P. Reiss, ACS Energy Lett., 2017, 2, 1076–1088.
6. S. Suresh, D. J. Rokke, A. A. Drew, E. Alruqobah, R. Agrawal and A. R. Uhl, Adv. Energy Mater., 2022, 12, 2103961.
7. I. E. Castelli, F. Hüser, M. Pandey, H. Li, K. S. Thygesen, B. Seger, A. Jain, K. A. Persson, G. Ceder and K. W. Jacobsen, Adv. Energy Mater., 2015, 5, 1400915.
8. J. Gierschner, J. Cornil and H. Egelhaaf, Adv. Mater., 2007, 19, 173–191.
9. L. G. Ferreira, M. Marques and L. K. Teles, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125116.
10. Y.-C. Wei, S. F. Wang, Y. Hu, L.-S. Liao, D.-G. Chen, K.-H. Chang, C.-W. Wang, S.-H. Liu, W.-H. Chan and J.-L. Liao, Nat. Photonics, 2020, 14, 570–577.
11. S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Nat. Commun., 2018, 9, 3405.
12. M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757.
13. J. Kangsabanik, M. K. Svendsen, A. Taghizadeh, A. Crovetto and K. S. Thygesen, J. Am. Chem. Soc., 2022, 144, 19872–19883.
14. Y. Gan, N. Miao, P. Lan, J. Zhou, S. R. Elliott and Z. Sun, J. Am. Chem. Soc., 2022, 144, 5878–5886.
15. M. Jain, J. R. Chelikowsky and S. G. Louie, Phys. Rev. Lett., 2011, 107, 216806.
16. M. P. Polak, R. Kudrawiec, R. Jacobs, I. Szlufarska and D. Morgan, Phys. Rev. Mater., 2021, 5, 124601.
17. X. Jiang, Q. Zheng, Z. Lan, W. A. Saidi, X. Ren and J. Zhao, Sci. Adv., 2021, 7, eabf3759.
18. R. Batra, L. Song and R. Ramprasad, Nat. Rev. Mater., 2021, 6, 655–678.
19. T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301.
20. V. Gladkikh, D. Y. Kim, A. Hajibabaei, A. Jana, C. W. Myung and K. S. Kim, J. Phys. Chem. C, 2020, 124, 8905–8918.
21. S. A. Tawfik, O. Isayev, M. J. Spencer and D. A. Winkler, Adv. Theory Simul., 2020, 3, 1900208.
22. C. Rudin, Nat. Mach. Intell., 2019, 1, 206–215.
23. A. Andreassen, I. Feige, C. Frye and M. D. Schwartz, Phys. Rev. Lett., 2019, 123, 182001.
24. K. A. Murphy and D. S. Bassett, Phys. Rev. Lett., 2024, 132, 197201.
25. A.-M. Nussberger, L. Luo, L. E. Celis and M. J. Crockett, Nat. Commun., 2022, 13, 5821.
26. M. S. Murillo, M. Marciante and L. G. Stanton, Phys. Rev. Lett., 2020, 125, 085503.
27. R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802.
28. Z.-K. Han, D. Sarker, R. Ouyang, A. Mazheika, Y. Gao and S. V. Levchenko, Nat. Commun., 2021, 12, 1833.
29. H. Wang, R. Ouyang, W. Chen and A. Pasquarello, J. Am. Chem. Soc., 2024, 146, 17636.
30. A. Mazheika, Y.-G. Wang, R. Valero, F. Viñes, F. Illas, L. M. Ghiringhelli, S. V. Levchenko and M. Scheffler, Nat. Commun., 2022, 13, 419.
31. M. De Bastiani, A. J. Mirabelli, Y. Hou, F. Gota, E. Aydin, T. G. Allen, J. Troughton, A. S. Subbiah, F. H. Isikgor and J. Liu, Nat. Energy, 2021, 6, 167–175.
32. G. Li, W.-H. Chang and Y. Yang, Nat. Rev. Mater., 2017, 2, 1–13.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cc00259a

‡ These authors contributed equally.

---