Electron paramagnetic resonance spectroscopy: toward the path of dihydrogen isotopologue detection in porous materials

Abstract

Electron paramagnetic resonance (EPR) spectroscopy is a powerful method to characterize the local framework structure of nanoporous materials during the dihydrogen isotopologue adsorption process. It also allows for exploring the adsorption sites of the dihydrogen isotopes and monitoring their desorption characteristics on the microscopic scale. The paramagnetic spin probes in the form of transition metal ions or organic radicals are required for EPR spectroscopy and are introduced either at the framework lattice position or in the pores of the metal–organic frameworks. This review highlights current advancements within the field of dihydrogen isotopologue detection as well as key findings related to the versatility of in situ continuous wave EPR and pulsed EPR experiments as toolkits for monitoring the adsorption–desorption process of dihydrogen isotopologues from the perspective of the framework as well as studying the host–guest interactions based on high-resolution advantages offered by using a pulsed EPR approach.

---

Muhammad Fernadi Lukman

Muhammad Fernadi Lukman obtained his BSc in Chemistry from the Chemistry Department, Universitas Gadjah Mada, Indonesia in 2017. He completed his MSc in the Advanced Spectroscopy in Chemistry program under the framework of the Erasmus+ joint master scholarship hosted by Lille University, France, and Leipzig University, Germany, in 2021. He is currently a doctoral researcher at Felix Bloch Institute for Solid State Physics, Faculty of Physics and Geosystem, Leipzig University, under the supervision of Prof. Andreas Pöppl. The project is part of Research Training Group 2721: Hydrogen isotopes 1, 2, 3 H funded by the German Research Foundation.

Andreas Pöppl

Andreas Pöppl received his Diploma in Physics and PhD from Leipzig University in 1987 and 1990. He completed his postdoctoral studies at the University of Houston, United States, in 1995 under the supervision of Prof. Larry Kevan. In the same year, he returned to Leipzig University as a research associate, was habilitated in 1990, and promoted to associate professor in 2003. His group's research program focuses on the application and development of solid state EPR methods for investigation of porous and functional materials.

---

1. Introduction

Hydrogen isotopologues such as deuterium and tritium are vital to support a multitude of fundamental research and their application in biomedicine and radioisotope tracing.¹ In addition, they are also potentially useful as a fuel for the nuclear fusion reactor, which is among future solutions for cleaner, sustainable, and long-term energy resources.² However, deuterium (D or ²H) is less abundant on earth with only up to 0.0184% mol fraction from the total hydrogen source.¹ On the other hand, tritium (T or ³H) is radioactive with a half-life of 12.3 years and even significantly less available than deuterium with only less than 1 in 10¹⁷ hydrogen atoms.³ Dihydrogen isotopologues exist as homonuclear molecules such as H₂, D₂, and T₂ and heteronuclear molecules such as HD, HT and DT.

Dihydrogen molecules (H₂), depending on the temperature, may exist in two nuclear spin isomers or allotropes: a nuclear singlet state with antiparallel (↑↓) nuclear spins, referred to as para-hydrogen (p-H₂), and nuclear spin triplet state with parallel (↑↑) configuration, known as ortho-hydrogen (o-H₂). Considering the Pauli principle, singlet p-H₂ must occupy even rotational states (rotational quantum numbers J = 0, 2, 4, …), while triplet o-H₂ occupies odd rotational states (J = 1, 3, 5, …). As J = 0 is the lowest rotational level of H₂, p-H₂ is the ground rotational state and o-H₂ is only realized in the rotationally excited state. The energy difference between the J = 0 and J = 1 rotational states is 120 cm⁻¹ (0.343 kcal mol⁻¹).⁴ At room temperature, o-H₂ predominates at equilibrium (75% o-H₂/25% p-H₂). In contrast, D₂ exhibits even rotational states (J = 0, 2, 4, …) with nuclear spins I = 0, 2 which are called ortho-D₂ (o-D₂) and the odd rotational states (J = 1, 3, 5, …) with the nuclear spin I = 1 termed as para-deuterium (p-D₂).

Currently, deuterium/hydrogen separation from the hydrogen on the industrial scale applies either the Girdler sulfide process or the H₂ cryogenic distillation at 24 K.⁵ The former is based on the chemical exchange between H₂S and H₂O which contains a few portions of D₂O in a closed-loop mechanism. The resulting D₂O is converted to D₂via an electrolysis process.⁶ Separately, the H₂ cryogenic distillation technique can be implemented at high pressures to separate H₂ from D₂ by exploiting their minor difference in boiling points: 20.3 K for H₂ and 23.7 K for D₂, respectively.^7,8 However, these methods are costly, energy-intensive, and have relatively low separation performance. Therefore, the nanoconfinement effect in nanoporous materials such as zeolites and metal–organic frameworks (MOFs) can be implemented to increase the efficiency of the dihydrogen isotopologue separation process.⁹

Fig. 1 depicts the D₂/H₂ separation performance in the form of selectivity factor S for several potential nanoporous materials, especially the most investigated MOFs and porous coordination polymers (PCPs) in the field of dihydrogen isotopologue separation. The selectivity is reported as a function of working temperature by Oh et al.¹⁰ It was found that ZIF-8 has its highest selectivity at 20 K whereas HKUST-1 works nicely at higher temperatures (77 K) but with relatively low selectivity. CPO-27(Co) appears to be reliable at 60 K with a selectivity of 12 and then reduces to 6 if measured at 80 K. These nice examples for D₂ and H₂ separation are thought to be driven by the nuclear quantum effects. It is important to note that two proposed mechanisms of separating hydrogen isotopologues via nuclear quantum effects are in general considered and are given below.

Fig. 1 Selectivity of hydrogen isotope adsorption (D₂ over H₂) for several porous frameworks as a function of working temperature. Reproduced from ref. 10 with permission from Wiley-VCH.

(1) Kinetic quantum sieving (KQS)

First proposed in 1995 by Beenakker and co-workers,⁹ the KQS effect can be explained using a relatively simple model for the adsorption of the molecules (hardcore spheres with diameter σ) in a cylindrical pore (diameter d) with a circular square well potential. Here a free motion between consecutive two collisions of the molecules is assumed whereas their motions are restricted in the axial direction due to the pore walls creating the potential well of depth ε. If the Broglie wavelength (λ) of the dihydrogen isotopologue molecules is in the range of λ ≈ d − σ, the pore may provide a noticeable diffusion barrier for the heavier isotopologue. The zero-point energy (ZPE) E₀ of a molecule with mass m in the narrow pore is given by⁹

E₀ ∼ 1/[m(d − σ)²] (1)

The density of molecules inside the pores per unit length (n) can be estimated under the equilibrium condition as⁹

where n_v is the gas density outside the pore, k is the Boltzmann constant, and T is the absolute temperature.

If the ZPE is smaller than the potential well (E₀ < ε) adsorption of the molecules at the pore or diffusion through the pore is possible. Otherwise, if E₀ > ε the zero-point motion of the molecules overcompensates the attractive interaction between the pore surface and the molecules.⁹ Differences in the ZPE of dihydrogen isotopologue molecules can be utilized to separate e.g. D₂ from H₂ using nanoporous materials at cryogenic temperatures if their pore diameter is very close to the kinetic diameter of the dihydrogen isotopologues. Thus, with this KQS effect, the molecular diffusivity of the hydrogen isotopologues can be discriminated by the E₀ of hydrogen isotopologues in such a way that heavier isotopes, such as D₂, will exhibit faster transport behaviour into the pore space than lighter isotopes, such as H₂. Fig. 1 represents the KQS effect of different pore sizes for ZIF-8 (0.34 nm) versus COF-1 (0.9 nm). As expected, this strongly influences the selectivity factor for ZIF-8, which is twice the value for COF-1.¹¹

(2) Chemical affinity quantum sieving (CAQS)

The CAQS is based on the thermodynamic effect by providing distinctive adsorptive sites for instance in the presence of stronger and weaker adsorptive sites in the framework in order to separate the hydrogen isotopologues. If the guest molecule is adsorbed on the surface of sites with stronger affinity or interaction, most translational and rotational degrees of freedom are restricted, except for vibrational motion. Vibrational motion is strongly dependent on ZPE. The heavier isotopologue has a lower ZPE than the lighter one and consequently a stronger binding affinity to the surface site.¹² This will result in distinct adsorption enthalpies for D₂ and H₂ in nanoporous materials having strong adsorption sites for hydrogen isotopologues. A significant gap in the adsorption enthalpies would allow preferential adsorption of the heavier isotopologue, which may improve the selectivity at relatively higher temperatures than the one obtained via the KQS effect.^13,14 In addition, irrespective of the pore size, the CAQS effect could be used to optimize the uptake of dihydrogen isotopologues.

In addition to the nuclear quantum effects, flexible MOFs^15–17 were also implemented to optimize D₂/H₂ separation processes. Specific characteristics of flexible MOFs are their responsiveness to external stimuli, such as temperature, gas pressure and type of guest molecules.¹⁵ In the case of dihydrogen isotopologue separation, adsorption uptake and selectivity are enhanced via the so-called pressure-induced¹⁸ and specific guest-induced flexibility.¹⁹ Typical representatives of flexible MOFs are DUT-8(Ni)¹⁹ and MIL-53(Al).¹⁸ Both materials show specific pore transformations at low temperatures in the presence of D₂ which are absent for H₂ and could be consequently utilized for D₂/H₂ separation.

2. Progress in dihydrogen isotopologue detection

Techniques for dihydrogen isotopologue detection are essential for the development of isotopologue separation technologies. Detection unit performance is often judged by its sensitivity, ease of technical implementation, cost, and efficiency.²⁰ In general, numerous analytical or spectroscopic methods have been utilized to detect dihydrogen isotopologues in the gas phase.^{6,10,12,21–28}

First of all, gas adsorption methods (e.g. volumetric or gravimetric) are fundamental tools for analyzing the adsorption properties such as the maximum uptake, the adsorption enthalpies and the characteristics of adsorption–desorption processes of dihydrogen isotopologues on nanoporous materials.^12,29,30 The chromatographic technique was also heavily implemented quantitatively back in the 1950s to study the separation of H₂, D₂, T₂, HD, HT and DT.^24,31–35 A stationary phase in the form of an alumina-based column covered by iron(III) oxide was used to separate these isotopologues at 77 K while the detection was conducted using an ionization chamber and electrometer.³²

In addition, infrared (IR) spectroscopy, in principle, is powerful in discriminating the vibration energies of a molecule based on the mass differences and the strength of the interaction. For example, diffuse reflectance IR spectroscopy is conducted to monitor the dynamics of the adsorbed H₂ in MOF-5 or IRMOF-1 at low temperatures where the enhancement of the optical absorption strength of a sample allows this technique to overcome weak IR activity of the adsorbed H₂.³⁶ The induced redshift in the vibrational frequencies allows the estimation of site-specific binding energies within 2.5 to 4 kJ mol⁻¹. Diffuse reflectance IR spectroscopy was also implemented to identify the presence of discrete primary (1°) and secondary (2°) sites during the adsorption of p-H₂, HD and D₂ gases on MOF-74 at 40 K³⁷ as shown in Fig. 2. The ZPE term is a substantial factor in explaining the discrepancy in the frequency shifts due to vibrational transition differences among dihydrogen isotopologues. In a separate work, Bordiga and co-workers³⁸ reported an IR spectroscopic study that suggests the interaction between coordinatively unsaturated Cu²⁺ sites in the paddle wheel units and the adsorbed H₂ gas at 20 K. They also mentioned that the HKUST-1 MOF system efficiently promotes the conversion of o-H₂ to p-H₂.

Fig. 2 (a) Vibrational spectra of dihydrogen isotopologues adsorbed on MOF-74 at 40 K. Vibrational bands associated with molecules adsorbed on the primary (1°) and secondary (2°) sites follow the trend predicted by simple reduced mass scaling (solid lines) and (b) structural representation of MOF-74. Adapted with permission from ref. 37. Copyright 2010 American Physical Society.

Recently, Asmis and co-workers³⁹ demonstrated the role of the H₂O ligand in the Cu(I)–H₂(D₂) bond strengthening of the gas phase Cu⁺(H₂O)(H₂)_n (n ≤ 3) clusters by combining a cryogenic ion-trap vibrational action spectroscopy aided by quantum chemical calculations. Again, ZPE's influence on the selectivity of the dihydrogen isotopologue is discussed in that work.

A combination of quadrupole mass spectrometry and temperature-programmed desorption developed by Hirscher and co-workers^{10,13,25,40,41} has also proven to be a powerful solution to support both qualitative and quantitative analysis of the hydrogen isotopologues that are adsorbed on nanoporous materials. This cryogenic thermal desorption spectroscopy (TDS) allows the analysis of pure dihydrogen isotope gases and gas mixtures and has developed into a kind of standard characterization method in this research area. It has a wide operating temperature range from 20 K to 1273 K under ultrahigh-vacuum conditions.⁴² TDS is applicable to distinguish multiple sorption sites of dihydrogen isotopologues in MOF. The strength of the interaction of the dihydrogen molecules with these multiple sorption sites can be judged by their respective desorption temperatures. One example of the synergistic effect between KQS and CAQS is presented in the study of the imidazole-MOF-74 for H₂/D₂ separation where at least three different sorption sites are proposed.⁴³ The presence of the imidazole group, in this case, maximizes the KQS effect, by blocking the diffusion of lighter isotopologues (H₂) into the 1D channels of MOF-74 while open metal sites can be used as the strong binding site (CAQS effect, reflected by the higher desorption temperature peak than the other two peaks at low temperatures) to preferably adsorb heavier isotopologues (i.e. D₂) as shown in Fig. 3.

Fig. 3 (Top) Structural representation of the imidazole-based MOF-74 altogether with its theoretical adsorptive sites and (down) the thermal desorption spectra for pure gas and 1 : 1 H₂/D₂ mixture gas at an exposure temperature of 25 K. Adapted with permission from ref. 43 Copyright 2017 American Chemical Society.

Diffraction-based methods such as X-ray powder diffraction (XRPD)^44,45 and neutron powder diffraction (NPD) have been employed to retrieve information about the phase transformation of flexible MOF structures triggered by the adsorption and desorption processes of guest molecules. However, only NPD, inelastic neutron scattering (INS) and quasielastic neutron scattering (QENS) were so far utilised to locate the position of D₂/H₂ since they are more sensitive toward atoms of light elements.^46–50 NPD experiments can provide structural information (crystallographically) about different possibilities for deuterium sorption sites in MOFs.^51,52 At least six probable positions of D₂ molecules were proposed using Rietveld refinement analysis during progressive fillings of D₂ gas in the HKUST-1 (Cu₃(BTC)₂, where BTC = 1,3,5-benzenetricarboxylate) system. The primary site for the adsorption is the coordinatively unsaturated Cu²⁺ site with a deuterium distance of about 2.39(1) Å from the Cu²⁺ ion.⁴⁶ In contrast, the most favourable sorption site for D₂ on the ZIF-8 framework is associated with the organic linkers instead of the ZnN₄ clusters⁵¹ as illustrated in the red map area in Fig. 4. In 2021, Long and co-workers⁴⁸ implemented the NPD to define the V²⁺–D₂ distance in a Kubas-type V₂Cl_2.8(btdd) MOF as a potential candidate for materials that can bind strongly and reversibly to hydrogen at ambient temperatures and moderate pressures (for hydrogen storage purposes).

Fig. 4 (a) (111) view of the real-space Fourier-difference scattering length density on ZIF-8 (yellow to red indicates the location of first adsorption sites) and (b) observed (dots), refined (line), and difference (noisy line) neutron powder diffraction profiles (λ = 2.079 Å, 3.5 K) for ZIF8 host lattice and ZIF8 with D₂ loading of 28 D₂/6 Zn. Adapted with permission from ref. 51 Copyright 2007 American Chemical Society.

In a different context, in situ NPD analysis was very useful for monitoring the crystal structure changes due to the pore opening transformation in the case of flexible DUT-8(Ni)¹⁹ and refining the very large pore structure due to the second-breathing transition at T < 25 K in the case of flexible MIL-53(Al).¹⁸ In addition, the INS method is used in parallel to obtain an insight into the potential energy surface of the adsorbed hydrogen molecules. Mulder and co-workers⁵³ suggested that the strongest adsorption site for hydrogen in the MIL-53(Cr) is situated near the organic linkers. The breathing modes due to dihydrogen adsorption are suggested to be driven by weak van der Waals interaction. Despite its strengths, the neutron-based methods are limited by the energy resolution as well as restricted experimental beamtime for routine research basis.³⁶

In principle, nuclear magnetic resonance (NMR) spectroscopy is also practically useful since this type of spectroscopy allows direct detection of dihydrogen isotopologues based on their nuclear spin properties. For instance, NMR was implemented to study the kinetics of equilibration between H₂, HD and D₂ in the gas phase and the surface of the ligands which contain Ru metal nanoparticles.⁵⁴ On the other hand, ¹H-NMR can be used to monitor the interconversion from the NMR-silent p-H₂ toward the NMR-active o-H₂ species within the interior cage of fullerene (C₆₀) and the presence of spin catalysts that are paramagnetic.^55,56 Separately, Huang's group⁵⁷ has applied ²H solid-state NMR spectroscopy to study the D₂ dynamics during adsorption process on various porous materials of the MOF-74 family. According to their study, the temperature-dependency of the linewidth of deuterium NMR spectra reflects the mobility of D₂ gas during adsorption on MOF-74. The D₂ is suggested to be less mobile in the Zn-MOF-74 in comparison to UiO-66 MOF due to a strong interaction between Zn open metal sites and the adsorbed D₂ molecules in the former material.^57,58

3. Electron paramagnetic resonance spectroscopy

Electron paramagnetic resonance (EPR) spectroscopy is a magnetic resonance technique applicable to systems containing unpaired electrons. Common systems with unpaired electron spins such as organic radicals, transition metal ions, rare earth ions, inorganic free radicals, photoexcited molecules or point defects of solids are the playgrounds for EPR utilisations.⁵⁹ EPR is also more sensitive than nuclear magnetic resonance (NMR) since the magnetic moment of an electron is significantly larger than that of a nucleus. However, we have to note that EPR is not applicable when the system under study is diamagnetic.⁶⁰ EPR spectroscopy can reveal information about the structural properties, coordination symmetry, magnetic properties, concentration and the electronic ground state of a paramagnetic species in a wide temperature range, with minimum sample preparation and versatility of materials states: solids (single crystals, polycrystalline and amorphous samples) and frozen solutions, liquids as well as also gas phase samples can be measured.^59,61

The electron is an elementary particle with an intrinsic angular momentum or spin. Therefore, the free electron exhibits a nonzero magnetic moment [small mu, Greek, vector] which is proportional to the spin angular momentum operator S⃑

[small mu, Greek, vector] = −g_eβ_eℏS⃑ (3)

where ℏ = h/2π, β_e is the Bohr magneton, and g_e = 2.0023 is the free electron g-factor. The spin operator Ŝ_z has two eigenvalues ℏm_S with m_S = ±1/2. So, if the z-direction is parallel to the external magnetic field vector B⃑₀, the Zeeman interaction causes a splitting into two energy levels E (m_S = ±1/2). The energy difference between two m_S states of a free electron dependent on the external magnetic field is derived as⁶⁰

ΔE = ℏω_S = g_eβ_eB₀ (4)

This interaction of the electron spin with a static magnetic field is known as electron Zeeman interaction. The resulting resonance frequency ω_S is characteristic and may reflect the chemical environment of the unpaired electron spin if embedded in an atomic or molecular orbital. In a continuous wave (CW) EPR experiment, the signal is detected as a result of the exact match between the energy difference from two different m_s states and the photon energy of the applied microwave (mw) radiation while sweeping the external magnetic field (see Fig. 5). The selection rule in EPR spectroscopy is Δm_s = ±1.

Fig. 5 Magnetic field dependence of the energy of the two spin states m_s = +1/2 (α state) and m_s = −1/2 (β state) of the unpaired electron (Zeeman effect). The resonance phenomenon originates from the absorption of microwave energy that matches the energy difference ΔE between the two m_s states.

In its general form, the EPR spectra are described by a spin Hamiltonian as follows:⁶¹

Ĥ = Ĥ_ez + Ĥ_zfs + Ĥ_hfi + Ĥ_nz + Ĥ_nqi

The first term is the electron Zeeman (ez) interaction Ĥ_ez. It can be described as the interaction between the electron spin and the applied external magnetic field B⃑₀. It is in general anisotropic and is parameterized by the tensor g. This electronic g tensor contains the spin–orbit coupling effect and encodes the information about coordination symmetry, ground state and its energy spacing to the excited states of the paramagnetic center.⁶¹

The second term is the so-called zero-field interaction (Ĥ_zfs), which is purely anisotropic and applicable only when we deal with S > 1/2 spin systems. The zero-field splitting (zfs) tensor D with principal values D_x, D_y, D_z is traceless; thus it can be parameterized just by using two parameters: the axial zfs parameter D = 3D_z/2 and the rhombic ZFS parameter E = (D_x − D_y)/2.⁶² The zfs term can be used to access information about the coordination symmetry of the paramagnetic centre as well as its bonding properties.⁶³

The third term (Ĥ_hfi) represents the hyperfine interaction (hfi), which describes the interaction between the electron spins and the surrounding nuclei which is usually anisotropic and parameterized by hfi tensors A_k. The hyperfine matrix A can be decomposed into two components: the isotropic component (Fermi contact interaction) and the anisotropic component (dipolar interaction):^59,63

A = a_isoI + T (6)

where I is the identity matrix, a_iso is the isotropic hfi parameter and T is the anisotropic, dipolar hfi tensor. Furthermore, the a_iso parameter can be estimated as⁶³where β_n is nuclear magneton and |ψ₀(0)|² is the probability of finding the spin carrying unpaired electron with the wave function ψ₀ of the electronic ground state at the nucleus. Please note that the electron spin density may also be significant when the unpaired electron resides in a p-, d- or f- orbitals; spin density at the nucleus is then induced by configuration interactions or spin polarization mechanisms.⁶³

On the other hand, the anisotropic hfi tensor T is a traceless and symmetric tensor with the elements^62,64,65

In the case of a simple point dipole approximation the anisotropic hfi tensor has principal values T_xx = T_yy = −T and T_zz = 2T with

The hfi tensors can originate from the central atom of the paramagnetic species bearing a major part of the unpaired spin density or can also be caused by so-called superhyperfine interactions (shfi) with ligand nuclear spins interacting with the electron spin. In that case, the shf tensors A_k may provide access to the distances between electron spin and the respective nuclei and provide valuable information about the spin density distribution across the coordinating ligands.⁶¹

The nuclear Zeeman interaction Ĥ_nz in the fourth term describes the interaction between the nuclear spins and the external magnetic field. The parameters g^k_n refer to the nuclear g-factors of the various coupled nuclear spins. Even though it is not resolved in the CW EPR experiment, this term is important for pulsed EPR techniques such as electron spin echo envelope modulation (ESEEM) and pulsed electron-nuclear double resonance (ENDOR).

The fifth term (Ĥ_nqi) contains the nuclear quadrupole interaction (nqi) with the traceless nqi tensors Q_k and arises only when the paramagnetic centre couples to nuclear spins I_k > 1/2. The tensors Q_k can be decomposed into two parameters: the quadrupole coupling constant e²qQ/ℏ and the asymmetry parameter η (0 > η > 1, η = 0 indicates axial symmetry whereas η > 0 indicates rhombic symmetry of the nucleus, respectively).⁶²

In terms of the technical operation, EPR spectroscopy can be divided into two sub-parts: the CW EPR and pulsed EPR. As the name suggests, the former approach utilizes continuous irradiation of monochromatic microwave energy while the external magnetic field B⃑₀ is swept to induce the resonance conditions for the EPR transitions.⁶² It is very useful as a first screening method to identify the paramagnetic species and to identify coupled nuclear spins via their hfi usually from the first coordination sphere with respect to the corresponding paramagnetic center.

Pulsed EPR spectroscopy offers a wide variety of sophisticated methods such as ESEEM and pulsed ENDOR experiments that allow obtaining information about interactions between the unpaired electrons and ligand nuclei due to the hyperfine, quadrupole and nuclear Zeeman interactions.^63,66–70 Pulsed EPR relies on the implementation of short, intense mw pulses (≈ 10–100 ns pulse length) to excite the electron spins similar to the use of radiofrequency pulses in NMR spectroscopy.

ESEEM experiments are performed by recording the electron spin echo intensity generated by the sequence of microwave pulses.⁷¹ The intensity of this echo is monitored as a function of one or two of the pulse intervals. This time domain (TD) trace is modulated by the nuclear spin transition frequencies ω_i (and their combination frequencies depending on the chosen pulse sequence) of the nuclear spins coupled to the unpaired electron spin and can be converted to the frequency domain via Fourier transformation as spectra that reveal exactly these nuclear spin transitions.^63,70,72 Among the frequently used ESEEM methods, the three pulse (3p) ESEEM, in particular, is promising to evaluate distant, weakly coupled D₂ or HD (without direct coordination to the spin probes) molecules up to a distance of approximately 0.8 nm from the paramagnetic centre. The 3p ESEEM sequence is based on the stimulated echo sequence (π/2)_mw–τ–(π/2)_mw–T–(π/2)_mw–τ-echo where the first pulse delay τ is fixed and the echo intensity is recorded in dependence on a stepwise increase of the second delay T.⁷³

Alternatively, HYSCORE (hyperfine sublevel correlation) spectroscopy has proven to be a powerful method to determine hfi and nqi parameters of more strongly coupled ligand nuclear spins. In the two-dimensional (2D) HYSCORE experiment (π/2)_mw–τ–(π/2)_mw–t₁–(π)_mw–t₂–(π/2)_mw–τ-echo, the time delays t₁ and t₂ are incremented separately, which leads to a correlated modulation of the four-pulse electron spin echo by the nuclear spin transition frequencies ω_i in the resulting two-dimensional 2D time domain pattern.⁷⁴ The frequency-domain spectrum is obtained by applying a 2D Fourier transformation. For example in the case of a simple S = ½, I = ½ spin system with nuclear Larmor frequency ω_I, the 2D frequency spectrum consists of correlation peaks at positions (ω_α, ω_β) and (ω_β, ω_α) in the second quadrant for the weak coupling case (|A| < 2ω_I), whereas in the case of the strong coupling (|A| > 2ω_I), these cross peaks appear in the first quadrant at (ω_α, −ω_β) and (ω_β, −ω_α). HYSCORE spectroscopy has the advantage of resolution improvement by reducing the peak overlap in one-dimensional (1D) ESEEM methods (two pulse ESEEM or three pulse ESEEM).⁶⁰ However, the 1D experiments require in general less measurement time.

Pulsed ENDOR spectroscopy such as the Davies ENDOR⁶⁷ or Mims ENDOR⁶⁶ experiments utilizes both mw and radiofrequency (rf) pulses to detect the nuclear spin transition frequencies of the coupled nuclear spins. The Davies ENDOR sequence (π)_mw–(π_rf)–(π/2)_mw–τ–(π)_mw–τ-echo uses a selective microwave π_mw pulse at the beginning of the experiment to invert the population of a particular EPR transition. During the time delay T, an rf π pulse π_rf is applied and if this is resonant with a nuclear spin transition, then it will alter the polarization across the initially excited EPR transition, which can be detected either using the Hahn echo sequence (π/2)_mw–τ–(π)_mw–τ-echo) or via free induction decay (FID) after a (π/2)_mw mw pulse. On the other hand, Mims ENDOR is based on the three-pulse stimulated echo and employs hard nonselective microwave pulses. The Mims ENDOR spectrum is recorded by stepwise sweeping selective RF π pulse applied during the second and third pulse and recording the stimulated echo intensity.⁶²

EPR spectral simulations are essential to extract the spin Hamiltonian parameters from the measured spectra. Based on the interpretation of these parameters (today often supported by quantum chemical computations) the nature of the paramagnetic centre can be identified and its electronic and geometric parameters can be determined. To date, several programs have been developed to help either EPR or non-EPR experts in simulating and interpret the EPR spectra, for example, the EasySpin⁷⁵ EPR toolbox or commercially available programs such as XSophe and SpinFit developed by Bruker.

For more advanced details or concepts of CW EPR, the reader is referred to a textbook by Weil and Bolton.⁶⁴ In addition, Schweiger and Jeschke cover a more in-depth explanation of pulsed EPR principles and applications.⁶³ The review from Roessler and Salvadori⁵⁹ shall provide the reader with a good starting point for learning the EPR method with several examples from chemical science research. In addition, an EPR handbook from Goldfarb and Stoll⁶² is available for an introductory but fairly extensive overview of the current EPR developments.

4. Case study I: selective adsorption of D₂ over H₂ on DUT-8(Ni_0.98 Co_0.02) using the in situ CW-EPR spectroscopy

Recently, there have been a growing number of reports about the versatility of in situ CW-EPR spectroscopy in monitoring a wide variety of chemical processes or reactions.^76–81In situ manifold setups for CW EPR investigations have also been implemented to study phase transitions in MOFs triggered by the adsorption–desorption of gaseous molecules,^82–84 which in principle can be employed to explore the adsorption process of dihydrogen isotopologues over nanoporous materials.

Bondorf and co-workers¹⁹ recently found that the flexible DUT-8(Ni) can selectively adsorb D₂ over H₂ at 23.3 K with a selectivity factor of 11.6 as determined from the TDS experiment. The attempt to verify this finding by taking the flexible DUT-8 (Ni_0.98Co_0.02) system (Fig. 6a) and subjecting it to the adsorption–desorption process using pure H₂ and D₂ gas while monitoring them separately has been done via in situ CW-EPR experiments.²⁶

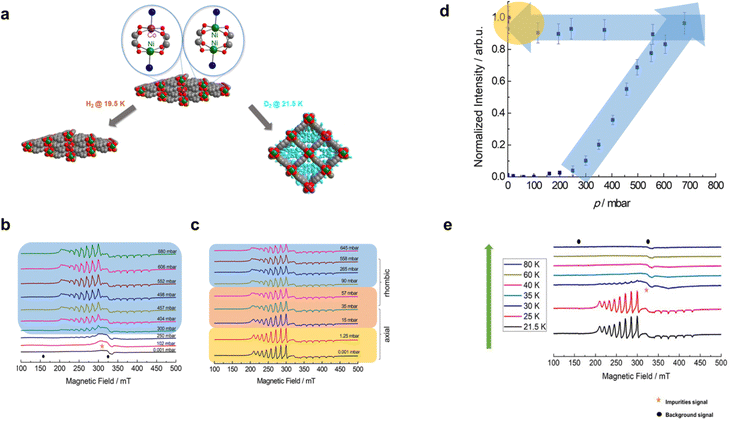Fig. 6 (a) Structural representation of mixed-metal Ni²⁺–Co²⁺ paddle wheel units. Blue, grey and red spheres indicate nitrogen, carbon and oxygen atoms, respectively. A schematic representation of the op phase and cp phase state in response to H₂/D₂ adsorption is also provided. (b) The series of CW-EPR spectra obtained in situ with variations of D₂ loading pressures in the adsorption branch from p = 0.001 mbar to p = 645 mbar recorded at 21.5 K. (c) Experimental spectra were recorded during the desorption stage from p = 645 mbar to p = 0.001 mbar. (d) The plot of EPR signal intensity of Ni²⁺–Co²⁺ species for DUT-8(Ni_0.98Co_0.02) normalized with the highest EPR intensity during adsorption and desorption stages (blue shaded arrows) and (e) CW-EPR spectra of DUT-8(Ni_0.98Co_0.02) with the variation of desorption temperatures at fixed p = 0.001 mbar. Adapted with permission from ref. 26 Copyright 2023 Royal Society of Chemistry.

According to the in situ CW-EPR results, it has been observed that the pore opening process only occurs for D₂ gas at the p = 250 mbar at 21.5 K, marked by the presence of an EPR signal assigned as open pore (op) species (Fig. 6b). This EPR signal for the op phase has been interpreted using an effective spin S = 1/2 ground state of the antiferromagnetically coupled mixed Ni²⁺–Co²⁺ paddle wheel unit interacting with its ⁵⁹Co nuclear spin (I = 7/2).⁸⁵ The EPR parameter for this species can be extracted via spectral simulation using Easyspin software⁷⁵ yielding a rhombic g-factor (g_xx = 2.65(4), g_yy = 2.59(4) and g_zz = 1.79(4)) and the hfi tensor A (A_xx = 510(10) A_yy = 465(10) and A_zz = 417(10)). Moreover, the pore-opening pressure at 250 mbar agrees well with the one obtained using volumetric sorption measurement.¹⁹ The double integration of op phase signal in the pressure-dependent CW-EPR spectra (Fig. 6d) was implemented during the adsorption–desorption processes. This gives us information about the relative concentration of the op phase when the D₂ pressure is increasing. In contrast, the op phase signal did not occur when the H₂ gas adsorbed on DUT-8 (Ni_0.98Co_0.02) from 0.001 mbar up to 929.2 mbar. These results confirm the selective intake of dihydrogen isotopologues (specifically D₂ over H₂) from the perspective of the EPR spin probe (Ni²⁺–Co²⁺ PWs) in the framework of flexible DUT-8.²⁶

It is also interesting to note the in situ CW EPR revealed the evolution of symmetry (lower to higher symmetry) of the Ni²⁺–Co²⁺ PWs unit during the D₂ desorption stage at the pressure below 35 mbar at 21.5 K (Fig. 6c). The desorption temperature is also decisive in accelerating the pore-closing transition (op to cp) as indicated by the reduction of op phase intensity until it is completely undetectable at T > 35 K (Fig. 6e). Thus, the changes in the local geometry of the spin probe can be used to sensitively monitor the overall framework transition during the pore opening or pore closing transition in the flexible DUT-8 (Ni_0.98Co_0.02) as a response toward dihydrogen isotopologue adsorption.

5. Case study II: pulsed EPR approach to unravel host–guest interactions between dihydrogen isotopologues and the Cu_2.97Zn_0.03(btc)₂ MOF

In the current section, we discuss the Cu_2.97Zn_0.03(btc)₂ system, a structural analogue of the HKUST-1 MOF (Fig. 7a) where 1% of the Cu²⁺ ions in the paddle-wheel units are substituted by Zn²⁺, resulting in the formation of paramagnetic Cu/Zn paddle-wheel units (S = 1/2 in the ground state). This variant of MOF is a well-known example which exhibits coordinatively unsaturated Zn²⁺ or Cu²⁺ metal sites that can strongly adsorb dihydrogen isotopologues.³⁸ The local environment of Cu²⁺ up to the second coordination sphere (proton shfi from the btc ligands) of such MOF has been analyzed extensively⁸⁶ using ENDOR spectroscopy and it is used as a basis to compare their local environment when dihydrogen isotopologues are adsorbed. CW-EPR results before and after dihydrogen isotopologues (H₂, D₂ and HD) adsorption implies that the spin Hamiltonian parameters of the Cu²⁺ ions in the Cu/Zn paddle wheel units did not change upon the adsorption, reflecting only negligible effect of potential adsorption on the ligand field at the Cu²⁺ ions. Furthermore, the shfi between the cupric ion and the proton and/or deuterium nuclear spins in the adsorbed hydrogen molecules are way too small to be resolvable in the CW EPR spectra.

Fig. 7 (a) Structural representation of Cu_2.97Zn_0.03(btc)₂ MOF (left) with mixed Zn–Cu paddlewheel units inside a black circle (right). (b) Davies-ENDOR spectrum of HD-loaded sample (1_DD) recorded at 339.8 mT: comparison of deuterium hf coupling with proton ENDOR spectrum by scaling factors (left) and Davies-ENDOR spectra of D₂ and HD-loaded samples, 1_DD and 1_HD respectively at deuterium Larmor frequency as well as the simulated spectrum at 339.8 mT (right). (c) Schematic representation of side-on coordination of rotating HD and D₂ with the deuterium quadrupole tensor Q_D orientation parallel to the C₄ axis. (d) The experimental (exp) and simulated (sim) HYSCORE spectra of Cu_2.97Zn_0.03(btc)₂ at 280 mT (related to g_zz position) after adsorption of D₂. Reproduced with permission from ref. 28 Copyright 2013 Taylor & Francis Ltd.

Since the resolution in the CW-EPR spectroscopy is inadequate to resolve such weak ligand shfi, pulsed EPR experiments (HYSCORE and ENDOR spectroscopy) were employed to clarify the position of HD and D₂ molecules with respect to the Cu²⁺ ions in the Cu/Zn paddle-wheel units.²⁸Fig. 7b displays the comparison of the proton and the deuterium ENDOR spectrum for HD- and D₂-loaded MOF at the same frequency scale using the scaling factor (g^D_n/g^H_n = 0.1535). The results demonstrate that the deuterium shfi is comparable to the proton shfi which reflects a similar form of coordination as well as the H/D distance with respect to the Cu²⁺ ions. Moreover, a deuterium nuclear quadrupole splitting of approximately 60 KHz can be deduced from the Davies ENDOR spectra of the HD-loaded sample at the magnetic field of 339.8 mT. HYSCORE spectra for D₂-loaded sample at 280 mT (Fig. 7d) show likewise a well-resolved deuterium nuclear quadrupole splitting signal with a similar nqi and shfi parameter as the one obtained via Davies ENDOR.²⁸

Employing orientation-selective⁶³ ENDOR and HYSCORE spectroscopy together with spectral simulations, it has been estimated that the g-tensor of the Cu²⁺ ions and the A^H/D and Q^D tensors are coaxial for both HD and D₂. The HD and D₂ molecules are suggested to be localised in the close environment of the Cu²⁺ of the paddle wheel units with side-on coordination where the H–D and D–D bond axis lies parallel to the CuO₄ plane and perpendicular to the C₄ axis (Fig. 7c). The tensors A^H/D were found to be purely dipolar with T^H = 3.517 MHz (HD), T^D = 0.552 MHz (HD), and T^D = 0.556 MHz (D₂). Using a point-dipole approximation (see eqn (9)) Cu–H and Cu–D distances of 0.28 nm were derived. In addition, the determination of the deuterium nqi tensor from these pulsed EPR experiments allowed the identification of the rotational state of adsorbed D₂ molecules on the Cu²⁺ site as a J = 1, m_J = ± 1 state.²⁸ However, H₂ molecules could not be detected at cryogenic temperatures in either HYSCORE or pulsed ENDOR experiments because of its predominant para-H₂ state, which has total nuclear spin, I_tot = 0.

Summarizing, the combination of ENDOR and HYSCORE spectroscopy provides microscopic information related to the position of dihydrogen isotopologues with respect to the paramagnetic centre; in this case, Cu²⁺ ions in the Cu/Zn paddle-wheel units. In addition, we can also learn that pulsed EPR has a much higher resolution for detecting weakly coupled D₂ or HD than the CW-EPR spectroscopy approach.^28,73 A complete approach involving both methods could complement each other to deduce the structural information in more detail toward host–guest interactions between MOFs and dihydrogen isotopologues. In an ideal case, the experimental findings could be supported by further quantum chemical approaches.

According to NPD experiments,⁴⁶ D₂ is also adsorbed at other sites in HKUST-1 more distant from the Cu²⁺ ions in the paddle wheels. Thus, 3p ESEEM spectroscopy was employed as a second pulsed EPR method to explore those other adsorption sites for dihydrogen isotopologues in this MOF material. The 3p ESEEM results of HD adsorbed over Cu_2.97Zn_0.03(btc)₂ at 6 K (Fig. 8c) reveal that two types of coupled deuterium nuclei contribute to the TD traces as well as frequency domain spectra, (1) distant, weakly coupled and (2) strongly coupled deuterium nuclei. The shfi and nqi coupling parameters for the strongly coupled deuterium nuclei have already been obtained from ENDOR and HYSCORE experiments²⁸ as discussed above. However, using only the strongly coupled nuclei data (indicated as HD(1) site) was not satisfactory to describe the 3p ESEEM traces. To address this, the analysis was complemented by the previously published NPD data for the HKUST-1 system⁴⁶ that contains the probable deuterium densities (HD positions) across the framework. These distant HD sites were considered in the computation of the TD traces of the 3p ESEEM experiment as distant, weakly coupled nuclei (Fig. 8a). Here, the corresponding dipolar shfi parameters T were computed from the NPD-derived HD positions again using a point-dipole approximation (eqn (9)) and assuming a negligible isotropic hfi. A significant improvement (Fig. 8b) is obtained by taking into account HD(1–3) sites in the 3p ESEEM time domain traces simulation. Furthermore, the incorporation of less than 20% HD (3–6) sites finally yielded the closest agreement of the simulation toward the 3p ESEEM experimental trace. To elucidate the HD desorption process, the 3p ESEEM experiments were performed at different temperatures, as illustrated in Fig. 9a. The results show a clear decrease of the overall deuterium modulation effect with rising temperature as likewise indicated by the temperature dependence (Fig. 9c, bottom) of the modulation depth parameter k_mod (see k_mod definition in Fig. 9b). The decrease of k_mod towards higher temperatures reflects the local HD desorption process from the Cu²⁺ sites which already starts below 12 K. In addition, the frequency domain spectrum reveals additional interesting aspect of the HD desorption process. The intensity ratio I_W/I_S of the distant, weakly (W) and strongly coupled (S) deuterium signal increases with rising temperature, indicating that HD molecules gradually desorb from HD(1) sites but tend to stay within the pores in proximity to Cu²⁺ centres (Fig. 9c). This can be presumably viewed as a dynamic process where the HD molecules desorbed from the Cu²⁺ sites diffuse through the nanoporous channels before they are expelled from the pores when a certain energy threshold is passed at much higher temperatures.

Fig. 8 (a) Variations of HD adsorption sites in Cu₃(btc)₂ as determined from NPD experiments.⁴⁶ Normalized (b) baseline-corrected time domain and (c) corresponding frequency domain 3p ESEEM simulations for different expected HD sites in Cu_2.97Zn_0.03(btc)₂. The experimental 3p ESEEM data recorded at 6 K are given for comparison. In addition, experimental and simulated TD traces with recovered decaying baseline are also provided. Reproduced with permission from ref. 27 Copyright 2015 American Chemical Society.

Fig. 9 (a) Time domain (TD) and (b) frequency domain (FD) of 3p ESEEM experiments of Cu_2.97Zn_0.03(btc)₂ after HD adsorption recorded at various temperatures. The weakly and strongly coupled deuterium signals in the FD are indicated by the asterisk and open circles, respectively. (b) The definition of the modulation depth parameter k_mod. (c) Temperature dependence of (top) the intensity ratio between the weakly and strongly coupled deuterium nuclei FD signals and (down) modulation depth parameter k_mod extracted from the TD traces at T = 420 ns. Reproduced with permission from ref. 27 Copyright 2015 American Chemical Society.

In the presented example of HKUST-1 MOF, 3p ESEEM spectroscopy supplemented by HYSCORE and pulsed ENDOR experiments has proven to be a powerful alternative to study the adsorption and desorption of dihydrogen isotopologues in the local environment of Cu²⁺ ions as opposed to another detection method, thermal desorption spectroscopy, which provides rather a macroscopic approach with the predominant focus on the temperature-dependent desorption of guest molecules from the nanoporous material. Direct microscopic information about the position of the hydrogen molecules in the pores and the nature of the adsorption sites is not readily accessible by TDS. However, it can be inferred that the pulsed EPR approach may provide exactly such information related to the positions of the dihydrogen isotopologues with respect to the paramagnetic spin probe (up to a limit of approximately 0.8 nm distance), the population of these sites as well as their adsorption strength towards the hydrogen molecules as reflected by the dihydrogen mobility within the pores. However, it must be noted that such specific information about the adsorption and desorption of dihydrogen isotopologues can only be obtained if suitable paramagnetic probes are present in the nanoporous material or if they can be incorporated beforehand.

6. Future directions and challenges

Looking forward, the combination of pulsed EPR spectroscopy and in situ techniques is highly desirable to measure the population of D₂ or HD sites in dependence on gas pressure during the adsorption and desorption processes. This approach allows more flexibility to monitor the adsorption–desorption processes with molecular resolution, as viewed from within the pore system, capable of resolving the interaction between the spin probe as the host entity and the dihydrogen isotopologues as the guest molecules. A wide pressure range of 10⁻³ mbar < p < 1000 mbar has already been proven to be advantageous in monitoring directly the pore opening/closing of flexible MOFs in the case of CW-EPR spectroscopy.²⁶ Thus, to some extent, it will be very beneficial as well in the case of pulsed EPR as a method with much higher resolution, providing information about the coupled nuclear spin, their ligand shfi and nqi parameters, to study the molecular interaction between dihydrogen isotopologues and the host material. Furthermore, in situ measurements involving dihydrogen isotopologue mixtures will be worthwhile to address since the separation of dihydrogen isotopologues in the practical case would require detection methods capable of analysing such gas mixtures.

Computational techniques such as density functional theory (DFT) and molecular dynamics (MD) simulation hold great promise for advancing our understanding of the dihydrogen isotopologues adsorption process in a more complex MOF system where individual or the combination of KQS and CAQS effects needs to be considered. The analysis of the EPR data obtained for dihydrogen isotopologues adsorbed in porous materials (shfi and deuterium nqi parameters, temperature-dependent site population) could largely benefit from supportive DFT and MD computations.

In addition, in principle, EPR spectroscopy can be further complemented by quadrupole mass spectrometry to allow the quantification of selectivity for dihydrogen isotopologue adsorption analogous to the case applied in the TDS methodologies. Furthermore, the integration of the volumetric sorption method parallel to the automation for the EPR spectral acquisition approach will be ideal for studying the structural transformation in flexible MOFs with much higher efficiency.

Finally, two challenges for the application of EPR methods in the field of dihydrogen isotopologue adsorption and separation still need to be addressed. First of all, the basic challenge for the EPR spectroscopy approach remains in the question of how to embed the spin probe in the porous host material since the majority of MOF systems are diamagnetic. It has been demonstrated that isomorphous substitution in the metal ion sites is a reliable way of introducing the paramagnetic centres into the MOF system.^87–90 However, one needs to ensure the compatibility of the incorporated metal ions in the framework so that the MOF structure and its properties can be largely preserved. Another approach studied by Fedin's group^91–95 is also available where organic radicals such as TEMPO can be incorporated in the pores of MOFs. It is also useful to sense the structural changes, for example, during the adsorption–desorption of guest molecules or application of a certain range of pressures and temperatures. The next question is correlated with the possibility of performing pulsed EPR measurements for the system under study. The relaxation properties of the spin probe are largely influenced by its chemical environment, concentration, the spin state of the paramagnetic centre itself and temperature. Because of short spin–lattice relaxation times, the application of pulsed EPR experiments is in general restricted to low temperatures. In most cases, pulsed EPR is applicable when the samples are magnetically diluted with low concentration of paramagnetic spins (minimum interactions with the neighbouring paramagnetic centres), thus increasing the transverse electron spin relaxation times to allow the application of mw and rf pulses, evolution and subsequent detection on a technically applicable timescale.⁶²

The second challenge is related to the detection of dihydrogen isotopologues that are magnetically inactive (for instance p-H₂ and p-T₂ under cryogenic temperatures). To address this issue, organic radicals or transition metal ions that have rather long spin–lattice relaxation times as a probe may be a solution to bring the detection to a higher temperature range so that the proportion of NMR active o-H₂ can be feasibly detected. However, organic radicals are in general prone to decomposition or ageing processes if compared to the transition metal ions, so this requires careful activation procedures and further chemical insight to anticipate the decomposition of the spin probe.

7. Conclusions

This feature article highlights the potential of in situ CW-EPR spectroscopy and hyperfine spectroscopy based on pulsed EPR methods (ESEEM and ENDOR) to be implemented in the study of dihydrogen isotopologue adsorption on nanoporous materials. In the field of dihydrogen isotopologue detection, several methods were discussed briefly in terms of their application potential and possible limitations, for instance, mass spectrometry, IR, NPD, TDS, and NMR. As an alternative, the EPR spectroscopic method is non-invasive and very sensitive to molecular-level changes as a result of host–guest interactions between the spin probe embedded in MOFs and the dihydrogen isotopologues. The first study case highlighted the power of the in situ CW-EPR approach to monitor the pore phase transitions via changes in the local structure of the spin probe in response to the adsorption of pure dihydrogen isotopologues. The favourability for adsorbing heavier dihydrogen isotopologues stems from the nuclear quantum effect that lowers the ZPE term. In addition, the second case discussed the applicability of pulsed EPR (ESEEM and ENDOR) to locate the exact position as well as the nature of the interaction of dihydrogen isotopologues in the vicinity of the Cu²⁺ spin probe in the Cu_2.97Zn_0.03(btc)₂ system (within 0.8 nm range). In the end, potential pitfalls were presented, and more progress is needed to anticipate the current challenges in using EPR spectroscopy for dihydrogen isotopologue detection.

Author contributions

M. F. L. conducted the draft writing & editing, literature research, and performed data analysis and interpretation. A. P. reviewed and edited the draft, designed the project and acquired the funding.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the DFG funding of GRK 2721: Hydrogen Isotopes 1, 2, 3 H with project number of 443871192 and FOR 2433 with project number of 279409724.

References

1. J. Atzrodt, V. Derdau, W. J. Kerr and M. Reid, Angew. Chem., Int. Ed., 2018, 57, 1758–1784.
2. R. J. Pearson, A. B. Antoniazzi and W. J. Nuttall, Fusion Eng. Des., 2018, 136, 1140–1148.
3. C. E. Housecroft and A. G. Sharp, Inorganic Chemistry, Pearson International, 5th edn, 2018.
4. Y. Li, X. Lei, S. Jockusch, J. Y. C. Chen, M. Frunzi, J. A. Johnson, R. G. Lawler, Y. Murata, M. Murata, K. Komatsu and N. J. Turro, J. Am. Chem. Soc., 2010, 132, 4042–4043.
5. H. K. Rae, ACS Symp. Ser., 1978, 17, 1–26.
6. J. Y. Kim, H. Oh and H. R. Moon, Adv. Mater., 2019, 31, 1805293.
7. H. Oh, S. B. Kalidindi, Y. Um, S. Bureekaew, R. Schmid, R. A. Fischer and M. Hirscher, Angew. Chem., Int. Ed., 2013, 52, 13219–13222.
8. G. M. Keyser, D. B. McConnell, N. Anyas-Weiss and P. Kirkby, ACS Symp. Ser., 1978, 126–133.
9. J. J. M. Beenakker, V. D. Borman and S. Y. Krylov, Chem. Phys. Lett., 1995, 232, 379–382.
10. H. Oh and M. Hirscher, Eur. J. Inorg. Chem., 2016, 4278–4289.
11. H. Oh, K. S. Park, S. B. Kalidindi, R. A. Fischer and M. Hirscher, J. Mater. Chem. A, 2013, 1, 3244–3248.
12. J. Park, A. Adhikary and H. R. Moon, Coord. Chem. Rev., 2023, 497, 215402.
13. L. Zhang, T. Wulf, F. Baum, W. Schmidt, T. Heine and M. Hirscher, Inorg. Chem., 2022, 61, 9413–9420.
14. I. Savchenko, A. Mavrandonakis, T. Heine, H. Oh, J. Teufel and M. Hirscher, Microporous Mesoporous Mater., 2015, 216, 133–137.
15. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062.
16. I. Senkovska, V. Bon, L. Abylgazina, M. Mendt, J. Berger, G. Kieslich, P. Petkov, J. L. Fiorio, J.-O. Joswig, T. Heine, L. Schaper, C. Bachetzky, R. Schmid, R. A. Fischer, A. Pöppl, E. Brunner and S. Kaskel, Angew. Chem., Int. Ed., 2023, 62, e202218076.
17. S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704.
18. J. Y. Kim, J. Park, J. Ha, M. Jung, D. Wallacher, A. Franz, R. Balderas-Xicohténcatl, M. Hirscher, S. G. Kang, J. T. Park, I. H. Oh, H. R. Moon and H. Oh, J. Am. Chem. Soc., 2020, 142, 13278–13282.
19. L. Bondorf, J. L. Fiorio, V. Bon, L. Zhang, M. Maliuta, S. Ehrling, I. Senkovska, J. D. Evans, J.-O. Joswig, S. Kaskel, T. Heine and M. Hirscher, Sci. Adv., 2022, 8, 7035.
20. S. M. Iordache, E. I. Ionete, A. M. Iordache, E. Tanasa, I. Stamatin and C. E. Ana Grigorescu, Int. J. Hydrogen Energy, 2021, 46, 11015–11024.
21. I. Weinrauch, I. Savchenko, D. Denysenko, S. M. Souliou, H. H. Kim, M. Le Tacon, L. L. Daemen, Y. Cheng, A. Mavrandonakis, A. J. Ramirez-Cuesta, D. Volkmer, G. Schütz, M. Hirscher and T. Heine, Nat. Commun., 2017, 8, 1–7.
22. A. J. W. Physick, D. J. Wales, S. H. R. Owens, J. Shang, P. A. Webley, T. J. Mays and V. P. Ting, Chem. Eng. J., 2016, 288, 161–168.
23. R. Muhammad, S. Jee, M. Jung, J. Park, S. G. Kang, K. M. Choi and H. Oh, J. Am. Chem. Soc., 2021, 143, 37.
24. C. Genty and R. Schott, Anal. Chem., 1970, 42, 7–11.
25. D. Cao, S. Peng, X. Chen, J. Hou, P. Chen, C. Xiao, Y. Gong and H. Wang, Anal. Methods, 2017, 9, 3067–3072.
26. M. F. Lukman, M. Mendt, V. Bon, S. Kaskel and A. Pöppl, Chem. Commun., 2023, 59, 9884–9887.
27. M. Šimenas, B. Jee, M. Hartmann, J. Banys and A. Pöppl, J. Phys. Chem. C, 2015, 119, 28530–28535.
28. B. Jee, M. Hartmann and A. Pöppl, Mol. Phys., 2013, 111, 2950–2966.
29. K. M. Thomas, Catal. Today, 2007, 120, 389–398.
30. O. T. Qazvini, V. J. Scott, L. Bondorf, M. Ducamp, M. Hirscher, F. X. Coudert and S. G. Telfer, Chem. Mater., 2021, 33, 8886–8894.
31. G. F. Shipman, Anal. Chem., 1962, 34, 877–878.
32. E. H. Carter and H. A. Smith, J. Phys. Chem., 1963, 67, 1512–1516.
33. W. A. Van Hook and P. H. Emmett, J. Phys. Chem., 1960, 64, 673–675.
34. P. L. Gant and K. Yang, Science, 1959, 129, 1548–1549.
35. J. King, J. Phys. Chem., 1963, 67, 1397.
36. S. A. Fitzgerald, K. Allen, P. Landerman, J. Hopkins, J. Matters, R. Myers and J. L. C. Rowsell, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 224301.
37. S. A. Fitzgerald, J. Hopkins, B. Burkholder, M. Friedman and J. L. C. Rowsell, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 104305.
38. S. Bordiga, L. Regli, F. Bonino, E. Groppo, C. Lamberti, B. Xiao, P. S. Wheatley, R. E. Morris and A. Zecchina, Phys. Chem. Chem. Phys., 2007, 9, 2676–2685.
39. E. G. Dongmo, S. Haque, F. Kreuter, T. Wulf, J. Jin, R. Tonner-Zech, T. Heine and K. R. Asmis, Chem. Sci., 2024, 15, 14635–14643.
40. F. Banijamali, A. Maghari, G. Schutz and M. Hirscher, Adsorption, 2021, 27, 925–935.
41. H. Oh, I. Savchenko, A. Mavrandonakis, T. Heine and M. Hirscher, ACS Nano, 2014, 8, 761–770.
42. F. Von Zeppelin, M. Haluška and M. Hirscher, Thermochim. Acta, 2003, 404, 251–258.
43. J. Y. Kim, R. Balderas-Xicohténcatl, L. Zhang, S. G. Kang, M. Hirscher, H. Oh and H. R. Moon, J. Am. Chem. Soc., 2017, 139, 15135–15141.
44. V. Bon, N. Busov, I. Senkovska, N. Bönisch, L. Abylgazina, A. Khadiev, D. Novikov and S. Kaskel, Chem. Commun., 2022, 58, 10492–10495.
45. H. Miura, V. Bon, I. Senkovska, S. Ehrling, S. Watanabe, M. Ohba and S. Kaskel, Dalton Trans., 2017, 46, 14002–14011.
46. V. K. Peterson, Y. Liu, C. M. Brown and C. J. Kepert, J. Am. Chem. Soc., 2006, 128, 15578–15579.
47. R. A. Pollock, J. H. Her, C. M. Brown, Y. Liu and A. Dailly, J. Phys. Chem. C, 2014, 118, 18197–18206.
48. D. E. Jaramillo, H. Z. H. Jiang, H. A. Evans, R. Chakraborty, H. Furukawa, C. M. Brown, M. Head-Gordon and J. R. Long, J. Am. Chem. Soc., 2021, 143, 6248–6256.
49. M. T. Kapelewski, T. Runčevski, J. D. Tarver, H. Z. H. Jiang, K. E. Hurst, P. A. Parilla, A. Ayala, T. Gennett, S. A. Fitzgerald, C. M. Brown and J. R. Long, Chem. Mater., 2018, 30, 8179–8189.
50. Y. Yabuuchi, H. Furukawa, K. M. Carsch, R. A. Klein, N. V. Tkachenko, A. J. Huang, Y. Cheng, K. M. Taddei, E. Novak, C. M. Brown, M. Head-Gordon and J. R. Long, J. Am. Chem. Soc., 2024, 146, 22759–22776.
51. H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2007, 129, 5314–5315.
52. C. M. Brown, Y. Liu, T. Yildirim, V. K. Peterson and C. J. Kepert, Nanotechnology, 2009, 20, 204025.
53. F. M. Mulder, B. Assfour, J. Huot, T. J. Dingemans, M. Wagemaker and A. J. Ramirez-Cuesta, J. Phys. Chem. C, 2010, 114, 10648–10655.
54. H. H. Limbach, T. Pery, N. Rothermel, B. Chaudret, T. Gutmann and G. Buntkowsky, Phys. Chem. Chem. Phys., 2018, 20, 10697–10712.
55. N. J. Turro, A. A. Martí, J. Y. C. Chen, S. Jockusch, R. G. Lawler, M. Ruzzi, E. Sartori, S. C. Chuang, K. Komatsu and Y. Murata, J. Am. Chem. Soc., 2008, 130, 10506–10507.
56. M. Frunzi, S. Jockusch, J. Y. C. Chen, R. M. K. Calderon, X. Lei, Y. Murata, K. Komatsu, D. M. Guldi, R. G. Lawler and N. J. Turro, J. Am. Chem. Soc., 2011, 133, 14232–14235.
57. Y. T. A. Wong, V. Martins, B. E. G. Lucier and Y. Huang, Chem. – Eur. J., 2019, 25, 1848–1853.
58. B. E. G. Lucier, Y. Zhang, K. J. Lee, Y. Lu and Y. Huang, Chem. Commun., 2016, 52, 7541–7544.
59. M. M. Roessler and E. Salvadori, Chem. Soc. Rev., 2018, 47, 2534.
60. M. Mendt, M. Simenas and A. Pöppl, Spectroscopic Methods in Mineralogy and Geology, John Wiley & Sons, Ltd, Weinheim, Germany, 2019, pp. 513–571.
61. V. Bon, E. Brunner, A. Pöppl and S. Kaskel, Adv. Funct. Mater., 2020, 30, 1907847.
62. D. Goldfarb and S. Stoll, EPR Spectroscopy: Fundamentals and Methods, John Wiley & Sons, Chichester, 2018.
63. A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, Oxford, 2001.
64. J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance: Elementary Theory and Practical Applications, John Wiley & Sons, Hoboken, 2nd edn, 2007.
65. V. Chechik, E. Carter and D. Murphy, Electron Paramagnetic Resonance, Oxford University Press, Oxford, 2nd edn, 2016.
66. W. B. Mims, Proc. R. Soc. London, Ser. A, 1965, 283, 452–457.
67. E. R. Davies, Phys. Lett. A, 1974, 47, 1–2.
68. S. Van Doorslaer, A. Schweiger and B. Kra, J. Phys. Chem. A, 2001, 105(31), 7554–7563.
69. C. Gemperle and A. Schweiger, Chem. Rev., 1991, 91, 1481–1505.
70. A. Ponti and A. Schweiger, Appl. Magn. Reson., 1994, 7, 363–403.
71. P. A. Narayana and L. Kevan, J. Magn. Reson., 1976, 23, 385–393.
72. A. Schweiger, Pure Appl. Chem., 1992, 64, 809–814.
73. L. Kevan, Acc. Chem. Res., 1987, 20, 1–7.
74. P. Höfer, J. Magn. Reson., Ser. A, 1994, 111, 77–86.
75. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
76. F. Wang, R. Büchel, A. Savitsky, M. Zalibera, D. Widmann, S. E. Pratsinis, W. Lubitz and F. Schüth, ACS Catal., 2016, 6, 3520–3530.
77. Y. Zhang, Y. Peng, J. Li, K. Groden, J. S. McEwen, E. D. Walter, Y. Chen, Y. Wang and F. Gao, ACS Catal., 2020, 10, 9410–9419.
78. J. Wolfram, A. Fischer, A. Brenig, D. Klose, J. A. van Bokhoven, V. L. Sushkevich and G. Jeschke, Angew. Chem., Int. Ed., 2023, 135, e202303574.
79. S. A. Bonke, T. Risse, A. Schnegg and A. Brückner, Nat. Rev. Methods Primers, 2021, 1, 1–20.
80. D. Nielsen, Q. Gao, T. V. W. Janssens, P. N. R. Vennestrøm and S. Mossin, J. Phys. Chem. C, 2023, 127, 12995–13004.
81. C. Drouilly, J. M. Krafft, F. Averseng, S. Casale, D. Bazer-Bachi, C. Chizallet, V. Lecocq, H. Vezin, H. Lauron-Pernot and G. Costentin, J. Phys. Chem. C, 2012, 116, 21297–21307.
82. M. Mendt, P. Vervoorts, A. Schneemann, R. A. Fischer and A. Pöppl, J. Phys. Chem. C, 2019, 123, 2940–2952.
83. D. M. Polyukhov, S. Krause, V. Bon, A. S. Poryvaev, S. Kaskel and M. V. Fedin, J. Phys. Chem. Lett., 2020, 11, 5856–5862.
84. I. Nevjestić, H. Depauw, K. Leus, G. Rampelberg, C. A. Murray, C. Detavernier, P. Van Der Voort, F. Callens and H. Vrielinck, J. Phys. Chem. C, 2016, 120, 17400–17407.
85. S. Ehrling, M. Mendt, I. Senkovska, J. D. Evans, V. Bon, P. Petkov, C. Ehrling, F. Walenszus, A. Pöppl and S. Kaskel, Chem. Mater., 2020, 32, 5670–5681.
86. B. Jee, K. Eisinger, F. Gul-E-Noor, M. Bertmer, M. Hartmann, D. Himsl and A. Pöppl, J. Phys. Chem. C, 2010, 114, 16630–16639.
87. A. Pöppl, S. Kunz, D. Himsl and M. Hartmann, J. Phys. Chem. C, 2008, 112, 2678–2684.
88. O. Kozachuk, M. Meilikhov, K. Yusenko, A. Schneemann, B. Jee, A. V. Kuttatheyil, M. Bertmer, C. Sternemann, A. Pöppl and R. A. Fischer, Eur. J. Inorg. Chem., 2013, 4546–4557.
89. M. Mendt, B. Jee, N. Stock, T. Ahnfeldt, M. Hartmann, D. Himsl and A. Pöppl, J. Phys. Chem. C, 2010, 114, 19443–19451.
90. M. F. Lukman, P. C. Bruzzese, W. Böhlmann, A. Schnegg and A. Pöppl, J. Phys. Chem. C, 2024, 128, 9141.
91. A. M. Sheveleva, D. I. Kolokolov, A. A. Gabrienko, A. G. Stepanov, S. A. Gromilov, I. K. Shundrina, R. Z. Sagdeev, M. V. Fedin and E. G. Bagryanskaya, J. Phys. Chem. Lett., 2014, 5, 20–24.
92. A. S. Poryvaev, A. M. Sheveleva, D. I. Kolokolov, A. G. Stepanov, E. G. Bagryanskaya and M. V. Fedin, J. Phys. Chem. C, 2016, 120, 10698–10704.
93. A. S. Poryvaev, D. M. Polyukhov, E. Gjuzi, F. Hoffmann, M. Fröba and M. V. Fedin, Inorg. Chem., 2019, 58, 8471–8479.
94. A. S. Poryvaev, D. M. Polyukhov and M. V. Fedin, ACS Appl. Mater. Interfaces, 2020, 12, 16655–16661.
95. D. M. Polyukhov, A. S. Poryvaev, S. A. Gromilov and M. V. Fedin, Nano Lett., 2019, 19, 6506–6510.

---