Understanding the Ag–S interface stability and electrocatalytic activity of CO₂ electroreduction in atomically precise Ag₂₅ nanoclusters

Abstract

Elucidating the catalytic properties of metal nanoclusters (NCs) with essentially the same structure but different core metals is of fundamental interest. Our current studies have demonstrated that the thiolated Ag₂₅(SR)₁₈ NC exhibits SR ligand leaching dynamics and electrocatalytic activity in CO₂ reduction distinct from those of its Au₂₅(SR)₁₈ NC structural analogue.

---

In recent years, small metal nanoclusters (NCs) made with atomic precision have attracted great attention in various fields such as catalysis, chemical sensing and bio-applications.^1–6 The use of atomically precise metal NCs could eliminate concerns of inhomogeneity, and their ultrasmall size (1–2 nm) minimizes the material gap between experiments and modelling, thus holding great promise in fundamental catalysis research.^7,8 In the large family of metal NCs protected by various ligands, the thiolate-protected metal NCs have attracted extensive research interest, wherein Au and Ag NCs are two extensively studied groups.^9–12 Thiolated Au NCs have been widely studied in many catalytic applications.^5,6,13,14 For example, gold NCs have been recognized for their exceptional electrocatalytic activities in electrocatalytic reduction of CO₂ to CO.¹⁵ The effects of cluster size, shape, surface ligands and heterometal doping have been extensively employed to modulate the electrocatalytic activity and selectivity of gold NCs.^16–19

Compared to the widely studied gold NCs, thiolated Ag NCs have been less extensively investigated, possibly due to their moderate stability, leading to a limited understanding of their catalytic properties,^20,21 In particular, there are few recent studies on Ag NCs for photocatalytic CO₂RR.^22,23 Investigating Ag-based catalysts is of great importance for uncovering new catalytic mechanisms and utilizing metals that are less expensive than Au. Note that the catalytic properties of metal NCs are highly sensitive to the packing of atomic structures, and a subtle disturbance to the structure, composition and morphology may cause a significant change in the electronic and catalytic behaviors. In this regard, a direct comparison of catalytic performances of materials with essentially identical structures but distinct metal cores is of particular interest but has been hardly been pursued. In the large family of thiolate-protected metal NCs, the well-characterized Ag₂₅(SR)₁₈ provides an ideal model to study the effect of the core since this cluster and Au₂₅(SR)₁₈ share essentially the same structure. They both feature an icosahedral M₁₃ core protected by six V-shaped motifs arranged in a quasi-Th symmetry (Fig. S1, ESI†),¹⁰ thus enabling a direct comparison of their catalytic activities.^10,24 Of note, recent studies have demonstrated that the Au–S interface in Au₂₅(SR)₁₈ NCs is unstable under electrochemical conditions, and would be attacked by water from electrolyte to lead to stripping of some of the thiolate ligands and hence expose under-coordinated Au atoms to the surface.^5,25,26 Since the Ag–S bond is expected to be stronger and more ionic than the Au–S bond based on the difference in electronegativity between S and these two metals, it would be interesting to determine whether the Ag–S interface would become destabilized under electrochemical environments. If the thiolate ligands in Ag₂₅(SR)₁₈ can be eliminated from the Ag–S interface, then it would be of great importance to investigate the electrocatalytic response of the exposed Ag sites in comparison to Au in the dethiolated Au₂₅ counterpart.

Therefore, to gain a better understanding of the catalytic mechanism of Ag NCs, we selected Ag₂₅(SR)₁₈ as our research model, and first performed density functional theory (DFT) calculations to investigate its dynamic stability in electrochemical conditions.^27–30 To reduce the computational cost, the SR ligands were simplified to be –SCH₃.⁵ The computational details are provided in ESI.† To simulate the cluster/water interface, Ag₂₅ and Au₂₅ were placed in respective periodic boxes, each with dimensions of 20 × 20 × 30 ų and surrounded by 90 explicit water molecules with a density of about 1 g cm⁻³ (Fig. S2, ESI†). The potential of the entire system was regulated by introducing different amounts of Na atoms into the aqueous layer while the overall system was kept charge neutral. In this way, U_RHE = (Φ – 4.44)/e + 0.0592 × pH would give a different applied potential U depending on the value of the work function (Φ) for each model.³¹ Under a neutral pH condition (pH = 7), the addition of 1, 2 and 3 Na atoms into the Ag₂₅/water system would thus yield potentials of, respectively, 0.33 V, −0.84 V and −1.10 V vs. reversible hydrogen electrode (RHE).

According to the previous studies,^5,26 the desorption of thiolate ligands from the Au₂₅(SR)₁₈ surface is promoted by H₂O attacking the S atom to initiate the weakening and breakage of Au–S bonds. In the case of Ag₂₅(SCH₃)₁₈ NCs, the –SR ligand would be expected to undergo a similar leaching process, and the corresponding control variable (CV) for H adsorption (step 1) and Ag–S breakage (step 2) are defined schematically in Fig. S3 (ESI†). Our constrained ab initio molecular dynamics (AIMD) simulations at 300 K indicated the dynamic behavior of the Ag–S interface to be strongly dependent on the applied potential (Fig. 1a). At a positive potential of 0.33 V (Fig. S4, ESI†), the Ag–S interface is very stable: an attack of water from the solution onto the ligated S atom to form an adsorbed S–H bond and solvated OH⁻ species would have to overcome a very high barrier of 1.28 eV. For the potential shifted negatively to −0.84 V, the barrier for the water attack forming an S–H bond decreases to 1.04 eV (Fig. 1b). Note that the water molecule prefers to attack the S atom from the exterior thiolate ligand initially coordinated to two staple Ag atoms (Fig. 1a). This picture is quite different from that for the previously reported Au₂₅(SR)₁₈ NC,⁵ where the water molecule tends to attack the interior thiolate ligand initially coordinated to one staple Au and one icosahedral surface Au. Formation of the S–H bond is accompanied by a weakening of and hence more easily breakable Ag–S bond (Fig. 1c). Note that at U_RHE = −0.84 V, only one staple Ag–S bond is broken with a small free energy barrier of 0.16 eV, while the other staple Ag still strongly interacts with the coordinated S atom (Fig. 1a). For the potential further decreased to U_RHE = −1.10 V, one of the staple Ag–S bonds first breaks spontaneously after the structural relaxation at 0.8 ps, followed by formation of an S–H bond with a moderate barrier of 0.67 eV, and the other staple Ag–S bond can be easily broken with a negligibly small barrier of 0.08 eV, which ultimately results in the complete removal of the –SCH₃ ligand, forming a free HSCH₃ molecule dissolved in solution and exposing two dethiolated Ag sites (exposed Ag–Ag bond length of 2.74 Å). These simulations indicated that the applied potential can significantly affect the leaching dynamics of the Ag–S interface, and a lower reduction potential could kinetically promote the removal of thiolate ligands.

Fig. 1 (a) Schematic of local structures formed during adsorption of *H onto the S site and during Ag–S bond breaking in Ag₂₅(SR)₁₈ at U_RHE = −0.84 V and −1.10 V. (b) Integral free energy curves for *H adsorption and (c) Ag–S bond breaking at U_RHE = −0.84 V and −1.10 V, respectively. The Ag, S, C, O and H atoms are shown as pale blue, yellow, grey, red and white spheres, respectively. The H from the attacking H₂O is colored in green.

As a comparison, we also performed AIMD simulations on the Au₂₅(SCH₃)₁₈ analogue in the same neutral environment. In this case, additions of one and two Na atoms into the water layer correspond to applied potential U_RHE values of 0.11 V and −0.60 V, respectively. Note that addition of 3 Na atoms would lead to severe deformation of the Au₂₅ NC due to an especially low potential produced (U_RHE = −1.30 V, Fig. S5, ESI†), which is beyond our consideration. Similar to the case in Ag₂₅, the ligand leaching in Au₂₅ was also found to be dependent on potential. At U_RHE = 0.11 V, adsorption of water-dissociation-derived H onto the S atom from the interior thiolate ligand has to overcome a high barrier of 1.13 eV (Fig. S6, ESI†). For the potential lowered to −0.60 V (Fig. 2), the attack of S by water becomes much more facile, and the formation of the S–H bond is accompanied by the consecutive breaking of the surface Au–S bond and the staple Au–S bond. Note the difference between the water attack site in Au₂₅ (interior thiolate) and that in Ag₂₅ (exterior thiolate). To understand this difference, we analysed the charge states of the two possible S sites. The Bader charge analysis carried out (Fig. S7, ESI†) revealed that in Ag₂₅, the exterior S site carries a more negative charge of −0.37|e| as compared to the interior S site (−0.35|e|); conversely, in Au₂₅, the analysis indicated the interior S to be more negatively charged (−0.30|e|) than the exterior S site (−0.12|e|). The S site bearing a more negative charge is prone to be attacked by H₂O and is hence more reactive. At 1.16 ps, the two breaking Au–S bonds reach an equilibrium length of greater than 3 Å, at which point the –SCH₃ ligand can be considered to be completely removed, and the two exposed Au atoms are bonded to each other with a shortened bond length of 2.71 Å. In particular, the negligible barrier of 0.07 eV (Fig. 2c) indicates that the thiolate leaching in Au₂₅ occurs spontaneously at a negative reduction potential. Notably, at a comparable reduction potential (−0.84 V in Ag₂₅vs. −0.60 V in Au₂₅), the leaching of thiolate from the Ag–S interface is kinetically more difficult than that from the Au–S interface, which is closely related to the difference between their M–S bond strengths.

Fig. 2 (a) Schematic of the local structures formed during *H adsorption and Au–S breaking in Au₂₅(SCH₃)₁₈ at U_RHE = −0.60 V. (b) Statistics of the relative distances between representative atoms and (c) the integral free energy curve during constrained DFT-MD simulations at U_RHE = −0.60 V.

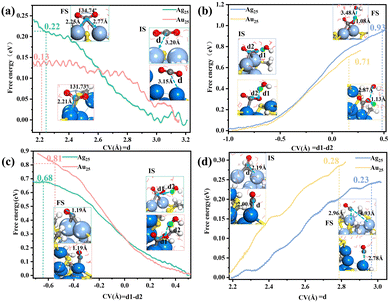
After the removal of–SR ligands, the dethiolated metal atoms can serve as the catalytically active sites. Our Bader charge analysis (Table S1, ESI†) revealed that the exposed two Ag atoms are positively charged (0.06|e| and 0.03|e|), while the exposed two Au atoms are negatively charged (−0.09|e| and −0.13|e|), with this difference between the exposed Ag and Au atoms implying that their catalytic properties could be different. We thus proceeded to investigate the dethiolated Ag₂₅ and Au₂₅ in the electrocatalytic CO₂ reduction reaction (CO₂RR). Fig. 3 shows the calculated integral free energy curves of the four elementary reaction steps for Ag₂₅ and Au₂₅ under the same neutral condition with two Na atoms added into the water layer. As shown in Fig. 3a, the CO₂ reactant can be effectively captured and activated at the exposed metal sites with very low kinetic barriers (0.22 eV in Ag₂₅ and 0.13 eV in Au₂₅). In Ag₂₅, the CO₂ is bonded to two staple Ag atoms in a bridging manner, while in Au₂₅, it is only singly bonded to the staple Au atom. After the activation step, the nearest water molecule would approach *CO₂ to form *COOH and a solvated OH⁻ species (Fig. 3b). This step has to overcome a relatively high barrier of about 0.93 eV in Ag₂₅, as compared to 0.71 eV in Au₂₅. Subsequently, the approach of another H₂O molecule to the O atom at the O–H end of *COOH leads to formation of adsorbed *CO and H₂O (Fig. 3c). This step needs to overcome a high barrier of 0.81 eV in Au₂₅, while in Ag₂₅, the barrier is only 0.68 eV. The final step corresponds to *CO desorption, forming CO gas and exposing the reactive metal sites (Fig. 3d). This step is very facile, and the desorption barrier is very low, about 0.23 eV in Ag₂₅ and 0.28 eV in Au₂₅. The above analysis indicated a different rate-determining step (RDS) of the CO₂RR for Ag₂₅ than for Au₂₅. In Ag₂₅, the highest potential barrier corresponds to the formation of *COOH, whereas in Au₂₅, the most difficult step is the formation of *CO. This analysis has thus demonstrated that changing the metal to another one with sufficiently different properties can change the RDS. We also examined the distributions of water density and hydrogen bonds at the cluster/water interface during the CO₂RR for Au₂₅ and Ag₂₅ (Fig. S8, ESI†). The results showed slightly denser water density at the Au₂₅/water interface, accompanied by more hydrogen bonds in Au₂₅ than in Ag₂₅. This observation suggested more water molecules to be accessible around the electrochemical interface of the Au₂₅ NC, thus facilitating the reaction kinetics for water and proton transfer during the CO₂RR.

Fig. 3 Comparison of the integral free energy curves between Ag₂₅ and Au₂₅ in (a) CO₂ activation, (b) *COOH formation, (c) *CO formation and (d) CO desorption as determined from constrained AIMD simulations. The local structures of the initial state (IS), final state (FS) and the defined collective variable (CV, d₁–d₂ or d) are shown in the insets.

Furthermore, to probe the CO₂RR selectivity, we also investigated its competitive hydrogen evolution reaction (HER). In the first Volmer step (Fig. S9a, ESI†), the dissociation of H₂O to form an *H intermediate requires a high barrier, of 1.45 eV in Ag₂₅ and 1.07 eV in Au₂₅, to be overcome. In the subsequent Heyrovsky step, the adsorbed *H would then combine with another H from water to produce H₂ and a solvated OH⁻ species. This step has to overcome a high barrier of 1.34 eV in Au₂₅ and 1.27 eV in Ag₂₅ (Fig. S9b, ESI†). Such a high barrier effectively inhibits HER at the exposed metal sites, thus ensuring the high selectivity of electroreduction of CO₂ to CO in both Ag₂₅ and Au₂₅.

To further probe whether ligand simplification would affect the reaction kinetics, we replaced the simplified –SCH₃ near the exposed metal site with the longer –SC₆H₁₃ ligand and calculated the corresponding free energy barriers of the CO₂RR (Fig. S10, ESI†) and HER (Fig. S11, ESI†). In contrast to the simplified –SCH₃, the long-chain –SC₆H₁₃ ligand facilitates CO₂ activation and *CO formation in Ag₂₅ as well as *COOH formation in Au₂₅. However, upon replacing the ligand, the energy barrier for the RDS (*COOH formation in Ag₂₅ and *CO formation in Au₂₅) remains almost unchanged for both NCs. In the HER process, the presence of the long-chain –SC₆H₁₃ greatly decreases the barrier for the Volmer and Heyrovsky steps, yet the barrier for the RDS is still higher than that in the CO₂RR, suggesting the higher selectivity for CO₂ electroreduction. These results indicated that the predicted reaction kinetics and selectivity based on the simplified –SCH₃ should be qualitatively reliable.

Furthermore, we conducted experiments to verify the prediction. As shown in Fig. S12 (ESI†), the Ag₂₅(SphMe₂)₁₈ NC (SphMe₂ = 2,4-dimethylbenzenethiol) sample exhibits characteristic absorption peaks at 390 nm, 490 nm, and 675 nm, while Au₂₅(PET)₁₈ (PET = phenylethylmercaptan) NC sample exhibits characteristic absorption peaks at 400 nm, 450 nm, and 670 nm, consistent with those reported in the literature.^24,32 Their performance in the CO₂RR was first evaluated by performing linear sweep voltammetry (LSV). As shown in Fig. 4a, the current density for each of the NCs is larger in CO₂-saturated electrolyte than in N₂-saturated electrolyte, suggesting greater involvement of current in the CO₂RR to CO. The CO faradaic efficiency (FE_CO) measurements (Fig. 4b) showed Au₂₅(PET)₁₈ achieving an FE_CO higher than that of Ag₂₅(SphMe₂)₁₈. The current density (j_CO) of Au₂₅(PET)₁₈ is also higher than that of Ag₂₅(SphMe₂)₁₈ (Fig. 4c). Moreover, from Fig. 4d, it is evident that the turnover frequency (TOF) value for Au₂₅(PET)₁₈ NCs is greater than that of Ag₂₅(SphMe₂)₁₈. These measurements suggested a better intrinsic activity and higher catalytic rate for Au₂₅(PET)₁₈ than for Ag₂₅(SphMe₂)₁₈. Additionally, the stability tests (Fig. 4e and f) indicated better FE_CO stability and current density stability demonstrated by Au₂₅(PET)₁₈ during continuous operation at −0.38 V for 16 hours. Evidently, these results agreed well with the theoretical predictions, where the inferior performance of Ag₂₅ could be correlated to its poorer ligand etching kinetics and higher RDS barrier in the CO₂RR process.

Fig. 4 Electrocatalytic CO₂RR performance in a CO₂ flow cell with 1 M KOH electrolyte. (a) LSV curves of Ag₂₅(SphMe₂)₁₈ and of Au₂₅(PET)₁₈, each in N₂-saturated or CO₂-saturated 1 M KOH electrolyte. (b) Faradaic efficiency of CO (FE_CO), (c) fractional current density of CO (j_CO), and (d) turnover frequency (TOF) of CO for Ag₂₅ and Au₂₅ at indicated potentials. (e) and (f) Tests of long-term stability of (e) Ag₂₅ and (f) Au₂₅ in the CO₂RR at −0.38 V.

In summary, our studies have demonstrated distinct interface dynamics and the CO₂RR mechanisms for Au₂₅ and Ag₂₅, which would be expected to inspire the development of functional nanostructures with enhanced catalytic properties through metal core engineering.

This work was supported by National Natural Science Foundation of China (No. 22473017 and No. 21805170) and Chongqing Science and Technology Commission (CSTB2024NSCQ-MSX0250).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. Chen, S. Wang, J. Zhong, Y. Song, J. Zhang, H. Sheng, Y. Pei and M. Zhu, Angew. Chem., Int. Ed., 2015, 127, 3188–3192.
2. Z. Chen, A. G. Walsh, X. Wei, M. Zhu and P. Zhang, J. Phys. Chem. C, 2022, 126, 12721–12727.
3. Y. Du, H. Sheng, D. Astruc and M. Zhu, Chem. Rev., 2019, 120, 526–622.
4. J. H. Lee, S. Kattel, Z. Xie, B. M. Tackett, J. Wang, C. J. Liu and J. G. Chen, Adv. Funct. Mater., 2018, 28, 1804762.
5. F. Sun, L. Qin, Z. Tang, G. Deng, M. S. Bootharaju, Z. Wei, Q. Tang and T. Hyeon, Chem. Sci., 2023, 14, 10532–10546.
6. Q. Yao, Z. Wu, Z. Liu, Y. Lin, X. Yuan and J. Xie, Chem. Sci., 2021, 12, 99–127.
7. R. Jin, G. Li, S. Sharma, Y. Li and X. Du, Chem. Rev., 2020, 121, 567–648.
8. S. Li, A. V. Nagarajan, Y. Li, D. R. Kauffman, G. Mpourmpakis and R. Jin, Nanoscale, 2021, 13, 2333–2337.
9. M. Hesari and Z. Ding, Acc. Chem. Res., 2017, 50, 218–230.
10. C. P. Joshi, M. S. Bootharaju, M. J. Alhilaly and O. M. Bakr, J. Am. Chem. Soc., 2015, 137, 11578–11581.
11. C. Liu, T. Li, H. Abroshan, Z. Li, C. Zhang, H. J. Kim, G. Li and R. Jin, Nat. Commun., 2018, 9, 744.
12. X. Zhu, L. Chen, Y. Liu and Z. Tang, POM, 2023, 2, 9140031.
13. P. Zhang, J. Phys. Chem. C, 2014, 118, 25291–25299.
14. F. Sun, C. Deng, S. Tian and Q. Tang, ACS Catal., 2021, 11, 7957–7969.
15. D. R. Kauffman, D. Alfonso, C. Matranga, H. Qian and R. Jin, J. Am. Chem. Soc., 2012, 134, 10237–10243.
16. S. Li, A. V. Nagarajan, D. R. Alfonso, M. Sun, D. R. Kauffman, G. Mpourmpakis and R. Jin, Angew. Chem., Int. Ed., 2021, 60, 6351–6356.
17. S. Li, D. Alfonso, A. V. Nagarajan, S. D. House, J. C. Yang, D. R. Kauffman, G. Mpourmpakis and R. Jin, ACS Catal., 2020, 10, 12011–12016.
18. X. Liu, E. Wang, M. Zhou, Y. Wan, Y. Zhang, H. Liu, Y. Zhao, J. Li, Y. Gao and Y. Zhu, Angew. Chem., Int. Ed., 2022, 134, e202207685.
19. J. Wang, F. Xu, Z. Y. Wang, S. Q. Zang and T. C. Mak, Angew. Chem., Int. Ed., 2022, 61, e202207492.
20. R. Jin, S. Zhao, Y. Xing and R. Jin, CrystEngComm, 2016, 18, 3996–4005.
21. S. Yoo, S. Yoo, G. Deng, F. Sun, K. Lee, H. Jang, C. W. Lee, X. Liu, J. Jang, Q. Tang, Y. J. Hwang, T. Hyeon and M. S. Bootharaju, Adv. Mater., 2024, 36, 2313032.
22. Y. Feng, F. Fu, L. Zeng, M. Zhao, X. Xin, J. Liang, M. Zhou, X. Fang, H. Lv and G. Y. Yang, Angew. Chem., Int. Ed., 2024, 63, e202317341.
23. Y. Xiong, H. Chen, Y. Hu, S. Yang, X. Xue, L. He, X. Liu, J. Ma and Z. Jin, Nano Lett., 2021, 21, 8693–8700.
24. M. Zhu, W. T. Eckenhoff, T. Pintauer and R. Jin, J. Phys. Chem. C, 2008, 112, 14221–14224.
25. H. Seong, V. Efremov, G. Park, H. Kim, J. S. Yoo and D. Lee, Angew. Chem., Int. Ed., 2021, 133, 14684–14691.
26. F. Sun, L. Qin, Z. Tang and Q. Tang, Chem. Sci., 2024, 15, 16142–16155.
27. H. Cao, Z. Zhang, J.-W. Chen and Y.-G. Wang, ACS Catal., 2022, 12, 6606–6617.
28. I. V. Chernyshova and S. Ponnurangam, Phys. Chem. Chem. Phys., 2019, 21, 8797–8807.
29. J. A. Gauthier, M. Fields, M. Bajdich, L. D. Chen, R. B. Sandberg, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 29278–29283.
30. S. Li, A. V. Nagarajan, X. Du, Y. Li, Z. Liu, D. R. Kauffman, G. Mpourmpakis and R. Jin, Angew. Chem., Int. Ed., 2022, 134, e202211771.
31. K. Xie, F. Wang, F. Wei, J. Zhao and S. Lin, J. Phys. Chem. C, 2022, 126, 5180–5188.
32. X. Liu, J. Yuan, C. Yao, J. Chen, L. Li, X. Bao, J. Yang and Z. Wu, J. Phys. Chem. C, 2017, 121, 13848–13853.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc06185c

‡ These two authors contributed equally to this work.

---