 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sustainable upgrading of biomass: a thermodynamic approach to fine-tuning product selectivity for glycerol oxidation†
Andrés F.
Pérez-Torres
*ab,
Heejung
Kong
 ab,
Fatwa F.
Abdi
ab,
Fatwa F.
Abdi
 c,
Roel
van de Krol
c,
Roel
van de Krol
 ab and
Marco
Favaro
ab and
Marco
Favaro
 *a
*a
aInstitute for Solar Fuels, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, Hahn-Meitner-Platz 1, 14109 Berlin, Germany. E-mail: andres.perez_torres@helmholtz-berlin.de; marco.favaro@helmholtz-berlin.de
bInstitut für Chemie, Technische Universität Berlin, Straße des 17. Juni 124, 10623 Berlin, Germany
cSchool of Energy and Environment, City University of Hong Kong, 83 Tat Chee Avenue, Kowloon, Hong Kong SAR, China
First published on 6th January 2025
Abstract
Calculated thermodynamic properties for the electrochemical glycerol oxidation at different temperatures and potentials indicate that external applied bias has a more significant influence on reaction selectivity than temperature.
Fossil fuel-derived hydrocarbons are central to the global economy, serving as the primary energy source for various industrial sectors and the main source of commodity chemicals.1 However, their use results in significant CO2 emissions, greatly contributing to global warming and environmental pollution. While substantial progress has been made in harnessing solar, wind, and geothermal energy, these sources cannot provide the organic carbon essential for the chemical industry. Consequently, alternative energy and renewable carbon sources are urgently needed for the chemical industry. Hybrid electrolysis—where biomass oxidation at the anode is coupled with the hydrogen evolution reaction (HER) at the cathode—enables the simultaneous, efficient production of essential carbon and hydrogen.2 This is particularly interesting given the substantial production of biomass waste; it is estimated that worldwide production of biomass waste amounts to around 100–400 gigatons per year (Gt per y).3 Assuming a carbon content of 50% and a global production of 140 Gt per y, the complete conversion of biomass waste to fuels and chemicals (by carbon content) could exceed the global demand for these goods by a factor of 45–300, depending on the product.3 Among the different biomass valorisation procedures (usually oxidation reactions), electrocatalytic valorisation is emerging as a sustainable approach over thermochemical processes due to milder reaction conditions, less waste generation, and the possibility of better selectivity control for the production of chemicals and fuels.1,3,4,5 Glycerol has drawn significant attention from academia and industry because it is an abundant and low-cost biomass-derived molecule that can be transformed into different C3, C2, and C1 compounds. Several of these products are widely used in the pharmaceutical, food, and cosmetics industry, reaching prices significantly higher than the starting material.6 For example, glyceric acid (GLAC) and dihydroxyacetone (DHA) can reach prices of 3290 and 702 € per g, while purified glycerol costs around 1.19 € per g.7 Despite promising advances reported thus far, the electrochemical glycerol oxidation reaction (GOR) currently lacks the necessary selectivity required for its practical deployment. The limitation comes from the complex reaction pathway, where several different products can be obtained by the transfer of a small number of electrons during the oxidation process (Table 1).
| Product | Total reaction | n |
|---|---|---|
| Dihydroxyacetone (DHA) | C3H8O3 → H2 + C3H6O3 | 2 |
| Glyceraldehyde (GLAD) | C3H8O3 → H2 + C3H6O3 | 2 |
| Lactic acid (LAC) | C3H8O3 → H2 + C3H6O3 | 2 |
| Glyceric acid (GLAC) | C3H8O3 + H2O → 2H2 + C3H6O4 | 4 |
| Hydroxypyruvic acid (HPAC) | C3H8O3 + H2O → 3H2 + C3H4O4 | 6 |
| Tartronic acid (TAC) | C3H8O3 + 2H2O → 4H2 + C3H4O5 | 8 |
| Mesoxalic acid (MESAC) | C3H8O3 + 2H2O → 5H2 + C3H2O5 | 10 |
| Glycolaldehyde (GCAD) | 2/3C3H8O3 → 2/3H2 + C2H4O2 | 4/3 |
| Acetic acid (AcOH) | 2/3C3H8O3 → 2/3H2 + C2H4O2 | 4 |
| Glycolic acid (GAC) | 2/3C3H8O3 + H2O → 5/3H2 + C2H4O3 | 10/3 |
| Glyoxylic acid (GLYX) | 2/3C3H8O3 + H2O → 8/3H2 + C2H2O3 | 16/3 |
| Oxalic acid (OXAC) | 2/3C3H8O3 + 2H2O → 11/3H2 + C2H2O4 | 22/3 |
| Formic acid (FAC) | 1/3C3H8O3 + H2O → 4/3H2 + CH2O2 | 8/3 |
| Carbon dioxide (CO2) | 1/3C3H8O3 + H2O → 7/3H2 + CH2O2 | 14/3 |
| Oxygen (O2) | 2H2O → 2H2 + O2 | 4 |
Important aspects for understanding the process, optimizing the reaction conditions, and designing the catalyst are the thermodynamic parameters of the reaction. However, despite the quite significant body of research performed on the GOR, there is a notable gap in the literature regarding the Gibbs free energy of reaction (ΔRG), the enthalpy of reaction (ΔRH), and the reversible potential (Erev) of the aforementioned oxidation pathways (Table 1). To calculate these values, the Gibbs free energy and enthalpy of formation (ΔfG and ΔfH, respectively) of the different molecules is needed, but this information is only available for glycerol (GLY), AcOH, GAC, FAC, CO2, H2, and O2.7,8 Furthermore, these data are usually computed for the molecules in their pure form at standard state conditions (298.15 K and 1 bar, referred as ΔfG° and ΔfH°), even though the reactions are performed in water at different temperatures. Consequently, it is often not possible to calculate the thermodynamic properties of most reactions. Even if estimation is feasible, ignoring the effects of water solvation and temperature variations may lead to erroneous values.
Recently, Ebeling et al.7 reported the thermodynamic properties of common GOR products. The reactions were modelled at infinite dilution in water at room temperature (298.15 K), using a combination of group additivity methods and machine learning. In this paper, we estimate the thermodynamic properties of various GOR at 1 bar, pH = 0 (meaning fully protonated species) and for temperatures ranging from 25 °C to 80 °C. Additionally, glycolaldehyde (GCAD), a major GOR product from BiVO4 photoanodes,9,10 is included in our calculations. The calculations were performed using a combination of information from databases, group additivity method (GANI)11 and thermodynamic models available in ASPEN Plus.12 The selected thermodynamic models (NTRL-NTH, NTRL-HOC, NTRL-RK, UNIF-DMD, WILS-NTH) were used to account for the effects of water solvation at infinite dilution and the change of temperature on the Gibbs energy of formation (ΔfG) and enthalpy of formation (ΔfH) for all molecules, except for H2, O2, and CO2. The properties of the latter were calculated in the gas phase, while considering non-ideal behaviour. The group additivity method was used to compute quantities only for molecules not reported in the database available in ASPEN Plus (Table S1, ESI†).
ΔfG for each molecule at different temperatures (T) was calculated using eqn (1) and (2):
| ΔfG(T) = ΔfGideal + ΔGE(T) | (1) |
| ΔfGideal = ΔfHideal − TΔSideal | (2) |
To select the most appropriate model, we calculated ΔfG° for the GOR products and compared them with experimental values tabulated in the literature (Table S2, ESI†). Note that ΔfG° was calculated using eqn (1) for temperature and pressure at standard state conditions. All the models, except for NTRL-HOC, give similar results with <1% variation among themselves and <5% difference compared to the experimental values (Tables S3 and S2, respectively, ESI†). For the case of NTRL-HOC, parameters needed for the calculations were not available in ASPEN Plus, so we were unable to calculate the thermodynamic properties of several molecules. Based on these results, we chose the NTRL-NTH model for further calculations. The determined ΔfG° for the possible products of GOR and the reaction pathways are reported in Fig. 1. The process can be described as an inner sphere reaction, in which the adsorption mode and site(s) on the catalyst surface leads to different C3 products. These products can be further oxidized to C2 and C1 products by different coupled C–C breaking reactions, including further oxidation by a desorption/re-adsorption process, a continuous reaction at the surface, or a combination of both. Despite the chemical similarity of the three hydroxyl groups present in glycerol, the product varies depending on which group is oxidized. Additionally, the presence of non-electrochemical steps13 further complicates the reaction pathway. As a result, achieving high selectivity for a specific product through GOR is challenging. Note that ΔfG° becomes more negative as we move toward more oxidized molecules containing the same number of carbon atoms. This indicates that the formation of more oxidized species is favoured in contrast to the reduced ones, except for the case of GLAD and DHA. As will be discussed in the following paragraphs, selectivity is highly dependent on the oxidation level of the product molecule. However, this does not guarantee that the reaction will proceed spontaneously under all conditions of temperature and pressure.
ΔRG was calculated using eqn (3), following the stoichiometry depicted in Table 1 and the values determined for ΔfG (Table S4, ESI†). Eqn (4) was used to calculate the reversible potential (Erev) based on the ΔRG; n is the number of electrons transferred in the reaction and F is the Faraday constant (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1). For the sake of simplicity and ease of comparison between the different products, we only calculated ΔRG and Erev for the direct conversion of glycerol to the selected products, without considering possible intermediates in the process.
485 C mol−1). For the sake of simplicity and ease of comparison between the different products, we only calculated ΔRG and Erev for the direct conversion of glycerol to the selected products, without considering possible intermediates in the process.
 | (3) |
 | (4) |
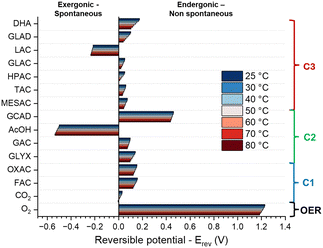 | ||
| Fig. 2 Reversible potential (Erev) at different temperatures for the oxidation of glycerol to different products (values can be found in Table S5, ESI†). | ||
Notably, the conversion processes of GLY to LAC and AcOH are spontaneous, suggesting that no energy input energy would be required for the reactions to occur. However, even though the formation of these molecules is thermodynamically favourable (exergonic), they are rarely reported as products in experimental studies, and the processes likely require an external energy input due to sluggish kinetics. In this context, it is important to note that the reported data are purely thermodynamic, and the electro-kinetics of each process are not considered. A competition between thermodynamic and kinetic control over the reaction likely plays a major role in defining the selectivity of the reaction. Additionally, other factors are not taken into account, for instance the electrolyte-solute interaction (reported to affect selectivity and activity9,16), the effect of the double layer on the electrocatalytic activity,17 the mass transport and hydrodynamics around the working electrode (known to affect the selectivity18), and the interaction/adsorption modes (which plays a role in selectivity13). Despite the limitations of our model, the thermodynamic data reported in this work provide general trends that are reflected in experimental results and can be used to study the effect of different reaction conditions on selectivity.
When considering the effect of temperature, the gradual decrease in Erev with increasing temperature reflects the endergonic nature of most reactions, except for LAC and AcOH (see ΔRH in Table S6, ESI†). By Le Chatelier's principle, the reaction equilibrium will be displaced toward products at higher temperatures and the magnitude of the change is directly proportional to the ΔRH. Thus, at higher temperatures a lower applied bias is needed to achieve the same current density and conversion rate of glycerol. However, our calculations show that the relative difference in Erev for the different products scales by about the same factor with temperature, and thus does not favour the formation of one product over the other. Consequently, from the thermodynamic perspective, temperature has no significant effect on selectivity. Notably, the oxidation of glycerol to CO2 becomes spontaneous at 80 °C, which may account for the experimental observations of increased CO2 production at elevated temperatures.1
In addition to temperature, the applied potential (Eapp) is another crucial parameter that can be adjusted to tune the selectivity of the GOR. The relation between potential and product concentrations is described by the Nernst equation (eqn (6)). When an external potential is applied to an electrochemical cell, the system is swept away from its equilibrium conditions and a new composition is achieved. This new composition will be dictated by the reaction quotient (Q): the smaller the value of Q, the higher the concentration of oxidation products (eqn (5) and (7)). To study the effect of different potentials on selectivity, we calculated Q using the Nernst equation and the number electrons necessary to produce 1 mol of oxidation product. For ease of interpretation, the natural logarithm of Q (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q) is displayed for the different products at different potentials in Fig. S1 (ESI†).
Q) is displayed for the different products at different potentials in Fig. S1 (ESI†).
| Ox + ne− ↔ Red | (5) |
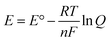 | (6) |
 | (7) |
The results suggest that product selectivity is influenced more by Eapp than T. When no potential is applied (Eapp = 0) i.e. at chemical equilibrium, most of the reactions are non-spontaneous and Q (in this case Keq) is displaced towards the reactants (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq > 0), except for the case of LAC and AcOH. At more positive potentials all the reactions shift toward the formation of products (ln
Keq > 0), except for the case of LAC and AcOH. At more positive potentials all the reactions shift toward the formation of products (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q < 0, Fig. S2, ESI†), but the extent of the shift is strongly influenced by the number of electrons involved in the reaction. The value of ln
Q < 0, Fig. S2, ESI†), but the extent of the shift is strongly influenced by the number of electrons involved in the reaction. The value of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q decreases by a proportionality constant of −nF/RT (or −n/0.0257 V−1) per volt of applied potential to the anode. For DHA, GLAD, LAC, GCAD, and AcOH, the shift to products is small compared to other molecules because only 1–2 electrons are involved in the reaction (Fig. S1 and S2, ESI†). In contrast, when more electrons are involved in the reaction, such as in the production of more oxidized molecules, Q is largely shifted toward the products with applied potential (Fig. S1 and S2, ESI†). This is the case of C3 products going from DHA to MESAC, C2 products from GCAD to OXAC, and even C1 products comparing FAC with CO2. These results may help to rationalize many experimental results where there is a selectivity shift or the formation of more oxidized molecules at higher applied potentials.19
Q decreases by a proportionality constant of −nF/RT (or −n/0.0257 V−1) per volt of applied potential to the anode. For DHA, GLAD, LAC, GCAD, and AcOH, the shift to products is small compared to other molecules because only 1–2 electrons are involved in the reaction (Fig. S1 and S2, ESI†). In contrast, when more electrons are involved in the reaction, such as in the production of more oxidized molecules, Q is largely shifted toward the products with applied potential (Fig. S1 and S2, ESI†). This is the case of C3 products going from DHA to MESAC, C2 products from GCAD to OXAC, and even C1 products comparing FAC with CO2. These results may help to rationalize many experimental results where there is a selectivity shift or the formation of more oxidized molecules at higher applied potentials.19
In conclusion, we found that the temperature has only a limited effect on the thermodynamics of the reaction, although a higher temperature help reducing the external energy input (i.e. the applied bias). However, this comes at the expense of the selectivity, since the complete mineralization of glycerol to CO2 is favoured by higher reaction temperatures. On the other hand, the effect of the applied potential on selectivity is significantly larger: as expected, increasing the applied bias favours the production of highly oxidized molecules due to the more efficient transfer of a higher number of electrons. Note that our calculations take into account only the thermodynamic aspect of GOR. However, the selectivity reported in experimental reports is likely due to the combination of the reaction thermodynamics and kinetics over the selected (photo)catalytic system.
The thermodynamic data reported in this study can be used in multiphysics modelling of hybrid (photo)electrolyzers in which the GOR constitutes the anodic process. For this reason, solution properties of glycerol and the different GOR products considered in this work have been calculated as a function of temperature and are available in Supplementary note 1 (ESI†) (viscosities and densities) and Supplementary note 2 (ESI†) (diffusion coefficients). Our calculation method is applicable to the investigation of other biomass oxidation reactions where the molecular structure of the products is known.
This work was supported by the European Innovation Council (EIC) via OHPERA (grant agreement 101071010) and PH2OTOGEN (grant agreement 101137889) projects.
Data availability
The data that support the findings of this study are available in the ESI.† Additionally, the calculated values for viscosity, density, and diffusion coefficient of glycerol and GOR products as a function of temperature can be downloaded as spreadsheets (.xlsx files).Conflicts of interest
There are no conflicts to declare.Notes and references
- J. Carneiro and E. Nikolla, Annu. Rev. Chem. Biomol. Eng., 2019, 10, 85–104 CrossRef CAS PubMed.
- J. Ma, X. Wang, J. Song, Y. Tang, T. Sun, L. Liu, J. Wang, J. Wang and M. Yang, Angew. Chem., Int. Ed., 2024, 63, e202319153 CrossRef CAS PubMed.
- F. W. S. Lucas, R. G. Grim, S. A. Tacey, C. A. Downes, J. Hasse, A. M. Roman, C. A. Farberow, J. A. Schaidle and A. Holewinski, ACS Energy Lett., 2021, 6, 1205–1270 CrossRef CAS.
- T. Werpy and G. Petersen, Top Value Added Chemicals from Biomass: Volume I – Results of Screening for Potential Candidates from Sugars and Synthesis Gas, National Renewable Energy Lab. (NREL), Golden, CO (United States), 2004 Search PubMed.
- Z.-H. Zhang, Z. Sun and T.-Q. Yuan, Trans. Tianjin Univ., 2022, 28, 89–111 CrossRef.
- G. Dodekatos, S. Schünemann and H. Tüysüz, ACS Catal., 2018, 8, 6301–6333 CrossRef CAS.
- K. M. Ebeling, D. Bongartz, S. Mürtz, R. Palkovits and A. Mitsos, Ind. Eng. Chem. Res., 2024, 63, 8250–8260 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed., W. M. Haynes, CRC Press, 95th edn, 2014 Search PubMed.
- H. Kong, S. Gupta, A. F. Pérez-Torres, C. Höhn, P. Bogdanoff, M. T. Mayer, R. van de Krol, M. Favaro and F. F. Abdi, Chem. Sci., 2024, 15, 10425–10435 RSC.
- A. M. Hilbrands, M. K. Goetz and K.-S. Choi, J. Am. Chem. Soc., 2023, 145, 25382–25391 CrossRef CAS PubMed.
- L. Constantinou and R. Gani, AIChE J., 1994, 40, 1697–1710 CrossRef CAS.
- Aspen Plus | Leading Process Simulation Software | AspenTech, https://www.aspentech.com/en/products/engineering/aspen-plus, (accessed September 10, 2024).
- T. Li and D. A. Harrington, ChemSusChem, 2021, 14, 1472–1495 CrossRef CAS PubMed.
- Z. G. Schichtl, S. K. Conlin, H. Mehrabi, A. C. Nielander and R. H. Coridan, ACS Appl. Energy Mater., 2022, 5, 3863–3875 CrossRef CAS.
- J.-A. Lin, I. Roh and P. Yang, J. Am. Chem. Soc., 2023, 145, 12987–12991 CrossRef CAS PubMed.
- X. Huang, Y. Zou and J. Jiang, ACS Sustainable Chem. Eng., 2021, 9, 14470–14479 CrossRef CAS.
- P. Li, Y. Jiao, J. Huang and S. Chen, JACS Au, 2023, 3, 2640–2659 CrossRef CAS PubMed.
- N. B. Watkins, Z. J. Schiffer, Y. Lai, C. B. I. Musgrave, H. A. Atwater, W. A. I. Goddard, T. Agapie, J. C. Peters and J. M. Gregoire, ACS Energy Lett., 2023, 8, 2185–2192 CrossRef CAS.
- M. C. Haryanto, R. Hartanto, T.-G. Vo and C.-Y. Chiang, J. Taiwan Inst. Chem. Eng., 2024, 158, 105087 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Thermodynamic data, viscosity, density, and diffusivity for glycerol and GOR products at different temperatures and concentration. See DOI: https://doi.org/10.1039/d4cc04967e |
| This journal is © The Royal Society of Chemistry 2025 |

