Single-atom vs. single-superatom as catalysts for ammonia production

Abstract

A new class of single-superatom catalyst (TiO, ZrO, and WC) supported on graphene is shown to outperform the stability and activity of their corresponding single-atom catalysts (Ni, Pd and Pt) for the electrochemical nitrogen reduction reaction. The results based on density functional theory point to a paradigm shift in catalyst design.

---

Ammonia (NH₃) is a critical global chemical, presently produced on a large scale through the one-step Haber–Bosch (H–B) process.^1,2 However, the extreme operating conditions and heavy dependence on fossil fuels render the H–B process highly expensive, energy-intensive, emission-heavy, and centralized.³ The electrocatalytic nitrogen reduction reaction (eNRR) has, therefore, received increasing attention owing to its milder operating conditions and its compatibility with renewable energy sources.⁴ However, eNRR is hindered by very low NH₃ yield, largely due to the challenges in activation of the dinitrogen (N₂) molecule. N₂ with a high bond energy (9.91 eV) and ionization potential (15.82 eV), and a negative electron affinity (−2.03 eV) is the most stable molecule in the atmosphere. It requires high temperature and pressure to break its triple bond to produce NH₃. Consequently, there is considerable interest in developing catalysts made of earth-abundant materials for the eNRR.

In the past decade, interest has shifted to the design and synthesis of single-atom catalysts (SACs) where individual atoms are dispersed on a substrate.^5,6 In spite of their distinct advantage over a range of chemical reactions, SACs have limitations;⁷ single atoms are inadequate when reactions with multiple molecules are required. Secondly, the atoms can migrate and coalesce to form clusters, diminishing the advantages of single-atom catalysts. While double atom catalysts (DACs) and triple atom catalysts (TACs) are being studied to overcome these shortcomings, no clear pathway exists for how to choose these atoms.^8,9 Atomic clusters show potential as advanced catalysts, but most of these studies¹⁰ are confined to the gas phase and, thus, do not have practical significance. This paper addresses this challenge by making use of lessons from cluster science.

Three decades ago, it was shown that clusters can be created by tailoring their size and composition such that they mimic the chemistry of atoms.¹¹ These clusters, called superatoms, can then be used to replace expensive metal atoms with earth-abundant species.^12,13 Note that while all superatoms are clusters, not all clusters are superatoms. In 2010, Castleman and co-workers showed that the spectroscopic signatures of TiO, ZrO, and WC are the same as those of their isoelectronic atoms Ni, Pd, and Pt, respectively.¹⁴ The authors suggested that the TiO, ZrO, and WC superatoms that mimic the chemistry of Ni, Pd, and Pt atoms, respectively, can be used as replacement catalysts. In an earlier work, it was shown that (ZrO)_n clusters do not react the same way with molecules as Pd_n clusters, thus casting doubt as to whether ZrO can be regarded as a replacement for Pd catalysts.¹⁵ However, this does not answer the question of whether a single Pd atom and a single ZrO superatom supported on a substrate would have the same chemistry. Note that for practical applications, catalysts do need to be supported on a substrate, but no work has been done to demonstrate this aspect. In a recent paper, we have shown that when the Li atom and its superatom Li₃O are supported on substrates like graphene, Cu(111), and Au(111), Li₃O outperforms the Li atom in activating CO₂.¹⁶ Note that Li is not a traditional catalyst.

Here, using first-principles calculations, we have studied the binding and activation of N₂ with isolated and supported TiO, ZrO, and WC superatoms and compared their properties with corresponding Ni, Pd, and Pt atoms. Our study addresses several questions: (1) do these atoms and their superatoms, while interacting with N₂, share the same chemistry in the gas phase? (2) When supported on a substrate, do these species maintain their gas-phase structure and properties? (3) Do the superatoms exhibit superior catalytic potential compared to the atoms in the eNRR?

Calculations are carried out using spin-polarized density-functional theory (DFT) methods implemented in the VASP^17,18 and Gaussian16¹⁹ codes. The electronic structures are studied by calculating the partial density-of-states (PDOS) and the crystal orbital Hamilton population (COHP) using the LOBSTER program.²⁰ The nudged elastic band (NEB) method²¹ is employed to determine the minimum energy migration pathways and transition states. For assessing thermal stability, ab initio molecular dynamics (AIMD) simulations are performed at 400 K for 4 ps with a timestep of 1 fs. The Gibbs free energy changes are calculated using the computational hydrogen electrode (CHE) model.²² Details of all computational methods are provided in the ESI.†

Note that N₂ is characterised by a triple bond, and it costs a significant amount of energy to stretch it. The energies, N≡N bond length, and vibrational frequency for the N₂ molecule using various basis sets are detailed in Table S1 of the ESI.† Moreover, an analysis of the energy and electronic structure of N₂ as a function of distance between the N atoms is provided in Fig. S1 of the ESI.†

We begin by studying the interaction of N₂ with isolated Ni, Pd, and Pt atoms and their corresponding superatoms, TiO, ZrO, and WC to ensure that they exhibit similar chemistry. Two typical adsorption configurations for the N₂ molecule, end-on and side-on, are considered (Fig. S2 of ESI†). The total energy calculations reveal that the N₂ molecule consistently prefers to bind to the transition metal sites in the end-on configuration (Fig. S3 of ESI†). The corresponding bond distances, binding energies, and Bader charges are presented in Table S2 of the ESI.† Following adsorption, the N≡N bond distances increase slightly from the original value of 1.1 Å on both the atoms and the corresponding superatoms. The binding energy of the N₂ molecule on the superatoms is consistently lower than that on the atoms. The amount of charge transferred from the superatoms is generally greater than that from the atoms, except in the case of Ni (TiO) where the charge transfer is nearly the same for both. Additionally, the charge density difference results indicate that charge depletion mainly occurs in the vicinity of the transition metal (TM) and the N≡N bond, while charge accumulation mainly takes place in the region of the TM–N* bond where N* refers to the nitrogen atom bonded to the TM. Thus, the atoms and their superatoms act as electron donors during the N₂ adsorption, and the strength of the N≡N bond is weakened. These results suggest that the atom and its superatom do exhibit similar chemistry.

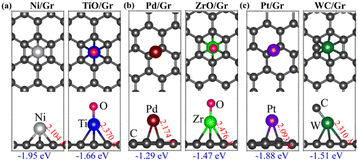
To simulate a real catalyst environment, we placed both the atoms and their superatoms on a graphene substrate. To ensure that the atoms and their superatoms are isolated on the surface, we utilized a large graphene supercell as the substrate and placed Ni (TiO), Pd (ZrO), and Pt (WC) at each of its symmetric sites (bridge, top, and hollow) (Fig. S4 of ESI†). Fig. 1 shows their energetically most favourable positions on the graphene surface. The Pd and Pt atoms exhibit the greatest stability when located at the bridge sites of graphene, which is in agreement with previous results.²³ On the other hand, all the superatoms as well as Ni prefer the hollow sites. The calculated binding energies of Ni (TiO), Pd (ZrO), and Pt (WC) on the graphene are −1.95 (−1.66), −1.29 (−1.47), and −1.88 (−1.51) eV, respectively.

Fig. 1 Top and side views of the most stable atomic configurations for (a) Ni (TiO), (b) Pd (ZrO), and (c) Pt (WC) single (super) atoms on a graphene substrate. The binding energy in eV and minimum bond distances in Å are depicted.

Next, we study the nitrogen reduction reaction (NRR), which involves a complex sequence of six electron-proton coupling steps, resulting in the formation of intermediate species and the release of two NH₃ molecules (N₂ + 6(H⁺ + e⁻) → 2NH₃). The first step in this reaction is the adsorption and activation of the N₂ molecule. Energetically, the most favourable configurations of the *N₂ on the atoms and superatoms supported on graphene are presented in Fig. 2 where the NN bond distances (d_NN) and the Gibbs free energy changes (ΔG) are also depicted. The *N₂ adopts a favorable end-on configuration (Fig. S5 of ESI†). Both the atom and superatoms on the surface act as active sites for N₂ adsorption. The NN bond distances are slightly larger in the superatoms compared to the corresponding single atoms, with the exception of Ni and TiO where the distances are nearly identical. This observation is further supported by the results of the ICOHP values (Fig. 2, right). The activation of the *N₂ molecule is attributed to the efficient transfer of electrons (Table S2 of ESI†). In addition, according to the PDOS results, there exist significant overlaps between N₂ and the atoms (superatoms) near the Fermi level, indicating strong orbital (particularly p–d) hybridization that activates N₂ (Fig. 2(b) middle and Fig. S6 of ESI†). In addition, the calculated ΔG values for the transition from N₂ to *N₂ on Ni (TiO), Pd (ZrO), and Pt (WC) supported on graphene are −1.46 (−0.38), −0.75 (−0.54), and −1.39 (−1.23) eV, respectively. These negative values indicate that the catalysts can effectively capture N₂ molecules without additional energy input. However, if the subsequent reaction step is energetically unfavourable (i.e., uphill in terms of free energy), the overall reaction could become more difficult to drive. The more negative free energy of the capture step might not be sufficient to offset the energy needed for the later steps, potentially complicating the overall reaction process. As known from previous studies, the first hydrogenation (*N₂ → *NNH) and the last hydrogenation (*NH₂ + H⁺ + e⁻ → *NH₃) steps in the NRR are likely to be energetically uphill. Could the superatoms exhibit a more favourable performance than the atoms?

Fig. 2 Left panels: The most stable atomic configurations for the adsorbed N₂ molecule on (a) Ni (TiO), (b) Pd (ZrO), and (c) Pt (WC) supported graphene surfaces where the N₂ bond distances and the Gibbs free energy changes for the transition from N₂ to *N₂ are depicted. Middle panels: Projected density of states (PDOS) for the *N₂ (in red) and Ni (TiO), Pd (ZrO), and Pt (WC) (in blue). Right panels: Crystal orbital Hamilton population (COHP) analysis for the N₂ bond, including the integrated COHP values (ICOHP), where antibonding and bonding states are illustrated in cyan and pink, respectively.

We further examine the first hydrogenation step, where a hydrogen atom is added to the adsorbed N₂ to form the *NNH intermediate. This step is a crucial and challenging step in the NRR process and typically requires a significant amount of activation energy and is often the rate-determining step. The most energetic atomic configurations of the *NNH intermediate on the Ni (TiO), Pd (ZrO), and Pt (WC) supported on graphene are presented in Fig. S7 of the ESI.† The results indicate that *NNH species preferentially adsorb onto the atoms and superatoms supported on graphene in the end-on configuration. The ICOHP values for the NN bond in *NNH species are lower compared to those in *N₂, suggesting that the first hydrogenation step significantly weakens the NN bond. This observation is consistent with the NN bond distances. The N=N bond lengths in *NNH species on the Ni (TiO), Pd (ZrO), and Pt (WC) supported on graphene are 1.207 (1.210), 1.201 (1.218), and 1.205 (1.221) Å, respectively.

Next, we examine the free energy changes for this reaction step for the NRR. The free energy changes in this reaction (*N₂ + H⁺ + e⁻ → *NNH) are 1.68 (0.98), 1.90 (0.82), and 1.67 (0.56) eV, respectively. These high positive free energy changes indicate that only the atoms supported on graphene require large free energies for the initial protonation step, suggesting their poor catalytic performance towards the NRR, regardless of the subsequent reduction steps.

In addition to the limited catalytic performance of the single atoms, we also investigate their stability against potential migration and coalescence on the graphene surface. This is further compared with the superatoms, which is crucial for SACs and single-superatom catalysts (SSACs). That is, if the atoms or superatoms can easily migrate between their energetically favorable sites on the surface, they might not remain isolated, which could lead to cluster formation or aggregation. To address this, we focus on Pd and ZrO on graphene despite their binding energies of 1.29 and 1.47 eV, respectively. The NEB results reveal the minimum energy path (MEP) where the top site of the graphene surface serves as the transition state with an energy barrier of 0.04 eV for the Pd atom (Fig. S8 of ESI†). This low energy barrier suggests that the Pd atom may not stay as an isolated atom on the graphene surface. Next, we performed the AIMD simulations at 400 K for 4 ps and monitored the trajectories of the Pd atom as well as that of ZrO on a large graphene supercell (including 400 carbon atoms). The results of the AIMD trajectories clearly illustrate the migration of the Pd atom towards the bridge sites while the ZrO superatom only vibrates around its minimum energetic position on the surface (Fig. 3).

Fig. 3 AIMD trajectories of Pd (upper panel) and ZrO (lower panel) supported on a large graphene surface at 400 K for 4 ps. The top (left, middle) and side views (right) are shown. The trajectories of Pd and ZrO are traced by lines, with colours transitioning from red (t = 0) to blue (t = 4 ps) indicate their positions over time.

Taking into account the high free energy values of all single atoms for the first hydrogenation step and the computational resources required, we further excluded the atoms from consideration in the following NRR steps. Instead, we only select the ZrO superatom supported on graphene for the following hydrogenation steps and evaluate its catalytic performance for the NRR. As the *N₂ is favorable with the end-on configuration on the ZrO supported on graphene, we consider two reaction pathways: the distal and alternating reaction paths in the following steps (Fig. S9 of ESI†). In the distal pathways, proton/electron (H⁺/e⁻) pairs continuously target the first nitrogen atom until the formation of the first NH₃. Subsequently, the second nitrogen atom is attacked continuously to produce the second NH₃. In contrast, in the alternating pathway, the (H⁺/e⁻) pairs alternately interact with two nitrogen atoms, resulting in the generation of two NH₃ molecules. We plot the Gibbs free energy diagram for the distal and alternating paths in Fig. 4. For the second hydrogenation step, the calculated free energy changes, ΔG (*NNH → *NHNH) = −0.54 eV and ΔG (*NNH → *NNH₂) = 0.06 eV, show that the alternating pathway is energetically more favorable than the distal pathway. All energies including the total energies, zero-point energies, and Gibbs free energies of the reaction intermediates are given in Table S3 of the ESI.† Our results reveal that the following mixed pathway is thermodynamically favourable (*NN → *NNH → *NHNH → *NHNH₂ → *NH → *NH₂ → *NH₃). In this reaction, the *NHNH₂ → *NH step is a short jump from the alternating to distal pathway. Moreover, *NH + NH₃(g) is energetically 0.67 eV higher than *NHNH₃. The maximum ΔG value (+0.82 eV) among all elementary steps is the first hydrogenation step (*N₂ → *NNH), which is the potential determining step. Furthermore, we calculated the overpotential, η = U_eq − U_lim where U_eq is the equilibrium potential of the NRR (about −0.16 V) and U_lim is the applied potential required to eliminate the energy barrier of the rate-limiting step, which can be determined as U_lim = −ΔG/e where ΔG is the free energy of the potential limiting step. As the limiting potential is calculated as 0.82 eV, the η value is (−0.16 V) – (−0.82 V) = 0.66 V. This value is lower than the overpotential of the NRR on the Ru(0001) stepped surface, which is the lowest overpotential among all bulk metal surfaces.²⁴

Fig. 4 (a) Optimized atomic structures of intermediates and (b) Gibbs free energy diagrams for NRR on the ZrO super-atom supported on graphene. The diagram illustrates the energy profiles for distal (in red) and alternating (in blue) reaction pathways.

In conclusion, we studied the adsorption, activation, and catalytic performance of superatoms for the NRR and compared them with their corresponding atoms. Our results reveal that superatoms outperform atoms in activating the N₂ molecule and exhibit low overpotential, which may open a new door to advance sustainable NH₃ production. We hope that our work will inspire further experimental and theoretical studies to explore the potential of superatoms for the NRR.

This work was partially supported by the U.S. Department of Energy, Office of Basic Energy Sciences (Award No. DE-FG02-96ER45579) and used resources from NERSC (Contract No. DE-AC02-05CH11231). We also thank the HPRC core facility at Virginia Commonwealth University for access to supercomputing resources.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

References

1. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636.
2. V. Smil, Nature, 1999, 400, 415.
3. M. D. Fryzuk, Nature, 2004, 427, 498.
4. S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490.
5. B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634.
6. A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65.
7. H. Jeong, S. Shin and H. Lee, ACS Nano, 2020, 14, 14355.
8. Y. Shao, Q. Yuan and J. Zhou, Small, 2023, 19, 2303446.
9. A. M. Roth-Zawadzki, A. J. Nielsen, R. E. Tankard and J. Kibsgaard, ACS Catal., 2024, 14, 1121.
10. (a) H. Himmel and M. Reiher, Angew. Chem., Int. Ed., 2006, 45, 6264; (b) Y. Y. Wang, X. Ding, Z. Ji, X. Huang and W. Li, Chem. Phys. Chem., 2023, 24, e202200952; (c) L.-H. Mou, Y. Li, Z.-Y. Li, Q.-Y. Liu, Y. Ren, H. Chen and S.-G. He, J. Phys. Chem. Lett., 2020, 11, 9990; (d) M. E. Kilic and P. Jena, J. Phys. Chem. A, 2024, 128, 1993; (e) T. Sengupta and S. N. Khanna, Commun. Chem., 2023, 6, 53; (f) R. Wang, G. Liu, S. K. Kim, K. H. Bowen and X. Zhang, J. Energy Chem., 2021, 63, 130; (g) X. Zhang, G. Liu, K. Meiwes-Broer, G. Ganteför and K. Bowen, Angew. Chem., Int. Ed., 2016, 55, 9644; (h) C. Kerpal, D. J. Harding, J. T. Lyon, G. Meijer and A. Fielicke, J. Phys. Chem. C, 2013, 117, 12153; (i) G. Liu, P. Poths, X. Zhang, Z. Zhu, M. Marshall, M. Blankenhorn, A. N. Alexandrova and K. H. Bowen, J. Am. Chem. Soc., 2020, 142, 7930; (j) M. E. Kilic and P. Jena, J. Phys. Chem. Lett., 2023, 14, 8697.
11. S. N. Khanna and P. Jena, Phys. Rev. Lett., 1992, 69, 1664.
12. P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755.
13. P. Jena, J. Phys. Chem. Lett., 2013, 4, 1432.
14. S. J. Peppernick, K. D. D. Gunaratne and A. W. Castleman, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 975.
15. S. Behera, N. King, D. Samanta and P. Jena, J. Chem. Phys., 2014, 141, 034301.
16. M. E. Kilic and P. Jena, Small, 2024, 2403888.
17. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
18. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
19. M. J. Frisch, et al., Gaussian 16 Rev. C.01, 2016.
20. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030.
21. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901.
22. (a) J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886; (b) A. A. Peterson and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251.
23. (a) K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430; (b) Y. Tang, Z. Yang and X. Dai, Phys. Chem. Chem. Phys., 2012, 14, 16566.
24. E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235.

---

Footnote

† Electronic supplementary information (ESI) available: Methods, N₂ molecule with energies and electronic properties, interaction of N₂ with isolated single atoms and superatoms, COHP analysis for TM–N, the most stable atomic configurations for the *NNH intermediate on single (super) atoms supported on graphene, MEP for a Pd single atom, distal and alternating pathways for the NRR. See DOI: https://doi.org/10.1039/d4cc04862h

---