Predicting the performance and stability parameters of energetic materials (EMs) using a machine learning-based q-RASPR approach

Abstract

The performance and stability are the two major areas of concern related to energetic materials (EMs). Balancing both the performance and stability simultaneously can result in the development of new advanced compounds that will not only perform better but at the same time be highly stable to physical/chemical/thermal stress. In this study, we aimed to predict some of the properties related to detonation performance (density, n = 12 805; gas-phase heat of formation, n = 2565) and thermal stability (decomposition temperature, n = 656; melting point, n = 19 667) of EMs using the quantitative Read-Across Structure–Property Relationship (q-RASPR) approach. q-RASPR, a combined application of quantitative structure–property relationship (QSPR) and RA methodologies, has shown an enhancement in the model predictivity, compared to the traditional QSPR method. The data sets collected from various sources were first curated to prepare high-quality data. After the structural representation of the data points and descriptor calculation, each data set was divided into the respective training and test sets. Different methodologies were employed to train the model, and the models so developed were validated based on the Organization for Economic Cooperation and Development (OECD) principles. Also, the developed models’ predictivity was checked using different ML algorithms. All the developed models showed good statistical quality with R² values (training set) ranging from 0.64 for decomposition temperature and 0.75 for the melting point to 0.94 for density and heat of formation data sets. Also, the external validation results were quite promising, which indicates that the predictive power of our developed models was significant. The models so developed can be used for examining the performance and heat resistance capacity of the newly developed compounds, screening of databases, modification of older derivatives, and/or the development of heat-resistant (non-thermo-labile) and impactful EMs.

---

1. Introduction

Energetic materials (EMs) are chemical entities or their mixtures containing significant amounts of energy in them. Depending upon their properties, formulations, and intended applications, the EMs are classified into 3 major classes – propellants, pyrotechnics, and explosives.¹ The major difference within the classes of EMs is the rate of energy released by them. Propellants and pyrotechnics take several seconds to release their energy through slow deflagration processes, and on the other hand, explosive compounds release their energy on the microsecond timescale. Although there are differences, they also share many chemical similarities among them. Identical ingredients, but in varying quantities, are present in explosives and propellants.²

There has been an increase in the demand for energetic materials (EMs) in civil, industrial, and military applications. The main concern related to the energetic materials is their performance as well as their safety/stability.³ The performance of EMs is related to their detonation velocity, detonation pressure, density, heat of formation, detonation heat, etc., while safety/stability refers to their sensitivity, detonation products, decomposition, melting, etc.^4–6 The safety evaluation of the energetic materials can also be done based on the impact sensitivity (h₅₀), electrostatic discharge, and friction tests.⁷ For a high detonation performance, the energy gap between the reactants and products should be high; in order to possess high stability, the energy gap between the reactants and their transition states should be large.⁸ Newly developed energetic compounds show improved performance and stability when compared to traditional energetic compounds like HMX (octogen), RDX (hexogen), TNT (trinitrotoluene), etc. Minimizing the effective cost involved in the production and screening is also a prime consideration.⁹ It is a tedious task to balance the high detonation performance and the sensitivity simultaneously, as most often, the enhancement of detonation performance comes at the cost of decreased sensitivity.¹⁰ Incorporation of explosophore groups like nitro, nitramino, azido, etc. into molecular structures helps to increase their detonation performance.^11,12

Thermal stabilization of the energetic materials is a prime goal of researchers to develop new compounds. As missiles and rockets travel at great speeds, they encounter intense friction with the atmosphere, causing a sudden rise in the temperature. Although traditional EMs have a good performance index, they lack thermal stability. The development of heat-resistant energetic materials helps to improve the sensitivity of compounds, as these compounds possess a high melting point maintaining high energy with appropriate sensitivity whenever exposed for a long time to a high-temperature environment. Compounds with a thermal decomposition temperature (T_dec) of 250 °C are classified as heat-resistant, whereas ultra-high temperature heat-resistant EMs have a thermal decomposition temperature of 350 °C or higher,^13,14 while the GHS regulation threshold of explosives is 500 °C.

Some of the traditional EMs like cyclotrimethylenetrinitramine (RDX) and 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX), which were used in perforating guns for deep well mining, have the T_dec values of 204 °C and 275 °C, respectively.^15–17 Because of their low heat resistance, the drilling depth was limited to only 4 km, and so these EMs are now replaced by 2,2′,4,4′,6,6′-hexanitrostilbene (HNS, T_dec = 318 °C) and 1,3,5-triamino-2,4,6-trinitrobenzene (TATB, T_dec = 350 °C), which exhibit lower sensitivity towards heat and can be used for drilling to a depth of 7 km.¹⁸

EMs, often called high-energy density materials (HEDMs), offer high energy during the process of deflagration or detonation due to their higher density. The detonation velocity is directly proportional to the density, while the detonation pressure is proportional to the square of the density.¹⁹ Also, compounds with a high positive heat of formation are preferred for the development of EMs.²⁰ The solid phase heat of formation can be used to evaluate the detonation performance of any EM and is calculated using Hess's law (eqn (1)).²¹

ΔH_s = ΔH_g − ΔH_sub (1)

where ΔH_s is the solid phase heat of formation, ΔH_g is the gas phase heat of formation, and ΔH_sub is the heat of sublimation.

The introduction of high-nitrogen-containing compounds has brought a revolutionary change in the field of energetic compounds. They possess a high positive heat of formation and show good thermal stability.^22,23 Also, these compounds are environment-friendly, as the final combustion products mostly comprise non-toxic gases such as dinitrogen (N₂).^24,25

The use of computational methodologies to design high-performance energetic compounds can significantly reduce the workload and also avoid the unintentional hazards related to them. It will not only save the cost of production but also reduce the time for the development and screening of the compounds. To date, many computational strategies like density functional theory (DFT), APC (atom pair contribution), AE (atom equivalents), quantitative structure–property relationship (QSPR), machine learning (ML), genetic function approximation (GFA), etc. have been employed to calculate different performance and sensitivity indexes of energetic compounds.^26–30 The quantitative structure–property relationship (QSPR) method can be used to correlate the physicochemical properties of a molecule with its structural features.³¹ Read-across (RA), on the other hand, serves as a platform to predict the activity/property/toxicity of molecules based on the similarities between the close-source compounds and the query compound.³² The q-RASPR (quantitative Read-Across Structure–Property Relationship) is a combined application of RA and QSPR. In comparison with the traditional QSPR technique, the q-RASPR approach shows better external predictivity for its models.^33,34 Fusion of the important structural and physicochemical features with the RA-derived similarity and error-based measures sets the benchmark for the development of q-RASPR models.³⁵ Along with conventional multiple linear regression (MLR) and partial least squares (PLS), machine learning (ML) algorithms like random forest (RF), adaptive boosting (AB), gradient boosting (GB), eXtreme gradient boosting (XGB), support vector machine (SVM), linear support vector machine (LSVM), ridge regression (RR), etc. can also be used to develop q-RASPR models, which can help to analyze a large dataset more accurately.^36–38

In the present work, we have developed 4 different models for the prediction of performance and thermal stability of the energetic materials. For the performance, two models each for density and gas-phase heat of formation have been developed, while two separate models for the decomposition temperature and melting point have been developed to evaluate the thermal stability of energetic materials. These developed models can be used for screening data for the selection, synthesis of new molecules, prediction of the detonation capacity, and thermal stability properties of unknown/newly synthesized energetic materials. This will help to reduce the time, hazards, and costs related to the development of energetic compounds.

2. Materials and methods

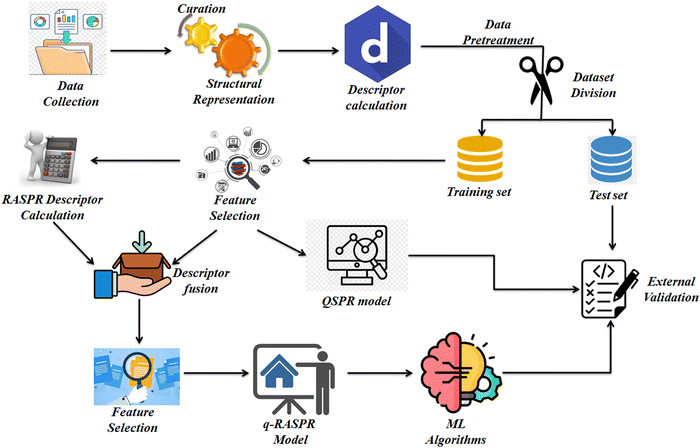
The detailed workflow we have used during the model development is presented in Fig. 1.

Fig. 1 Schematic workflow for the model development.

2.1. Data set preparation, curation, and structural representation

It is crucial to have high-quality data while building computational models. Therefore, we collected four data sets with their experimental data, each containing information about the one of the properties like decomposition temperature, melting point, density, and heat of formation from previously published literature sources.^28,39 The data taken from these 2 literature sources are all experimental data. The T_dec data were derived in-house by Wespiser et al.,³⁹ the Bradley melting point data set was used by Wespiser et al. for the melting point data set, the density data set was collected from the Crystallography Open Database by Wespiser et al., and the heat of formation data contain different types of compounds with their experimental data, which are also clearly mentioned in the literature.²⁸ The data set used by Wespiser et al.³⁹ contains some other organic compounds also with their experimental data for heat of formation and densities. This was done so as to extract the features that correspond to high positive heat of formation and higher densities of the compounds. These features can help to get insights into how the densities and heat of formation are affected by the presence of certain features in the compounds. The determination of these features will help to design new better performing EMs with less sensitivity.

To ensure accuracy, we curated the collected data to remove any duplicates, inorganic compounds, or mixtures, if present. After the curation process, we were left with 656, 19 667, 12 805, and 2565 data points for the decomposition temperature (°C), melting point (°C), density (g cm⁻³), and gas phase enthalpy of formation data (kJ mol⁻¹) sets, respectively. We made all the curated data sets available in the Excel sheets in SI-1 (ESI†). The SMILES (Simplified Molecular Identity Line Entry System) notation was used for the representation of all data points, and MarvinSketch v-5.11.5⁴⁰ was used to prepare the structures, which were then subjected to aromatization, the addition of explicit hydrogens and 2D cleaning as necessary.

2.2. Descriptor calculation and data pre-treatment

The molecular structures so prepared were used to calculate the descriptors (quantitative values derived from the molecular structural information) for the respective data sets using the AlvaDesc software v2.0.6.⁴¹ Nine different classes of highly interpretable 2D descriptors like molecular properties, functional group counts, atom type E-state indices, atom-centered fragments, 2D atom pairs, connectivity indices, constitutional indices, ring descriptors, and extended topochemical atom (ETA) indices were calculated for all data sets.

The calculated descriptor set was then subjected to the pre-treatment process where the descriptors having high inter-correlation (>0.8) or having constant/null values were removed from the descriptor set. The final pre-treated files were used for further division of the data set into training and test sets.

2.3. Dataset division

To check the predictive power of the model, there is a requirement to check the predictions for external compounds in addition to those included in the development of the model. To do so, the data set was divided into training and test sets. The training set was used for the development of the model while the test set validates the predictivity of the developed model. We have divided all the data sets into the respective training and test sets in a 3 : 1 ratio. Based on different algorithms, the data sets were divided using the Dataset-DivisionGUI1.2 tool freely available from https://teqip.jdvu.ac.in/QSAR_Tools/. The information on the number of compounds in the individual training and test sets after the division along with the division algorithm applied is provided in Table 1. The details of the data sets are provided in SI-1 (ESI†).

Table 1 List of training and test compounds in data sets and the applied division algorithm

Data set	No. of compounds		Division algorithm
	Training	Test
Decomposition temperature (Tdec)	424	141	Property-sorted
Melting point (Tm)	14 750	4917	Property-sorted
Density	9604	3201	Property-sorted
Heat of formation (ΔHf°) (gas phase)	1923	642	Kennard–Stone

---

Additionally, for the density data set, we have also prepared a true external set of 37 energetic compounds with their experimental density (g cm⁻³) collected from Rice and Brydr.⁴²

After the division of the dataset into the respective training and test sets, we further pre-treated the training and test set descriptor matrix to remove the null/constant descriptors, and the final training and test sets so obtained were used for the feature selection process.

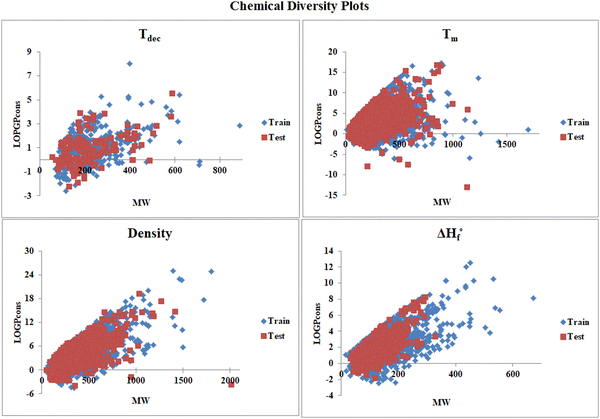
Fig. 2 presents the chemical diversity plot (MW vs. LOGPcons) prepared using the molecular weight and LOGPcons for all the data sets to investigate the diversity in the chemical nature of the compounds present in the respective training and test sets of the individual data set.

Fig. 2 Chemical diversity plots.

2.4. Feature selection and QSPR model development

The selection of the potential features from the descriptor pool that are closely related to the activity/property/toxicity of the compound is a key step during the development of QSAR models.⁴³ There are several variable selection methods like step-wise selection, all possible subset selection, genetic algorithm, factor analysis, etc.⁴⁴ In this work, we used step-wise and genetic algorithms to prepare a pool of important descriptors and then used the all-subset selection method to finalize the set of descriptors for the final models. The features are selected based on the MAE-based criteria (the training set only without any involvement of the test set). A grid search was performed using the pool of selected features for the generation of several MLR models using the Best Subset Selection tool v2.1 available from https://teqip.jdvu.ac.in/QSAR_Tools/. The final robust PLS QSPR model was selected based on the cross-validation (Q_LOO²) results with a lower number of latent variables (LVs). The final model so obtained was then used for read-across-based similarity prediction.

2.5. RA predictions

For the calculation of RA-based similarity predictions, we have used the default values of the hyperparameters, i.e. σ = 1 and γ = 1, and the number of closed training/source compounds (CTC) to be 10. Using the default hyperparameters and a Java-based tool Read-Across-v4.2 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home, we have calculated the similarity predictions of the test set compounds for different similarity algorithms such as Gaussian kernel-based, Laplacean kernel-based, and Euclidean distance-based similarity algorithms. Furthermore, based on the MAE_test results, we have chosen the best similarity measure for the representation of predictions from the individual data sets.

2.6. RASPR descriptor calculation

The calculation of the similarity and error-based RASPR descriptors is the first and foremost step needed to build a q-RASPR model.⁴⁵ The calculation of the RASPR descriptors (for the best similarity measure obtained from RA prediction) is done after the division process, which is different from the calculation of structural and physicochemical descriptors that are calculated before the data set division. This is because here the test/query set RASPR descriptors are calculated based on their similarity to the training/query set compounds. For the calculation of the test set RASPR descriptors, both the training and test sets (containing the structural and physicochemical descriptors) were used, while the training set RASPR descriptors were calculated from the training set only.

2.7. Feature selection and q-RASPR model development

The descriptor matrix of the QSPR model was fused with the 18 calculated similarity and error-based RASPR descriptors. The prepared descriptor pool was then used for the feature selection using a step-wise process or performing a grid search through the Best Subset Selection tool v2.1 available from https://teqip.jdvu.ac.in/QSAR_Tools/. The optimal number of descriptors selected in the model was based on the leave-one-out cross-validated (Q_LOO²) results, and the same features were used to develop the final PLS model. The PLS model was developed for all sets except for the melting point data set where a univariate model was developed.

2.8. Statistical quality and validation metrics

After the development of a model, the model needs to be validated internally as well as externally. The OECD principle 4 describes the different validation metrics needed to judge the predictive potential of a model.⁴⁶ To check the statistical quality and validate the model internally, we have used the determination coefficient (R²), leave-one-out cross-validated Q² (Q_LOO²), mean absolute error (MAE_train), and root mean square error of the calibration set (RMSE_C).⁴⁷ The external validation was done based on Q_F1², Q_F2², mean absolute error (MAE_test), and root mean square error of the prediction set (RMSE_P). Both the internal and external validation tests were done based on the MAE-based criteria as Q² metrics do not always provide a good reflection of the prediction quality.⁴⁸

2.9. Application of ML algorithms

We have also applied different machine learning algorithms to check the predictivity of our developed PLS q-RASPR model. Here, we have used 7 different supervised ML algorithms such as random forest (RF), support vector machine (SVM), linear support vector machine (LSVM), adaptive boosting (AB), gradient boosting (GB), extreme gradient boosting (XGB), and ridge regression (RR) to build various regression models.^49–54 These machine learning modeling methods are described in SI-2 (ESI†). The training and test set descriptors and response values of the developed PLS model were scaled before the application of ML algorithms using a Java-based tool Scale1.0 freely available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. Different ML models were developed for each property data set (except T_m) using a Python-based tool RSLv2.2 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. We have used the default setting of the hyperparameters for the development of the ML models.

2.10. Applicability domain (AD)

As per the OECD principle 3, the defined applicability domain (AD) represents the validity of the developed q-RASPR model. The chemicals employed in the model development define the chemical structure space, which is represented by the AD.⁵⁵ To check whether the compounds in the test set are within the chemical space of the training set used for the modeling, we have used the DModX (distance to model X) approach with 99% confidence level (only for the PLS models) using the SIMCA software https://landing.umetrics.com/downloads-simca.⁵⁶ The compounds within the AD can be predicted precisely, whereas the compounds outside the AD are termed outliers. The DModX approach was used for defining the AD of T_dec, density, and ΔH_f° data sets, while for the T_m data set, we used the leverage approach⁴⁴ for determining the AD.

3. Results and discussion

3.1. QSPR model development

We have developed 4 different QSPR models for the prediction of 4 different properties of energetic compounds. Three models (T_dec, density, and ΔH_f°) were developed using the PLS regression algorithm, while one of the models [for the melting point (T_m)] was developed using multiple linear regression (MLR).

Detailed information on the development of the QSPR models is provided in SI-2 (ESI†). The regression equations for each model along with their metrics for the training set and the test set are tabulated in Table S1 given in SI-2 (ESI†). The definition of the individual descriptors for all the QSPR models is tabulated in Table S2 of SI-2 (ESI†).

3.2. Chemical read-across (RA) predictions

The structural and physicochemical features of the developed QSPR model were used to evaluate the similarity-based RA predictions. The default setting of the hyperparameters (σ = 1, γ = 1, no. of closed source/training compounds = 10) was used to perform the read-across predictions for the 3 different similarity algorithms like Laplacian kernel-based (LK), Gaussian kernel-based (GK), and Euclidean distance-based (ED) similarity algorithms. The prediction results show that the Laplacean kernel-based similarity algorithm has the best predictivity for T_dec, T_m, and ΔH_f°, whereas the Gaussian kernel-based similarity algorithm shows the best performance for the density data set. The results of RA predictions are shown in Table 2. The default hyperparameters of each similarity measure were used to calculate the RASPR descriptors for each of the data sets.

Table 2 Read-across predictions for different data sets

Metrics
Properties	Q F1 ^2	Q F2 ^2	MAEP^a	RMSEP^a	Similarity measure
a Non-standardized values.
T dec	0.645	0.645	41.756	53.037	LK
T m	0.736	0.736	34.075	46.520	LK
Density	0.925	0.925	0.039	0.052	GK
ΔHf°	0.924	0.924	49.100	70.787	LK

---

3.3. q-RASPR model development

The motive behind the development of the q-RASPR model is to increase the external predictivity of the model over the traditional QSPR model. The calculated RASPR descriptors are composed of different similarity, error, concordance and predictive functions from the structural and physicochemical descriptors. These calculated RASPR descriptors were clubbed with the previously selected structural and physicochemical descriptors to form the new descriptor matrix for the individual training and test sets. The prepared training set was further used for the selection of the prominent features for the development of the model. To develop the q-RASPR model for T_dec and ΔH_f°, a grid search was performed on the fused descriptor matrix (obtained from the fusion of QSPR and RASPR descriptors) to develop several MLR models using the Best Subset Selection tool v2.1 freely available from https://teqip.jdvu.ac.in/QSAR_Tools/. The best MLR model was selected based on the leave-one-out (LOO) cross-validation results, and the same was used further to develop the final PLS q-RASPR model with a lower number of LVs, which are optimized using LOO Q². For the density dataset, a forward step-wise feature selection method was used to develop the MLR model, and further, the PLS algorithm was applied to obtain the final PLS q-RASPR model. Both grid-search and step-wise selection were performed for the T_m dataset, and in both cases a univariate q-RASPR model with RA function (LK) as the only descriptor was obtained. The final model equations for individual models with their internal and external validation metrics are tabulated in Table 3.

Table 3 Model equations and validation metrics for the developed q-RASPR models

Property	Model equation	Training set metrics^a	Test set metrics^a
a Non-standardized MAE and RMSEP values are shown.
T dec (PLS model)	T dec = 144.449 + 2.684 × C% − 43.374 × B01[O−O] − 15.109 × B03[N–O] + 8.425 × Hy− 8.311 × LOGP99 + 19.520 ×nArNO2 + 16.965 × C − 005 − 8.233 × B01[N–N] + 0.596 × RA function (LK) − 0.870 × SE (LK)	n training = 424	n test = 141
		R ^2 = 0.620	Q F1 ^2 = 0.676
		Q LOO ^2 = 0.600	Q F2 ^2 = 0.676
		MAEtr = 42.313	MAEte = 41.383
		RMSEC = 55.013	RMSEP = 50.683
	Descriptors = 10, LVs = 5
T m (univariate model)	T m = 9.081 + 0.952 × RA function (LK)	n training = 14 750	n test = 4917
		R ^2 = 0.746	Q F1 ^2 = 0.741
	Descriptor = 1
		Q LOO ^2 = 0.746	Q F2 ^2 = 0.741
		MAEtr = 33.959	MAEte = 34.297
		RMSEC = 46.005	RMSEC = 46.520
Density (PLS model)	Density = 0.425 + 0.042 × AMW − 0.690 × Mp + 0.082 × MCD + 0.741 × RA function (GK) − 0.049 × CVsim (GK)	n training = 9604	n test = 3201
		R ^2 = 0.940	Q F1 ^2 = 0.939
	Descriptors = 5, LVs = 4	Q LOO ^2 = 0.940	Q F2 ^2 = 0.939
		MAEtr = 0.035	MAEte = 0.035
		RMSEC = 0.047	RMSEP = 0.047
ΔHf° (PLS model)	ΔHf° = 28.972 + 1.020 × RA function (LK) − 0.298 × SD Activity (LK) − 1.884 × nCsp3	n training = 1924	n test = 643
		R ^2 = 0.943	Q F1 ^2 = 0.931
		Q LOO ^2 = 0.942	Q F2 ^2 = 0.931
	Descriptors = 3, LVs = 2
		MAEtr = 61.718	MAEte = 47.158
		RMSEC = 103.603	RMSEP = 67.630

---

Additionally, to evaluate the predictivity of the developed PLS q-RASPR model for the density dataset, we have collected a true external set of 37 energetic compounds from Rice and Byrd⁴³ and calculated the validation metrics for the same. The result shows that our model can predict new compounds accurately.

Q_F1² = 0.883, MAE = 0.073, RMSE = 0.088

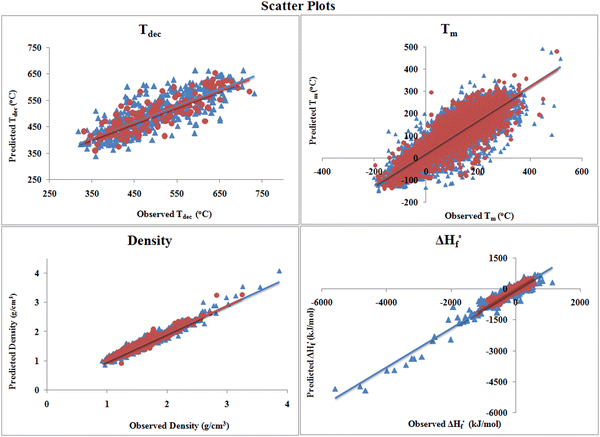
The scatter plots shown in Fig. 3 reveal that there is a high correlation between the observed and predicted values. As in the individual plots, the scattering is not much, which indicates that the quality of the developed models is good. The distribution of the heat of formation data set in Fig. 3 shows that only a few (approx. 14) compounds are present far from the clusters of training (1924) and test (643) sets, which are very small in number with respect to the whole training set compounds. Also, the division algorithm used here was based on the Kennard–Stone method, which divides the data set based on the descriptor matrix and not based on properties/response.

Fig. 3 Scatter plots for the individual PLS models.

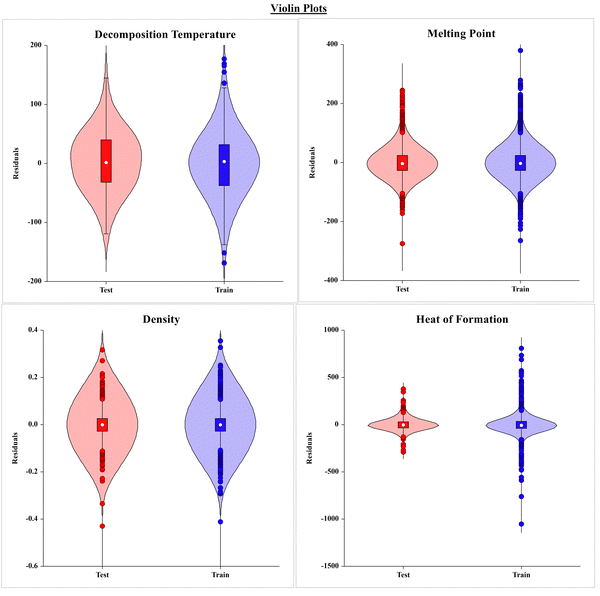
The violin plots shown in Fig. 4 present the frequency of compounds with the residual values (i.e. observed and predicted) in the training and test sets of the respective models for each property. The graph seems to be more flattened in the middle portion, indicating that there are more compounds in the training and test sets with lower residual values, and the tapered end at both the ends of the violin represents the lower number of compounds with high residuals.

Fig. 4 The violin plot of each model presents the variation in the residual values for compounds in the respective training and test sets. The width of the plot represents the frequency/number of data points for the given residuals.

3.4. PLS plot interpretation

Models were developed from all the datasets, except for the melting point (T_m) dataset, using PLS regression, as the final model of the T_m data set contains only a single descriptor. Hence, a univariate model has been reported to determine T_m instead of reporting it in the form of a PLS model, which represents several original descriptors with a lower number of latent variables (LVs).

We have used the DModX (Distance to Model X) approach to check the numbers of outliers present in the training and test sets respectively (except for the melting point data set). The DModX-AD plots of the developed PLS models are given in Fig. S1–S3 in SI-2 (ESI†). The applicability domain of the univariate model for the melting point was calculated using the leverage approach. The leverage values for the individual data points of training and test sets were calculated using the Java-based tool Hi_Calculator-v2.0 (accessible from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home). William's plot (see Fig. S4 in SI-2, ESI†) represents the outliers from the training and test sets of the melting point data set with leverage values higher than the critical h* value (0.0004). The percentage (%) of compounds as outliers in the training and test sets of the respective models is shown in the bar graph in Fig. S5 in SI-2 (ESI†).

To check the impact of the descriptors (i.e. X-variables) on the properties (Y-variable), we have developed the loading plot (Fig. S6 in SI-2, ESI†) using the first 2 PLS components. The variables that are more dispersed from the origin have a high impact on the model. We have also used the VIP plot (see Fig. S7 in SI-2, ESI†) to interpret the importance of the respective descriptors according to their VIP values in the model. The coefficient plot representing the standardized regression coefficient values for each descriptor of the individual model and the score plots for each model are given in Fig. S8 and S9 in SI-2 (ESI†). As the score plot for each model (Fig. S9, ESI†) has been developed using the first 2 components (t1 and t2) of the model, the compounds outside the ellipse can be considered outliers for the model with 2 latent variables. The ellipse indicates the applicability domain of the model, as defined by Hotelling's t² (a multivariate generalization of Student's t-test). The AD study shows that the compounds present far away from the ellipse are just not the outliers based on the 2 components of the model but they are also outliers for the whole descriptor space, which is shown in the DModX applicability domain (AD) plots (Fig. S1–S3, ESI†).

The bubble plot (Fig. 5) collectively represents the VIP values (the size of bubble) of the descriptors with their standardized regression coefficient values (Y-axis) of the PLS models.

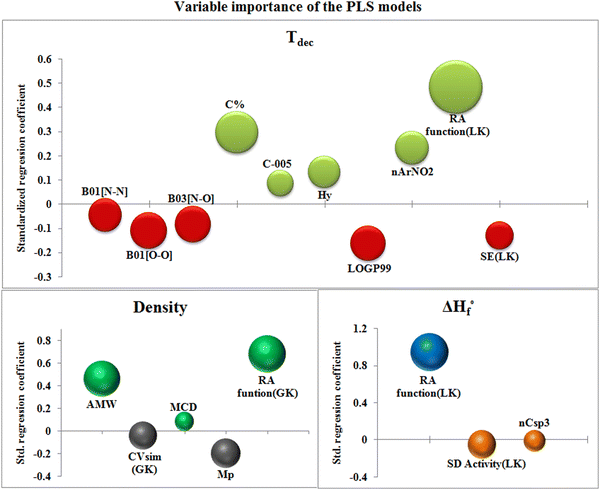Fig. 5 Bubble plots for the respective PLS models representing variable importance and standardized regression coefficients.

3.5. Prediction through ML models

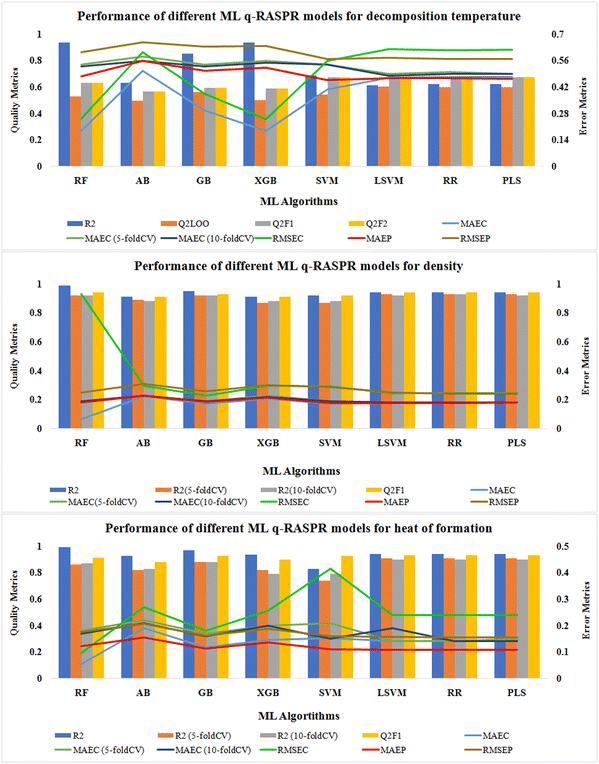
We have also developed various ML models for the individual data sets (except T_m) to predict the respective properties. Here, 7 different ML algorithms were used to develop the models. Scale1.0 (a Java-based tool) was used for scaling the descriptors and response values of both the training set and the test set. The default values of the hyperparameters for each algorithm were used during the model development process. The statistics for the model quality and predictivity are reported in Tables S3–S5 (ESI†). We have also performed 5-fold and 10-fold cross-validation and noted MAE_C (CV) to check the quality of our developed models. For the density and ΔH_f° data sets, 5-fold and 10-fold cross-validated R² values were determined to check the robustness of the developed models, as LOO-CV is not appropriate for such large data sets. The graphical representation of various quality and error metrics for different ML-based q-RASPR models is shown in Fig. 6.

Fig. 6 Comparison of quality and error metrics of different q-RASPR models.

In the case of T_dec, the external validation metrics of the PLS model infer that it has better predictivity in comparison to the other developed ML models in terms of Q_F1², Q_F2², and RMSE_P.

For the density data set, the external predictions of the LSVM, RR, and PLS models were similar in terms of Q_F1² and Q_F2² but the error for the LSVM model in terms of MAE_P was the least among all the models. Therefore, the LSVM model can be considered to be the best-performing model for the prediction of density.

For the prediction of gas-phase heat of formation, the RR model shows its better predictivity with the least error in terms of MAE_P and cross-validated MAE_C.

After the feature selection process, the selected features were used to build an MLR model, and then the same descriptor set was used for the development of a PLS model. For the read-across predictions the selected structural and physicochemical features used to develop the MLR/PLS models were used to develop a read-across hypothesis. The optimal descriptor set is thus not method-dependent, as the same descriptor set shows good performance for different methods, both linear (QSPR) and non-linear (RA), and also for different ML methods in our study.

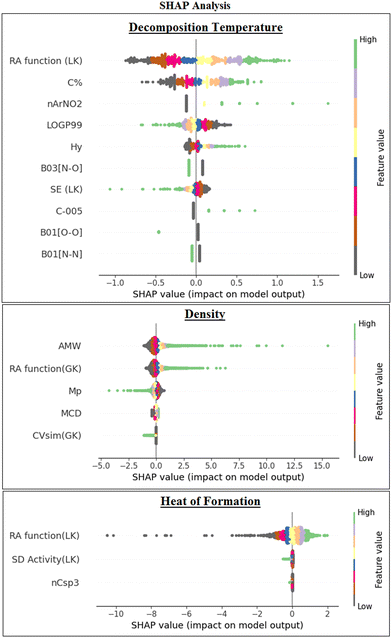
We have also performed the Shapley Additive exPlanations (SHAP) analysis⁵⁷ (Fig. 7) for the final ML models to investigate the impact/importance of the descriptors in the model predictions. It was found in all the 3 models that the descriptors having high feature values and positive SHAP values contribute positively to the predictions and vice versa. The features that are more dispersed along the X-axis have a high impact on the model.

Fig. 7 Determination of feature importance through the SHAP summary plots.

3.6. Descriptor interpretation of the PLS q-RASPR models

The final PLS q-RASPR models for different properties of EMs have been presented in the form of mathematical equations in Table 3, while the descriptions of the descriptors with their contribution to the models are listed in Table 4. The descriptor influences on the properties with suitable examples are discussed below:

Table 4 List of descriptors with their definitions and contributions to the PLS q-RASPR models

Descriptor	Definition	Type	Model	Contribution
C%	Percentage of carbon atoms	Constitutional indices	T dec	Positive (+ve)
B01[O–O]	Presence/absence of O–O at topological distance 1	2D atom pairs	T dec	Negative (−ve)
B01[N–O]	Presence/absence of N–O at topological distance 3	2D atom pairs	T dec	Negative (−ve)
Hy	Hydrophilic factor	Molecular property	T dec	Positive (+ve)
LOGP99	Wildman–Crippen octanol–water coefficient (LogP)	Molecular property	T dec	Negative (−ve)
nArNO2	Number of nitro (–NO2) groups (Aromatic)	Functional group count	T dec	Positive (+ve)
C-005	CH3X	Atom centered fragment	T dec	Positive (+ve)
B01[N–N]	Presence/absence of N–N at topological distance 1	2D atom pairs	T dec	Negative (−ve)
AMW	Average molecular weight	Constitutional indices	Density	Positive (+ve)
Mp	Mean atomic polarizability (scaled on the C-atom)	Constitutional indices	Density	Negative (−ve)
MCD	Molecular cyclized degree	Ring descriptor	Density	Positive (+ve)
nCsp3	Number of sp^3 hybridized C-atoms	Constitutional indices	ΔHf°	Negative (−ve)
RA function	A composite function derived from read-across	RASPR descriptors	T dec, Tm, density, ΔHf°	Positive (+ve)
SE (LK)	Weighted standard error of the closed source compounds' response values	RASPR descriptors	T dec	Negative (−ve)
CVsim (GK)	Coefficient of variance of similarity values of closed source compounds'	RASPR descriptors	Density	Negative (−ve)
SD_Activity (LK)	Weighted standard deviation of the closed source compounds' observed response values	RASPR descriptors	ΔHf°	Negative (−ve)

---

3.6.1. Interpretation of descriptors for the T_dec model. In the decomposition temperature (T_dec) model, the descriptors RA function (LK), C%, nArNO₂, Hy, and C-005 contribute positively to the decomposition temperature, which means that any increase or decrease in the values of the above-mentioned descriptors will result in the simultaneous increase or decrease, respectively, in the T_dec of the compounds. On the other hand, the descriptors B01[N–N], B01[O–O], B03[N–O], LOGP99, and SE (LK) have negative contributions to the T_dec. The positive contribution of the RA function (LK) can be represented by compounds 452 (RA function (LK) = 673.168, T_dec = 608.15 °C), 151 (RA function (LK) = 587.517, T_dec = 573.15 °C), and 19 (RA function (LK) = 378.162, T_dec = 397.15 °C). The presence of 55.56% and 6.67% of carbon in compounds 187 (T_dec = 536.55 °C) and 78 (T_dec = 383.15 °C) confirms the positive contribution of the descriptor C%. The presence of 8 nitro groups in 300 (T_dec = 658.15 °C), 3 in 262 (T_dec = 587.15 °C), and none in 343 (T_dec = 526.65 °C) shows the positive contribution of the descriptor nArNO₂ in the model. The hydrophilic factor Hy contributes positively to the model, which can be represented by compounds 113 (Hy = 6.992, T_dec = 511.15 °C) and 11 (Hy = −0.200, T_dec = 468.15 °C). The atom-centered fragment C-005 represents the fragment CH₃X (where X is an electronegative atom, here oxygen). The positive contribution of CH₃X can be represented by compounds 536 (CH₃X = 3, T_dec = 655.15 °C) and 223 (CH₃X = 0, T_dec = 623.15 °C). The T_dec value of 180 is 620.95 °C, and it does not contain any N–N, O–O, and N–O bonds at the topological distances of 1, 1, and 3, respectively. But in compounds 51 (T_dec = 461.15 °C), 184 (T_dec = 471.15 °C), and 103 (T_dec = 381.15 °C) the presence of these bonds corresponds to a decrease in their T_dec. The negative contribution of LOGP99 can be presented by compounds 177 (LOGP99 = 7.830, T_dec = 359.15 °C) and 443 (LOGP99 = −0.882, T_dec = 503.65 °C). Also, the negative contribution of the RASPR descriptor SE (LK) can be described by compounds 364 (SE (LK) = 88.991, T_dec = 364.65 °C) and 277 (SE (LK) = 22.036, T_dec = 448.15 °C).

3.6.2. Interpretation of the RA function descriptor in the T_m model. The RASPR descriptor, RA function (LK), is the only descriptor in the univariate model for the melting point. This RA-derived composite function contributes positively towards the property prediction. The positive contribution of RA function (LK) can be represented by compounds 19 458 (T_m = 481 °C), 12 637 (T_m = 360 °C), 17 948 (T_m = 117.5 °C), and 16 (T_m = −100.67 °C) with their respective feature values 491.162, 328.358, 114.91, and −108.684.

3.6.3. Interpretation of descriptors for the density model. The density of a compound can be calculated as the ratio of molecular mass to its volume. The descriptor AMW in the developed model stands for the Average Molecular Weight of the compound and contributes positively to the prediction of the density. As we know that density is directly correlated with the mass of the compound, as the AMW increases the density of the molecule also increases simultaneously. Compounds 223 and 551 with molecular densities of 3.866 and 3.546 have average molecular weights of 53.57 and 41.53 respectively. Again, compounds 12 764 and 12 765 with densities of 1.027 and 1.03 have AMWs of 4.88 and 4.89 respectively. The constitutional descriptor Mp represents the mean atomic polarizability (scaled on the C-atom) and contributes negatively to the model prediction. The polarizability is directly proportional to the volume of the compound, which has an indirect relation with the density. So, the increase in the polarizability indicates a decrease in the density of the compound. This can be easily illustrated by 337 with a mean polarizability value of 0.532 having a molecular density of 1.859 g cm⁻³, while 12 351 has a molecular density of 1.696 g cm⁻³ with only 0.852 Mp value. The descriptor MCD (Molecular Cyclized Degree) shows a positive impact on the model predictivity. MCD represents the ratio of number of atoms present in the ring to the total number of atoms in the molecule. The cyclic molecules have a higher density due to the stronger London forces, which is because the ring system allows for a larger area of contact. The density of 11 446 is 1.254 g cm⁻³ with a degree of cyclization of 0.857, whereas with 0.75 degree of cyclization, 8403 has a density of 1.171 g cm⁻³. The RASPR descriptor, RA function (GK), is a composite descriptor derived from the read-across and contributes positively to the prediction of density. This can be seen in 223, 7347, 8127, and 12 773 having descriptor values of 3.546, 1.715, 1.268, and 1.024 corresponding to their densities in the order of 3.866, 1.764, 1.325, and 1.041, respectively. CVsim (GK) indicates the coefficient of variance of the similarity values of the closed source compounds and shows a negative contribution in the model. When the variation between the similarity values increases among the close training compounds, it indicates that the prediction is not so reliable for the test set compound. Compounds 9129 (CVsim (LK) = 0.005, d = 1.323 g cm⁻³) and 1335 (CVsim (LK) = 3.162, d = 1.184 g cm⁻³) verify the negative contribution of CVsim (LK).

3.6.4. Interpretation of descriptors for the ΔH_f° model. In the ΔH_f° model, the descriptor RA function (LK) contributes positively to the model. Compounds 849, 569, and 102 with the descriptor values of 693.341, 407.732, and −4455.65 have the enthalpies of formation of 681.4 kJ mol⁻¹, 364 kJ mol⁻¹, and −4806.4 kJ mol⁻¹ respectively. Another RASPR descriptor, SD_Activity (LK), has a negative contribution to the model. Compounds 120 (SD_Activity (LK) = 876.004, ΔH_f° = −1551 kJ mol⁻¹), 2353 (SD_Activity (LK) = 62.293, ΔH_f° = −272 kJ mol⁻¹), and 1825 (SD_Activity (LK) = 6.991, ΔH_f° = −227.4 kJ mol⁻¹) confirm that the increase in the weighted standard deviation of closed source compounds' response values results in the decrease in the amount of ΔH_f°. The descriptor nCsp3 represents the number of sp³ hybridized C-atoms in the molecule and represents a negative contribution to the model. The ΔH_f° of compounds 279 (nCsp3 = 0, ΔH_f° = 147.45 kJ mol⁻¹) and 280 (nCsp3 = 6, ΔH_f° = −48.9 kJ mol⁻¹) shows that the hydrogenation of the latter compound increases the number of sp³ hybridized carbons from 0 to 6, which leads to a decrease in the value of ΔH_f° of the molecules.

4. Comparison of the quality of q-RASPR models with QSPR models

4.1. Comparison with our QSPR models

We have compared the q-RASPR models with our own developed QSPR models for all 4 properties. The validation metrics for all the developed models are shown in Table S1 (QSPR models) (ESI†) and Table 3 (q-RASPR models). The comparative results depict that the prediction quality has been enhanced for all the q-RASPR models when compared to their corresponding QSPR models. The number of descriptors in the q-RASPR models was also lower than the descriptors present in the QSPR models, which shows that with a lower number of regressors (except in the case of decomposition temperature), our q-RASPR models can efficiently predict the compounds having identical chemical information.

4.2. Comparison with the previous models

The process of performing curation is most important to obtain a noise-free data set, to develop a relevant model with a high degree of acceptance. While performing curation on the obtained data set, we have found that the data set used by the authors³⁹ contains several duplicate compounds and mixtures as well. Previously, the authors³⁹ prepared two QSPR models for the T_dec and T_m data sets, and two semi-empirical additivity scheme models for the density and ΔH_f° data sets. Apart from this, they developed deep-learning models using the MPNN (Message Passing Neural Network) algorithm for all the data sets. The validation metrics of the training sets were not reported by the authors and at the same time, the feature selection process or the final features in the developed models were also not reported. Also, for the T_dec and ΔH_f° data sets, only the external test set results were reported.

For easy interpretability and reproducibility of our developed models, we have mentioned the descriptors (both the number and types) of our QSPR and q-RASPR models (refer to Table 4). This information can be used for the prediction of properties of newly developed compounds or compounds whose properties are not known yet using our models. Wespiser et al.³⁹ did not mention the descriptor number and type for the models, which challenges the reproducibility of their developed models.

A comparison of the results for the test set prediction quality of our QSPR and q-RASPR models with the previously developed QSPR and MPNN models is presented in Table 5. We can state that our T_dec q-RASPR model reports a lower RMSE_P error compared to the QSPR and MPNN models developed previously. The q-RASPR model for T_m shows a good predictive quality with only a single descriptor [i.e. RA function (LK)] for a very large data set. Although the prediction quality of our q-RASPR model does not exceed the previous QSPR and/or MPNN models, a model with a single descriptor with this much accuracy for a large data set is quite remarkable. Comparing the results for the density data set, we infer that with only 5 descriptors in the final model, the model shows a very minute difference in the error estimation both with respect to MAE and RMSE. Also, the quality and prediction of our PLS q-RASPR model for ΔH_f° were almost similar to those of the MPNN DL model.

Table 5 Comparison of our q-RASPR models with our own QSPR models and previously developed models

Property	Models	No. of descriptors	R ^2	MAEP	RMSEP
T dec	QSPR^39	Not defined	0.82	39	53.6
	MPNN^39	Not defined	0.83	40	53
	QSPR (our work)	10	0.621	44.919	54.814
	q-RASPR (our work)	10	0.676	41.383	50.683
T m	QSPR^39	Not defined	0.93	25.2	35.8
	MPNN^39	Not defined	0.95	20.2	30.1
	QSPR (our work)	29	0.67	39.626	52.501
	q-RASPR (our work)	1	0.741	34.3	46.52
Density	QSPR^39	Not defined	0.98	0.031	0.040
	MPNN^39	Not defined	0.98	0.034	0.046
	QSPR (our work)	6	0.928	0.037	0.051
	q-RASPR (our work)	5	0.939	0.035	0.047
ΔHf°	QSPR^39	Not defined	0.972	23.4	30.8
	MPNN^39	Not defined	0.94	47.9	67.4
	QSPR (our work)	11	0.932	47.903	67.412
	q-RASPR (our work)	3	0.931	47.158	67.63

---

Therefore, we can infer that, with much less model complexity, our q-RASPR models with few features can efficiently predict the enlisted properties, and the developed models are also easily reproducible.

5. Conclusion

In the present work, the authors report the development of q-RASPR models for the prediction of different properties of energetic compounds associated with their energetic performance and thermal stability. We have used properties like the decomposition temperature and melting point for the prediction of the thermal stability of compounds, and for the evaluation of performance, we have used density and gas phase heat of formation. Firstly, we developed QSPR models through a feature selection process for individual data sets and then used the structural and physicochemical features of the developed models for the calculation of the RASPR descriptors. The calculated RASPR descriptors were then fused with those structural and physicochemical descriptors. Again for each modeled response, the feature selection process was employed for the fused descriptor matrix to develop an MLR q-RASPR model based on the cross-validation results, and finally, with a lower number of LVs, a PLS q-RASPR model was developed. Several ML-based models were also prepared for the prediction of the properties associated with the energetic compounds. Furthermore, we have also checked the model quality by using 5-fold and 10-fold cross-validation tests (in terms of R² and MAE), which also reflect the absence of any over-fitting.

The models so developed in the study were found to be robust and predictive, and they can be used during the early developmental stages of energetic compounds for screening purposes. This will help to select the best compound with better performance and thermal stability. These models can also be used for the development of new efficient energetic materials or for the prediction of the properties of newly developed molecules. Thus, the models can be useful for the designing and manufacturing of new energetic compounds at a low cost and a fast rate with a decrease in the hazards associated with them during the experiments.

Data availability

The data sets associated with this modeling analysis are available in the ESI.†

Author contributions

SKP – data curation, formal analysis, validation, writing – original draft and KR – conceptualization, resources, supervision, writing – reviewing and editing.

Conflicts of interest

No potential conflict of interest.

Acknowledgements

SKP acknowledges Souvik Pore (souvikpore123@gmail.com) for the detailed discussion of ML modeling. SKP conveys his sincere gratitude to the All India Council for Technical Education (AICTE), New Delhi for the PG scholarship as financial aid.

References

1. J. P. Agrawal, High Energy Materials: Propellants, Explosives and Pyrotechnics, John Wiley & Sons, 2010.
2. L. E. Fried, M. R. Manaa, P. F. Pagoria and R. L. Simpson, Annu. Rev. Mater. Res., 2001, 31, 291–321.
3. A. K. Sikder and N. Sikder, J. Hazard. Mater., 2004, 112, 1–5.
4. M. H. Keshavarz, J. Hazard. Mater., 2009, 166, 762–769.
5. N. Chandrasekaran, C. Oommen, V. S. Kumar, A. N. Lukin, V. S.Abrukov and D. A. Anufrieva, Propellants, Explos., Pyrotech., 2019, 44, 579–587.
6. M. Suceska, M. Dobrilovic, V. Bohanek and B. Stimac, Z. Anorg. Allg. Chem., 2021, 647, 231–238.
7. Q. L. Yan and S. Zeman, Int. J. Quantum Chem., 2013, 113, 1049–1061.
8. F. Jiao, Y. Xiong, H. Li and C. Zhang, CrystEngComm, 2018, 20, 1757–1768.
9. D. C. Elton, Z. Boukouvalas, M. S. Butrico, M. D. Fuge and P. W. Chung, Sci. Rep., 2018, 8, 9059.
10. T. T. Vo, J. Zhang, D. A. Parrish, B. Twamley and J. N. Shreeve, J. Am. Chem. Soc., 2013, 135, 11787–11790.
11. J. Rein, J. M. Meinhardt, J. L. H. Wahlman, M. S. Sigman and S. Lin, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv-2021-16f6w-v2.
12. L. Wang, L. Zhai, W. She, M. Wang, J. Zhang and B. Wang, Front. Chem., 2022, 10, 871684.
13. Z. Zhang, W. Geng, W. Yang, Q. Ma, W. Li, G. Fan and Y. Chen, Propellants, Explos., Pyrotech., 2021, 46, 593–599.
14. C. Li, M. Zhang, Q. Chen, Y. Li, H. Gao, W. Fu and Z. Zhou, Chem. - Eur. J., 2017, 23, 1490–1493.
15. J. Liu, L. X. Wang, Q. Li, J. B. Zeng, S. Zhou, W. Jiang and F. S. Li, J. Explos. Propellants, 2012, 35, 46–50.
16. S. Zhang, Z. Gao, Q. Jia, N. Liu, J. Zhang and K. Kou, Appl. Surf. Sci., 2020, 515, 146042.
17. Q. Huang, X. Liu, Y. Xiao, L. Luo, G. Luo, B. Jin, R. Peng and S. Chu, J. Energ. Mater., 2021, 39, 1–9.
18. R. Zhang, Y. Xu, F. Yang, P. Wang, Q. Lin, H. Huang and M. Lu, Def. Technol., 2023 DOI:10.1016/j.dt.2023.09.005.
19. M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23–35.
20. T. M. Klapötke, J. Stierstorfer and A. U. Wallek, Chem. Mater., 2008, 20, 4519–4530.
21. P. W. Atkins, J. De Paula and J. Keeler, Atkins' Physical Chemistry, Oxford University Press, Oxford, 2023.
22. V. D. Ghule, R. Sarangapani, P. M. Jadhav and R. K. Pandey, J. Mol. Model., 2011, 17, 2927–2937.
23. L. Wang, L. Zhai, W. She, M. Wang, J. Zhang and B. Wang, Front. Chem., 2022, 10, 871684.
24. M. Jaidann, S. Roy, H. Abou-Rachid and L. S. Lussier, J. Hazard. Mater., 2010, 176, 165–173.
25. P. Yin, Q. Zhang and J. N. Shreeve, Acc. Chem. Res., 2016, 49, 4–16.
26. V. D. Ghule, R. Sarangapani, P. M. Jadhav and R. K. Pandey, J. Mol. Model., 2011, 17, 2927–2937.
27. R. V. Tsyshevsky, O. Sharia and M. M. Kuklja, Molecules, 2016, 21, 236.
28. D. Mathieu, J. Chem. Inf. Model., 2018, 58, 12–26.
29. S. V. Bondarchuk, Z. Zhang, C. Chen, L. Wen, J. Zhang and Y. Liu, J. Phys. Chem. A, 2023, 127, 10506–10516.
30. S. V. Bondarchuk, FirePhysChem., 2022, 2, 272–278.
31. A. R. Katritzky, V. S. Lobanov and M. Karelson, Chem. Soc. Rev., 1995, 24, 279–287.
32. Assessment, Read-Across. Framework (RAAF). 2017, https://echa.europa.eu/documents/10162/13628/raaf_en.pdf/614e5d61-891d-4154-8a47-87efebd1851a (accessed on 07 September 2023).
33. A. Banerjee, A. Gajewicz-Skretna and K. Roy, Mol. Inform., 2022, 42, 2200261.
34. S. K. Pandey, A. Banerjee and K. Roy, Mater. Adv., 2023, 4, 5797–5807.
35. A. Banerjee and K. Roy, Mol. Divers., 2022, 26, 2847–2862.
36. G. K. Uyanık and N. Güler, Procedia Soc. Behav. Sci., 2013, 106, 234–240.
37. S. Wold, M. Sjostrom and L. Eriksson, Chemometr. Intell. Lab. Syst., 2001, 58, 109–130.
38. A. Varnek and I. Baskin, J. Chem. Inf. Model., 2012, 52, 1413–1437.
39. C. Wespiser and D. Mathieu, Propellants Explos. Pyrotech., 2023, 48, e202200264.
40. MarvinSketch software, https://www.chemaxon.com (accessed on 31 August 2023).
41. A. Mauri, in Ecotoxicological QSARs, ed. K. Roy, 2020, pp. 801–820.
42. B. M. Rice, J. J. Hare and E. F. Byrd, J. Phys. Chem. A, 2007, 111, 10874–10879.
43. Z. Bursac, C. H. Gauss, D. K. Williams and D. W. Hosmer, Source Code Biol. Med., 2008, 3, 1–8.
44. K. Roy, S. Kar and R. N. Das, Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press, NY, 2015.
45. A. Banerjee and K. Roy, Chem. Res. Toxicol., 2023, 36, 446–464.
46. P. Gramatica, QSAR Comb. Sci., 2007, 26, 694–701.
47. K. Roy, Expert Opin. Drug Discovery, 2007, 2, 1567–1577.
48. K. Roy, R. N. Das, P. Ambure and R. B. Aher, Chemom. Intell. Lab. Syst., 2016, 152, 18–33.
49. L. Breiman, Mach. Learn., 2001, 45, 5–32.
50. Q. Wu, C. J. Burges, K. M. Svore and J. Gao, Inf. Retr., 2010, 13, 254–270.
51. J. H. Friedman, Comput. Stat. Data Anal., 2002, 38, 367–378.
52. T. Chen and C. Guestrin, Proc. ACM SIGKDD Int. Conf., 2016, 785–794.
53. W. S. Noble, Nat. Biotechnol., 2006, 24, 1565–1567.
54. A. E. Hoerl and R. W. Kennard, Technometrics, 1970, 12, 69–82.
55. K. Roy, S. Kar and P. Ambure, Chemom. Intell. Lab. Syst., 2015, 45, 22–29.
56. S. Wold, M. Sjöström and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109.
57. R. Rodriguez-Perez and J. Bajorath, J. Comput.-Aided Mol. Des., 2020, 34, 1013–1026.

---

Footnote

† Electronic supplementary information (ESI) available: SI-1 contains the data sets in .xlsx format. SI-2 contains the PLS plots. See DOI: https://doi.org/10.1039/d4ya00215f

---