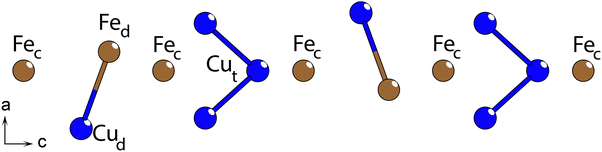Synthesis and properties of La₁₈Fe₅Cu₄S₂₆O₈, a compound containing large magnetic clusters

Abstract

A new quinary oxysulfide, La₁₈Fe₅Cu₄S₂₆O₈, was synthesized by solid-state reaction, and is found to crystallize in a novel type structure. X-Ray diffraction on powder and single crystal samples reveal an orthorhombic lattice, which can be described with the Cmcm (no. 63) space group, with lattice constants a = 9.7999(2) Å, b = 26.1186(3) Å and c = 9.7767(1) Å. The matrix of the crystal structure is built up of layers of [La₉O₄]-units connected by sulfur ions and interspaced with transition metal arrangements. The structure exhibits a guest-in-host arrangement where the guest constitutes 1D chains of transition metal ions with substantial static disorder, which can be simulated using several split positions with partial occupancies. AC and DC magnetic susceptibility (χ) measurements reveal the formation of magnetic spin domains below ∼15 K; AC data indicate that the domain wall motions are thermally activated because Arrhenius-like frequency dependencies on both the real and imaginary parts of χ(T) are observed. However, the spin domains should have relatively large sizes because there is a significant entropy release during the domain formation, as indicated by specific heat measurements. Temperature-dependent ⁵⁷Fe-Mössbauer spectroscopy data reveal that the compound lacks magnetic order down to 20 K, but exhibits signatures of spin-freezing at 6 K. Hence, it is suggested that the title compound exhibits large magnetic clusters with significant spin dynamics at high temperatures, which freeze into a disordered state at low temperatures.

---

Introduction

The vast majority of all research into inorganic compounds has focused on exploring the range of oxides or, more generally, on mono-anionic compounds. The cations are typically regarded as the source of a compound's properties, and anions are considered akin to a background element on which the cationic structure is built.

Multi-anion systems often exhibit structural ordering of the component anions.^1,2 According to Hume-Rothery,³ two different anions with ionic radii differing more than approximately 15% should not form solid solutions. Above this limit, the structures will assume an ordered arrangement. Compared with conventional mono-anionic compounds, these ordered phases offer a range of atomic environments, structural symmetries, and, by extension, properties that would not be attainable within the same structure for a mono-anionic compound. In recent years, interest in multianionic compounds has started to rise. The potential of multianionic compounds for novel structures,² catalysis,⁴ tunable properties,⁵ iron-based superconductivity,⁶ and more, along with the many unexplored phase diagrams, makes multi-anion compounds promising for further exploration.

The increased complexity of multianion crystal structures typically manifests in the form of lower crystal structure symmetry, but some families of compounds are additionally prone to structural disorder. A couple of examples of such behavior are some members of the La–Cu–S–O phase system,^7,8 as well as a quinary relative of this system, La₁₄TME₆CuS₂₄O₄ (TME = Cr, Fe).⁹ The manifestation of structural disorder within a crystal structure has significant, and potentially valuable, effects on its physical properties. The potential value of disordered systems is evident from the major interest high-entropy alloys have attracted over recent years,^10,11 but attention to the physical properties emerging from disorder within otherwise ordered phases has been comparatively lacking. In this paper, we expand upon the knowledge in this field by introducing a new example of such a phase.

This paper presents a new quinary compound, La₁₈Fe₅Cu₄S₂₆O₈, henceforth referred to as LFCSO, its synthesis, crystal structure, heat capacity, and its electric and magnetic properties, the latter properties both of which are significantly influenced by the disordered nature of the compound. The compound was discovered during a cursory search for novel compounds in the La–Fe–TME–S–O phase diagram (TME = transition metal). Several of the properties are also compared to density functional theory calculation results.

Experimental section

Sample preparation

All sample handling prior to the completion of the synthesis procedure took place within an argon-filled glove box (H₂O and O₂ < 1 ppm). A mixture of about 0.5 g with a nominal composition of La₁₈Fe_4.8Cu_4.4S₂₆O₈, with constituents La filings (Thermo Scientific, 99.9%), La₂O₃ powder (Molycorp, 99.99%), Fe powder (Alfa Aesar, 99%), Cu powder (>99%) and S chunks (>99%), were mixed into a homogenous powder in an agate mortar, and pressed into a 13 mm diameter pellet with 3 tons of force. These pellets were broken, and the fragments were placed in a corundum crucible. The crucible was sealed in an evacuated silica ampoule using an oxygen–hydrogen torch. The sample was heated in a muffle furnace, with an initial ramp of 1 °C min⁻¹ to 400 °C, resting at this temperature for 5 hours. Then, the temperature was ramped at 5 °C min⁻¹ up to 1000 °C, resting at this temperature for 24 hours before the furnace was turned off and allowed to cool at ambient rate. The cooled sample was returned to the glove box for two intermediate regrinds and repelletizations, followed by 60 and finally 96 hours at 1000 °C, with a 5 °C min⁻¹ ramp up, again turning off the furnace at the end. Alternate synthesis temperatures were attempted, but they did not improve the product.

The single crystals, used for structure determination, were obtained from samples synthesized with a nominal composition La₁₈Fe_4.666Cu_4.666S₂₆O₈, i.e. with slightly higher Cu/Fe ratio, using the same heating program.

The black, crystalline product appeared to be stable under ambient conditions. The individual crystallites lacked habitus, as observed under optical microscope. Most grain edges were round, rather than exhibiting typical crystalline features.

Obtaining completely pure samples of LFCSO proved challenging, with some degree of secondary phases consistently appearing over a range of compositions with varying Cu/Fe ratios. X-Ray diffraction (XRD) analysis reveals La₁₀S_14+xO_1−x¹² as the most prevalent extrinsic phase, observed in all syntheses, while LaCuS₂¹³ is the resulting secondary impurity if an excess of copper is employed. Attempted synthesis with stoichiometries of La₁₈Fe_4.9Cu_4.2S₂₆O₈ or La₁₈Fe₅Cu₄S₂₆O₈ results in at least one Fe-based impurity, possibly La_3.22Fe_1.1S₆,¹⁴ and one minor unidentified phase.

The title stoichiometry was determined from single crystal XRD data by refining partial occupancies for an optimal fit, but due to the disorder in the crystal structure and similar atomic form factors of Cu and Fe, the here presented composition is a close approximation of the true one.

X-Ray structure determination

Powder X-ray diffraction (pXRD) data were obtained using a BRUKER D8 Discover with a Bragg–Brentano geometry, with a Ge(111) Johanssen monochromator, CuKα₁ X-rays, and Lynxeye detector. A silicon zero-background plate covered with silicone grease was used as sample holder. The single crystal data, both room- and low-temperature (100 K), were collected using a BRUKER D8 Venture single crystal diffractometer with a MoKα InCoatec microfocus X-ray source using a photon 100 detector. The sample was cooled down for the low-temperature measurement by a nitrogen gas blower. The structure solution and refinement were successful by using the JANA2006 software.¹⁵ JANA2006 was also used for the fitting of lattice parameters from the pXRD data.

Physical property measurement system (PPMS)

The electric, magnetic and heat capacity properties were determined using quantum design PPMS. For the heat capacity measurements in the range 2–300 K, sintered polycrystalline pellets were used with the non-adiabatic thermal relaxation approach, and the sample was equilibrated for 15 minutes at each temperature before measurements. Two sequential measurements were carried out at each temperature. Sample coupling stayed at least 92% throughout all measurements. The magnetic measurements were performed on a powdered sample from a ground pellet in a polypropylene sample holder. For DC magnetic determination, field-cooling (FC) and zero field-cooling (ZFC) measurements were carried out in the range 2–300 K with applied magnetic fields of 100 mT and 1 T. A magnetic relaxation measurement was carried out by field-cooling the sample to 5 K under 100 mT, and leaving the sample in the applied magnetic field during 100, 1000 and 10 000 seconds, to try for ageing effects.^16,17 The magnetic field was removed, and the change in magnetization with time was measured after the fields removal. The AC susceptibility of the sample was measured by applying a 5 Oe AC field with frequencies ranging from 10 Hz to 10 kHz.

The electric resistance measurements utilized the same PPMS instrument to control the temperature, but the resistance across the sample was measured utilizing a MASTECH® MAS830L multimeter with a two-point measurement approach. The electrodes were fastened to a sintered pellet using silver-paint. The resistance was measured during a constant ramping of the temperature by 5 K min⁻¹ between 10–300 K, both up and down, and by 1 K min⁻¹ between 2–10 K. Due to the resistance measurement range of the multimeter, the second set of measurements between 2–10 K was done with a different range setting and lower accuracy. The average measured values between cooling and heating ramps were used for analysis. It was noted that the final resistivity of the sample at 300 K after the measurements had irreversibly increased by about 1% compared with the initial value.

Scanning electron microscopy (SEM) and energy dispersive X-ray (EDX) analyses

SEM imaging and EDX analyses were performed with a Hitachi SU8230 field emission scanning electron microscope with an XFlash 6|10 EDX detector. An acceleration voltage of 15 keV was used for both SEM and EDX. EDX composition analysis was carried out by determining the elemental composition of 19 separate crystallites and averaging the obtained values. The heaviest element, lanthanum, was used to normalize the absolute composition. Oxygen content was not determined due to the major inaccuracies for such light elements.

Mössbauer spectroscopy

⁵⁷Fe Mössbauer spectra were collected between 295 K and 6 K utilizing a standard WissEl spectrometer operated in constant acceleration mode, and a Janis SHI 850-5 closed cycle refrigerator. The source was a ⁵⁷Co/Rh source. About 33 mg of powdered LFCSO was mixed with BN and distributed in an acrylic glass sample container with a 13 mm inner diameter.

Isomer shifts are reported relative to α-iron. The data evaluation utilized the MossWinn program¹⁸ using the thin absorber approximation.

Density functional theory (DFT)

DFT was employed to determine whether the atomic arrangements, used to describe the disorder in the crystal structure, correspond to local minima in the energy landscape, or if the arrangements are unstable in the ground state. The band structure was subsequently determined for the final structure.

The calculations were done with the Vienna ab initio simulation package (VASP),^19,20 using generalized gradient approximation (GGA) as formulated by Perdew–Burk–Ernzerhof (PBE)²¹ for the exchange–correlation energy. The calculations use projected augmented-wave (PAW) pseudopotentials,²² with a plane-wave energy cutoff of 500 eV and self-consistent-field energy convergence criteria of 10⁻⁶ eV. The convergence criterion for ionic relaxation was set to all forces being less than 0.01 eV Å⁻¹. To account for the strong correlation of the Fe-3d orbitals, a Hubbard U_eff repulsion term of 3 eV is added under the rotationally invariant Dudarev approach during structural relaxation and magnetic configuration calculations.²³ Certain sections of the relaxed crystal structure was found to be dependent on the applied U_eff. However, the utilization of U_eff = 3 eV resulted in calculated band gaps significantly larger than the experimental measurements would imply. Thus, electronic structure calculations were carried both with U_eff = 3 eV, as well as without an applied Hubbard potential, utilizing the same relaxed cell, to confirm whether agreement with experimental data could be obtained by tuning U_eff.

The sampling of the Brillouin zone during structural relaxation of the unit cells used a 2 × 1 × 2 gamma-centered grid, with the supercell grids adjusted accordingly. Final energy calculations used slightly higher 3 × 1 × 3 (for unit cells) and 2 × 1 × 3 (for the 2 × 1 × 1 supercell) grids, according to the standard unit cell axes. The band structure calculations were split into seven partial calculations, using the Γ-point as a common reference included in all calculations. A full DOS calculation is not included, due to the achievable quality being too low from computational limitations. It should be emphasized that, due to the size and number of atoms of the unit cell, the k-point densities were the upper limit of what could be used with the computational capacity available in a reasonable amount of time. As such, proper convergence of properties with respect to k-point density has not been rigorously observed, so the margin of error for the calculations may be larger than ideal. As such, the relative energy differences between various configurations are largely treated qualitatively in this work, with less emphasis given to the precise energy differences. Integration over the Brillouin zone was carried out with Gaussian smearing with a width of 0.02 eV. While the compound is known to be magnetic, all calculations related to determining the ordering of the chains were non-magnetic due to the potential complexity of the unknown magnetic arrangement.

The structural relaxation calculations were carried out on the unit cell, a 2 × 1 × 1 or a 1 × 1 × 2 supercell as necessary for a given coordination of the disordered sections. The unit cell was kept fixed, while the atomic positions were relaxed. For determining the magnetic arrangement, the same three cells were employed. For the final determination of band properties, the most favorable 2 × 1 × 1 supercell structure and magnetic configurations were used. The whole unit cell, including the lattice parameters, were allowed to relax, while the angles of the unit cell were kept fixed at 90°. The final energy calculations used the tetrahedron method with Blöchl corrections for smearing.

Results

Crystal structure

The single crystal structure determination of LFCSO shows that the phase crystallizes in the orthorhombic space group Cmcm (no. 63), with lattice constants a = 9.7971(3) Å, b = 26.1193(8) Å, c = 9.7671(3) Å, and V = 2499.3(2) ų at room temperature. No distinct structural change or reduction of disordered arrangements were observed with a temperature reduction to 100 K, except a 0.56% decrease in unit cell volume. The overall structure is shown in Fig. 1. The parameters from the structure refinement are given in Tables 1 and 2. An alternate version of Table 2 with additional information is provided in the ESI,† Table S1.

Fig. 1 The overall structure of the unit cell of La₁₈Fe₅Cu₄S₂₆O₈, viewed along two different cell axes.

Table 1 Results of refinement of the structure of LFCSO against single-crystal XRD data at room temperature. From the data obtained at 100 K, only the lattice parameters are shown

Formula	La18Fe5Cu4S26O8
Radiation	Mo Kα (λ = 0.71073 Å)
Instrument	BRUKER D8 Venture
Physical appearance	Specular black, irregular habitus
Crystal system	Orthorhombic
Space group	Cmcm (no. 63)
Formula weight (g mol^−1)	2004.76
Temperature (K)	293	100
a (Å)	9.7971(3)	9.7767(3)
b (Å)	26.1193(8)	26.0630(8)
c (Å)	9.7671(3)	9.7539(3)
V (Å^3)	2499.3(2)	2485.4(2)
Z	2
ρ calc (g cm^−3)	5.301
Independent reflections	2857
No. of variables	98
GOF (obs) on F^2	1.99
GOF (all) on F^2	1.87
R 1 (obs) (%)	3.49
R 1 (all) (%)	4.71
wR2 (obs) (%)	8.92
wR2 (all) (%)	9.23
CCDC ID	2306781

---

Table 2 Structural parameters for LFCSO, as refined from single-crystal X-ray data at 293 K

Atom	x	y	z	Occ.
La1	0.5	0.42836(2)	0.53727(4)	1
La2	0.5	0.32992(2)	0.25	1
La3	0.78807(3)	0.32055(1)	0.53350(3)	1
La4	0.77609(4)	0.43308(2)	0.25	1
Fe1	0	0.24876(6)	0.25	1
Fe2	0.5	0.0102(1)	0	0.5
Fe3	0.5681(7)	0.0952(2)	0.1944(6)	0.125
Cu1	0.5	0.0948(2)	0.1631(5)	0.25
Cu2	0.3300(5)	0.0603(2)	0.1494(5)	0.25
Cu3	0.2925(5)	0.0538(2)	0.2058(5)	0.125
S1	0	0.23198(7)	0.4868(2)	1
S2	0.5	0.48045(9)	0.25	1
S3	0.2356(2)	0.26844(7)	0.25	1
S4	0.5	0.0139(1)	0.25	1
S5	0	0.3240(1)	0.75	1
S6	0	0.39215(8)	0.4370(2)	1
S7	0.2465(2)	0	0	1
S8	0.3210(2)	0.38384(8)	0.75	1
O1	0.6535(3)	0.3770(2)	0.4046(3)	1

---

The overall structure (Fig. 1) may be regarded in terms of ordered and disordered components. The ordered components, consisting of the lanthanum, oxygen, sulfur, and part of the copper positions, may be fully described within the Cmcm space group. The matrix of the structure may be considered as a composition of [La₉O₄] units, linked together with sulfide ions. The [La₉O₄] units are formed by the nine lanthanum positions tetrahedrally coordinating the four oxygen positions (Fig. 2). The preference of the oxygen ions to coordinate with the lanthanum ions over the transition metal elements is in accordance with the hard-soft acid–base principle.

Fig. 2 The [La₉O₄] unit, which constitutes the primary building block of the LFCSO matrix.

The [La₉O₄] units are ordered in layers along the ac-plane, with alternating shifted stacking along the b-axis. Each adjacent layer exhibits [La₉O₄] units arranged with the reverse orientation along the b-axis. Two [La₉O₄] planes with an ac-axis shift are interspaced by an ordered iron layer, where the iron positions (consisting of the Fe1 ions, as per Table 2) are tetrahedrally surrounded by four [La₉O₄] units. [La₉O₄] planes shifted only along the c-axis, are interspaced by disordered chains of iron and copper positions, henceforth referred to as the Fe/Cu-chains. These chains extend parallel with the c-axis, and extend alternatingly into the adjacent [La₉O₄] planes with a regular periodicity spanning the c-axis. A simplified representation of the structure, emphasizing the structural sub-units, is shown in Fig. 3.

Fig. 3 A simplified representation of the structural elements comprising LFCSO. The red elements represent the [La₉O₄] units, the brown elements represent the Fe-positions in the ordered Fe-layer, and the blue elements represent the disordered cation chains. The remaining space (empty in this figure), is filled with sulfide ions.

There are three different coordinations of lanthanum ions in the structure. All lanthanum positions are coordinated to eight anions, with 1-, 2-, and 4-fold bonding to oxygen, forming distorted square antiprismatic structures with the S and O ions arranged on opposite sides of the La ions (Fig. 4). The stacking of the [La₉O₄] units towards the iron layers results in the structure exhibiting significant voids. These voids appear to occur as a simple consequence of the structure not allowing for any favorable coordination site, with any potential ionic position within the void being too close to an ion with the same sign of charge.

Fig. 4 The coordination of lanthanum ions in LFCSO. Depending on the particular coordination, 0, 2 or 3 of the oxygen positions are replaced with sulfur.

The ordered iron layer exhibits Fe ions coordinated in a square planar arrangement, with a distortion of the coordination towards a tetrahedral coordination. The Fe ions are individually arranged in the La–S lattice, without connecting faces, edges or vertices with each other. As previously mentioned, in the structure between the Fe and oxide layers, voids form that are centered directly above and below the Fe positions, with respect to the b-axis. It should be noted that the adjacent iron layers are arranged such that any antiferro-magnetic coupling between them would be frustrated.

The Fe/Cu-chains extend parallel with the c-axis as discrete chains, with Fe and Cu positions distributed within two roughly circular ranges in the ab-plane around a central axis (Fig. 5), separated into an inner and an outer ring. Through the center of the Fe/Cu-chains, there is a vertex-linked chain of Fe–S polyhedra (henceforth referred to as the Fe_c positions, labelled as Fe2 in Table 2). Nominally, these Fe_c ions appear to be octahedrally coordinated, but local distortions in the position of the cation along the b-axis results in the chain becoming a sequence of square pyramidal-coordinated Fe_c ions instead. The Fe_c position is split between two adjacent positions above and below the center axis of the Fe/Cu-chains.

Fig. 5 Disordered section of the structure located perpendicularly off the Fe–S chain.

Only the disordered chains break with the Cmcm space group symmetry, exhibiting a local lowered symmetry. There are several potential atom positions suggested by SC-XRD data, of which several are closer than allowed. In the Cmcm space group, the chain is described by four symmetrically inequivalent sites, which amount to fourteen different positions in the lattice, per unit of the disordered section (28 positions for a single chain, per unit cell). Of the four inequivalent sites, two are trigonal planar positions, situated one in each of the two rings. The third site is a distorted tetrahedral position with two pairs of roughly equal length distances to the adjacent sulfur positions situated in the inner ring. The final position may be considered as a trigonal planar position, situated in the outer ring, with a slight distortion towards a tetrahedral arrangement where one interatomic distance to the adjacent sulfur is significantly elongated.

The three trigonal planar positions are assumed to be occupied by copper, while the distorted tetrahedral position is assumed to be occupied by iron, in accordance with the common bonding behaviors of Cu⁺ and Fe²⁺ species. There are compounds where iron assumes a trigonal planar arrangement, such as in Cs₉Fe₂S₇,²⁴ but these are very rare, and the oxidation state of Fe is uncertain in that report.

The observed structure average from diffraction is considered to be a composite of two symmetrically distinct arrangements, with either two or three atoms in each arrangement (Fig. 6). The arrangement with two atoms (one Fe and one Cu) has four equivalent spatial distributions, (henceforth individually referred to as the Fe_d (crystallographic label Fe3 in Table 2) and Cu_d (crystallographic label Cu3 in Table 2) positions, respectively), while the arrangement with three atoms has two equivalent spatial distributions, each with three Cu atoms (crystallographic labels Cu1 and Cu2 in Table 2). The cation–cation distance in the doubly and triply occupied arrangements are 3.07 Å and 2.63 Å, respectively, which are, while on the shorter end, plausible; Cu–Cu distances of 2.62 Å are observed in LaCuS₂,²⁵ while Fe–Fe distances of 2.87 Å occur in La₄FeS₇,²⁶ both chemically similar compounds to LFCSO. One interatomic distance that seems problematic is a Cu–S distance of 2.02 Å. This might be an artifact from the smeared electron density, as the two other Cu–S distances of the trigonal planar arrangement are 2.32 and 2.49 Å. At an appropriately centered position between these three sulfur positions, each Cu–S distance would be roughly ∼2.25 Å, which is a more common value.

Fig. 6 The two symmetrically inequivalent configurations of ions in the disordered section of the structure. The simultaneously occupied positions are indicated by the colored lines. The arrangement of the atomic positions in this illustration are viewed directly along the b-axis.

A ratio of 1 : 1 between the 2- and 3-fold occupied arrangements results in the nominal composition of LFCSO. Arranging an appropriate ratio of the di- and tri-occupied coordinations, respectively, a range of viable compositions with respect to Fe and Cu emerge, making exact determination of the composition of LFCSO improbable from just the crystal structure.

It should be emphasized that precise determination of atomic species, occupancy and atomic positions in the disordered region is not possible with the data available, and the structure suggested here is a compromise that fulfills the criteria of composition, charge balancing, sensible structural motif giving rise to the observed disorder, and an acceptable refinement of the single crystal XRD data.

The disorder in the structure persists if the structure is refined in the P1 space group, so it is improbable that the wrong space group was selected. The disorder is also found to remain unchanged under low temperature single crystal XRD carried out at 100 K, suggesting that the disorder is static in nature.

From the standpoint of the experimental data available, it is fully possible that the observed disorder is, in fact, a composite image from an ordered chain, and the true unit cell in fact has a longer c-axis. One possibility is that the individual chains are fully ordered, but the different chains are either ordered out of phase with each other, or disordered relative to each other. A second possibility is that the structure might be incommensurate as compared with the host-lattice along the disordered chain. However, precession images from the measured single crystal data do not suggest any incommensurate periodicities, within resolution limits. The diffraction peaks were sharp, and no diffuse scattering was observed.

DFT: structural considerations

Structural relaxation by DFT showed that the two suggested cation arrangements (including the symmetrical equivalents), proposed from the experimental data, do correspond to local minima in the energy landscape (with U_eff = 3 eV). As mentioned in the methods section, the stability of this structure does depend on the applied Hubbard potential.

To derive the theoretically favorable crystal structure from the experimental superposition, the postulates for the most energetically favorable arrangements for the occupation within each chain were found to be the following:

(1) Each successive disordered section along a single chain alternates between double and triple occupation.

(2) The two mirrored Cu positions of the triply occupied arrangement are aligned closest to the Fe_d position. Equivalently, the Cu position situated on the mirror plane is aligned closest to the Cu_d position.

(3) The two applicable configurations of the doubly occupied arrangement from postulate 2, occur in alternating sequence along the same chain.

As a consequence of postulations 1 and 2, each chain would exhibit directionality and phase, with each cation configuration being arranged with the same alignment, and on the same side of the chain, relative to the b-axis. The resulting sequence is illustrated in Fig. 7. The total observed disorder is then the sum of all chains being in one of two phases, with one of two orientations for a total of four potential arrangements each chain may assume (eight, if the alternating sequence from postulate 3 is taken into consideration). With regards to the structure of the individual chains, there are two possibilities for the full description: if the doubly occupied positions are regarded as a disordered, split occupation, the chains may be regarded as exhibiting a local mirror plane symmetry perpendicular to the a-axis, agreeing with basic unit cell axes. If they are regarded as ordered, the local symmetry of the individual chains exhibits a glide plane along the c-axis, again with the mirror plane perpendicular to the a-axis, with a doubled c-axis relative to the base unit cell.

Fig. 7 The most energetically favorable repeating sequence of ionic arrangements, as suggested by DFT. The Fe_c correspond to the center Fe-chain. The Fe_d and Cu_d positions correspond to the doubly occupied Fe and Cu positions, respectively. The Cu_t corresponds to the triply occupied copper arrangement. The arrangement of the atomic positions in this illustration are viewed directly along the b-axis.

Adjacent chains arranged along the a-axis are predicted to have preferred orientations relative to each other. Having adjacent chains with the same relative occupancy modulation phase is energetically unfavorable, and the same applies to the chain orientation. The former is the more significant in terms of energy: adjacent chains with the same phase increase the energy of the system by about 55 meV formula unit⁻¹. A parallel chain orientation results in a comparatively small 16 meV formula unit⁻¹ increase in energy. Having different phase and orientation of all adjacent chains is thus the most favorable configuration.

As a final point for this section, exchanging the Fe and Cu ions in the calculation cell, the calculations would converge towards abnormal magnetic states. While these spurious states were not closely investigated, they appear to correspond with Fe⁺ and Cu²⁺ configurations, which is an unreasonable state that does not agree with the stoichiometry, the synthesis conditions, nor thermodynamic stability. These states were accompanied by a significant increase in the system energy, which provides a further indicator that the nominal structure is more correct.

Powder XRD

For accurate determination of lattice parameters, refinement from pXRD is more suited compared with single crystal determination. Refining the lattice parameters of LFCSO from the pXRD data, one obtains a = 9.7999(2) Å, b = 26.1186(3) c = 9.7767(1) Å and V = 2502.47(2) ų. Superimposing the LFCSO crystal structure, as determined by single crystal, to the powder diffraction data results in discrepancies. The shown refinement (Fig. 8) is using the structure refined from single crystal data, with all parameters except the lattice vectors held constant, as the disordered part of the structure is too complex to refine by pXRD. LFCSO appears to exhibit a preferential orientation, such that the [2 6 2] lattice plane reflection, in particular, appears disproportionally large. While the intensities of the calculated and measured peaks differ significantly for the larger peaks, the two diffractograms are at least in general qualitative agreement. At higher angles, the agreement is substantially better.

Fig. 8 Refinement of pXRD data against the crystal structure determined by single crystal XRD. Open circles are observations, the full black line is the Rietveld refinement, vertical lines are Bragg positions, and the blue line displays the difference Y_obs–Y_calc.

There are a couple of impurity peaks in the sample; one set is known to be from La₁₀S_14+xO_1−x, the second is suspected to be either La₂O₂S²⁷ or LaCuS₂,²⁵ although the peaks are too few and weak to be certain.

SEM and EDX analysis

The SEM images suggest that LFCSO crystallites lack habitus, exhibiting rounded surfaces and edges (Fig. 9). There are distinct crystalline domains visible, which grow in intertwining arrangements, as could be expected from crystal growth during sintering of a pellet. The presence of both rounded and straight edges, as well as a range of surface roughness, suggests different crystallinity through the sample. The EDX analyses gave the composition for LFCSO shown in Table 3.

Fig. 9 Three different SEM images (a)–(c) of LFCSO, demonstrating that both rounded and straight grain edges can be found, representing less and more crystallinity, respectively, throughout the sample. Also, a range of surface roughness suggests different crystallinity.

Table 3 The averaged composition of LFCSO as determined by EDX, referenced to the heaviest element, La

Element	Composition
La	18.0(4)
Fe	5.2(4)
Cu	4.2(3)
S	25.2(6)

---

The average chemical composition matches decently the expected stoichiometric ratio La₁₈Fe₅Cu₄S₂₆O₈, with the nominal composition falling within the standard deviation for all elements except sulfur, which is still close. The uncertainty in the measurements is unfortunately substantial for the elements present in a smaller proportion, rendering the precise stoichiometry of Fe and Cu too uncertain to determine by this method.

Mössbauer spectroscopy

Temperature dependent Mössbauer spectra of LFCSO are shown in Fig. 10. The spectra confirm that LFCSO is magnetically disordered down to at least 20 K. In the spectra between room temperature (RT) and 20 K one can identify a quite sharp central quadrupole doublet with nearly temperature-independent quadrupole splitting QS (QS ∼ 0.85 mm s⁻¹) and a broader part with a temperature-dependent QS. The sharper component revealing an isomer shift IS ∼ 0.66 mm s⁻¹ at RT (IS ∼ 0.80 mm s⁻¹ at 20 K) can be assigned to distorted square planar Fe(1)²⁺ sites with high spin configuration that form the ordered quite isolated Fe layers. The T-independent QS reflects the pronounced splitting of the d-orbitals in the approximately square planar ligand field which is expected to stabilize orbitals with local z components owing to the lack of an axial ligand. Nearly temperature-independent QS of ∼1.1–1.3 mm s⁻¹ has been reported for Fe²⁺ oxides with square planar coordination like SrFeO₂,²⁸ Sr₃Fe₂O₅,²⁹ or Sr₂FeO₃.³⁰ The electronic structure of SrFeO₂ was analyzed in detail and it was concluded that its electronic and magnetic state is determined by double occupancy of the 3d_z² orbital.^31,32 The latter is favored by the hybridization between the 3d_z² and the 4s orbitals in square planar coordination geometry, which is also reflected in the quite small IS values of these oxides (∼0.5 mm s⁻¹ at RT). The isomer shifts are determined by the s electron density at the nucleus. In LFCSO the IS values for Fe(1) are somewhat larger corresponding to a smaller s electron density at the nucleus which might indicate that the 3d_z²–4s hybridization is less pronounced. A detailed investigation of the electronic structure of the distorted Fe(1)S₄ layers is required for more profound clues.

Fig. 10 Mössbauer spectra of LFCSO at the indicated temperatures. Dots, black lines, and colored lines correspond to the experimental data, calculated spectra, and component spectra, respectively. Fitting of the spectra was performed with three components with an intensity ratio 2 : 2 : 1 as suggested by the crystal structure analysis.

The remaining part of the spectra comprises the Fe2 and Fe3 sites which, however, cannot be identified unambiguously in the broad and poorly structured spectra. Considering the crystal structure model, the spectra between RT and 20 K were described by three quadrupole doublets with fixed intensity ratio Fe1 : Fe2 : Fe3 = 2 : 2 : 1. While the central component assigned to the ordered Fe1 square planar units is sharp, pronounced line broadening for the Fe2 and Fe3 components suggests local atomic disorder and fitting with two components is somewhat arbitrary. The Mössbauer parameters obtained at 100 K are summarized in Table 4. The isomer shifts of all sites are in agreement with Fe²⁺ high spin. The temperature dependence of QS for the Fe2 and Fe3 subspectra can be attributed to non-cubic contributions to the electric field gradient in tetrahedral and square pyramidal Fe²⁺ high spin (3d⁶) configuration owing to unequal temperature-dependent orbital populations in the respective ligand field.

Table 4 Parameters obtained from fitting the Mössbauer spectrum of LFCSO at 100 K with three components assigned to Fe1, Fe2, and Fe3 sites with the intensity ratio 2 : 2 : 1. IS, QS, and Γ denote the isomer shift, quadrupole splitting, and linewidth, respectively

	IS (mm s^−1)	QS (mm s^−1)	Γ (mm s^−1)
Fe1	0.774(5)	0.855(9)	0.246(10)
Fe2	0.947(11)	2.13(2)	0.44(3)
Fe3	0.70(3)	2.15(4)	0.44

---

At 6 K an inward collapse of the spectrum is apparent which indicates the onset of spin freezing or magnetic ordering in the low-temperature region, in agreement with the susceptibility and heat capacity studies described below. The collapse particularly affects the outer signals attributed to Fe2 and Fe3 sites while the apparent splitting of the spectrum may indicate that the Fe1 quadrupole doublet may be still discernible.

Magnetic properties

Over the majority of the temperature range 2–300 K, LFCSO exhibits typical Curie-paramagnetism (Fig. 11). Magnetization measurements at room temperature showed no discernable indication of ferromagnetic impurities. Fitting the Curie–Weiss formula with a diamagnetic contribution, , to the curves results in diamagnetic constant contributions of χ₀ = −0.003(1) emu Oe⁻¹ mol⁻¹ and χ₀ = −0.0037(9) emu Oe⁻¹ mol⁻¹ for the 100 mT and 1 T measurements, respectively. A relatively strong diamagnetic contribution is expected, as the bulk of the composition consists of heavy, diamagnetic species, and there seems to be diamagnetic contributions from the sample holder, yet the total diamagnetic signal is irrelevant for most calculations here because the sample signal is strong.

Fig. 11 Susceptibility measurements for LFCSO against temperature at 100 mT (a) and 1 T (b) of applied external fields, respectively. The top insert in both graphs is a close-up of the regions where the FC and ZFC measurements diverge. The bottom insert is the inverse susceptibility against temperature.

The Weiss constant θ is −21(3) K at 1 T, while the 100 mT measurement gave a value around zero. The effective magnetic moment, determined using the equation

where k_B is the Boltzmann constant, N_A is the Avogadro number, μ_B is the Bohr magneton, and C is the molar Curie constant as fitted from the Curie–Weiss formula, gives effective iron magnetic moments of μ_eff = 7.1(2)μ_B and μ_eff = 8.5(2)μ_B for 100 mT and 1 T, respectively. These values correspond to a total of about 6 and 8 unpaired electrons formula unit⁻¹, respectively. From the synthesis conditions, the neutrality condition, and the DFT calculations, we assume that all Cu in the compound is in a diamagnetic Cu⁺ state. Further assuming a nominal spin S = 2 for all Fe²⁺ sites, with negligible spin–orbit coupling effects, these values correspond to approximately two paramagnetic Fe²⁺ ions. This would suggest either the presence of both high- and low-spin states of Fe, or a not fully paramagnetic high temperature regime. By assuming a large range of magnetic interaction strengths, the more distanced Fe positions in the ordered iron layer interact comparatively weakly, relative to the close coupling between the Fe positions in the Fe/Cu-chains. Hence, it is possible that only the iron layer (Fe1 positions) which constitutes 2/5 of the total Fe, is in a paramagnetic state, while the Fe/Cu-chains retain at least some degree of local ordering up to 300 K. Being 1D chains, the associated transition to complete paramagnetism would take place over a very broad temperature range, and would be difficult to isolate under the dominant observed signal from the paramagnetic layer.

The divergence between the FC and ZFC curves appears at about 9.75 K and 7.75 K, for applied fields of 100 mT and 1 T, respectively (Fig. 11, upper insert). The behavior observed in the curves is characteristic for magnetic domains, such as those in e.g. superparamagnets, spin-glasses, magnetic cluster glasses, or mictomagnets. The possibility of the material being a spin-glass was evaluated by ageing of relaxation measurements of the field-cooled spin-state (data not shown). No significant effect was observed, which indicates the freezing is not spin-glass-like.

The frequency dependence measurements of the AC susceptibility with temperature exhibited a clear relation (Fig. 12). Plotting the relative positions of susceptibility maxima in an Arrhenius plot (Fig. 12, insert), reveals a linear relationship with an activation energy of 27(2) meV per atom for reversing the magnetic moment. Compared with the average thermal energy of electrons at 15 K, 1.3 meV, this activation energy is significantly larger than would be expected for a spin-glass or a superparamagnet,³³ where magnetic spins rearrangements include smaller domains with lower activation energies. It should be noted that the observed activation energy is comparable to the thermal energy of electrons at room temperature, but no effect is observed in the susceptibility curves around 300 K. With respect to the domain-like magnetism observed, the large imaginary component of the AC susceptibility (almost 10%), and the strong shift in the AC susceptibility maximum with the magnetic field frequency, one may suggest that LFCSO is a magnetic cluster glass with large, coupled spin domains, which do not extend into a state of complete ordering.

Fig. 12 AC susceptibility of LFCSO in the temperature range 5–15 K. The real contribution is given above, while the imaginary component is below. The top-left insert is the Arrhenius plot of the natural logarithm of the magnetic field frequencies resulting in susceptibility maxima, against inverse temperature. The corresponding red lines are the fitted least-squares linear equations.

Further, the Arrhenius-like behavior of the frequency-dependent shift shows that the compound is either a superparamagnet, or a magnetic cluster glass.

DFT: magnetism

The lattice of magnetic ions in LFCSO may be thought of as two parts: the Fe/Cu-chains, and the iron layers, which mutually interact in a difficult-to-predict manner. The magnetic structure may be described with four significant interactions (I1–I4, each I incudes a set of magnetic couplings J), which are illustrated in Fig. 13: internal Fe/Cu-chain interactions (labeled I1), interactions between adjacent Fe/Cu-chains (labeled I2), internal Fe-layer interactions (labeled I3), and finally the interaction between the Fe/Cu-chains and the Fe-layers (labeled I4). From calculations, there are several magnetic configurations with nearly degenerate energy contending to be the most favorable.

Fig. 13 A partial illustration of the crystal structure, showing the sections of the crystal structure each magnetic interaction label corresponds with, as utilized in the magnetic discussion.

Starting with the I1 interactions, these may be considered in two parts: the central Fe_c–S–Fe_c chain is predicted to assume an AFM arrangement, as would be expected from the Goodenough–Kanamori rules.^34,35 The Fe_d position is situated such that it is aligned closer with one of the two Fe_c positions of the central chain; the DFT calculations consistently predict that the most favorable arrangement of the Fe_d magnetic moment is in parallel with the closer Fe_c neighbor.

Following the predicted ordering of the chains, which was described previously, the doubly occupied sections of the chain are all situated such that the magnetic spins of the Fe_d positions are arranged in parallel, resulting in each chain exhibiting a sum magnetic moment, essentially acting as a ferrimagnetic domain. This sum moment is involved in both I2 and I4, which results in complex interactions through the structure. This would happen regardless of whether the magnetic alignment of the Fe_d positions have FM or AFM type interaction with their closest Fe_c neighbor.

The I3 interactions result in the most favorable magnetic configuration within the Fe-layer being a simple AFM arrangement with the closest adjacent Fe positions.

It is difficult to determine the most favorable magnetic configuration with respect to the I2 and I4 interactions, as there are many potential configurations with similar energy. Certain interactions are so weak that the energy difference between different configurations is on the scale of 1 meV or less per formula unit. Note the calculations have limited precision, and only consider a partial structure.

Qualitatively, the most favorable I4 interaction was found to be a FM arrangement between the sum moment of the chains and the closest Fe positions in the adjacent Fe-layer, situated directly adjacent along the b-axis. Thus, depending on the orientation of the magnetic moment of the chains on opposite sides of the Fe-layer, the AFM I3 and FM I4 interactions may end up competing.

According to DFT, the I2, I3 and I4 interactions are rather weak, on the order of 1 meV formula unit⁻¹. In comparison, the I1 interaction energy is predicted to be two orders of magnitude greater, in excess of 150 meV formula unit⁻¹. Hence, the DFT calculations may be considered to lend credence to the previously postulated hypothesis that only the Fe-layer undergoes a magnetic transition at ∼10 K, while the Fe/Cu-chains retain at least local coupling up to a substantially higher temperature.

Heat capacity

The heat capacity and heat capacity divided by temperature of LFCSO with temperature is shown in Fig. 14.

Fig. 14 Upper: Heat capacity of LFCSO with temperature and the Dulong–Petit limit. Below: The heat capacity of LFCSO divided by the temperature, against the temperature. The shaded area of the inset corresponds to the integral for the magnetic entropy contribution.

The C_P/T reveals a non-phononic contribution to the heat capacity at about 15 K and down to the lower limit of the measurement range, which matches the observed behavior of magnetic freezing in this temperature range in the absence of external magnetic fields. The low temperature anomaly on the heat capacity curve covers the critical region for proper fitting of a Debye model curve, thus rendering this method unavailable. A simple fitting of a second order polynomial was used to crudely integrate for the entropic energy released in the anomalous region, giving a contribution of 4.74 J mol⁻¹ K⁻¹. This is marginal compared with the 66.91 J mol⁻¹ K⁻¹ one would expect for the magnetic entropy of high-spin Fe²⁺ ions, as per the equation

S = RN ln(2J + 1)

where S is the entropy contribution, R is the ideal gas constant, N is the number of magnetic ions per formula unit, and J is the total spin moment per magnetic ion. There are several possible contributions which may cause this, but returning to the previous postulation that only the iron layer undergoes a magnetic transition in the measured temperature range, the expected entropy contribution becomes 26.76 J mol⁻¹ K⁻¹.

In this case there is still a significant, if smaller, discrepancy between the theoretical and measured values. Other potential contributions for the discrepancy include the cutoff of the measurement at 2 K prior to attainment of complete ordering, entropic contribution from magnetic ordering across a larger temperature range than is apparent, or finally inherent disorder in the magnetic structure, which would agree with the depiction of this compound as a magnetic cluster glass.

Electric conductivity

The electric resistance of LFCSO with temperature (Fig. 15) is comparatively low for a semiconductor, in agreement with the black appearance of the material. Compared with a conventional semiconductor, the increase in resistivity with decreasing temperature is too low. The conductivity cannot be modelled by simple thermal excitation of electrons across a band gap, as it exhibits no simple Arrhenius relation.

Fig. 15 Resistance of LFCSO against temperature, measured with a two-point method. The red curve in the main graph is the low-temperature fitted Mott variable-range hopping model, while the green line is the full graph fitting. The red line in the insert is the linear fit of the low temperature region for the natural log of the resistance against T^−1/2.

At low temperatures, the data provides an excellent fit with the Mott variable-range hopping model, described by the equation³⁶

where the parameter d represents the dimensionality of the conduction, R is the resistance, T is the absolute temperature, T₀ is a characteristic temperature, and R₀ is a prefactor.

In the low-temperature range, between 2 K and 30 K, an excellent fit is attained with d = 1, where T₀ = 9.23(9) K (refining with respect to d gives 1.17(3) as the best fit) suggesting that electric conduction in the lowest temperature range predominantly could occur along the one-dimensional Fe–S chains, separated by insulating layers of La–S. The inset shows the natural logarithm of the resistance against T^−1/2, showing the linear relation that emerges (Fig. 15). The prefactor R₀ could not be determined with any agreeable precision with the measurement methodology employed.

Across the full temperature range, the best fit is attained with d = 2, where T₀ = 41.1(6) K. Refining with respect to the parameter d gives d = 1.76 and T₀ = 29(2) K, suggesting possibly a combination of 1D and 2D modes of conduction. The obvious candidates, from simple structural considerations, for the primary sites of conduction is thus the Fe/Cu-chains at the lowest temperatures, with the iron layers significantly contributing after a threshold temperature is surpassed.

The fitting results in a decent overall agreement, but it is not ideal, as residue of the fitting exhibit systematic, nearly linear trends at higher temperatures. This effect is likely a composite of conduction in higher dimensionality than the 2D planes gradually coming into effect, along with other mechanisms of conduction, which would be difficult to decompose into separate contributions.

The agreement with the Mott model supports the presented structure as exhibiting some degree of inherent disorder, and further implies the presence of localized charge-carrier states.

DFT: electronic structure

Without an applied U_eff, the band gap is about 0.25 eV, which is generally in line with the experimentally observed results. This band structure is shown in Fig. 16. The transition is indirect, occurring across two different transitions, X–T and X–R. The energy levels of the two symmetry points are practically identical within the available accuracy. With an applied Hubbard potential U_eff = 3 eV, LFCSO still exhibits an indirect band gap, although across different transitions (U–Γ or Z–Γ), as well as with a much wider band gap of 1.43 eV (the U_eff = 3 eV band structure is provided in the ESI,† Fig. S1). The character of the transition also depends significantly on the applied U_eff value. With U_eff = 3 eV, the valence band maximum (VBM) consists of a mixture of S-3p and Cu-3d states, centered on the triply occupied disordered site. The Γ-point conduction band minimum (CBM) is dominated by Fe-3d states originating from the Fe_d-positions. With U_eff = 0 eV, on the other hand, both the VBM and CBM are dominated by Fe-3d states originating from the Fe_c-positions. It is notable in the band structure that there is a discernable difference in the energy of the bands depending on the local magnetic environment.

Fig. 16 Band structure of LFCSO, calculated with an applied U_eff = 0 eV. The zero point of the energy scale is set to the Fermi level. Black and red bands represent spin-up and spin-down states, respectively.

A particular point of note in the band structure is that the energy bands near the CBM lie comparatively close in energy, with local variation of less than one meV without an applied U_eff, and with local magnetic shifts in energy introducing further fine structure into the bands.

Unfortunately, as this band structure is based on the incomplete atomic configuration of the calculation cell, there is necessarily error in the structure. The effect of the incomplete representation is unknown, but a more complete representation would presumably decrease the degeneracy of the electron bands further.

Referring back to the postulated mechanism for the electronic conductivity, the band structure calculations qualitatively support the view of chain- followed by plane-conduction. The conduction band edge is dominated by Fe/Cu-chain positions, followed by the Fe positions in the iron layer at higher energies. The calculated difference in energy is somewhat too large for the corresponding experimental temperature range, however, with differences of at least about 60 meV between the chain and plane iron states.

Discussion

The main question, pertaining to the properties of LFCSO, is the origin of the magnetic cluster glass behavior. As the exact structure of LFCSO, and whether or not it is prone to non-stoichiometry, substitutions, defects or intrinsic disorder, is still unknown, this is a potential origin of the properties. It should be noted that LFCSO exhibits the same FC/ZFC behavior for at least two different Fe : Cu ratio synthesis compositions, so the properties are at least not highly susceptible to synthesis conditions.

Magnetic cluster glass properties have been attributed as a consequence of magnetic frustrations, disordered magnetic interactions, and competing ferro- and antiferromagnetic interactions,³⁷ which fits well with the observations from the DFT results of many states with similar energy. As previously postulated, it is possible that only the iron layers undergo a complete magnetic transition in the measured temperature range, so the obvious inference would be to assign the magnetic cluster glass characteristic to the arrangement of the Fe-layer spin states. However, as the DFT calculations predict the spin orientation of the Fe ions in the plane to preferentially align parallel with the magnetic ordering of adjacent Fe/Cu-chains, and Mössbauer data suggest no long-ranged magnetic order, the description of the magnetic structure is likely a compound effect which depends on the exact structural arrangement.

With the data available at this point, the most suitable description of the magnetic behavior would be as follows: at high temperatures, the weakly interacting Fe-layer is in a paramagnetic state. Concurrently, the Fe/Cu-chains are not ordered, but exhibit significant coupling between the adjacent Fe-positions within each chain, resulting in the absence of the corresponding magnetic moments from measurements. Further, the chains also exhibit significant spin dynamics at high temperatures. At the magnetic transition temperature, the spin dynamics freeze in, resulting in a disordered magnetic state with competing FM and AFM interactions, which is a known cause of magnetic cluster glass formation.

Conclusions

Powder and single crystals of La₁₈Fe₅Cu₄S₂₆O₈ were obtained by mixing a ratio of La, La₂O₃, Fe, Cu and S corresponding to the nominal composition La₁₈Fe_4.8Cu_4.4S₂₆O₈. The crystal structure was determined by combined single crystal and pXRD determination. The compound assumes an original crystal structure is largely described by the Cmcm space group, but the structure exhibits a significant degree of static disorder in the positions of the transition metal elements. The static nature of this disorder was indicated by low temperature single crystal XRD. Resistivity measurements reinforce the disordered representation of LFCSO as the electric behavior is well described by the Mott variable-range hopping model for a single dimension of conduction at low temperature. Magnetic cluster glass formation is observed below about 15 K, as suggested by magnetic and heat capacity measurements, as well as Mössbauer spectroscopy, which is attributed to the influence of competing AFM and FM interactions.

Data availability

Crystallographic data for the subject compound has been deposited at the CCDC repository under ID 2306781 and can be obtained from https://www.ccdc.cam.ac.uk/structures/. Additional data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

E. H. F. and M. V. would like to thank the Norwegian Research Council (NFR) for their financial support through project 301711.

Notes and references

1. S. J. Clarke, P. Adamson, S. J. C. Herkelrath, O. J. Rutt, D. R. Parker, M. J. Pitcher and C. F. Smura, Inorg. Chem., 2008, 47, 8473.
2. M. Valldor, Inorganics, 2016, 4, 23.
3. W. Hume-Rothery and H. M. Powell, Z. Kristallogr. – Cryst. Mater., 1935, 91, 23.
4. G. Yadav and M. Ahmaruzzaman, Mater. Res. Bull., 2022, 152, 111836.
5. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772.
6. G. Wu, et al. , J. Phys.: Condens. Matter, 2009, 21, 142203.
7. F. Q. Huang, P. Brazis, C. R. Kannewurf and J. A. Ibers, J. Solid State Chem., 2000, 155, 366.
8. G. H. Chan, M.-L. Liu, L.-D. Chen, F.-Q. Huang, D. E. Bugaris, D. M. Wells, J. R. Ireland, M. C. Hersam, R. P. Van Duyne and J. A. Ibers, Inorg. Chem., 2008, 47, 4368.
9. E. H. Frøen and M. Valldor, ACS Omega, 2024, 9, 22145.
10. E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515.
11. D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 122, 448.
12. P. Besançon, D. Carré and P. Laruelle, Acta Crystallogr., Sect. B, 1973, 29, 1064.
13. M. Julien-Pouzol, S. Jaulmes, A. Mazurier and M. Guittard, Acta Crystallogr., Sect. B, 1981, 37, 1901.
14. K. Cenzual, L. M. Gelato, M. Penzo and E. Parthé, Z. Kristallogr. – Cryst. Mater., 1990, 193, 217.
15. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. – Cryst. Mater., 2014, 229, 345.
16. L. Lundgren, P. Svedlindh, P. Nordblad and O. Beckman, Phys. Rev. Lett., 1983, 51, 911.
17. M. Alba, M. Ocio and J. Hammann, Europhys. Lett., 1986, 2, 45.
18. Z. Klencsár, E. Kuzmann and A. Vértes, J. Radioanal. Nucl. Chem., 1996, 210, 105.
19. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
20. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
22. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
23. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
24. W. Bronger and U. Ruschewitz, J. Alloys Compd., 1993, 197, 83.
25. S. Strobel, P. Lauxmann and T. Schleid, Z. Naturforsch. B, 2005, 60, 917.
26. G. Collin, F. Rouyer and J. Loriers, C. R. Seances Acad. Sci., Ser. C, 1968, 266, 689.
27. B. Morosin, Acta Crystallogr., Sect. B, 1973, 29, 2647.
28. Y. Tsujimoto, C. Tassel, N. Hayashi, T. Watanabe, H. Kageyama, K. Yoshimura, M. Takano, M. Ceretti, C. Ritter and W. Paulus, Nature, 2007, 450, 1062.
29. H. Kageyama, et al. , Angew. Chem., Int. Ed., 2008, 47, 5740.
30. C. Tassel, L. Seinberg, N. Hayashi, S. Ganesanpotti, Y. Ajiro, Y. Kobayashi and H. Kageyama, Inorg. Chem., 2013, 52, 6096.
31. H. J. Xiang, S. H. Wie and M. H. Whangbo, Rev. Lett., 2008, 100, 167207.
32. J. M. Pruneda, J. Íñiguez, E. Canadell, H. Kageyama and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 115101.
33. J. A. Mydosh, Spin Glasses: An Experimental Introduction, CRC Press, London, 1st edn, 1993.
34. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87.
35. J. B. Goodenough, Phys. Rev., 1955, 100, 564.
36. N. F. Mott, Philos. Mag., 1969, 19, 835.
37. S. Mahana and D. Topwal, Appl. Phys. Lett., 2017, 110, 102907.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2306781. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc03067b

---