Donor incomplete ionization and mobility enhancement in ultra-thin silicon-on-insulator films doped by phosphorus end-terminated polymers

Abstract

Ex situ doping of ultra-thin silicon-on-insulator (SOI) substrates is performed by using polymers terminated with a doping containing moiety. The injection of P impurity atoms is investigated confining the same P dose of ∼ 1 × 10¹³ cm⁻² in a progressively thinner device layer, with thickness values (H_SOI) from 6 to 70 nm. The dopant concentration is determined by Time-of-flight secondary ion mass spectroscopy (ToF-SIMS) measurements. Sample resistivity (ρ), carrier concentration (n_e) and mobility (μ) are determined combining sheet resistance and Hall measurements in van der Pauw configuration. Almost complete activation and full ionization of the injected dopants is observed at room temperature in the samples with H_SOI ≥ 30 nm. The ionization fraction progressively drops to 5% when reducing the thickness of the device layer. Dopant incomplete ionization is accompanied by an increase in electron mobility, with values significantly larger than those reported for bulk Si. In the SOI samples with H_SOI > 20 nm, the fraction of ionized P atoms at room temperature is perfectly described by the 3D bulk model of Altermatt et al. For H_SOI ≤ 20 nm, the bulk model must be corrected to account for the effect of interface states and dielectric mismatch between Si and surrounding SiO₂.

---

Introduction

The microelectronics industry is heading into the age of ultra-scaled stacked 3D device architectures, such as gate-all-around field-effect transistors (GAAFETs).¹ These transistors, in which the gate surrounds a Si nanosheet channel, are a direct evolution of FinFETs, designed to offer better channel control, be faster, and less power-consuming.^2,3 This transition poses technological and fundamental problems regarding dopant incorporation, activation and ionization in Si-based nanostructures.⁴ In this respect, there have been extensive theoretical and experimental studies regarding dopants in 0D and 1D silicon nanostructures,^5–7 but limited results are reported on 2D systems like doped ultra-thin Si films.^8,9

Ex situ doping of ultra-scaled Si nanostructures by standard ion implantation is difficult because the release of energy by the impinging ions determines severe damages in the Si crystal that are difficult to restore. To overcome the limitations associated with conventional top-down doping techniques, the use of dopant end-terminated polymers was proposed as an alternative bottom-up approach to achieve semiconductor doping.¹⁰ Polymers are employed to create a δ-layer source of dopants at the interface between a SiO₂ capping layer and the underlying Si substrate.¹¹ The dopants are driven-in via high temperature annealing in a rapid thermal processing (RTP) system. This mild approach is compatible with mass production of advanced microelectronic components and was demonstrated not to introduce significant contaminations in the sample during the process.¹² In particular, the incorporation of P dopants in a silicon-on-insulator (SOI) substrate with device layer thickness ∼30 nm using this doping strategy was already investigated.¹¹ The experimental data demonstrated that drive-in of the dopants at 1000 °C for 100 s results in a uniform dopant concentration throughout the entire device layer with high activation rates (η_a > 90%) and electrical properties compatible with those reported for a P-doped bulk Si.¹³ This doping technology represents a simple tool to introduce dopant impurities in ultra-thin Si films and study their activation, providing useful information to support current transition toward the next generation of microelectronics devices.

In this work, the drive-in of P impurity atoms in ultra-thin Si films was investigated confining the same P dose in SOI samples with progressively thinner device layers. Time-of-flight secondary ion mass spectrometry (ToF-SIMS) data were combined with sheet resistance and Hall measurements at room temperature to investigate the effect of the reduction of the device layer thickness (H_SOI) on the activation and ionization of P impurity atoms.

Experimental

1 × 1 cm² SOI dies were cleaved from lightly doped p-type SOI wafers with (149.6 ± 0.1) nm thick buried oxide (BOX) and (71 ± 1) nm thick Si device layer. The device layer was thinned down following an oxidation procedure described in a previous paper,¹¹ developed to produce ultra-thin SOI films with no evidence of sample degradation associated with high temperature oxidation.¹¹ In particular, no significant differences in terms of oxygen diffusion into the device layer were observed between the pristine and the thinned SOI samples when performing the oxidation process in O₂ atmosphere at T ≤ 1100 °C. Accordingly, to prevent any possible oxygen contamination and modification of the Si/SiO₂ interfaces prior to the doping process, the thinning of the device layers was performed by an oxidation process at T = 1000 °C. A P dopant δ-layer source was formed at the interface between the Si device layer and a 10 nm thick SiO₂ capping layer, using a poly(methylmetachrylate) end-terminated by a P-containing moiety (PMMA-P) grafted to the substrate. PMMA-P is characterized by an average molar mass M_n = 7.5 kg mol⁻¹ and polydispersity index Đ = 1.14. More details are reported in previous publications.^10,14–16 The samples underwent a high temperature treatment in a RTP system at temperatures ranging from 900 to 1100 °C in N₂ atmosphere to promote the drive-in of P atoms into the Si device layer. Finally, after removal of the SiO₂ capping layer, circular aluminum metal contacts were deposited by thermal evaporation in a square van der Pauw (VDP) geometry at the corners of each sample using a shadow mask. Spectroscopic ellipsometry (SE) was used to monitor H_SOI at each step of the doping process, from oxidation to metal deposition. Sample preparation was optimized to produce SOI films with H_SOI ranging from 6 to 70 nm. To guarantee accurate determination of the effective H_SOI values and proper correlation with electrical characteristics, the thickness of each sample was determined at the end of the process, just before the electrical characterization of the sample. Sheet resistance and Hall measurements were performed in VDP configuration.¹⁷ ToF-SIMS measurements were performed in a IONTOF IV system using Cs⁺ ions for sputtering and Ga⁺ ions for analysis. Depth scale calibration was performed by individually measuring the sputter rate in each of the SOI samples. The Si/SiO₂ interfaces were determined by the spikes in ³⁰Si signals, while H_SOI was accurately determined by SE. To obtain quantitative information about the P concentration, the counts measured by the ToF-SIMS were converted into atom concentrations (atoms cm⁻³) following a calibration protocol fully described in a previous publication.¹⁸ In particular, P⁻ secondary ion signal was normalized on the ³⁰Si⁻ secondary ion signal that was selected as a reference. Subsequently, the normalized P signal was calibrated using a relative sensitivity factor that was determined considering a set of samples implanted with P at the same energy but different doses in order to verify the linearity of the calibration over a broad range of concentrations.

Results and discussion

The P concentration profiles in the different SOI samples upon drive-in at 1000 °C for 100 s are reported in Fig. 1. The ToF-SIMS depth profiles of the 50 and 70 nm thick SOI samples show a P concentration gradient throughout the device layer. The observed concentration profile is correctly predicted by Fick's law of diffusion for thick SOI films.¹⁹ Conversely, when H_SOI ≤ 30 nm, P atoms reach the buried Si/SiO₂ interface during diffusion, starting to segregate at the interface and rediffuse into the device layer. This results in a flattening of the concentration profile, as observed by ToF-SIMS analysis, which demonstrates that the P concentration remains constant within experimental variation throughout the entire film thickness in the case of the samples with H_SOI ≤ 30 nm.

Fig. 1 ToF-SIMS P depth profiles of SOI samples with H_SOI ranging from 6 to 70 nm upon drive-in at 1000 °C. Grey dashed lines indicates the position of the BOX interface.

Fig. 2a shows the total P dose (N_D) injected in the device layer, computed as the integral of the P concentration depth profile obtained by ToF-SIMS analysis. Data were obtained by averaging the P doses obtained across several samples annealed in the same RTP conditions with the same nominal H_SOI. In the case where just one sample was prepared, the error bar was assumed to be around 10% of the dose determined from calibrated ToF-SIMS depth profiles. In the SOI samples with H_SOI > 6 nm, N_D is found to be constant within experimental error. The average P dose was determined to be N_D ∼ (1.0 ± 0.2) × 10¹³ cm⁻². The N_D reduction that is observed in the 6 nm thick sample suggests that, in the case of ultra-thin SOI, a fraction of P atoms is lost because of P diffusion in the BOX, in agreement with previous studies about P diffusivity in Si and SiO₂ under similar annealing conditions.¹¹ Moreover, Fig. 1 shows an increasingly higher P signal at the device layer/BOX interface when reducing H_SOI, suggesting a significant P accumulation at the interface in ultra-thin films. It is worth noting that, although important matrix effects are expected to occur at the buried Si/SiO₂ interface, preventing a quantitative estimation of the effective amount of P segregated at this interface by the ToF-SIMS signals, a qualitative comparison of the P concentration profiles in this region is assumed to be reliable since were obtained from samples that are nominally identical since they were cut from the same wafer and experienced the same thermal treatment. The combination of these P segregation and diffusion phenomena accounts for the low P dose in the 6 nm thick device layer.

Fig. 2 (a) The total P dose computed from analysis of ToF-SIMS depth profiles (black) and the dose of charge carriers obtained by Hall measurements (blue) versus H_SOI upon drive-in at 1000 °C. Dashed lines correspond to different dopant activation rates. (b) Sheet resistance R_s (black) and carrier mobility μ (blue) versus H_SOI. In the inset, μ versus the average carrier concentration n_e. Blue solid line indicates electron mobility in bulk Si.¹³

Fig. 2a shows the dose of free electrons (N_e) in the device layer, obtained by Hall measurements at room temperature, as a function of H_SOI. In the limit of full ionization, the free carrier dose is assumed as an indicator of the dose of electrically active P atoms. Accordingly, the activation rate η_a is computed as the ratio η_a = N_e/N_D. Almost complete activation and full ionization is achieved when H_SOI ≥ 30 nm, consistently with previous results.¹¹ Apparently, the activation progressively drops when decreasing H_SOI below this threshold value, achieving a minimum η_a ∼ 5% when H_SOI ∼ 6 nm.

Fig. 2b reports the sheet resistance (R_s) and the carrier mobility (μ) values as a function of H_SOI. The carrier mobility (μ) is computed by combining R_s and Hall measurements according to the equation

μ = (qN_eR_s)⁻¹,

where q is the elemental charge. The R_S value progressively increases when reducing of H_SOI. Conversely, the mobility progressively decreases until H_SOI ∼ 20 nm, consistent with the idea of increased Coulomb scattering that correlates with the progressive increase in carrier concentration, that is observed taking into account the progressive reduction of H_SOI. These mobility values are perfectly compatible with those reported for bulk Si¹³ as shown in the inset of Fig. 2b. Interestingly, a strong increase in electron mobility is observed when H_SOI < 20 nm, with values higher than those reported for bulk Si. This trend is consistent with data in the literature for highly doped SOI samples and can be explained assuming that H_SOI reduction causes a transition from 3D to quasi-2D Coulomb scattering.²⁰

Fig. 3a depicts a schematic representation of ionized impurities and the effect of Coulomb scattering on an electron moving in a thick or ultra-thin doped SOI. When H_SOI is similar to the average distance between ionized impurities , the number of Coulomb scattering ions surrounding an electron decreases because no ions exist outside the Si device layer plane. The reduced number of neighbor ionized dopants results in reduced Coulomb scattering and leads to enhanced mobility.²⁰ To effectively describe this effect, it is necessary to consider both H_SOI and the concentration of ionized scattering centers. Following the procedure described by Kadotani et al.,²⁰ we consider a new variable defined as H_SOI/d_ave. Interestingly, the relative mobility, i.e. the mobility increase with respect to the mobility expected for bulk Si, is found to increase when decreasing H_SOI/d_ave (Fig. 3b). When H_SOI/d_ave ∼ 1, a significant rise of the relative mobility is observed, with values even double those expected for bulk Si. It is worth noting that data follow the same universal curve irrespective of the annealing temperature, indicating that the model provides a consistent picture of the system. Fig. 3b reports the electron mobility values of the SOI films annealed at 1000 °C for 100 s (red open circles). The results obtained from two other sets of samples are also shown in Fig. 3b. These SOI samples were prepared and characterized following the same sample preparation protocol but varying the temperature of the drive-in process of the dopants from 900 (blue open circles) to 1100 °C (green open circles). The duration of each annealing was properly adjusted to inject into the device layer the same N_D ∼ 1.0 × 10¹³ cm⁻². As shown in Fig. 3b, our experimental data, that were obtained from different sets of samples annealed in different RTP conditions, are fully compatible with those reported by Kadotani et al. (black closed symbols), particularly for the ultra-thin SOI samples, where the increased electron mobility is observed.²⁰

Fig. 3 (a) Schematic representation of ionized impurities and the effect of Coulomb scattering on an electron in a thick or ultra-thin SOI. (b) Relative mobility versus H_SOI/d_ave, for SOI samples upon drive-in at different temperatures. Experimental data obtained in ultra-thin samples upon drive-in of the dopants at 900, 1000, and 1100 °C (open circles) are compared to those reported by Kadotani et al.²⁰ (black closed circles).

Data in Fig. 2a demonstrated a significant η_a reduction for H_SOI < 20 nm. In principle, this η_a reduction could be ascribed to incomplete ionization associated to the variation of P concentration in the conductive channel. Fig. 4 shows the average P concentration in the device layer as obtained by ToF-SIMS analysis. P concentration progressively increases as H_SOI is reduced. The average electron carrier concentration n_e reported in Fig. 4, is derived as the ratio between the N_e value, obtained by Hall measurements, and H_SOI. The model of incomplete ionization proposed by Altermatt et al.²¹ predicts that the fraction of ionized P impurity atoms in bulk Si changes with the concentration of the dopants and exhibits a clear minimum at n_D ∼ 2 × 10¹⁸ atoms cm⁻³. However, the model predicts that more than 80% of the dopants is expected to be ionized and, considering the P concentration range of this work, the percentage of ionized impurities is expected to increase as the P concentration increases, i.e., reducing H_SOI. The P concentration expected to be ionized at room temperature computed using the parametrization of Abenante²² of the model proposed by Altermatt et al.²¹ is shown (red solid line) in Fig. 4. The model correctly predicts, within the experimental error, the values recorded for the SOI samples with H_SOI ≥ 20 nm but does not account for the strong decrease in η_a observed in ultra-thin SOI. When H_SOI < 20 nm, the model developed for bulk Si cannot be directly applied because interface and quantum confinement effects are expected to occur.

Fig. 4 The average P concentration obtained by ToF-SIMS analysis (black) and the carrier concentration computed by Hall measurements (blue) versus H_SOI upon drive-in at 1000 °C. The measured electron concentration corrected considering the effect of the D_IT, the electron concentration predicted by the incomplete ionization model of Altermatt et al.²¹ and the range predicted by the 1D dielectric mismatch model of Bjork et al.²³ corrected considering the reduction of E_I, are shown for comparison.

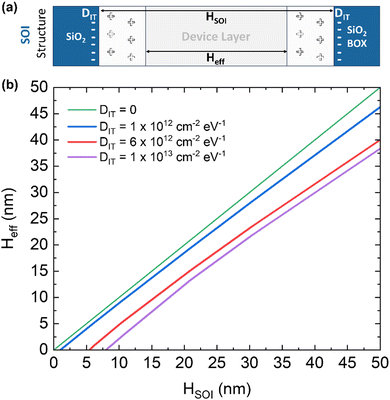
The first interface effect to be considered is the presence of interface state traps between the Si device layer and the surrounding oxides. Fig. 5a shows a scheme elucidating the effect of interface states in n-type-doped SOI. Interface states trap negative charges at the Si/SiO₂ interface, resulting in a depletion of mobile charges near the interface.²⁴ As a result, the effective thickness of the conductive channel (H_eff) is lower than the physical thickness of the device layer (H_SOI). The dimensions of the depleted region can be computed by solving the 1D Poisson equation, assuming both interfaces are identical, considering the full depletion approximation and imposing the charge neutrality condition. Fig. 5b shows H_eff plotted against H_SOI for various density of interface states (D_IT) values. As D_IT increases, H_eff is reduced considerably. It is worth noting that the graph was computed considering the average dopant concentration in the device layer obtained by ToF-SIMS analysis, which increases as H_SOI is reduced. Higher n_D leads to smaller depletion regions created by interface states, ultimately resulting in a small difference between H_SOI and H_eff. Fig. 5b suggests a maximum D_IT value of ∼6 × 10¹² cm⁻² eV⁻¹. Above this threshold value, the model predicts that the 6 nm thick SOI should be fully depleted, resulting in no conduction during the electrical characterization. The correct D_IT value could vary when H_SOI is reduced. In particular, we expect a higher D_IT value as n_D is increased due to the enhanced segregation of the P dopants at the interfaces, potentially causing additional traps and doping-induced defects.²⁵ Additionally, according to the literature, D_IT values between 1 and 6 × 10¹² cm⁻² eV⁻¹ are appropriate for non-passivated Si/SiO₂ interfaces.^26,27

Fig. 5 (a) Schematic representation of the effect of trapped charge carries at the interfaces, reducing the effective thickness of the conductive channel (H_eff). (b) H_effversus H_SOI calculated solving the Poisson equation considering the average P concentration obtained by ToF-SIMS analysis.

Accordingly, to correctly compute the average carrier concentration in the conductive layer, we must divide the Hall dose by H_eff. The corrected carrier concentration value in the conductive channel varies in the blue range shown in Fig. 4, which was computed considering the reduction of H_eff for D_IT values ranging between 1 and 6 × 10¹² cm⁻² eV⁻¹. Fig. 4 clearly indicates that there is no significant difference when comparing the lower limit to the one without any effect of interface states. However, increasing the D_IT to 6 × 10¹² cm⁻² results in a significant increase in the average carrier concentration in the conductive channel. The reduced dimensions of the conductive channel could contribute to the significant η_a reduction observed in Fig. 2a. However, the correct D_IT value may differ from the proposed upper limit, and even after considering the effects of interface states, the experimental data for ultra-thin SOI differ significantly from the values predicted by the model proposed by Altermatt et al.²¹ (Fig. 4).

The second interface effects to be considered is the dielectric mismatch between Si and SiO₂. This effect was highlighted in Si nanowires by Bjork et al.²³ Nanostructures usually exhibit sharp dielectric interfaces with their surroundings. These dielectric mismatches are responsible for significant self-energy corrections to the band structure.²⁸ When an electron is injected into a solid, it repels nearby valence electrons.²⁹ In nanostructures this charge accumulates around the dielectric interfaces in the vicinity of the impurity, leading to an extra term in the Coulomb potential.²⁸ The interaction between the electron and these image charges is responsible for the additional self-energy correction to the band structure. The total charge seen far from the impurity as well as the potential is asymptotically unscreened.³⁰ Diarra et al. theoretically studied dopant deionization due to dielectric mismatch between a nanowire and its surroundings. This additional contribution to the tight-band Hamiltonian leads to a strong increase in the ionization energy of the dopants.³⁰ Using their model, an expression for the change in impurity ionization energy (E_I) with respect to the ionization energy in bulk Si (E^BULK_I) is obtained:

where R is the effective radius of the nanowire, ε_in and ε_out are the dielectric constants of Si and surrounding respectively and F is a function of the dielectric ratio of the wire to the surroundings given by Niquet et al.²⁸

The geometry of our system is planar rather than circular. However, following the 1D parametrization given by eqn (1), that we believe is accounting for the maximum contribution of the dielectric mismatch between Si and the surrounding, it is possible to determine the carrier concentration expected in the conductive channel, considering the contribution of dielectric mismatch. Moreover, in our system, n_D increases when H_SOI is reduced. As a consequence, E^BULK_I cannot be kept constant, as it decreases when n_D is increased.²¹E^BULK_I was then evaluated using the incomplete ionization model of Altermatt et al.²¹ We assume that the two opposite contributions to E_I, caused by the increase in n_D and the effect of dielectric mismatch can be independently determined and that their overall effect can be accounted by a simple additive procedure. The R parameter in eqn (1) was assumed as H_eff/2. The carrier concentration values expected considering the effect of the dielectric mismatch are reported in the bronze range in Fig. 4, for D_IT values between 1 and 6 × 10¹² cm⁻² eV⁻¹. When D_IT increases, H_eff decreases, resulting in a higher E_I correction from eqn (1). Fig. 4 clearly demonstrates that interface effects start to be significant only when H_SOI < 20 nm. Above this thickness value, any variation of the D_IT produces no significant changes. Interestingly, the model significantly underestimates the fraction of ionized P impurities when H_SOI ≥ 20 nm. The same effect was observed in the original paper of Bjork et al., in which less than 30% of dopants were assumed to be ionized at room temperature, even in the case of thick nanowires (R ≥ 30 nm) and high P concentrations (n_D = 3 × 10¹⁹ cm⁻³). In this respect, it is worth noting that the 1D dielectric mismatch parametrization is based on the incomplete ionization model of Xiao et al.,³¹ which assumes a constant E^BULK_I and strongly overestimates the incomplete ionization in bulk Si when n_D > 10¹⁸ cm⁻³.²¹ Correctly, when H_SOI ≥ 20 nm, the experimental results were perfectly described by the incomplete ionization model for bulk Si of Altermatt et al. (red line in Fig. 4) further supporting the idea that above this threshold the system behaves like bulk silicon. Conversely, when H_SOI < 20 nm, E_I rapidly increases, and the proposed model predicts a significant dopant incomplete ionization. In particular, the model underestimates the ionization observed in the 6 nm thick SOI when D_IT = 1 × 10¹² cm⁻² eV⁻¹ but tremendously overestimates the ionization when D_IT = 6 × 10¹² cm⁻² eV⁻¹, with n_e values dropping lower than 3 × 10¹⁶ cm⁻³. In this D_IT range, n_e values predicted by the 1D dielectric mismatch model overlap the n_e values measured and corrected to account for the reduction of H_eff. Consequently, the strong incomplete ionization observed in ultra-thin SOI samples could be tentatively described by the increase in E_I, assuming a D_IT value in the proposed range.

Conclusions

In conclusion, this work investigates the electrical properties of P doped ultra-thin SOI. The annealing treatment efficiently promotes diffusion and incorporation of P atoms in the SOI. If H_SOI ≥ 20 nm, the percentage of active dopants at room temperature is perfectly described by the incomplete ionization model of Altermatt et al.²¹ and the samples behave as bulk-like, perfectly matching the electrical properties of a similarly doped bulk Si substrate.¹¹ If H_SOI < 20 nm, a significant increase in carrier mobility is observed, with values even greater than those reported for bulk Si.¹³ Moreover, a significant dopant incomplete ionization is observed for ultra-thin SOI, with η_a values dropping below 5%. Accordingly, the model developed for bulk Si²¹ must be corrected considering the contribution of interface effects due to depleted regions resulting from interface traps and dielectric mismatch between Si and SiO₂. The proposed model was able to qualitatively describe the experimental data in the case of ultra-thin SOI, but it significantly overestimates the effect of incomplete ionization when H_SOI ≥ 20 nm. A 2D parametrization to account for the dielectric mismatch contribution in planar geometry would be necessary to improve the accuracy of the proposed model and properly discriminate between interface effects and quantum confinement corrections that were not considered in this study, even though they are expected to play a role in SOI samples with H_SOI < 10 nm, i.e. when H_SOI is approximately 2 times the effective Bohr radius of P in Si.³²

Author contributions

Andrea Pulici: writing – original draft, investigation, formal analysis, data curation. Stefano Kuschlan: writing – review & editing, investigation. Gabriele Seguini: writing – review & editing, investigation. Marco De Michielis: writing – review & editing, investigation, formal analysis, data curation. Riccardo Chiarcos: writing – review & editing. Michele Laus: writing – review & editing, supervision. Marco Fanciulli: writing – review & editing, supervision. Michele Perego: writing – original draft, supervision, formal analysis, data curation, conceptualization.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

This work was financially supported by the Italian project DONORS (grant number 2022WBPHKF). The project received funding from the Italian programme for Research Projects of outstanding National Interest (PRIN) in the framework of the National Recovery and Resilience Plan (PNRR).

References

1. H. Mertens, R. Ritzenthaler, A. Hikavyy, M. S. Kim, Z. Tao, K. Wostyn, S. A. Chew, A. De Keersgieter, G. Mannaert, E. Rosseel, T. Schram, K. Devriendt, D. Tsvetanova, H. Dekkers, S. Demuynck, A. Chasin, E. Van Besien, A. Dangol, S. Godny, B. Douhard, N. Bosman, O. Richard, J. Geypen, H. Bender, K. Barla, D. Mocuta, N. Horiguchi and A. V.-Y. Thean, 2016 IEEE Symposium on VLSI Technology, 2016, pp. 1–2.
2. M. G. Bardon, Y. Sherazi, D. Jang, D. Yakimets, P. Schuddinck, R. Baert, H. Mertens, L. Mattii, B. Parvais, A. Mocuta and D. Verkest, 2018 IEEE Symposium on VLSI Technology, 2018, pp. 143–144.
3. P. Ye, T. Ernst and M. V. Khare, IEEE Spectr., 2019, 56, 30–35.
4. R. Duffy, F. Meaney and E. Galluccio, ECS Meet. Abstr., 2020, MA2020-01, p. 1316.
5. M. Perego, C. Bonafos and M. Fanciulli, Nanotechnology, 2009, 21, 025602.
6. E. Arduca and M. Perego, Mater. Sci. Semicond. Process., 2017, 62, 156–170.
7. Z. Sun, O. Hazut, B.-C. Huang, Y.-P. Chiu, C.-S. Chang, R. Yerushalmi, L. J. Lauhon and D. N. Seidman, Nano Lett., 2016, 16, 4490–4500.
8. J. M. Yang, J. Lee, T.-E. Park, D. Seo, J. M. Park, S. Park, J. Na, J. Kwon, H.-J. Lee, J. Ryu and H.-J. Choi, Electron. Mater. Lett., 2019, 15, 208–215.
9. C. Barri, E. Mafakheri, L. Fagiani, G. Tavani, A. Barzaghi, D. Chrastina, A. Fedorov, J. Frigerio, M. Lodari, F. Scotognella, E. Arduca, M. Abbarchi, M. Perego and M. Bollani, Nanotechnology, 2020, 32, 025303.
10. M. Perego, G. Seguini, E. Arduca, A. Nomellini, K. Sparnacci, D. Antonioli, V. Gianotti and M. Laus, ACS Nano, 2018, 12, 178–186.
11. A. Pulici, S. Kuschlan, G. Seguini, F. Taglietti, M. Fanciulli, R. Chiarcos, M. Laus and M. Perego, Mater. Sci. Semicond. Process., 2023, 163, 107548.
12. M. Perego, F. Caruso, G. Seguini, E. Arduca, R. Mantovan, K. Sparnacci and M. Laus, J. Mater. Chem. C, 2020, 8, 10229–10237.
13. S. M. Sze and K. K. Ng, Physics of Semiconductor Devices, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2006.
14. V. Gianotti, D. Antonioli, K. Sparnacci, M. Laus, C. Cassino, F. Marsano, G. Seguini and M. Perego, J. Anal. Appl. Pyrolysis, 2017, 128, 238–245.
15. M. Perego, S. Kuschlan, G. Seguini, R. Chiarcos, V. Gianotti, D. Antonioli, K. Sparnacci and M. Laus, ACS Appl. Polym. Mater., 2021, 3, 6383–6393.
16. R. Chiarcos, M. Laus and M. Perego, Eur. Polym. J., 2024, 208, 112849.
17. L. J. van der PAUW, Semiconductor Devices: Pioneering Papers, World Scientific, 1991, pp. 174–182.
18. M. Mastromatteo, E. Arduca, E. Napolitani, G. Nicotra, D. De Salvador, L. Bacci, J. Frascaroli, G. Seguini, M. Scuderi, G. Impellizzeri, C. Spinella, M. Perego and A. Carnera, Surf. Interface Anal., 2014, 46, 393–396.
19. A. Fick, Ann. Phys., 1855, 170, 59–86.
20. N. Kadotani, T. Takahashi, T. Ohashi, S. Oda and K. Uchida, J. Appl. Phys., 2011, 110, 034502.
21. P. P. Altermatt, A. Schenk and G. Heiser, J. Appl. Phys., 2006, 100, 113714.
22. L. Abenante, AIP Adv., 2023, 13, 015109.
23. M. T. Björk, H. Schmid, J. Knoch, H. Riel and W. Riess, Nat. Nanotechnol., 2009, 4, 103–107.
24. V. Schmidt, S. Senz and U. Gösele, Appl. Phys. A: Mater. Sci. Process., 2007, 86, 187–191.
25. J. Snel, Solid-State Electron., 1981, 24, 135–139.
26. H. Angermann, Th Dittrich and H. Flietner, Appl. Phys. A: Mater. Sci. Process., 1994, 59, 193–197.
27. W. Lu, C. Leendertz, L. Korte, J. A. Töfflinger and H. Angermann, Energy Procedia, 2014, 55, 805–812.
28. Y. M. Niquet, A. Lherbier, N. H. Quang, M. V. Fernández-Serra, X. Blase and C. Delerue, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165319.
29. J. C. Inkson, Many-Body Theory of Solids, Springer US, Boston, MA, 1984.
30. M. Diarra, Y.-M. Niquet, C. Delerue and G. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045301.
31. G. Xiao, J. Lee, J. J. Liou and A. Ortiz-Conde, Microelectron. Reliab., 1999, 39, 1299–1303.
32. J. W. Orton, The Story of Semiconductors, OUP, Oxford, 2004.

---