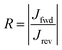DOI:
10.1039/D4TC01807A
(Paper)
J. Mater. Chem. C, 2024,
12, 15588-15595
Temperature dependence of charge transport in molecular ensemble junctions†
Received
2nd May 2024
, Accepted 27th August 2024
First published on 28th August 2024
Abstract
Understanding charge transport across molecule–electrode interfaces is essential for advancing organic electronic devices, yet its underlying mechanisms remain incompletely understood. Here, we investigate the temperature dependence of conductivity in molecular junctions under various biasing regimes. By examining devices with both low and high current rectification, we identify the conditions leading to temperature-activated transport and the less common phenomenon where conductance decreases with increasing temperature. The current increase with temperature is consistent with previous findings in similar systems and is attributed to thermally assisted tunneling and incoherent tunneling processes. Notably, the discovery of the regime with a negative temperature coefficient for conductance provides the first experimental validation of theoretical frameworks that unify Landauer formalism with Marcus theory, which we attribute to entropic effects influencing the molecular conformation. These measurements have also captured the emergence of new electronic states arising from the co-assembly of molecules containing electron donor and acceptor moieties. Our results decipher key aspects related to charge transport in molecular junctions and leveraging these insights holds significant promise for accelerating the development of more complex devices that exploit electrode–molecule interfaces for tunable functionality.
Introduction
Molecular junctions are simplified test structures that facilitate the study of charge transport at molecule–electrode interfaces, a critical phenomenon underlying the function of diverse electronic devices, including field-effect transistors, light-emitting diodes, memristors and more.1–4 In the field of molecular electronics alone, an impressive number of functionalities that rely on the processes occurring at molecule–electrode interfaces have been developed, including molecular diodes,5–7 sensors,8–10 molecular transistors,11 memory,12–18 and other optoelectronic devices.19–21 Given the channel dimensions in these devices (3 nm or less), coherent tunneling, as described by the Landauer formalism, is considered the dominant charge transport mechanism.22–24 The signature of coherent tunneling is a temperature independent charge transport. Consequently, any observed temperature dependence of conductivity within these length scales is typically attributed to extrinsic factors such as contact effects and thermally assisted tunneling caused by the thermal broadening of the Fermi distribution of the electrodes and molecular orbitals.25–28 At slightly larger length-scales, in the range 4–7 nm, incoherent tunneling, described by Marcus theory, becomes dominant.29–33 This mechanism involves thermally activated charge transport that proceeds via a sequence of nuclear tunneling events. Recently, however, deviations from these conventions have been reported, with proteins exhibiting long range tunneling up to 7 nm,34,35 and thermally activated transport being found in molecular rectifiers at length scales shorter than 3 nm.5,36,37 Indeed, the temperature dependence of charge transport in molecular junctions is complex and depends both on the magnitude and polarity of the applied bias.38 Control of these rich dependencies has led to the design and engineering of novel device functionalities,36,37,39 and enabled highly efficient current rectification where coherent tunneling dominates transport during one polarity of the voltage and incoherent tunneling governs the opposite one.5,37 Temperature independent incoherent tunneling has also been observed in gated structures, where the magnitude of the applied voltage controls the transition from the direct to the inverted Marcus regimes.36,37 The apparently conflicting reports on temperature dependence of charge transport in molecular junctions underscore the critical need for a deeper understanding of the fundamental nanoscale processes governing this phenomenon. Such knowledge is essential for the development of novel electronic devices and the optimization of existing ones.
In this study, we conduct a detailed investigation of the temperature dependence of charge transport across molecular junctions, specifically focusing on devices exhibiting both low and high rectification behavior. Our measurements revealed distinct transport mechanisms in the studied self-assembled monolayers (SAMs) depending on temperature range, the magnitude and sign of the applied voltage and the structure of the rectifying molecule. Under reverse bias, transport is dominated by coherent tunneling in aliphatic non-rectifying SAMs, a mechanism with minimal temperature dependence outside of the effects of thermally assisted tunnelling near resonance. In contrast, forward bias exhibits thermally activated transport over a wider voltage range, either indicative of multiple conductive molecular orbitals or of incoherent tunneling. A similar thermally activated tunneling was observed in the forward bias regime when we measured an efficient molecular rectifier based on an aromatic SAM. Interestingly, under reverse bias, we found voltage regimes where transport was characterized by a negative temperature coefficient. We attributed this rarely observed temperature response to temperature-induced entropic effects within the molecular ensemble junction (MEJ). Essentially, at high temperatures the molecules gain more conformational freedom, and charging of the polarizable tail groups within the SAM impacts the voltage dependence of the activation energy. The observed temperature and voltage dependence of charge transport aligns well with the theoretical framework proposed by Sowa and Marcus,40,41 which combines Marcus theory with the Landauer formalism; however, more quantitative analysis is needed to confirm this agreement. We further investigated SAMs formed by co-assembling molecules with electron donor and acceptor groups, where the formation of charge transfer (CT) states between the two SAMs has been shown to enhance rectification.42 We found that the presence of CT influences the temperature response of the mixed SAMs, where a 0.3 V shift in the bias at which the junction reaches resonance was observed. This shift reflects the altered position of the key molecular orbital involved in transport relative to the Fermi energy, implying that resonance will occur at a higher bias, leading to enhanced molecular rectification. Our findings provide insights into the complex phenomena occurring at molecule–electrode interfaces, thus advancing molecular electronics and related fields.
Experimental
Molecular ensemble junctions were investigated in metal–SAM–metal configurations utilizing EGaIn (eutectic gallium–indium) as the top electrode and degenerately doped n-type silicon substrates (resistivity of 0.001 to 0.005 Ω cm) capped with a (∼2 nm) native oxide layer as the bottom electrode (Fig. 1a). The molecules self-assembled on the native oxide and MEJs were formed with nearly 100% yields, while also avoiding expensive electrode evaporation and/or template-stripping processes.7,43 Before SAM deposition, the Si substrates were cleaned using a previously reported procedure:43 the Si substrates were diced with dimensions of 1 × 1 cm2, submerged in acetone at 85 °C for 10 min, and immediately rinsed with acetone and isopropyl alcohol (IPA). Then they were submerged in IPA at 85 °C for 10 min, followed by an IPA rinse and dried using a nitrogen stream. Next, the substrates were exposed to ultraviolet ozone for 10 min, rinsed with deionized water, and dried again with a stream of nitrogen. This cleaning procedure effectively removes surface contaminants to facilitate SAM deposition without significantly altering the native silicon oxide layer on the highly doped silicon substrate.43 SAM deposition has been performed following the procedures previously established and optimized to ensure the formation of a high-quality monolayer, with minimal byproducts.7,10,42,44,45 The clean substrates were placed in glass containers filled with 7 mM SAM solutions in chloroform inside a nitrogen glovebox (O2 < 0.1 ppm, H2O < 0.1 ppm). After approximately 16–20 hours, the samples were thoroughly rinsed with chloroform, then IPA, and finally dried again with nitrogen.
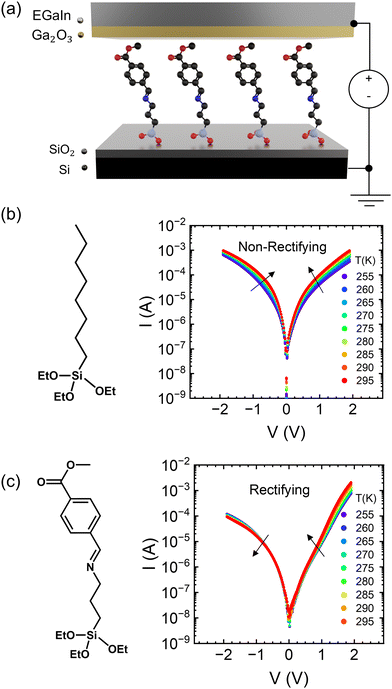 |
| | Fig. 1 (a) Device structure of molecular ensemble junctions. (b) Molecular structure and current–voltage characteristics as a function of temperature in the OTES non-rectifying SAM. (c) Molecular structure and current–voltage characteristics as a function of temperature in the CMPTM rectifying SAM. | |
Two different SAMs have been studied as model systems. The first one (n-octyltriethoxysilane, referred to as OTES) (Fig. 1b) consists of a triethoxysilane head connected to a long aliphatic chain. Typical current–voltage characteristics measured on this SAM are presented in Fig. 1b. Current rectification is quantified by the rectification ratio:
where
Jfwd is the current density under a forward bias and
Jrev is the current density at the same bias magnitude, but at the opposite polarity. We will refer to this compound as a “non-rectifying SAM” since its does not rectify current when included in a molecular junction (
R ≈ 1). The second SAM efficiently rectifies current and thus is a “rectifying SAM”, with
R ≈ 1000.
42 It consists of a similar head, but has a substituted aromatic tail with a sigma-bonded decoupling bridge ((
E)-1-(4-carbomethoxy-phenyl)
N-(3-(triethoxysilyl)propyl)methanimine, CMPTM) (
Fig. 1c).
42 Details on the synthesis and characterisation of SAMs have been reported elsewhere.
46 The MEJs were electrically characterized in dark, under vacuum, in a Lake Shore Cryotronics TTPX cryogenic probe station, using a Keithly 2614B Source Meter. The bottom electrode was grounded, and the voltage was swept from 0 to 2 V to record the forward bias response, followed by 0 to −2 V for the reverse bias. Hence, electrons are injected from the bottom electrode in the forward bias regime, and from the top during reverse bias.
Results and discussion
In Fig. 1b we show the temperature dependence of current at different voltages for the non-rectifying SAM. It can be observed that charge transport exhibits a positive temperature dependence regardless of voltage polarity. In contrast, the rectifying SAM displays distinct temperature responses depending on the bias regime: the forward bias current increases with temperature, whereas the reverse bias current decreases with increasing temperature (Fig. 1c). To better understand the temperature response of our molecular junctions, Arrhenius plots were generated for both sample types. Fig. 2a depicts the current density J in forward bias for the non-rectifying SAM, while Fig. 2b shows J for the rectifying SAM under the same conditions. Similarly, Fig. 2c and d include the corresponding results acquired in the reverse bias sweep. The y-axis data were normalized with respect to the value recorded at 250 K (lowest temperature) and each curve corresponds to a different applied voltage. In the positive bias regime (Fig. 2a and b), both SAMs display similar temperature-activated behavior of the current, with a progressively more pronounced response at higher voltages. Under the reverse bias (Fig. 2c and d) the dependence of current on temperature of the two types of SAMs differs significantly. The OTES non-rectifying SAM junctions exhibit temperature activated behavior throughout the tested voltage range, albeit with a complex interplay between activation energy and applied bias (Fig. 2c). Conversely, the rectifying CMPTM SAMs display a gradual transition from a positive to negative temperature response with increasing negative bias (Fig. 2d). To quantify the changes in the current with temperature shown in Fig. 2a–d, we calculated the activation energy Ea in each SAMs by using the Arrhenius expression:
Ea = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[J/J0] ln[J/J0] |
where kB is the Boltzmann constant and T is temperature. The dependence of activation energy on the applied voltage is shown in Fig. 2e and f for the OTES and CMPTM, respectively. All activation energies are the average of 3 or more junctions. In the non-rectifying SAM, (Fig. 2e) at low bias voltages the activation energy initially increases with increasing voltage, but then this trend reverses at higher voltages. The dashed vertical lines indicate the boundaries between the different regimes, where region I marks the off-resonant regime, II is near-resonant regime, and III is resonant regime. We illustrate the negative temperature response in Fig. 2d as a ‘negative activation energy’ in Fig. 2f; however, this is for convenience purposes only and we make no implications that a negative activation energy is characteristic to these devices. This region corresponds to regime IV, which only occurs in the rectifying SAMs and corresponds to the off-resonant regime in the presence of entropic effects, as we will describe below.
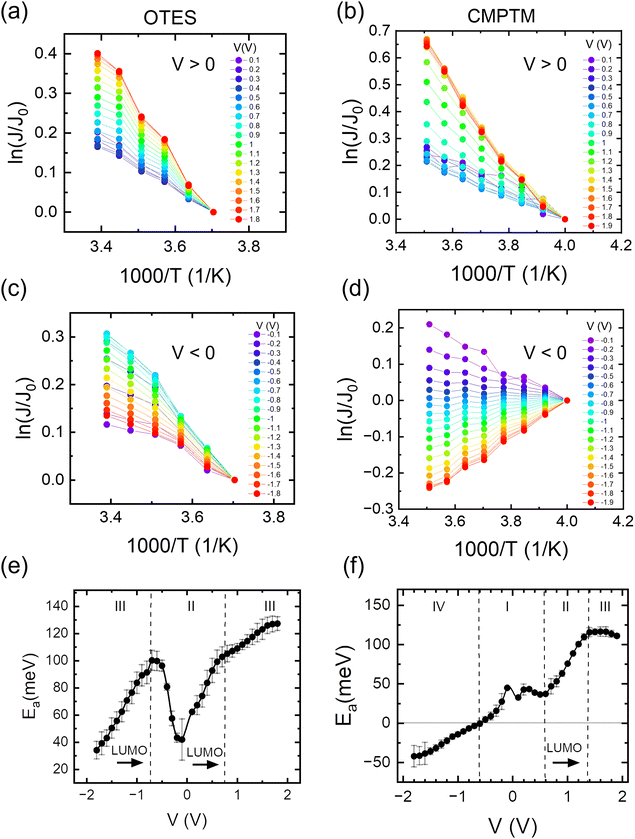 |
| | Fig. 2 Arrhenius plots in the OTES (a) and (c) and CMPTM (b) and (d) SAM, respectively. The weighted average of the activation energies versus voltage calculated from the corresponding Arrhenius plots for the OTES (e) and CMPTM (f) SAMs. Label I represents off-resonant regime, II is near-resonant regime, III is resonant regime and IV is off-resonant regime in the presence of entropic effects. | |
To understand these graphs, we will first refer to the relevant theories of charge transport. Traditionally, transport in molecular ensembles has been described as coherent tunneling using the Landauer Formalism.22–24 Within this framework, the current–voltage (I–V) relationship is expressed by the following equation:
| | 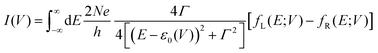 | (1) |
where
N represents the total number of molecules,
Γ is the electrode/molecule coupling constant,
E is energy and
ε0 is the energetic position of the molecular orbital responsible for facilitating transport: the HOMO (highest occupied molecular orbital) or LUMO (lowest unoccupied molecular orbital).
fL(
E;
V) and
fR(
E;
V) are the Fermi distributions of the left and right electrodes, respectively. This model attributes current rectification to the asymmetric bias-induced shift of the conductive molecular orbital,
ELUMO(
V) =
ELUMO +
γeV where
γ is the orbital shift coefficient. For the case of incoherent charge transport, following Marcus theory, the electron transfer rates are:
40,47,48| | 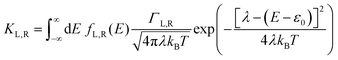 | (2a) |
and
| |  | (2b) |
where
KL,R is the electron transfer rate onto the molecule,
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) L,R
L,R is the electron transfer rate onto the electrode,
λ is reorganization energy, and assuming
ΓL,R is constant with energy. The two theories have been unified by Sowa and Marcus in a generalized equation where the charge transfer rate is defined by:
40,41| | 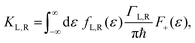 | (3a) |
| | 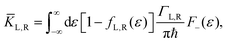 | (3b) |
and
| | 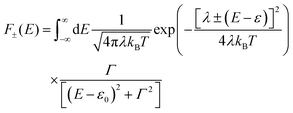 | (3c) |
where
Γ is the average electrode/molecule coupling constant (
Γ = (
ΓL +
ΓR)/2). In
Fig. 3a–c we show the different energetic landscapes that give rise to the
Ea evolution presented in
Fig. 2. Here we assume that the LUMO acts as the orbital facilitating charge transport (the interpretation would remain consistent if the transport were instead mediated by the HOMO). S and T label the energy levels of the bottom electrode (substrate) and top electrode, respectively, when an external voltage is applied. Considering resonant tunneling as the dominant transport mechanism, the conductance of the molecular junction depends on the tunneling probability and transport is more efficient when the energy level of the molecular orbital lies within the transmission window. Consequently, the relative placement of this orbital to the electrode energy levels plays a critical role in determining the temperature dependence of charge transport. For a comprehensive description of the application of the single-level model to describe the
I–
V characteristics in molecular junctions, we recommend the insightful perspective recently published by Frisbie and collaborators.
38 When the orbital resides outside of the transmission window (
Fig. 3a) the system operates in the off-resonance regime and charge transport exhibits minimal temperature dependence (
eqn (3)), resembling coherent tunneling. This behavior contrasts with Marcus theory, which predicts a strong temperature dependence even under off-resonant conditions.
41 As the applied bias shifts the conductive orbital closer to the transmission window (
Fig. 3b), the junction transitions to a near-resonance regime, where small variations in the Fermi level broadenings of the electrodes and conductive orbitals can lead to significant temperature responses in coherent tunneling referred as thermally assisted tunneling. This behavior is also reflected in
eqn (3), which predicts an increase in activation energy within the near-resonance regime. Once the molecular orbitals are placed deep within the transmission window (
Fig. 3c), the system enters the resonance regime, where thermal effects on tunneling become negligible, resulting in a weak temperature dependence.
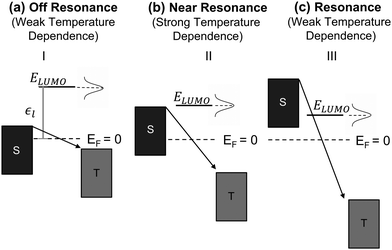 |
| | Fig. 3 Energetic landscape of charge transport in a molecular junction governed by eqn (3) when LUMO is the orbital responsible for facilitating transport. ε1 represents the energetic position of LUMO, which is placed off resonance in panel (a), near resonance in (b), and in resonance (c). | |
In the following, we will analyze the voltage dependence of Ea depicted in Fig. 2e and f by invoking the energetic landscapes described in Fig. 3. While recognizing the importance of contact effects, we will consider a simplified model that excludes their contribution. The OTES molecule is characterized by a small γ and ε0,44 thus, based on eqn (1), at low bias the LUMO enters the near-resonance regime independent of the polarity of the voltage. Indeed, Fig. 2e (regime II) shows a sharp rise in Ea as the voltage |V| increases from 0 V to ∼±0.7 V, which is consistent with the energy level diagram in Fig. 3b. As the voltage becomes more negative, the LUMO transitions towards resonance (regime III), where transport is governed by eqn (3) and corresponds to the energy picture in Fig. 3c. Consequently, Ea exhibits a gradual decline. This behavior aligns with thermally assisted coherent transport, but contradicts Marcus theory which predicts the highest activation energy in the off-resonant regime, steadily decreasing towards resonance.41 Interestingly, a similar response is observed when a molecule enters the inverted Marcus regime, which is unexpected for non-redox active molecules like OTES.37 At the other side of regime II, when V > 0.7 V, the molecular orbital is approaching resonance and the system enters regime III of the forward bias. The minor increase in Ea suggests that other molecular orbitals also participate in transport and their relative alignment with the electrode Fermi levels contributes to Ea. The small difference in Ea in the forward and reverse bias resonant regimes is attributed to the non-zero γ, which can cause a higher-energy orbital to enter the transmission window under one bias but not the other.44
The rectifying SAM, CMPTM, is characterized by a larger γ and ε0 (εl in this case since LUMO facilitates transport) compared to OTES, which promotes a clear off-resonance regime (Fig. 3a) in the low voltage range, with minimal temperature dependence – regime I of Fig. 2f.44 Under forward bias conditions, Ea gradually increases in the voltage interval 0.6 V < V < 1.4 V, suggesting that the system transitions to the near-resonance condition (Fig. 3b), as indicated by regime II of Fig. 2f. After that point, the LUMO enters resonance (Fig. 3c), as confirmed by the negligible dependence of Ea on the applied voltage.36 Under reverse bias (negative voltage), the LUMO resides permanently in the off-resonant regime. Under the assumption of purely coherent tunneling, this regime typically exhibits negligible temperature dependence. However, our measurements consistently reveal a negative temperature coefficient in this regime, marked as a negative Ea, as shown in Fig. 2f (regime IV). Negative temperature response, while less common, have been previously observed in alkyl monolayers,49 and attributed to the temperature-dependent structural changes within the SAMs. Upon cooling, the SAMs became more rigid and adopted a straighter conformation. This transformation led to an increase in the number of conducting molecules (N) within the junction and a reduction in average tilt angle, ultimately reducing the overall SAM thickness (Fig. S1, ESI†). Collectively, these processes effectively reduced the entropy, S, of the system, resulting in the observed negative temperature response.49 While we suspect that similar temperature-dependent conformational changes occur in our SAMs, given the distinct nature of the molecule–substrate interface in our system, a direct comparison is difficult and additional experimental characterization is necessary to definitively validate this hypothesis. The presence of aromatic rings in the structure of CMPTM enhances the intermolecular interactions between neighboring molecules through π–π stacking. Since the negative temperature response was shown to be driven by van der Waals interactions between neighboring molecules within alkyl SAMs, it is not surprising that CMPTM SAMs produce an enhanced temperature response. The bias-sensitivity of the negative Ea in our samples can be attributed to local heating effects, biased-sensitive molecule–electrode couplings,50 and/or to effects induced from the charging of the tail groups. A bias-induced dependence of N on V has been found in high-performance molecular rectifiers,5 and adopted to model current–voltage characteristics in CMPTM.44 These findings support the hypothesis that temperature-induced structural changes should be considered when modeling rectification within MEJs with aromatic molecular structures. We recognize that the temperature-dependent conductivity observed in our SAMs near and during resonance could also be interpreted within the theoretical framework proposed by Migliore et al.51,52 While the Marcus–Sowa generalized theory appears to better describe the data across all regimes (off-resonant, near-resonant, and resonant), a definitive assessment of the relative merits of these models would necessitate quantitative modelling of the experimental data and comprehensive analysis.
Next, we will examine the temperature response of mixed SAMs. Co-assembling SAMs terminated with strong electron donor and acceptor termini is a versatile tool for tuning the properties of molecular assemblies by manipulating the resulting CT state.42 For example, we have shown that a charge transfer process between the electron-donor moiety of (3-aminopropyl)triethoxysilane (APTES) and the electron-acceptor moiety of CMPTM enhances the rectifying properties of the mixed SAM.42 The efficiency of charge transfer is influenced by the spatial proximity of donor and acceptor molecules within the mixed SAMs. While achieving absolute control over the arrangement of molecules within the monolayer is challenging, our fabrication methods have been optimized to promote a well-mixed monolayer and mitigate the formation of large-scale phase separation or island formation. To test the temperature response in the presence of a CT state, CMPTM was co-assembled with APTES at a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 ratio (Fig. 4a). The temperature dependence of the current in the mixed SAMs is plotted in Fig. 4b. Generally, the behavior is similar to that of pure CMPTM, but subtle differences are clearly observed in the dependence of the Ea on V, especially for regimes II (near-resonance) and III (resonance) within the forward bias, which we are comparing in Fig. 4c. Specifically, we found a consistent shift of ∼0.3 V in the voltage point where the Ea plateaus, with the transition point occurring at higher voltage values in the mixed SAMs. This suggests that the transition from near-resonance to resonance is occurring at higher voltages in the mixed SAMs since the facilitating molecular orbital is placed further away from the Fermi energy of the contacts. A significant increase in εl would effectively increase the width of the off-resonant regime of the molecular rectifier (Fig. 3a), leading to a reduction in the reverse bias current. These findings are in agreement with previous observations that the addition of APTES results in a new electronic state within the SAM that enhances molecular rectification.
30 ratio (Fig. 4a). The temperature dependence of the current in the mixed SAMs is plotted in Fig. 4b. Generally, the behavior is similar to that of pure CMPTM, but subtle differences are clearly observed in the dependence of the Ea on V, especially for regimes II (near-resonance) and III (resonance) within the forward bias, which we are comparing in Fig. 4c. Specifically, we found a consistent shift of ∼0.3 V in the voltage point where the Ea plateaus, with the transition point occurring at higher voltage values in the mixed SAMs. This suggests that the transition from near-resonance to resonance is occurring at higher voltages in the mixed SAMs since the facilitating molecular orbital is placed further away from the Fermi energy of the contacts. A significant increase in εl would effectively increase the width of the off-resonant regime of the molecular rectifier (Fig. 3a), leading to a reduction in the reverse bias current. These findings are in agreement with previous observations that the addition of APTES results in a new electronic state within the SAM that enhances molecular rectification.
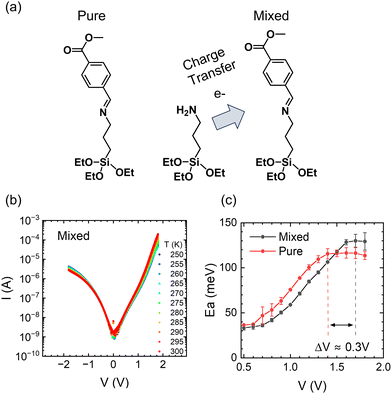 |
| | Fig. 4 Schematic of CT occurring between co-assembled CMPTM/APTES molecules (a). The current–voltage characteristics as a function of temperature for the mixed SAMs of CMPTM:APTES (b) along with the corresponding activation energies (c). | |
Conclusions
In summary, we employed temperature-dependent conductivity measurements to investigate the charge transport mechanisms in rectifying and non-rectifying SAMs. We explained the observed activation energy dependence on voltage by considering the interplay between the participating molecular orbital's energy level, its relative position to electrode Fermi levels, and their respective shifts under applied bias. We identified both resonant and near-resonant regimes in both SAMs. Notably, the off-resonant regime was only observed in the rectifying SAM, attributed to its larger orbital shift coefficient and greater energy difference compared to the electrode Fermi level. We also discovered significant entropic effects in the off-resonant regime of the rectifying SAM, supporting the hypothesis that the number of conducting molecules depends on the applied bias and temperature. The temperature and voltage dependence of current observed in our molecular junctions have been discussed within the theoretical frameworks combining Landauer formalism with Marcus theory. Remarkably, these measurements have proven sufficiently sensitive to detect the energetic shift of the facilitating molecular orbital induced by the presence of charge transfer states in a co-assembled donor–acceptor SAM. These findings offer valuable insights into charge transport mechanisms within molecule–electrode junctions. Such knowledge is critical not only for the development of novel and improved molecular-scale electronic devices, but also for the progress of all optoelectronic devices, which rely on the complex processes occurring at the molecule–electrode interfaces.
Author contributions
The manuscript was written through contribution of all authors. All authors have given approval to the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was partially supported by the National Science Foundation under award ECCS-1810273.
References
- D. M. Adams, L. Brus, C. E. D. Chidsey, S. Creager, C. Creutz, C. R. Kagan, P. V. Kamat, M. Lieberman, S. Lindsay, R. A. Marcus, R. M. Metzger, M. E. Michel-Beyerle, J. R. Miller, M. D. Newton, D. R. Rolison, O. Sankey, K. S. Schanze, J. Yardley and X. Zhu, J. Phys. Chem. B, 2003, 107, 6668–6697 CrossRef CAS.
- V. R. I. Kaila, J. R. Soc., Interface, 2018, 15, 20170916 CrossRef PubMed.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- N. Amdursky, D. Marchak, L. Sepunaru, I. Pecht, M. Sheves and D. Cahen, Adv. Mater., 2014, 26, 7142–7161 CrossRef CAS.
- X. Chen, M. Roemer, L. Yuan, W. Du, D. Thompson, E. del Barco and C. A. Nijhuis, Nat. Nanotechnol., 2017, 12, 797–803 CrossRef CAS PubMed.
- L. Yuan, R. Breuer, L. Jiang, M. Schmittel and C. A. Nijhuis, Nano Lett., 2015, 15, 5506–5512 CrossRef CAS PubMed.
- Z. A. Lamport, A. D. Broadnax, B. Scharmann, R. W. Bradford, A. DelaCourt, N. Meyer, H. Li, S. M. Geyer, T. Thonhauser, M. E. Welker and O. D. Jurchescu, ACS Appl. Mater. Interfaces, 2019, 11, 18564–18570 CrossRef CAS.
- H. Atesci, V. Kaliginedi, J. A. C. Gil, H. Ozawa, J. M. Thijssen, P. Broekmann, M. Haga and S. J. van der Molen, Nat. Nanotechnol., 2018, 13, 117–121 CrossRef CAS PubMed.
- C. W. Fuller, P. S. Padayatti, H. Abderrahim, L. Adamiak, N. Alagar, N. Ananthapadmanabhan, J. Baek, S. Chinni, C. Choi, K. J. Delaney, R. Dubielzig, J. Frkanec, C. Garcia, C. Gardner, D. Gebhardt, T. Geiser, Z. Gutierrez, D. A. Hall, A. P. Hodges, G. Hou, S. Jain, T. Jones, R. Lobaton, Z. Majzik, A. Marte, P. Mohan, P. Mola, P. Mudondo, J. Mullinix, T. Nguyen, F. Ollinger, S. Orr, Y. Ouyang, P. Pan, N. Park, D. Porras, K. Prabhu, C. Reese, T. Ruel, T. Sauerbrey, J. R. Sawyer, P. Sinha, J. Tu, A. G. Venkatesh, S. VijayKumar, L. Zheng, S. Jin, J. M. Tour, G. M. Church, P. W. Mola and B. Merriman, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2112812119 CrossRef CAS PubMed.
- R. P. Sullivan, E. Castellanos-Trejo, R. Ma, M. E. Welker and O. D. Jurchescu, Nanoscale, 2023, 15, 171–176 RSC.
- E. C. P. Smits, S. G. J. Mathijssen, P. A. van Hal, S. Setayesh, T. C. T. Geuns, K. A. H. A. Mutsaers, E. Cantatore, H. J. Wondergem, O. Werzer, R. Resel, M. Kemerink, S. Kirchmeyer, A. M. Muzafarov, S. A. Ponomarenko, B. de Boer, P. W. M. Blom and D. M. de Leeuw, Nature, 2008, 455, 956–959 CrossRef CAS.
- J. E. Green, J. Wook Choi, A. Boukai, Y. Bunimovich, E. Johnston-Halperin, E. DeIonno, Y. Luo, B. A. Sheriff, K. Xu, Y. Shik Shin, H.-R. Tseng, J. F. Stoddart and J. R. Heath, Nature, 2007, 445, 414–417 CrossRef CAS PubMed.
- F. Schwarz, G. Kastlunger, F. Lissel, C. Egler-Lucas, S. N. Semenov, K. Venkatesan, H. Berke, R. Stadler and E. Lörtscher, Nat. Nanotechnol., 2016, 11, 170–176 CrossRef CAS.
- Y. Han, C. Nickle, Z. Zhang, H. P. A. G. Astier, T. J. Duffin, D. Qi, Z. Wang, E. del Barco, D. Thompson and C. A. Nijhuis, Nat. Mater., 2020, 19, 843–848 CrossRef CAS PubMed.
- S. Kumar, M. Merelli, W. Danowski, P. Rudolf, B. L. Feringa and R. C. Chiechi, Adv. Mater., 2019, 31, 1807831 CrossRef PubMed.
- M. Carlotti, S. Soni, S. Kumar, Y. Ai, E. Sauter, M. Zharnikov and R. C. Chiechi, Angew. Chem., 2018, 130, 15907–15911 CrossRef.
- M. C. Walkey, C. R. Peiris, S. Ciampi, A. C. Aragonès, R. B. Domínguez-Espíndola, D. Jago, T. Pulbrook, B. W. Skelton, A. N. Sobolev, I. Díez Pérez, M. J. Piggott, G. A. Koutsantonis and N. Darwish, ACS Appl. Mater. Interfaces, 2019, 11, 36886–36894 CrossRef CAS PubMed.
- Y. Liu, X. Qiu, S. Soni and R. C. Chiechi, Chem. Phys. Rev., 2021, 2, 021303 CrossRef.
- C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445 CrossRef CAS.
- W. Du, T. Wang, H.-S. Chu, L. Wu, R. Liu, S. Sun, W. K. Phua, L. Wang, N. Tomczak and C. A. Nijhuis, Nat. Photonics, 2016, 10, 274–280 CrossRef CAS.
- M. Galperin and A. Nitzan, Phys. Chem. Chem. Phys., 2012, 14, 9421–9438 RSC.
- B. S. Kim, J. M. Beebe, Y. Jun, X.-Y. Zhu and C. D. Frisbie, J. Am. Chem. Soc., 2006, 128, 4970–4971 CrossRef CAS PubMed.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. Daniel Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801 CrossRef.
- Z. Xie, I. Bâldea and C. D. Frisbie, J. Am. Chem. Soc., 2019, 141, 3670–3681 CrossRef CAS.
- M. Poot, E. Osorio, K. O’Neill, J. M. Thijssen, D. Vanmaekelbergh, C. A. van Walree, L. W. Jenneskens and H. S. J. van der Zant, Nano Lett., 2006, 6, 1031–1035 CrossRef CAS.
- S. H. Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486 CrossRef CAS.
- M. Kamenetska, J. R. Widawsky, M. Dell’Angela, M. Frei and L. Venkataraman, J. Chem. Phys., 2017, 146, 092311 CrossRef.
- H. B. Li, Y.-F. Xi, Z.-W. Hong, J. Yu, X.-X. Li, W.-X. Liu, L. Domulevicz, S. Jin, X.-S. Zhou and J. Hihath, ACS Sens., 2021, 6, 565–572 CrossRef CAS.
- Q. Lu, K. Liu, H. Zhang, Z. Du, X. Wang and F. Wang, ACS Nano, 2009, 3, 3861–3868 CrossRef CAS PubMed.
- T. Hines, I. Diez-Perez, J. Hihath, H. Liu, Z.-S. Wang, J. Zhao, G. Zhou, K. Müllen and N. Tao, J. Am. Chem. Soc., 2010, 132, 11658–11664 CrossRef CAS.
- D. Taherinia, C. E. Smith, S. Ghosh, S. O. Odoh, L. Balhorn, L. Gagliardi, C. J. Cramer and C. D. Frisbie, ACS Nano, 2016, 10, 4372–4383 CrossRef CAS.
- A. Vilan, D. Aswal and D. Cahen, Chem. Rev., 2017, 117, 4248–4286 CrossRef CAS.
- Q. V. Nguyen, P. Martin, D. Frath, M. L. Della Rocca, F. Lafolet, S. Bellinck, P. Lafarge and J.-C. Lacroix, J. Am. Chem. Soc., 2018, 140, 10131–10134 CrossRef CAS.
- K. S. Kumar, R. R. Pasula, S. Lim and C. A. Nijhuis, Adv. Mater., 2016, 28, 1824–1830 CrossRef CAS.
- Z. Futera, X. Wu and J. Blumberger, J. Phys. Chem. Lett., 2023, 14, 445–452 CrossRef CAS PubMed.
- L. Yuan, L. Wang, A. R. Garrigues, L. Jiang, H. V. Annadata, M. Anguera Antonana, E. Barco and C. A. Nijhuis, Nat. Nanotechnol., 2018, 13, 322–329 CrossRef CAS.
- Y. Han, C. Nickle, M. S. Maglione, S. K. Karuppannan, J. Casado-Montenegro, D.-C. Qi, X. Chen, A. Tadich, B. Cowie, M. Mas-Torrent, C. Rovira, J. Cornil, J. Veciana, E. del Barco and C. A. Nijhuis, Adv. Sci., 2021, 8, 2100055 CrossRef CAS.
- D. Taherinia and C. D. Frisbie, Phys. Chem. Chem. Phys., 2023, 25, 32305–32316 RSC.
- H. Yan, A. J. Bergren, R. McCreery, M. L. Della Rocca, P. Martin, P. Lafarge and J. C. Lacroix, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5326–5330 CrossRef CAS.
- J. K. Sowa, J. A. Mol, G. A. D. Briggs and E. M. Gauger, J. Chem. Phys., 2018, 149, 154112 CrossRef PubMed.
- J. K. Sowa and R. A. Marcus, J. Chem. Phys., 2021, 154, 034110 CrossRef CAS PubMed.
- R. P. Sullivan, J. T. Morningstar, E. Castellanos-Trejo, R. W. Bradford, Y. J. Hofstetter, Y. Vaynzof, M. E. Welker and O. D. Jurchescu, Sci. Adv., 2022, 8, eabq7224 CrossRef CAS PubMed.
- Z. A. Lamport, A. D. Broadnax, D. Harrison, K. J. Barth, L. Mendenhall, C. T. Hamilton, M. Guthold, T. Thonhauser, M. E. Welker and O. D. Jurchescu, Sci. Rep., 2016, 6, 38092 CrossRef CAS.
- R. P. Sullivan, J. T. Morningstar, E. Castellanos-Trejo, M. E. Welker and O. D. Jurchescu, Nano Lett., 2023, 23, 10864–10870 CrossRef CAS.
- C. Tyznik, M. Waldrip, R. P. Sullivan, M. Mirhosseini, A. Berry, S. Dwyer, H. Y. Cakir, T. Coffey, Y.-L. Loo and O. D. Jurchescu, ACS Appl. Electron. Mater., 2023, 5, 5343–5351 CrossRef CAS.
- S. R. Banks, J. T. Morningstar and M. E. Welker, Molbank, 2021, 2021, M1251 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- H. Shpaisman, O. Seitz, O. Yaffe, K. Roodenko, L. Scheres, H. Zuilhof, Y. J. Chabal, T. Sueyoshi, S. Kera, N. Ueno, A. Vilan and D. Cahen, Chem. Sci., 2012, 3, 851–862 RSC.
- Z.-F. Liu and J. B. Neaton, J. Phys. Chem. C, 2017, 121, 21136–21144 CrossRef CAS.
- A. Migliore and A. Nitzan, ACS Nano, 2011, 5, 6669–6685 CrossRef CAS.
- A. Migliore, P. Schiff and A. Nitzan, Phys. Chem. Chem. Phys., 2012, 14, 13746–13753 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Chemical structures and an illustration of structural changes of self-assembled monolayers with temperature. See DOI: https://doi.org/10.1039/d4tc01807a |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
John T.
Morningstar
b,
Manikanta
Makala
a,
John T.
Morningstar
b,
Manikanta
Makala
 a,
Mark E.
Welker
a,
Mark E.
Welker
 b and
Oana D.
Jurchescu
b and
Oana D.
Jurchescu
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[J/J0]
ln[J/J0]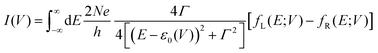
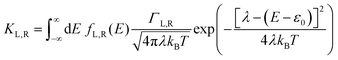

![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) L,R is the electron transfer rate onto the electrode, λ is reorganization energy, and assuming ΓL,R is constant with energy. The two theories have been unified by Sowa and Marcus in a generalized equation where the charge transfer rate is defined by:40,41
L,R is the electron transfer rate onto the electrode, λ is reorganization energy, and assuming ΓL,R is constant with energy. The two theories have been unified by Sowa and Marcus in a generalized equation where the charge transfer rate is defined by:40,41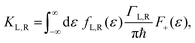
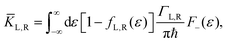
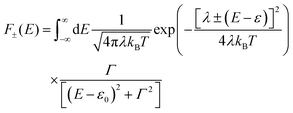

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 ratio (Fig. 4a). The temperature dependence of the current in the mixed SAMs is plotted in Fig. 4b. Generally, the behavior is similar to that of pure CMPTM, but subtle differences are clearly observed in the dependence of the Ea on V, especially for regimes II (near-resonance) and III (resonance) within the forward bias, which we are comparing in Fig. 4c. Specifically, we found a consistent shift of ∼0.3 V in the voltage point where the Ea plateaus, with the transition point occurring at higher voltage values in the mixed SAMs. This suggests that the transition from near-resonance to resonance is occurring at higher voltages in the mixed SAMs since the facilitating molecular orbital is placed further away from the Fermi energy of the contacts. A significant increase in εl would effectively increase the width of the off-resonant regime of the molecular rectifier (Fig. 3a), leading to a reduction in the reverse bias current. These findings are in agreement with previous observations that the addition of APTES results in a new electronic state within the SAM that enhances molecular rectification.
30 ratio (Fig. 4a). The temperature dependence of the current in the mixed SAMs is plotted in Fig. 4b. Generally, the behavior is similar to that of pure CMPTM, but subtle differences are clearly observed in the dependence of the Ea on V, especially for regimes II (near-resonance) and III (resonance) within the forward bias, which we are comparing in Fig. 4c. Specifically, we found a consistent shift of ∼0.3 V in the voltage point where the Ea plateaus, with the transition point occurring at higher voltage values in the mixed SAMs. This suggests that the transition from near-resonance to resonance is occurring at higher voltages in the mixed SAMs since the facilitating molecular orbital is placed further away from the Fermi energy of the contacts. A significant increase in εl would effectively increase the width of the off-resonant regime of the molecular rectifier (Fig. 3a), leading to a reduction in the reverse bias current. These findings are in agreement with previous observations that the addition of APTES results in a new electronic state within the SAM that enhances molecular rectification.