 Open Access Article
Open Access ArticleMagnetic anisotropy evolution with Fe content in electrodeposited Ni100−xFex thin films†
A.
Begué
 ab,
N.
Cotón
ab,
N.
Cotón
 a and
R.
Ranchal
a and
R.
Ranchal
 *ac
*ac
aDpto. Física de Materiales, Fac. CC. Físicas, Universidad Complutense de Madrid, Ciudad Universitaria s/n, Madrid 28040, Spain. E-mail: rociran@ucm.es
bFac. Ciencias, Universidad de Zaragoza, Zaragoza 50009, Spain
cInstituto de Magnetismo Aplicado, UCM-ADIF-CSIC, Las Rozas 28232, Spain
First published on 5th June 2024
Abstract
In this study, we have experimentally and theoretically determined how the magnetic anisotropy of Ni100−xFex thin films evolves as a function of the Fe content in electrodeposited samples. When the Fe content is below 12 at%, stripe domains are promoted once the thickness exceeds a critical value. For an Fe content of 7 at%, the transcritical shape is present in the hysteresis loop for a thickness of 600 nm. However, for compositions equal to or above 12 at%, we have not found evidence of stripe domains, as indicated by the absence of the transcritical shape in the hysteresis loops for layer thicknesses as high as 1 μm even if a magnetic field is applied perpendicular to the sample plane during growth. All the studied layers are polycrystalline with a 〈111〉 texture. The experimental results are understood in the framework of a theoretical model which considers different contributions to the magnetic anisotropy: magnetocrystalline, magnetoelastic, magnetostatic and from pairs. Out-of-plane anisotropy promoted by columnar growth has not been considered as the saccharine-based electrolyte used for the electrodeposition prevents it. In fact, the magnetic anisotropy related to pairs, which is not generally taken into account in models for Ni100−xFex, appears to play a crucial role in these thin films. Fitting of the experimental results to this model reveals that the local anisotropy generated by pairs can be as high as 3.30 × 106 J m−3. This theoretical and experimental combined investigation highlights the relevance of all these fundamental mechanisms for the understanding and tuning of magnetic materials.
1. Introduction
Control of magnetic anisotropy is a key issue when dealing with magnetic materials, and in particular for thin films. While for some applications perpendicular magnetic anisotropy (PMA) is crucial to increase for example the magnetic storage capacity1–5 or to create spin textures such as skyrmions or stripe domains,6–9 it might be considered a disadvantage for other applications such as giant magnetoimpedance (GMI) sensors in which the need for soft magnetic properties is crucial.10–12 Since optimum performance of GMI sensors is obtained for a thickness of around 1 μm, the insertion of layers is required to avoid the formation of stripes once the thickness exceeds the critical value for their formation, which is around 200 nm for sputtered Ni80Fe20 layers11 or even lower for materials with a higher PMA such as FePt.13 Generally, the presence of stripe domains can be identified in the in-plane (IP) hysteresis loops, which exhibit what it is known as the “transcritical shape”,14–16 characterized by a linear behaviour in the magnetization curve as the magnetic saturated state is reached14–19 and an increase of coercivity in comparison to thinner samples without stripes.14Ni100−xFex alloys have been broadly studied due to their low coercivity and large saturation magnetization (Msat).10–12,14,17,18,20 In sputtered Ni80Fe20 thin films, the appearance of stripe domains has been previously reported when a certain critical thickness is exceeded due to columnar growth.10,14 The possibility of avoiding columnar growth through electrodeposition in continuous mode by adding saccharine to the electrolyte has been reported. This addition enables smooth and uniform deposition while preventing columnar growth in NiCu and Ni80Fe20 alloys.21,22 However, in our previous investigation of electrodeposited Ni90Fe10 thin films grown from a saccharine-based electrolyte, we have shown that when the electrolyte is not stirred, stripe domains are formed for thicknesses above 0.8 μm.17 Moreover, when the electrolyte is not stirred and stripes are promoted, the critical thickness for their formation can be reduced if a perpendicular magnetic field to the sample plane is applied during growth.18
Here, we have systematically investigated the evolution of the magnetic anisotropy in electrodeposited Ni100−xFex layers obtained from a saccharine-based electrolyte in a compositional range between 7 ≤ x ≤ 48 at% Fe. The effect of the thickness and even of a perpendicular magnetic field applied during growth has also been assessed. The interplay between magnetocrystalline, magnetoelastic, magnetostatic and even magnetic anisotropy from pairs plays a crucial role on the evolution of the anisotropy of these 〈111〉 textured films.
2. Experimental section
Ni100−xFex layers were grown by electrodeposition on glass substrates covered with a Ti/Au bilayer to increase electrical conductivity. We have used a three-electrode cell with a platinum mesh as a counter electrode and an Ag/AgCl (3 M NaCl) reference electrode. A PalmSens EmStat3+Blue potentiostat was used to perform the depositions at room temperature in non-rotating substrates in a horizontal position. The electrolyte was not magnetically stirred during growth. To deposit the samples, an electric potential of −1.2 V was used. The electrolyte had a fixed composition for H3BO3 (0.4 M), NiSO4·6H2O (0.7 M) and saccharine (17 mM). To tune the Ni100−xFex composition, the concentration of FeSO4·7H2O ranged from 20 mM to 80 mM.The growth time of Ni100−xFex was adjusted to reach the expected thicknesses (t) by means of Faraday's law:
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485, 34 C mol−1), d is the density of the electrodeposited material, S is the area of the sample, and Matom is the molecular mass. A set of calibration samples was firstly deposited in which the layer thickness was measured by atomic force microscopy (AFM). These samples were used to adjust the formula of Faraday's law to take into account hydrogen evolution.
485, 34 C mol−1), d is the density of the electrodeposited material, S is the area of the sample, and Matom is the molecular mass. A set of calibration samples was firstly deposited in which the layer thickness was measured by atomic force microscopy (AFM). These samples were used to adjust the formula of Faraday's law to take into account hydrogen evolution.
We have used X-ray diffractometry (XRD) in the Bragg–Brentano configuration to study the structural properties. Measurements were performed using D8 Bruker equipment using the Cu Kα wavelength (λ = 1.54056 Å). The composition of the alloys was measured by energy-dispersive X-ray spectroscopy using JEOL JSM 7600F equipment at 15 kV. In-plane hysteresis loops were measured using a homemade magneto-optical Kerr effect (MOKE) setup in the longitudinal configuration, employing p-polarized light from a laser with a wavelength of 650 nm operating at 10 kHz.
3. Experimental results
The IP hysteresis loops shown in Fig. 1a for Ni93Fe7 layers with thicknesses ranging from 600 nm to 1.4 μm exhibit the transcritical shape, consistent with our previous results on Ni90Fe10 films where stripe domains are promoted when deposition is performed under non-stirring conditions.17 MOKE hysteresis loops appear reversed due to the inversion in Kerr signal promoted by Ni.23 However, IP hysteresis loops do not exhibit the transcritical shape related to the presence of stripe domains even when the thickness is as high as 1.4 μm if the Fe content increases to 12 at% (Fig. 1b).Upon comparing 1 μm thick layers with different compositions, it is evident that the transcritical shape is not present once the Fe content is equal to or higher than 12 at% (Fig. 2a). In the Ni90Fe10 layers electrodeposited from a saccharine-based electrolyte, we have previously reported that the formation of stripe domains can be enhanced by applying an external magnetic field perpendicular to the sample plane.18 However, for Ni80Fe20 this procedure is not effective even when the layer thickness is 1 μm (Fig. 2b).
To understand the evolution of the magnetic anisotropy in these Ni100−xFex alloys, XRD characterization was performed (Fig. 3a). All the layers exhibit an fcc crystal structure as revealed by the diffraction peaks present in all the patterns which is in agreement with the fact that that this crystal structure is kept up to an Fe content as high as ca. 90 at% in Ni100−xFex alloys.20 In addition, all the studied thin films exhibit a 〈111〉 texture regardless of the composition. Therefore, the evolution of the magnetic anisotropy appears to be strongly dependent on the Fe content that controls the formation of stripe domains in electrodeposited Ni100−xFex films being not possible to achieve its formation for compositions equal to or above 12 at%. We have studied the correlation between Fe content and the coherent domain size (D) by means of Scherrer's formula:24
 | (2) |
4. Theoretical model
To explain the loss of domain stripes occurring around Fe 12 at%, we have developed a model based on the magnetic anisotropies involved in these alloys. The sign of the total anisotropy of the films is defined taking into account that the magnetocrystalline anisotropy constant is typically defined as K1 < 0 when the magnetization lies along the 〈111〉 directions, and K1 > 0 for perpendicular directions (i.e. 〈100〉 direction).20 From MOKE loops we see that for compositions below Fe 12 at%, the anisotropy is negative, as the magnetization points in the out-of-plane (OOP) direction, which is parallel to the 〈111〉 direction in these textured films. On the other hand, for compositions equal to or above Fe 12 at%, the anisotropy has to be positive as the magnetization lies in the sample plane.The total magnetic anisotropy, Ktotal, of the films is the sum of the different anisotropies involved:
| Ktotal = Kmc + Kme + Kms + Kpairs | (3) |
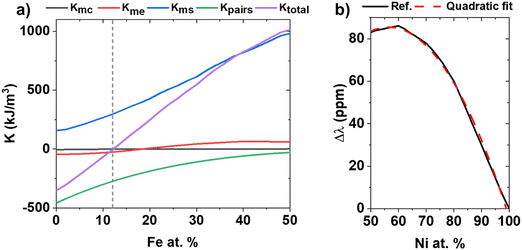 | ||
| Fig. 4 (a) Dependency of the different magnetic anisotropies with respect to Fe content (at%). The dashed line at Fe 12 at% indicates the change of sign in Ktotal. (b) Excess magnetostriction (Δλ) obtained from the references (black)20 with its quadratic fit (dashed-red). | ||
K mc is determined by the values of anisotropy constant K1 for each composition of the Ni100−xFex alloy, with no consideration of K2 due to its low contribution to the anisotropy. We have introduced in our calculation the data of K1 for every composition reported by Cullity.20
K me is calculated as:
 | (4) |
 is the microstrain and Y is the Young's modulus. The value of λp can be obtained as the average of random orientations of the grains, which depend on the magnetostriction constants λ100 and λ111 for each composition. It is calculated as λp = (2λ100 + 3λ111)/5.20 The microstrain is determined by applying the Williamson–Hall method to the (111) XRD peak as
is the microstrain and Y is the Young's modulus. The value of λp can be obtained as the average of random orientations of the grains, which depend on the magnetostriction constants λ100 and λ111 for each composition. It is calculated as λp = (2λ100 + 3λ111)/5.20 The microstrain is determined by applying the Williamson–Hall method to the (111) XRD peak as  .24 From the values of
.24 From the values of  obtained at each composition, we performed a linear fit in order to extrapolate the values of
obtained at each composition, we performed a linear fit in order to extrapolate the values of  to compositions for which we do not have data (see ESI†). The Young's modulus for each Ni100−xFex composition is obtained from the literature.25
to compositions for which we do not have data (see ESI†). The Young's modulus for each Ni100−xFex composition is obtained from the literature.25
Due to the shape of the samples, there is a significant magnetostatic anisotropy leading the magnetization to lie in the sample plane of the thin films. The magnetostatic anisotropy for a film is calculated as:
 | (5) |
In many metallic alloys, there is also a non-negligible contribution to the magnetic anisotropy due to the formation of pairs, denoted as Kpairs in this work. Chikazumi already reported that in Ni100−xFex alloys featuring the Ni3Fe superlattice, the anisotropy exhibits a decrease in its value26 that is attributed to the ordered superlattice, while disordered configurations, where Fe or Ni atoms are first neighbors, serve to enhance a local uniaxial anisotropy along the direction of pair formation.27 For other Fe-based alloys such as FeGa, Cullen et al. developed a model to calculate the induced anisotropy by pairs, resulting in 5 × 107 J m−3 for Ga-pairs in the Fe matrix.28 This Cullen's model is based on the premise that the excess magnetostriction, Δλ, depends quadratically on the composition. In the studied Ni100−xFex alloys, the addition of Fe to the Ni matrix results in a reduction in coherence length as shown in the reduction of the crystallite size with increasing Fe atomic content (Fig. 3b). The introduction of Fe atoms diminishes this magnetic anisotropy within the Ni matrix, resulting in a reduction of local uniaxial anisotropy. By adapting the model initially formulated for Ga-pairs by Cullen to Ni-pairs, we can effectively express the observed excess magnetostriction:
 | (6) |
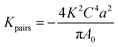 | (7) |
5. Conclusions
In conclusion, this study has provided valuable insights into the evolution of the magnetic anisotropy in electrodeposited Ni100−xFex alloys across a range of Fe contents spanning from 7 to 48 at%. Regardless of the composition, all the layers are polycrystalline with a 〈111〉 texture. We have developed a theoretical model for the magnetic anisotropy evolution that accounts for the observed experimental results obtained in a saccharine-based electrolyte in which columnar growth is avoided. Our research underscores the complex interplay between composition, crystalline structure, and different sources of magnetic anisotropies as: magnetocrystalline, magnetoelastic, magnetostatic and from pairs. By elucidating these relationships, we advance our understanding of the fundamental mechanisms governing magnetic behavior in thin films. Due to the use of a saccharine-based electrolyte for the layer growth, the contribution from columnar growth has not been considered. Further research could explore the generalization of the model to magnetic systems where this constraint does not apply, such as in Ni100−xFex sputtered layers.10,14Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
A. Begué: investigation; methodology; writing – original draft; writing – review & editing. N. Cotón: investigation; data curation; validation; writing – review & editing. R. Ranchal: conceptualization; methodology; funding adquisition; supervision; writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been financially supported through the project PID2021-122980OB-C51 (AEI/FEDER) of the Spanish Ministry of Science and Innovation. A. B. would like to acknowledge the funding received from the Ministry of Universities and the European Union-Next Generation for the Margarita Salas fellowship. We thank CNME at UCM for the use of JEOL JSM 7600F, and CAI Difracción de rayos-X at UCM for XRD measurements, respectively.References
- B. Dieny and M. Chshiev, Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications, Rev. Mod. Phys., 2017, 89, 025008 CrossRef.
- R. Sbiaa, H. Meng and S. N. Piramanayagam, Materials with perpendicular magnetic anisotropy for magnetic random access memory, Phys. Status Solidi RRL, 2011, 5, 413–419 CrossRef CAS.
- C. A. Brondin, S. Ghosh, S. Debnath, F. Genuzio, P. Genoni, M. Jugovac, S. Bonetti, N. Binggeli, N. Stojić, A. Locatelli and T. O. Menteş, Tailoring Magnetic Anisotropy in Ultrathin Cobalt by Surface Carbon Chemistry, Adv. Electron. Mater., 2024, 10, 2300579 CrossRef CAS.
- K. Wang, X. Fu, L. Yu, Z. Guo, J. Liu, G. Jagadish Kumar and R. Xiong, Perpendicular magnetic anisotropy properties of Co2FeSi/Pt multilayers deposited on amorphous dielectric Ta2O5, Mater. Sci. Eng., B, 2024, 301, 117173 CrossRef CAS.
- S. Bhatti, R. Sbiaa, A. Hirohata, H. S. Fukami and S. N. Piramanayagam, Spintronics based random access memory: a review, Mater. Today, 2017, 20, 530–548 CrossRef.
- Y.-C. Li, Y.-H. Huang, C.-C. Huang, Y.-T. Liu and C.-F. Pai, Field-free switching in symmetry-breaking multilayers: the critical role of interlayer chiral exchange, Phys. Rev. Appl., 2023, 20, 024032 CrossRef CAS.
- R. Wiesendanger, Nanoscale magnetic skyrmions in metallic films and multilayers: a new twist for spintronics, Nat. Rev. Mater., 2016, 1, 16044 CrossRef CAS.
- D. Petti, S. Tacchi and E. Albisetti, Review on magnonics with engineered spin textures, J. Phys. D: Appl. Phys., 2022, 55, 293003 CrossRef CAS.
- S. Luo, M. Song, X. Li, Y. Zhang, J. Hong, X. Yang, X. Zou, N. Xu and L. You, Reconfigurable Skyrmion Logic Gates, Nano Lett., 2018, 18, 1180–1184 CrossRef CAS.
- E. Fernández, A. V. Svalov, G. V. Kurlyandskaya and A. Garcia-Arribas, GMI in nanostructured FeNi/Ti multilayers with different thicknesses of the magnetic layers, IEEE Trans. Magn., 2013, 49, 18–21 Search PubMed.
- G. V. Kurlyandskaya, A. V. Svalov, E. Fernandez, A. Garcia-Arribas and J. M. Barandiaran, FeNi-based magnetic layered nanostructures: Magnetic properties and giant magnetoimpedance, J. Appl. Phys., 2010, 107, 09C502 CrossRef.
- M. A. Corrêa, F. Bohn, C. Chesman, R. B. da Silva, A. D. C. Viegas and R. L. Sommer, Tailoring the magnetoimpedance effect of NiFe/Ag multilayer, J. Phys. D: Appl. Phys., 2010, 43, 295004 CrossRef.
- N. R. Álvarez, J. E. Gómez, A. E. Moya Riffo, M. A. Vicente Álvarez and A. Butera, Critical thickness for stripe domain formation in FePt thin films: Dependence on residual stress, J. Appl. Phys., 2016, 119, 083906 CrossRef.
- M. Romera, R. Ranchal, D. Ciudad, M. Maicas and C. Aroca, Magnetic properties of sputtered Permalloy/molybdenum multilayers, J. Appl. Phys., 2011, 110, 083910 CrossRef.
- A. Hubert and R. Schäfer, Magnetic domains, Springer, 2011 Search PubMed.
- N. Saito, H. Fujiwara and Y. Sugita, A New Type of Magnetic Domain Structure in Negative Magnetostriction Ni-Fe Films, J. Phys. Soc. Jpn., 1964, 19, 1116–1125 CrossRef CAS.
- N. Cotón, J. P. Andrés, E. Molina, M. Jaafar and R. Ranchal, Stripe domains in electrodeposited Ni90Fe10 thin films, J. Magn. Magn. Mater., 2023, 565, 170246 CrossRef.
- N. Cotón, J. P. Andrés, M. Jaafar, A. Begué and R. Ranchal, Tuning the out-of-plane magnetic textures of electrodeposited Ni90Fe10 thin films, J. Appl. Phys., 2024, 135, 093905 CrossRef.
- M. Coïsson, G. Barrera, F. Celegato and P. Tiberto, Rotatable magnetic anisotropy in Fe78Si9B13 thin films displaying stripe domains, Appl. Surf. Sci., 2019, 476, 402–411 CrossRef.
- B. D. Cullity, in Introduction to magnetic materials, ed. C. D. Graham, IEEE/Wiley, Hoboken, N.J, 2nd edn, 2009 Search PubMed.
- M. Troyon and L. Wang, Influence of saccharin on the structure and corrosion resistance of electrodeposited multilayers, Appl. Surf. Sci., 1996, 103, 517–523 CrossRef CAS.
- A. Kotelnikova, T. Zubar, T. Vershinina, M. Panasyuk, O. Kanafyev, V. Fedkin, I. Kubasov, A. Turutin, S. Trukhanov, D. Tishkevich, V. Fedosyuk and A. Trukhanov, The influence of saccharin adsorption on NiFe alloy film growth mechanisms during electrodeposition, RSC Adv., 2022, 12, 35722–35729 RSC.
- A. Green and B. W. J. Thomas, A simple hysteresis loop plotter using the transverse Kerr effect, J. Sci. Instrum., 1966, 43, 399–401 CrossRef.
- V. D. Mote, Y. Purushothani and B. N. Dole, Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles, J. Theor. Appl. Phys., 2012, 6, 6 CrossRef.
- H. M. Ledbetter and R. P. Reed, Elastic Properties of Metals and Alloys, I. Iron, Nickel, and Iron-Nickel Alloys, J. Phys. Chem. Ref. Data, 1973, 2, 531–618 CrossRef CAS.
- S. Chikazumi, Ferromagnetic Properties and Superlattice Formation of Iron-Nickel Alloys (II), J. Phys. Soc. Jpn., 1950, 5, 333–338 CrossRef.
- S. Chikazumi and T. Oomura, On the Origin of Magnetic Anisotropy Induced by Magnetic Annealing, J. Phys. Soc. Jpn., 1955, 10, 842–849 CrossRef CAS.
- J. Cullen, P. Zhao and M. Wuttig, Anisotropy of crystalline ferromagnets with defects, J. Appl. Phys., 2007, 101, 123922 CrossRef.
- K. Inoue, H. Shima, A. Fujita, K. Ishida, K. Oikawa and K. Fukamichi, Temperature dependence of magnetocrystalline anisotropy constants in the single variant state of L1-type FePt bulk single crystal, Appl. Phys. Lett., 2006, 88, 102503 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc01189a |
| This journal is © The Royal Society of Chemistry 2024 |



