Evidence for efficient anchoring in nitroxyl radical thin films: an experimental XPS/NEXAFS and theoretical DFT/TD-DFT study

Abstract

Studies of persistent organic radical films on conductive metal surfaces can pave the way for diverse applications such as improved spin probes and labels, data control and storage, spintronics, and quantum computing. We grew monolayer films of three nitroxyl radicals (NRs), viz. TEMPO and two carbamoyl-proxyl radicals (nit8 and nit9) under ultra-high vacuum conditions on Au(111) and Cu(111) surfaces. The electronic properties of the films and NR adsorption mechanisms were analyzed by means of X-ray photoelectron (XPS) and absorption (NEXAFS) spectroscopies, with the aid of density functional theory (DFT) and time-dependent DFT computations performed on large unit cells (rev-PBE) and clusters (CAM-B3LYP). We found that all three NRs physisorb weakly on Au. In the case of nit8 and nit9, H-bonded monolayers are formed that recline parallel to the Au surface. Stronger interactions with Cu resulted in chemisorption and robust films, with nit8 and nit9 exhibiting upright orientation due to the amide group acting as an efficient binding anchor. Conversely, TEMPO binds to Cu necessarily via NO which is observed to lead to the destruction of the spin-carrying NO functionality. Computational evidence highlighted the decisive role of Cu surface defects in the partial fragmentation of the CONH₂ anchor upon chemisorption of nit8 and nit9.

---

Introduction

Interest in thin films has been rising steadily over the last few decades owing primarily to the need for gradual miniaturization of technological devices.¹ Organic materials offer the possibility to grow nanoscale thin films with several desirable properties, such as transparency, low-cost fabrication, and flexible chemical design, coupled with an overall lower environmental impact relative to their heavy metal and inorganic counterparts.² As a result, whole classes of cutting-edge devices implementing organic thin films have been developed and studied, notably for applications in solar cells,³ transistors,^4,5 sensing, and light-emitting diodes.⁶ However, identifying efficient and reproducible fabrication methods for nanoscale materials still faces major challenges.

Functionalization of surfaces via thin film growth of persistent organic free radicals (FRs) has been an increasingly attractive topic in materials science.^7,8 The prolonged stability of persistent FRs is typically achieved by enabling the delocalization of unpaired spin(s) over several centres and/or shielding the radical centre with vicinal bulky groups to inhibit dimerization.⁹ Each persistent FR molecule adsorbed on a surface furnishes the intrinsic magnetic spin moment as an additional potentially controllable information-carrying degree of freedom.¹⁰

A majority of the research activity concerning surfaces functionalized with persistent FRs has been devoted to advancing the methods of their preparation and their microscopic and spectroscopic characterization, as well as the rational design and fine-tuning of their properties, with an eye on possible future applications.⁷ The primary aim is to achieve low-dimensional neatly ordered assemblies of persistent FRs physisorbed or chemisorbed on (semi)conducting surfaces, preserving their unpaired spins and with known spin magnetic coupling. Such materials could lead to major technological advances, e.g. in improved data control and storage,¹⁰ spintronics,¹¹ and eventually quantum computing.^12,13

Nitroxyl radicals (NRs; Fig. 1) make an important class of persistent FRs with numerous applications, such as magnetic resonance imaging (MRI) contrasting agents;¹⁴ energy stores,¹⁵ catalysts;^16,17 initiators and inhibitors in free radical polymerizations,^18,19 (nano)antioxidants²⁰etc. Thus far, we have extensively studied the electronic structure of FRs in the gas phase with special emphasis on NRs,^21–25 by means of ultraviolet photoelectron spectroscopy (UPS), X-ray photoelectron spectroscopy (XPS) and near-edge X-ray absorption fine structure spectroscopy (NEXAFS) at the C, N and O K-edges. The assignment of the XPS and NEXAFS spectra of NRs was aided by quantum chemical calculations, specifically density functional theory (DFT) and time-dependent DFT (TD-DFT) computations of the core electron binding energies (CEBEs) and core excitations. These studies provided deeper insights into the delocalization and stabilization of the unpaired spin density, conformation and fine vibrational structure of NRs, and the electronic effects of the NR ring substituents. More recently, the spectroscopic characterization of NRs was extended to the gas phase resonant photoelectron spectroscopy (ResPES) measurements at the N and O K-edges.²⁵ This helped elucidate the role of the singly occupied molecular orbital (SOMO) in the de-excitation of the core-hole.²⁵

Fig. 1 From left to right: structures and atom enumeration of TEMPO, nit9, and nit8. The “nit8” and “nit9” designations for the two carbamoyl-proxyl radicals are taken from our earlier work. The numbers in italic refer to the atom designations discussed in the text.

As a continuation of our work on NRs, we currently present a spectroscopic study and theoretical modelling of the adsorption of three NRs, viz. TEMPO, nit8, and nit9 (Fig. 1), in ultra-high vacuum (UHV) conditions on gold and copper(111) surfaces. The thus-obtained molecular films are characterized by means of the XPS and NEXAFS techniques to probe the core and unoccupied levels. The structures and energetics in these systems and the NR adsorption mechanisms are deduced from DFT and TD-DFT computations. Some of the previously studied systems of direct relevance to the present work are described in ref. 26–39.

We demonstrate that molecular films of nit8 and nit9 can be successfully grown at room temperature (RT) on Au(111) and Cu(111). At RT, the TEMPO films can only be grown on Cu(111) whereas, in order to obtain a stable TEMPO monolayer on Au(111), liquid nitrogen (LN₂)-cooling is required. In all cases, NRs are deposited onto the substrates directly, without interposition of extra molecular linkers. This, besides allowing difficult synthesis processes to be circumvented, can also lead to enhanced spin magnetic interactions.³⁶ Evidence is presented for the physisorption on Au(111) and the chemisorption on Cu(111), and detailed mechanisms, supported by spectroscopic and computational data, are proposed for both. We note that, as a conducting metal substrate, Cu is still rarely studied in this context, compared to the more inert and amenable Au. Also rare are studies on the potential of the CONH₂ group as a chemisorptive anchor for surface functionalization; still, we observe its particularly strong affinity for Cu surfaces and find it to be crucial for preserving the NO group and thus the magnetism of nit8 and nit9 films.

Experimental methods

The preparation methods, the achieved outcomes and the beamline where the experiments were realized are summarized in Table 1. Nit8, nit9 and TEMPO film growth and characterization on RT Au(111) and Cu(111) were realized at the material science beamline (MSB). TEMPO thin film experiments on the LN₂ – cooled surfaces have been performed at the VUV photoemission beamline (VUV). Both beamlines are located at Elettra, the Italian synchrotron facility. MSB⁴⁰ is a bending magnet beamline, operating in the 22–1000 eV range of photon energies. The analysis chamber, with a base pressure of 2 × 10⁻¹⁰ mbar, is equipped with a SPECS PHOIBOS 150 hemispherical electron analyzer and a dual-anode Mg/Al K_α X-ray source, an ion gun, and a sample manipulator with a K-type thermocouple attached to the rear side of the sample. Surface preparation was realized by repeated cycles of sputtering (1 kV, 30 min, 10⁻⁶ mbar Ar pressure) and annealing (5 min at 550 °C). Prior to nit8 (nit9) deposition, the substrates were allowed to cool back to RT. Nit8 (nit9) (Merck, 99%) was evaporated in the preparation chamber (base pressure lower than 10⁻⁹ mbar) from a resistively heated quartz crucible after carefully degassing to the evaporation temperature (ca. 55 °C), during a 5 min deposition at 3 × 10⁻⁷ mbar. As TEMPO (Merck, 99%) already sublimates at RT, it was kept in a CF quartz tube outside the preparation chamber and purged prior to the deposition by a few cycles of LN₂ freeze-and-pump. After the surface preparation, TEMPO was dosed on Au(111) and Cu(111), during a 5 min deposition, in a pressure range of 4 × 10⁻⁸ to 7 × 10⁻⁷ mbar (preparation chamber base pressure ca. 3 × 10⁻⁸ mbar). The monolayer thicknesses were estimated by considering the attenuation of Au 4f and Cu 2p peaks after evaporation, measured using the Al K_α X-ray source. The XPS spectra were collected at normal emission (60° incidence), at hν = 630 eV, 500 eV and 410 eV for O 1s, N 1s and C 1s core levels, respectively. Binding and photon energy calibration and photon energy resolution (ΔE) were evaluated considering the kinetic energy position of the Fermi edge and its Gaussian broadening, measured on the freshly cleaned surfaces. The ΔE values for O, N and C 1s were respectively 500, 400 and 300 meV on Au(111) and 600, 400 and 350 meV on Cu(111). The NEXAFS measurements for O, N and C K-edges were performed in the Auger-electron yield mode at grazing incidence and normal incidence geometry, i.e., with the polarization vector of the incident radiation perpendicular or almost parallel to the substrate surface. The thus-obtained spectra were normalized with respect to the reference spectra acquired on the freshly prepared Au(111) and Cu(111) surfaces. In order to rule out the contribution from the adventitious carbon present on the beamline mirrors, the Au 4f intensity of the freshly prepared surface was also measured and then used to treat the C K-edge NEXAFS spectrum.

Table 1 Procedures and beamlines employed for NR growth. RT = room temperature, LN₂ = liquid N₂ temperature, MSB = material science beamline, VUV = VUV spectroscopy beamline

Growth successful?	TEMPO		nit8		nit9
	Au	Cu	Au	Cu	Au	Cu
RT – MSB	No	Yes	Yes	Yes	Yes	Yes
LN2 – VUV	Yes	Yes	—	—	—	—

---

VUV⁴¹ is an undulator beamline operating in the 20–750 eV range of photon energies. The analysis chamber, with a base pressure lower than 10⁻¹⁰ mbar, is equipped with a R4000 Scienta hemispherical electron analyzer and a sample manipulator with a liquid He cryostat. Surface preparation and TEMPO purging were realized following the same procedure already used at MSB. TEMPO was then dosed on Au(111) and Cu(111) kept at LN₂ temperature, during a 5 s deposition at 2 × 10⁻⁶ mbar (preparation chamber base pressure ca. 2 × 10⁻⁸ mbar). The subsequent XPS characterization was performed keeping the samples at LN₂ temperature, with hν = 660 eV for O 1s and 515 eV for C 1s and N 1s. The sample was scanned during acquisition in order to avoid beam irradiation damages. The film thicknesses were estimated considering the attenuation of Au 4f and Cu 3p peaks after TEMPO evaporation. The XPS spectra were calibrated using the standard CEBEs of Au 4f and Cu 3p levels, evaluated for the freshly prepared surfaces. The ΔE values for the O, N and C 1s XPS evaluated considering the experimental and beamline parameters are between 500 meV and 600 meV. Gaussian and Voigt profiles were employed to simulate, respectively, the gas phase and the film core level spectral features in the fitting analysis. More details about the fitting analysis and the fitting parameter are found in Table S4 (ESI†). For the sake of clarity, background baselines have been subtracted from the spectra after fitting. The core level stoichiometry has been evaluated normalizing the peak area obtained from the fit analysis by the photoionization cross sections and the analyzer transmission function.

Computational methods

We computed the C 1s, N 1s and O 1s core-ionization and core-excitation energies of the three NRs adsorbed on Au and Cu surfaces. To this end, we employed the Siesta^42,43 (version 4.1.5) and Orca (version 5.0.3) quantum chemistry codes.^44,45 To model the XPS spectra, the CEBEs were approximated as the energies of the spin orbitals pertaining to the C, N, and O 1s levels (effectively the Koopmans’ approximation). For the structures with doublet multiplicity, the energies of the β-spin orbital set were used. These were shown to approximate the ionizations to the triplet-coupled state of the cation well in open-shell systems.⁴⁶ To model the NEXAFS spectra, the restricted single excitation space (RSES) TD-DFT excitation energies and oscillator strengths were used. The excitations were restricted to originate from the C 1s, N 1s, and O 1s levels and up to 150 roots were afforded in each case. To alleviate the comparison with the measured XPS and NEXAFS spectral features, the DFT and RSES-TD-DFT spectra had to be shifted upwards by several eV. The details on deriving the optimal shifts are given in the Computational results section. The remaining technical details of the calculations are provided in the ESI.†

Experimental results

XPS

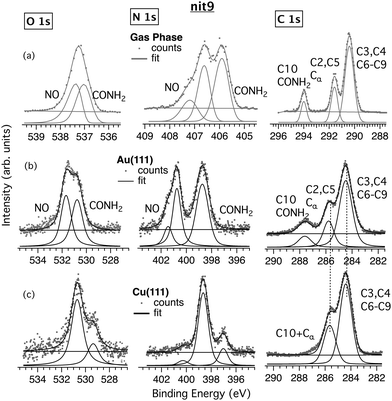
The results for nit8 and nit9 are similar; therefore, in the following we will mainly discuss nit9 (Fig. 2 and 4) and TEMPO (Fig. 3 and 5), assuming the nit9 results are extendable to nit8, if not stated otherwise. Nit8 spectra on Au(111) and Cu(111) are given in the ESI† (Fig. S6). Table S1 (ESI†) summarizes the assignments of the core level signals for nit8 and nit9.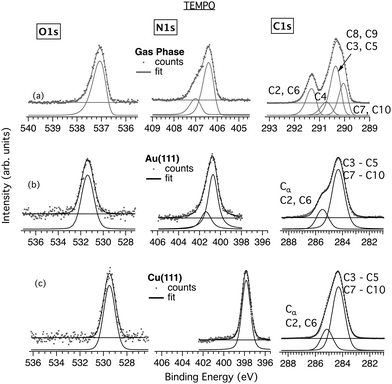

Fig. 2 Comparison of nit9 O, N and C 1s core levels in (a) gas phase, and in thin films deposited onto (b) Au(111), and (c) Cu(111) surfaces. Vertical dashed lines are added as a guide for better visualization of the peak alignment.

Fig. 3 Comparison of TEMPO O, N and C 1s core levels in (a) gas phase, and in thin films deposited onto (b) Au(111) and (c) Cu(111) surfaces.

For nit8 and nit9, overview XPS spectra, together with the zoomed in core levels, are shown in Fig. S1 and S2 (ESI†), indicating a successful growth at RT and a neat preparation. At RT, TEMPO core levels were detectable on Cu(111) but not on Au(111) (Fig. S3, ESI†). To achieve a successful deposition of TEMPO on Au, cooling of the substrate was required to increase the sticking coefficient. A successful growth of TEMPO on Au(111) was achieved, and the overview spectra confirmed the absence of external contaminants on either substrate (Fig. S4, ESI†). To check whether the films grown under the RT and LN₂ conditions are consistent, subsequently similar preparation was conducted for the Cu substrate. The core levels of TEMPO/Cu from RT and LN₂ preparations were found to be entirely analogous, indicating in both cases a suitable preparation and successful realization of neat films (Fig. S5, ESI†).

For all three NRs, we note that attempts to further increase the film thickness by successive depositions were unsuccessful. Thus, we assume that a saturated monolayer was formed after the first deposition whereas the formation of overlayers is disfavored because of the too weak interactions between the adsorbate molecules.

The average thickness of the nit9 (nit8) monolayer is 2.8 Å (3.1 Å) on Au and approximately twice this value, 5.3 Å (5.8 Å), on Cu. Similarly, the thickness of the TEMPO monolayer is 2 Å on Au and 4.7 Å on Cu. The films grown on Au showed a low stability under beam irradiation. In contrast, those on Cu were significantly more robust, without changes in the core level spectra even after prolonged acquisitions.

These differences already indicated fundamentally different adsorption geometries and mechanisms. Confirmation was obtained by comparing the measured core levels with the previously obtained gas phase results,^22,23 as shown in Fig. 2 and 3. Note that the gas and film XPS spectra are characterized by a different CEBE scale, due to the use of two different energy references, namely the vacuum level and the Fermi level, reflecting the presence of the surface work function. Therefore, for ease of comparison, the spectra in Fig. 2 and 3 are graphically aligned using different energy axes.

The XPS spectra of nit9 deposited on Au (Fig. 2b) are similar to the gas phase spectra (Fig. 2a). The C 1s film spectrum is characterized by the same three main bands displayed by the corresponding gas phase spectrum. The bands are attributable to the three classes of C atoms with clearly resolved CEBEs: the amide C (C10) at 287.6 eV (294 eV in gas phase); the C2 and C5 atoms (C_α) bonded to the N atom of the NO group at 285.8 eV (291.6 eV in gas phase); and the remaining six C atoms, all of which are bonded only to C or H atoms, at 284.5 eV (290.4 eV in gas phase). We obtain the expected intensity ratio for the three bands of 6 : 2 : 1.

The gas phase and nit9/Au N 1s spectra are also similar (Fig. 2a and b). The gas phase spectrum exhibits two main peaks at 406.7 eV and 405.9 eV, which have been attributed to the nitroxide and amide N atoms, respectively.^22,23 In the film the corresponding peaks are found at 400.8 and 398.7 eV. The nitroxide N atom has a larger CEBE because it is bonded to the more electronegative O atom and thus is more depleted of the charge. Analogous observations apply to the nitroxide and amide O atoms, measured respectively at 537.3 and 536.9 eV in the gas phase, and at 531.7 and 530.8 eV in the film (Fig. 2). It can be seen (Table S1, ESI†) that in N 1s and O 1s XPS, the two peaks on Au are significantly more separated than in the gas phase, viz. 2.1 vs. 0.8 eV for N 1s and 0.9 vs. 0.4 eV for O 1s, and similar results are found for nit8. A plausible explanation for this is given in the Computational results section (vide infra).

A third, less intense peak is visible in the gas phase N 1s spectrum at 407.2 eV (Fig. 2a). This peak is typical of open-shell molecules, e.g. NO,⁴⁷ and is due to the energy splitting between the singlet (S) and triplet (T) coupled unpaired N 1s and SOMO electrons. It is also visible in the NR/Au films (Fig. 2b, 3b and Fig. S6, ESI†) and corresponds to the small-intensity shoulder on the high energy side of the main NO component, i.e. the “NO (weak)” signals (Table S1, ESI†).

The C/N/O stoichiometry agrees reasonably with the theoretical 9 : 2 : 2 ratio (see Table S2, ESI†). Overall, the XPS data suggest that the structure of nit9 is well-preserved after the deposition on the Au(111) surface.

Focusing on the nit9 (nit8) films on Cu, it is crucial to note that the band corresponding to the amide C has practically disappeared (Fig. 2c and Fig. S6, ESI†). Furthermore, the intensity ratio of the two remaining C 1s bands peaking at 285.6 and 284.4 eV has changed with respect to the adsorption on Au and is closer to 1 : 2 (3 : 6). Thus, the C10 atom, which was strongly unshielded in the gas phase and for nit9/Au, is here pushed much closer to C_α, with the corresponding bands now overlapping. The significantly lower C10 CEBE suggests that this atom cannot be anymore bonded to the two highly electronegative atoms but probably only to one of them. This implies that the CONH₂ functionality undergoes a profound chemical transformation following the deposition of nit9 (nit8) on Cu. On the other hand, the low CEBE side of the C 1s XPS is comparable to the Au film and gas phase spectra, suggesting that the ring structure and the methyl C atoms of nit9 remain intact.

The N 1s and O 1s XPS spectra on Cu (Fig. 2c) provide further clues. Both are very different from the weakly interacting nit9/Au system. These spectra show a main and a less intense peak at 398.6 eV and 397.0 eV and 530.7 eV and 529.4 eV, respectively. The N 1s signals with similar characteristics were observed previously in the XPS spectra of peptides adsorbed onto the Cu(110) facet.⁴⁸ In particular, the lowest CEBE component was empirically attributed to amine and amide N atoms in strong interaction with the Cu surface atoms. Thus, the appearance of the small intensity peaks on the low CEBE side of the main peaks can here similarly be explained in terms of the strong CONH₂-substrate interactions. These weaken the C–N and C–O bonds and enhance the screening of the N and O cores by the Cu surface charge density.

Overall, the XPS data suggest that nit9 (nit8) can bind to the Cu surface via CONH₂ with a subsequent, at least partial, decomposition of this anchor. At the same time, the adsorbate stoichiometry is roughly maintained (Table S2, ESI†), indicating that there is no significant C, N or O desorption from the surface.

Fig. 3 shows the core levels obtained from the TEMPO/Au (Fig. 3b) and TEMPO/Cu (Fig. 3c) films on the LN₂-cooled substrates and a comparison with the previously recorded gas phase data (Fig. 3a). The results of TEMPO deposition on the RT and LN₂-cooled Cu(111) are very similar, as proved by their comparison in Fig. S5 (ESI†). The two bands at 291.4 eV and 290.4 eV in the gas phase C 1s spectrum appear broadened and less resolved in the films. Thus, the peak corresponding to the C atoms bonded to N at 285.5 eV (C2 and C6) appears on Au as a high-energy shoulder to the main band at 284.3 eV, with an area ratio of the two bands of 2.8 (cf. 7 : 2 = 3.5 in the gas phase). On Cu, the two bands, located at 285.2 eV and 284.3 eV, are even closer, with an area ratio of 2.4. The N 1s S–T splitting, clearly visible in the gas phase, is barely discernible in the Au film spectra (Fig. 3b).

Importantly, the N 1s and O 1s CEBEs of TEMPO are significantly lower on Cu than on Au. The corresponding values are 400.8 eV and 531.4 eV on Au and 397.8 and 529.5 eV on Cu. This indicates that TEMPO binds strongly to the Cu surface via the NO group and that the interaction is much stronger on Cu than on Au. In order to lower the N and O CEBEs to this extent, the Cu surface must transfer a significant charge to the NO functionality, possibly inducing its decomposition. In contrast, there is no shift between the main peaks of the C 1s film spectra on Au and Cu. Thus, the C skeleton of TEMPO looks unaffected by the adsorption and by the type of substrate. The film stoichiometry is reasonable (Table S3, ESI†), indicating no relevant change in the chemical composition of the molecular layer.

NEXAFS

Further information on the adsorption mechanisms and geometries was obtained from NEXAFS at the O, N and C K-edges. Fig. 4 shows the NEXAFS spectra of the nit9 films on Au and Cu in normal and grazing incidence geometries (NI and GI, respectively). Again, only the results for nit9 and TEMPO films are discussed as nit8 spectra are very similar to those obtained for nit9 and are displayed in Fig. S7 (ESI†). For comparison, we also show our previously measured gas phase spectra assigned using the TD-SRC2-BLYP method.²⁴ The film resonance assignments are based on these data, which are presently also corroborated by the TD-CAM-B3LYP method (see the Computational results section). The gas phase and film NEXAFS spectra have directly comparable energy scales.⁴⁹

Fig. 4 NEXAFS spectra of nit9 in the gas phase and adsorbed onto the Au(111) and Cu(111) surfaces at O K-edge (a) and (d), N K-edge (b) and (e) and C K-edge (c) and (f). Vertical dashed lines are added as guides for better visualization of the peak alignment.

The gas phase and Au film spectra are clearly similar, again indicating a largely preserved structure of nit9 upon adsorption on Au(111). The O K-edge NEXAFS of nit9/Au (Fig. 4a) is characterized by two strong resonances at 529.7 and 531.4 eV. Due to the strong similarity between the film and gas phase data,²⁴ we can attribute these peaks to the O1(1s) → π*(NO) and O2(1s) → π*(CONH₂) transitions, respectively. Also similar to the gas phase, the N K-edge nit9/Au spectrum (Fig. 4b) shows a strong resonance at 399.3 eV due to the N1(1s) → π*(NO) transition.

In contrast, the O K-edge and N K-edge spectra of nit9/Cu (Fig. 4d and e) are much more difficult to interpret, reflecting the complex chemistry at the nit9/Cu interface. Only the C K-edge spectrum (Fig. 4c and f) looks similar for both substrates, showing the same two strong resonances as in the gas phase spectrum (ca. 285 eV and 288 eV). These were attributed to transitions from the C3, C4, and C10 1s levels to mainly π*(CONH₂).²⁴ The C atoms involved are part of the π-system, which conjugates CONH₂ to the C=C double bond. Considering the (partial) decomposition of the CONH₂ anchor inferred from the nit9/Cu XPS spectra, the similarity between the nit9/Au and nit9/Cu C 1s NEXAFS suggests that a part of this π-system may still be preserved in some form in the nit9/Cu films (see the Computational section).

Next, we focus on the dichroic behavior of the resonances for the two substrates in GI and NI. On Au, the π resonances observed at the O and N K-edges (Fig. 4a and b) are stronger in GI than in NI, while the σ resonances, starting from ca. 537 and 407 eV, respectively, show the opposite behavior, although less evident at the N K-edge. On Cu, despite the noisier and less clear spectra, the resonance intensities at the O and N K-edges (Fig. 4d and e) suggest the opposite behavior: the π resonances are stronger in NI than in GI while the σ resonances are slightly stronger in GI. Considering that the polarization vector of the incoming photon beam is perpendicular to the direction of the light (and changes with respect to the surface depending on the incidence angle of the light), we conclude that, on average, nit9 is flat on Au and upright on Cu. This is in line with the measured film thicknesses on the two substrates (vide ante).

Focusing on TEMPO, the NEXAFS spectra were only obtained for the film grown on Cu(111) at RT. As mentioned above, attempts to grow TEMPO/Au films at RT were unsuccessful. In addition, the NEXAFS characterization of TEMPO films grown on the LN₂-cooled Au(111) could not be performed due to beamtime contingencies. The results are shown in Fig. 5 together with the previously obtained gas phase data.

Fig. 5 NEXAFS spectra of TEMPO in the gas phase and adsorbed onto the Cu(111) surface at O K-edge (a), N K-edge (b) and C K-edge (c). Vertical dashed lines are added as guides for better visualization of the peak correspondence between the gas phase and molecular films.

Some of the features of the gas phase spectra are still recognizable in the TEMPO/Cu film (Fig. 5a and b). Thus, the strong gas phase O(1s) → π*(NO) and N(1s) → π*(NO) transitions at 529.3 eV and 399.4 eV²⁴ appear to have their core-to-valence counterparts in the Cu film spectra at slightly different photon energies of 529.6 eV and 398.9 eV. The Rydberg manifold of the film exhibits maxima at about 534 eV for O K-edge and 405 eV for N K-edge, at significantly lower photon energies than in the gas phase (ca. 538 eV and 408 eV respectively).²⁴

For the C K-edge (Fig. 5c), the similarity between the gas phase and TEMPO/Cu film spectra is more pronounced, and all the major gas phase resonances are also visible in the film spectra. This again suggests that the C skeleton is comparatively less affected by the interaction with the Cu surface and that the binding is mainly via the NO group. The strongest gas phase core-to-valence transition occurs at 286.9 eV and was previously assigned to originate from the quasi-equatorial CH₃ groups, viz. C7(C10)(1s) → π*(NO).²⁴ However, an analogous assignment for the TEMPO/Cu system is doubtful knowing that the XPS spectra indicate a very strong NO–Cu interaction, possibly leading to the scission of the N–O bond and disintegration of the NO chromophore (vide ante). Higher in energy, the most intense transitions are of Rydberg origin, such as those at 287.2 eV and 288 eV.

The dichroism observed in NI and GI seems to indicate an upright geometry and adsorption via the NO group. Conversely, in the case of the C K-edge, the entire spectrum is attenuated on moving from GI to NI, which may indicate a lack of an ordered arrangement of the TEMPO rings. However, the film thickness, estimated at ∼4.7 Å, is similar to nit8 and nit9 on Cu. Thus, a strong upright chemisorption of TEMPO on Cu(111) seems the most likely.

Computational results

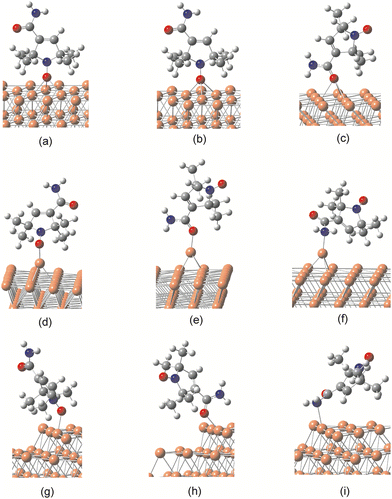
We next examine computational models of adsorption that can potentially explain the key features in the XPS and NEXAFS spectra of the three NRs. The most challenging differences with respect to the gas phase are seen in the XPS spectra of nit8/nit9 on Cu. These include the almost complete disappearance of the amide signal in the C 1s, and the appearance of a single well-resolved smaller peak on the low-energy side of the main signal in the N 1s and O 1s spectra (Fig. 2 and Fig. S6, ESI†).

We commence by optimizing the geometries of the NRs adsorbed onto the Cu and Au surface. Three different models of the Cu slab were considered: the flat (111) surface and two common types of defects. Fig. 6 shows the possible modes of binding to the surface via the NO or CONH₂ group for the nit9/Cu system. Analogous structures were optimized for nit8 and TEMPO. For the adsorption onto Au only the ideal, defect-free Au(111) surface was considered (vide infra). The corresponding adsorption energies are collected in Tables 2 and 3. The coordinates of the optimized unit cells and lattice vectors are provided in the ESI.† Several partial density of states (PDOS) plots given in the ESI† (Fig. S8–S10) provide additional information on the bonding of NRs onto the Au and Cu surfaces.

Fig. 6 Various considered modes of binding in the nit9/Cu system: (a) Cu-flat NO (fcc); (b) Cu-flat NO (hcp); (c) Cu-flat >CO; (d) Cu-adatom NO; (e) Cu-adatom >CO; (f) Cu-adatom NH₂; (g) Cu-step NO; (h) Cu-step >CO; and (i) Cu-step NH₂.

Table 2 Energies (eV) and minimum distances (Å) for the adsorption on the flat Cu(111) surface, Cu adatoms and Cu monoatomic steps

Surface	Cu flat			Cu adatom			Cu step
Type of adsorption	–NO fcc	–NO hcp	>CO hcp	–NO top	–NH2 top	>CO top	–NO top	–NH2 top	>CO top
Bond	Cu–O	Cu–O	Cu–O	Cu–O	Cu–N	Cu–O	Cu–O	Cu–N	Cu–O
d min (Å) – nit8	2.14	2.16	2.59	1.95	2.12	2.04	2.13	2.42	2.11
d min (Å) – nit9	2.14	2.12	2.51	1.96	2.10	1.99	2.12	2.36	2.10
d min (Å) – TEMPO	2.17	2.21	—	1.88	—	—	2.12	—	—
E ads (eV) – nit8	−1.05	−1.00	−0.86	−1.16	−0.95	−0.99	−0.75	−0.65	−0.87
E ads (eV) – nit9	−1.13	−1.10	−0.83	−1.06	−0.98	−0.96	−0.73	−0.69	−0.97
E ads (eV) – TEMPO	−1.00	−0.96	—	−0.82	—	—	−0.75	—	—

---

Table 3 Energies (eV) and minimum distances (Å) for the adsorption on the flat Au(111) surface

Type of adsorption	–NO fcc	–NO hcp	>CO hcp	Parallel
Bond	Au–O	Au–O	Au–O
d min (Å) – nit8	2.87	2.95	2.85	—
d min (Å) – nit9	2.86	2.93	2.93	—
d min (Å) – TEMPO	3.15	3.04	—	—
E ads (eV) – nit8	−0.50	−0.53	−0.44	−0.76
E ads (eV) – nit9	−0.49	−0.50	−0.44	−0.74
E ads (eV) – TEMPO	−0.50	−0.49	—	−0.45

---

Flat surfaces

Cu. On the flat surfaces, NRs prefer to bind via NO to hollow fcc or hollow hcp sites, while other possibilities such as on-top or bridge adsorption sites are disfavored. The differences in E_ads between the fcc and hcp sites are minor, generally within 0.05 eV (Table 2). The O atom resides 1.5–1.6 Å above the surface and is coordinated to three Cu atoms with Cu–O distances in the range of 2.1–2.3 Å.

These Cu–O distances are 0.1–0.3 Å longer than typical Cu–O single bonds,⁵⁰ indicating that a closer approach and a stronger binding to the Cu surface is sterically hindered by the four vicinal CH₃ groups. The distances to the flat surface are slightly larger for TEMPO, suggesting larger steric hindrances for the 6-membered ring due to the more open C–N–C angle.

In the case of nit8/nit9, the N–O axis is tilted by ca. 15° with respect to the surface normal vector. For the more symmetric TEMPO, the tilt is much smaller, about 7°. The π(N–O) orbital is thus not parallel to the surface, suggesting its significant involvement in the bonding. Upon adsorption, the NO bond lengthens by ca. 0.14 Å relative to the isolated NRs, whereas the vicinal C–N bonds are only slightly shortened (<0.01 Å). Conversely, the distant CONH₂ group does not undergo significant structural changes when nit8/nit9 binds to the surface via NO. In addition, nit8/nit9 could bind to the flat surface via the amide O atom, which also prefers the hollow adsorption site (Fig. 6c). However, in this case the Cu–O distances are ca. 0.4 Å longer, and this adsorption mode is predicted to be only weakly competitive to the adsorption via NO (ca. 0.2–0.3 eV smaller E_ads; Table 2).

Au. The flat Au surface shows a much weaker affinity for the NO and CONH₂ functionalities, with the adsorption energies generally halved compared to the adsorption on Cu (Table 3). The shortest Au–O distances range from 2.9 to 3.0 Å, which is much longer than the Au–O distance of 2.17 Å for the adsorption of the O atom on Au(111)⁵¹ or the Au–O bonds of 2.0–2.4 Å typically seen for the ligands coordinated to Au.⁵² Also noteworthy are the 0.1–0.3 Å longer Au–O distances for the TEMPO adsorption. However, the binding energies for all three NRs remain similar.

Since we observed a significantly smaller thickness of the NR films on Au than on Cu, we additionally optimized the structures in which the NRs lie parallel to the flat Au surface. The computations suggest that the reclining orientation reduces the thickness by ca. 1 Å compared to the upright orientation, i.e. the adsorption via either NO or CONH₂. The reclining NRs are indeed predicted to interact more strongly with Au (by >0.2 eV, Table 3). Importantly, the reclining orientation of nit8/nit9 allows for the strong H bonds between CONH₂ groups of neighboring molecules (vide infra), as is also suggested by the XPS data. To describe them explicitly, much larger unit cells containing at least two H-bonded nit8/nit9 molecules would be required. On the other hand, for TEMPO the reclining orientation implies mainly the noncovalent interactions with the Au surface, whose appropriate description requires van der Waals-corrected density functionals. It has been observed, however, that the differences with respect to the uncorrected parent functionals are typically small (within 0.05 eV).⁵³

Surface defects

Cu. Modeling adsorption only on ideally flat metal facets is insufficient to gain a deeper insight into the adsorption dynamics on realistic surfaces.⁵⁴ In particular, metals with comparatively low cohesive energies such as Cu (3.49 eV per atom)⁵⁵ are prone to rapidly developing ubiquitous structural defects such as terraces, steps and dislocations, depending on the preparation conditions.⁵⁶ These involve low-coordinated mobile Cu atoms that act as hubs for catalytic transformations of adsorbates.⁵⁷ Importantly, the adsorption itself, especially at high coverages, can promote major restructurings and thus further activation of the surface.⁵⁷

To investigate the role of common surface defects, we additionally studied the binding of NRs onto: (a) a single atom island (adatom), one per unit cell and located above the hcp-hole; and (b) monatomic steps at the edge of the 10-atom equilateral terrace created by removing 6 top-layer metal atoms from the unit cell (Fig. 6d–i). Both types of defects involve exposed Cu atoms protruding from the surface. Apart from being more reactive, such atoms can greatly reduce the steric hindrance, allowing a closer approach of the NRs to the surface.

We have found that the preferred mode of binding to the adatom or the monoatomic step is on-top (Fig. 6d–f). Avoiding the steric clash with the CH₃ groups leads to shortening of the nearest Cu–O distances by up to 0.5 Å compared to adsorption on the flat Cu surface (Table 3). The binding is generally stronger on the adatoms than on the steps. For the adsorption via NO, the Cu–N–O angle is 126°, indicating that the in-plane and out-of-plane N–O orbitals play comparable roles in the binding to the Cu adatoms. The NO group of nit8/nit9 binds to the adatom as strongly as to the flat Cu surface. In contrast, the E_ads of TEMPO is significantly reduced on the adatom.

For the adsorption via CONH₂, the Cu–O and Cu–N axes approximately follow the direction of the lone pairs on the O and N atoms; the Cu–O–C and Cu–N–C angles for the structures in Fig. 6e and f are 139° and 118°, respectively. In the case of the binding via NH₂, the nit8/nit9 ring is positioned quasi-parallel to the surface (Fig. 6f) to avoid the largely unfavorable C–N rotation that has been extensively studied in amides.⁵⁸ However, the structures with both carbonyl and amino groups bonded to the Cu surface exhibit significantly elongated C=O and C–NH₂ bonds. Consequently, these structures likely play a role in the disintegration of the CONH₂ anchor on the Cu steps (see the section on the mechanism below).

Crucially, the computed energies of adsorption indicate that the binding to the adatom via either the NH₂ or the CO part of the amide becomes closely competitive with the binding via the NO group (Table 2). Furthermore, in the case of monatomic step defects, E_ads is already clearly in favor of the adsorption via CO. Thus, E_ads for the adsorption via amide O and N atoms generally increases on defects. Conversely, in the case of the adsorption via NO, E_ads remains about the same on adatoms but is less favorable on monatomic steps. The reason for this is that the exclusively electron-donating CONH₂ group is more attracted to the electronically poorer undercoordinated Cu atoms. On the other hand, the paramagnetic NO center is in principle redox-flexible, being capable of acting as an electron acceptor, forming the nitrosyl (NO⁻) anion, or as an electron donor, forming the nitrosonium (NO⁺) cation. However, concerning the adsorption onto the present substrates, the electron-accepting role of NO prevails (see the discussion on atomic charges below).

Au. Deviations from the ideal flatness of the Au(111) surface are mainly due to a 22 × √3 periodic reconstruction of the top layer, which is unique to Au.⁵⁹ This gives rise to the corrugation pattern resembling a herringbone with some of the top-layer Au atoms slightly puckered above the surface (by ca. 0.2 Å).⁶⁰ It has been shown however that ignoring this reconstruction and assuming that the Au(111) surface is perfectly flat introduces only small errors in the computed adsorption energies.⁶¹ We still note that a slightly stronger binding was observed at the so-called elbow sites of the Au herringbone.⁶²

Atomic charges

The computed Voronoi atomic charges⁶³ further quantify type and extent of the interaction of NRs with the Cu and Au surfaces (Tables S6 and S7, ESI†). These show that NO bonded to Cu generally acts as an electron acceptor, receiving more charge from the flat surface than from the step atom. In contrast, CONH₂ bonded to Cu donates the charge to the surface, and the donation is more efficient on the steps. Both N and O atoms accept (donate) the charge in NO (CONH₂). Interestingly, on the flat Cu surface, within the NO group, the N atom receives twice more charge than O.

We next analyze the differences between α and β spin densities (Δ_αβ) based on the Mulliken charges (Tables S8 and S9, ESI†), specifically, the sum of Δ_αβ for NO N and O atoms. In non-bonded NRs, this sum is >0.9e, confirming the presence of the single unpaired electron localized on NO. Importantly, when NRs bind to flat Cu via NO, the Δ_αβ differences reduce to zero, which implies the full saturation of the NO radical centre and thus the complete loss of magnetism. However, the saturation is only partial when NO binds to the Cu steps (Δ_αβ(N) + Δ_αβ(O) ≈ 0.7e). Conversely, binding via the N and O atoms of CONH₂, either on the flat Cu or on the step, fully preserves the unpaired spin density (Δ_αβ(N) + Δ_αβ(O) > 0.9e).

On the other hand, the charge transfer between NRs and Au surfaces is comparatively small, reflecting generally weaker interactions with the Au surface. The Mulliken spin densities also show that the deposition on Au largely preserves the magnetism of the NR films. Thus, regardless of the mode of adsorption the Δ_αβ(N) + Δ_αβ(O) sum remains around 0.9e. The same holds when the NRs recline parallel to the Au surface (Table S9, ESI†).

Modeling XPS

Fig. 7 shows the computed C, N, and O 1s CEBEs in the nit9/Cu system for all the adsorbate/adsorbent geometries investigated (Table 2). The computed C, N, and O 1s XPS spectra require upshifting by several eV to match the measured peaks. The magnitudes of the shifts were determined from the nit9/Au system, as this has an easily assignable XPS spectrum that clearly corresponds to gas phase XPS (Fig. S15, ESI†). As the same DFT method and basis set were used to model the adsorption on Au and Cu, the same shifts had to be applied consistently to the core energies computed for the NR/Cu systems. This is important, considering that the interpretation and assignment of the bands are much more challenging for the Cu substrate and depend critically on the shifts used. Correlating the one-electron energies of the core orbitals with CEBEs comes with an important caveat because it neglects the effect of the core-hole relaxation that subtly reflects the chemical environment of the core-ionized atom.²³ The performance of the (TD-)DFT methods used here is calibrated by computing the gas phase XPS and NEXAFS spectra of the three NRs (Fig. S11, S12 and Table S5, ESI†).

Fig. 7 Experimental XPS spectra and computed C, N, and O 1s CEBEs for the different modes of adsorption of nit9 on the flat Cu surface, on Cu adatoms, and on Cu monoatomic steps (“w/o” stands for “without”); see Fig. 6 for the structures. The upward energy shifts of 5.0 (C 1s), 5.4 (N 1s), and 7.5 eV (O 1s) were applied to the modelled spectra.

Au XPS. The XPS spectra of the NR/Au films are similar to the gas phase data for all three NRs. An important difference is the >1 eV larger separation of the NO and CONH₂ peaks in the N 1s spectra of nit8/nit9 on Au (Fig. 2, Fig. S6 and Table S1, ESI†). This is a clear indication that on Au nit8/nit9 molecules aggregate into dimers held together by relatively strong intermolecular H bonds that can form between the two CONH₂ groups. The H bonding increases the negative charge on the donor N atom and shifts the CONH₂ N 1s CEBE to lower energies while leaving the NO N 1s CEBE unaffected. The structures of such H-bonded dimers of nit8 and nit9, optimized in the gas phase, are shown in Fig. S22 (ESI†). An inspection of the core orbital energies confirms the larger separation (by 0.3–0.4 eV) between NO and CONH₂ N 1s CEBEs in the dimers compared to the monomers. Interestingly, the separation of N 1s peaks in the nit8/Au system is by 0.4 eV smaller than for nit9/Au (Table S1, ESI†). This suggests that the stronger intermolecular H bonds are formed in nit9, which can be explained in terms of the conjugation of CONH₂ with the vicinal C=C bond.

The analogous difference in the peak separation between the gas-phase and the nit8/Au (nit9/Au) films is also observed in the O 1s XPS spectra; however, the effect here is comparatively minor (Table S1, ESI†), viz. only 0.3 (0.5 eV) larger separation in the O 1s XPS of nit8/Au (nit9/Au); indeed, the O 1s orbital energy differences between the nit8 (nit9) monomers and H-bonded dimers come out very small, <0.1 eV.

Overall, we conclude that the energy differences between the NO and CONH₂ XPS peaks are larger in the nit8/Au and nit9/Au films than in the gas-phase. This is primarily seen in the N 1s and to a less extent in the O 1s XPS, and is consistent with the formation of the weakly physisorbed H-bonded dimers. This is also in line with the parallel orientation of the nit8/nit9 monolayers on Au, which allows for the formation of such H-bonded dimers.

Cu XPS. The C 1s XPS results of nit8/nit9 on Cu (Fig. 2 and Fig. S6, ESI†) reveal that the strongly deshielded signal due to the amide C (C10) almost disappears, but that none of the C atoms is missing. It is clear from Fig. 7 that no model that preserves the CONH₂ group is able to reproduce this particular spectral feature, as the C10 CEBE is never sufficiently red-shifted to appear below the main signal. To satisfactorily explain this greatly reduced CEBE, it has to be assumed that C10 is no longer bonded to the two highly electronegative atoms. This in turn suggests that either one of the C–NH₂ or C=O bonds on the Cu surface is greatly extended or completely broken in a homolytic manner, which may ultimately lead to complete detachment of the NH₂ or O fragments. The primary sites for the (partial) decomposition of the CONH₂ anchor and binding of the resulting nit8/nit9 residues should be the surface defects, such as steps, which are more reactive and where the strong steric hindrances can be relieved.

As a model for the decomposition, we consider four plausible fragments of nit8/nit9 (Fig. 8) that could possibly remain on the Cu surface after the partial decomposition of the CONH₂ group. These are: (a) the fragment without NH₂ (the C–NH₂ bond is broken); (b) the fragment without O (the C=O bond is broken); (c) the NH₂ fragment; and (d) the O atom. The fragments (a) and (b) are computed as bonded to the monoatomic Cu steps via C10, while the smaller fragments (c) and (d) are bonded to the flat Cu surface. The bridge as the preferred adsorption mode for the NH₂ fragment agrees with a previous study, as does the 1.1 Å distance of the O atom from the Cu surface.⁶⁴

Fig. 8 Fragments of nit9 bonded onto the Cu surface: (a) nit9 w/o NH₂ (Cu step); (b) nit9 w/o O (Cu step); (c) NH₂ (bridge site; flat Cu); (d) O atom (hcp site; flat Cu). Analogous fragments are considered for nit8 (see ESI† for the structures).

Both (a) and (b) fragments have C10 firmly bonded to the Cu step atom with a Cu–C10 distance of ca. 2 Å. In both fragments, the C10 CEBE is shifted closer to the C2 and C3 CEBEs, which is now in much better agreement with the observed C 1s XPS spectra (Fig. 7; “step w/o O” and “step w/o NH₂”). Similarly, the N 1s and O 1s CEBEs of the NH₂ and O fragments adsorbed on the flat Cu surface agree well with the weaker signals observed on the low-energy side of the main peaks (Fig. 7). The different intensity of the two N 1s and O 1s XPS signals reflects the two possible pathways of the CONH₂ decomposition, viz. the C–NH₂ and C=O dissociation. Thus, the 397.0 eV signal is weak because it is due only to the NH₂ fragment whereas the one at 398.7 eV is strong because it is due to the two overlapping contributions, viz. the NO group and the N atom of the “step w/o O” structure (Fig. 7).

It is thus seen that the N 1s BE of NO is pushed down as low as 398.7 eV (Fig. 7). Considering the standard relationship between CEBEs and partial atomic charges²³ this substantially lowered value is attributable to the long-range effects of the Cu surface. Since NO acts as the electron-acceptor (vide ante), the closer it is to the Cu surface, the more lowered are the N 1s and O 1s BEs. Exactly the opposite holds for the CONH₂ group which acts exclusively as the electron-donor. Although the BEs of NO in “step w/o O” and “step w/o NH₂” are indeed lowered relative to the other models (with the exception of the “flat NO”), the BEs still come out higher than the main 398.7 eV peak (Fig. 7). However, this error would be reduced if the herein neglected relaxation of the final N 1s core-hole state were taken into account.

It is noteworthy that the COOH group in 3CP also plays the role of a strong anchor on the Cu(110) surface, but the occurrences upon the chemisorption seem to be fundamentally different; namely, COOH loses the H atom and its O atoms bind symmetrically to Cu via the bridge bonding-mode.²⁸ Here, however, such a simple dehydrogenation would not be sufficient to explain the spectral data, in particular the significantly reduced C10 XPS signal. Therefore, we conclude that the CONH₂ anchor decomposes to a much greater extent than the COOH does.

This decomposition does not seem to produce stable species that would desorb from the Cu surface, e.g. the recombination of two O atoms to form O₂ does not occur because the O content remains unchanged within the experimental error (Table S2, ESI†). Other conceivable degradation pathways for anchored CONH₂ include the industrially important dehydrogenation of primary amides to nitriles.⁶⁵ However, it is unlikely that such a transformation would proceed to completion on the clean Cu surface, knowing that special catalysts, dehydrating substances, and/or high temperatures are usually required;⁶⁵ in particular, no traces of water from dehydration were presently observed. Nevertheless, our data provide evidence that, at ambient temperatures and UHV conditions, the clean Cu surface is at the very least capable of initiating the process of CONH₂ decomposition by catalyzing the scission of the C=O and C–NH₂ bonds.

According to Table 3, binding of the NRs via NO should also occur, especially on flat portions of the Cu surface. In this case, the N 1s signals of NO and CONH₂ are found to be much closer than on Au or in the gas phase (Fig. 7; “flat NO”), due to the substantial charge donation that NO receives from the Cu surface. However, in the TEMPO/Cu system, where there is no alternative to the binding via NO, the XPS spectra provide clear clues as to the fate of the chemisorbed NO group (Fig. 3 and Fig. S18, ESI†). In this case, as anticipated above, the NO functionality is likely to decompose. In fact, a model in good agreement with these data involves the scission of the N–O bond leading to the highly screened N and O atoms. The O content is close to the stoichiometric value (Table S3, ESI†), therefore the eliminated O atom likely remains bonded to the Cu surface at a hollow site (the 529.4 eV signal), whereas TEMPO without O binds to the surface via the N atom (the 397.8 eV signal; the optimized structure is given in the ESI†). This results in a strong Cu–N bond which for steric reasons should only be realizable at the exposed (e.g. step) Cu atoms.

The computations suggest that a fraction of potentially undamaged NO groups would be visible in the spectra towards higher N 1s and O 1s CEBEs; however, in particular, the O 1s XPS is very noisy in this region and so any additional signal cannot be clearly confirmed. Overall, the NO radical center is likely quantitatively decomposed upon chemisorption on Cu; consequently, the TEMPO/Cu thin films should be largely devoid of magnetism.

On the other hand, in the case of nit8 (nit9), the strongly attenuated amide C 1s signal (Fig. 2c and Fig. S6c, ESI†) reveals that the binding via NO is largely superseded by the binding via the CONH₂ anchor. As discussed above, for nit8/nit9 the adsorption via CONH₂ is preferred to the adsorption via NO primarily on Cu adatoms or steps (Table 3), whereas for TEMPO, Cu steps are required to have sterically favorable conditions that allow the predicted NO fragmentation. All these elements highlight the critical role of Cu defects. It should be noted that, prior to the deposition, the hexagonal diffraction pattern of the Cu(111) surface was guaranteed by a thorough annealing and further verified by the LEED (low-energy electron diffraction). Therefore, similarly to previous works,^57,66 an adsorption-induced surface reconstruction of Cu is likely to occur, which in turn strongly influences the surface adsorption dynamics of the NR thin films.

Modeling NEXAFS

Fig. 9 shows the experimental GI and NI NEXAFS spectra of the nit9/Cu films with the superimposed TD-DFT excitation energies and oscillator strengths. The data for the nit9/Au system are shown in Fig. S17 (ESI†). The corresponding data for nit8 are given in Fig. S16 and S21 (ESI†), and for TEMPO in Fig. S20 (ESI†). The optimal energy shifts for the computed C, N, and O 1s core excitation energies are derived from the gas phase modeling of the nit9 NEXAFS using the identical TD-DFT method (Fig. S12, ESI†).

Fig. 9 Experimental NEXAFS spectra and computed C, N, and O 1s core excitations for the different modes of adsorption of nit9 on the flat Cu surface and Cu monoatomic steps (“w/o” denotes “without”); see Fig. 6 for the structures. The upward energy shifts of 10.2 (C 1s), 12.2 (N 1s), and 13.8 eV (O 1s) were applied to the modelled spectra.

Au NEXAFS. The positions and intensities of the core-excitations for the gas phase and the nit9/Au film are very similar, and, after the upshift, both computed spectra agree well with the experimental data (Fig. S12 and S17, ESI†). Accordingly, the previous assignments of the gas phase spectra²⁴ are essentially unchanged for the nit9/Au system.

As discussed above, the parallel orientation of the nit9 monolayer above the Au surface enables the formation of intermolecular H bonds between the nit9 monomers. The H bonds have a subtle effect on the energies of the core levels, especially the π*(CONH₂) virtual orbitals. To check whether the NEXAFS data are consistent with this hypothesis, we computed the (gas phase) core-excited spectra of nit9 monomers and H-bonded dimers (Table S10, ESI†). The aim was to correlate the computed monomer and dimer spectra respectively with the gas phase and nit9/Au measured NEXAFS spectra.

The key differences are most obvious in the O K-edge spectra. The experimental data show that, in the nit9/Au O K-edge NEXAFS, the two strong transitions, viz. O1(1s) → π*(NO) and O2(1s) → π*(CONH₂), are 0.17 eV further apart than in the gas phase. The TD-DFT computed difference in the separation between the two peaks is 0.22 eV, which agrees well with this value. We conclude that the nit9/Au NEXAFS also supports the hypothesis that H-bonded aggregates are formed when nit9 monomers recline parallel to the Au surface. The successful use of the gas phase models for comparison with the Au film spectra confirms the very weak interaction of nit9 with the Au surface and the negligible involvement of the Au surface states in the observed NEXAFS transitions.

We also considered a model consisting of one NR molecule weakly physisorbed via NO onto the fcc (or hcp) hole of the flat Au surface (“flat via NO”; Fig. 9). This model does not involve the intermolecular H-bonding and indeed deviates more from the experiment because it predicts the smaller distance between the two N 1s XPS peaks and the poorer CEBE of the C10 atom (Fig. S14 and S15, ESI†). Interestingly, the KS-DFT MO spectrum of this model exhibits the orbital energy inversion between the π*(N–O) SOMO and several of the doubly occupied MOs (DOMO) localized mainly on the Au cluster. The corresponding unoccupied level in the β-spin set is also found above the LUMO, which is also seen from the PDOS plots (Fig. S10, ESI†). Organic radical materials exhibiting the SOMO–DOMO inversions are of interest as they show promise for applications such as OLEDs and spintronics.⁶⁷

Cu NEXAFS. For modeling the NEXAFS spectra of the nit9/Cu films, we used the same structures and binding modes considered above for modeling the XPS (Fig. 6–8). Focusing on the C K-edge NEXAFS, the computations provide evidence that even after the partial decomposition of the CONH₂ anchor, i.e. with NH₂ or O removed, the remnants of the amide π-system can still give rise to the three strong transitions from the C3, C4, and C10 core levels (Fig. 9). The lower peak, observed at 285.4 eV (nit8) and 284.6 eV (nit9), is much weaker and blue-shifted in nit8 (Fig. S7, ESI†) because of the absence of the C=C double bond. At the same time, no strong transitions are predicted from the C core levels to the π*(NO) virtual orbital. Overall, the C K-edge NEXAFS spectral features do not seem to be drastically changed in the structures with the partially decomposed CONH₂ compared to the “flat via NO” structure where CONH₂ is intact (Fig. 9). This explains the apparent similarity between the C K-edge nit9/Au and nit9/Cu NEXAFS (Fig. 4).

On the other hand, the N 1s and O 1s spectra reveal more about the state of the NO radical center. Crucially, the transitions to the SOMO, viz. N2 1s (O2 1s) → π*(NO), remain very strong in the structures bonded onto Cu steps via C10 (“w/o O” and “w/o NH₂”; Fig. 9). Conversely, when nit9 binds to the flat Cu surface via NO (“flat via NO”; Fig. 9), the surface donates enough charge to the SOMO to make it doubly occupied (Table S8, ESI†). As a result, the transitions to π*(NO) are largely attenuated, and the only prominent low-lying transitions remain from the N1 and O1 core levels to π*(CONH₂). However, these transitions are predicted to be relatively weak. While the high fuzziness of the experimental spectra hampers unequivocal assignments, the prominent spikes observed at 399.2 and 400.0 eV in the N K-edge (NI) and at 530.0, 532.0, and 532.4 eV in the O K-edge (NI) could originate from the transitions to π*(NO). We note that the complex jaggedness of the N K-edge and O K-edge NEXAFS concurs with the presence of small N- and O-containing fragments attached to the Cu surface (Fig. 9 and Fig. S20, S21, ESI†).

Similarly to the XPS, the NEXAFS spectra of the TEMPO/Cu films are consistent with the decomposition of the NO functionality leading to the formation of the Cu–N bond and the detached O atom. Accordingly, the low-lying N K-edge peak observed at the GI (398.9 eV; Fig. 5 and Fig. S20, ESI†) originates from the transition to the σ*(Cu–N) LUMO. The similar GI spike at 529.6 eV in the O K-edge NEXAFS corresponds well to the lowest transition in the O atom/Cu system (Fig. S20, ESI†). Conversely, due to the charge donation to the π*(NO) SOMO level and its consequent saturation, the “flat via NO” structure does not provide any strong transitions in the lower regions of the N and O K-edge NEXAFS, which is contrary to what is observed.

Mechanism of the CONH₂ decomposition

Here we tentatively discuss possible initial steps of the CONH₂ anchor decomposition in the nit9/Cu system. We first note that the binding of the C=O or NH₂ group on top of the Cu step atom already significantly increases the C=O and C–NH₂ bond lengths relative to the free CONH₂ group (taken from the structure in Fig. 6b). Thus, the C=O bond elongates from 1.245 Å (Fig. 6b) to 1.269 Å (Fig. 6h), and the C–NH₂ bond from 1.388 Å (Fig. 6b) to 1.425 (Fig. 6i).

The next step in the mechanism plausibly involves a structure where nit9 becomes bonded to the Cu surface simultaneously via C=O and NH₂, which should further activate the C=O and C–NH₂ bonds rendering them more vulnerable to the scission. While an exhaustive investigation of the mechanism falls outside the present scope, we present one such optimized structure in Fig. S23 (ESI†). Here, C=O is tilted from its on-top position and now bridges the two Cu step atoms (d(Cu–O) = 2.173 and 2.295 Å) while NH₂ binds on-top to the terrace Cu atom (d(Cu–NH₂) = 2.172 Å). Importantly, the C=O and C–NH₂ bonds thereby become even more elongated, 1.307 and 1.471 Å, respectively. This structure lies 20 kcal mol⁻¹ above that in Fig. 6h.

We also attempt a rough estimate of the overall reaction energy corresponding to the reactants in Fig. 6h or i converting into the products in Fig. 8a (the C–NH₂ bond breaks) or 8b (the C=O bond breaks), respectively accompanied by the chemisorption of the NH₂ (Fig. 8c) or O (Fig. 8d) fragments. The full details of the computation are given in Table S11 (ESI†). Both reactions come out as only slightly endothermic; viz. 8.8 kcal mol⁻¹ for the C=O and 7.3 kcal mol⁻¹ for the C–NH₂ scission. However, the largest positive contribution to these estimates comes from the C=O and C–NH₂ bond energies which were currently evaluated in vacuo. Consequently, the reaction energies corrected for the actual scission of these bonds taking place on the Cu surface should be significantly lower and likely exothermic.

Conclusions

In this work we have shown that monolayer films of NRs such as TEMPO, nit8 and nit9 can be efficiently grown on the Au(111) and Cu(111) surfaces by evaporation under UHV conditions. The thus-obtained molecular films were analyzed using XPS and NEXAFS spectroscopic techniques and DFT/TD-DFT computations. Our main findings point to the fundamentally different behavior of NRs on the two surfaces, namely physisorption on Au and chemisorption on Cu.

NRs interact only weakly with the Au surface preferring the parallel to the upright orientation accompanied by the formation of dimers held together by the H bonds between the two CONH₂ groups. TEMPO also prefers the parallel orientation on Au, thus avoiding the NO⋯Au interaction, even in the absence of the possibility of intermolecular H bonding.

On the Cu substrate, nit8 and nit9 are mostly chemisorbed via the CONH₂ group, which then undergoes a partial decomposition. The key spectral evidences include the loss of the amide C signal and the extra small peaks in the N and O 1s XPS spectra, together with the complexly jagged N and O K-edge NEXAFS spectra. The computations highlight the decisive role of the Cu surface defects in this process. Therefore, the defects are crucial in preserving the NO radical center and consequently the magnetism of the nit8/Cu and nit9/Cu films.

On the other hand, in the absence of an alternative anchor, the binding of TEMPO onto the Cu surface takes place necessarily via the NO functionality. As a result, the SOMO level becomes saturated when NO receives a charge from the Cu surface. The XPS and NEXAFS spectra and the corresponding computational models consequently indicate the complete destruction of the NO functionality and thus the loss of the magnetism in the TEMPO/Cu thin films.

Finally, we offer a perspective on the application potential of the thin films obtained by the direct grafting of three NRs onto the Au and Cu surface. Despite the challenges encountered, the results open up exciting prospects for the development of advanced applications and functional materials. On the Au surface, the preference for a parallel orientation and the formation of H-bonded dimers suggest the possibility of assembling ordered structures with conserved magnetic properties, provided that such films could be efficiently immobilized. On the other hand, nit8 and nit9 Cu films show remarkable robustness. On the more reactive Cu surface, despite the partial decomposition of the CONH₂ anchors, the preservation of the NO functionality represents a particularly promising feature. Optimizing the anchoring reactivity via appropriate passivation of the Cu surface could lead to stable thin films with preserved magnetic properties paving the way for applications such as sensing, data storage, catalysis and spintronics. Thus, our research offers a detailed insight into the promising future of thin films obtained from the NR grafting, underlining the richness of possibilities that arise from the active management of surface-molecule interactions.

Author contributions

All authors have given approval to the final version of the manuscript. R. T. and I. L.: conceptualization, formal analysis, methodology, data curation, analysis, writing; S. M., V. K., M. J., G. B., A. C., C. G., F. G., S. D’A.: M. d. S., P. M. S.: investigation, software, writing – review and editing, P. M., N. T.: investigation, writing – review and editing; M. C.: investigation, conceptualization, supervision, funding.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work of I. Lj. is supported in full by the Croatian Science Foundation under the project numbers IP-2020-02-9932 and IP-2022-10-4658. I. Lj. gratefully acknowledges the computational time at the Isabella cluster (isabella.srce.hr) administered by the University of Zagreb Computing Center (SRCE). P. M. S. and P. M. acknowledge the partial support through the project EUROFEL-ROADMAP ESFRI of the Italian MUR. We acknowledge Elettra Sincrotrone Trieste for providing access to its synchrotron radiation facilities (proposals nr. 20207147, 20210154, 20222194). The CERIC-ERIC consortium and the Czech Ministry of Education, Youth and Sports (project LM2023072) are acknowledged for financial support. Fabio Zuccaro is acknowledged for technical support during beamtime preparation and realization.

Notes and references

1. T. M. Christensen, Understanding Surface and Thin Film Science, CRC Press, Boca Raton, FL, 1st edn, 2023.
2. Z. A. Lamport, M. R. Cavallari, K. A. Kam, C. K. McGinn, C. Yu and I. Kymissis, Adv. Funct. Mater., 2020, 30, 2004700.
3. K. L. Chopra, P. D. Paulson and V. Dutta, Prog. Photovolt: Res. Appl., 2004, 12, 69.
4. N. Wang, A. Yang, Y. Fu, Y. Li and F. Yan, Acc. Chem. Res., 2019, 52, 277.
5. H. Klauk, Chem. Soc. Rev., 2010, 39, 2643.
6. J. Song, H. Lee, E. G. Jeong, K. C. Choi and S. Yoo, Adv. Mater., 2020, 32, 1907539.
7. M. Mas-Torrent, N. Crivillers, R. Concepció and J. Veciana, J. Chem. Rev., 2012, 112, 2506.
8. M. B. Casu, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 39.
9. Z. X. Chen, Y. Li and F. Huang, Chem, 2021, 7, 288.
10. A. Cornia, D. R. Talham and M. Affronte, Thin Layers of Molecular Magnets in Molecular Magnetic Materials: Concepts and Applications, ed. B. Sieklucka and D. Pinkowicz, Wiley-VCH Verlag, 1st edn, 2017, pp. 187–229.
11. M. Mas-Torrent, N. Crivillers, V. Mugnaini, I. Ratera, C. Rovira and J. Veciana, J. Mater. Chem., 2009, 19, 1691.
12. M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490.
13. L. Tesi, F. Stemmler, M. Winkler, S. S. Y. Liu, S. Das, X. Sun, M. Zharnikov, S. Ludwigs and J. van Slageren, Adv. Mater., 2023, 35, 2208998.
14. G. M. Rosen, L. K. Griffeth, M. A. Brown and B. P. Drayer, Radiology, 1987, 163, 239.
15. T. Janoschka, M. D. Hager and U. S. Schubert, Adv. Mater., 2012, 24, 6397.
16. R. A. Sheldon and I. W. C. E. Arends, J. Mol. Catal. A: Chem., 2006, 251, 200.
17. S. Wertz and A. Studer, Green Chem., 2013, 15, 3116.
18. J. Nicolas, Y. Guillaneuf, C. Lefay, D. Bertin, D. Gigmes and B. Charleux, Prog. Polym. Sci., 2013, 38, 63.
19. D. Yang, C. Feng and J. Hu, Polym. Chem., 2013, 4, 2384.
20. D. Genovese, A. Baschieri, D. Vona, R. E. Baboi, F. Mollica, L. Prodi, R. Amorati and N. Zaccheroni, ACS Appl. Mater. Interfaces, 2021, 13, 31996.
21. I. Ljubić, A. Kivimäki, M. Coreno, S. Kazazić and I. Novak, Phys. Chem. Chem. Phys., 2018, 20, 2480.
22. B. Kovač, I. Ljubić, A. Kivimäki, M. Coreno and I. Novak, Phys. Chem. Chem. Phys., 2014, 16, 10734.
23. I. Ljubić, J. Chem. Theory Comput., 2014, 10, 2333.
24. I. Ljubić, A. Kivimäki and M. Coreno, Phys. Chem. Chem. Phys., 2016, 18, 10207.
25. R. Totani, I. Ljubić, A. Ciavardini, C. Grazioli, F. Galdenzi, M. de Simone and M. Coreno, Phys. Chem. Chem. Phys., 2022, 24, 1993.
26. N. Niermann, T. H. Degefa, L. Walder, V. Zielke, H.-J. Steinhoff, J. Onsgaard and S. Speller, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 235424.
27. P. Krukowski, W. Kozlowski, W. Olejniczak, Z. Klusek, M. Puchalski, P. Dabrowski, P. J. Kowalczyk, K. Gwozdzinski and G. Grabowski, Appl. Surf. Sci., 2008, 255, 1921.
28. A. Robin, L. Marnell, J. Bjork, M. S. Dyer, P. S. Bermudez, S. Haq, S. D. Barrett, M. Persson, A. Minoia, R. Lazzaroni and R. Raval, J. Phys. Chem. C, 2009, 113, 13223.
29. A. Bencini, G. Rajaraman, F. Totti and M. Tusa, Superlattices Microstruct., 2009, 46, 4.
30. O. Swiech, N. Hrynkiewicz-Sudnik, B. Palys, A. Kaim and R. Bilewicz, J. Phys. Chem. C, 2011, 115, 7347.
31. F. Grillo, H. Früchtl, S. M. Francis, V. Mugnaini, M. Oliveros, J. Veciana and N. V. Richardson, Nanoscale, 2012, 4, 6718.
32. N. Crivillers, M. Mas-Torrent, C. Rovira and J. Veciana, J. Mater. Chem., 2012, 22, 13883.
33. R. Kakavandi, S.-A. Savu, S. Sorace, D. Rovai, M. Mannini and M. B. Casu, J. Phys. Chem. C, 2014, 118, 8044.
34. V. Lloveras, E. Badetti, K. Wurst, V. Chechik, J. Veciana and J. Vidal-Gancedo, Chem. Eur. J., 2016, 22, 1805.
35. L. Zhang, Y. B. Vogel, B. B. Noble, V. R. Gonçales, N. Darwish, A. Le Brun, J. J. Gooding, G. G. Wallace, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2016, 138, 9611.
36. M. R. Ajayakumar, I. Alcón, S. T. Bromley, J. Veciana, C. Rovira and M. Mas-Torrent, RSC Adv., 2017, 7, 20076.
37. M. B. Casu, Acc. Chem. Res., 2018, 51, 753.
38. M. R. Ajayakumar, C. Moreno, I. Alcón, F. Illas, C. Rovira, J. Veciana, S. T. Bromley, A. Mugarza and M. Mas-Torrent, J. Phys. Chem. Lett., 2020, 11, 3897.
39. L. Poggini, A. Lunghi, A. Collauto, A. Barbon, L. Armelao, A. Magnani, A. Caneschi, F. Totti, L. Sorace and M. Mannini, Nanoscale, 2021, 13, 7613.
40. https://www.elettra.eu/elettrabeamlines/material_science.html .
41. https://www.elettra.eu/elettra-beamlines/vuv.html .
42. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
43. A. García, N. Papier, A. Akhtar, E. Atracho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerdá, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. Gale, P. García-Fernandez, V. M. García-Suárez, S. García, G. Huhs, S. Illera, R. Korytár, P. Koval, I. Lebedeva, L. Lin, P. López-Tarifa, S. G. Mayo, S. Mohr, P. Ordejón, A. Postnikov, Y. Pouillon, M. Pruneda, R. Robles, D. Sánchez-Portal, J. M. Soler, R. Ullah, V. W.-Z. Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108.
44. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
45. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, 1327.
46. O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2002, 117, 9154.
47. A. Rüdel, U. Hergenhahn, K. Maier, E. E. Rennie, O. Kugeler, J. Viefhaus, P. Lin, R. R. Lucchese and A. M. Bradshaw, New J. Phys., 2005, 7, 189.
48. (a) C. Méthivier, V. Humblot and C.-M. Pradier, J. Phys. Chem. C, 2016, 120, 27364; (b) V. Feyer, O. Plekan, N. Tsud, V. Lyamayev, V. Chab, V. Matolin, K. C. Prince and V. Carravetta, J. Phys. Chem. C, 2010, 114, 10922.
49. Because in the NEXAFS electrons are photoexcited and not ionized the substrate work function, which causes the misalignment in the XPS BEs, does not need to be taken into account.
50. D. P. Woodruff, C. F. McConville, A. L. D. Kilcoyne, T. Lindner, J. Somers, M. Surman, G. Paolucci and A. M. Bradshaw, Surf. Sci., 1988, 201, 228.
51. T. A. Baker, C. M. Friend and E. Kaxiras, J. Phys. Chem. C, 2009, 113, 3232.
52. E. Langseth, A. Nova, E. A. Tråseth, F. Rise, S. Øien, R. H. Heyn and M. A. Tilset, J. Am. Chem. Soc., 2014, 136, 10104.
53. J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
54. T. Waldmann, C. Nenon, K. Tonigold, H. E. Hoster, A. Groß and R. J. Behm, Phys. Chem. Chem. Phys., 2012, 14, 10726.
55. C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc, Hoboken, NJ, 8th edn, 2005, p. 50.
56. Z. Qu, X. Wang, X. Shen and H. Zhou, Nanomaterials, 2022, 12, 4278.
57. B. Eren, D. Zherebetskyy, L. L. Patera, C. H. Wu, H. Bluhm, C. Africh, L.-W. Wang, G. A. Somorjai and M. Salmeron, Science, 2016, 351, 475.
58. C. R. Kemnitz and M. J. Loewen, J. Am. Chem. Soc., 2007, 129, 2521.
59. Q. Guo, F. Yin and R. E. Palmer, Small, 2005, 1, 76.
60. P. Li and F. Ding, Sci. Adv., 2022, 8, eabq2900.
61. F. Hanke and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235422.
62. R. Vranik, V. Stetsovych, S. Feigl and S. Müllegger, Surf. Sci., 2020, 700, 121676.
63. C. F. Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189.
64. L. Xu, J. Lin, Y. Bai and M. Mavrikakis, Topics Catal., 2018, 61, 736.
65. M. Ganesan and P. Nagaraaj, Org. Chem. Front., 2020, 7, 3792.
66. X. Lian, P. Xiao, R. Liu and G. Henkelman, Chem. Mater., 2017, 29, 1472.
67. S. Kasemthaveechok, L. Abella, J. Crassous, J. Autschbach and L. Favereau, Chem. Sci., 2022, 13, 9833.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional computational details; Cartesian coordinates and lattice vectors of the optimized unit cells; Tables S1–S11; and Fig. S1–S23. See DOI: https://doi.org/10.1039/d4tc00427b

‡ These authors contributed equally.

---