Open Access Article
Open Access ArticleHost–guest complexes of perylene bisimide-based metallacage and fullerenes for efficient photoinduced charge separation†
O. A.
Stasyuk
 a,
M.
Solà
a,
M.
Solà
 *a and
A. J.
Stasyuk
*a and
A. J.
Stasyuk
 *ab
*ab
aInstitut de Química Computacional i Catàlisi and Departament de Química, Universitat de Girona, C/ Maria Aurèlia Capmany 69, 17003 Girona, Catalonia, Spain. E-mail: miquel.sola@udg.edu; antony.stasuk@gmail.com
bFaculty of Chemistry, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland
First published on 2nd December 2023
Abstract
The discovery of coordination-driven self-assembly has greatly expanded the field of organic macrocyclic compounds. This approach enables the construction of precise supramolecular complexes, known as metallacages, assembled from organic ligands coordinated with metal centers. Metallacages come in various sizes and shapes, making them capable of hosting guest molecules of different sizes. In this work, we report the ground and excited state properties of non-covalent complexes between various fullerenes (C60, C70, Sc3N@C80, Sc3CH@C80, and Sc4O3@C80) and Pt6PBI3 metallacage, composed of perylene bisimide units and organoplatinum nodes. These complexes exhibit thermodynamically favorable photoinduced charge transfer from endohedral metallofullerenes to metallacage that occurs within picoseconds. Among the systems considered, the Pt6PBI3⊃Sc3N@C80 complex stands out as the most promising candidate for use in photovoltaics due to its ability for fast charge separation and slow charge recombination.
Introduction
Organic macrocyclic compounds, such as crown ethers,1 cryptands,2 and cavitands3,4 became widespread and firmly established in the routine life of chemists almost immediately after their discovery.5 Due to their ability to engage in multiple non-covalent interactions and selectively bind small cationic species, they are widely used as phase transfer catalysts,6,7 specific metal cation sensors,8,9 or even as compounds that facilitate ion transport across cell membranes (ionophore) in biological applications.10 Cyclodextrins are another type of macrocyclic compound composed of glucopyranoside sugar molecules bound together in rings of various sizes. Depending on their size, they can accommodate neutral or charged molecules.11 This ability, in combination with very low toxicity, allows cyclodextrins to find broad applications as drug delivery agents in numerous official approved medicines.12–14 However, due to the narrow cavity size, their host–guest chemistry is limited to small molecules and often has restricted use in polar protogenic environments. Porous organic cages15 with shape-stable structures are of particular interest in supramolecular chemistry due to their internal cavities of different size and ability to bind to guest molecules, such as fullerenes.16–18 Charge-separated states with long lifetimes were observed in porphyrin-based organic cages with encapsulated C60/C70 fullerenes.17,19The discovery of coordination-driven self-assembly has significantly expanded host–guest chemistry.20–22 This powerful tool allows for precise construction of supramolecular complexes, such as metal–organic cages or metallacages, in various shapes and sizes.23,24 Metal–organic cages are molecular assemblies of organic ligands coordinated with either metal cations or metal oxide clusters of different nuclearities, resulting in architectures with inherent porosity. Similar to other macrocyclic compounds, metal–organic cages are capable of binding various organic guests. At the same time, since the size and shape of metal–organic cages can vary broadly, the size of the guest molecule can also differ significantly.25,26
Since the majority of metallacages are constructed from rigid organic fragments, enhancing non-covalent interactions is a natural approach to facilitate their hosting ability.27,28 Therefore, the ideal building blocks for preparation of metallacages with promising host–guest chemistry are extended π-conjugated organic ligands, such as polycyclic aromatic hydrocarbons,29–31 porphyrins,32–36 or rylene bisimides.37–40
In 2013, Würthner and co-workers first synthesized and characterized a giant tetrahedral host (M4L6), assembled from octahedral Fe(II) ions and linear perylene bisimide (PBI) dyes with 2,2′-bipyridine groups.41 The reported cage, with an edge length of 3.9 nm and an estimated internal volume of more than 950 Å3, exhibits broad and strong absorption in the visible region (up to 650 nm). Moreover, it demonstrates a total of 7 highly reversible electrochemical oxidation and reduction waves. The ability to encapsulate C60 fullerene was demonstrated through UV-Vis and NMR spectroscopy, as well as mass spectrometry. It is important to note that spectroscopic measurements suggest that each cage can accommodate two fullerenes. The evolution of this work led to the synthesis of a structurally similar metallacage in which Fe(II) ions were replaced by Zn(II) ions.42 This replacement dramatically enhanced the cage's fluorescence quantum yield. The new cage also demonstrates the ability to accommodate aromatic guests, coronene and perylene, with host–guest ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, respectively.
3, respectively.
In 2020, Fang, Stang, and their co-workers reported a novel supramolecular complex constructed through the coordination-driven self-assembly of o-tetrapyridyl perylene bisimide with cis-(PEt3)2Pt(OTf)2.43 The synthesized metallacage (Pt6PBI3) has the shape of a trigonal prism and possesses an inner cavity with a diameter of 14.7 Å. A cavity of this size is suitable for accommodating both C60 and C70 fullerenes, providing free rotation of the fullerenes inside it. However, as has been demonstrated, the cage exhibits a greater affinity towards C70. This, combined with the possibility of fabricating monomolecular membranes, opens up broad application perspectives for Pt6PBI3 and its host–guest complexes.
In this work, we report a theoretical study of the electronic and photophysical properties of the host–guest complexes of Pt6PBI3 and various fullerenes. We conduct a comprehensive analysis of the photoinduced electron transfer (PET) occurring in the complexes by means of DFT/TDA-DFT method. The obtained results show that the Pt6PBI3 metallacage exhibits a strong electron acceptor nature. The complexes formed with fullerene guests can exhibit either intense fluorescence or pronounced PET properties.
Computational methods
Geometry optimizations were performed utilizing the DFT BLYP44,45 exchange–correlation functional along with the empirical D3(BJ) dispersion correction46,47 and def2-SVP basis set.48,49 The calculations were performed within the ORCA 5.0.3 program.50,51 Energy decomposition analysis (EDA) at BLYP-D3(BJ)/TZP level was performed using the Amsterdam density functional (ADF) program.52 For electronic structure calculations and vertical excitation energies, the TDA formalism53 with the range-separated CAM-B3LYP functional54 and def2-SVP basis set48,49 was employed in Gaussian 16 (rev. A.03).55 Population analysis was performed within Mulliken,56 Löwdin,57 Hirshfeld,58 and CM559 schemes. Solvent effects were accounted using a COSMO-like polarizable continuum model (C-PCM) with acetonitrile as a solvent (dielectric constant ε = 35.69).60,61 Topological analysis of the electron density distribution was conducted using the “quantum theory of atoms in molecules” (QTAIM). Properties of electron density at the bond critical points (BCPs), such as electron density [ρ(r)], its Laplacian [∇2ρ(r)], potential energy density [V(r)], kinetic energy density [G(r)], and total electron energy density [H(r)] were evaluated using the AIMALL suite.62 Chemcraft 1.8 program63 was utilized for molecular structures and frontier molecular orbitals visualization. Further methodological details, including analysis of excited states, calculation of electron transfer rates, reorganization and interaction energies are available in the ESI.†Results and discussion
Ground state properties of Pt6PBI3 metallacage and its complexes with C60/C70 fullerenes
The encapsulation of C60 and C70 fullerenes in Pt6PBI3 metallacage was experimentally carried out in acetone solution and robustly confirmed by a combination of multinuclear NMR and mass-spectrometry.43 A series of NMR measurements taken over an extended period of time for a very dilute solution of Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes revealed no indication of complex instability. The electronic complementarity between the metallacage and fullerenes, along with their ability to undergo reversible electrochemical oxidation/reduction suggests strong electronic communication between the units in both ground and excited states. However, cyclic voltammetry and spectroscopic studies indicated that fullerene encapsulation has only a limited effect on the electronic nature of the metallacage, suggesting weak electronic communication between the host and guest units.To gain deeper insights into the behavior of the Pt6PBI3 metallacage and the fullerenes in their free state and within the corresponding host–guest complexes, a detailed comparison of their electronic properties was conducted. The optimized ground state (GS) geometries of the Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes are shown in Fig. 1.
 | ||
| Fig. 1 Structure of Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes. HOMO and LUMO energies of Pt6PBI3, C60, and C70 in free state and in the corresponding complexes. | ||
It is well known that fullerenes possess strong electron-acceptor properties. As depicted in Fig. 1, the lowest unoccupied molecular orbital (LUMO) of the metallacage is almost 1 eV lower in energy than LUMO of C60/C70, indicating its exceptionally strong electron-acceptor capabilities. In the Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes, the LUMO remains localized on the cage, and its energy is nearly identical to that of the isolated metallacage. The nature of the highest occupied molecular orbital (HOMO) is somewhat different in the complexes with C60 and C70. In Pt6PBI3⊃C60, the HOMO is delocalized over both host and guest units in a ratio of 0.64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.36, respectively. Meanwhile, in Pt6PBI3⊃C70, the degree of HOMO localization increases to a ratio of 0.88
0.36, respectively. Meanwhile, in Pt6PBI3⊃C70, the degree of HOMO localization increases to a ratio of 0.88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.12. Thus, the destabilization of the HOMO observed during the complex formation is attributed to its partial delocalization over the fullerene units. Given the strong electron-acceptor properties of the metallacage, we checked the charge separation between host and guest units in the GS. However, population analysis performed within commonly used schemes did not reveal any significant charge transfer between the units, charge separation in GS does not exceed 0.1 e (Table S1, ESI†). Thus, the slight differences in orbital energies observed upon complexation, coupled with the absence of GS charge separation, validate the limited electronic communication between the metallacage and fullerenes, which has been previously observed in the electrochemical and spectroscopic studies.43
0.12. Thus, the destabilization of the HOMO observed during the complex formation is attributed to its partial delocalization over the fullerene units. Given the strong electron-acceptor properties of the metallacage, we checked the charge separation between host and guest units in the GS. However, population analysis performed within commonly used schemes did not reveal any significant charge transfer between the units, charge separation in GS does not exceed 0.1 e (Table S1, ESI†). Thus, the slight differences in orbital energies observed upon complexation, coupled with the absence of GS charge separation, validate the limited electronic communication between the metallacage and fullerenes, which has been previously observed in the electrochemical and spectroscopic studies.43
To assess the stability of the complexes, we calculated the interaction energy (ΔEint) between the Pt6PBI3 cage and C60/C70 units, as well as the deformation energy (ΔEdef) associated with the distortion of the units from their equilibrium geometries to the geometries they adopt in the complexes. For Pt6PBI3⊃C60 and Pt6PBI3⊃C70, ΔEint is −61.5 and −78.3 kcal mol−1, while ΔEdef is 5.4 and 9.8 kcal mol−1, respectively. The most of the deformation energy is attributed to the cage deformation, with deformation of the fullerenes contributing less than 10%. To analyze the nature of the host–guest interactions, we employed the Morokuma-like interaction energy decomposition analysis64 implemented in the ADF program.52 The EDA decomposes the interaction energy into four components: electrostatic (ΔEelstat), Pauli repulsion (ΔEPauli), orbital interactions (ΔEoi), and dispersion correction (ΔEdisp). This decomposition enables us to assess the role of the specific interactions in the systems.
Table 1 represents the EDA analysis results showing similar nature of host–guest interactions in the complexes. Dispersion dominates (63%), followed by electrostatic attraction (24–25%), and orbital interactions (12–13%). The destabilizing term (ΔEPauli) is 92.6 for Pt6PBI3⊃C60 and 112.5 kcal mol−1 for Pt6PBI3⊃C70. The complex with C70 also has higher deformation energy compared to Pt6PBI3⊃C60. Overall, based on the complexation energy values, Pt6PBI3⊃C70 complex is more stable than Pt6PBI3⊃C60, confirming the greater cage affinity to C70 observed in the experiment.43
| Complex | Energy terms | ΔEint | ΔEdef | ΔEcomplex | ||||
|---|---|---|---|---|---|---|---|---|
| ΔEPauli | ΔEelstat | ΔEoi | ΔEdisp | Cage | Fullerene | |||
| a Relative values (in parentheses) are given as a percentage and express the contribution to the sum of all attractive energy terms: ΔEelstat + ΔEoi + ΔEdisp. Complexation energy: ΔEcomplex = ΔEint + ΔEdef. | ||||||||
| Pt6PBI3⊃C60 | 92.57 | −37.17 (24%) | −19.88 (13%) | −97.04 (63%) | −61.52 | 5.14 | 0.56 | −56.10 |
| Pt6PBI3⊃C70 | 112.52 | −47.15 (25%) | −23.39 (12%) | −120.27 (63%) | −78.29 | 9.41 | 0.40 | −68.48 |
We used QTAIM calculations65 to analyze the host–guest interaction topology in the Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes, considering various topological parameters at BCPs (Table S2, ESI†). Numerical values of these parameters can provide information on the nature of interactions.66 In both complexes, the analysis revealed only one type of interactions: C⋯C contacts between fullerene and host cage linkers. These interactions can be described as weak, closed-shell non-covalent interactions. Considering the π-conjugated nature of the guest and PBI units, the C⋯C contacts can be attributed to π⋯π interactions. No interactions of fullerenes with other metallacage parts were observed due to their spatial separation. In Pt6PBI3⊃C60, 11 BCPs for π⋯π interactions were detected, while replacing C60 with C70 increases the number of BCPs to 15 in Pt6PBI3⊃C70. QTAIM molecular graphs for both complexes are depicted in Fig. S1, ESI.† Considering the similar electron density characteristics at BCPs in both complexes but the higher number of BCPs in Pt6PBI3⊃C70, the results correlate well with its stronger interaction energy. The non-covalent interaction (NCI) index analysis67 showed qualitatively similar NCI isosurface arrangements in both complexes, resembling the metallacage shape. In particular, three distinct areas between PBI linkers and fullerene were observed. The reduced density gradient (RDG) plots and NCI isosurfaces are presented in Fig. S2 and S3, ESI.†
Singlet excited states of Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes
Our results revealed relatively low LUMO energy for both the Pt6PBI3 cage and C60/C70 fullerenes: −3.82 and −2.71/−2.80 eV, respectively (Fig. 1). A very low-lying LUMO of Pt6PBI3 suggests its potential as a strong electron acceptor, capable of oxidizing fullerene under photoexcitation. However, study by Fang, Stang, and co-workers indicates only marginal changes in the UV-Vis spectrum of the cage upon fullerene inclusion.43 To get deeper understanding of the processes taking place under photoexcitation, we performed simulations of excited states using the TDA-DFT method at the CAM-B3LYP-D3(BJ)/def2-SVP//BLYP-D3(BJ)/def2-SVP level of theory (see ESI† for computational details). The TDA-DFT performs well in reproducing experimental absorption and emission spectra of a series of medium-sized conjugated molecules68 and is computationally feasible method for excited state simulations of large systems. Moreover, the range-separated CAM-B3LYP functional performs well for prediction of excitation energy and is particularly effective in modeling charge transfer processes in fullerene-based complexes, yielding a mean absolute percentage error of 6.3% for charge transfer rate values.69The complexes were split into two fragments: Pt6PBI3 and C60/C70 fullerene. We examined the electron density distribution for the 40 lowest singlet excited states. These states can be categorized into three types: (1) locally excited (LE) states, in which the exciton is mostly localized on either fullerene (LEGuest) or Pt6PBI3 (LEHost) with charge separation (CS) below 0.1 e; (2) charge transfer (CT) states with significant charge separation (CS > 0.8 e); and (3) mixed states, involving both LE and CT contributions (0.1 e < CS < 0.8 e).
The gas-phase energies of the 40 lowest-lying singlet excited states of Pt6PBI3⊃C60 range from 2.50 to 3.28 eV. The first excited state, at 2.50 eV, corresponds to the LEGuest state with exciton localization on C60 (Table 2). The LEHost state was found at 2.73 eV, i.e. 0.23 eV higher in energy compared to LEGuest. The lowest CT state with 0.81 e transferred lies at 2.98 eV and can be described as [Pt6PBI3]−⊃[C60]+. In the case of Pt6PBI3⊃C70, the first 40 excited states have the energy range from 2.29 to 3.14 eV. The lowest-lying excited state, at 2.29 eV, is the LEGuest state. The energy of the LEHost state is very similar to that in Pt6PBI3⊃C60 and equal to 2.71 eV. Since the HOMO energy of C70 is slightly higher than that of C60, this fullerene should have a slightly improved electron-donor capability. Indeed, the energy of the CT state is 2.63 eV, which is 0.35 eV lower compared to the CT state in the complex with C60. Similar to Pt6PBI3⊃C60, this state results from an electron transfer from C70 fullerene to the metallacage.
| Supramolecular system | ||||
|---|---|---|---|---|
| Pt6PBI3⊃C60 | Pt6PBI3⊃C70 | |||
| VAC | ACN | VAC | ACN | |
| a Mixed state with significant contributions of both LE and CT. | ||||
| LEGuest (C60/C70) | ||||
| E x | 2.500 | 2.499 | 2.289 | 2.284 |
| Transition (CI coef.) | H−2–L+3 (0.20) | H−1–L+4 (0.24) | H–L+3 (0.45) | H–L+3 (0.48) |
| f | <0.001 | 0.001 | <0.001 | <0.001 |
| X | 0.922 | 0.902 | 0.930 | 0.908 |
| LEHost (Pt6PBI3) | ||||
| E x | 2.727 | 2.698 | 2.711 | 2.678 |
| Transition (CI coef.) | H−8–L (0.13) | H−5–L+2 (0.20) | H−3–L+2 (0.14) | H−3–L+1 (0.25) |
| f | 0.015 | 0.027 | 0.205 | 0.207 |
| X | 0.865 | 0.868 | 0.888 | 0.885 |
| Most intense absorption band | ||||
| E x | 2.792 | 2.741 | 2.789a | 2.739 |
| Transition (CI coef.) | H–L+2 (0.28) | H−5–L+1 (0.27) | H−6–L+5 (0.05) | H−5–L (0.23) |
| f | 1.787 | 2.199 | 1.266 | 1.193 |
| Localization | Pt6PBI3 | Pt6PBI3 | Pt6PBI3 | Pt6PBI3 |
| X | 0.887 | 0.860 | 0.754 | 0.833 |
| CT (C60/C70 → Pt6PBI3) | ||||
| E x | 2.982 | 2.678 | 2.632 | 2.305 |
| Transition (CI coef.) | H−2–L+2 (0.17) | H−4–L+2 (0.21) | H−2–L+2 (0.23) | H−1–L+1 (0.47) |
| f | 0.030 | 0.027 | 0.009 | 0.006 |
| CT | 0.813 | 0.885 | 0.858 | 0.928 |
To understand how polar environment affects electronic excitations, we used a COSMO-like model60,61,70–72 with acetonitrile solvent. For the Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes, GS dipole moments are 0.87 and 2.11 D, respectively. Their rather small values are due to symmetric structure of the metallacage and fullerene fragments. With Pt(II) centers, o-tetrapyridyl PBI and triflate counterions, both complexes are expected to have high solvation energies in the GS. In particular, their solvation energies are similar and equal to −5.29 and −5.28 eV. The change in the dipole moment (Δμ) due to GS → LEGuest/LEHost excitations is small and hardly exceeds 1 D, keeping the solvation energies in both LEGuest and LEHost states similar to those in the GS. Solvation data for both complexes are given in Table S3, ESI.† The dipole moment changes from GS to CT states are usually much larger than those to LE states due to charge separation. In our study, Pt6PBI3⊃C60 and Pt6PBI3⊃C70 showed relatively small changes, namely 11.84 and 14.47 D, due to high symmetry and efficient charge delocalization. Solvation of the complexes stabilizes CT states, lowering their energies from 2.96 to 2.68 eV and from 2.63 to 2.31 eV for Pt6PBI3⊃C60 and Pt6PBI3⊃C70, respectively. Thus, stabilization of the CT states significantly reduces the energy gap between the CT and the lowest excited state (LEGuest), making CT population possible from this state.
The method of Ulstrup and Jortner73,74 was employed to estimate charge separation (kCS) and charge recombination (kCR) rates using four parameters, such as electronic coupling of initial and final states (Vij), solvation reorganization energy (λs), reaction Gibbs energy (ΔG0), and Huang–Rhys factor (Seff). We used an effective frequency of 1600 cm−1, corresponding to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond stretching. Testing the effect of the selected frequency on the rate did not reveal significant changes (Table S4, ESI†). The kCS and kCR rates calculated in ACN are listed in Table 3.
C bond stretching. Testing the effect of the selected frequency on the rate did not reveal significant changes (Table S4, ESI†). The kCS and kCR rates calculated in ACN are listed in Table 3.
| Complex Pt6PBI3 ⊃ Cxx | Transition | ΔG0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|Vij| | λ | S eff | k x | τ |
|---|---|---|---|---|---|---|---|
| a Gibbs energy difference between the given states. b Effective value of the Huang–Rhys factor Seff = λi/ħωeff, where ħωeff is set to 1600 cm−1. | |||||||
| Pt6PBI3⊃C60 | LEGuest → CT | 0.179 | 2.34 × 10−3 | 0.744 | 1.26 | 4.95 × 106 | 202.1 |
| CT → GS | −2.678 | 2.87 × 10−2 | 0.724 | 1.15 | 7.32 × 106 | 136.6 | |
| Pt6PBI3⊃C70 | LEGuest → CT | 0.021 | 2.42 × 10−3 | 0.683 | 1.12 | 3.54 × 108 | 2.8 |
| CT → GS | −2.305 | 1.24 × 10−2 | 0.680 | 1.10 | 3.23 × 107 | 31.0 | |
In Table 3, Pt6PBI3⊃C60 complex shows charge separation with positive Gibbs energy, taking place in the inverted Marcus region (|ΔG0| > λ). The rate of this process is 4.95 × 106 s−1. At the same time, charge recombination (CT → GS) occurs in a deep inverted Marcus region (|ΔG0| ≫ λ). The rates for CS and CR differ by less than two times, with CR surpassing CS. The predicted kCS/kCR ratio suggests that the CT state formation is unlikely in Pt6PBI3⊃C60. In turn, Pt6PBI3⊃C70 has near-zero Gibbs energy for CS, therefore this process is more thermodynamically favorable than in Pt6PBI3⊃C60. The CS and CR rates for Pt6PBI3⊃C70 are significantly faster compared to Pt6PBI3⊃C60, the processes occur in nanoseconds (2.8 ns for CS and 31.0 ns for CR). The slower CR than CS implies a detectable CT state lifetime, although formation of the CT state has not been observed in UV-Vis experiment.43 The fluorescence measurements for empty metallacage and both complexes with fullerenes show minimal difference in fluorescence decay. The amplitude weighted average fluorescence lifetimes are 2.42, 2.56, and 2.71 ns for Pt6PBI3, Pt6PBI3⊃C60, and Pt6PBI3⊃C70, respectively. Thus, radiative deactivation of excited state is much faster than CT state generation for Pt6PBI3⊃C60 (2.6 ns vs. 202.1 ns) and comparable for Pt6PBI3⊃C70 (2.7 ns vs. 2.8 ns).
Hence, the absence of experimental detection of the CT state in the studied complexes results from faster radiative deactivation (fluorescence) than CT state formation. Notably, in Pt6PBI3⊃C60, the formation of the CT state is also slower than non-radiative charge recombination. Fig. 2 highlights the fluorescence and charge transfer processes following photoexcitation of the Pt6PBI3⊃C60 and Pt6PBI3⊃C70.
 | ||
| Fig. 2 Summary of the excited state processes for Pt6PBI3⊃C60 and Pt6PBI3⊃C70 in ACN. Fluorescence rates are taken from ref. 43. | ||
Facilitating electron transfer using endohedral metallofullerenes
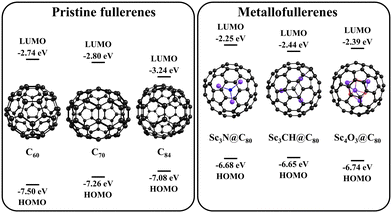
It is known that an increase in the size of fullerene leads to an increase in its donor abilities. A comparison of the HOMO and LUMO energies of pristine C60, C70, and C84 fullerenes (Fig. 3) clearly demonstrates an increase in their HOMO energy from −7.50 eV for C60 to −7.08 eV for C84. The observations made based on the HOMO energy are in a good agreement with the experimentally measured ionization energies of fullerenes, which are equal to 7.57, 7.36, and 7.17 eV for C60, C70, and C84, respectively.75As the electron-acceptor properties of Pt6PBI3 proved insufficient to withdraw electron from C60 and C70 fullerenes, we hypothesized that replacing these pristine fullerenes with more effective electron donors could facilitate charge transfer. Earlier, we demonstrated that metal nitride endohedral fullerenes effectively donate electrons in complexes with carbon-rich acceptors, such as pristine fullerenes and γ-graphynes.76,77 Guided by these results, we aimed to evaluate the feasibility of the PET in a series of complexes composed of the Pt6PBI3 metallacage and various endohedral Ih-C80-based metallofullerenes. As it can be seen in Fig. 3, the HOMO energies of endohedral metallofullerenes are higher compared to those of the pristine fullerenes of a similar size, suggesting better donor properties, even surpassing those of C84 fullerene. This change can be explained by a partial charge transfer between the metal cluster and fullerene cage, thus the electronic structure of the considered metallofullerenes M@C80 can be represented as Mδ+@C80δ−. Importantly, the host size is suitable to accommodate these metallofullerenes, given their diameter is only 20% larger than that of C60. As cluster-encapsulated fullerenes, we selected three experimentally obtained systems: scandium nitride (Sc3N@C80),78 hydrogenated scandium carbide (Sc3CH@C80),79,80 and scandium oxide (Sc4O3@C80)81 endohedral fullerenes (Fig. 3). The structures of Pt6PBI3⊃Sc3N@C80, Pt6PBI3⊃Sc3CH@C80, and Pt6PBI3⊃Sc4O3@C80 were optimized using the BLYP-D3(BJ) functional and def2-SVP basis set.
Given that the metallofullerenes are larger than C60 and C70, we first checked the stability of the new complexes. The analysis performed according to the same scheme as for Pt6PBI3⊃C60 and Pt6PBI3⊃C70 revealed some interesting features of these systems. First, the deformation energy of new complexes is noticeably higher than that of complexes with pristine fullerenes. At the same time, the main contribution to the deformation energy is made by the deformation of metallacage, as in the C60 and C70 based complexes. Second, the interaction energies are higher compared to Pt6PBI3⊃C60 and Pt6PBI3⊃C70 due to the larger dispersion correction term. Overall, the complexation energies range from −63.9 to −67.8 kcal mol−1 (Table S5, ESI†). Note that the nature of the interactions in all studied complexes is very similar. Thus, the stability of the new complexes is in between of the energy range for Pt6PBI3⊃C60 and Pt6PBI3⊃C70. Therefore, the binding affinity of the metallacage to the studied fullerenes is in the following order: C70 > Sc4O3@C80 > Sc3N@C80 > Sc3CH@C80 > C60. Since the complexes with pristine fullerenes were successfully synthesized and isolated, we are convinced that the synthesis of the proposed complexes with metallofullerenes is also possible.
Fig. 4 shows that LUMO in all cases is located on one of the PBI subunits of the metallacage. Its energy is almost equal to the LUMO energy in Pt6PBI3⊃C60 and Pt6PBI3⊃C70. In turn, due to the better electron-donor ability of the endohedral metallofullerenes, the HOMO energy in their complexes is in between –7.39 and –7.49 eV, which is higher than the HOMO energies predicted for the complexes with pristine fullerenes (−8.14 and −7.99 eV for Pt6PBI3⊃C60 and Pt6PBI3⊃C70). In addition, the HOMO in the metallofullerene-based complexes is fully localized on the fullerene, unlike the originally described complexes with pristine fullerenes (Fig. 1). The mentioned differences should facilitate the photoinduced electron transfer in the new systems. To test this assumption, we analyzed the electron density distribution for their 40 lowest singlet excited states.
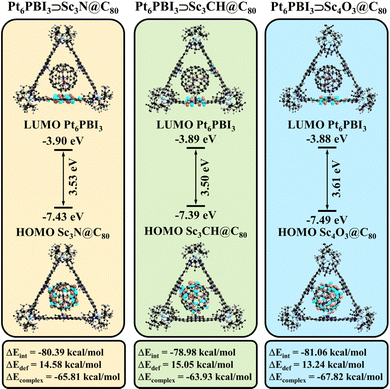 | ||
| Fig. 4 Structure and HOMO/LUMO energies (in eV) of Pt6PBI3⊃Sc3N@C80, Pt6PBI3⊃Sc3CH@C80, and Pt6PBI3⊃Sc4O3@C80 complexes. | ||
In all cases, the energies of the excited states in the gas-phase vary from 2.1 to 3.1 eV. The LE state energies of both LEGuest and LEHost turned out to be similar. The CT state in the complexes of interest is characterized by energies from 2.15 to 2.35 eV, depending on the particular complex. It is much lower than the CT state energies in Pt6PBI3⊃C60 and Pt6PBI3⊃C70 (Table 4). Usually, the energies of the CT states correlate well with the HOMO–LUMO energy gap. It is important to note that for the Pt6PBI3⊃Sc3CH@C80 complex, the CT state is the lowest excited state, even in the gas-phase. For other complexes, the energy difference between the CT state and the lowest LE state, with the exciton localized on the fullerene, does not exceed 0.15 eV. The frontier MOs representing the LE and CT states for the Pt6PBI3⊃Sc3N@C80, Pt6PBI3⊃Sc3CH@C80, and Pt6PBI3⊃Sc4O3@C80 complexes are shown in Fig. S4–S6, ESI.†
| Supramolecular system | |||
|---|---|---|---|
| Pt 6 PBI 3 ⊃XXX@C 80 | |||
| Sc3N@C80 | Sc3CH@C80 | Sc4O3@C80 | |
| LEGuest (XXX@C80) | |||
| E x | 2.116 | 2.215 | 2.235 |
| Transition (CI coef.) | H−4–L+4 (0.77) | H–L+3 (0.86) | H–L+3 (0.37) |
| f | 0.013 | <0.001 | <005 |
| X | 0.923 | 0.920 | 0.886 |
| LEHost (Pt6PBI3) | |||
| E x | 2.812 | 2.747 | 2.756 |
| Transition (CI coef.) | H−13–L+3 (0.25) | H−7–L () | H−5–L+2 (0.37) |
| f | 0.446 | 0.439 | 0.431 |
| X | 0.872 | 0.881 | 0.889 |
| CT (XXX@C80 → Pt6PBI3) | |||
| E x | 2.260 | 2.152 | 2.347 |
| Transition (CI coef.) | H−4–L (0.40) | H–L+2 (0.74) | H−1–L (0.55) |
| f | 0.014 | 0.013 | 0.010 |
| CT | 0.894 | 0.883 | 0.834 |
The GS solvation energies of Pt6PBI3⊃Sc3N@C80, Pt6PBI3⊃Sc3CH@C80, and Pt6PBI3⊃Sc4O3@C80 complexes turned out to be very close to those of the C60 and C70 based complexes and are equal to −4.83, −5.18, and −5.31 eV, respectively. The difference in dipole moments of the GS and both LEGuest and LEHost states is quite small and does not exceed 3.5 D. As expected, the solvation energies of these LE states are very similar to the solvation energies of GS. At the same time, the difference in dipole moments of GS and CT states in the complexes of interest is large: 10 D for Pt6PBI3⊃Sc3N@C80 and 21 D for Pt6PBI3⊃Sc3CH@C80 and Pt6PBI3⊃Sc4O3@C80. Subsequently, the difference in solvation energies between GS and CT states is −0.34 eV for the complex with Sc3N@C80, and −0.58 and −0.54 eV for the complexes with Sc3CH@C80 and Sc4O3@C80. Detailed solvation data in ACN are given in Table S6, ESI.† It is important to note that stabilization of the CT state is sufficient to reorder the LEGuest and CT states in all complexes of interest. Fig. 5 shows the energies of the GS, LE, and CT states in the gas-phase and in ACN, as well as the simulated absorption spectra for all metallofullerene-based complexes.
The higher solvation energy of the CT states in Pt6PBI3⊃Sc3CH@C80 and Pt6PBI3⊃Sc4O3@C80 compared to the Sc3N@C80 based complex can be explained by different charge delocalization over the host fragment measured by inverse participation ratio (IPR), which counts the number of atoms involved in the charge delocalization. For Pt6PBI3⊃Sc3N@C80, Pt6PBI3⊃Sc3CH@C80, and Pt6PBI3⊃Sc4O3@C80, the calculated IPR values for the Pt6PBI3 host unit are 51.9, 27.5, and 28.4 (see Table S7 for details, ESI†). Charge delocalization over endohedral metallofullerene units is apparently less significant due to their lower accessibility to the solvent. The IPR value for the Sc3N@C80, Sc3CH@C80, and Sc4O3@C80 units are 30.4, 20.0, and 24.8. Thus, higher charge delocalization and subsequently IPR values for both host and guest subunits in Pt6PBI3⊃Sc3N@C80 are responsible for its lower solvation in the CT state.
According to Table 4, GS → CT transitions in all complexes with metallofullerenes are characterized by a low oscillator strength, making direct population of the CT states through light absorption difficult. However, they can be generated by a decay of LE states. The kCS and kCR rates were calculated using the semi-classical approach.73,74 The main parameters used in calculation, as well as the rate values are given in Table 5.
| Complex Pt6PBI3⊃Cxx | Transition | ΔG0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|Vij| | λ | S eff | k x | τ |
|---|---|---|---|---|---|---|---|
a Gibbs energy difference between the given states.
b Effective value of the Huang–Rhys factor Seff = λi/ħωeff, where ħωeff is set to 1600 cm−1, which corresponds to the stretching of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. C bonds.
|
|||||||
| Pt6PBI3⊃Sc3N@C80 | LEGuest → CT | −0.191 | 5.83 × 10−3 | 0.412 | 1.11 | 4.94 × 1011 | 2 |
| CT → GS | −1.920 | 5.25 × 10−2 | 0.401 | 1.05 | 7.47 × 108 | 1339 | |
| Pt6PBI3⊃Sc3CH@C80 | LEGuest → CT | −0.600 | 5.94 × 10−3 | 0.534 | 1.02 | 4.95 × 1011 | 2 |
| CT → GS | −1.577 | 3.46 × 10−2 | 0.531 | 1.00 | 3.60 × 1010 | 28 | |
| Pt6PBI3⊃Sc4O3@C80 | LEGuest → CT | −0.422 | 8.85 × 10−3 | 0.500 | 1.11 | 1.28 × 1011 | 1 |
| CT → GS | −1.807 | 5.26 × 10−2 | 0.488 | 1.05 | 6.49 × 109 | 154 | |
Photoinduced electron transfer in the studied complexes is characterized by a negative Gibbs energy in the range from −0.19 to −0.60 eV. The estimated rates of CT generation are very high, thus the process occurs on a picosecond timescale. Characteristic time is 2, 2, and 1 ps, for Pt6PBI3⊃Sc3N@C80, Pt6PBI3⊃Sc3CH@C80, and Pt6PBI3⊃Sc4O3@C80, respectively. The CR reaction proceeds in a deep inverted Marcus region (|ΔG0| ≫ λ) and its rate varies considerably from complex to complex. In particular, for Pt6PBI3⊃Sc3N@C80, charge recombination is almost three orders of magnitude slower than the corresponding charge separation. At the same time, for Pt6PBI3⊃Sc3CH@C80, the charge recombination is only 14 times slower than charge separation. The Pt6PBI3⊃Sc4O3@C80 complex is located in the middle, with a ratio of charge separation time to charge recombination time of approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150. Considering the fact that PET depends not only on the rate of charge separation, but also on the efficiency of hole and electron extraction, the ideal combination for practical usage is characterized by fast charge separation and slow charge recombination. Therefore, it can be concluded that the Pt6PBI3⊃Sc3N@C80 complex is the best candidate among the considered systems for use as active layer in photovoltaic devices.
150. Considering the fact that PET depends not only on the rate of charge separation, but also on the efficiency of hole and electron extraction, the ideal combination for practical usage is characterized by fast charge separation and slow charge recombination. Therefore, it can be concluded that the Pt6PBI3⊃Sc3N@C80 complex is the best candidate among the considered systems for use as active layer in photovoltaic devices.
Conclusions
Using the DFT method, we showed that the Pt6PBI3 metallacage constructed from perylene bisimide units and organoplatinum nodes features an appropriately sized internal cavity, allowing it to form stable complexes not only with pristine C60 and C70 fullerenes but also with Sc3N@C80, Sc3CH@C80, and Sc4O3@C80 metallofullerenes. Our calculations reveal that the binding affinities of the studied fullerenes to Pt6PBI3 follows this order: C70 > Sc4O3@C80 > Sc3N@C80 > Sc3CH@C80 > C60.The TDA-DFT results indicate that the metallacage has a lower LUMO energy than C60 and a high ability to delocalize an excess charge, ensuring its excellent electron-acceptor properties. However, the electron affinity of the metallacage is insufficient to withdraw an electron from C60 or C70 fullerenes. Charge separation in the Pt6PBI3⊃C60 and Pt6PBI3⊃C70 complexes is characterized by a small positive Gibbs energy and occurs within nanoseconds. Charge recombination is also fast in both complexes, serving as a competitive deactivation channel for the CT state. Moreover, the formation of the CT state in such complexes is hindered by the rapid radiative deactivation channel (fluorescence) of the corresponding LE states, which occurs more quickly than CT state formation.
However, replacing pristine fullerenes with metallofullerenes enables photoinduced electron transfer from fullerene to metallacage, a thermodynamically favorable process occurring within picoseconds. Importantly, in all cases, charge recombination is one to three orders of magnitude slower than the corresponding charge separation. Among the studied complexes, Pt6PBI3⊃Sc3N@C80 demonstrates the best ratio of fast charge separation and relatively slow charge recombination, making it a highly promising candidate for photovoltaic systems.
Author contributions
O. A. S. investigation, formal analysis, writing – original draft, writing – review & editing. M. S. supervision, writing – review & editing, funding acquisition. A. J. S. investigation, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support from the Spanish Ministerio de Ciencia e Innovación (Network RED2018-102815-T, project PID2020-113711GB-I00, and Juan de la Cierva contract IJC2019-039846-I to A.J.S.), the Catalan Conselleria de Recerca i Universitats of the Generalitat de Catalunya (project 2021SGR623) and the University of Girona (María Zambrano fellowship REQ2021_C_31 to O.A.S.). A. J. S. gratefully acknowledges Poland's high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grants no. PLG/2022/016045 and PLG/2022/015981.References
- C. J. Pedersen, Cyclic polyethers and their complexes with metal salts, J. Am. Chem. Soc., 1967, 89(26), 7017–7036 CrossRef CAS.
- B. Dietrich, J. M. Lehn and J. P. Sauvage, Diaza-polyoxa-macrocycles et macrobicycles, Tetrahedron Lett., 1969, 10(34), 2885–2888 CrossRef.
- A. Lledó, R. J. Hooley and J. Rebek, Recognition of Guests by Water-Stabilized Cavitand Hosts, Org. Lett., 2008, 10(17), 3669–3671 CrossRef PubMed.
- F. R. Pinacho Crisóstomo, A. Lledó, S. R. Shenoy, T. Iwasawa and J. Rebek, Recognition and Organocatalysis with a Synthetic Cavitand Receptor, J. Am. Chem. Soc., 2009, 131(21), 7402–7410 CrossRef PubMed.
- G. Montà-González, F. Sancenón, R. Martínez-Máñez and V. Martí-Centelles, Purely Covalent Molecular Cages and Containers for Guest Encapsulation, Chem. Rev., 2022, 122(16), 13636–13708 CrossRef PubMed.
- D. Landini, F. Montanari and F. M. Pirisi, Crown ethers as phase-transfer catalysts in two-phase reactions, J. Chem. Soc., Chem. Commun., 1974, 21, 879–880 RSC.
- D. Vidal, M. Costas, A. Lledó and A. Deep Cavitand, Receptor Functionalized with Fe(II) and Mn(II) Aminopyridine Complexes for Bioinspired Oxidation Catalysis, ACS Catal., 2018, 8(4), 3667–3672 CrossRef CAS.
- G. W. Gokel, W. M. Leevy and M. E. Weber, Crown Ethers:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sensors for Ions and Molecular Scaffolds for Materials and Biological Models, Chem. Rev., 2004, 104(5), 2723–2750 CrossRef CAS PubMed.
Sensors for Ions and Molecular Scaffolds for Materials and Biological Models, Chem. Rev., 2004, 104(5), 2723–2750 CrossRef CAS PubMed. - J. Li, D. Yim, W.-D. Jang and J. Yoon, Recent progress in the design and applications of fluorescence probes containing crown ethers, Chem. Soc. Rev., 2017, 46(9), 2437–2458 RSC.
- H.-J. Schneider and A. K. Yatsimirsky, Selectivity in supramolecular host–guest complexes, Chem. Soc. Rev., 2008, 37(2), 263–277 RSC.
- F. Cramer, W. Saenger and H. C. Spatz, Inclusion Compounds. XIX.1a The Formation of Inclusion Compounds of α-Cyclodextrin in Aqueous Solutions. Thermodynamics and Kinetics, J. Am. Chem. Soc., 1967, 89(1), 14–20 CrossRef CAS.
- Martindale: The Complete Drug Reference, ed. S. C. Sweetman, Pharmaceutical Press, London, England, UK, 2011 Search PubMed.
- K. Uekama, F. Hirayama and T. Irie, Cyclodextrin Drug Carrier Systems, Chem. Rev., 1998, 98(5), 2045–2076 CrossRef CAS PubMed.
- T. Wimmer, Cyclodextrines, in Ullmann’s Encyclopedia of Industrial Chemistry, 2003, DOI:10.1002/14356007.e08_e02.
- T. R. Cook, Y.-R. Zheng and P. J. Stang, Metal–Organic Frameworks and Self-Assembled Supramolecular Coordination Complexes: Comparing and Contrasting the Design, Synthesis, and Functionality of Metal–Organic Materials, Chem. Rev., 2013, 113(1), 734–777 CrossRef CAS PubMed.
- H. Wang, Y. Jin, N. Sun, W. Zhang and J. Jiang, Post-synthetic modification of porous organic cages, Chem. Soc. Rev., 2021, 50(16), 8874–8886 RSC.
- X. Yang, S. Huang, M. Ortiz, X. Wang, Y. Cao, O. Kareem, Y. Jin, F. Huang, X. Wang and W. Zhang, Truxene-based covalent organic polyhedrons constructed through alkyne metathesis, Org. Chem. Front., 2021, 8(17), 4723–4729 RSC.
- M. Ortiz, S. Cho, J. Niklas, S. Kim, O. G. Poluektov, W. Zhang, G. Rumbles and J. Park, Through-Space Ultrafast Photoinduced Electron Transfer Dynamics of a C70-Encapsulated Bisporphyrin Covalent Organic Polyhedron in a Low-Dielectric Medium, J. Am. Chem. Soc., 2017, 139(12), 4286–4289 CrossRef CAS PubMed.
- C. Zhang, Q. Wang, H. Long and W. Zhang, A Highly C70 Selective Shape-Persistent Rectangular Prism Constructed through One-Step Alkyne Metathesis, J. Am. Chem. Soc., 2011, 133(51), 20995–21001 CrossRef CAS PubMed.
- X. Yu, B. Wang, Y. Kim, J. Park, S. Ghosh, B. Dhara, R. D. Mukhopadhyay, J. Koo, I. Kim, S. Kim, I.-C. Hwang, S. Seki, D. M. Guldi, M.-H. Baik and K. Kim, Supramolecular Fullerene Tetramers Concocted with Porphyrin Boxes Enable Efficient Charge Separation and Delocalization, J. Am. Chem. Soc., 2020, 142(29), 12596–12601 CrossRef CAS PubMed.
- T. R. Cook and P. J. Stang, Recent Developments in the Preparation and Chemistry of Metallacycles and Metallacages via Coordination, Chem. Rev., 2015, 115(15), 7001–7045 CrossRef CAS PubMed.
- Y. Inokuma, M. Kawano and M. Fujita, Crystalline molecular flasks, Nat. Chem., 2011, 3(5), 349–358 CrossRef CAS PubMed.
- S. Chakraborty and G. R. Newkome, Terpyridine-based metallosupramolecular constructs: tailored monomers to precise 2D-motifs and 3D-metallocages, Chem. Soc. Rev., 2018, 47(11), 3991–4016 RSC.
- F. M. Steudel, E. Ubasart, L. Leanza, M. Pujals, T. Parella, G. M. Pavan, X. Ribas and M. von Delius, Synthesis of C60/[10]CPP-Catenanes by Regioselective, Nanocapsule-Templated Bingel Bis-Addition, Angew. Chem., Int. Ed., 2023, 62(42), e202309393 CrossRef CAS PubMed.
- M. Pan, K. Wu, J.-H. Zhang and C.-Y. Su, Chiral metal–organic cages/containers (MOCs): From structural and stereochemical design to applications, Coord. Chem. Rev., 2019, 378, 333–349 CrossRef CAS.
- Y. Sun, C. Chen, J. Liu and P. J. Stang, Recent developments in the construction and applications of platinum-based metallacycles and metallacages via coordination, Chem. Soc. Rev., 2020, 49(12), 3889–3919 RSC.
- F. J. Rizzuto, L. K. S. von Krbek and J. R. Nitschke, Strategies for binding multiple guests in metal–organic cages, Nat. Rev. Chem., 2019, 3(4), 204–222 CrossRef.
- C. García-Simón, M. Costas and X. Ribas, Metallosupramolecular receptors for fullerene binding and release, Chem. Soc. Rev., 2016, 45(1), 40–62 RSC.
- V. Martínez-Agramunt, S. Ruiz-Botella and E. Peris, Nickel-Cornered Molecular Rectangles as Polycyclic Aromatic Hydrocarbon Receptors, Chem. – Eur. J., 2017, 23(27), 6675–6681 CrossRef PubMed.
- P. P. Neelakandan, A. Jiménez and J. R. Nitschke, Fluorophore incorporation allows nanomolar guest sensing and white-light emission in M4L6 cage complexes, Chem. Sci., 2014, 5(3), 908–915 RSC.
- J. J. Perry Iv, P. L. Feng, S. T. Meek, K. Leong, F. P. Doty and M. D. Allendorf, Connecting structure with function in metal–organic frameworks to design novel photo- and radioluminescent materials, J. Mater. Chem., 2012, 22(20), 10235–10248 RSC.
- W. Meng, B. Breiner, K. Rissanen, J. D. Thoburn, J. K. Clegg and J. R. Nitschke, A Self-Assembled M8L6 Cubic Cage that Selectively Encapsulates Large Aromatic Guests, Angew. Chem., Int. Ed., 2011, 50(15), 3479–3483 CrossRef CAS PubMed.
- T. Lin, X. S. Shang, P. N. Liu and N. Lin, Multicomponent Assembly of Supramolecular Coordination Polygons on a Au(111) Surface, J. Phys. Chem. C, 2013, 117(44), 23027–23033 CrossRef CAS.
- M. Boccalon, E. Iengo and P. Tecilla, Metal–Organic Transmembrane Nanopores, J. Am. Chem. Soc., 2012, 134(50), 20310–20313 CrossRef CAS PubMed.
- E. Iengo, P. Cavigli, D. Milano and P. Tecilla, Metal mediated self-assembled porphyrin metallacycles: Synthesis and multipurpose applications, Inorg. Chim. Acta, 2014, 417, 59–78 CrossRef CAS.
- C. García-Simón, C. Colomban, Y. A. Çetin, A. Gimeno, M. Pujals, E. Ubasart, C. Fuertes-Espinosa, K. Asad, N. Chronakis, M. Costas, J. Jiménez-Barbero, F. Feixas and X. Ribas, Complete Dynamic Reconstruction of C60, C70, and (C59N)2 Encapsulation into an Adaptable Supramolecular Nanocapsule, J. Am. Chem. Soc., 2020, 142(37), 16051–16063 CrossRef PubMed.
- C.-C. You and F. Würthner, Self-Assembly of Ferrocene-Functionalized Perylene Bisimide Bridging Ligands with Pt(II) Corner to Electrochemically Active Molecular Squares, J. Am. Chem. Soc., 2003, 125(32), 9716–9725 CrossRef CAS PubMed.
- A. Sautter, D. G. Schmid, G. Jung and F. Würthner, A Triangle−Square Equilibrium of Metallosupramolecular Assemblies Based on Pd(II) and Pt(II) Corners and Diazadibenzoperylene Bridging Ligands, J. Am. Chem. Soc., 2001, 123(23), 5424–5430 CrossRef CAS PubMed.
- V. Blanco, M. D. García, C. Peinador and J. M. Quintela, Self-assembly of new fluorescent Pd(II) and Pt(II) 2,7-diazapyrenium-based metallocycles and study of their inclusion complexes and [3]catenanes, Chem. Sci., 2011, 2(12), 2407–2416 RSC.
- S. Lin, X. Chang, Z. Wang, J. Zhang, N. Ding, W. Xu, K. Liu, Z. Liu and Y. Fang, High-Performance NMHC Detection Enabled by a Perylene Bisimide-Cored Metallacycle Complex-Based Fluorescent Film Sensor, Anal. Chem., 2021, 93(48), 16051–16058 CrossRef CAS PubMed.
- K. Mahata, P. D. Frischmann and F. Würthner, Giant Electroactive M4L6 Tetrahedral Host Self-Assembled with Fe(II) Vertices and Perylene Bisimide Dye Edges, J. Am. Chem. Soc., 2013, 135(41), 15656–15661 CrossRef CAS PubMed.
- P. D. Frischmann, V. Kunz and F. Würthner, Bright Fluorescence and Host–Guest Sensing with a Nanoscale M4L6 Tetrahedron Accessed by Self-Assembly of Zinc–Imine Chelate Vertices and Perylene Bisimide Edges, Angew. Chem., Int. Ed., 2015, 54(25), 7285–7289 CrossRef CAS PubMed.
- X. Chang, S. Lin, G. Wang, C. Shang, Z. Wang, K. Liu, Y. Fang and P. J. Stang, Self-Assembled Perylene Bisimide-Cored Trigonal Prism as an Electron-Deficient Host for C60 and C70 Driven by “Like Dissolves Like”, J. Am. Chem. Soc., 2020, 142(37), 15950–15960 CrossRef CAS PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- ORCA - an ab initio density functional, and semiempirical program package, version 5.0.3.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606 Search PubMed.
- E. J. Baerends, et al., ADF 2018, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314(3), 291–299 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393(1), 51–57 CrossRef CAS.
- M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; G. A. Petersson; H. Nakatsuji; X. Li; M. Caricato; A. V. Marenich; J. Bloino; B. G. Janesko; R. Gomperts; B. Mennucci; H. P. Hratchian; J. V. Ortiz; A. F. Izmaylov; J. L. Sonnenberg; D. Williams-Young; F. Ding; F. Lipparini; F. Egidi; J. Goings; B. Peng; A. Petrone; T. Henderson; D. Ranasinghe; V. G. Zakrzewski; J. Gao; N. Rega; G. Zheng; W. Liang; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell; J. A. Montgomery.; J. E. Peralta; F. Ogliaro; M. J. Bearpark; J. J. Heyd; E. N. Brothers; K. N. Kudin; V. N. Staroverov; T. A. Keith; R. Kobayashi; J. Normand; K. Raghavachari; A. P. Rendell; J. C. Burant; S. S. Iyengar; J. Tomasi; M. Cossi; J. M. Millam; M. Klene; C. Adamo; R. Cammi; J. W. Ochterski; R. L. Martin; K. Morokuma; O. Farkas; J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23(10), 1833–1840 CrossRef CAS.
- P. O. Löwdin, On the Non-Orthogonality Problem Connected with the Use of Atomic Wave Functions in the Theory of Molecules and Crystals, J. Chem. Phys., 1950, 18(3), 365–375 CrossRef.
- F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44(2), 129–138 CrossRef CAS.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8(2), 527–541 CrossRef CAS PubMed.
- A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt, Calculation of UV/Vis Spectra in Solution, J. Phys. Chem., 1996, 100(9), 3349–3353 CrossRef CAS.
- T. A. Keith AIMAll, version 19.10.12; TK Gristmill Software: Overland Park, KS, 2019. (https://aim.tkgristmill.com).
- G. A. Zhurko, Chemcraft 1.80 (build 523b) - graphical program for visualization of quantum chemistry computations. (https://chemcraftprog.com).
- K. Morokuma, Why do molecules interact? The origin of electron donor-acceptor complexes, hydrogen bonding and proton affinity, Acc. Chem. Res., 1977, 10(8), 294–300 CrossRef CAS.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91(5), 893–928 CrossRef CAS.
- S. J. Grabowski, What Is the Covalency of Hydrogen Bonding?, Chem. Rev., 2011, 111(4), 2597–2625 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132(18), 6498–6506 CrossRef CAS PubMed.
- A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, Is the Tamm-Dancoff Approximation Reliable for the Calculation of Absorption and Fluorescence Band Shapes?, J. Chem. Theory Comput., 2013, 9(10), 4517–4525 CrossRef CAS PubMed.
- P. Besalú-Sala, A. A. Voityuk, J. M. Luis and M. Solà, Evaluation of charge-transfer rates in fullerene-based donor–acceptor dyads with different density functional approximations, Phys. Chem. Chem. Phys., 2021, 23(9), 5376–5384 RSC.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Electron Transfer in a Li+-Doped Zn-Porphyrin–[10]CPP⊃Fullerene Junction and Charge-Separated Bands with Opposite Response to Polar Environments, J. Phys. Chem. B, 2020, 124(41), 9095–9102 CrossRef CAS PubMed.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Photoinduced electron transfer in nanotube⊃C70 inclusion complexes: phenine vs. nanographene nanotubes, Chem. Commun., 2020, 56(83), 12624–12627 RSC.
- A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Photoinduced electron transfer in mechanically interlocked suit[3]ane systems, J. Mater. Chem. C, 2021, 9(30), 9436–9445 RSC.
- J. Ulstrup and J. Jortner, The effect of intramolecular quantum modes on free energy relationships for electron transfer reactions, J. Chem. Phys., 1975, 63(10), 4358–4368 CrossRef CAS.
- J. Jortner, Temperature dependent activation energy for electron transfer between biological molecules, J. Chem. Phys., 1976, 64(12), 4860–4867 CrossRef CAS.
- O. V. Boltalina, I. N. Ioffe, L. N. Sidorov, G. Seifert and K. Vietze, Ionization Energy of Fullerenes, J. Am. Chem. Soc., 2000, 122(40), 9745–9749 CrossRef CAS.
- M. Izquierdo, B. Platzer, A. J. Stasyuk, O. A. Stasyuk, A. A. Voityuk, S. Cuesta, M. Solà, D. M. Guldi and N. Martín, All-Fullerene Electron Donor–Acceptor Conjugates, Angew. Chem., Int. Ed., 2019, 58(21), 6932–6937 CrossRef CAS PubMed.
- O. A. Stasyuk, A. A. Voityuk, M. Solà and A. J. Stasyuk, γ-graphynes with extended polyyne chains for efficient photoinduced electron transfer in complexes with fullerenes, Carbon, 2023, 215, 118460 CrossRef CAS.
- S. Stevenson, G. Rice, T. Glass, K. Harich, F. Cromer, M. R. Jordan, J. Craft, E. Hadju, R. Bible, M. M. Olmstead, K. Maitra, A. J. Fisher, A. L. Balch and H. C. Dorn, Small-bandgap endohedral metallofullerenes in high yield and purity, Nature, 1999, 401(6748), 55–57 CrossRef CAS.
- M. Krause, F. Ziegs, A. A. Popov and L. Dunsch, Entrapped Bonded Hydrogen in a Fullerene: the Five-Atom Cluster Sc3CH in C80, ChemPhysChem, 2007, 8(4), 537–540 CrossRef CAS PubMed.
- K. Junghans, M. Rosenkranz and A. A. Popov, Sc3CH@C80: selective 13C enrichment of the central carbon atom, Chem. Commun., 2016, 52(39), 6561–6564 RSC.
- S. Stevenson, M. A. Mackey, M. A. Stuart, J. P. Phillips, M. L. Easterling, C. J. Chancellor, M. M. Olmstead and A. L. Balch, A Distorted Tetrahedral Metal Oxide Cluster inside an Icosahedral Carbon Cage. Synthesis, Isolation, and Structural Characterization of Sc4(μ3-O)2@Ih-C80, J. Am. Chem. Soc., 2008, 130(36), 11844–11845 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting information is available and includes a detailed computational methodology, characteristics of interactions between fullerenes and metallacage (QTAIM, NCI, and energy decomposition data), charge separation values and rates of photoinduced electron transfer. Cartesian coordinates for all studied systems are also provided. See DOI: https://doi.org/10.1039/d3tc03412g |
| This journal is © The Royal Society of Chemistry 2024 |