Uncovering cation disorder in ternary Zn_1+xGe_1−x(N_1−xO_x)₂ and its effect on the optoelectronic properties

Abstract

Ternary nitride materials, such as ZnGeN₂, have been considered as hopeful optoelectronic materials with an emphasis on sustainability. Their nature as ternary materials has been ground to speculation of cation order/disorder as a mechanism to tune their bandgap. We herein studied the model system Zn_1+xGe_1−x(N_1−xO_x)₂ including oxygen – which is often a contaminant in nitride materials – using a combination of X-ray and neutron diffraction combined with elemental analyses to provide direct experimental evidence for the existence of cation swapping in this class of materials. In addition, we combine our results with UV-VIS spectroscopy to highlight the influence of disorder on the optical bandgap.

---

Introduction

The general suitability of nitride materials for optoelectronic applications has long been demonstrated¹ and even culminated in the nobel prize for (In,Ga)N based blue LED materials – the famous III–V materials.^2–4 Besides their application as LEDs, a number of studies also evaluated the potential of nitride materials for photovoltaic applications.⁵ Growing concern, however, is associated with the use of scarce and toxic elements in photovoltaic applications,⁶ as their use will become more and more widespread. Particularly, indium is one of the scarcest elements⁷ and its use would hence potentially impede their widespread application. With the choice of trivalent cations that can replace In³⁺ being limited, a strategy that has been proven fruitful is the replacement of the trivalent cations with equimolar amounts of divalent and tetravalent cations. A similar strategy has been used to replace In³⁺/Ga³⁺ in Cu(In,Ga)S₂ (CIGS) with Zn²⁺ and Sn⁴⁺ to arrive at Cu₂ZnSnS₄ (CZTS)^8–10 as well as in double perovskites, such as Cs₂AgInBr₆, where Ag⁺ and In³⁺ replace the toxic Pb²⁺ in lead halide perovskites.^11,12

For nitrides, a combination of divalent Zn²⁺ and a tetravalent cation of group 14 (Si⁴⁺, Ge⁴⁺, and Sn⁴⁺) has been proven to yield materials with a suitable optical bandgap and stability that can be produced in the form of thin-films and bulk materials with the general formula ZnMN₂ (M = Si, Ge, Sn).^13–15 The transition from binary to ternary nitride materials not only allows the more traditional bandgap tuning mechanism through alloying of different tetravalent cations – similar to Al, Ga, In alloying in III–V's – but the particular arrangement of different cation types influences the bandgap, too.^16–25 While a compound with fully statistical distribution of the cations would crystallise isostructurally to (In,Ga)N in the wurtzite-type structure in the hexagonal space group P6₃mc,²⁶ this crystal structure type does not allow for ordering in the crystal structure, since there is only one crystallographic position for the cations.²⁷ Instead, fully or partially ordered compounds crystallise in the β-NaFeO₂-type structure in the orthorhombic space group Pna2₁, a subgroup of P6₃mc.^27–29 Herein, the cation and anion positions are split in two distinct crystallographic sites on the general Wyckoff position 4a and hence allow a great degree of freedom in the crystal structure.

A number of theoretical works have studied the influence of cation ordering on the bandgap of the material,^20,23,30 showing a strong trend to bandgap narrowing when cation disorder is introduced. Such trends were also observed experimentally and attempts to rationalise the degree of disorder based on the lattice constants have proven some success.^14,31,32 However, there are two fundamental problems when studying the order phenomena in these materials: (a) Zn²⁺ and Ge⁴⁺, the cations in the best studied material of this series, are isoelectronic and hence hardly distinguishable using standard X-ray diffraction (XRD) techniques and (b) the accidental or voluntary introduction of oxygen into the compounds appears to cause a similar phenomenon of narrowing the optical bandgap.^26,33 We could recently show that compounds made through ammonolysis of Zn₂GeO₄ follow the general formula Zn_1+xGe_1−x(N_1−xO_x)₂ within the technologically relevant reaction region.³³ While neither of the pairs Zn²⁺/Ge⁴⁺, and O²⁻/N³⁻ can be distinguished confidently using standard XRD, the neutron scattering lengths of the elements (b_Zn = 5.68 fm, b_Ge = 8.185 fm, b_O = 5.803 fm, and b_N = 9.36 fm)³⁴ allow a clear distinction between the elements and hence permit the unambiguous quantification of order/disorder in Zn_1+xGe_1−x(N_1−xO_x)₂.

Herein, we present a systematic approach to study the cation order in Zn_1+xGe_1−x(N_1−xO_x)₂ directly using powder neutron diffraction (PND). By studying the trilogy of chemical compositions, optical properties and cation order, we are able to deconvolute the effects of oxygen and intrinsic disorder on the bandgap for the first time and show that both effects – although resulting in similar trends – are unrelated to each other.

Experimental section

Samples of Zn_1+xGe_1−x(N_1−xO_x)₂ with varying compositions were prepared using a method described earlier.^26,33,35

X-ray fluorescence (XRF) measurements of the metals were used to determine the overall chemical composition of the samples. The calculation was based on the general formula, since we could show that this approach yields in reliable overall compositions.

UV-Vis measurements (UV-VIS) were performed using a PerkinElmer Lambda 750S spectrometer using a praying mantis diffuse reflectance sample holder and a 100 mm integrating sphere as the detector. The data interpretation was conducted through Kubelka–Munk treatment³⁶ combined with a Tauc-plot.³⁷ An exponent for a direct allowed bandgap was used in the Tauc-plot.³⁸

Powder X-ray diffraction (XRD) was performed using a Bruker D8 advance powder diffractometer with Ni-filtered Cu-Kα radiation (λ = 1.5418 Å) in the range of 15° ≤ 2θ ≤ 140° with a step width of 0.02° and LaB₆ as the internal standard.

Powder neutron diffraction (PND) was performed using either the E9 powder diffractometer³⁹ at the BERII research reactor of Helmholtz-Zentrum Berlin or the D2B powder diffractometer at the Institut Laue-Langevin.⁴⁰

Anomalous X-ray diffraction data for Rietveld refinement were collected at the KMC-2 Diffraction station at KMC-2 beamline,⁴¹ BESSY II, Berlin, Germany. Samples were mounted in symmetric reflection geometry using a zero-background silicon sample holder and an area sensitive gas detector (Vantec 2000, Bruker AXS). The instrumental resolution function was determined from a sample of LaB₆. A preliminary energy-dependent scan of one sample determined the positions of the absorption edges as established by the increase of the fluorescence background as 9660(2) eV and 11 102(2) eV. These values did not deviate significantly from the literature values of 9659 eV (Zn–K) and 11 103 eV (Ge–K).⁴²

Full powder diffraction sets were collected at energies of 8048 eV (λ = 1.5406 Å, equivalent to Cu Kα₁), 9649 eV (below Zn–K absorption edge), and 11 093 eV (below Ge–K edge).

Rietveld refinements were performed using Fullprof-Suite.⁴³ For the neutron diffraction samples, both XRD and NPD were refined simultaneously for each sample in order to combine the accuracy of lattice constants and contrast between cations and anions from XRD with the contrast of the cation pair Zn²⁺/Ge⁴⁺ and the anion pair O²⁻/N³⁻. The background was modelled by linear interpolation between positions with little contribution from Bragg peaks. Symmetric Thompson–Cox–Hastings pseudo-Voigt functions were used for the peak shape. Anisotropic domain size broadening according to Scherrer was refined by symmetry-adapted spherical harmonics up to second order. Further details on the anomalous diffraction refinement procedure may be found in the ESI,† in particular the form factors used for N³⁻ and O²⁻ anions.⁴⁴

Types of cation disorder in Zn_1+xGe_1−x(N_1−xO_x)₂

To signify disordered cations clearly, we use notation in the form of Zn_Ge for zinc residing at the germanium position, Ge_Zn for germanium residing at the zinc position and Zn_Zn and Ge_Ge for the respective atoms residing at their conventional crystallographic position (Fig. 1). An ideal, fully ordered ZnGeN₂ would show the anti-sites Ge_Ge and Zn_Zn.

Fig. 1 Schematic of the cation occupation of the two cation sites of the β-NaFeO₂ structure type. The left-hand case has no intrinsic disorder and a certain degree of extrinsic disorder (Zn_Ge), while the right-hand case depicts the same composition with extrinsic (Zn_Ge) and intrinsic ( and ) disorders.

Two distinct and independent types of disorder must be regarded in the zinc germanium oxide nitride materials as produced from the ammonolysis of Zn₂GeO₄. As a consequence of the reaction mechanism, no sub-stoichiometric amounts of cations or anions are expected, i.e. the ratio of cations to anions is always 1 : 1.³³ This fact, on the other hand, in combination with the decrease in overall anion charge when the oxygen amount increases means that all oxide nitrides are rich in Zn resulting in Zn/Ge > 1. As a consequence, a certain amount of Zn that is commensurate with the oxygen content necessarily resides at the Ge position, as there is more than one equivalent of Zn in such a compound, while it contains less than one equivalent of Ge. The amount of Zn_Ge in an otherwise completely ordered sample (notably Ge_Zn = 0) would hence correspond to the extrinsic disorder, since it is a direct consequence of the composition (Fig. 1, left).

On the other hand, one could imagine a situation, where a Zn atom swaps sites with a Ge atom, thus a pair of Zn_Ge and Ge_Zn are formed simultaneously. We will refer to this as intrinsic disorder (named and ), since it is independent of the chemical composition and can exist, in principle, at any oxygen level in any compound (Fig. 1, right). This latter is also the kind of disorder that has been investigated computationally in terms of its influence on the bandgap. Complete disorder in stoichiometric ZnGeN₂ – i.e. without any extrinsic disorder – is reached when Zn_Ge = Ge_Zn = 0.5 is observed. In this case, both elements are statistically distributed over both cation positions, rendering them indistinguishable from each other.

Refinement strategy for neutron powder diffraction

As a consequence of the group–subgroup relationship between the wurtzite type structure and the β-NaFeO₂-type structure, the differences in the diffraction patterns mostly occur in split reflections and only weak supplementary reflections for the latter crystal structure. Since differences in stoichiometry and cation disorder cause a quasi-continuous change between the wurtzite-type structure and the β-NaFeO₂-type structure, there are cases where the split reflections, which are significant for ordered or partially ordered materials, overlap to a large degree. In such cases, the exact peak positions – indicative for the lattice constants – and the exact intensities – indicative for the atomic arrangement – are not straightforward to separate due to a strong peak overlap. In order to ease this problem, we have combined neutron and X-ray powder diffraction measurements in a simultaneous refinement (see Fig. 2 for a representative example). Hereby, we profit from the typically much narrower peaks in X-ray diffraction (due to a better instrumental resolution) for the exact determination of the reflection positions and the distinction between isoelectronic atoms in neutron diffraction.

Fig. 2 Rietveld plots of Zn_1.032Ge_0.968(N_0.968N_0.032)₂ using neutron diffraction and X-ray diffraction (inset). Experimental values: red dots, calculated values: black line, difference: blue line and calculated reflection positions: green stacks. The calculated positions are given for the title phase (top) and LaB₆ (bottom) was used as the internal standard.

Still, the complex convolution of chemical compositions and four atomic sites on general positions makes such a refinement prone to errors and potentially unstable. Therefore, we introduced our knowledge of the chemical composition as a constraint on the composition into the refinement. We were recently able to elucidate the reaction mechanism for the later stages of the ammonolysis reaction and can therefore determine the chemical composition from XRF measurements with good confidence.³³ Two important conclusions can be drawn from the reaction model: the chemical composition of the full compound is only dependent on one variable x and the crystallographic sites are fully occupied, since the cation-to-anion ratio in Zn_1+xGe_1−x(N_1−xO_x)₂ is always 1 : 1. An important drawback is the fact that the results for multiple phase samples, in which traces of decomposition products, such as Ge and Ge₃N₄, are present cannot be treated in this way, since the chemical composition of the whole sample is no longer indicative for the ternary oxide nitride phase. Using this strategy, we have achieved stable refinements throughout the series of single-phase products studied. Fig. 3 shows exemplarily the resulting cation distribution for a series of Zn_1+xGe_1−x(N_1−xO_x)₂ compounds. It has to be noted that there is always some Ge on the Zn site.

Fig. 3 Cation distributions determined by the simultaneous refinement of neutron and X-ray powder diffraction data for a series of Zn_1+xGe_1−x(N_1−xO_x)₂ compounds. The x-axis shows the oxygen content, and the y-axis shows the cation site occupancy.

Structural studies of Zn_1+xGe_1−x(N_1−xO_x)₂

Are extrinsic and intrinsic disorders correlated?

As shown in Fig. 4, the oxygen content of the synthesised Zn_1+xGe_1−x(N_1−xO_x)₂ compounds can be tuned by the synthesis conditions: reaction time (t) and reaction temperature (T).

Fig. 4 Oxygen content x in Zn_1+xGe_1−x(N_1−xO_x)₂ compounds in dependence on the synthesis conditions (reaction time t and reaction temperature). The different reaction temperature series are colour-coded.

If intrinsic (cation swapping) and extrinsic (compositional) disorders would go hand-in-hand, there should be a clear trend in the plot of intrinsic disorder 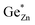vs. the oxygen content. The latter corresponds to extrinsic disorder, i.e. Zn_Ge, that is commensurate with the oxygen content. It is evident on the first glance that there is no such correlation in the data (Fig. 5).

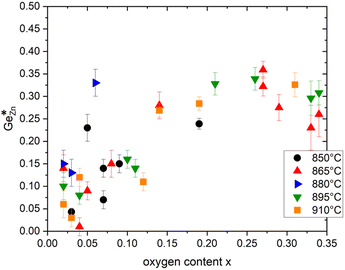Fig. 5 Plot of the intrinsic disorder versus oxygen content x for Zn_1+xGe_1−x(N_1−xO_x)₂ compounds synthesized at different temperatures.

While there appears to be a general trend in the sense that the high oxygen content, which corresponds to high extrinsic disorder, tends to go hand in hand with high intrinsic disorder, and the samples are pretty scattered, signifying that there is no causal relationship between both. Also, there are Zn_1+xGe_1−x(N_1−xO_x)₂ compounds with the same oxygen content x but different values of intrinsic disorder

This is a most significant point, since it not only proves that both types of disorder exist, but also that they are not correlated to each other. Therefore, both effects can be regarded independent of each other and we look at the relationship between the intrinsic disorder and the reaction conditions in order to explore, whether the intrinsic disorder can be tuned through the reaction conditions. Still, one has to bear in mind that for the oxide nitride system, both effects exist at the same time, and hence need to be regarded simultaneously. This influences the trends and a strictly mathematical trend can only be expected for either, if the other does not influence this specific parameter.

Order parameter

The Zn_1+xGe_1−x(N_1−xO_x)₂ compounds synthesised crystallize either in the β-NaFeO₂-type structure and show different degrees of cation disorder (as shown in Fig. 5) or in the wurtzite-type structure with a statistic distribution of the cations and hence full cation disorder. To describe the different levels of cation disorder, an order parameter has been introduced. 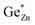The order parameter is equal to 1 for full order (no intrinsic disorder, i.e.) and equal to 0 for full disorder and is calculated according towhere describes the intrinsic disorder and Ge is the Ge-content in Zn_1+xGe_1−x(N_1−xO_x)₂. Different levels of cation disorder correspond to different values of the order parameter and can be tuned by the synthesis conditions (see Fig. 6).

Fig. 6 Order parameter in dependence on the synthesis conditions reaction time t and reaction temperature. The different reaction temperature series are colour-coded.

Influences on the lattice constants

While the hexagonal crystal system of the wurtzite-type structure restricts the lattice parameters a and b to be equal, this restriction is lifted in the orthorhombic β-NaFeO₂-type structure. The distortion of the lattice in the latter case can, therefore, be conveniently described by the ratio of these lattice constants. Since a rather complex change of the unit cells occurs in this group–subgroup relationship,²⁷ we first calculate pseudo-hexagonal lattice constants from the orthorhombic lattice constants as demonstrated previously.³³ The lattice distortion a is calculated according to

Again, there is an overall trend between the lattice distortion and both extrinsic and intrinsic disorders, but this trend is not straightforward enough to allow the prediction of any variable on the basis of another (see Fig. 7 and 8). This is most probably due to the fact that both disorder effects affect the lattice distortion in a similar manner.

Fig. 7 Plot of the lattice distortion α versus.

Fig. 8 Plot of the lattice distortion α versus the extrinsic disorder .

Intrinsic disorder and reaction conditions

Theoretical studies agree that the ordered state is energetically more favourable than any disordered state in this system but with different energy differences.^23,25,31 At a first glance, one could therefore assume that the higher thermal energy at higher temperatures would provoke a higher degree of disorder in the final product, but this is not the case in our experiments. Instead, there is a general trend that samples with comparable reaction times exhibit less disorder when they are produced at higher temperatures (Fig. 6). The higher thermal activation allows the overcoming of the activation energy for cation swapping and the energetic difference between the ordered and disordered states appears to be high enough to lock the cations in their energetically favoured environment.

Furthermore, this trend is even clearer for the dwelling times. Longer times at the same reaction temperature produce smaller levels of intrinsic disorder. The combination of the reaction time and the reaction temperature therefore allows directing the reaction into one particular composition. We found that the reaction conditions producing the smallest amount of intrinsic disorder in our experiments are 865 °C and 18.3 h of dwelling times with . This sample is, within the experimental error, completely ordered Zn_1+xGe_1−x(N_1−xO_x)₂. It is worth noting that this sample is also with the lowest extrinsic disorder, but has a nominal composition of Zn_1.035(9)Ge_0.965(9)(N_0.965(9)O_0.035(9))₂ and is hence not completely oxygen free. Since traces of oxygen are very often found in nitride materials, it is an important information that even with such small amounts of oxygen, the material can be virtually fully ordered.

Cumulating the information gained under different reaction conditions allows an experimental window to be defined, in which a variable degree of disorder can be achieved (Fig. 9). It is evident that the tuneable time window is much smaller at higher temperatures than at lower temperatures. Using higher temperatures may therefore be a key to achieving full order efficiently, while lowering the temperature allows for finer tuning of the degree of disorder. The determination of the reaction window is therefore highly beneficial for the directed conduction of the reaction in further experiments.

Fig. 9 Overview of intrinsic disorder and reaction conditions. Between the lines for full disorder (OP = 1) and order (OP = 0) the level of cation disorder can be tuned by the reaction conditions.

Bandgap energy trends

The bandgap energy values tend to become the lower, the higher the oxygen content and the extrinsic cation disorder is (Fig. 10). This trend is similar to the previous data acquired using different synthesis methods, with varying degrees of oxygen composition.⁴⁵ As outlined, however, the chemical composition is not sufficient to characterise the sample, since intrinsic and extrinsic disorders are not strictly correlated. All synthesized Zn_1+xGe_1−x(N_1−xO_x)₂ compounds lie in a band gap energy range of 2.7–3.5 eV, which also is very much in line with previous studies.

Fig. 10 Oxygen content x in Zn_1+xGe_1−x(N_1−xO_x)₂versus the optical bandgap E_g. Open symbols refer to Zn_1+xGe_1−x(N_1−xO_x)₂ with full cation disorder. The star marks the Zn_1+xGe_1−x(N_1−xO_x)₂ compound with the lowest degree of cation disorder. The triangle shows the theoretical value [23].

A key question in this study was the question, as to whether the intrinsic disorder really affects the bandgap energy in the way it was predicted theoretically. As with many of the other values, there are some degrees of scattering of values around the general trend that the bandgap energy decreases with the decreasing order parameter (Fig. 11). Therefore, the extrinsic disorder (Fig. 10) and intrinsic disorder (Fig. 11) both affect the optical bandgap in a similar manner, but independently of each other. Since both effects are heavily intertwined, the exact reaction conditions need to be precisely met, in order to reliably produce a distinct composition with a certain disorder and hence an exact bandgap.

Fig. 11 Order parameter versus optical bandgap E_g. The star marks the Zn_1+xGe_1−x(N_1−xO_x)₂ compound with nearly full cation order.

The situation becomes much clearer when considering the trend of the optical bandgap within time series at distinct temperatures (Fig. 12). A correlation is very clear in these series, which is in line with thermodynamic considerations outlined earlier. This indicates that the prolongation of the reaction time monotonically influences the intrinsic disorder rather than the extrinsic disorder. Therefore, the level of intrinsic disorder can be influenced straightforwardly through the choice of the reaction temperature. In combination with the choice of the appropriate reaction time, a targeted formulation of composition and intrinsic disorder can be achieved. However, since the reaction is strongly kinetically influenced, the concrete combinations will be highly dependent on the amount of the material produced and hence should be adjusted to the system in use.

Fig. 12 Trend of the optical bandgaps as a function of the dwelling times at different reaction temperatures.

Conclusions

We first demonstrated the direct experimental evidence of cation swapping in the ternary nitride (oxide nitride) system Zn_1+xGe_1−x(N_1−xO_x)₂, which was previously predicted computationally. Using a combination of X-ray and neutron diffraction, we showed that not only intrinsic cation disorder in the form of cation swapping exists in these compounds, but also a second form of disorder exists, which is not directly correlated with the first. This extrinsic disorder is directly related to the oxygen content and hence to the composition of the compound. Both disorder types influence the bandgap energy in similar, but unrelated ways. Using structural evidence, we therefore show for the first time that the predicted bandgap tuning mechanism through cation swapping truly exists in these materials. Further studies in the future will be revealing the individual contributions of the different types of disorder to ideally allow the individual tuning of both types independently of each other.

Author contributions

Su.S. conceived the initial idea for the study. J.B., Su.S. and Z.W. developed the experimental plan and designed the experiments. Z. W. and J. B. conducted the synthesis experiments. J.B., Z.W., St.S., A.F. and Su.S. conducted the neutron diffraction experiments. Z.W. performed the data refinement. Su.S., J.B. and Z.W. performed the data interpretation. J.B. wrote the manuscript with input from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Z.W. would like to acknowledge the MatSEC graduate school of HZB for PhD studentship. Helmholtz-Zentrum Berlin, Institut Laue-Langevin and Paul-Scherrer Institut are acknowledged for the provision of beamtime under proposal numbers 182-07291-EF/R (HZB), 5-21-1126, EASY-601, EASY-602, EASY-1012, and EASY-1013 (ILL). The authors would like to thank Galina Gurieva for assistance with the neutron measurements.

Notes and references

1. T. Matsuoka, Int. J. Optomechatronics, 2015, 9, 1–8.
2. P. Von Dollen, S. Pimputkar and J. S. Speck, Angew. Chem., Int. Ed., 2014, 53, 13978–13980.
3. I. Akasaki, Angew. Chem., 2015, 127, 7860–7873.
4. J. Heber, Nat. Phys., 2014, 10, 791.
5. N. Lu and I. Ferguson, Semicond. Sci. Technol., 2013, 28, 074023.
6. D. Shin, B. Saparov and D. B. Mitzi, Adv. Energy Mater., 2017, 7, 1602366.
7. A. A. Yaroshevsky, Geochem. Int., 2006, 44, 48–55.
8. D. M. Többens, G. Gurieva, S. Levcenko, T. Unold and S. Schorr, Phys. Status Solidi B, 2016, 253, 1890–1897.
9. S. Schorr, G. Gurieva, M. Guc, M. Dimitrievska, A. Pérez-Rodríguez, V. Izquierdo-Roca, C. S. Schnohr, J. Kim, W. Jo and J. M. Merino, J. Phys. Energy, 2019, 2, 012002.
10. L. E. Valle Rios, K. Neldner, G. Gurieva and S. Schorr, J. Alloys Compd., 2016, 657, 408–413.
11. J. Breternitz, S. Levcenko, H. Hempel, G. Gurieva, A. Franz, A. Hoser and S. Schorr, J. Phys. Energy, 2019, 1, 025003.
12. F. Igbari, Z.-K. Wang and L.-S. Liao, Adv. Energy Mater., 2019, 9, 1803150.
13. N. C. Coronel, L. Lahourcade, K. T. Delaney, A. M. Shing and H. A. Atwater, Earth-Abundant ZnSnxGe1–xN2 Alloys as Potential Photovoltaic Absorber Materials. In 2012 38th IEEE Photovoltaic Specialists Conference; 2012; pp 003204–003207. https://doi.org/10.1109/PVSC.2012.6318259.
14. A. L. Greenaway, C. L. Melamed, M. B. Tellekamp, R. Woods-Robinson, E. S. Toberer, J. R. Neilson and A. C. Tamboli, Annu. Rev. Mater. Res., 2021, 51, 591–618.
15. W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, Nat. Mater., 2019, 18, 732–739.
16. T. D. Veal, N. Feldberg, N. F. Quackenbush, W. M. Linhart, D. O. Scanlon, L. F. J. Piper and S. M. Durbin, Adv. Energy Mater., 2015, 5, 1501462.
17. N. Feldberg, J. D. Aldous, W. M. Linhart, L. J. Phillips, K. Durose, P. A. Stampe, R. J. Kennedy, D. O. Scanlon, G. Vardar, R. L. Field, T. Y. Jen, R. S. Goldman, T. D. Veal and S. M. Durbin, Appl. Phys. Lett., 2013, 103, 042109.
18. J. J. Cordell, J. Pan, A. C. Tamboli, G. J. Tucker and S. Lany, Phys. Rev. Mater., 2021, 5, 024604.
19. E. W. Blanton, K. He, J. Shie and K. Kash, J. Cryst. Growth, 2017, 461, 38–45.
20. M. S. Haseman, M. R. Karim, D. Ramdin, B. A. Noesges, E. Feinberg, B. H. D. Jayatunga, W. R. L. Lambrecht, M. Zhu, J. Hwang, K. Kash, H. Zhao and L. J. Brillson, J. Appl. Phys., 2020, 127, 135703.
21. D. Skachkov, P. C. Quayle, K. Kash and W. R. L. Lambrecht, Phys. Rev. B, 2016, 94, 205201.
22. D. Skachkov, A. P. Jaroenjittichai, L. Huang and W. R. L. Lambrecht, Phys. Rev. B, 2016, 93, 155202.
23. P. C. Quayle, E. W. Blanton, A. Punya, G. T. Junno, K. He, L. Han, H. Zhao, J. Shan, W. R. L. Lambrecht and K. Kash, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205207.
24. A. Punya, T. R. Paudel and W. R. L. Lambrecht, Phys. Status Solidi C, 2011, 8, 2492–2499.
25. S. Lany, A. N. Fioretti, P. P. Zawadzki, L. T. Schelhas, E. S. Toberer, A. Zakutayev and A. C. Tamboli, Phys. Rev. Mater., 2017, 1, 035401.
26. J. Breternitz, Z. Wang, A. Glibo, A. Franz, M. Tovar, S. Berendts, M. Lerch and S. Schorr, Phys. Status Solidi A, 2019, 216, 1800885.
27. J. Breternitz and S. Schorr, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, 208–216.
28. P. C. Quayle, Acta Crystallogr., Sect. A: Found. Adv., 2020, 76, 410–420.
29. P. C. Quayle and J. Breternitz, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, 217–221.
30. W. R. L. Lambrecht, E. Alldredge and K. Kim, Phys. Rev. B, 2005, 72, 155202.
31. C. L. Melamed, J. Pan, A. Mis, K. Heinselman, R. R. Schnepf, R. Woods-Robinson, J. J. Cordell, S. Lany, E. S. Toberer and A. C. Tamboli, J. Mater. Chem. C, 2020, 8, 8736–8746.
32. C. L. Melamed, M. B. Tellekamp, J. S. Mangum, J. D. Perkins, P. Dippo, E. S. Toberer and A. C. Tamboli, Phys. Rev. Mater., 2019, 3, 051602.
33. Z. Wang, D. Fritsch, S. Berendts, M. Lerch, J. Breternitz and S. Schorr, Chem. Sci., 2021, 12, 8493–8500.
34. V. F. Sears, Neutron News, 1992, 3, 26–37.
35. R. Viennois, T. Taliercio, V. Potin, A. Errebbahi, B. Gil, S. Charar, A. Haidoux and J.-C. Tédenac, Mater. Sci. Eng. B, 2001, 82, 45–49.
36. P. Kubelka and F. Munk, Z. Techn. Phys., 1931, 12, 593–601.
37. Y. Feng, S. Lin, S. Huang, S. Shrestha and G. Conibeer, J. Appl. Phys., 2015, 117, 125701.
38. J. Tauc, Mater. Res. Bull., 1968, 3, 37–46.
39. A. Franz and A. Hoser, J. Large-Scale Res. Facil., 2017, 3, 103.
40. A. W. Hewat, Materials Science Forum, 1986, vol. 9, pp. 69–80.
41. Helmholtz-Zentrum für Materialien und Energie, J. Large-Scale Res. Facil., 2016, 2, A49.
42. E. A. Merritt, X-ray Anomalous Scattering, http://skuld.bmsc.washington.edu/scatter/, accessed June 2014.
43. J. Rodruigez-Carvajal, Fullprof.2k. 2012: ILL-JRC.
44. P. C. Schmidt and A. Weiss, Z. Naturforsch. A, 1979, 4, 1471–1481.
45. R. R. Schnepf, J. J. Cordell, M. B. Tellekamp, C. L. Melamed, A. L. Greenaway, A. Mis, G. L. Brennecka, S. Christensen, G. J. Tucker, E. S. Toberer, S. Lany and A. C. Tamboli, ACS Energy Lett., 2020, 5, 2027–2041.

---

Footnotes

† Electronic supplementary information (ESI) available: Table of experimental results. See DOI: https://doi.org/10.1039/d3tc02650g

‡ Current address: FH Münster University of Applied Sciences, Stegerwaldstr. 39, 48565, Steinfurt, Germany.

---