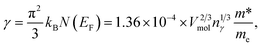Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Massive reduction in lattice thermal conductivity and strongly enhanced thermoelectric properties in Ge- and Se-doped CoSbS†
H. Sajida
Kousar‡
a,
Divya
Srivastava‡
b,
Antti J.
Karttunen
a,
Maarit
Karppinen
 *a and
Girish C.
Tewari
*a and
Girish C.
Tewari
 *a
*a
aDepartment of Chemistry and Materials Science, Aalto University, FI-00076 Aalto, Finland. E-mail: girish.tewari@aalto.fi; maarit.karppinen@aalto.fi
bDepartment of Physics and Astronomy, University of Turku, FI-20014, Finland
First published on 30th October 2024
Abstract
The thermoelectric figure-of-merit (ZT) can be significantly enhanced through the introduction of substitutional point defects of different elements, leading to pronounced scattering of phonons and consequently reducing lattice thermal conductivity. In this study, we deliberately induced atomic disorder in the paracostibite-structured CoSbS by substituting Sb with Ge. This approach was guided by density functional theory calculations, which revealed that the 12.5% Ge (1/8) substituted CoSbS exhibited characteristics of a degenerate p-type semiconductor; the Fermi level shifted within the valence band, creating hole pockets and flat energy bands. Experimentally, single-phase Co(Sb1−xGex)S samples could be synthesized up to x = 0.1. For these samples a massive reduction in lattice thermal conductivity due to softening of the low energy acoustic phonon modes and strong scattering of phonons from defects could be realized. Moreover, we investigated the effects of additional Se-for-S substitution for Co(Sb,Ge)(S,Se). This synergistic co-substitution approach allowed – along with the remarkably reduced thermal conductivity – a substantial enhancement in electrical conductivity owing to the increased charge carrier concentration. Notably, we achieved a ZT value as high as 0.10 at 400 K for the Co(Sb0.9Ge0.1)(S0.95Se0.05) sample. This novel co-substitution scheme thus outlines a prominent avenue for the CoSbS-based materials towards true applications in thermoelectric devices.
Introduction
Finding an efficient, sustainable, and environmentally friendly thermoelectric (TE) material is an important goal for bringing the TE heat-to-electricity energy conversion into a broader range of applications ranging from body-heat powered implantable medical devices to versatile solid-state heat pumps.1–3 Thermoelectric performance of a TE device is related to its electrical and thermal transport properties according to the dimensionless figure-of-merit, ZT = σS2T/κ, where σ is electrical conductivity, S is the Seebeck coefficient, κ is thermal conductivity, and T is absolute temperature. The average ZT of a competitive TE device must be higher than 1 in the entire application temperature range. Currently, the efficiency of TE devices is inferior to other energy-conversion technologies because of the low performance of the state-of-the-art TE materials. Hence, the true application breakthroughs of TE devices depend on the advances in higher-performance material development.4 Moreover, in a practical thermoelectric generator, mutually complementary and highly performing p- and n-type TE materials are needed to maximize the energy conversion efficiency.Low enough thermal conductivity is a key constraint towards the high-performance TE materials, and the most popular strategies to reduce the thermal conductivity of a given material are chemical doping and nanostructuring. Moreover, active research is carried out to discover entirely new materials with intrinsically low thermal conductivity, like Skutterudite and clathrate materials which follow the Slack's phonon-glass electron-crystal concept.5
Another material challenge to be addressed is the fact that the current state-of-the-art TE materials such as Bi2Te3,6–9 and PbTe,10–13 are composed of scarce (e.g. Te) and toxic (e.g. Pb) elements. In recent years, sulphur-based TE materials such as Cu12Sb4S13 (ref. 14) have drawn considerable attention due to the high abundancy and non-toxicity of sulphur. For some of the sulphur-based TE materials relatively low thermal conductivity and high ZT values have been reported.14–19 However, for most of these p-type semiconductors the n-type counterparts have not been found.20,21 or if found, have shown inferior TE performances.22,23
Among the various sulphur-based TE material candidates, CoSbS offers high band degeneracy near band edge24–31 and – as recently discovered by us – bipolar semiconductor nature which is a rare but extremely exciting feature considering the possibility to pair up n- and p-type TE legs made from a single base material.32 From density functional theory (DFT) calculations it has been predicted that for optimized CoSbS, ZT values up to 1 at 600 K could be possible if the high thermal conductivity value (8 W m−1 K−1 at room temperature, RT) could be significantly lowered.33 Additionally, the thermodynamic stability of this material has been confirmed from both experimental observations and first principle calculations, that it remains stable up to 1000 K.33–35 Different nanostructuring and doping schemes have been devised to enhance the TE performance of CoSbS. It has been hypothesized that doping could increase the density of states, electron effective mass, carrier concentration, acoustic phonon scattering and consequently the ZT value. In the early efforts, partial Ni-for-Co substitution in nanostructured CoSbS was found to boost the power factor (PF = σS2) up to ∼1600 μW m−1 K−2 at 773 K, but at the expense of high thermal conductivity of 3.5 W m−1 K−1, resulting in ZT ≈ 0.35 at 773 K.36 In another study for the same chemical composition synthesized through ball milling thermal conductivity was efficiently suppressed thanks to strong electron–phonon scattering such that a ZT value of 0.05 was obtained even at the low temperature of 400 K (0.5 at 873 K).37 Also, a number of investigations have focused on the optimization of carrier concentration, phonon scattering, and thermal transport properties through partial Se-for-S and Te-for-Sb substitutions.34,38–44 In the latter case, when excess Te at the Sb site was introduced to obtain PF ≈ 2150 μW m−1 K−2, the dominating electron–phonon scattering reduced the thermal conductivity to 2.73 W m−1 K−1 at 766 K (ZT ≈ 0.45).43 In another study, ZT ≈ 0.62 was reached at 730 K for a sample co-doped with Se and Te, owing to suppressed thermal conductivity (3.0 W m−1 K−1) solely due to mass disordered scattering; for the same sample the RT value of ZT was 0.18.38 So far the highest ZT values (0.65 at 873 K and 0.07 at 400 K) have been reported for Ni-for-Co and Te-for-S co-doped CoSbS, thanks to enhanced carrier mobility and slightly suppressed thermal conductivity.45
In the realm of TE materials, substitution of Sb with Ge in so-called skutterudite and half-Heusler materials has proven to be highly effective in diminishing thermal conductivity.46–50 In the present study, inspired by these results, we carried out first-principles DFT calculations for Ge-for-Sb substituted CoSbS to guide the experimental efforts to enhance the TE performance of CoSbS. According to the DFT prediction, a p-type degenerate semiconductor could be realized with a moderate (12.5%) Ge content. Experimentally, we achieved simultaneous increase in electrical conductivity and decrease in thermal conductivity upon the Ge-substitution, up to the ∼10% solubility limit of Ge at the Sb site. Most impressively, through co-doping this Ge-doped Co(Sb0.9Ge0.1)S phase with 5% Se at the S site, a record-high low-temperature (400 K) ZT value of 0.10 could be reached.
Experimental details
A series of polycrystalline Co(Sb1−xGex)S samples with the nominal Ge content x varying from 0 to 0.2 were synthesized through solid-state synthesis from appropriate quantities of elemental precursors, i.e., Co powder (99.8%), Sb shots (99.99%), and S shots (99.99%). The precursors were carefully mixed inside a glove box, after which the mixed powder was pelletized, and sealed in quartz ampoules under vacuum for a heat treatment in a furnace. The first heat treatment was carried out at 850 °C for 24–48 h inside a tube furnace at the rate of 17° h−1 with a 24 h dwell at 400 °C, followed by natural cooling to room temperature. The resultant charge was grounded and thoroughly homogenized using an agate mortar and pestle in an argon-filled glovebox, then the powders were again pressed into pellets and sealed in quartz ampoules under vacuum for the second heat treatment at 800 °C for 24 h followed by natural cooling.Additionally, one Ge and Se co-doped sample was synthesized with the nominal composition of Co(Sb0.9Ge0.1)(S0.95Se0.05) (x = 0.1 & y = 0.05); also Se was introduced in elemental form (99.999%). Here the sample synthesis progressed in three steps to ensure the synthesis of the desired material while avoiding the formation of undesirable secondary phases like germanium selenide. First, a sulphur-deficient CoSb0.9Ge0.1S0.95 sample was synthesized from pulverized precursor elements using the same mixing and heating strategy as mentioned above. Then the resultant charge was mixed with selenium and homogenized inside a glove box, pressed into pellets, and sealed in quartz ampoule under vacuum and placed in a box furnace for a second heat treatment at 800 °C for 24 h (heating rate 27° h−1). Finally, the resultant mixture was homogenized in glove box, pressed into pellets, sealed in a quartz ampoule under vacuum and annealed at 750 °C for 24 h followed by natural cooling.
Each sample was characterized for the phase purity and crystal structure determination by X-ray diffraction (XRD; PANanalytical X'Pert PRO MPD Alpha-1; Cu Kα1 radiation). The low-temperature transport properties 2–400 K were measured using a physical property measurement system (PPMS; Quantum Design; equipped with 9 T magnet). Electrical resistivity, Seebeck coefficient and thermal conductivity were measured simultaneously using the thermal transport option (TTO) available in PPMS. Hall measurements were carried out using a standard four-point-probe technique. For the TTO measurement we make four linear probe connections to a rectangular shape (roughly 10 mm × 4 mm × 1 mm) sample along its length. A heater is attached to one end probe and two thermometers are attached to middle probes. In isothermal condition the heater applies heat to one end of the sample and the temperature difference and the Seebeck voltage are measured simultaneously from the middle probes at the steady state. The Seebeck voltage is divided by temperature difference to get Seebeck coefficient. The thermal conductivity was estimated by using sample dimensions and temperature difference.
The electronic structure of Ge-doped CoSbS was computed through DFT calculations using the Quantum Espresso software package.51,52 This analysis utilized the generalized gradient approximation (GGA) method, specifically the Perdew–Burke–Ernzerhof (PBE)53 exchange–correlation functional. Scalar-relativistic ultrasoft pseudopotentials were sourced from the GBRV high-throughput pseudopotentials library. Spin–orbit coupling (SOC) was not included in the calculations. The plane wave basis cut-off was taken to be 70 Ry. The Monkhorst–Pack scheme was employed to generate a 13 × 13 × 13 k-point grid to ensure efficient coverage of reciprocal space. Convergence was achieved using a threshold of 10−8 Ry for self-consistency of reciprocal space. We previously investigated the electronic band structure of the CoSbS phase and here we have plotted it for making a comparison with Ge-doped CoSbS.27,32 First-principles calculations were also conducted to investigate the phonon band structures for both CoSbS and Ge-doped CoSbS. The PHONOPY code was utilized for these calculations, with Quantum Espresso serving as the force calculator.54,55 The force constant calculations were performed on a 2 × 2 × 1 supercell, consisting of 96 atoms. The Monkhorst–Pack scheme was utilized to generate a 3 × 3 × 3 k-point mesh for sampling the Brillouin zone, and convergence tests were performed to ensure accuracy in the force constants and phonon dispersion results.
Results and discussion
Structural analysis
The CoSbS compound is known to exist in two crystalline forms, as a semiconducting paracostibite (Pbca) and a metallic costibite (Pnm21);24,29,38 both structures are of orthorhombic symmetry but the unit cell sizes are different, such that there are 8 formula units in the former and 2 formula units in the latter.24–27,29,31 For the TE application, the semiconductor paracostibite phase in which Co forms tilted corner- and edge-sharing octahedra with three Sb and three S atoms, is preferred due to the larger Seebeck coefficient values, high band degeneracy,26,27,30 and thermodynamic stability.33,35 The lattice parameters of the non-substituted paracostibite CoSbS are: a = 5.834 Å; b = 5.948 Å, and c = 11.654 Å.26,27The X-ray diffraction patterns recorded for the present Co(Sb1−xGex)(S1−ySey) samples are displayed in ESI (Fig. S1†), and the refined lattice parameters are presented in Fig. 1. With increasing Ge substitution level in Co(Sb1−xGex)S the single-phase paracostibite is obtained up to x = 0.1. For the x > 0.1 samples, peaks of the costibite phase appear along those of the paracostibite phase. From Rietveld refinement, we estimated the costibite content at 3.5% for the x = 0.15 sample and at 52% for the x = 0.2 sample. For the rest of the experiments, we excluded the multiphase samples with x > 0.1. Likewise, the XRD pattern for the Ge and Se co-doped x = 0.1 & y = 0.05 sample confirmed its phase purity as only peaks of the paracostibite phase were observed. Fig. 1 shows that the orthorhombic lattice parameters monotonically decrease with increasing Ge content up to x = 0.1, as expected when the larger Sb is replaced with the smaller Ge. Similarly, when the larger Se is introduced to the S site the lattice parameters increase, as expected. From the Rietveld refinement results (Table S1†) it is seen that the refined occupancies of the Ge (at the Sb site) and Se (at the S site) substituents closely follow the nominal x and y values, respectively. For the multiphase x = 0.15 sample the two-phase Rietveld refinement gave the Ge occupancy at 0.138 indicating that the solubility limit of Ge in the paracostibite phase is around 14%.
 | ||
| Fig. 1 Lattice parameters plotted against Ge-content x for the Co(Sb1−xGex)(S1−ySey) samples; the red symbols indicate the lattice parameters of the x = 0.1 & y = 0.05 sample. | ||
Band structure
The Ge-for-Sb substituted CoSbS model is created by methodically replacing one of the eight Sb atoms at position 8c (−x + 1/2, y + 1/2, z) by Ge atom in the CoSbS unit cell (Pbca), equivalent to the Ge substitution level of 12.5%. The DFT-optimized lattice parameters for this Co(Sb0.875Ge0.125)S phase are: a = 5.82 Å, b = 5.94 Å, and c = 12.60 Å. Germanium is smaller than antimony, allowing it to occupy the Sb lattice position without inducing significant strain or deformation in the crystal structure. The overall decrease in unit cell volume is less than 2% compared to pristine CoSbS.27,32 The inclusion of Ge induces a slight alteration in the bonding interactions among adjacent atoms, resulting in a modest decrease in bond length by 1 to 4% when compared to pristine CoSbS.The band structure of pristine CoSbS (black) and Ge-doped CoSbS (blue) are illustrated in Fig. 2. The band structure is calculated along the high-symmetry points of the first Brillouin zone (BZ) of the orthorhombic lattice. It is apparent from Fig. 2(a) that Ge-doped CoSbS exhibits characteristics of a metal, while the pristine CoSbS is a semiconductor with an indirect bandgap of 0.38 eV.27,32 Germanium acts as an acceptor atom since it has one less valence electron than antimony. When the Ge dopant is added into CoSbS, it introduces energy bands that overlap the top of the valence band. As a result, the Fermi level lies within the valence band. Therefore, Ge-doped CoSbS is a p-type degenerate semiconductor with a higher electrical conductivity than CoSbS. This behaviour is evident from projected density of state (DOS) in Fig. 2(b), where the energy bands near the Fermi level primarily originate from the 3d orbitals of Co, 4p orbitals of Ge, and 3p orbitals of S. To discern the contribution of atoms near the Fermi level more clearly, we have plotted the normalized projected DOS per atom in Fig. 2(c), which is the total projected DOS divided by the number of atoms in the unit cell. This normalization accommodates variations in system size and ensures that the DOS is expressed on a per-atom basis.
 | ||
| Fig. 2 (a) Electronic band structure of CoSbS (black) and Co(Sb0.875Ge0.125)S (blue), (b) total and projected DOS, and (c) DOS per individual atoms for Co(Sb0.875Ge0.125)S. | ||
The calculated phonon dispersion relations for CoSbS and Ge-doped CoSbS are shown in Fig. 3. From these calculations, both phases appear to be dynamically stable; the remaining minor imaginary frequencies near the Gamma point are most likely due to numerical issues which would be mitigated by using an even denser k-point sampling and a larger phonon supercell in the force constant calculations. As illustrated in Fig. 3, Ge-doping leads to a slight hardening of the high-frequency optical phonon modes, but these modes are somewhat less dispersive compared to those in the CoSbS system. In CoSbS, the tranverse acoustic phonons (TA1 and TA2) are degenerate. However, Ge-doping lifts the degeneracy. In the Ge-doped CoSbS system, the TA1 branch softens and becomes less dispersive along the Γ–X–S–U–R path, with a softening of −5 meV observed at the U point. Notably, an additional phonon mode emerges around 33 meV, which is nearly dispersion-less over a significant portion of the Brillouin zone. Fig. 4 illustrates the phonon density of states (PDOS) and the projected PDOS. The projected PDOS shows that Sb is the primary contributor in the low-energy region (below 20 meV), Co is the main contributor in the intermediate region (20–35 meV), and S dominates the high-energy region. Contributions from other atoms are small but noticeable across all three regions. When Ge replaces one of the Sb atoms, it alters the local environment and bonding for Co, Sb, and S atoms in the crystal structure. Ge doping in the CoSbS lattice shifts the projected PDOS to lower energy levels and significantly affects the projected PDOS of Co, Sb, and S at low energy. The contribution of Ge to the projected PDOS above 25 meV is minimal. Compared to CoSbS, the low energy peaks in Ge-doped CoSbS are softened, and additional shoulders appear at lower energy around 8 meV and at an intermediate energy region around 33 meV. These extra shoulders/peaks in the PDOS arise from less dispersive TA1 and longitudinal optical branches over an extended volume of the Brillouin zone, respectively. The softer dispersion and flat TA1 branch in Ge-doped CoSbS lead to a suppressed phonon group velocity (vg = ∇kω, ω is angular frequency of phonon). Doping CoSbS with the lighter element Ge leads to phonon softening and a flat low-frequency TA branch, in line with experimental findings for TE Mg3(Sb,Bi)2. Mg3(Sb,Bi)2 exhibits soft phonons and an unusually flat low-frequency TA branches when compared with the ternary compound AMg2(Sb,Bi)2 (A = Ca or Yb).56
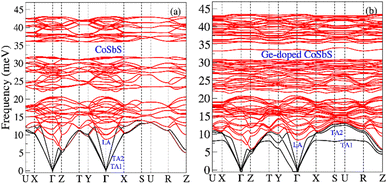 | ||
| Fig. 3 Calculated phonon dispersions (a) CoSbS and (b) Ge-doped CoSbS (Co(Sb0.875Ge0.125)S). The black lines represent the acoustic phonon modes, while the red lines depict the optical phonon modes. | ||
Charge carrier concentration
Hall-effect measurements were conducted to determine the charge carrier type and concentration in Co(Sb1−xGex)(S1−ySey) samples; Fig. 5 displays the temperature dependence of Hall coefficient (RH) and charge carrier concentration (nH), as well as the Hall resistance (RXY) versus magnetic field (B) data measured at different temperatures. At low temperatures, RH roughly follows the 1/T behaviour expected for semiconductors. However, at the higher temperatures starting from ca. 300 K, RH and nH exhibit a complex temperature dependence and remain essentially unchanged, resembling the behaviour expected for degenerate semiconductors. The linear RXYversus B behaviour indicates a single type of charge carriers, and the positive RXY values obtained indicate p-type conduction for all samples (both doped and non-doped). However, a sharp decrease in RXY (and consequently in RH) along with the systematic increase in charge carrier concentration are observed upon the Ge doping. The charge carrier concentration increases from the value of 8.22 × 1018 cm−3 determined for the non-doped x = 0 sample at 400 K to 1.3 × 1020 and 3.46 × 1020 cm−3 for the x = 0.05 and x = 0.1 samples, respectively. The highest charge carrier concentration value (9.52 × 1020 cm−3) was found for the x = 0.1 & y = 0.05 sample. The increased charge carrier concentration observed for the doped samples correlates well with the modifications seen in the electronic band structure, where the Fermi level was found to shift upon the Ge-for-Sb substitution into the valence band, creating hole pockets. This shift is indicative of a p-type semiconducting behaviour, as it facilitates the generation of holes as the primary charge carriers. Apparently, the introduction of Ge at the Sb site in the lattice alters the electronic structure, effectively reducing the band gap and enabling the Fermi level to move into positions where it can enhance the hole concentration.Thermoelectric transport properties
All the four single-phase Co(Sb1−xGex)(S1−ySey) samples were systematically characterized for their thermoelectric transport properties. The temperature dependent electrical resistivity (ρ), Seebeck coefficient (S) and power-factor are presented in Fig. 6, 400 K density of state effective mass (m*) (Pisarenko plot) in Fig. 7 and the thermal conductivity and figure-of-merit (ZT) data in Fig. 8. | ||
| Fig. 6 Temperature-dependent electrical transport properties for the Co(Sb1−xGex)(S1−ySey) samples: (a) electrical resistivity, (b) Seebeck coefficient, and (c) power factor. | ||
 | ||
| Fig. 7 n (log scale) versus |S| for Co(Sb1−xGex)(S1−ySey) samples. The dashed line is fitting with eqn (3). | ||
 | ||
| Fig. 8 Temperature-dependent (a) thermal conductivity, and (b) ZT for the Co(Sb1−xGex)(S1−ySey) samples. | ||
Electrical resistivity
From Fig. 6(a), a typical semiconducting behaviour is evident for all the samples, with ρ decreasing as temperature increases. At 400 K, a sharp decrease in ρ is observed with increasing x in Co(Sb1−xGex)S, attributable to the gradually increasing charge carrier concentration. It is important to emphasize that electronic transport properties are significantly affected by the aliovalent Ge-for-Sb substitution, which introduces additional holes in the valence band.We estimated the activation energy (band gap) for the measured samples using the Arrhenius equation in the high-temperature range, by linearly fitting ln(ρ) versus 1/T; these results are presented in Table 2. For the non-doped x = 0 sample, the activation energy is found to be 0.30 eV; this value then decreases rapidly with (hole) doping to 0.08 eV for x = 0.05, to 0.049 eV for x = 0.1, and to 0.048 eV for x = 0.1 & y = 0.05.
Seebeck coefficient
From Fig. 6(b), the positive S values seen for all Co(Sb1−xGex)(S1−ySey) samples (including the x = 0 sample) confirm the results of Hall measurements indicating p-type electrical conduction with holes as the dominant charge carriers. The 400 K S value of 370 μV K−1 for the x = 0 sample increases to a maximum value of 590 μV K−1 around 190 K before rapidly decreasing with a further decrease in temperature. Below 100 K, S reaches a minimum and remains constant until 50 K. Below 50 K, the resistance of the sample (x = 0) becomes very large (around 30 MΩ), preventing the TTO setup from measuring reliable S values.For all the x > 0 samples, the S values are lower due to the strongly enhanced charge carrier concentration. For these samples, S rapidly increases with increasing temperature up to ∼50 K, then gently decreases until 150 K, after which it increases again, albeit more slowly, above 150 K. Among all the doped samples, those with x = 0.1 and x = 0.1 & y = 0.05 exhibit the highest S, measuring 182 μV K−1 and 170 μV K−1, respectively. The large S values in our Co(Sb1−xGex)(S1−ySey) samples may be due to the high density of state effective masses (m*) near the Fermi level. The m* value can be estimated by fitting the n-dependent S data to the following equations based on the single parabolic band (SPB) model (Pisarenko plot).
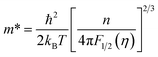 | (1) |
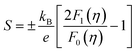 | (2) |
 and the reduced Fermi energy
and the reduced Fermi energy 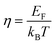 , and EF, Fermi energy. The fitting requires numerical calculations of Fermi integral, which makes it rather complex to obtain the m* from SPB model. A much simpler equation by using nonlinear regression analysis to SBP model was developed by Lee et al.,57 and given by
, and EF, Fermi energy. The fitting requires numerical calculations of Fermi integral, which makes it rather complex to obtain the m* from SPB model. A much simpler equation by using nonlinear regression analysis to SBP model was developed by Lee et al.,57 and given by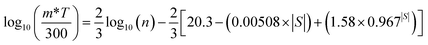 | (3) |
 and evaluated simply by substituting the experimentally measured |S| (in μV K−1). This equation can be applied to estimate m* accurately without complex Fermi integral calculation for different materials and the accuracy is within 10% of the SBP model. We analysed our data with this model and the results are presented in Fig. 7, showing the fitted m* values for different samples.
and evaluated simply by substituting the experimentally measured |S| (in μV K−1). This equation can be applied to estimate m* accurately without complex Fermi integral calculation for different materials and the accuracy is within 10% of the SBP model. We analysed our data with this model and the results are presented in Fig. 7, showing the fitted m* values for different samples.
The m* value was determined for the x = 0 and x = 0.05 samples at 1.4me, increasing to 2.4me and 3.2me for the x = 0.1 and x = 0.1 & y = 0.05 samples, respectively. The large m* values in these samples could be responsible for the relatively high S for Ge-doped samples. These observations indicate that Ge doping in the CoSbS system has a beneficial influence on the electronic band structure.
Power factor
From Fig. 6(c), the power factor is significantly enhanced for the Co(Sb1−xGex)(S1−ySey) samples, particularly for x = 0.1 which measures 300 μW m−1 K−2, and for the x = 0.1 & y = 0.05, with a power factor measured at 240 μW m−1 K−2 at 400 K.Thermal conductivity
The temperature-dependent thermal conductivity is presented for the Co(Sb1−xGex)(S1−ySey) samples in Fig. 8(a). For x = 0, thermal conductivity increases with temperature to 9.75 W m−1 K−1 at 100 K, then decreases to a value of 5.17 W m−1 K−1 at 400 K.For the doped samples, significantly suppressed thermal conductivity values are seen thorough the temperature range investigated. The 400 K value of 1.32 W m−1 K−1 seen for the x = 0.1 & y = 0.05 sample is the lowest thermal conductivity value measured for the CoSbS system to date. The rapid drop in thermal conductivity is due to the sharp decrease in lattice thermal conductivity (κl) presented in Fig. 9(c). The sharp decrease in κl could be reasonably explained by fitting the data with the Debye–Callaway model in the next section. However, from the phonon dispersion curve and PDOS (Fig. 3 and 4) we believe that the sharp drop in κl might be related to the significant broadening of phonon dispersion and reduction in the phonon lifetime due to Ge-doping. In the thermoelectric Zintl compounds Mg3Sb2 and Mg3Bi2 it was shown that replacing Mg with heavier atoms (Ca or Yb) influences the scattering of phonons and plays a major role in modulating κl.56 Other reports on the disordered systems also reveal enhanced phonon scattering due to disordered behavior.58,59 In present samples Ge/Se doping in CoSbS could lead to lattice disorder and reduce phonon life time and hence κl.
 | ||
| Fig. 9 Temperature-dependence of (a) heat capacity, (b) Debye fit at low temperature, (c) lattice thermal conductivity, and (d) phonon mean-free-path for the Co(Sb1−xGex)(S1−ySey) samples. | ||
Figure-of-merit
The dimensionless ZT is calculated using the measured values of σ, S, and κ, and the temperature dependence of ZT is depicted in Fig. 8(b). It is observed that the ZT value rises to 0.1 for the x = 0.1 & y = 0.05 sample at 400 K. The ZT values at 400 K are compared with those of other doped compositions of CoSbS in Table 1, showing approximately similar or surpassing the previously reported values for the CoSbS system.34,37,45Heat capacity
In Fig. 9(a) we show the heat capacity data for the samples. At low temperature data is analysed using Debye model presented in Fig. 9(b): in Debye model the temperature dependence of heat capacity is given by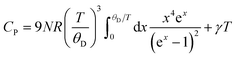 | (4) |
where Vmol is the molar volume, nγ the number of electrons in the formula unit, m* is the density of states effective mass.
| Sample | ρ (Ω m) | Activation energy (eV) | S (μV K−1) | κ (W m−1 K−1) | PF (W m−1 K−2) | ZT | θ D (K) | γ (J mol−1 K−2) | Density (g cm−3) |
|---|---|---|---|---|---|---|---|---|---|
| x = 0 | 0.025 | 0.30 | 370 | 5.17 | 5.32 × 10−6 | 4.23 × 10−4 | 248 | 3.71 × 10−3 | 6.739 |
| x = 0.05 | 3.69 × 10−4 | 0.08 | 124 | 3.14 | 4.09 × 10−5 | 0.005 | 256 | 6.48 × 10−3 | 6.715 |
| x = 0.1 | 1.11 × 10−4 | 0.049 | 182.3 | 1.91 | 2.41 × 10−4 | 0.063 | 264 | 5.21 × 10−3 | 6.879 |
| x = 0.1 & y = 0.05 | 8.8 × 10−5 | 0.048 | 170 | 1.32 | 3.0 × 10−4 | 0.10 | 230 | 0.0135 | 6.812 |
Lattice thermal conductivity and phonon mean free path
The κl is calculated by subtracting the electronic contribution (κe) – estimated using Wiedeman–Franz law (κe = LσT) from the electrical conductivity σ, from the experimental thermal conductivity value; the results are presented in Fig. 9(c). The. Lorentz number (L) is a constant (2.44 × 10−8 W Ω K−2) for metals and degenerate semiconductors. However, in case of non-degenerate semiconductors L shows significant deviation and converges to 1.5 × 10−8 W Ω K−2 at high temperatures where acoustic phonon scattering dominates the conduction.60 This is found to be correlated to an increase in the absolute value of S. Recently, a first-order correction to the degenerate limit of L depending on the absolute value of S is given by L = 1.5 + exp(−|S|/116) (where L is in 10−8 W Ω K−2 and S in μV K−1) was proposed by Kim et al.60 for non-degenerate semiconductors. This equation was found to estimate the value of L within 5% for single parabolic band/acoustic phonon scattering assumption. We used this relation for the estimation of L for our samples, see Fig. S3.† For all the samples, the κe value was found to be small, and the thermal conductivity dominated by κl. The massive reduction in thermal conductivity of Co(Sb1−xGex)(S1−ySey) samples is due to strongly reduced κl. The temperature dependence of phonon mean free path (MFP) was then evaluated using Fourier's law (κl = (1/3)CPρdνlk) with the Debye model, where ρd, ν, and lk are density, phonon velocity, and MFP of the phonons involved in the thermal conductivity. The ν was estimated from θD for each sample. From Fig. 9(d), the phonon MFP increases with decreasing temperature; the 2 K values are given in Table 3. The MFP for the x = 0 sample is 2.06 μm, and it strongly decreases with Ge-doping to 1.46 μm for x = 0.05, to 0.21 μm for x = 0.1 and to 0.18 μm for x = 0.1 & y = 0.05.| Sample | d (10−6) m | A (10−42 s3) | B (10−18 s K−1) | l k (μm) |
|---|---|---|---|---|
| x = 0 | 0.504 | 2.44 | 2.37 | 2.06 |
| x = 0.05 | 0.407 | 152.7 | 0.064 | 1.46 |
| x = 0.1 | 0.769 | 22.03 | 2.35 | 0.208 |
| x = 0.1 & y = 0.05 | 0.449 | 21.47 | 5.09 | 0.182 |
Mechanism leading to low lattice thermal conductivity
To explain the massive reduction in κl along the Ge-for-Sb substitution we fitted the data to the Debye–Callaway model.61,62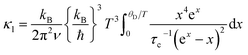 | (5) |
 and τc is the phonon relaxation time. In our data fitting we only considered grain boundary scattering, point defect scattering, and phonon–phonon Umklapp scattering mechanisms. The relaxation time is calculated as
and τc is the phonon relaxation time. In our data fitting we only considered grain boundary scattering, point defect scattering, and phonon–phonon Umklapp scattering mechanisms. The relaxation time is calculated aswhere, τB, τD, and τU represent the relaxation time for grain boundary scattering, point defect scattering and dissipative phonon–phonon scattering, respectively. The fitting parameter d stands for the grain size, while A and B are constants; the values obtained (Table 3) indicate the contribution of different scattering mechanisms on the thermal conductivity. The relaxation time for boundary scattering, the parameter d, is approximately same for all the studied samples. The point defect scattering coefficient A was found to be extremely large for the substituted Co(Sb1−xGex)(S1−ySey) samples in comparison to the non-substituted CoSbS sample. It increased approximately by 62 times for x = 0.05 and 10 times for x = 0.1, and x = 0.1 & y = 0.05, and is the dominant contributing factor to the lattice thermal conductivity. The Umklapp scattering coefficient B decreased significantly for x = 0.05, remained roughly the same for x = 0.1 and increased by 2 times for x = 0.1 & y = 0.05.
The Ge-for-Sb substitution causes point defects in lattice which enhances the phonon scattering and lowers the MFP. The volume defects/point defect clusters are clearly visible in the SEM image of the x = 0.1 sample (Fig. 10(c)). The significantly smaller values of MFP for the Ge-substituted samples presented in Fig. 9(d) (2 K value in Table 3) also support the scheme of phonons being predominantly scattered by defects.
Conclusions
This study has uncovered Ge as a highly effective substituent for Sb to enhance the thermoelectric properties of CoSbS. Since this substitution is not isoelectronic, it significantly impacts the electron transport properties, leading to a notable increase in electrical conductivity because of increased charge carrier concentration. Concurrently, the Ge-for-Sb substitution contributes to a substantial reduction in lattice thermal conductivity in CoSbS (75% reduction for the 10% Ge and 5% Se co-substituted sample) which we attributed to a significant softening of the acoustic phonons, resulting in a flatter dispersion curve and extensive point defect scattering. Thus, a remarkably low thermal conductivity value of 1.32 W m−1 K−1 at 400 K was achieved; this is the lowest value reported for this system.The 400 K ZT value is significantly improved up to 0.10. This represents a 236-fold enhancement in ZT compared to the pristine CoSbS, primarily due to a substantial increase in electrical conductivity resulting from a higher charge carrier density and significantly reduced lattice thermal conductivity. This study thus not only underscores the potential of Ge doping, but also presents a promising direction for further enhancement of the thermoelectric properties of CoSbS.
Finally, we like to emphasize that the present study covers only the TE characteristics of the Co(Sb,Ge)(S,Se) system up to 400 K, but we foresee that at higher temperatures the system could show highly competitive ZT values, owing to its impressively low thermal conductivity values compared to state of art TE materials presented in Fig. 11.
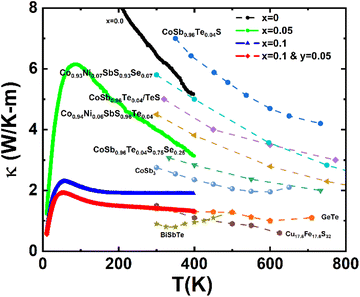 | ||
| Fig. 11 Thermal conductivity of Co(Sb1−xGex)(S1−ySey) as a function of temperature, in comparison to other typical thermoelectric materials. | ||
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Girish C. Tewari, Divya Srivastava and Maarit Karppinen conceived and designed the study. Girish C. Tewari and Maarit Karppinen supervised the study. Sajida Kousar synthesized the samples and together with Girish C. Tewari performed the experimental investigation and data analysis. Divya Srivastava performed the first-principles calculations. Sajida Kousar, Girish C. Tewari and Maarit Karppinen wrote the original draft, and finalized the paper. All authors participated in the final writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the funding from the Finnish Cultural Foundation (Project THERMOF), and the use of the RawMatTERS Finland Infrastructure (RAMI) at Aalto University. HSK thanks the funding from Jenny and Antti Wihuri Foundation.References
- I. Petsagkourakis, K. Tybrandt, X. Crispin, I. Ohkubo, N. Satoh and T. Mori, Sci. Technol. Adv. Mater., 2018, 19, 836–862 CrossRef CAS PubMed
.
- Y. Yang, X. J. Wei and J. Liu, J. Phys. D: Appl. Phys., 2007, 40, 5790–5800 CrossRef CAS
.
- E. Bell Lon, Science, 2008, 321, 1457–1461 CrossRef CAS PubMed
.
- A. Shakouri, Annu. Rev. Mater. Res., 2011, 41, 399–431 CrossRef CAS
.
-
G. A. Slack, Handbook of Thermoelectrics, CRC Press, 1995 Search PubMed
.
- J. He, M. G. Kanatzidis and V. P. Dravid, Mater. Today, 2013, 16, 166–176 CrossRef CAS
.
- W. Liu, K. C. Lukas, K. McEnaney, S. Lee, Q. Zhang, C. P. Opeil, G. Chen and Z. Ren, Energy Environ. Sci., 2013, 6, 552–560 RSC
.
- A. M. Adam, E. Lilov and P. Petkov, Superlattices Microstruct., 2017, 101, 609–624 CrossRef CAS
.
- R. Venkatasubramanian, E. Siivola, T. Colpitts and B. O'Quinn, Nature, 2001, 413, 597–602 CrossRef CAS PubMed
.
- Y. Pei, A. LaLonde, S. Iwanaga and G. J. Snyder, Energy Environ. Sci., 2011, 4, 2085–2089 RSC
.
- K. Biswas, J. He, I. D. Blum, C. I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed
.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Sceince, 2008, 321, 554–557 CrossRef CAS PubMed
.
- O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M. H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden and B. C. Sales, Nat. Mater., 2011, 10, 614–619 CrossRef CAS PubMed
.
- X. Lu, D. T. Morelli, Y. Xia, F. Zhou, V. Ozolins, H. Chi, X. Zhou and C. Uher, Adv. Energy Mater., 2012, 3, 342–348 CrossRef
.
- Q. Tan, L.-D. Zhao, J.-F. Li, C.-F. Wu, T.-R. Wei, Z.-B. Xing and M. G. Kanatzidis, J. Mater. Chem. A, 2014, 2, 17302–17306 RSC
.
- Y. He, T. Day, T. Zhang, H. Liu, X. Shi, L. Chen and G. J. Snyder, Adv. Mater., 2014, 26, 3974–3978 CrossRef CAS PubMed
.
- H. S. Kousar, D. Srivastava, M. Karppinen and G. C. Tewari, Z. Anorg. Allg. Chem., 2023, 649, e202300079 CrossRef CAS
.
- G. C. Tewari, H. Sajida Kousar, D. Srivastava and M. Karppinen, J. Magn. Magn. Mater., 2024, 590, 171688 CrossRef CAS
.
- G. C. Tewari, T. S. Tripathi, H. Yamauchi and M. Karppinen, Mater. Chem. Phys., 2014, 145, 156–161 CrossRef CAS
.
- R. Chetty, A. Bali and R. C. Mallik, J. Mater. Chem. C, 2015, 3, 12364–12378 RSC
.
- K. H. Lim, M. Li, Y. Zhang, Y. Wu, Q. Zhou, Q. Wang, X. Yang, P. Liu, W.-J. Wang, K. W. Wong, K. M. Ng, Y. Liu and A. Cabot, J. Mater. Sci. Technol., 2024, 171, 71–79 CrossRef CAS
.
- J. Leszczyński, K. Kapera, A. Mizera, P. Nieroda and A. Koleżyński, Materials, 2022, 15, 4115 CrossRef PubMed
.
- D. P. Weller, G. E. Kunkel, A. M. Ochs, D. T. Morelli and M. E. Anderson, Mater. Today Phys., 2018, 7, 1–6 CrossRef
.
- L. J. Cabri, D. C. Harris and j. M. Stewart, Am. Mineral., 1970, 55, 10–17 CAS
.
- L. J. Cabri, D. C. Harris and J. M. Stewart, Can. Mineral., 1970, 10, 232–246 CAS
.
- R. Carlini, C. Artini, G. Borzone, R. Masini, G. Zanicchi and G. A. Costa, J. Therm. Anal. Calorim., 2010, 103, 23–27 CrossRef
.
- H. S. Kousar, D. Srivastava, M. Karppinen and G. C. Tewari, J. Phys.: Condens. Matter, 2019, 31, 405704 CrossRef CAS PubMed
.
- R. Henry, J. Steger, H. Nahigian and A. Wold, Inorg. Chem., 1975, 14, 2915–2917 CrossRef CAS
.
- J. F. Rowland, E. J. Gabe and S. R. Hall, Can. Mineral., 1975, 13, 188–196 Search PubMed
.
- Q. Du, M. Abeykoon, Y. Liu, G. Kotliar and C. Petrovic, Phys. Rev. Lett., 2019, 123, 076602 CrossRef CAS PubMed
.
- M. A. Zakrzewski, E. A. J. Burke and H. W. Nugteren, Can. Mineral., 1980, 18, 165–171 CAS
.
- H. S. Kousar, D. Srivastava, A. J. Karttunen, M. Karppinen and G. C. Tewari, APL Mater., 2022, 10, 091104 CrossRef CAS
.
- S. Bhattacharya, R. Chmielowski, G. Dennler and G. K. H. Madsen, J. Mater. Chem. A, 2016, 4, 11086–11093 RSC
.
- Y. You, X. Su, S. Hao, W. Liu, Y. Yan, T. Zhang, M. Zhang, C. Wolverton, M. G. Kanatzidis and X. Tang, J. Mater. Chem. A, 2018, 6, 15123–15131 RSC
.
- J. Yang, D. Yang, Y. Wang, X. Quan and Y. Li, J. Solid State Chem., 2021, 302, 122443 CrossRef CAS
.
- D. Parker, A. F. May, H. Wang, M. A. McGuire, B. C. Sales and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 045205 CrossRef
.
- Z. Liu, H. Geng, J. Shuai, Z. Wang, J. Mao, D. Wang, Q. Jie, W. Cai, J. Sui and Z. Ren, J. Mater. Chem. C, 2015, 3, 10442–10450 RSC
.
- R. Chmielowski, S. Bhattacharya, S. Jacob, D. Pere, A. Jacob, K. Moriya, B. Delatouche, P. Roussel, G. Madsen and G. Dennler, Sci. Rep., 2017, 7, 46630 CrossRef CAS PubMed
.
- R. Chmielowski, S. Bhattacharya, W. Xie, D. Péré, S. Jacob, R. Stern, K. Moriya, A. Weidenkaff, G. K. H. Madsen and G. Dennler, J. Mater. Chem. C, 2016, 4, 3094–3100 RSC
.
- Y. You, X. Su, W. Liu, Y. Yan, T. Hu, C. Uher and X. Tang, RSC Adv., 2017, 7, 34466–34472 RSC
.
- D. Srivastava, G. C. Tewari and M. Karppinen, J. Phys.: Condens. Matter, 2014, 26, 505501 CrossRef PubMed
.
- Y. You, X. Su, W. Liu, Y. Yan, J. Fu, X. Cheng, C. Zhang and X. Tang, J. Solid State Chem., 2018, 262, 1–7 CrossRef CAS
.
- G. Guélou, F. Failamani, P. Sauerschnig, J. Waybright, K. Suzuta and T. Mori, J. Mater. Chem. C, 2020, 8, 1811–1818 RSC
.
- W. Huang, H. Zhu, Q. Liu, S. Duan, M. Yang, X. Liu and T. Su, J. Alloys Compd., 2024, 970, 172555 CrossRef CAS
.
- W. Gao, Y. Yang, M. Deng, B. Sun, Y. Fu, X. Wei, Y. Li, Z. Liu and J. Sui, J. Mater. Chem. A, 2022, 10, 19829–19838 RSC
.
- G. Joshi, H. Lee, Y. Lan, X. Wang, G. Zhu, D. Wang, R. W. Gould, D. C. Cuff, M. Y. Tang, M. S. Dresselhaus, G. Chen and Z. Ren, Nano Lett., 2008, 8, 4670–4674 CrossRef CAS PubMed
.
- D. shaheen, M. S. Javed, H. Shah, S. Hussain, M. A. Ahmad, R. Raza, M. Saleem and X. Zhou, Ceram. Int., 2018, 44, 12610–12614 CrossRef
.
- X. W. Wang, H. Lee, Y. C. Lan, G. H. Zhu, G. Joshi, D. Z. Wang, J. Yang, A. J. Muto, M. Y. Tang, J. Klatsky, S. Song, M. S. Dresselhaus, G. Chen and Z. F. Ren, Appl. Phys. Lett., 2008, 93, 193121 CrossRef
.
- X. Zhao, X. Li, L. Chen, Y. Pei, S. Bai, X. Shi and T. Goto, Jpn. J. Appl. Phys., 2008, 47, 7470–7473 CrossRef CAS
.
- K. K. Johari, R. Bhardwaj, N. S. Chauhan, B. Gahtori, S. Bathula, S. Auluck and S. R. Dhakate, ACS Appl. Energy Mater., 2020, 3, 1349–1357 CrossRef CAS
.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens.Matter, 2017, 29, 465901 CrossRef CAS PubMed
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens.Matter, 2009, 21, 395502 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens.Matter, 2023, 35, 353001 CrossRef CAS PubMed
.
- A. Togo, J. Phys. Soc. Jpn., 2022, 92, 012001 CrossRef
.
- J. Ding, T. Lanigan-Atkins, M. Calderón-Cueva, A. Banerjee, D. L. Abernathy, A. Said, A. Zevalkink and O. Delaire, Sci. Adv., 2021, 7, eabg1449 CrossRef CAS PubMed
.
- K. H. Lee, S.-i. Kim, J.-C. Lim, J. Y. Cho, H. Yang and H.-S. Kim, Adv. Funct. Mater., 2022, 32, 2203852 CrossRef CAS
.
- Q. Ren, M. K. Gupta, M. Jin, J. Ding, J. Wu, Z. Chen, S. Lin, O. Fabelo, J. A. Rodríguez-Velamazán, M. Kofu, K. Nakajima, M. Wolf, F. Zhu, J. Wang, Z. Cheng, G. Wang, X. Tong, Y. Pei, O. Delaire and J. Ma, Nat. Mater., 2023, 22, 999–1006 CrossRef CAS PubMed
.
- M. K. Gupta, J. Ding, D. Bansal, D. L. Abernathy, G. Ehlers, N. C. Osti, W. G. Zeier and O. Delaire, Adv. Energy Mater., 2022, 12, 2200596 CrossRef CAS
.
- H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506 CrossRef
.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS
.
- J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta07047j |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |