Fast Mg-ion insertion kinetics in V₂Se₉

Abstract

V₂Se₉ displays facile electrochemical insertion of up to 1.6 Mg²⁺ per unit formula with fast diffusion (coefficients of 10⁻¹⁰–10⁻¹² cm² s⁻¹) surpassing best-in-class materials like Mo₆S₈. Detailed structural characterization of synchrotron X-ray diffraction data with ab initio Maximum Entropy Method analysis reveals Mg²⁺ insertion into octahedral sites within the large vdW space between [V₄Se₁₈]_∞ chains. Fast rate performance is attributed to low structural perturbation and low diffusion barriers, calculated by bond valence pathway analysis, resulting from the low charge-per-size of anionic selenium. X-ray photoelectron spectroscopy and X-ray absorption spectroscopy reveal that reversible insertion of Mg²⁺ is facilitated by V⁵⁺/V³⁺ redox. V₂Se₉ demonstrates that selenides, despite their larger molecular weight, offer potential as fast-rate positive electrode materials for magnesium batteries over well-explored oxides and sulfides.

---

Introduction

Performance limitations, safety concerns, and the availability of the necessary raw materials for rechargeable Li-ion batteries have created a demand for innovative energy storage technologies beyond lithium.^1,2 The high natural abundance, low cost and high volumetric capacity of magnesium (3833 mA h cm⁻³) compared to that of lithium (2046 mA h cm⁻³) and sodium (1125 mA h cm⁻³) make rechargeable Mg batteries an appealing alternative.^3–6

The most significant challenge preventing the commercialization of magnesium batteries is a lack of suitable positive electrode materials capable of suitable kinetics for Mg²⁺ insertion. Despite the comparable ionic radii of Mg²⁺ and Li⁺ (0.57 vs. 0.59 Å),⁷ the high charge density of Mg²⁺ results in strong electrostatic interaction between the anionic sub-structure of the host electrode and the inserting ion.^8,9 As a result, Mg-storage is hindered both thermodynamically, with limited reaction reversibility; and kinetically, with sluggish Mg²⁺ insertion into the host structure.¹⁰

Increasing the polarizability of the anion framework has resulted in improved kinetic performance of insertion electrodes: layered VSe₂ and TiSe₂ demonstrate faster Mg²⁺ migration than the isostructural sulfide and oxide materials, albeit at a lower working potential.^11–17 Similarly, capacity retention has been improved in well-studied electrode materials like the Chevrel phase Mo₆S_8−xSe_x (0 < x ≤ 2)^18,19 and CuS_1−xSe_x (0 < x ≤ 0.25)^20–22 by partial substitution of S for Se. The enhanced kinetics of Mg²⁺ storage following the trend of Se > S > O can be attributed to both weakening electrostatic interactions as well as increasing anionic radii resulting in larger channels for Mg²⁺ diffusion.²³

Recently, one-dimensional chain materials like VS_4,^24–27 V₂PS₁₀,²⁸ and TiS₃ (ref. 29 and 30) have attracted interest as positive electrode materials for Mg batteries. Their structures are comprised of one-dimensional chains formed from trans-facially connected [MS₈] polyhedra bound loosely by weak van der Waals (vdW) forces with large inter-chain spacing (5.38 Å in VS₄); through which Mg²⁺ can diffuse. These materials are noted for the complex insertion mechanisms, emanating from anionic redox on the disulfide (S₂)²⁻ site.³¹ The highly active anion chemistry of these materials provides motivation to explore S/Se substitution.

The structure of V₂Se₉, like VS₄ and V₂PS₁₀, consists of infinite one-dimensional chains of [V₄Se₁₈]_∞ formed by trans-facial stacking of distorted rectangular anti-prismatic [VSe₈] polyhedra. These chains extend along the [302] direction and are weakly bound by vdW forces. The large anionic radius of Se results in large inter-chain spacings of 6.366–6.610 Å for V₂Se₉, significantly longer than those observed in VS₄ and V₂PS₁₀. The oxidation states in V₂Se₉ can be considered by the asymmetric unit V₂⁵⁺(Se₂)^2–₄Se²⁻, where all Se are coordinated to a V⁵⁺ metal center and exist in either a (Se₂)²⁻ or Se²⁻ oxidation state (a detailed structural description is provided in the ESI, Fig. S1 and Table S1†).

Recently, V₂Se₉ was investigated as an electrode material in monovalent Li⁺ and Na⁺ batteries and was shown to operate by a combination of insertion and conversion mechanisms.^32–34 Initially, up to nine Li⁺ or Na⁺ are inserted between the [V₄Se₁₈]_∞ chains by an intercalation-type process. At lower potentials, conversion reactions result in the formation of metallic V and either Li₂Se or Na₂Se.

Herein, Mg²⁺ insertion into V₂Se₉ with fast kinetics is reported. Through detailed structural analysis of synchrotron X-ray diffraction (SXRD) data, combined with maximum entropy method analysis and bond valence diffusion pathway analysis, Mg²⁺ sites are located within the structure and highlight the inter-connected three-dimensional diffusion pathways and low structural perturbation as the origin of fast Mg²⁺ insertion. Ex situ X-ray photoelectron (XPS) and X-ray absorption spectroscopic (XAS) characterization and Raman spectroscopy were used to elucidate an insertion mechanism resulting from a reversible V⁵⁺/V³⁺ redox couple, with no evidence of parasitic conversion reactions which were seen for Mg²⁺ insertion into VS₄.

Experimental section

V₂Se₉ synthesis

Powdered vanadium (99.5% Alfa Aesar) and selenium (99.5% Sigma Aldrich) were combined in stoichiometric quantities in an agate pestle and mortar in an inert Ar atmosphere in a glovebox (MBraun LabMaster 130; H₂O and O₂ levels < 0.1 ppm) before being pressed into pellets (13 mm diameter at 0.5 tonnes) and sealed in fused silica ampules under a vacuum of 1 × 10⁻⁵ mbar before heating to 623.15 K in a Carbolite RHF 1600 furnace for 21 days using heating and cooling rates of 5 K min⁻¹ (Fig. S2 and Table S2†). After synthesis, the pellets were collected and homogenized by further grinding. Elemental analysis by ICP-OES yielded a composition of V_2.00(2)Se_9.4(3) (Fig. S3 and Table S3†). TEM-EDX yielded a Se/V ratio of 4.31(18) (Fig. S4 and S5 and Table S4†). Further details for ICP-OES, TEM and TEM-EDX measurements is provided in the ESI.† Se and VSe₂ were observed as minor impurity phases by XRD in the as-made V₂Se₉ and the Mg-intercalated powders. The relative weight ratios of these impurity phases did not change between the pristine and intercalated materials.

Electrochemical cell assembly and testing

Stainless steel coin cells (CR2032, Pi-KEM) assembled under an inert Ar atmosphere inside a glovebox (MBraun LabMaster Pro-Eco) with O₂ and H₂O levels < 0.1 ppm. Positive electrodes consisted of a slurry of V₂Se₉ powder, sieved through a 20 μm mesh (Impact Test Systems), conductive carbon (Pi-KEM, dried), and binder (PVDF, dried) in proportions of 70 : 20 : 10 w/w combined with in N-methyl-2-pyrrolidone. The slurry was cast onto carbon-coated aluminium foil and cut into disks (16 mm diameter) and dried under vacuum overnight. Active material loadings were typically between 0.25 and 0.35 mg cm⁻², with an electrode thickness of 100 μm. Negative electrodes consisted of polished Mg foil discs with a diameter of 18 mm. Electrodes were separated by Whatman GF/D borosilicate glass fibre membranes soaked with 500–750 μL of an electrolyte consisting of a 0.5 M solution of magnesium bis(trifluoromethane)sulfonimide (Mg(TFSI)₂, 99.5%, Solvionic) dissolved in a mixture of dimethoxyethane (DME, Sigma Aldrich, anhydrous, inhibitor-free, 99.5%) and 1-methoxypropyl-2-amine (MPA, Sigma Aldrich, 99%) in a 3.84/1 w/w ratio (Fig. S6†).³⁵ The Mg(TFSI)₂ had been dried at 220 °C under a dynamic vacuum of ≈5 mbar for 12 h. DME was further dried over activated molecular sieves (Sigma Aldrich, 3 Å, heated to 250 °C under vacuum). MPA was degassed by freeze–pump–thaw with liquid N₂ and dried by distillation over CaH₂ before storing over activated molecular sieves. A final water content of <10 ppm was recorded by Karl-Fischer titration (Table S5†). Electrolyte stability was confirmed by cyclic voltammetry and Mg plating and stripping (Fig. S7 and S8†).

Electrochemical measurements were conducted using a BioLogic VSP300 potentiostat at 30 °C. Galvanostatic charge–discharge was performed between potential limits of 0.8–2.2 V vs. Mg²⁺/Mg at current densities of 20–200 mA g⁻¹, recording the change in potential every 5 mV. Ex situ cell testing was performed on powder-based Swagelok cells. The cathode composition was 70% active material, 30% carbon black, without binder with typical loadings of 15–20 mg. Cells were discharged and charged with a constant current of 20 mA g⁻¹ to the required potentials. Powders were collected, washed in DME, and dried under vacuum at 60 °C for 12 h.

Potentiostatic Intermittent Titration Technique (PITT) utilised chronoamperometric pulses imposed from open circuit potential to 0.8 V vs. Mg²⁺/Mg with an interval of 20 mV until the current reach 0.75 mA g⁻¹ at each potential step. Diffusion coefficients (D) were calculated by differentiation of the finite-diffusion Cottrell equation for the long-time region:

where I is current (A), n number of transferred electrons, F Faraday constant (96 485 C mol⁻¹), A surface area (cm²), ΔC for concentration gradient within the particles, t for time (s) and a for particle radius (cm).

X-ray diffraction (XRD) techniques

Synchrotron X-ray diffraction (SXRD) was performed at Diamond Light Source, U.K., on high-resolution beamline I11.^36,37 The patterns were recorded in the transmission mode [0° < 2θ < 90°] using a position sensitive detector (PSD, λ = 0.824399 Å) at room temperature on samples introduced into 0.3 mm diameter borosilicate glass capillaries. Rietveld refinements were carried out using TOPAS Academic Version 7.³⁸ The background was fitted manually using a 36-part linear profile. Fundamental parameters of the beamline were modelled, including Lorentz-polarization, la, lo and lh Voight coefficients, source-to-sample radius & slit widths. Peak profiles were fitted using the Stephens model in the monoclinic setting (b-axis unique). Simple axial model was initially constrained to 5.0 before being refined after initial peak profile fitting.

Maximum Entropy Method (MEM) was used to calculate electron density distributions. The observed structure factor was extracted from data using a Rietveld refinement performed in Jana 2006.³⁹ The refinement models were taken from Topas refinements and atomic positions were kept fixed. Peak profiles were fit empirically using a pseudo-Voight function and the Stephens model for anisotropic strain broadening in the monoclinic setting, as was done in Topas. The background was fit manually using a 60-point linear interpolation to ensure that peak intensities were extracted to the highest degree of accuracy. The electron densities were generated with MEM using the Sakata–Sato algorithm in BayMEM⁴⁰ on a grid of 300 × 300 × 300 voxels and run till the combined FG constraint met its convergence criteria of 1.0. Electron densities were visualized using VESTA.⁴¹

Mg²⁺ diffusion pathways in V₂Se₉ were analyzed by bond valence pathway analysis (BVPA) using the software SoftBV GUI (Version 1.3.1).⁴² Three-dimensional energy landscape maps were generated for Mg²⁺ ion diffusion using soft bond valence parameters calculated using the CIF generated from SXRD data for V₂Se₉. Maximum voxel resolution of 0.1 Å was applied. The resulting volumetric data was visualized using an isosurface level of 5.0 α₀⁻³ (α₀: Bohr radius) using the VESTA software.⁴¹

Elemental analysis

Scanning Transmission Electron Microscopy (STEM) imaging, and EDX analysis were performed using a Cs-corrected TEM/STEM Jeol 2100FCs microscope operating at 200 kV. For EDX mapping, a JEOL silicon drift detector (SDD) was used with a detection area of 100 mm².

Further details regarding Transmission Electron Microscopy (TEM) and Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES) can be found in the ESI.†

Raman spectroscopy

Ex situ Raman measurements were collected using a Raman microscope (Renishaw, in via reflex coupled with an inverted Leica microscope), with a 532 nm laser as the excitation source (power <300 μW), focused onto the sample using a ×50 objective (Olympus). The collected Raman spectra were baseline-corrected. The spectral measurement time was 60 seconds with 5 accumulations to ensure a good signal-to-noise ratio and well-resolved peaks. To check for potential laser damage, V₂Se₉ was measured with varying laser intensities and exposure times. No changes in the spectra were observed up to 10% power for 60 seconds.

X-ray photoelectron and X-ray absorption analysis

X-ray Photoelectron Spectroscopy (XPS) analysis was performed using a Thermo NEXSA XPS fitted with a monochromatic Al Kα X-ray source (1486.7 eV), a spherical sector analyser and multichannel resistive plate, 128 channel delay line detectors. All data were recorded at 19.2 W with an X-ray beam size of 400 × 200 μm². Survey scans were recorded at a pass energy of 200 eV, and high-resolution scans were recorded at a pass energy of 40 eV. Electronic charge neutralization was achieved using a dual-beam low-energy electron/ion source (Thermo Scientific FG-03). The ion gun was operated at a current of 150 μA and a voltage of 45 V. All sample data were recorded at a pressure below 10⁻⁸ Torr and at 294 K. Data was processed using CasaXPS (v2.3.19PR1.0) using a Shirley background and peak fitting with Gaussian–Lorentzian functions. The Fermi edge of Ni foil measured using the same equipment was used to calibrate the data and eliminate any effects of surface charging.

X-ray Absorption Spectroscopy (XAS) was measured at beamline B18 (ref. 43) at Diamond Light Source, U.K. Pellets of sample diluted with cellulose were prepared with an optimized density for X-ray absorption measurements in transmission mode at the V K-edge (5465 eV) and the Se K-edge (12 658 eV) at ambient temperature. The samples were hermetically sealed in Al pouches under argon. The spectra were calibrated by fixing the maximum of the derivative of V and Se foil references placed after the samples for the corresponding edges, respectively, and normalized with the Athena software.⁴⁴

Results and discussion

Cyclic voltammetry was used to probe the operational potential window and redox activity of V₂Se₉ towards electrochemical (de)insertion of Mg²⁺ in 0.5 M magnesium bis(trifluoromethane)sulfonimide (Mg(TFSI)₂) in dimethoxyethane (DME) and 1-methoxy-2-propylamine (3.84 : 1 w/w) electrolyte (Fig. S6–S8 and Table S5†). From an open circuit potential (OCP) of 1.8 V vs. Mg²⁺/Mg the cell potential was swept at a rate of 100 μV s⁻¹ while the reductive potential was lowered, from 0.9 V to 0.2 V (Fig. 1a). When cycled between 0.8 V and 2.4 V, a sharp reductive peak is observed at 1.72 V, with additional weaker peaks observed at 1.36 V, 1.25 V and 1.13 V. Strong oxidative peaks are observed above 1.6 V, centered at 1.72 V and 1.95 V, though several smaller less resolved peaks are also present. The inflection at 2.4 V was shown to be oxidation of the electrolyte solution, which continued as the potential was further increased. This observation is similar to other reports which use Mg(TFSI)₂ electrolyte solutions in the literature and is in-line with the potential at which [TFSI]⁻ has been shown to corrode Al in Li-ion based systems.^45,46 When the potential is swept below 0.6 V there is an almost immediate loss of redox activity, suggesting the system undergoes irreversible changes below ca. 0.7 V (Fig. S9†). Low-potential conversion reactions are observed in V₂Se₉ in Li⁺ and Na⁺ cells when cycled below 1.5 V vs. Li⁺/Li (0.83 V vs. Mg²⁺/Mg) and 1.0 V vs. Na⁺/Na (0.66 V vs. Mg²⁺/Mg).^32–34 Similar conversion reactions are likely occurring with Mg²⁺ at potentials below 0.7 V. This is indeed the case for structurally related one-dimensional chain materials containing sulfur, such as VS₄ and TiS₃, which display low-potential conversion reactions in which MgS and metallic V are formed.^47–49 While the formation of Li₂Se and Na₂Se is shown to be reversible, the formation of MgS is not, and results in significant capacity decay over the first few cycles. It is therefore reasonable to expect that the formation of MgSe is also irreversible. The large charge-per-size of Mg²⁺ compared to Li⁺ and Na⁺ will result in stronger Mg–Se bonding in MgSe than Li–Se and Na–Se bonds in Li₂Se and Na₂Se, respectively. As such, a suitable potential window of 0.8 V to 2.2 V was selected for galvanostatic cycling.

Fig. 1 (a) Cyclic voltammogram recorded for Mg_xV₂Se₉ at a sweep rate of 100 μV s⁻¹ between 0.8 V and 2.4 V. (b) Voltage profiles of cycles 1–12 for V₂Se₉ in 0.5 M Mg(TFSI)₂ in dimethoxyethane/1-methoxypropyl-2-amine (3.84/1, w/w) at 200–600 mA g⁻¹. (c) Potentiostatic intermittent titration technique of the discharge of V₂Se₉ to calculate the Mg²⁺ diffusion coefficients as a function of potential, from 1.3 V to 0.8 V. (d) Second cycle discharge potential profile for V₂Se₉/carbon loose powder electrode in a Swagelok cell at a current density of 50 mA g⁻¹ for ex situ analysis. Spheres represent the potentials at which cells were stopped and the materials collected: cyan for discharged (magnesiated) Mg_xV₂Se₉ and orange for charged (de-magnesiated) Mg_xV₂Se₉. Typically, a second discharge capacity of 90 mA h g⁻¹ (i.e., 1.35 Mg²⁺/V₂Se₉) is achieved by 0.8 V. Samples of Mg_xV₂Se₉ were collected at 1.6 V (x = 0.15); 1.3 V (x = 0.47); and 0.8 V (x = 1.35) during discharge; and 1.65 V (x = 0.97) and 2.2 V (x = 0.00) during charging.

During the first cycle, an initial discharge capacity of 107 mA h g⁻¹ is observed at a current density of 200 mA g⁻¹. The first cycle shows a different initial potential profile to subsequent cycles. The potential drops rapidly to 1 V, suggesting a large overpotential activation for Mg²⁺ insertion whereas upon further cycling, Mg begins to be inserted at a much higher potential of 1.6 V. Subsequent cycles achieve a decreasing amount of capacity from 106 to 88 mA h g⁻¹ (i.e., 1.6–1.3 Mg²⁺/V₂Se₉) at 200 mA h g⁻¹ with potential profiles remaining similar; with plateaus at 1.75 V, 1.50 V and 1.35 V (Fig. 1b), consistent with the peak positions observed in cyclic voltammetry. The capacity decreases at higher current densities, with 50 mA h g⁻¹ (0.76 Mg²⁺/V₂Se₉) at 400 mA g⁻¹ and 31 mA h g⁻¹ (0.47 Mg²⁺/V₂Se₉) at 600 mA g⁻¹ being maintained for multiple cycles. This is lower than the capacity achieved by the insertion of Li⁺ or Na⁺ into V₂Se₉, which can be estimated to be 300 mA h g⁻¹ from insertion reactions alone.^32,33 This can likely be attributed to the associated thermodynamic and kinetic difficulties with the insertion of high charge-per-size Mg²⁺ relative to Li⁺ and Na⁺.

Mg²⁺ de-insertion appears to be a more complex process with voltage hysteresis observed during charging. Plateaux are observed at 1.65 V, 1.72 V, and 1.85–1.90 V, again in agreement with peaks observed during cyclic voltammetry. An extended plateau is observed above 2.1 V that originates from the oxidation of the electrolyte as the potential approaches the upper limit of the electrochemical stability window (Fig. S8†), accounting for the larger capacity observed on charging.⁵⁰ As a result, this difference in capacity is observed for cycles at slower rates, with higher current densities achieving higher coulombic efficiencies (Fig. S10†).

Magnesium insertion diffusion was studied using Potentiostatic Intermittent Titration Technique (PITT); the calculated diffusion coefficients from the selected points are illustrated in Fig. 1c. The Mg²⁺ diffusion coefficients in Mg_xV₂Se₉ are ≈10⁻¹⁰–10⁻¹² cm² s⁻¹, and change as a function of potential indicating Mg content-dependent insertion kinetics. The kinetic performance of V₂Se₉ towards Mg²⁺ insertion is faster than V₂PS₁₀ (10⁻¹⁴–10⁻¹¹ cm² s⁻¹ between 1.5 and 0.1 V)²⁸ and Mo₆S₈ (10⁻¹⁴–10⁻¹¹ cm² s⁻¹ between 1.4–1.0 V);^18,51 and is comparable to monovalent charge carrier (Li⁺, Na⁺) insertion into layered oxide materials.^52,53 The observed rapid kinetics of V₂Se₉ can be attributed to the low-charge-density selenide framework, helping to overcome the sluggish kinetics of Mg batteries.

To understand the storage mechanism of V₂Se₉, Swagelok-type cells with cathodes consisting of approximately 20 mg of 70/30 w/w V₂Se₉/carbon black powder (no binder) were used to prepare samples of Mg_xV₂Se₉ for ex situ diffraction, XPS, and XAS measurements. Typically, a second discharge capacity of 90 mA h g⁻¹ (i.e., 1.35 Mg²⁺/V₂Se₉ giving Mg_1.35V₂Se₉) is achieved by 0.8 V (Fig. 1d). The lower capacity is the result of reduced conductivity between the loose powder electrode in Swagelok cells compared to cast electrodes in coin cells. The long plateau above 2.1 V is attributed to electrolyte oxidation, as previously discussed.

STEM-EDX false color micrographs shown in Fig. 2 confirm that Mg is homogeneously distributed throughout the bulk of V₂Se₉ crystallites after insertion. ICP-OES analysis gives a composition of Mg_1.20(3)V_2.00(8)Se_9.4(5), in good agreement with the expected Mg content from the electrochemical discharge capacity (Table S6†). Ex situ SXRD analysis was performed on Mg_xV₂Se₉ (0 ≤ x ≤ 1.35) prepared at various potentials during discharge: 1.6 V (x = 0.15); 1.3 V (x = 0.47); 0.8 V (x = 1.35); and recharge: 1.65 V (x = 0.97) and 2.2 V (x = 0.00).

Fig. 2 STEM dark field and false color EDX micrographs of (a) V₂Se₉ (b) and Mg_1.35V₂Se₉ (after discharge to 0.8 V; shown in for separate areas) using an acceleration voltage of 200 kV with a probe current of 7.475 nA. V is shown in blue, Se in green and Mg in orange. The Mg content cannot be resolved due to overlap between the Mg K_a (1.253 keV) and Se L_a (1.379 keV) peaks. Mg signal is within the limits of noise in V₂Se₉. For Mg_1.35V₂Se₉ Mg is homogeneously inserted throughout the crystallite.

Analysis of SXRD data for Mg_1.35V₂Se₉ (discharged to 0.8 V vs. Mg²⁺/Mg) indicates that the structural symmetry (C2/c) and framework of V₂Se₉ is retained for cycled Mg_xV₂Se₉ (Fig. 3a). Fourier difference analysis reveals two separate regions of electron density as suitable positions for Mg²⁺ within the unit cell (Fig. 3b and c and S11†). Magnesium was placed on each of these sites with an initial occupancy of 1.0 (equivalent to Mg₂V₂Se₉) before refinement. The proximity of magnesium positions to V and Se sites was restrained using a penalty function during final refinement, and the B_iso values for both Mg sites were constrained to be equal. The final structural model (shown in Fig. 3a) achieved fit statistics of R_wp = 0.521%, improved from 0.624% for a model without any Mg present (Fig. S12 and Table S7†).

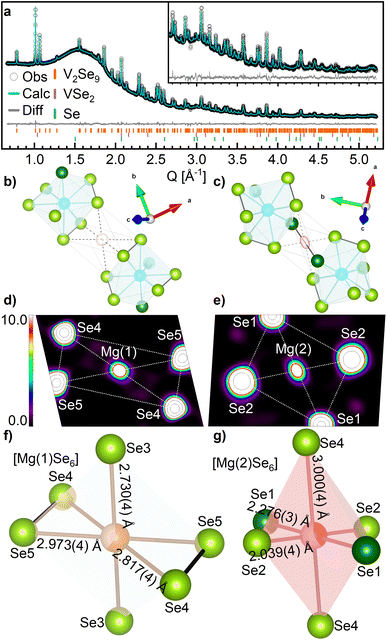Fig. 3 (a) Rietveld refinement of Mg_1.35V₂Se₉ against SXRD data collected at I11 beamline. Observed data are shown by white circles. The calculated fit is shown by the cyan line. The difference between the calculated and observed data are shown by the grey line. The Bragg reflection positions of V₂Se₉, VSe₂ and Se are given by the orange, purple and green ticks, respectively. Inset is an enlarged region of the fit between 2.5–5.2 Å⁻¹. Refined parameters are summarized in Table S7.† (b–g) Coordination of Mg sites in Mg_1.35V₂Se₉. V is shown by blue spheres, Mg(1) by orange spheres, Mg(2) by red spheres, Se²⁻ by dark green spheres and Se¹⁻ by light green spheres. Se–Se bonds are shown by bold black lines and V–Se and Mg–Se bonds are shown by grey lines. Electron density isosurfaces of the Mg(1) and Mg(2) sites in Mg_1.35V₂Se₉ generated by (b and c) Fourier difference analysis and (d and e) maximum entropy method. 2D planes bisect the MgSe₆ octahedrons in the equatorial plane (see Fig. S13†). (f and g) Local coordination environments of Mg(1) and Mg(2).

The location of the two refined Mg positions is further confirmed through analysis of the SXRD data via maximum entropy method (MEM) calculations by generating the electron density distribution ab initio from the observed diffraction data.⁴⁰ Analysis was performed on both pristine V₂Se₉ and Mg_1.35V₂Se₉ to visualize the change in charge density upon reduction of the host structure. Fig. 3d and e shows electron density observed between neighboring [V₄Se₁₈]_∞ chains of Mg_1.35V₂Se₉ which is not present in V₂Se₉, further confirming Mg is present on these sites (Fig. S13†). Notably, the electron density observed on the Mg sites is more localized than that of the larger, and therefore less densely charged, neighboring Se sites.

The refined occupancies of the two Mg sites were 0.596(19) and 0.402(16), providing a refined composition of Mg_0.99(3)V₂Se₉, compared to Mg_1.35V₂Se₉ calculated from electrochemical capacity. Identification of discrete Mg sites suggests a homogeneous distribution of Mg²⁺ within bulk V₂Se₉, indicative of an insertion-type electrochemical process. Additionally, no metallic V or MgSe is observed via ex situ diffraction measurements, suggesting that no conversion processes take place when cycling between 0.8–2.2 V.

Mg is octahedrally coordinated to Se in Mg_1.35VSe₉, with MgSe₆ octahedra located in the vdW space between neighboring [V₄Se₁₈]_∞ chains. Selenide materials containing octahedral MgSe₆ units involving Se²⁻ only, such as spinel MgM₂Se₄ (M = In, Al, Sc),⁵⁴ olivine Mg₂MSe₄ (M = Ge, Si, Sn)⁵⁵ and Mg₂P₂Se₆ (ref. 56) have average Mg–Se distances of 2.74(9) Å with a range of 2.3–3.3 Å (Fig. S14†), and average polyhedral volumes of 27.2(4) ų. In Mg_1.35V₂Se₉, Mg(1) is coordinated entirely to Se¹⁻ anions with an average Mg–Se distance of 2.84(12) Å and an octahedral volume of 21.51 ų (Fig. 3f). Mg(2) is coordinated to four Se¹⁻ and two Se²⁻ anions with an average Mg–Se distance of 2.4(5) Å and an octahedral volume of 17.85 ų (Fig. 3g). The smaller Mg(2) octahedra is attributed to a lower Mg occupancy and the smaller anionic radius of Se²⁻. Additionally, the mixed coordination of Mg(2) to Se¹⁻ and Se²⁻ results in a larger octahedral distortion index than that of Mg(1) (0.154 compared to 0.031) due to different anionic radii and charge densities.⁵⁷

Each VSe₈ polyhedron shares faces with two MgSe₆ octahedra, with one Mg(1) and one Mg(2); likewise, each MgSe₆ octahedron shares two opposite, and identical, faces with two separate VSe₈ polyhedra from neighboring [V₄Se₁₈]_∞ chains. Every (Se₂)²⁻ group is coordinated to at least one Mg²⁺ site. Mg(1) shares two triangular faces with VSe₈ formed between Se(1)²⁻, Se(2)¹⁻ and Se(4)²⁻. Mg(2) shares two triangular faces formed between Se(3)¹⁻, Se(4)¹⁻, and Se(5)²⁻, such that two edges of Mg(2) Se₈ octahedron is formed by the (Se₂)²⁻ bond between Se(4) and Se(5) (Fig. 4a). In this way, chains of [V₄Se₁₈]_∞ that are separated by vdW gaps in V₂Se₉ are connected in Mg_1.35V₂Se₉ through Se–Mg–Se bonds (Fig. 4b).

Fig. 4 The structure of Mg_1.35V₂Se₉. V is shown by blue spheres, Mg(1) by orange spheres, Mg(2) by red spheres, Se²⁻ by dark green spheres and Se¹⁻ by light green spheres. Se–Se bonds are shown by bold black lines and V–Se and Mg–Se bonds are shown by grey lines. (a) The coordination of Mg sites around V₂Se₉. (b and c) Chains of [V₄Se₁₈]_∞ that are separated by vdW space in V₂Se₉ are connected through Se–Mg–Se bonding in Mg_1.35V₂Se₉ in the (011) plane. V–V interchain distances across Mg sites are provided.

The structural model for Mg_1.35V₂Se₉ was used as a starting model for refinement against SXRD data for other ex situ samples of Mg_xV₂Se₉ after discharging (0 ≤ x ≤ 1.35): 1.6 V (x = 0.15); 1.3 V (x = 0.47); 0.8 V (x = 1.35); and after charging: 1.65 V (x = 0.97) and 2.2 V (x = 0.00). Refined Rietveld parameters and fits are given in Fig. S15 and Tables S8–S11.†

Refinement of Mg site occupancies shows Mg content in Mg_xV₂Se₉ increases as potential is decreased (Fig. S16a†). After discharging from the OCV (1.8 V) to 1.6 V the occupancy of Mg(1) increases to 0.227(17), while Mg(2) is only 0.061(17). Mg(1) occupancy continues to increase rapidly to 0.553(14) by 1.3 V and more slowly to 0.596(11) by 0.8 V; suggesting that Mg(1) is filled more easily in the earlier stages of electrochemical discharge, as would be expected given the larger octahedral volume and low charge density Se¹⁻ coordination of this site. The occupancy of Mg(2) increases to 0.263(14) by 1.3 V and 0.402(12) by 0.8 and is therefore filled more easily in the later stages of discharge, but to a lesser degree than Mg(1). This supports the measured PITT data (Fig. 1c), which shows faster kinetics in the early stages of Mg insertion before decreasing later in the discharge process. The preferential occupation of Mg(1) over Mg(2) is likely attributed to favorable kinetics associated with the interaction of high-charge density Mg²⁺ with the lower charge density Se¹⁻ (to which Mg(1) has a higher coordination) compared to Se²⁻. None of the Mg sites observed through ex situ structural analysis are fully occupied and, likely, the higher capacities recorded for non-ex situ cells (Fig. 1b and d) are the result of greater occupancy of these sites with increased Mg insertion due to the difference in cell preparation. Upon charging from 0.8 to 2.2 V, refinement shows that magnesium is de-intercalated from Mg_1.35V₂Se₉, reforming V₂Se₉.

To better understand the facile Mg²⁺ insertion kinetics observed by PITT, Mg²⁺ ion conduction pathway energy landscapes were calculated from soft bond valence parameters by bond valence pathway analysis (BVPA) (further details are given in the ESI†).⁵⁸ 2D and 2D Mg²⁺ diffusion pathways are observed in V₂Se₉, with energy barriers ranging from 0.140 to 0.742 eV (Fig. S17 and S18†).^44–46

Locally, this results in minimal strain induced on the individual [VSe₈] polyhedra, which is evidenced by minimal change to average V–Se and Se–Se distances between V₂Se₉ and Mg_1.35V₂Se₉ (2.57(5) Å to 2.55(4) Å for V–Se; and 2.716(12) Å to 2.728(18) Å for Se–Se, respectively). The relatively small changes in V–Se distances are in line with other vanadium chalcogenide materials after electrochemical insertion of Mg²⁺: V–O distances in MgV₂O₅ increase by only 0.03 Å compared to V₂O₅ (1.49 Å to 1.52 Å)⁵⁹ and V–S distances in Mg_1.5VS₄ increase by only 0.04 Å compared to VS₄ (2.40 Å to 2.44 Å).²⁵ The lower charge density of Se, compared to O and S, as well as the lower Mg/V ratio for Mg_1.35V₂Se₉ result in little to no change in the average V–Se bond length between V₂Se₉ and Mg_1.35V₂Se₉. The minimal change in Se–Se distances between V₂Se₉ and Mg_1.35V₂Se₉ indicates that (Se₂)²⁻ bonds are maintained after Mg²⁺ insertion, unlike VS₄ (ref. 25) and V₂PS₁₀ (ref. 28) where S–S bonds break upon discharge (increasing in length by up to 15%). A full comparison of bond lengths for V₂Se₉ and Mg_xV₂Se₉ (0 ≤ x ≤ 1.35) is provided in Table S12.†

More significant structural perturbation is observed in the relative positions of the [V₄Se₁₈]_∞ chains across the vdW space, which are influenced by the location of the Mg sites. The V–V interchain distances between vanadium sites adjacent to Mg(1) increase by 0.1% (from 7.394(9) Å in V₂Se₉ Å to 7.401(9) Å) in Mg_1.35V₂Se₉ (Fig. 4b and c). This is different to the V–V interchain distances between vanadium adjacent to the lesser occupied Mg(2) site contract by 2% (from 6.625(10) Å to 6.495(9) Å). This suggests that at low levels of Mg²⁺ occupancy, the selenium anionic framework of the [V₄Se₁₈]_∞ chains are attracted towards the high charge density intercalated ion. For x(Mg) = 1.35 in Mg_1.35V₂Se₉, this attractive force dominates, and the distance between [V₄Se₁₈]_∞ chains decreases in all directions (Fig. S16b†).^25,28,59 The shortest inter-chain Se–Se distances decrease from 3.443(6) to 3.419(7) Å for Se₁–Se₂ and from 3.521(4) Å to 3.419 Å for Se₂–Se₅. This leads to contraction of the a, b, and c lattice parameters, each with an approximately equal induced strain of 0.1%, resulting in a 0.3% decrease in unit cell volume from 1063.225(19) ų in V₂Se₉ to 1059.511(18) ų in Mg_1.35V₂Se₉ (Fig. S16c†). After charging, the unit cell returns to 1062.988(13) ų, with lattice parameters close to that of V₂Se₉.

Spectroscopic methods were used to further examine the changes in the electronic structure of V₂Se₉ upon Mg insertion. Both V₂Se₉ and Mg_1.35V₂Se₉ crystalize in C2/c symmetry (crystal class 2/m). Group-theory analysis identifies 33 Raman active modes for V₂Se₉. V and 4 of the Se sites that make up the (Se₂)²⁻ groups occupy 8f Wyckoff positions, each with 3 A_g and 3 B_g active modes, while Se²⁻ occupies a 4e site with 1 A_g and 2 B_g active modes (Tables S13–S15†).^60,61 Low structural symmetry results in overlapping modes and produces the convoluted spectra observed for V₂Se₉ in Fig. 5a. Similarly to Raman spectra of isostructural Nb₂Se₉ (ref. 62) and related VS₄,⁴⁷ the spectrum can be divided into two regions; with phonons in the low-wavenumber range, between 105 and 175 cm⁻¹, assigned to V–V and V–Se bending and stretching modes, and a high-wavenumber range, between 268 and 346 cm⁻¹ (relating to shorter chemical bonds), assigned to Se–Se stretching and twisting as Se cage-breathing (Table S16†).

Fig. 5 (a) Ex situ Raman spectroscopy of V₂Se₉ (black), Mg_1.35VSe₉ (orange) after discharging to 0.8 V and V₂Se₉ after charging (Ch) to 2.2 V (cyan). (b and c) XPS spectra of Mg_xV₂Se₉ collected at various stages of discharge/charge. (b) Mg 2p collected at a pass energy of 200 eV and scaled using the Se 3d signal. (c) Se 3d XPS collected at a pass energy of 40 eV. Both Se 3d5/2 and Se 3d3/2 contributions are shown for each Se species: (Se₂)²⁻ (light blue) and Se²⁻ (orange). The sum of orbital contributions is shown as the purple envelope relative to the observed data (black circles). The Se 3d5/2 and 3d3/2 spin–orbit components of each oxidation state were constrained based on relative position, Δ = 0.86 eV, and intensity ratio = 0.735. The relative areas of Se²⁻/(Se₂)²⁻ for V₂Se₉ were constrained at 1/8, to reflect the nominal formula V₂⁵⁺(Se₂)^2–₄Se²⁻. Normalized (d) Se K-edge and (e) V K-edge XANES data measured in transmission for V₂Se₉ (black), Mg_1.35V₂Se₉ (discharged 0.8 V, orange), and V₂Se₉ (charged 2.2 V, cyan). Inset panels show enlarged profile of the absorption edges at 12 658 eV and 5465 eV, respectively.

Ex situ Raman spectra collected for Mg_1.35V₂Se₉ (Fig. 5a) contain similar 33 Raman active A_g and B_g modes as V₂Se₉ as the octahedrally coordinated Mg²⁺ occupies 4a and 4b Wyckoff positions and possess no Raman active modes (Table S15†). The decrease in the intensity of signals observed between 268 and 346 cm⁻¹ is the result of electron delocalization away from (Se₂)²⁻ towards the Raman inactive Mg site, to which all (Se₂)²⁻ are coordinated, resulting in reduced polarizability, and dampening of the Raman signal.⁶³ Additionally, coordination of (Se₂)²⁻ to Mg²⁺, as well as the presence of Mg sites between [V₄Se₁₈]_∞ chains, will limit the movement of Se sites to stretching, twisting, and breathing, further decreasing signal intensity. After charging to 2.2 V intense peaks in the high-wavenumber range are recovered supporting Mg de-insertion from the bulk.

X-ray photoelectron spectroscopy (XPS) measurements show the formation of peaks at 1303.2 eV, 89.0 eV, and 49.8 eV in Mg_1.35V₂Se₉ after discharge that are not present in V₂Se₉. These signals relate to Mg 1s, Mg 2s, and Mg 2p core levels, respectively (Fig. S22†), and relate to Mg insertion after discharging to 0.8 V. The low energy of the Mg 2p signal corresponds to higher kinetic energy electrons and is capable of probing deeper than Mg 1s and Mg 2s, and as such suggests that Mg is present beyond the immediate surface in Mg_1.35V₂Se₉.⁶⁴ The intensities of the Mg peaks is much lower after charging to 2.2 V, supporting Mg de-insertion (Fig. 5b), with the slight Mg signal that remains likely being due to the presence of surface species, which would explain why this feature is more prominent for the more surface sensitive Mg 1s and Mg 2s cores than Mg 2p.⁶⁵

The Se 3d XPS signals contain contributions from both Se²⁻ and (Se₂)²⁻ oxidation states (Fig. 5c and S23†). In V₂Se₉, the binding energy of the Se²⁻ 3d_5/2 signal is at 53.4 eV; comparable to other vanadium selenide materials containing Se²⁻.^66–68 The higher oxidation state Se¹⁻ 3d_5/2 signal is at a higher binding energy of 54.4 eV due to the increased interaction between the photo-emitted electron and the ion core.⁶⁹ The (Se₂)²⁻ 3d_5/2 signal is maintained at 54.4 eV in both V₂Se₉ and Mg_1.35V₂S₉. The Se²⁻ 3d_5/2 shows a slight shift in Mg_1.35V₂Se₉ relative to V₂Se₉ (from 54.7 eV to 53.7 eV) though its position is maintained after charging to 2.2 V. This is indicative of slight irreversible structural change occurring upon initial discharging supported by the signal broadening observed for both 0.8 V and 2.2 V samples. The relative areas of the Se²⁻/(Se₂)²⁻ signals is maintained at close to 1/8 (as in V₂Se₉); suggesting that Se is redox inactive between 0.8-2.2 V for x(Mg) 0 ≤ x ≤ 1.35, in agreement with the structural analysis via SXRD.

X-ray Absorption Near-Edge Spectroscopy (XANES) measurements of Se and V K-edges were used to monitor changes in the oxidation state of bulk Mg_xV₂Se₉ at the various stages of electrochemical cycling. Similarly to the Se 3d XPS measurements, there is no change in Se edge position observed by XANES upon discharge or charge (Fig. 5d). An average Se oxidation state between −1.08 and −1.11 is maintained between V₂Se₉, Mg_1.35V₂Se_9, and after charging to V₂Se₉ indicating the redox inactivity of Se (Fig. S24†). This differs from VS₄ (ref. 25) and V₂PS₁₀ (ref. 28) which show changing contributions from signals relating to S²⁻ and (S₂)²⁻ as S–S bonds are broken and reformed. Se has a lower electronegativity compared to S, meaning Se²⁻ is less readily formed than S²⁻ or O²⁻ which may explain why V₂Se₉ is anionic redox-inactive. While reversible cleavage of (Se₂)²⁻ has been observed in molecular systems,⁷⁰ in solid materials Se–Se bonding is almost certainly less prone to redox activity than S–S or O–O. Cleavage of (Se₂)²⁻ bonding in Mg_xV₂Se₉ may be the cause of irreversible electrochemistry below 0.8 V. The V K-edge XANES edge position decreases from 5471.0 eV for V₂Se₉ to 5470.5 eV for Mg_1.35V₂Se₉ after discharge, indicating a reduction from V⁵⁺ (Fig. 5e). Insertion of 0.675 Mg²⁺ per V requires the reduction of V⁵⁺ to V^3.65+. Upon charging, the vanadium edge energy and absorption profile return to that of V₂Se₉ (5471.0 eV), suggesting reversible redox processes take place on the V site and are responsible for Mg intercalation.

Conclusions

V₂Se₉ is capable of storing up to 1.6 Mg²⁺ (106 mA h g⁻¹) within the vdW spaces between its constituent one-dimensional chains. Detailed structural characterization by SXRD and MEM supports homogeneous distribution of Mg²⁺ ions within V₂Se₉, supporting an insertion-type electrochemical process without the formation of metallic V or MgSe that would be associated with a conversion-type reaction. Insertion of Mg²⁺ is facilitated by reversible redox on the V site, while (Se₂)²⁻ is not redox active over the achieved levels of discharge. The octahedral coordination of Mg²⁺ results in minimal strain on the [VSe₈] polyhedra, allowing for small changes in bond distances during Mg insertion, resulting in V₂Se₉ displaying exceptional Mg²⁺ diffusion kinetics, with diffusion coefficients surpassing state-of-the-art cathode materials such as Mg₂Mo₆S₈. Calculated bond valence parameters support diffusion pathways with low energy barriers to ion mobility are available to inserting Mg²⁺. The one-dimensional structure of V₂Se₉ combined with the low charge density of coordinating (Se₂)²⁻ and Se²⁻ anions enables rapid access to Mg²⁺ sites which enhances kinetic performance. Despite the larger mass of Se relative to S, V₂Se₉ can achieve comparable capacity to high-performance sulfide materials like Mo₆S₈, whilst operating with faster diffusion kinetics, helping to overcome the kinetic limitations that have perpetually hindered Mg²⁺ electrodes. This work motivates further investigation of tuning the anion chemistry of the wide range of known low-dimensional transition metal chalcogenides to improve kinetic performance of multivalent electrodes.

Data availability

The data supporting this article have been included as part of the ESI.† Underlying data collected as part of this work is available via the University of Liverpool data repository at https://datacat.liverpool.ac.uk/id/eprint/2676. The CIF files for the structures of V₂Se₉ and Mg_1.35V₂Se₉ are deposited with CSD accession codes 2357643 and 2357642, respectively.

Author contributions

Matthew A. Wright: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft, writing – review & editing; Jungwoo Lim, Raul A. Pacheco Muino: formal analysis, investigation, visualization, data curation; Anna E. Krowitz, Cara J. Hawkins, Mounib Bahri: investigation; Luke M. Daniels, Ruiyong Chen, Luciana Gomes Chagas: conceptualization, supervision, writing – review & editing; James Cookson, Paul Collier, Alan V. Chadwick, Nigel D Browning: funding acquisition, resources; John B. Claridge: conceptualization, supervision; Laurence J. Hardwick, Matthew J. Rosseinsky: conceptualization, funding acquisition, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded under the Engineering and Physical Sciences Research Council (EPSRC; EP/V026887). M. A. W. thanks Johnson Matthey for studentship funding. We acknowledge the ICSF Faraday Institution project “CATMAT – Next Generation Li-ion Cathode Materials” [grant number FIRG016] for funding J. L. We acknowledge NSG and EPSRC for funding A. E. K. We acknowledge Diamond Light Source for access to beamline I11 under CY31578 and for access to B18 under the Energy Materials BAG. The X-Ray Photoelectron (XPS) data collection was performed by Ms Cara J. Hawkins at the EPSRC National Facility for XPS (“HarwellXPS”), operated by Cardiff University and UCL, under Contract No. PR16195.

References

1. M. Armand and J. M. Tarascon, Nature, 2001, 414, 359–367.
2. M. Mao, T. Gao, S. Hou and C. Wang, Chem. Soc. Rev., 2018, 47, 8804–8841.
3. J. Heelan, E. Gratz, Z. Zheng, Q. Wang, M. Chen, D. Apelian and Y. Wang, JOM, 2016, 68, 2632–2638.
4. R. Davidson, A. Verma, D. Santos, F. Hao, C. Fincher, S. Xiang, J. Van Buskirk, K. Xie, M. Pharr, P. P. Mukherjee and S. Banerjee, ACS Energy Lett., 2019, 4, 375–376.
5. E. Levi, Y. Gofer and D. Aurbach, Chem. Mater., 2010, 22, 860–868.
6. C. Ling, D. Banerjee and M. Matsui, Electrochim. Acta, 2012, 76, 270–274.
7. R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767.
8. Y. Liang, H. Dong, D. Aurbach and Y. Yao, Nat. Energy, 2020, 5, 646–656.
9. Z. Guo, S. Zhao, T. Li, D. Su, S. Guo and G. Wang, Adv. Energy Mater., 2020, 10, 1903591.
10. M. Mao, T. Gao, S. Hou and C. Wang, Chem. Soc. Rev., 2018, 47, 8804–8841.
11. Y. Liang, R. Feng, S. Yang, H. Ma, J. Liang and J. Chen, Adv. Mater., 2011, 23, 640–643.
12. X. Sun, P. Bonnick, V. Duffort, M. Liu, Z. Rong, K. A. Persson, G. Ceder and L. F. Nazar, Energy Environ. Sci., 2016, 9, 2273–2277.
13. M. Liu, A. Jain, Z. Rong, X. Qu, P. Canepa, R. Malik, G. Ceder and K. A. Persson, Energy Environ. Sci., 2016, 9, 3201–3209.
14. H. D. Yoo, Y. Liang, H. Dong, J. Lin, H. Wang, Y. Liu, L. Ma, T. Wu, Y. Li, Q. Ru, Y. Jing, Q. An, W. Zhou, J. Guo, J. Lu, S. T. Pantelides, X. Qian and Y. Yao, Nat. Commun., 2017, 8, 339.
15. X. Sun, P. Bonnick and L. F. Nazar, ACS Energy Lett., 2016, 1, 297–301.
16. Y. Gu, Y. Katsura, T. Yoshino, H. Takagi and K. Taniguchi, Sci. Rep., 2015, 5, 12486.
17. D. Tao and F. Xu, Mater. Lett., 2021, 300, 130221.
18. M. D. Levi, E. Lancri, E. Levi, H. Gizbar, Y. Gofer and D. Aurbach, Solid State Ionics, 2005, 176, 1695–1699.
19. G. S. Suresh, M. D. Levi and D. Aurbach, Electrochim. Acta, 2008, 53, 3889–3896.
20. C. Du, Z. Han, H. Peng, J. Tian, X. Yang, T. Xia, X. Ma, Y. Zhu and C. Cao, J. Power Sources, 2022, 546, 231673.
21. D. Chen, Y. Zhang, X. Li, J. Shen, Z. Chen, S. Cao, T. Li and F. Xu, Chem. Eng. J., 2020, 384, 123235.
22. Y. Cao, Y. Zhu, C. Du, X. Yang, T. Xia, X. Ma and C. Cao, ACS Nano, 2022, 16, 1578–1588.
23. M. Mao, X. Ji, S. Hou, T. Gao, F. Wang, L. Chen, X. Fan, J. Chen, J. Ma and C. Wang, Chem. Mater., 2019, 31, 3183–3191.
24. Z. Li, B. P. Vinayan, P. Jankowski, C. Njel, A. Roy, T. Vegge, J. Maibach, J. M. G. Lastra, M. Fichtner and Z. Zhao-Karger, Angew. Chem., Int. Ed., 2020, 59, 11483–11490.
25. S. Dey, J. Lee, S. Britto, J. M. Stratford, E. N. Keyzer, M. T. Dunstan, G. Cibin, S. J. Cassidy, M. Elgaml and C. P. Grey, J. Am. Chem. Soc., 2020, 142, 19588–19601.
26. E. D. Grayfer, E. M. Pazhetnov, M. N. Kozlova, S. B. Artemkina and V. E. Fedorov, ChemSusChem, 2017, 10, 4805–4811.
27. Y. Wang, Z. Liu, C. Wang, X. Yi, R. Chen, L. Ma, Y. Hu, G. Zhu, T. Chen, Z. Tie, J. Ma, J. Liu and Z. Jin, Adv. Mater., 2018, 30, 1802563.
28. M. A. Wright, T. W. Surta, J. A. Evans, J. Lim, H. Jo, C. J. Hawkins, M. Bahri, L. M. Daniels, R. Chen, M. Zanella, L. G. Chagas, J. Cookson, P. Collier, G. Cibin, A. V. Chadwick, M. S. Dyer, N. D. Browning, J. B. Claridge, L. J. Hardwick and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2024, 63, e202400837.
29. M. Arsentev, A. Missyul, A. V Petrov and M. Hammouri, J. Phys. Chem. C, 2017, 121, 15509–15515.
30. K. Taniguchi, Y. Gu, Y. Katsura, T. Yoshino and H. Takagi, Appl. Phys. Express, 2016, 9, 11801.
31. A. M. Abakumov, S. S. Fedotov, E. V. Antipov and J.-M. Tarascon, Nat. Commun., 2020, 11, 4976.
32. S. Oh, C. Woo, J. Ahn, T. Y. Kim, X. Dong, Y. Kim, K. H. Choi, S. Chae, X. Zhang, H.-S. Bang, J. Kang, J. Jeon, H.-S. Oh, W.-S. Yoon, H. K. Yu and J.-Y. Choi, ACS Appl. Mater. Interfaces, 2023, 15, 55745–55752.
33. S. Hwang, S. Oh, W. Choi, S. Chae, J. Ahn, W. Lee, H.-S. Oh, J.-Y. Choi and W.-S. Yoon, J. Alloys Compd., 2024, 980, 173541.
34. L. Liu, S. Xu, F. Tang, M. Wu, W. Yang, C. Xu and X. Rui, Chem. Commun., 2023, 59, 11365–11368.
35. S. Hou, X. Ji, K. Gaskell, P.-F. Wang, L. Wang, J. Xu, R. Sun, O. Borodin and C. Wang, Science, 2021, 374, 172–178.
36. N. Tartoni, S. P. Thompson, C. C. Tang, B. L. Willis, G. E. Derbyshire, A. G. Wright, S. C. Jaye, J. M. Homer, J. D. Pizzey and A. M. T. Bell, J. Synchrotron Radiat., 2007, 15, 43–49.
37. S. P. Thompson, J. E. Parker, J. Potter, T. P. Hill, A. Birt, T. M. Cobb, F. Yuan and C. C. Tang, Rev. Sci. Instrum., 2009, 80, 75107.
38. A. A. Coelho, J. Appl. Crystallogr., 2000, 33, 899–908.
39. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr.–Cryst. Mater., 2014, 229, 345–352.
40. S. van Smaalen, L. Palatinus and M. Schneider, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 459–469.
41. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
42. L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Chem. Mater., 2021, 33, 625–641.
43. A. J. Dent, G. Cibin, S. Ramos, A. D. Smith, S. M. Scott, L. Varandas, M. R. Pearson, N. A. Krumpa, C. P. Jones and P. E. Robbins, J. Phys.: Conf. Ser., 2009, 190, 12039.
44. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
45. A. Abouimrane, J. Ding and I. J. Davidson, J. Power Sources, 2009, 189, 693–696.
46. I. Shterenberg, M. Salama, H. D. Yoo, Y. Gofer, J.-B. Park, Y.-K. Sun and D. Aurbach, J. Electrochem. Soc., 2015, 162, A7118.
47. Y. Wang, Z. Liu, C. Wang, X. Yi, R. Chen, L. Ma, Y. Hu, G. Zhu, T. Chen, Z. Tie, J. Ma, J. Liu and Z. Jin, Adv. Mater., 2018, 30, 1802563.
48. S. Dey, J. Lee, S. Britto, J. M. Stratford, E. N. Keyzer, M. T. Dunstan, G. Cibin, S. J. Cassidy, M. Elgaml and C. P. Grey, J. Am. Chem. Soc., 2020, 142, 19588–19601.
49. K. Taniguchi, Y. Gu, Y. Katsura, T. Yoshino and H. Takagi, Appl. Phys. Express, 2016, 9, 11801.
50. S. Hou, X. Ji, K. Gaskell, P.-F. Wang, L. Wang, J. Xu, R. Sun, O. Borodin and C. Wang, Science, 2021, 374, 172–178.
51. E. Lancry, E. Levi, Y. Gofer, M. D. Levi and D. Aurbach, J. Solid State Electrochem., 2005, 9, 259–266.
52. N. Phattharasupakun, M. M. E. Cormier, E. Lyle, E. Zsoldos, A. Liu, C. Geng, Y. Liu, H. Li, M. Sawangphruk and J. R. Dahn, J. Electrochem. Soc., 2021, 168, 90535.
53. S. G. Lim, M. S. Kwon, T. Kim, H. Kim, S. Lee, J. Lim, H. Kim and K. T. Lee, ACS Appl. Mater. Interfaces, 2022, 14, 33129.
54. P. Dotzel, H. Schäfer and G. Schön, Z. Anorg. Allg. Chem., 1976, 426, 260–268.
55. K. Wu, X. Su, Z. Yang and S. Pan, Dalton Trans., 2015, 44, 19856–19864.
56. W. Klingen, G. Eulenberger and H. Hahn, Sci. Nat., 1968, 55, 229–230.
57. J. Glinnemann, H. E. King Jr, H. Schulz, Th. Hahn, S. J. La Placa and F. Dacol, Z. Kristallogr., 1992, 198, 177–212.
58. L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Chem. Mater., 2021, 33, 625–641.
59. Y. Xu, X. Deng, Q. Li, G. Zhang, F. Xiong, S. Tan, Q. Wei, J. Lu, J. Li, Q. An and L. Mai, Chem, 2019, 5, 1194–1209.
60. G. F. Koster, J. O. Dimmock and R. G. Wheeler, The Properties of the Thirty-Two Point Groups, The MIT Press, Cambridge, 1963.
61. S. L. Altmann and P. Herzig, Point-group Theory Tables, Clarendon Press, Oxford, 1994, 704.
62. J. Lee, B. J. Kim, Y. K. Chung, W. G. Lee, I. J. Choi, S. Chae, S. Oh, J. M. Kim, J. Y. Choi and J. Huh, J. Raman Spectrosc., 2020, 51, 1100–1107.
63. Y. Matsuda, N. Kuwata, T. Okawa, A. Dorai, O. Kamishima and J. Kawamura, Solid State Ionics, 2019, 335, 7–14.
64. J. F. Watts and J. Wolstenholme, An Introduction to Surface Analysis by XPS and AES, John Wiley & Sons, 2019.
65. C. Du, W. Younas, Z. Wang, X. Yang, E. Meng, L. Wang, J. Huang, X. Ma, Y. Zhu and C. Cao, J. Mater. Chem. A, 2021, 9, 3648–3656.
66. T. G. Ulusoy Ghobadi, B. Patil, F. Karadas, A. K. Okyay and E. Yilmaz, ACS Omega, 2017, 2, 8319–8329.
67. S. Chae, C. Woo, G. H. Gu, T. Y. Kim, J. Jeon, H. J. Kwon, S. Oh, K. H. Choi, X. Dong, J. Ahn, G. Asghar, H.-S. Oh, H. K. Yu, H. W. Kim and J.-Y. Choi, ACS Appl. Nano Mater., 2023, 6, 16242–16252.
68. K.-Y. Hwa, A. Ganguly, A. Santhan and T. S. Kanna Sharma, Chemosphere, 2021, 282, 130874.
69. J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-Ray Photoelectron Spectroscopy, Perkin-Elmer, 1981, vol. 3.
70. X. Wang, S. Zhang, X. Wang, Y. Su, Y. Qiu and Z. Zhang, Nat. Commun., 2014, 5, 1–7.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04469j

---