Enhancing carbon dioxide capture under humid conditions by optimizing the pore surface structure

Abstract

Metal–organic frameworks (MOFs) exhibit significant potential for mitigating carbon emissions due to their high porosity and tunability. Despite numerous reports on CO₂ capture by MOF sorbents, a common challenge is their poor selectivity for CO₂ over water. Moreover, in-depth studies are much needed to elucidate the relationships among the pore surface structure, hydrophobicity, and CO₂ uptake capacity/selectivity. In this work, we investigate the factors influencing CO₂ adsorption capacity and selectivity under humidity in a series of isoreticular pillar-layer structures, Ni₂(L)₂(dabco) (L = bdc, ndc, adc). Our study shows that increasing ligand conjugation not only results in increased hydrophobicity, decreased pore size and BET surface area, but also leads to the change of primary binding sites of water molecules and higher binding energy of CO₂, all of which contribute to largely increased CO₂ uptake capacity under humid conditions. Additionally, increasing ligand conjugation and consequently hydrophobicity slow down and reduce competitive water adsorption drastically. Notably, the MOF made of ligand with the highest conjugation, Ni₂(adc)₂(dabco), exhibits significantly enhanced CO₂ adsorption in N₂/CO₂ binary mixtures under relatively high humidity (50% RH), with an increase of ∼31% and ∼36% for the composition of 15/85 and 50/50, respectively, compared to dry conditions. An experimental FTIR study and DFT theoretical calculations confirm that H₂O occupies different primary binding site in Ni₂(bdc)₂(dabco) and Ni₂(adc)₂(dabco), and under humid conditions a higher binding energy of CO₂ is achieved with preferential H₂O/CO₂ co-adsorption in Ni₂(adc)₂(dabco), potentially creating additional adsorption sites for CO₂.

---

Introduction

Global warming has pushed us to the edge of an epoch of frequent unpredictable natural disaster occurrences. In order to limit global warming to 1.5 °C, it is essential for greenhouse gas (GHG) emissions to reach their peak no later than 2024 and decrease by 43% by 2030.^1,2 Managing emissions and cutting down the existing GHG via negative emissions technologies (NETs) are of vital importance besides developing renewable energy.^3,4 Conventional NETs predominantly rely on aqueous phase adsorption of CO₂via amine or inorganic basic solutions, which lack long-term sustainability due to their highly corrosive nature, bulky volume occupancy, and intensive regeneration energy consumption. A more efficient and low-cost alternative NET is currently being extensively explored by the entire scientific community.⁵

Acclaimed as “magic sponges” for cleaning air, porous solid sorbents have been considered as the solution for the next generation of adsorption-based NETs.⁶ Metal–organic frameworks (MOFs), composed of metal ions or clusters and various organic ligands, represent solid sorbents with immense potential for practical applications to slow down global warming.^5,7–13 Having pore sizes reaching down to the angstrom level, these crystalline microporous materials exhibit expansive inner surface areas, high selectivities, systematic structural tunability, and lower energy consumption for regeneration.^14,15 Although numerous MOFs have achieved high CO₂ uptake capacity under certain conditions, further improvement in the selective adsorption and capture of CO₂ from gas mixtures is much needed, especially under moisture and/or dilution concentrations.^16–18 In contrast to its smaller size, the higher polarizability and quadruple moment of CO₂ (3.3 Å) enable its effective separation from competitive components such as N₂ (3.64 Å) and O₂ (3.46 Å) from their gas mixtures via pore size and sorbent-gas interaction control.^19–21 The real challenge lies in achieving selective adsorption of CO₂ over H₂O (2.64 Å) under humid conditions while keeping the MOF structure intact; especially in such cases H₂O and CO₂ usually compete at the same binding sites. Owing to their much smaller size, polar water molecules can readily penetrate into microporous sorbents and form a hydrogen-bonded network inside the pore space, which further accelerates their accumulation.¹⁸ Moreover, water vapor can competitively break the original coordination bonds between ligands and metals and bind to the open metal sites under a high humidity environment,^22,23 which often causes serious degradation of the MOF structure and destroy the porosity.¹⁹ Water molecules with higher binding energy often pre-occupy the competing binding sites in the MOF structure during the adsorption of a gas mixture and suppress the uptake of CO₂, which refers to “water poisoning”.²⁴ Notwithstanding a comparatively weaker host–guest interaction, physisorption can be one of the possible solutions to surpass water interference to attain a notable level of adsorption capacity through adeptly tailoring the pore size to an appropriate range and modifying their pore surface structures.^17,18 Furthermore, the regeneration energy can be significantly lower. An excellent example is the recently reported MOF adsorbent, CALF-20,¹⁸ featuring ultra-small pores and physisorption of CO₂. Due to its exceptional performance in CO₂ capture under both dry and humid conditions, CALF-20 has already entered the initial phase for commercialization. However, achieving a small pore size alone may not be sufficient to provide a complete solution as it does not necessarily address the competitive adsorption of water molecules. Therefore, an adsorption pathway that favors CO₂ adsorption over H₂O under humid conditions and a comprehensive understanding of such processes is yet to be developed.

One possible approach to diminish water interference while enhancing CO₂ uptake is to modify the pore surface structure by changing the properties of the binding sites, which may alter the competitivity of the competing molecules. In 2016, Ding et al. demonstrated a strategy for boosting CO₂ uptake by partitioning the channels of MOF-5 with in situ polymerization of aromatic acetylenes to simultaneously decrease pore size and increase hydrophobicity.²⁵ Inspired by this work, we target to systematically study a series of isoreticular pillar-layer type MOFs, Ni₂(L)₂(dabco). By alternating the ligand conjugation, we show that the pore size, surface area, hydrophobicity, and pore surface structure can all be optimized concurrently to enhance CO₂ uptake under competitive water co-adsorption. The use of nonpolar aromatic groups is a straightforward and effective method to tune the hydrophobicity and pore surface structure of MOFs. As depicted in Scheme 1, changing the ligand conjugation can not only efficiently optimize the pore surface structure but also lead to the decrease of competitive adsorption of CO₂ and H₂O, as well as giving rise to new binding sites for CO₂. The pillar-layer type MOF presented in Scheme 1 is made of two ligands, a linker and a pillar. In the low-conjugation pore environment (Scheme 1, left), CO₂ and H₂O each preferentially bind to the linker site. However, in the binary mixture, they compete for the same site, resulting in the suppression of CO₂ uptake since H₂O binds more strongly with the linker. On the other hand, in the case of a high-conjugation pore environment (Scheme 1, right), the preferential binding site of water is shifted to the more hydrophilic pillar ligand due to significantly reduced interaction between H₂O and the linker ligand, thereby freeing this site for CO₂. In the binary mixture, the competition between H₂O and CO₂ will be significantly reduced owing to the formation of energy-favorable H₂O/CO₂ co-adsorption, which also potentially creates new binding sites for CO₂ to enhance its uptake capacity under humid conditions.

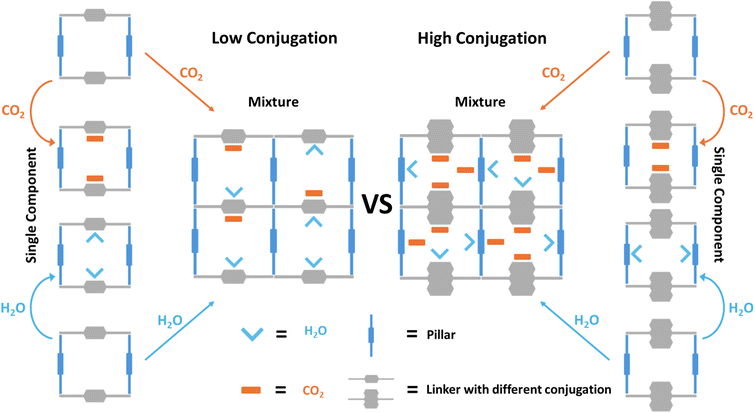Scheme 1 Schematic showing the ligand conjugation effect on the pore surface structure and competitive binding sites of CO₂ and H₂O.

We have successfully synthesized three members of the Ni₂(L)₂(dabco) MOFs. All of them are made of the same pillar ligand (1,4-diazabicyclo[2,2,2]octane, dabco) but different linker ligands within the layer with paddle-wheel Ni₂ dimers. The dicarboxylate linker ligands vary from one benzene ring (1,4-benzenedicarboxylic acid, H₂bdc), to two benzene rings (1,4-naphthalenedicarboxylic acid, H₂ndc) and three benzene rings (9,10-anthracenedicarboxylic acid, H₂adc). All three isoreticular MOFs, namely Ni₂(adc)₂(dabco) (1), Ni₂(ndc)₂(dabco) (2), and Ni₂(bdc)₂(dabco) (3), are structurally characterized. Their pore size and surface area decrease with the increasing size and conjugation of the ligands, and their corresponding hydrophobicity is in the order of 3 < 2 < 1. Yet their CO₂ uptake demonstrates a reverse trend of 1 > 2 > 3. Compound 1 reaches a CO₂ uptake of 3.03 mmol g⁻¹ at 298 K and 101.3 kPa, which is 1.75 times that of compound 3. Moreover, the decreased adsorption amount and rate of water from 3 to 1 show the effectiveness of changing the ligand conjugation to increase the hydrophobicity of the framework. Compound 1 exhibits a very interesting and rare adsorption behavior, with its CO₂ uptake significantly increased under humid conditions, as confirmed by both dynamic adsorption and column breakthrough experiments. In situ FTIR measurements and ab initio calculations have verified the change of water binding sites and H₂O/CO₂ co-adsorption, leading to partial replacement of H₂O by CO₂ in Ni₂(adc)₂(dabco) under humid conditions. The current study is a neat example of tuning the pore surface structure to minimize competitive adsorption and to enhance CO₂ uptake under humidity.

Results and discussion

Characterization of the structure and physical properties

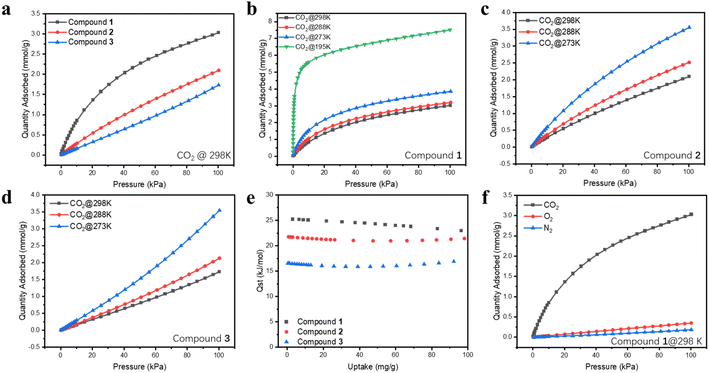
The isoreticular Ni₂(L)₂(dabco) structural series is formed by a paddle-wheel Ni₂(COO)₄ node, a neutral N-donor pillar ligand dabco, and a dicarboxylate ligand L with different hydrophobicity (L = bdc, ndc, adc) (Fig. 1a). The pillar-layer structures feature a three-dimensional (3D) network with one-dimensional (1D) channels through a- and c-axes (Fig. 1b and c). As the micrometer-sized crystals of compound 1 were too small to obtain a satisfactory structure solution by the single crystal XRD method, we synthesized isostructural Zn₂(adc)₂(dabco) single crystals under similar conditions and solved its crystal structure (Fig. S2 and Table S1†). The well matched PXRD patterns of the simulated Zn₂(adc)₂(dabco) and Ni₂(L)₂(dabco) series confirmed their isostructural nature (Fig. 2a). In addition to Ni and Zn, other isostructural M₂(adc)₂(dabco) (M = Mg, Ca, Cu, Co) were also successfully synthesized (Fig. S3†). The Ni₂(L)₂(dabco) series was chosen for further study since Ni₂(adc)₂(dabco) outperforms the other isostructural compounds in CO₂ uptake (Fig. S5a†). Structure analysis revealed that compounds 1–3 crystallize in the tetragonal crystal system, with the space group I4/mcm. Each Ni²⁺ is 5-coordinated by four oxygen atoms from four different carboxylate groups and one N-donor which forms a square pyramidal coordination environment. Thermogravimetric (TG) analysis of compounds 1, 2 and 3 after solvent exchange in methanol for two days showed that the initial weight losses were 4.1%, 19.2%, and 32.7%, respectively, attributed to the solvent removal prior to 100 °C. All three samples remained stable up to ∼400 °C (Fig. 2b). The permanent porosity of the Ni₂(L)₂(dabco) series was estimated using N₂ absorption data collected at 77 K (Fig. 2c). The Brunauer–Emmett–Teller (BET) surface areas are 637 m² g⁻¹, 779 m² g⁻¹, and 1609 m² g⁻¹, for compounds 1, 2 and 3, respectively. The pore size distributions based on the Horvath–Kawazoe (H–K) function are 3.57, 3.81 and 4.08 Å for compounds 1, 2 and 3, respectively, demonstrating a monotonic increase (Fig. 2d). This is well expected, as the surface area and pore size increase/decrease as the size of ligand decreases/increases.

Fig. 1 (a) The chemical components of the Ni₂(L)₂(dabco) series; (b) 3D pillar-layer structure of compound 1 viewed along the a-axis; (c) 1D channels along the c-axis with decreased pore diameters from compounds 3 to 1. Color code: C – grey; O – red; N – blue; Ni – green.

Fig. 2 (a) PXRD patterns of isoreticular Ni₂(L)₂(dabco) MOFs and simulated pattern of Zn₂(adc)₂(dabco); (b) the TG plots of the Ni₂(L)₂(dabco) series; (c) N₂ adsorption–desorption isotherms at 77 K; and (d) pore size distribution (H–K function) of the Ni₂(L)₂(dabco) series.

Single component CO₂ adsorption analysis

Single-component CO₂ adsorption isotherms were obtained at different temperatures to evaluate the adsorption performance of compounds 1–3. Before measurements, solvent exchange was carried out on each sample in MeOH for two days, with the supernatant replaced by fresh MeOH every 8 hours. Activation was subsequently done under dynamic vacuum at 393 K for 3 hours. The results showed a reverse trend between the uptake amount and BET surface area: compound 1 has the lowest BET surface area but the highest CO₂ uptake over the entire pressure range from 0 to 101 kPa. It reaches an adsorption capacity of 3.03 mmol g⁻¹ (67.9 cm³ g⁻¹ STP) at 298 K and 101.3 kPa, while compound 2 and compound 3 can only take up 2.09 mmol g⁻¹ and 1.73 mmol g⁻¹, respectively, under the same conditions (Fig. 3a). Despite its smaller BET surface area (39.6% compound 3), the CO₂ loading of compound 1 is 1.75 times that of compound 3 at 101 kPa. Moreover, the CO₂ adsorption profile of compound 1 shows a much steeper slope in the low-pressure area (<15 kPa), and the uptake capacity is 1.12 mmol g⁻¹ at 15 kPa, 4.7 times that of compound 3 (0.24 mmol g⁻¹). In addition, the uptake capacity of compound 1 remains significantly higher than those of others at different temperatures (Fig. 3b–d). It also outperformed all other members of the isostructural M₂(adc)₂(dabco) series (M = Zn, Cu, Co, Mg, Ca) (Fig. S5a†). Based on these data, it is clear that smaller pore size and an increased degree of conjugation within the pore environment give rise to stronger interactions between CO₂ and the MOF host, as reflected by the Q_st values (Fig. 3e). This phenomenon is particularly notable in the low partial pressure area. At zero loading, compound 1 has the highest isosteric heat (25.2 kJ mol⁻¹), compared to 21.7 kJ mol⁻¹ and 16.5 kJ mol⁻¹ for compounds 2 and 3, respectively (Fig. 3e). Furthermore, the CO₂ binding energies from the theoretical calculations, 42.61 and 30.27 kJ mol⁻¹ for compounds 1 and 3, are fully consistent with the experimental data, as discussed below. Considering other gas components in the air mixture, compound 1 adsorbs a very small amount of N₂ and O₂ at 298 K (Fig. 3f). The calculated IAST selectivity of CO₂/N₂ (15 : 85) for compound 1 gives a very high value at zero loading (Fig. S14†).

Fig. 3 The single-component CO₂ adsorption isotherms (up to 1 bar) of (a) compounds 1–3 at 298 K; (b) compound 1 at 195 K, 273 K, 288 K, and 298 K; (c) compound 2 and (d) compound 3 at 273 K, 288 K, and 298 K; (e) the isosteric heats (Q_st) of CO₂ adsorption of compounds 1–3 calculated from isotherms collected at 273, 288, and 298 K; (f) single component adsorption isotherms of N₂ and O₂ at 298 K and up to 1 bar on compound 1 in comparison with CO₂.

CO₂ adsorption under humid conditions

To assess the effect of water vapor on the MOF sorbents and the CO₂ adsorption performance under humid conditions, dynamic adsorption isotherms of water vapor and CO₂/N₂ binary mixtures were collected in a gravimetric adsorption analyzer by exposing the samples to variable relative humidity (RH) and monitoring their weight changes. The results show that after optimizing the pore surface structure by increasing the conjugation of ligands, water molecules were significantly impeded from entering the pores. Adsorption kinetics profiles clearly show that the adsorption was slow in all three cases, and the adsorbed amount of water follows the trend: 3 > 2 > 1 throughout the entire RH range being tested (Fig. 4a). The static vapor adsorption isotherms show that the water adsorption capacity in compounds 1–3 remains relatively low under 15 mbar (∼50% RH). Above this pressure both compounds 2 and 3 illustrate a sharp surge far surpassing compound 1 (Fig. S5b†). Compound 1 has a very low equilibrium adsorption capacity of water vapor compared to some top-performing CO₂ sorbents (Fig. 4b and d).^{17,18,26–33} A more detailed comparison of its performance with other prototype MOFs is provided in Table S2.† Compound 1 takes up the highest amount of CO₂ under similar RH from CO₂/N₂ mixtures, demonstrating its outstanding performance under humidity. Note that the rate of CO₂ adsorption was much faster than that of H₂O, as shown in Fig. 4c for binary CO₂/N₂ mixtures (15/85 and 50/50) at 303 K (30 °C). For CO₂, the adsorption equilibrium was reached within several minutes, while for H₂O, only ∼12% of its maximum capacity was reached at 30 minutes (Fig. 4c). More interestingly and strikingly, the uptake of CO₂ under humid conditions (50% RH) increased by a large amount, 30.6% and 36.1% for both CO₂/N₂ mixtures (15/85 and 50/50) compared to dry conditions (Fig. 4c), which was further confirmed by the increased retention time from column breakthrough experiments. In addition, the sample exhibits high stability. No obvious capacity loss was observed after six-consecutive adsorption cycles (Fig. S15†), and its PXRD pattern remained nearly identical to those of the as-made and simulated patterns upon exposure to open air for 1.5 months (Fig. S15 and S16†), further confirming the robustness and recyclability of this compound.

Fig. 4 (a) Dynamic adsorption kinetics of water vapor in compounds 1–3 at 303 K; (b) adsorption isotherm of water vapor at 298 K; (c) adsorption kinetics of CO₂ (in 15/85 and 50/50 binary mixtures of CO₂/N₂ under dry and 50% RH conditions) and H₂O (95% RH) in compound 1 at 303 K; (d) comparisons of single component CO₂ uptake (1 bar, 298 K) and H₂O vapor uptake at 298 K of compound 1 with those of previously reported best-performing MOFs.

Separation of CO₂/N₂ binary mixtures by column breakthrough experiments

The column breakthrough experiments were carried out to assess the selectivity of CO₂ over N₂ under both dry and wet conditions to mimic practical separation processes and to evaluate the CO₂ adsorption performance under competitive adsorption of water molecules. In all cases, N₂ gas was eluted out quickly after a delay between 50 and 125 s g⁻¹, while CO₂ was retained in the column for various time periods after the departure of N₂. The CO₂ retention times under dry conditions are 500 s g⁻¹, 170 s g⁻¹, and 110 s g⁻¹, for compounds 1, 2 and 3, respectively (Fig. 5a–c). These results are consistent with their single component CO₂ adsorption behaviors. On the other hand, under wet conditions (at 50% RH), the retention time of compound 3 decreases slightly, while it increases significantly for compound 1, about 20% compared to that under dry conditions (Fig. 5a). The decrease in the retention time for compound 3 is likely due to the competitive adsorption of water at the same binding site and the increase in the retention time for compound 1 is fully consistent with the observed ∼30.6% increase in the CO₂ uptake amount in Fig. 4c under the same RH. In order to understand this desirable yet rare behavior, we further carried out in situ FT-IR spectroscopic experiments and ab initio calculations to elucidate the role and the binding site of water molecules during the co-adsorption process and how it facilitated the enhanced CO₂ adsorption in compound 1.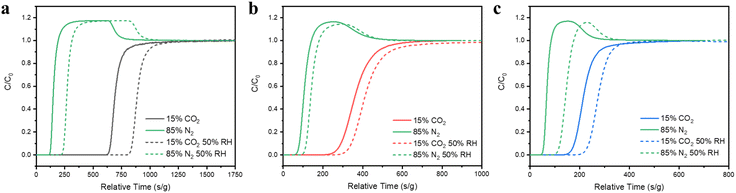

Fig. 5 Experimental column breakthrough curves of compound (a) 1, (b) 2, and (c) 3 for CO₂/N₂ (15/85) binary mixtures under dry (solid line) and wet (dashed line) conditions at 1.0 bar and 298 K.

In situ FTIR study

To reveal the competitive and co-adsorption of CO₂ and H₂O in compound 1 under humid conditions, we further conducted in situ infrared (IR) spectroscopic experiments. After sample activation, CO₂ alone was measured first in a dry sample. Given that the gas phase CO₂ spectrum was prohibitively high (no signal on the detector) above 10 torr and thus it was impossible to directly observe the adsorbed CO₂ in the presence of a gas phase, the gas CO₂ was evacuated by pumping the cell and the spectra were immediately collected within 5 seconds of evacuation once the pressure of CO₂ drops below 500 mTorr (negligible gas-phase IR absorption). The adsorbed CO₂ was detected by its characteristic ν_as(CO₂) band at 2334 cm⁻¹ as shown in Fig. 6a.³⁴ After fully evacuating CO₂ under vacuum, the sample was then exposed to water moisture at 11 torr, equivalent to 50% RH at 24 °C. The adsorbed H₂O was typified by its stretching (v) and bending (β) bands, respectively (see Fig. 6b bottom and Fig. S6†). A closer inspection reveals the β(H₂O) band shows two components at 1637 and 1625 cm⁻¹, which correspond to two types of H₂O in compound 1 as later verified by theoretical calculations. The two blue-shift differently in reference to gas phase H₂O at 1595 cm⁻¹ due to their different strength of H bonding interaction with the sample.^35–37 The larger shift points to a stronger interaction, whereas the smaller one indicates a weaker interaction with the structure.^35,36 Along with water adsorption, we see the perturbation of phonon modes of the MOF, e.g., stretching bands of the COO⁻ group in the region 1600–1400 cm⁻¹,^10,38 as indicated by the derivative-like feature, which is caused by water inclusion.¹⁰ Keeping water moisture inside, we further introduced CO₂. The time dependent spectra were recorded to monitor the impact of CO₂ on pre-adsorbed H₂O. As shown in Fig. 6b, the β(H₂O) band diminishes significantly by around 50% after exposure to CO₂ for 15 min, indicating that half of pre-adsorbed water was displaced by CO₂ which indicates an energy-favorable process. The loss mainly occurred on the 1625 cm⁻¹ component, suggesting the higher susceptibility of weakly bound H₂O to be displaced by incoming CO₂. From this displacement phenomenon, we can conclude that the thermodynamically favorable co-adsorption configurations of H₂O and CO₂ play a dominant role when the low concentration of water moisture exists. The final adsorption of CO₂ was further measured through monitoring the ν_as(CO₂) band after evacuating gas phase CO₂. Interestingly, the ν_as(CO₂) band shows a slight blue shift (+2 cm⁻¹) compared with the value observed in the dry sample (Fig. 6a). Given the sensitivity of the ν_as(CO₂) position to its chemical environment, we infer that the binding/interaction of CO₂ within compound 1 is enhanced due to the presence of co-adsorbed H₂O, which further assists CO₂ to bind onto the sites that are not accessible under dry conditions, as further verified by the subsequent ab initio calculation.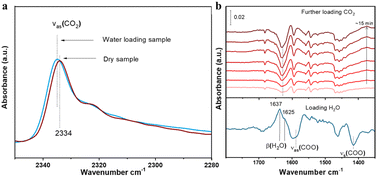

Fig. 6 (a) IR spectra of adsorbed CO₂ into dry (activated) and water-loaded (∼50% RH) compound 1. CO₂ was loaded at ∼120 torr and 24 °C in both cases. (b) IR spectra of loading H₂O (bottom line) and CO₂ (top lines) sequentially into the compound 1 sample. The bottom spectrum was referenced to the activated sample to show the adsorbed H₂O. The top six spectra were referenced to the bottom one to show the changes of pre-adsorbed H₂O upon further loading CO₂. The β(H₂O) band was analyzed and presented here as the v(OH) band of H₂O is partially masked by the combination bands of gas phase CO₂ (Fig. S7†). Notation and acronym: ν, stretch; β, bending; as, asymmetric; and s, symmetric.

Theoretical calculations of the CO₂ binding energies and binding sites

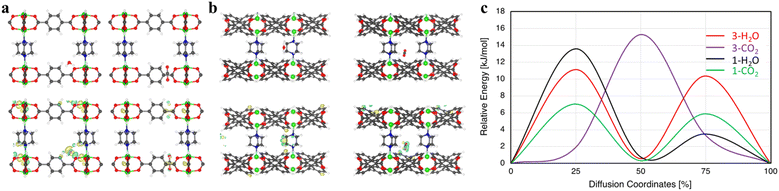
Here, we chose two MOFs, compounds 1 and 3, to illustrate the trends and mechanisms of adsorption. We made use of an ab initio thermal annealing method and GCMC with the help of VASP and RASPA, respectively, for an efficient sampling of the configurational space.^39,40 Several low-energy configurations were identified and further subjected to full ab initio geometry optimization. There is a clear distinct binding spot for CO₂ in both 1 and 3 and H₂O in compound 3 (Fig. 7). However, two low-energy configurations were found for H₂O in compound 1 (Fig. S8†). The CO₂ binding energies in compounds 1 and 3 at the most favorable site are 42.61 and 30.27 kJ mol⁻¹, respectively. Hence, the binding of CO₂ is significantly stronger with compound 1 in comparison with compound 3. These results explain the significantly higher single-component CO₂ uptake in compound 1 and align with our experimental results.

Fig. 7 (a) (Top) H₂O (left) and CO₂ (right) optimum binding locations in compound 3. (Bottom) Guest interaction with compound 3. (b) (Top) H₂O (left) and CO₂ (right) optimum binding spots in compound 1. (Bottom) Guest interaction with compound 1. Yellow and blue represent charge accumulation and depletion, respectively, at an iso-value of 0.0005 e Å⁻³. (c) Diffusion energy barrier for H₂O and CO₂ in compounds 1 and 3. Note: diffusion coordinate describes the progress of the molecules along their diffusion pathway, 0% means no translation and 50% corresponds to a translation halfway through the unit cell.

Similarly, the H₂O binding energies were calculated to be 45.72 and 33.19 kJ mol⁻¹ in compounds 1 and 3, respectively. Upon further inspection, we found that, although CO₂ and H₂O in compound 3 mainly interact with the bdc linker, there are clear distinctions. The main interaction of H₂O is with the oxygen of the bdc linker; however, CO₂ strongly interacts with the C–C connected to O of the bdc linker (Fig. 7a). It can also be seen that H₂O only interacts with one linker while CO₂ interacts with two of the nearby linkers (Fig. S9†). On the other hand, the interaction of guest molecules and preferential binding sites are very different in compound 1. For example, CO₂ only interacts with the adc linker while due to the hydrophobic nature of adc, H₂O's main interaction is with the pillar ligand dabco, with a secondary interaction at the adc linker (Fig. S8†). Due to the presence of different binding pockets for water, we find two low-energy structures with two H₂O molecules, respectively (Fig. S10†). The separations between them are in the range of ∼2.12–1.94 Å, depending on the configuration. Moreover, the water–water interaction is quite visible even at two water molecules per pore (Fig. S11†).

We further study the kinetics of guest molecules in both compounds 1 and 3 (Fig. 7c). It is observed that the guest molecules show different diffusion behavior in these MOFs. The diffusion energy barrier for H₂O is 11.13 kJ mol⁻¹vs. 15.28 kJ mol⁻¹ for CO₂ in compound 3. Consequently, a faster diffusion of H₂O is found in compound 3 in comparison with CO₂. However, an opposite behavior in compound 1 is noted where we see a much faster diffusion of CO₂ compared to H₂O. The diffusion barrier for CO₂ and H₂O in compound 1 is 7.04 and 13.59 kJ mol⁻¹, respectively, suggesting almost two times faster kinetics for CO₂. These outcomes are in perfect agreement with our experimental observations, showing that CO₂ is adsorbed much faster compared with water in dynamic adsorption in compound 1.

How could compound 1 capture CO₂ with an increased capacity when water molecules are present in the system with competitive co-adsorption, especially when water has a higher binding energy and demonstrates obvious water–water interactions in the pore? The favorability of co-adsorption configuration over lower water loading has been reported in TIFSIX-3-Ni, and the CO₂ binding energy is notably higher than that of H₂O in these systems.⁴¹ However, for compound 1, as the water interaction is stronger than that of CO₂, why does the CO₂ uptake increase when water co-adsorption is present in the mixture? To unlock this mystery, our next step was to study CO₂/H₂O co-adsorption and their preferential binding sites in detail.

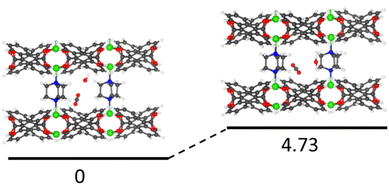
For compound 1, we found two low energy preferential co-adsorption configurations as shown in Fig. 8. The total binding energy of the most favorable co-adsorption configuration (1H₂O + 1CO₂) is 94.5 kJ mol⁻¹, which is stronger than the binding of 2H₂O. Additionally, the secondary co-adsorption configuration is just 4.73 kJ mol⁻¹ higher in energy compared to the most favorable one. Given the small difference in energy, both types of co-adsorption likely occur under humid conditions. In this configuration, the pillar ligand offers a new binding site for CO₂ which is not accessible under dry conditions. Since the H₂O molecules at the secondary binding site can be partially replaced by CO₂ based on the results from the IR experiments, this explains the ∼30% increase in CO₂ uptake and prolonged retention time under the humid conditions for compound 1. Such synergistic effects of H₂O/CO₂ co-adsorption that enhances the CO₂ binding energy and adsorption capacity are quite rare, especially in ultra-microporous materials (Fig. S12†).⁴¹ Note that there is an increase in CO₂ binding energy when water is present in the structure. For example, in two favorable co-adsorption states, the binding energy of CO₂ is 50.62 kJ mol⁻¹ and 44.05 kJ mol⁻¹, respectively, which are both higher than that of CO₂ in a single component adsorption experiment (42.61 kJ mol⁻¹).

Fig. 8 The two low energy co-adsorption configurations of H₂O/CO₂ in compound 1.

To summarize, the higher binding energy and faster kinetics of CO₂ upon adsorption in compound 1 can be attributed to its higher conjugation and hydrophobicity. Conversely, much slower water kinetics and changes in the pore surface environment hinder water accumulation within pores. The adsorption enhancement achieved in this study further highlights the importance of optimizing the pore surface structure through ligand functionalization.

Conclusions

We have successfully synthesized a series of isoreticular Ni₂(L)₂(dabco) MOFs using ligands with different degrees of conjugation. The increase in the conjugation level of the ligands correlates with an increase in ligand size and a decrease in pore size and surface area, resulting in a different pore surface structure. Compound 1 with the lowest BET surface area and the smallest pore size reaches 1.75 times higher CO₂ uptake capacity compared to compound 3 with the largest BET surface area and pore size and the lowest hydrophobicity under dry conditions. The calculated CO₂ isosteric heats of adsorption and binding energies are fully consistent with these experimental observations. The enhancement of CO₂ uptake is more prominent in the lower pressure region. More significantly, compound 1 exhibits a substantial increase in CO₂ uptake (>31%) in binary CO₂/N₂ mixtures under humid conditions, as confirmed by both dynamic adsorption isotherm and column breakthrough measurements. The possible reasons are elucidated by in situ FTIR analysis along with theoretical ab initio calculations that suggest that the co-adsorption configuration of H₂O and CO₂ is favorable and generates extra binding sites to accommodate more CO₂, leading to an enhancement of CO₂ uptake. Optimizing the pore surface structure of MOFs by increasing ligand conjugation can be an effective approach to significantly enhance CO₂ adsorption, both under single component dry conditions and in gas mixtures with competitive water co-adsorption under humid conditions.

Experimental section

Synthesis of H₂adc

The dicarboxylic linker 9,10-anthracenedicarboxylic acid (H₂adc) was synthesized according to a reported procedure with some modifications.⁴² In a 500 mL two-necked round bottom flask, 8 grams of 9,10-dibromoanthracene were dissolved in 300 mL of dry ether and stirred at 0 °C. Meanwhile, 33 mL of 1.6 M n-butyllithium was added to the mixture under nitrogen protection and kept stirring for 2 hours. Pure carbon dioxide gas was purged into the resulting yellowish mixture at −78 °C (dry ice and acetone bath) and the entire reaction mixture was stirred overnight. A bright yellow solid was precipitated out once the water and hydrochloric acid (6 M) were added to the solution. The solid was filtered, washed with a copious amount of fresh water and collected. The yield is 90%. ¹H NMR (500 MHz, DMSO-d₆, δ): 8.04 (dd, 4H, Ar H), 7.66 (dd, 4H, Ar H). The peaks of H₂adc were assigned and integrated to confirm the structure (Fig. S1†). The synthesis of this ligand was scaled up to 20 g and can be scaled up further with appropriate reaction vessels.

Synthesis of Ni₂(L)₂(dabco)

The Ni₂(L)₂(dabco) MOF series were synthesized via similar solvothermal reactions with some modifications and improvements to the previous procedure. Ni(NO₃)₂·6H₂O (145 mg, 0.5 mmol), 1,4-diazabicyclo[2,2,2]octane (dabco, 56 mg, 0.5 mmol) and 0.5 mmol of ligands (H₂adc 133 mg, or H₂ndc 108 mg, or H₂bdc 83 mg) were dispersed in 10 mL of DMF solution in a 20 mL glass vial. The mixture was then stirred at room temperature for 2 hours followed by filtering using a syringe Nylon filter. The clear filtrate was collected and sealed in a new vial, which was then put into an oven pre-heated to 120 °C and reacted for two days. The crystalline precipitates were filtered and washed with fresh DMF and MeOH several times. The yields were calculated based on the ligand amount and were 53%, 73%, and 71% for compounds 1, 2 and 3, respectively. The products were characterized by powder X-ray diffraction (PXRD) and thermogravimetric (TG) analysis. The largest batch we have achieved was ∼5 g and the synthesis procedure can also be modified to larger scales.

Gas adsorption measurements

Prior to the gas adsorption test, the as-made samples were first washed thoroughly with DMF and then soaked in fresh MeOH for two days to allow solvent exchange to complete. Around 80 mg of exchanged sample was activated at 393 K under dynamic vacuum for three hours prior to adsorption experiments. Gas adsorption measurements were carried out on a Micromeritics 3Flex volumetric adsorption analyzer. The BET surface area and pore size distribution were determined based on the nitrogen adsorption–desorption data at 77 K. Liquid nitrogen, dry ice-isopropyl alcohol bath, and a circulating-bath digital temperature controller were used for measurements at 77 K, 195 K, and temperatures around room temperature, respectively.

The single-component dynamic adsorption isotherms for CO₂ and H₂O vapor were collected in a gravimetric adsorption analyzer TGA Q50 (TA Instruments). The bubbler contained water-run ultrahigh purity N₂ as the carrier gas. The partial pressure of CO₂ or H₂O was adjusted by controlling the ratio of pure N₂ gas and CO₂ or saturated water vapor. Approximately 20 mg of exchanged samples was activated under a constant N₂ flow at 393 K for 60 min. Adsorbed amounts were monitored continuously by weight changes in the sample throughout the measurements.

Isosteric heat of adsorption (Q_st)

To determine the affinity between the scaffold and the adsorbates, the Clausius–Clapeyron equation⁴³ was employed to calculate the adsorption heats for CO₂ on compounds 1–3, which is defined as follows:
where Q_st stands for the adsorption heat of CO₂, P and T represent the pressure and temperature. R is the universal gas constant and n_a is the adsorbed amount in moles. Before the calculation, the isotherms tested at 273 K, 288 K, and 298 K were fitted using the virial equation:⁴⁴

where P is the pressure described in pascals, N is the adsorbed amount in mmol g⁻¹, T is the temperature in kelvin, a_i and b_j are virial coefficients, and m and n are the number of coefficients used to describe the isotherms.

In situ infrared (IR) spectroscopic measurements

In situ IR measurements were performed on a Nicolet™ iS50 FTIR spectrometer using a liquid N₂-cooled mercury cadmium telluride (MCT-A) detector. The spectrometer is equipped with a vacuum cell that is placed in the main compartment with the sample at the focal point of the infrared beam. To avoid the direct pressing of the MOF sample that may cause damage to the crystalline structure, the sample (∼5 mg) was made into a slurry form by mixing with a small amount of methanol and pasted onto a KBr pellet. The powder sample was dried and directly attached to the KBr pellet after blowing a nitrogen stream for a minute, and then transferred into the cell that is connected to a vacuum line for evacuation. The sample was activated by evacuation at 150 °C for 3 h and then cooled back to room temperature for CO₂ adsorption measurement. H₂O was loaded by exposing the sample to ∼11 torr water vapor at 24 °C for ∼5 min until adsorption reaches saturation. CO₂ loading was followed by introducing 80 torr gas into the cell and keeping for ∼15 min.

Computational and simulation details

To deepen our understanding of molecular-level guest–guest and guest–host interactions, ab initio calculations were carried out utilizing the VASP code.^45,46 These calculations captured the necessary van der Waals interactions through the non-local vdW-DF1 functional with a plane-wave basis set and in conjunction with standard PAW pseudopotentials.^47–50Γ-Point sampling along with a kinetic energy cutoff of 600 eV gave well-converged results. The geometry optimization criteria were: 10⁻⁶ eV for SCF loops and 0.005 eV Å⁻¹ for Hellmann–Feynman forces. The binding energy (E_b) is calculated from the energy difference between the loaded MOF (E_total) and the individual fragments (activated empty MOF and isolated gas-phase energy of the molecule):

E_b = E_MOF + E_guest − E_total

Diffusion energy barriers were determined using the climbing-image nudged elastic band method (cNEB), a transition-state search algorithm,⁵¹ and five transition images were selected.

Column breakthrough measurements

Breakthrough tests were carried out at 298 K and 1 bar in an auto mixed-gas breakthrough apparatus (BSD-MAB) equipped with a vapor generator. The mass of compounds 1–3 filled into the column (I.D. 6 mm and length 80 mm) was 0.273 g, 0.51 g, and 0.79 g, respectively. The adsorbents were activated at 120 °C for 2 h under purging helium gas (20 mL min⁻¹). When the temperature was cooled down to 25 °C, the helium flow was stopped and the feed gas mixtures (CO₂/N₂, 15/85; v/v, dry or wet) at a flow rate of 10 mL min⁻¹ were introduced into the adsorption column. The wet feed gas was pre-mixed with a relative humidity of 50%. The gases at the outlet were analyzed using a mass spectrometer (MKS). After the adsorption reached equilibrium, the column was purged with helium gas (20 mL min⁻¹) at 100 °C for 2 h for desorption.

Data availability

Crystallographic data for Zn-DABCO-ADC have been deposited at the CCDC under 2360909 and can be obtained from https://doi.org/10.5517/ccdc.csd.cc2k7qcx. All data supporting this research (like PXRD, TGA, adsorption isotherms, NMR, FT-IR, etc.) are included in the main article and/or ESI.†

Author contributions

G. Z.: methodology, investigation, formal analysis, visualization, and writing – original draft; F. X.: investigation and formal analysis; S. U., T. T.: computational investigation and formal analysis; H. W., L. M.: investigation and formal analysis (breakthrough); K. T., S. M.: investigation and formal analysis (IR); S. T.: investigation (single-crystal); J. L.: conceptualization, supervision, validation, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful for the financial support from the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award No. DE-SC0019902. This research used the Advanced Light Source (ALS), which is a DOE Office of Science User Facility under Contract No. DE-AC02-05CH11231.

Notes and references

1. J. Terhaar, T. L. Frölicher, M. T. Aschwanden, P. Friedlingstein and F. Joos, Nat. Clim. Change, 2022, 12, 1136–1142.
2. L. Espinal, D. L. Poster, W. Wong-Ng, A. J. Allen and M. L. Green, Environ. Sci. Technol., 2013, 47, 11960–11975.
3. E. S. Sanz-Pérez, C. R. Murdock, S. A. Didas and C. W. Jones, Chem. Rev., 2016, 116, 11840–11876.
4. S. Xiang, Y. He, Z. Zhang, H. Wu, W. Zhou, R. Krishna and B. Chen, Nat. Commun., 2012, 3, 954.
5. H. Lyu, O. I.-F. Chen, N. Hanikel, M. I. Hossain, R. W. Flaig, X. Pei, A. Amin, M. D. Doherty, R. K. Impastato, T. G. Glover, D. R. Moore and O. M. Yaghi, J. Am. Chem. Soc., 2022, 144, 2387–2396.
6. A. Samanta, A. Zhao, G. K. H. Shimizu, P. Sarkar and R. Gupta, Ind. Eng. Chem. Res., 2012, 51, 1438–1463.
7. M. Ding, R. W. Flaig, H.-L. Jiang and O. M. Yaghi, Chem. Soc. Rev., 2019, 48, 2783–2828.
8. J. Cure, E. Mattson, K. Cocq, H. Assi, S. Jensen, K. Tan, M. Catalano, S. Yuan, H. Wang, L. Feng, P. Zhang, S. Kwon, J.-F. Veyan, Y. Cabrera, G. Zhang, J. Li, M. Kim, H.-C. Zhou, Y. J. Chabal and T. Thonhauser, J. Mater. Chem. A, 2019, 7, 17536–17546.
9. G. Zhang, F. Xie, T. M. Osborn Popp, A. Patel, E. M. Cedeño Morales, K. Tan, R. Crichton, G. Hall, J. Zhang, A. J. Nieuwkoop and J. Li, CrystEngComm, 2023, 25, 1067–1075.
10. K. Tan, N. Nijem, P. Canepa, Q. Gong, J. Li, T. Thonhauser and Y. J. Chabal, Chem. Mater., 2012, 24, 3153–3167.
11. A. M. Plonka, D. Banerjee, W. R. Woerner, Z. Zhang, N. Nijem, Y. J. Chabal, J. Li and J. B. Parise, Angew. Chem., Int. Ed., 2013, 52, 1692–1695.
12. Z. Zhang, Y. Zhao, Q. Gong, Z. Li and J. Li, Chem. Commun., 2013, 49, 653–661.
13. H. Wu, R. S. Reali, D. A. Smith, M. C. Trachtenberg and J. Li, Chem.–Eur. J., 2010, 16, 13951–13954.
14. Z. Hu, Y. Wang, B. B. Shah and D. Zhao, Adv. Sustainable Syst., 2019, 3, 1800080.
15. W. Fan, X. Zhang, Z. Kang, X. Liu and D. Sun, Coord. Chem. Rev., 2021, 443, 213968.
16. C. E. Bien, K. K. Chen, S.-C. Chien, B. R. Reiner, L.-C. Lin, C. R. Wade and W. S. W. Ho, J. Am. Chem. Soc., 2018, 140, 12662–12666.
17. H. A. Evans, D. Mullangi, Z. Deng, Y. Wang, S. B. Peh, F. Wei, J. Wang, C. M. Brown, D. Zhao, P. Canepa and A. K. Cheetham, Sci. Adv., 2022, 8, eade1473.
18. J.-B. Lin, T. T. T. Nguyen, R. Vaidhyanathan, J. Burner, J. M. Taylor, H. Durekova, F. Akhtar, R. K. Mah, O. Ghaffari-Nik, S. Marx, N. Fylstra, S. S. Iremonger, K. W. Dawson, P. Sarkar, P. Hovington, A. Rajendran, T. K. Woo and G. K. H. Shimizu, Science, 2021, 374, 1464–1469.
19. O. H. P. Gunawardene, C. A. Gunathilake, K. Vikrant and S. M. Amaraweera, Atmosphere, 2022, 13, 397.
20. F. Raganati, F. Miccio and P. Ammendola, Energy Fuels, 2021, 35, 12845–12868.
21. J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
22. N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575–10612.
23. P.-Q. Liao, H. Chen, D.-D. Zhou, S.-Y. Liu, C.-T. He, Z. Rui, H. Ji, J.-P. Zhang and X.-M. Chen, Energy Environ. Sci., 2015, 8, 1011–1016.
24. S. Zuluaga, E. M. A. Fuentes-Fernandez, K. Tan, F. Xu, J. Li, Y. J. Chabal and T. Thonhauser, J. Mater. Chem. A, 2016, 4, 5176–5183.
25. N. Ding, H. Li, X. Feng, Q. Wang, S. Wang, L. Ma, J. Zhou and B. Wang, J. Am. Chem. Soc., 2016, 138, 10100–10103.
26. C. Chen, X. Feng, Q. Zhu, R. Dong, R. Yang, Y. Cheng and C. He, Inorg. Chem., 2019, 58, 2717–2728.
27. J. A. Coelho, A. M. Ribeiro, A. F. P. Ferreira, S. M. P. Lucena, A. E. Rodrigues and D. C. S. d. Azevedo, Ind. Eng. Chem. Res., 2016, 55, 2134–2143.
28. V. B. López-Cervantes, E. Sánchez-González, T. Jurado-Vázquez, A. Tejeda-Cruz, E. González-Zamora and I. A. Ibarra, Polyhedron, 2018, 155, 163–169.
29. A. Masala, J. G. Vitillo, G. Mondino, C. A. Grande, R. Blom, M. Manzoli, M. Marshall and S. Bordiga, ACS Appl. Mater. Interfaces, 2017, 9, 455–463.
30. W. P. Mounfield and K. S. Walton, J. Colloid Interface Sci., 2015, 447, 33–39.
31. Z. H. Rada, H. R. Abid, J. Shang, H. Sun, Y. He, P. Webley, S. Liu and S. Wang, Ind. Eng. Chem. Res., 2016, 55, 7924–7932.
32. P. Singh, H. D. Singh, A. H. Menon and R. Vaidhyanathan, Chem. Commun., 2023, 59, 5559–5562.
33. N. S. Wilkins, J. A. Sawada and A. Rajendran, Adsorption, 2020, 26, 765–779.
34. K. I. Hadjiivanov, D. A. Panayotov, M. Y. Mihaylov, E. Z. Ivanova, K. K. Chakarova, S. M. Andonova and N. L. Drenchev, Chem. Rev., 2021, 121, 1286–1424.
35. T. Seki, K.-Y. Chiang, C.-C. Yu, X. Yu, M. Okuno, J. Hunger, Y. Nagata and M. Bonn, J. Phys. Chem. Lett., 2020, 11, 8459–8469.
36. A. Nalaparaju, R. Babarao, X. S. Zhao and J. W. Jiang, ACS Nano, 2009, 3, 2563–2572.
37. K. Tan, S. Zuluaga, Q. Gong, P. Canepa, H. Wang, J. Li, Y. J. Chabal and T. Thonhauser, Chem. Mater., 2014, 26, 6886–6895.
38. K. Tan, P. Canepa, Q. Gong, J. Liu, D. H. Johnson, A. Dyevoich, P. K. Thallapally, T. Thonhauser, J. Li and Y. J. Chabal, Chem. Mater., 2013, 25, 4653–4662.
39. S. Ullah, S. Jensen, K. Tan, G. Zhang, T. Jenkins, A. Elias, M. D. Gross, J. Li and T. Thonhauser, Chem. Mater., 2022, 34, 3246–3252.
40. D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101.
41. S. Ullah, K. Tan, D. Sensharma, N. Kumar, S. Mukherjee, A. A. Bezrukov, J. Li, M. J. Zaworotko and T. Thonhauser, Angew. Chem., Int. Ed., 2022, 61, e202206613.
42. H. S. Quah, L. T. Ng, B. Donnadieu, G. K. Tan and J. J. Vittal, Inorg. Chem., 2016, 55, 10851–10854.
43. O. L. I. Brown, J. Chem. Educ., 1951, 28, 428.
44. E. N. Parker, Phys. Rev., 1954, 96, 1686–1689.
45. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
46. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
47. K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 066501.
48. D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Käck, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. Murray, A. Puzder, H. Rydberg, E. Schröder and T. Thonhauser, J. Phys.: Condens. Matter, 2009, 21, 084203.
49. T. Thonhauser, V. R. Cooper, S. Li, A. Puzder, P. Hyldgaard and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125112.
50. T. Thonhauser, S. Zuluaga, C. A. Arter, K. Berland, E. Schröder and P. Hyldgaard, Phys. Rev. Lett., 2015, 115, 136402.
51. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, PXRD, NMR, TGA, FT-IR, and theoretical calculation as well as crystal structure and single crystal data. CCDC 2360909. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ta06019a

---